Is π halogen bonding or lone pair⋯π interaction formed between borazine and some halogenated compounds?

Abstract

Borazine, “inorganic benzene”, exhibits some different properties from benzene although both of them are isostructural and isoelectronic. It was known that benzene is favorable to form halogen bonds with halogenated molecules. However, borazine more easily forms lone pair–π interactions with halogenated molecules, but for stronger halogen donors it can also form halogen bonds. The halogen bonds formed by borazine are stronger than the corresponding lone pair–π interactions. It was found that the pair–π interactions can be changed into halogen bonds with the increase of interaction strength. The dispersion energy plays a main role in stabilizing the weakly bonded complexes, while the electrostatic energy is dominant in the strongly bonded complexes. This is different from the nature of the respective benzene complexes.

---

1. Introduction

Halogen bonding, a highly directional noncovalent interaction between a covalently-bonded halogen atom and a negative site,¹ has been widely investigated, due to its potential applications in molecular recognition,² crystal engineering,³ and biological systems.⁴ Dihalogen molecules can form π halogen bonds with some usual π systems, such as benzene, thiophene, furan, and pyridine, and the structures and properties of these complexes have been extensively studied using experimental and theoretical methods.^5–7 However, C–X⋯π halogen bonds have more important practical value in crystal engineering,⁸ drug design,⁹ and protein–ligand complexation,¹⁰ although only sporadic studies have been performed for them.¹¹ The induction interaction plays a dominant role in stabilizing benzene–X₂ (X = Cl, Br, I) complexes,¹² while the dispersion interaction is primarily responsible for the stability of benzene–halocarbon complexes.¹³

Lone pair–π interaction between a neutral electron-rich molecule and an electron-poor π ring is another important noncovalent interaction. It has been found in a number of biological systems^14–16 and supramolecular systems.^17,18 A detailed analysis of the Cambridge Structure Database has shown that such an interaction is not unusual in organic compounds,¹⁹ but it has been rather unexplored,²⁰ due to the general belief that it is mostly repulsive.²¹ Another possible reason is its weak interaction strength with interaction energy smaller than 3 kcal mol⁻¹ in most cases.²² This weak strength leads to the fact that it is seldom present alone in complicated systems and it often coexists with other types of interactions.^23–25 In the benzene–dimethylether complex, where only lone pair–π interaction exists, a substantial part of the stabilization stems from dispersion energy.²⁶

Borazine (B₃N₃H₆), isolated in 1926 by Stock and Pohland,²⁷ exhibits some similarity with benzene in its physical properties, because it is isostructural and isoelectronic with benzene, thus it is called “inorganic benzene”.²⁸ People have shown great interest in borazine and its derivatives due to their potentials as building blocks in materials' science. They can act as precursors for nonoxidic ceramics containing B–N bonds and boron nitride nanotubes or other nanostructures.²⁹ They also have the potential to act as chemical H₂ storage materials.^30–32 Very recently, Kervyn and co-workers³³ reported the first bottom-up preparation of borazine-based supermolecular architectures on metal surfaces, which are rationalized as a delicate interplay of short-range van der Waals attractions between neighboring molecules and long-range Coulomb repulsions between deprotonated charged molecules. It has been demonstrated that borazine can form π hydrogen-bonded complexes with the first-row hydrides (BH₃, CH₄, NH₃, H₂O, and HF) and electrostatic and dispersion energies play an important role in the formation of these complexes.³⁴ Interestingly, borazine can participate not only in anion–π interactions with anions (F⁻, Cl⁻, Br⁻, NO₃⁻, and BF₄⁻)³⁵ but also in cation–π interactions with cations (Li⁺, Na⁺, and K⁺).³⁶

In the present paper, we designed some complexes of borazine and halogenated compounds. Selected halogenated compounds include XF, XCN, XCCH, and XCF₃ (X = F, Cl, Br, and I), which usually act as halogen donors in halogen bonds.^37–39 Bonding energy and geometrical parameters have been investigated for these complexes. Our interest is in determining the interaction type between borazine and the halogenated compounds, that is, is the main force between them π halogen bonding or lone-pair–π interaction? To answer this question, we performed natural bond orbital (NBO) and symmetry-adapted perturbation theory (SAPT) calculations. In addition, we also considered the substitution effect on the interaction type.

2. Calculation methods

The structures of complexes and monomers were determined using the MP2 method with the aug-cc-pVDZ basis set for all atoms except the I atom. For iodine, pseudopotentials with the aug-cc-pVDZ-PP basis set were used to account for relativistic effects. Symmetry constrain has been imposed for the C_3,v geometries. Frequency calculations were performed at the same level for the obtained structures to confirm the minima on their potential surfaces. The interaction energy is the difference between the energy of the complex and the sum of the isolated monomers in their minima configuration. The basis set superposition error (BSSE) was obtained using the full counterpoise method proposed by Boys and Bernardi⁴⁰ to correct the interaction energy. All calculations were carried out using the Gaussian09 package.⁴¹

Molecular electrostatic potentials (MEPs) on the 0.001 electrons per bohr³ contour of the electronic density have been calculated with the Wave Function Analysis-Surface Analysis Suite (WFA-SAS) program⁴² at the MP2/aug-cc-pVDZ level. Natural bond orbital (NBO) analyses were carried out using NBO 3.1 version⁴³ implemented in Gaussian 09 to provide an insight into the bonding nature of these complexes. The symmetry adapted perturbation theory (SAPT) method using the SAPT2008 program⁴⁴ was used to decompose the interaction energy at the MP2/aug-cc-pVDZ level.

3. Results and discussion

3.1. MEPs of borazine

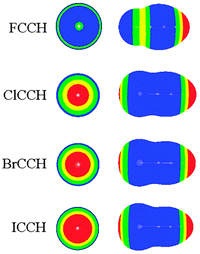
It was known that MEPs are a very effective method for predicting the possibility of intermolecular interactions.⁴⁵ Thus we plotted the MEPs map of borazine in Fig. 1. One can conclude that the hydrogen atoms connected with the boron atoms are basic (blue and negative MEPs), while those connected with the nitrogen atoms are acidic (red and positive MEPs). Thus both types of hydrogen atoms in borazine can be respectively used as the proton donors and acceptors in hydrogen bonds.³⁴ With respect to the hydrogen atom, the nitrogen atom shows greater electronegativity, while the boron atom exhibits smaller electronegativity. Thus the MEPs on the nitrogen atoms are negative (blue MEPs) and those on the boron atoms are positive (green MEPs). Additionally, the central site of the borazine ring has negative MEPs, although they are smaller than those on the N atoms. Thus both the nitrogen atoms and the ring center in borazine can be taken as basic centers in intermolecular interactions. It is also observed that the region of negative MEPs on the N atom in borazine is discrete, in agreement with the conclusion that borazine is nonaromatic.⁴⁶ Comparing the MEPs of borazine and benzene (Fig. S1, ESI†), one can see that the negative MEPs at the ring center and carbon atoms in benzene are more negative than those found in borazine. This further shows that borazine is an electron-deficient π system with respect to benzene.²²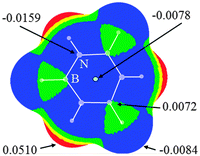

Fig. 1 Molecular electrostatic potentials of borazine. Color ranges, in eV, are: red, greater than 0.02; yellow, between 0.02 and 0.01; green, between 0.01 and 0; blue, less than 0.

3.2. Interactions between borazine and halogenated compounds

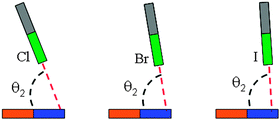
On the basis of the MEPs of borazine, more than one site of Lewis bases and acids are observed. Thus the interaction modes between borazine and halogenated compounds would be diverse. Here we are concerned only with the interactions between the ring center or N of borazine (1) and the halogen atom, although other types of complexes are also possible, which are shown in Fig. S2 in ESI.† The sketched structures of 1-XY (Y = F, CN, CCH, and CF₃) are shown in Fig. 2 and their optimized structures are shown in Fig. S3 (ESI†). There are two structures for each halogen atom: 1-XY-a and 1-XY-b. The X atom in structure 1-XY-a points to the ring center of borazine with C_3,v symmetry. Three F atoms are located over the three B atoms of borazine in the 1-XCF₃-a complex. In structure 1-XY-b the halogen atom combines with the N atom of borazine, not being perpendicular to the ring plane. For the halogen-bonded complexes of benzene–X₂, X = halogen atom, there are three types of π halogen bonds:⁴⁷ the halogen atom points to the center of the benzene ring, the middle of the C–C bond, and the C atom, respectively.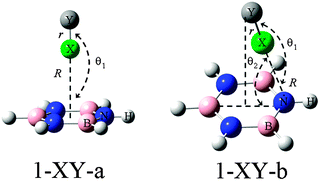

Fig. 2 Structures of complexes of borazine (1) with XY (X = F, Cl, Br, and I; Y = F, CN, CCH, and CF₃).

In Table 1, we summarized the structural parameters in all complexes. Here we pointed out that the planar structure of borazine has small deformation for the 1-XY-b complex. The Y-X⋯N angle (θ₁) almost amounts to 180° in the complexes except for 1-ClCF₃-b. For the 1-XY-b complex, the angle θ₂ becomes larger with the increase of the halogen atomic number (Fig. 3). The geometrical difference in structure b can be explained with the size of the σ-hole on the interacting halogen atom. MEPs maps of XCCH (X = F, Cl, Br, and I) are shown in Fig. 4. When X varies from F to I, the region of the positive MEPs (σ-hole) on the halogen atomic surface becomes bigger, while the area of the negative MEPs on the halogen atomic surface becomes smaller. Other halogenated compounds show a similar change in the size of the σ-hole with the increase of the halogen atomic number. The negative area (lone pair electrons) on the halogen atom could have an attractive interaction with the electron-deficient ring center of borazine and this interaction becomes weaker for the heavier halogen. Simultaneously, the bigger positive region results in a stronger halogen bond between the N and X atoms. The change in the strength for both interactions is jointly responsible for the larger θ₂ in the heavier halogen complex. This angle is bigger than 90° in 1-XY-b (XY = Cl₂, Br₂, I₂) complexes but is smaller than 90° in other b complexes. For 1-XY-b (XY = Cl₂, Br₂, I₂) complexes, the dihalogen molecules are almost perpendicular to the plane of 1. The distance between the F atom and the ring center of borazine is about 3.0 Å in the 1-FY-a (Y = F, CN, CCH, and CF₃) complexes with small interaction energy (Table 2). The weak interaction in the 1-FY complex has a negligible effect on the change in the F–Y bond length and the frequency shift of the respective bond stretch vibration. The X⋯N distance shows an irregular change for the different series of 1-XY-b (X = Cl, Br, and I) complexes. With the increase of the X atomic radius, it becomes shorter in the 1-XCN-b complex and larger in the 1-XCF₃-b complex, however, in the 1-XCCH-b complex, it grows in the order of Br < I < Cl and in the 1-XF-b complex in the order of Br < Cl < I. Even so, the X⋯N distances in all b complexes are smaller than the sum of van der Walls radii of the respective atoms (3.3 Å for Cl and N atoms, 3.4 Å for Br and N atoms, 3.6 Å for I and N atoms). However, the interaction energy shows a consistent change in the 1-XY-b (X = Cl, Br, and I) complex. Namely, the interaction energy becomes more negative with the increase of the halogen atomic number. This is in agreement with the most positive MEP on the halogen atomic surface.⁴⁸ The interaction energy is also related to the Y substitutent and becomes more negative in the order of Y = CF₃ < CCH < CN < F. It is also found that the b type complexes are more stable than the corresponding a type complexes. Both types of complexes are less stable than halogen-bonded complexes of benzene–X₂.⁴⁷ This further shows that borazine is a weaker Lewis base than benzene.

Table 1 Binding distance (R, Å), change in the X–Y bond length (Δr, Å), and bond angles (θ, degree) in the complexes at the MP2/aug-cc-pVDZ level

	R	Δr	θ 1		R	Δr	θ 1	θ 2
1-FF-a	2.963	0.002	180.0	1-FF-b	2.672	0.013	178.6	84.4
1-ClF-a	3.176	0.004	180.0	1-ClF-b	2.576	0.030	179.4	93.4
1-BrF-a	3.200	0.005	180.0	1-BrF-b	2.548	0.038	179.2	95.0
1-IF-a	3.261	0.007	180.0	1-IF-b	2.644	0.036	179.2	96.4
1-FCN-a	2.980	−0.001	180.0	1-FCN-b	—	—	—	—
1-ClCN-a	3.235	—	180.0	1-ClCN-b	3.250	0.001	180.0	76.5
1-BrCN-a	3.252	—	180.0	1-BrCN-b	3.139	0.004	180.0	82.3
1-ICN-a	3.330	0.002	180.0	1-ICN-b	3.126	0.012	180.0	85.8
1-FCCH	2.976	−0.002	180.0	1-FCCH-b	—	—	—	—
1-ClCCH-a	3.273	—	180.0	1-ClCCH-b	3.283	0.000	176.4	75.5
1-BrCCH-a	3.289	—	180.0	1-BrCCH-b	3.189	0.002	179.6	79.5
1-ICCH-a	3.376	0.002	180.0	1-ICCH-b	3.197	0.008	179.4	82.3
1-FCF3-a	2.976	−0.002	180.0	1-FCF3-b	—	—	—	—
1-ClCF3-a	3.283	−0.002	180.0	1-ClCF3-b	3.312	−0.002	173.7	75.7
1-BrCF3-a	3.308	−0.003	180.0	1-BrCF3-b	3.230	−0.002	178.8	80.5
1-ICF3-a	3.383	−0.003	180.0	1-ICF3-b	3.237	0.000	179.5	83.8

---

Fig. 3 Dependence of the angle θ₂ on the nature of the halogen atom in the 1-XY-b complex.

Fig. 4 Molecular electrostatic potentials of XCCH (X = F, Cl, Br, and I). Color ranges, in eV, are: red, greater than 0.02; yellow, between 0.02 and 0.01; green, between 0.01 and 0; blue, less than 0.

Table 2 Interaction energy corrected for BSSE (ΔE, kJ mol⁻¹), frequency shift of X–Y stretch vibration (Δν, cm⁻¹), and number of imaginary frequencies (N) in the complexes at the MP2/aug-cc-pVDZ level

	ΔE	Δν	N		ΔE	Δν	N
1-FF-a	−3.70	−10	2	1-FF-b	−5.10	−63	0
1-ClF-a	−8.69	−10	2	1-ClF-b	−18.81	−92	0
1-BrF-a	−10.69	−11	2	1-BrF-b	−27.00	−76	0
1-IF-a	−12.62	−12	2	1-IF-b	−32.37	−55	0
1-FCN-a	−3.91	0	0	1-FCN-b	—	—	—
1-ClCN-a	−9.01	−2	2	1-ClCN-b	−9.37	−4	0
1-BrCN-a	−10.44	−1	2	1-BrCN-b	−11.66	−8	0
1-ICN-a	−12.23	−2	2	1-ICN-b	−15.02	−14	0
1-FCCH	−2.45	3	0	1-FCCH-b	—	—	—
1-ClCCH-a	−6.98	−1	2	1-ClCCH-b	−7.30	−3	0
1-BrCCH-a	−8.11	−1	2	1-BrCCH-b	−9.06	−6	0
1-ICCH-a	−9.53	−1	2	1-ICCH-b	−11.60	−11	0
1-FCF3-a	−2.11	0	3	1-FCF3-b	—	—	—
1-ClCF3-a	−6.77	−1	3	1-ClCF3-b	−6.94	−1	0
1-BrCF3-a	−7.90	−1	3	1-BrCF3-b	−8.53	−2	0
1-ICF3-a	−9.29	−1	3	1-ICF3-b	−10.77	−3	0

---

The interaction strength is weak in most complexes except some XF complexes. Thus we plan to enhance it by the substitution effect. Specifically, the H atom of B–H or N–H bond in 1-BrCF₃ complex is replaced with CN, Li, and CH₃, respectively. The obtained complexes are represented as B-R-1-BrCF₃ and N-R-1-BrCF₃, where the bold atom indicates the substitution site and R represents substituents. The corresponding results are given in Table 3. The electron-withdrawing group CN leads to a weakening of the interaction strength with less negative interaction energy, while the electron-donating group Li results in an enhancement of the interaction strength with more negative interaction energy. The enhancing effect of Li is more prominent than the weakening effect of CN. The N substitution effect is more prominent whether for the Li enhancing effect or for the CN weakening effect, due to its direct participation in the interaction. The interaction energy in the N-Li-1-BrCF₃ complex is about 2.5 times as much as that in the 1-BrCF₃ complex. The prominent effect of Li stubstitutent has been reported for the halogen-bonded complex of HCCBr–NCH.⁴⁹ A similar enhancing effect is also found for the CH₃ substituent, although its effect is smaller than that of Li substitution. This indicates that the methyl group plays an electron-donating role in this interaction, which is similar to that in hydrogen bonds.⁵⁰ Considering the possible Br⋯Li interaction in the N-Li-1-BrCF₃ complex, the θ₁ angle decreases by about 12° and the θ₂ angle increases by about 40°. Both angles change a little in other substituted complexes. In general, the enhancing interaction shortens the binding distance, while the weakening interaction enlarges it. The binding distance is an exception in the N-CN–1–BrCF₃ complex.

Table 3 Interaction energy corrected for BSSE (ΔE, kJ mol⁻¹), binding distance (R, Å), change in the X–Y bond length (Δr, Å), bond angles (θ, degree), and frequency shift of the X–Y stretch vibration (Δν, cm⁻¹) in the complexes at the MP2/aug-cc-pVDZ level

	ΔE	R	Δr	θ 1	θ 2	Δν
B-CN-1-BrCF3-b	−7.01	3.240	0.001	173.4	79.8	−1
N-CN-1-BrCF3-b	−6.60	3.213	0.001	171.7	82.7	0
B-Li-1-BrCF3-b	−14.42	3.178	−0.005	174.0	81.5	−4
N-Li-1-BrCF3-b	−21.66	2.888	0.018	166.6	120.2	−9
B-CH3-1-BrCF3-b	−10.13	3.178	−0.001	175.5	81.6	−2
N-CH3-1-BrCF3-b	−11.10	3.089	−0.001	176.0	86.3	−3

---

3.3. NBO and SAPT analyses

To unveil the interaction nature in the above types of complexes, we fall back on the NBO and SAPT analyses. For each type of complex, two orbital interactions are analyzed, and their strengths are estimated with second-order perturbation energy (E) given in Table 4. The two orbital interactions are BD_B–N → BD*_X–Y and LP_X → BD*_B–N, as shown in Fig. 5, and the perturbation energies are represented as E₁ and E₂, respectively. In the former the π bonding orbital in borazine acts as the donor orbital (Lewis bases), while in the latter the lone pair bonding orbital on the halogen atom acts as the donor orbital. The former orbital interaction corresponds to halogen bonding, while the latter orbital interaction suggests lone pair–π interactions. One can see that for the 1-XY-a complex the E₂ value is larger than the E₁ one, indicating that the interaction in the 1-XY-a complex should belong to lone pair–π interactions. This also goes for most 1-XY-b complexes except the 1-XF-b (X = Cl, Br, and I) complex, in which the E₁ value is larger than the E₂ one and the ratio of E₁/E₂ increases for the heavier halogen atom. This means that halogen bonding is present in the 1-XF-b (X = Cl, Br, and I) complex.

Table 4 Second-order perturbation energies due to the BD_B–N → BD*_X–Y (E₁, kJ mol⁻¹) and LP_X → BD*_B–N (E₂, kJ mol⁻¹) orbital interactions and charge transfer (CT, me) in the complexes

	E 1	E 2	CT		E 1	E 2	CT
1-FF-a	0.75	9.20	−4.8	1-FF-b	8.94	22.49	−0.4
1-ClF-a	2.88	17.18	−9.7	1-ClF-b	70.31	54.00	33.5
1-BrF-a	5.52	21.69	−9.8	1-BrF-b	122.01	73.69	53.3
1-IF-a	9.91	27.88	−9.4	1-IF-b	138.90	81.13	48.2
1-FCN-a	0.00	7.61	−2.4	1-FCN-b	—	—	—
1-ClCN-a	1.13	12.08	−4.3	1-ClCN-b	2.84	16.30	−4.0
1-BrCN-a	2.63	15.92	−1.0	1-BrCN-b	9.20	24.24	0.9
1-ICN-a	5.39	19.86	−2.3	1-ICN-b	21.57	33.36	6.0
1-FCCH	0.00	7.82	−3.5	1-FCCH-b	—	—	—
1-ClCCH-a	0.88	11.33	−6.2	1-ClCCH-b	2.26	16.47	−6.4
1-BrCCH-a	2.01	15.26	−6.6	1-BrCCH-b	6.81	23.58	−5.4
1-ICCH-a	4.01	18.89	−5.6	1-ICCH-b	14.21	31.10	−1.3
1-FCF3-a	0.00	9.74	−2.8	1-FCF3-b	—	—	—
1-ClCF3-a	0.75	10.83	−4.4	1-ClCF3-b	2.13	16.43	−4.7
1-BrCF3-a	2.01	14.04	−4.4	1-BrCF3-b	6.69	21.57	−3.2
1-ICF3-a	4.64	17.35	−3.3	1-ICF3-b	15.55	28.38	1.2

---

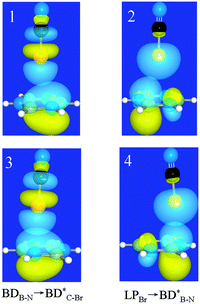Fig. 5 Schematic diagrams of two orbital interactions in 1-BrCN-a (1 and 2) and 1-BrCN-b (3 and 4) complexes.

To further provide evidence for the above results, charge transfer from borazine to the halogenated molecule was also calculated. The charge transfer is negative in the 1-XY-a complex, showing that borazine gains electrons in the 1-XY-a complex. This is consistent with the electron-withdrawing role of borazine in the lone pair–π interaction. Likely, the charge transfer is also negative in most 1-XY-b complexes except 1-XF-b (X = Cl, Br, and I), 1-BrCN-b, and 1-IY-b (Y = CN, and CCH, CF₃) complexes. This means that for most 1-XY-b complexes borazine also gains electrons. However, this negative charge transfer is changed to positive in the 1-XF-b (X = Cl, Br, and I), 1-BrCN-b, and 1-IY-b (Y = CN, CCH, and CF₃) complexes. The positive charge transfer in the 1-BrCN-b and 1-IY-b (Y = CN, CCH, and CF₃) complexes is inconsistent with the magnitude of the respective orbital interactions. We think that other interactions such as polarization interaction, besides the orbital interactions, are also responsible for the charge transfer in these complexes. The positive charge transfer in the 1-XF-b (X = Cl, Br, and I) complex supports the electron-donating role of borazine in the formation of the halogen bond. With the increase of the halogen atomic mass, the magnitude of negative charge transfer in the 1-XY-b complex becomes smaller and is even changed to positive one in some complexes.

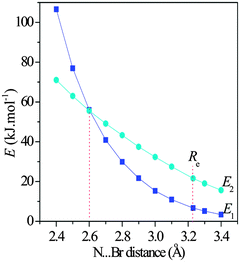
One finds the stronger halogen bonding interaction in the 1-XF-b (X = Cl, Br, and I) complex but the weaker lone pair–π interaction in other complexes. Thus we studied the dependence of the interaction type on the binding distance. One can see from Fig. 6 that with the shortening of the Br⋯N distance in the 1-BrCF₃-b complex the values of E₁ and E₂ are both increased. The E₂ value almost increases linearly, while the E₁ one displays an exponential increase. However, the slope of their change is different. Interestingly, the E₁ value is smaller than the E₂ one with the Br⋯N distance larger than 2.6 Å, both values are equal at 2.6 Å, and the E₁ value is greater than the E₂ one with the Br⋯N distance shorter than 2.6 Å. Thus the lone pair–π interaction is changed into the halogen bond with the shortening of the binding distance (stronger interaction). This result indicates that the interaction strength can change the interaction type.

Fig. 6 Dependence of E₁ and E₂ on the N⋯Br distance in the 1-BrCF₃-b complex.

The interaction energies in both types of complexes are decomposed into five terms: electrostatic energy (E_elst), exchanged energy (E_exch), induction energy (E_ind), dispersion energy (E_disp), and δE_int,r^HF, and the related results are given in Table 5, while the detailed components are presented in Tables S1 and S2 in ESI.† For the 1-FY-a (Y = CN, CCH, and CF₃) complex, the E_disp term has a greater contribution than the E_elst one and the E_ind contribution is very small. A similar result is also found in the 1-ClY-a (Y = CN, CCH, and CF₃) complex. For the 1-BrY-a (Y = CN, CCH, and CF₃) complex, the E_elst term is close to the E_disp term and is even larger in some cases, and the E_ind contribution is still smallest. However, the E_elst contribution is negative for the 1-FF-a complex. For the other dihalogen complexes, the E_elst contribution is dominant although the other two attractive terms are also important. For the 1-XY-b (X = Cl and Br; Y = CN, CCH, and CF₃) complex, the E_elst contribution is still dominant, while the E_ind contribution is small. Thus the physical origin of the interaction between borazine and halogenated molecule depends on the interaction type and the nature of the halogen atom. In summary, the dispersion energy is the main force responsible for the weaker interactions, while the electrostatic energy has a main contribution to the stronger interactions.

Table 5 Electrostatic energy (E_elst), exchange energy (E_exch), induction energy (E_ind), dispersion energy (E_disp), and δE_int,r^HF. All are in kJ mol⁻¹

	E elst	E exch	E ind	E disp	δE int,r ^HF
Note: Data in parentheses are for the b complex. δEint,r^HF collects all third- and higher-order induction and exchange-induction terms.
1-FF-a	5.01(−24.62)	10.85(46.69)	−5.31(−4.26)	−3.09(−8.23)	−0.35(−0.98)
1-ClF-a	−12.00(−61.90)	16.84(101.15)	−2.68(−16.72)	−8.94(−20.86)	−1.92(−24.48)
1-BrF-a	−19.48(−105.04)	26.12(154.93)	−6.48(−45.77)	−12.91(−30.05)	−3.93(−34.37)
1-FCN-a	−7.90	27.78	−0.75	−13.21	−1.59
1-ClCN-a	−9.27(−12.00)	15.62(20.13)	−1.30(−1.63)	−9.86(−10.83)	−0.96(−1.52)
1-BrCN-a	−15.76(−24.83)	24.11(36.35)	−3.59(−5.89)	−13.96(−16.05)	−2.19(−4.39)
1-FCCH-a	−1.55	8.80	−0.21	−5.14	−0.38
1-ClCCH-a	−7.06(−9.70)	14.56(19.24)	−0.54(−0.84)	−9.66(−10.70)	−0.74(−1.21)
1-BrCCH-a	−13.00(−20.77)	22.70(33.28)	−2.05(−3.72)	−13.63(−15.59)	−1.65(−3.23)
1-FCF3-a	−2.42	8.78	0.04	−4.60	−0.36
1-ClCF3-a	−7.77(−10.12)	13.59(18.00)	−0.92(−1.17)	−8.99(−10.03)	−0.81(−1.31)
1-BrCF3-a	−13.38(−19.90)	20.73(30.04)	−2.80(−4.39)	−12.75(−14.55)	−1.88(−3.71)

---

4. Conclusions

The complexes of borazine and four halogenated molecules XF, XCN, XCCH, and XCF₃ (X = F, Cl, Br, and I) have been investigated. Two structures (a and b) are studied: the halogen atom in structure a points to the ring center of borazine and combines with the N atom of borazine in structure b. The structure a is stabilized by a lone pair–π interaction although it is not located at the minima on the potential surface in most complexes. The structure b is also combined with a lone pair–π interaction in most complexes except the dihalogen systems, where a halogen bond with large interaction energy is present. NBO analysis indicates that with the increase of interaction strength between the two molecules the lone pair–π interaction may change to the halogen bonding interaction. SAPT results show that the dispersion energy plays a main role in stabilizing the weakly bonded complexes, while the electrostatic energy is dominant in the strongly bonded complexes.

Acknowledgements

This work was supported by the Outstanding Youth Natural Science Foundation of Shandong Province (JQ201006), the Program for New Century Excellent Talents in University, the National Natural Science Foundation of China (51278443), and Open Project of State Key Laboratory of Supramolecular Structure and Materials (sklssm201321).

References

1. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757.
2. A. Caballero, N. G. White and P. D. Beer, Angew. Chem., Int. Ed., 2011, 50, 1845–1848.
3. P. Politzer and J. S. Murray, ChemPhysChem, 2013, 14, 278–294.
4. P. Auffinger, F. A. Hays, E. Westhof and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16789–16794.
5. S. A. Cooke, C. M. Evans, J. H. Holloway and A. C. Legon, J. Chem. Soc., Faraday Trans., 1998, 94, 2295–2302.
6. Z. X. Wang, B. S. Zheng, X. Y. Yu, X. F. Li and P. G. Yi, J. Chem. Phys., 2010, 132, 164104.
7. Y. L. Zeng, X. Y. Zhang, X. Y. Li, L. P. Meng and S. J. Zheng, ChemPhysChem, 2011, 12, 1080–1087.
8. D. S. Reddy, D. C. Craig and G. R. Desiraju, J. Am. Chem. Soc., 1996, 118, 4090–4093.
9. Y. X. Lu, Y. Wang and W. L. Zhu, Phys. Chem. Chem. Phys., 2010, 12, 4543–4551.
10. K. S. Yeung, Drug Discovery Today, 2011, 15, 158.
11. X. Liang, T. Sun and Y. B. Wang, Chem. J. Chin. Univ., 2012, 33, 541–547.
12. Y. X. Lu, J. W. Zou, Y. H. Wang and Q. S. Yu, J. Chem. Phys. A, 2007, 334, 10781–10788.
13. N. Nagels, D. Hauchecorne and W. A. Herrebout, Molecules, 2013, 18, 6829–6851.
14. M. Egli and R. V. Gessner, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 180–184.
15. S. Sarkhel, A. Rich and M. Egli, J. Am. Chem. Soc., 2003, 125, 8998–8999.
16. A. Jain, C. S. Purohit, S. Verma and R. Sankararamakrishnan, J. Phys. Chem. B, 2007, 111, 8680–8683.
17. J. Zukerman-Schpector, A. Otero-de-la-Roza, V. Luaña and E. R. T. Tiekink, Chem. Commun., 2011, 47, 7608–7610.
18. A. Das, S. R. Choudhury, C. Estarellas, B. Dey, A. Frontera, J. Hemming, M. Helliwell, P. Gamez and S. Mukhopadhyay, CrystEngComm, 2011, 13, 4519–4527.
19. T. J. Mooibroek, P. Gamez and J. Reedijk, CrystEngComm, 2008, 10, 1501–1515.
20. G. A. DiLabio and E. R. Johnson, J. Am. Chem. Soc., 2007, 129, 6199–6203.
21. W. Gung, B. Y. Zou, Z. Xu, J. C. Amicangelo, S. Ma and H. C. Zhou, J. Org. Chem., 2008, 73, 689–693.
22. T. J. Mooibroek, P. Gamez and J. Reedijk, CrystEngComm, 2008, 10, 1501–1515.
23. G. A. DiLabio and E. R. Johnson, J. Am. Chem. Soc., 2007, 129, 6199–6203.
24. A. Nijamudheen, D. Jose, A. Shine and A. Datta, J. Phys. Chem. Lett., 2012, 3, 1493–1496.
25. C. Estarellas, A. Frontera, D. Quiñonero and P. M. Deyà, Cent. Eur. J. Chem., 2011, 9, 25–34.
26. J. Ran and P. Hobza, J. Chem. Theory Comput., 2009, 5, 1180–1185.
27. A. Stock and E. Pohland, Ber. Dtsch. Chem. Ges., 1926, 59, 2210–2215.
28. E. Wiberg and A. Bolz, Ber. Dtsch. Chem. Ges., 1940, 73, 209–232.
29. H. F. Bettinger, T. Kar and E. Sanchez-Garcia, J. Phys. Chem. A, 2009, 113, 3353–3359 , and references cited here.
30. T. J. Carter, J. W. Kampf and N. K. Szymczak, Angew. Chem., Int. Ed., 2012, 51, 13168–13172.
31. A. Staubitz, A. P. M. Robertson and I. Manners, Chem. Rev., 2010, 110, 4079–4124.
32. N. C. Smythe and J. C. Gordon, Eur. J. Inorg. Chem., 2010, 509–521.
33. S. Kervyn, N. Kalashnyk, M. Riello, B. Moreton, J. Tasseroul, J. Wouters, T. S. Jones, A. D. Vita, G. Costantini and D. Bonifazi, Angew. Chem., Int. Ed., 2013, 52, 7410–7414.
34. J. Y. Wu, H. Yan, H. Chen, G. L. Dai and A. G. Zhong, Comput. Theor. Chem., 2012, 984, 51–56.
35. A. Bauzá, D. Quiñonero, P. M. Deyà and A. Frontera, Chem. Phys. Lett., 2012, 530, 145–150.
36. R. Miao, G. S. Yang, C. M. Zhao, J. Hong and L. G. Zhu, THEOCHEM, 2005, 715, 91–100.
37. R. Y. Li, Z. R. Li, D. Wu, Y. Li, W. Chen and C. C. Sun, J. Phys. Chem. A, 2005, 109, 2608–2613.
38. D. J. R. Duarte, M. M. de las Vallejos and N. M. Peruchena, J. Mol. Model., 2010, 16, 737–748.
39. G. Valerio, G. Raos, S. V. Meille, P. Metrangolo and G. Resnati, J. Phys. Chem. A, 2000, 104, 1617–1620.
40. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. A. Yazyev, J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. A. Dapprich, D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
42. F. A. Bulat, A. Toro-Labbé, T. Brinck, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679–1691.
43. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
44. R. Bukowski, W. Cencek, P. Jankowski, B. Jeziorski, M. Jeziorska, S. A. Kucharski, V. F. Lotrich, A. J. Misquitta, R. Moszynski, K. Patkowski, R. Podeszwa, S. Rybak, K. Szalewicz, H. L. Williams, R. J. Wheatley, P. E. S. Wormer and P. S. Zuchowski, SAPT2008: An Ab initio Program for Many-Body Symmetry-Adapted Perturbation Theory Calculations of Intermolecular Interaction Energies, Version 2008.2.
45. J. M. Campanario, E. Bronchalo and M. A. Hidalgo, J. Chem. Edu., 1994, 71, 761–766.
46. J. J. Engelberts, R. W. A. Havenith, J. H. Lenthe, L. W. Jenneskens and P. W. Fowler, Inorg. Chem., 2005, 44, 5266–5272.
47. E. Munusamy, R. Sedlak and P. Hobza, ChemPhysChem, 2011, 12, 3253–3261.
48. P. Politzer, J. S. Murray and M. C. Concha, J. Mol. Model., 2007, 13, 643–650.
49. J. B. Cheng, R. Li, Q. Z. Li, B. Jing, Z. B. Liu, W. Z. Li, B. A. Gong and J. Z. Sun, J. Phys. Chem. A, 2010, 114, 10320–10325.
50. Q. Z. Li, G. S. Wu and Z. W. Yu, J. Am. Chem. Soc., 2006, 128, 1438–1439.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp54006e

---