 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermophoresis of charged colloidal rods
Zilin
Wang
a,
Hartmut
Kriegs
a,
Johan
Buitenhuis
a,
Jan K. G.
Dhont
*ab and
Simone
Wiegand
a
aICS-3 Soft Condensed Matter, Jülich, Germany. E-mail: j.k.g.dhont@fz-juelich.de; s.wiegand@fz-juelich.de
bInstitute of Physics, Heinrich-Heine- Universität, D-40225 Düsseldorf, Germany
First published on 19th July 2013
Abstract
The thermal diffusion behavior of dilute solutions of very long and thin, charged colloidal rods (fd-virus particles) is studied using a holographic grating technique. The Soret coefficient of the charged colloids is measured as a function of the Debye screening length, as well as the rod-concentration. The Soret coefficient of the fd-viruses increases monotonically with increasing Debye length, while there is a relatively weak dependence on the rod-concentration when the ionic strength is kept constant. An existing theory for thermal diffusion of charged spheres is extended to describe the thermal diffusion of long and thin charged rods, leading to an expression for the Soret coefficient in terms of the Debye length, the rod-core dimensions, and the surface charge density. The thermal diffusion coefficient of a charged colloidal rod is shown to be accurately represented, for arbitrary Debye lengths, by a superposition of spherical beads with the same diameter of the rod and the same surface charge density. The experimental Soret coefficients are compared with this and other theories, and are contrasted against the thermal diffusion behaviour of charged colloidal spheres.
1 Introduction
Thermal diffusion, which is also known as the Ludwig–Soret effect, is the phenomenon where mass transport is induced by a temperature gradient in a multi-component system. For sufficiently small gradients, the mass flux induced by a temperature gradient ∇T is equal to −DT∇T, where DT is the thermal diffusion coefficient. Thermal diffusion leads to gradients ∇c in concentration, which in turn give rise to a mass flux equal to −D∇c, where D is the mass diffusion coefficient. The two fluxes counter balance in a stationary state, from which it follows that the ratio of the concentration gradient and the temperature gradient in such a stationary state is equal to the Soret coefficient ST = DT/ρD, where ρ is the number density of colloids. The Soret coefficient can be regarded as a response function, which measures the concentration gradient induced per unit of temperature gradient. Note that often a slightly modified definition of the thermal diffusion coefficient is used in experimental contexts,1 which contains an additional prefactor related to concentration (as discussed by Ning et al.,2 and in Section 4 of the present paper).In many previous studies, attempts have been made for mixtures of non-polar liquids to relate the Soret coefficient to the mass of the molecules, their moment of inertia, and the viscosity and thermal expansion coefficient.1 In aqueous systems, where the situation is more complicated, hydrogen bonds and the charge effect are of significant importance.3,4
With the advent of new experimental techniques in the last few years, it became possible to investigate the thermal diffusion behaviour of relatively slowly diffusing macromolecules. A number of experimental studies have been performed on charged macromolecules, such as DNA, ionic surfactants, surface modified polystyrene spheres and silica colloids.2,5–8 For charged silica Ludox particles it was found that the Soret coefficient increases with increasing Debye length and slightly drops at large Debye lengths, of the order of the core-radius of the colloids. For all investigated concentrations at room temperature, a negative Soret coefficient has been observed for this system.2 Another study reveals an increasing linear dependence of the Soret coefficient with the Debye length for carboxyl-modified polystyrene beads.5 Here, the Debye length is always very small as compared to the particle radius. Apart from colloids, a study of micellar solutions with the ionic surfactant sodium dedecyl sulphate also shows that raising the Debye length leads to an increase of the Soret coefficient.7
To gain a better understanding of the microscopic mechanism of the thermal diffusion process of macromolecules, several theoretical approaches have been developed. The first theory was published by Ruckenstein in 1981,9 where a connection between thermophoresis of solid colloidal particles and the Marangoni effect is made. Later, models for single spherical particles have been derived in terms of surface potential, independently by Morozov and Piazza.6,10 A few years later, Bringuier and Bourdon proposed an expression for ST in terms of the total internal energy of a particle, based on the kinetic theory of Brownian motion.11 Independently, Fayolle et al.12 and later Duhr and Braun13 derived an expression for the Soret coefficient for charged colloids with thin double layers, which was subsequently generalized by Dhont and Briels14 to arbitrary Debye lengths. All these theoretical approaches apply only to spherical colloids, while little is known about non-spherical colloids. The present paper is devoted to thermal diffusion of very long and thin, charged colloidal rods.
Fd-virus suspensions are widely used as model systems for colloidal rods. Suspensions of fd-virus particles have been shown to exhibit several liquid-crystalline phases (for an overview see ref. 15), and have been used for studies on the response of rod-like colloids to shear flow16,17 and electric fields.18 Their suspensions are stable up to 65 °C,19 and are highly monodisperse. The wild type fd-virus has a molecular weight of 1.64 × 107 g mol−1, a contour length L of 880 nm, a radius a of 3.4 nm, and a persistence length LP of 2.2 μm. The ratio of the persistence length to contour length LP/L = 2.5 indicates that these rods are semi-flexible, which leads to a deviation of isotropic–nematic coexistence concentrations as predicted by Onsager for stiff rods.15,20 Above pH 4 these particles are negatively charged and interact via a combination of electrostatic repulsion and hard-core interactions. The net surface charge can be increased or decreased by increasing or decreasing the solution pH, respectively.21
In the present paper we use fd-virus suspensions to investigate the thermal diffusion behaviour of very long and thin, charged colloidal rods. The paper is structured as follows. First, we describe the experimental details. In the subsequent section we extend the Dhont–Briels model14 for spherical colloids to rod-shaped particles. In the results and discussion section we present experimental results for thermal diffusion coefficients and mass diffusion coefficient, where both the ionic strength and concentration are independently and systematically varied. The experimental results are compared to our theory and other theories, and also to former experimental results for spherical colloids. The main conclusions and remarks with respect to possible future work close the paper.
2 Experimental details
2.1 Sample preparation and characterization
The fd-virus was prepared following a standard biological protocol using the XL1-Blue strain of E. coli as the host bacteria.22 The obtained virus was purified by repetitive centrifugation (108![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g) and then re-dispersed in the chosen buffers. Tris(hydroxymethyl)aminomethane (Tris) with concentrations of 82.15, 15.09, 6.11, 3.29, and 2.05 mM was used as buffer solution. The pHs of all buffer solutions were adjusted to 8.2 by adding concentrated HCl solution. Finally the virus was dialyzed in each chosen buffer and used as stock solutions to prepare the further concentration series for the measurements. The five concentrations of Tris are chosen such that the resulting Debye lengths are varied with equal increments. The studied fd-virus concentration is 1 mg ml−1 for the fixed-concentration measurements, and in the range of 0.4–1.8 mg ml−1 and 0.6–2.2 mg ml−1 for the fixed-buffer concentration and the fixed-volume fraction measurements, respectively. Concentrations were determined by UV absorption (NanoDrop ND-1000, Peqlab). All measurements were performed at 20 °C.
000g) and then re-dispersed in the chosen buffers. Tris(hydroxymethyl)aminomethane (Tris) with concentrations of 82.15, 15.09, 6.11, 3.29, and 2.05 mM was used as buffer solution. The pHs of all buffer solutions were adjusted to 8.2 by adding concentrated HCl solution. Finally the virus was dialyzed in each chosen buffer and used as stock solutions to prepare the further concentration series for the measurements. The five concentrations of Tris are chosen such that the resulting Debye lengths are varied with equal increments. The studied fd-virus concentration is 1 mg ml−1 for the fixed-concentration measurements, and in the range of 0.4–1.8 mg ml−1 and 0.6–2.2 mg ml−1 for the fixed-buffer concentration and the fixed-volume fraction measurements, respectively. Concentrations were determined by UV absorption (NanoDrop ND-1000, Peqlab). All measurements were performed at 20 °C.
2.2 Infrared thermal diffusion forced Rayleigh scattering (IR-TDFRS)
A detailed description of the recently modified IR-TDFRS can be found in the paper by Blanco et al.3 This setup is optimized for aqueous systems and has been used to study the transport properties in different aqueous systems of non-ionic surfactants,2 saccharide solutions23 and anisotropic bio-colloids.3The normalized heterodyne scattered intensity ζthhet(t), assuming an ideal excitation with a step function, is given by,
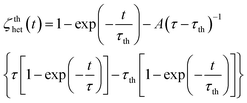 | (1) |
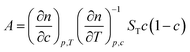 | (2) |
3 Theoretical description
The force on a charged colloidal particle due to the presence of an electric double layer has been shown in ref. 14 to be mainly due to the change of the internal energy of the electric double layer as the ambient temperature changes on moving the colloid. The additional forces due to the temperature-gradient induced deformation of the double layer are relatively small in polar solvents like water.14 Let FW denote the force acting on the colloid due to the temperature dependence of the internal energy of the double layer. This force is connected to the work d![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) to reversibly pull the colloid from a box with temperature T over a distance dz to a box with temperature T + dT, by the relation FWdz = −d
to reversibly pull the colloid from a box with temperature T over a distance dz to a box with temperature T + dT, by the relation FWdz = −d![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) (see Fig. 1). The work d
(see Fig. 1). The work d![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) can be calculated, as far as the contribution from the electric double layer is concerned, by considering the alternative path as depicted in Fig. 1. First the surface of the colloid is reversibly de-charged. The work involved in de-charging the colloid is −W(dl)(T), that is, W(dl)(T) is the reversible work to charge-up the colloidal particle. Then the un-charged colloid is pulled from the box with temperature T to the box with temperature T + dT. As far as the double layer is concerned, there is no work involved, simply because the double layer is no longer present for the neutral colloid. Then the colloid is re-charged, which requires the work +W(dl)(T + dT). Hence, d
can be calculated, as far as the contribution from the electric double layer is concerned, by considering the alternative path as depicted in Fig. 1. First the surface of the colloid is reversibly de-charged. The work involved in de-charging the colloid is −W(dl)(T), that is, W(dl)(T) is the reversible work to charge-up the colloidal particle. Then the un-charged colloid is pulled from the box with temperature T to the box with temperature T + dT. As far as the double layer is concerned, there is no work involved, simply because the double layer is no longer present for the neutral colloid. Then the colloid is re-charged, which requires the work +W(dl)(T + dT). Hence, d![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) = W(dl)(T + dT) − W(dl)(T) = dTdW(dl)(T)/dT. It follows that the force is equal to FW = −(dT/dz)(dW(dl)/dT). The connection of the force to the thermal diffusion coefficient is found from force balance on the diffusive time scale, that is, once the colloid is moving, the friction force Ffr = −γv with the solvent balances with FW, where γ is the friction coefficient and v is the velocity of the colloid. The thermal-gradient induced velocity of the colloid is thus equal to v = FW/γ. Substitution of this expression for the velocity into the continuity equation ∂ρ/∂t = −d(vρ)/dz (where ρ is the number density of the colloids) and expansion with respect to gradients in temperature and deviations of the temperature from the ambient temperature then lead to ∂ρ/∂t = DTd2T/dz2, where the thermal diffusion coefficient is equal to14,24
= W(dl)(T + dT) − W(dl)(T) = dTdW(dl)(T)/dT. It follows that the force is equal to FW = −(dT/dz)(dW(dl)/dT). The connection of the force to the thermal diffusion coefficient is found from force balance on the diffusive time scale, that is, once the colloid is moving, the friction force Ffr = −γv with the solvent balances with FW, where γ is the friction coefficient and v is the velocity of the colloid. The thermal-gradient induced velocity of the colloid is thus equal to v = FW/γ. Substitution of this expression for the velocity into the continuity equation ∂ρ/∂t = −d(vρ)/dz (where ρ is the number density of the colloids) and expansion with respect to gradients in temperature and deviations of the temperature from the ambient temperature then lead to ∂ρ/∂t = DTd2T/dz2, where the thermal diffusion coefficient is equal to14,24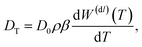 | (3) |
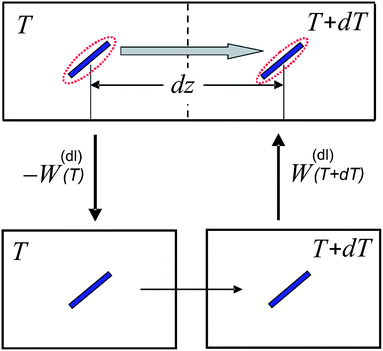 | ||
| Fig. 1 The alternative path to move the colloid from a box with temperature T over a distance dz to the neighbouring box with temperature T + dT. W(dl)(T) is the reversible work that is required to charge the colloid. The colloid is the blue rod, while the red dashed lines are used to indicate the presence of the double layer. | ||
For the calculation of the temperature derivative of the reversible energy to charge the colloidal particle, analytical results can be obtained within the Debye–Hückel approximation. The work required to add a charge dq to the surface of the colloid, homogeneously distributed over its surface, is equal to Ψs(q)dq, where Ψs(q) is the potential at the surface of the colloid with the total charge equal to q. Since within the Debye–Hückel approximation the surface potential is proportional to the charge, the work to charge the colloid up to a total charge equal to Q is given by
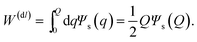 | (4) |
This result is valid for arbitrary double-layer thickness.25 The relationship between the surface potential and the total charge for a spherical colloid reads
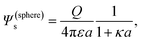 | (5) |
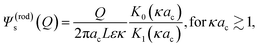 | (6) |
Combining the above results it is found that the thermal diffusion coefficient can be written in terms of the surface charge density σ and the Bjerrum length lB as
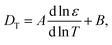 | (7) |
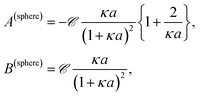 | (8) |
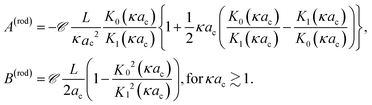 | (9) |
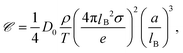 | (10) |
For the cylindrical colloid there are two limiting situations, where either κac ≪ 1 or κac ≫ 1. In the first case of very thick double layers compared to the cylindrical core radius, the core of the rod may be considered as a string of L/2ac beads of radii ac. The extended double layer structure of each bead is essentially unaffected by the presence of the relatively small excluded volume of the neighbouring beads, so that within the linearized Poisson–Boltzmann approach the structure of the double layer of the cylinder is well approximated by a sum of the spherical double layers of the beads. Except for the diffusion coefficient D0, which is different for a sphere and a rod, the thermal diffusion coefficient of the rod is now a sum of the thermal diffusion coefficients of the beads, that is,
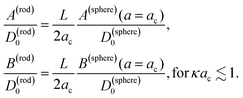 | (11) |
The expression for the thermal diffusion coefficient in the other limiting case of thin double layers is given by eqn (9). May be surprisingly, this expression predicts, like for the thick double layers, that the thermal diffusion coefficient of a rod is simply a superposition of the thermal diffusion coefficients of the beads (with radii ac). This can be analytically verified by substitution of the two leading terms in an asymptotic expansion of the two Bessel functions. Numerical results are given in Fig. 2. Fig. 2a and b show that for κac ≳ 2 the result in eqn (9) is quite accurately approximated by a representation of 2ac/L beads with each having a thermal diffusion coefficient given in eqn (8) with a = ac, where there is an increasing accuracy for thinner double layers. The thermal diffusion coefficient DT in dimensionless form is plotted in Fig. 2c for a cylinder and the corresponding bead model, with the value d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε/d
ε/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T = −1.43 for water. As can be seen, the approximation of the thermal diffusion coefficient of a rod by that of a string of spheres becomes more accurate on decreasing the Debye length.
T = −1.43 for water. As can be seen, the approximation of the thermal diffusion coefficient of a rod by that of a string of spheres becomes more accurate on decreasing the Debye length.
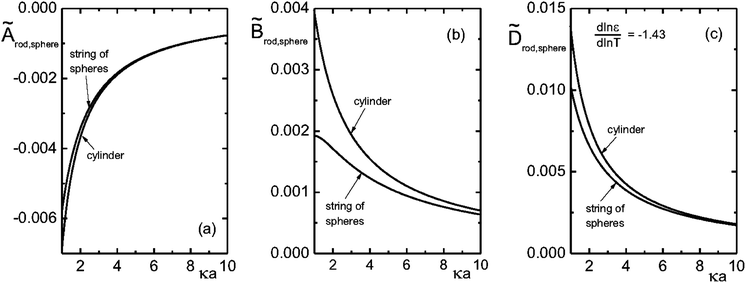 | ||
Fig. 2 The dimensionless quantities à = CA, ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) = CB and = CB and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) T = CDT, where C = T16πεa/βD0ρQ2 as a function of κa (with a = ac for the rods), where Q is the monomer charge. T = CDT, where C = T16πεa/βD0ρQ2 as a function of κa (with a = ac for the rods), where Q is the monomer charge. | ||
The conclusion from the above analysis is that both for thick and thin double layers, the thermal diffusion coefficient of a rod-like colloid can be accurately approximated by L/2ac times the thermal diffusion coefficient (7) and (8) of a spherical colloid with radius a = ac, with the same surface charge density as the rod. From the above analysis we thus find that the Soret coefficient S(rod)T = D(rod)/ρD(rod)0 is equal to
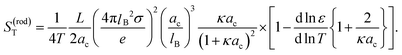 | (12) |
This superposition of thermal diffusion coefficients of spherical beads to approximate the thermal diffusion coefficient of a rod is valid for arbitrary Debye lengths, and will be used in the sequel for a comparison with experimental data for the thermal diffusion coefficient of fd-viruses.
4 Experimental results
Measurements of the mass diffusion coefficient and the thermal diffusion coefficient are performed, where the fd number concentration (defined as the number of fd-virus particles per unit volume) as well as the Debye length are varied independently. The Debye length is tuned by adjusting the concentration of the buffer Tris–HCl solution. Since the acid dissociation constant pKa of Tris is 8.2 and the pH of all the buffers are adjusted to 8.2, the ionic strength I is half the value of the total molar concentration of Tris. The Debye length κ−1 can be calculated from (with NA Avogadro's number)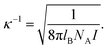 | (13) |
An effective volume fraction ϕ can be defined, which characterizes the importance of interactions between rods. The effective volume fraction depends on the fd number concentration and the Debye length. Due to inter-particle charge–charge interactions, the apparent radius of the core of the fd-virus particles increases by an amount that is approximately given by the Debye length. The effective volume fraction is defined as the volume fraction of rods with a core radius of ac + κ−1. Alternatively the apparent radius can be calculated as suggested by Onsager,20 based on equality of the second virial coefficient of charged rods and the equivalent hard rods with the corresponding apparent core radius. We shall be satisfied with the former simple approximation, as it does not affect our conclusions.
There are thus three parameters of interest: the number concentration of fd viruses, the Debye length, and the effective volume fraction. We therefore performed the following set of experiments:
(a) The Debye length is varied with a constant number concentration of fd-virus particles (of 1 mg ml−1).
(b) The number concentration of fd-virus particles is varied with a fixed Debye length (where the buffer concentration is chosen equal to 6.11 mM).
(c) The effective volume fraction is fixed to 0.0037 with appropriate simultaneous variation of both the fd-virus concentration and the Debye length.
These experimental paths are illustrated in Fig. 3a–c, respectively. Although in our suspensions the state of the system is always isotropic, the rods in these figures are sketched with the same orientation for clarity.
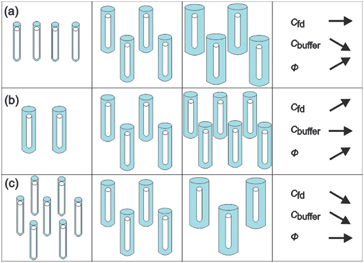 | ||
| Fig. 3 Illustration of the chosen experimental paths. The white rods present the core of fd-viruses and the blue parts are used to indicate the extent of the electric double layers. For clarity the rods have been drawn with the same orientation. In the experiments, however, the systems are isotropic. (a) The number concentration of fd-viruses is constant while the Debye length is increased by decreasing the buffer concentration. (b) The number concentration of fd viruses is increased at a constant Debye length. (c) Both the number concentration of fd viruses and the Debye length are changed in such a way that the effective volume fraction remains constant. | ||
The aim of this work is to probe the thermal diffusion behaviour of single fd-virus particles as a function of the Debye length, without the intervening effects of inter-particle interactions. In order to probe whether inter-particle interactions affect the measured mass diffusion and thermal diffusion coefficients, we performed a series of experiments as a function of the effective volume fraction. The open symbols in Fig. 4 are experimental data for the Soret coefficient and the mass- and thermal diffusion coefficient at a constant buffer concentration, and thus a fixed Debye length. The effective volume fraction for this series of experiments is changed by only changing the fd-virus concentration (path (b)). As can be seen from the lower panel in Fig. 4 (the open symbols), the thermal diffusion coefficient is insensitive to interactions, and is essentially constant up to an effective volume fraction of about 0.0065. The mass diffusion coefficient, however, significantly increases with increasing effective volume fraction, as can be seen from the middle panel (again the open symbols). The blue triangle at low concentration is taken from the literature.26,27 On the other hand, when the effective volume fraction is increased at a constant fd-virus number concentration (1 mg ml−1) by increasing the Debye length (path (a)), significant changes are observed (see the filled symbols in Fig. 4), also for the thermal diffusion coefficient. Since inter-particle interactions are not significant as far as the thermal diffusion coefficient is concerned, its variation with the buffer concentration must be due to the variation of the double-layer thickness. In order to obtain experimental values for the single-particle Soret coefficient S0T, we will use the Debye-length dependent thermal diffusion coefficient (filled symbols in the bottom panel in Fig. 5) and the mass diffusion coefficient at infinite dilution D0 = 2.3 × 10−8 cm2 s−1 from the literature.26,27 The upper panel in Fig. 5 shows Soret coefficients obtained from the diffraction signal (cf.eqn (1) and (2)) corresponding to the ratio of the experimental values for the two diffusion coefficients.
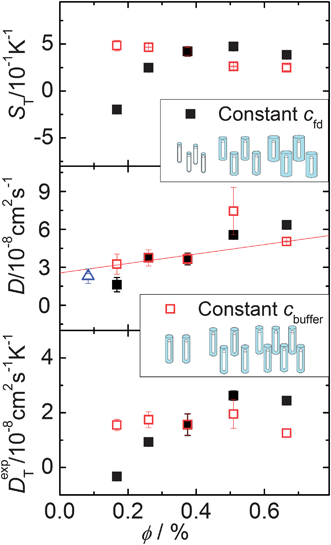 | ||
| Fig. 4 S T, D and DT as a function of the effective volume fraction. Solid squares present measurements with fixed cfd = 1 mg ml−1. Open squares illustrate measurements with constant cbuffer = 6.11 mM. The open triangle presents the data of the bulk diffusion coefficient from the literature.26,27 The red line is a guide to the eye. | ||
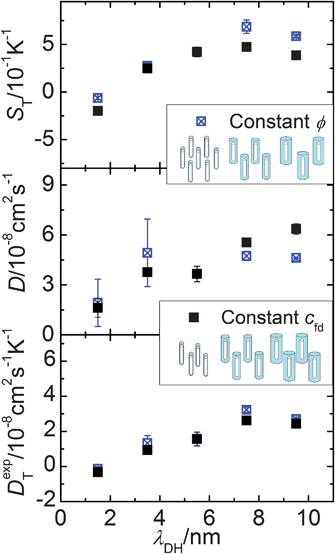 | ||
| Fig. 5 S T, D and DT as a function of the Debye length. Solid squares present measurements with fixed cfd = 1 mg ml−1. Empty with center cross-symbols are measurements with constant ϕ = 0.0037. | ||
To further establish the Debye-length dependence of the mass- and thermal diffusion coefficients, we performed experiments at a fixed effective volume fraction of 0.0037 (path (c)), by appropriate simultaneous variation of both the fd number concentration and the Debye length. The Soret coefficient and the mass- and thermal diffusion coefficients along this path are plotted in Fig. 5 by the open (with center-cross) symbols as a function of the Debye length. The filled symbols in Fig. 5 refer to data obtained along path (a), where the fd number concentration is fixed to 1 mg ml−1, and the Debye length is varied by changing the buffer concentration. The two sets of data points in the lower panel for the thermal diffusion coefficient coincide to within experimental error, which again confirms the insignificant inter-particle interactions.
5 Comparison of experiments with theory
We compare the single-particle Soret coefficient S0T as a function of the Debye length with the theory that has been developed in Section 3. We note that the thermal diffusion coefficient is sometimes defined differently from the theoretical expressions given in Section 3. The definition of the thermal diffusion coefficient DexpT in experimental work relates to DT used in most of the theoretical studies (as in Section 3) through DT = ρc(1 − c)DexpT, where ρ is the colloid number density and c is the volume fraction of colloids.2In order to asses the importance of the finite extent of the electric double layer, we include a comparison to eqn (12) in the asymptotic limit of very thin double layers, where κac → ∞. For such thin double layers we have from eqn (12),
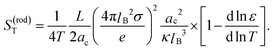 | (14) |
The corresponding expression for spherical particles (without the factor L/2ac) has been derived independently by Fayolle et al.12 and Duhr and Braun.13 There is so far no extension of Ruckenstein's theory9 to rod-like colloids. It is not obvious that we can simply take Ruckenstein's expression for the Soret coefficient for spheres and multiply that with the number of beads to obtain the corresponding expression for rods. We will therefore refrain from a comparison with any possible extension of Ruckenstein's theory to rods.
The result in eqn (12) and the above expression account only for the contribution of the electric double layer to the Soret coefficient. There is an additional “ideal gas” contribution equal to 1/T, and contributions due to thermal properties of, for example, the solvation layer and the core of the colloids. These contributions are insensitive to salt concentration, so that they determine the “offset” in plots of the Soret coefficient as a function of the Debye length. The offset and the surface charge density σ are used as fitting parameters in a comparison of experiments with theory. Fig. 6 shows the Soret coefficient S0T = DT/D0 determined from the measured thermal diffusion coefficient DT and the diffusion at infinite dilution D0 as a function of the Debye length. The fits are plotted in Fig. 6, while the offset and surface charge density for the best fits to various theories are given in Table 1. The solid line (blue) is a fit to limiting expression (eqn (14)) for very thin double layers. The fit is slightly improved by accounting for the finite extent of the electric double layer, as discussed in Section 3 (the dashed green line). Similar results have been found for charged spherical particles (Ludox silica particles),2,13 of which the experimental data are presented in Fig. 6 as open circles, which fitted with the model described in Section 3 for spherical colloids.
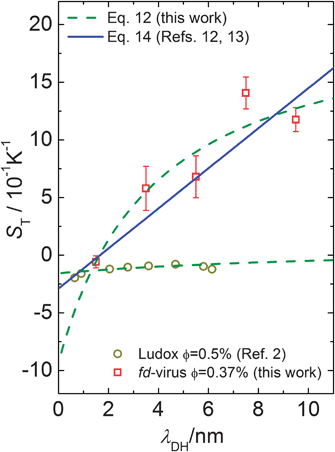 | ||
| Fig. 6 The Soret coefficient ST as a function of the Debye length. In contrast to Fig. 4 and 5 the open squares present the calculated S0T = DT/D0 for the fd-virus with an effective volume fraction of ϕ = 0.0037 and the open circles show ST of Ludox silica particles. The data of the fd-virus are fitted by the two models discussed in the main text. The data of Ludox particle are fitted by Dhont's model for spheres.2 | ||
| Model | σ/e nm−2 | Offset |
|---|---|---|
| Eqn (14) (based on ref. 12 and 13) | 0.023 ± 0.002 | −0.74 |
| Eqn (12) (this work) | 0.050 ± 0.003 | −1.39 |
| Calculated free surface charge | 0.066 |
The question now is whether the surface charge density of σ = (0.050 ± 0.003) e nm−2 that is found from the fit to our theory is a reasonable value. Fd-virus consists of a DNA strand that is covered by 2700 proteins, which carry a bare charge of 9.5 ± 0.5 negative elementary charges per nm. According to a calculation by Buitenhuis,28 about 90% of these groups at pH = 8.2 are dissociated, so that the total bare charge of an fd particle is equal to N = 7500 ± 400 e. A large fraction of this surface charge is neutralized by ion-condensation. According to Manning's ion-condensation theory,29,30 the ratio b/lB < 1 of the typical distance b = L/N between the charges on a cylindrical rod and the Bjrerrum length lB is equal to the fraction of bare charges that is not neutralized by condensed ions (for monovalent ions). Since lB = 0.71 nm for water at room temperature, it is found that b/lB is equal to 0.16 ± 0.01. The total number of charges close to the surface of an fd particle that determine the structure of the diffuse electric double layer is thus equal to 1239 ± 66, which corresponds to surface charge densities of 0.066 ± 0.004 e nm−2 (where the indicated error is certainly much smaller than the actual error that are implicit in the approximations made in the theory on which this estimate is based). This value of the surface charge density is in reasonable agreement with the experimentally found surface charge density of 0.050 ± 0.003. The surface charge density obtained from a fit to the same theory for very thin double layers gives a significantly lower surface charge density (see Table 1).
Within Manning's ion-condensation theory, there is no dependence of the number of condensed ions on the overall ionic strength, which suggests that the contribution of the condensed ions to the thermal diffusion coefficient is independent of the Debye length. The contribution of the condensed ions to DT is thus incorporated in the offset as introduced earlier, while the Debye-length dependence of DT is determined by the diffuse electric double layer.
6 Conclusion
In this work we explored the thermal diffusion behaviour of filamentous wild type fd-virus. These virus particles are used as a model system for very long and thin, and relatively stiff rod-like colloids. A theory is proposed, which predicts that the thermal diffusion coefficient of a rod is equal to that of a spherical bead with a diameter equal to that of the rod-core, and with the same surface charge density, multiplied by the aspect ratio of the rod (which is equal to the number of beads). Such a superposition of spherical beads to represent the thermal diffusion coefficient of a rod is accurate for arbitrary Debye lengths, including very thin double layers. Thermal diffusion coefficients are measured with Thermal Diffusion Forced Rayleigh Scattering (TDFRS), where an infra-red laser is used to create a temperature grating through the excitation of a vibrational mode of the water molecules. In a series of experiments the fd concentration and the Debye length were varied independently. We also performed experiments where the fd number concentration and the ionic strength are changed in combination, such that the effective volume fraction is fixed. Contrary to the mass diffusion coefficient, the thermal diffusion coefficient is found to be essentially independent of the fd concentration. The measured Soret coefficients are well described by the theory that we developed in this paper. Comparing with experiments, there are two adjustable parameters: the ionic-strength independent contribution to the Soret coefficient and the surface charge density. The surface charge density that we find from the fit with theory compares reasonably well with the theoretically predicted value.Future developments related to charged colloids could include (i) the extension of the theory beyond the Debye–Hückel approximation and (ii) the thermal diffusion of other types of non-spherical colloids, like disks, and of charged rods with varying flexibility.
Acknowledgements
We thank Pavlik Lettinga and Peter Lang for fruitful discussions and we are grateful for experimental advice from Donald Guu. We acknowledge financial support due to the Deutsche Forschungsgemeinschaft grant Wi 1684.References
- P. Polyakov, J. Luettmer-Strathmann and S. Wiegand, J. Phys. Chem. B, 2006, 110, 26215–26224 CrossRef CAS.
- H. Ning, J. K. G. Dhont and S. Wiegand, Langmuir, 2008, 24, 2426–2432 CrossRef CAS.
- P. Blanco, H. Kriegs, M. P. Lettinga, P. Holmqvist and S. Wiegand, Biomacromolecules, 2011, 12, 1602–1609 CrossRef CAS.
- Z. Wang, H. Kriegs and S. Wiegand, J. Phys. Chem. B, 2012, 116, 7463–7469 CrossRef CAS.
- S. Duhr and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19678–19682 CrossRef CAS.
- R. Piazza and A. Guarino, Phys. Rev. Lett., 2002, 88, 208302 CrossRef.
- R. Piazza, S. Iacopini and B. Triulzia, Phys. Chem. Chem. Phys., 2004, 6, 1616–1622 RSC.
- S. A. Putnam and D. G. Cahill, Langmuir, 2005, 21, 5317–5323 CrossRef CAS.
- E. Ruckenstein, J. Colloid Interface Sci., 1981, 83, 77–81 CrossRef CAS.
- K. Morozov, J. Magn. Magn. Mater., 1999, 201, 248–251 CrossRef CAS.
- E. Bringuier and A. Bourdon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 011404 CrossRef CAS.
- S. Fayolle, T. Bickel, S. Le Boiteux and A. Würger, Phys. Rev. Lett., 2005, 95, 208301 CrossRef.
- S. Duhr and D. Braun, Phys. Rev. Lett., 2006, 96, 168301 CrossRef.
- J. K. G. Dhont and W. J. Briels, Eur. Phys. J. E, 2008, 25, 61–76 CrossRef CAS.
- Z. Dogic and S. Fraden, in Phase Behavior of Rod-Like Viruses and Virus-Sphere Mixtures, ed. G. Gompper and M. Schick, Wiley-VCH, Weinheim, 2006, vol. 2, pp. 1–78 Search PubMed.
- M. Ripoll, P. Holmqvist, R. G. Winkler, G. Gompper, J. K. G. Dhont and M. P. Lettinga, Phys. Rev. Lett., 2008, 101, 168302 CrossRef CAS.
- K. G. Kang, M. P. Lettinga, Z. Dogic and J. K. G. Dhont, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 026307 CrossRef.
- K. Kang and J. K. G. Dhont, Soft Matter, 2010, 6, 273–286 RSC.
- J. X. Tang and S. Fraden, Biopolymers, 1996, 39, 13–22 CrossRef CAS.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS.
- K. Purdy, PhD thesis, Brandeis University, 2004.
- J. Sambrook and D. Russell, Molecular Cloning: A Laboratory Manual, Cold Spring Harbor Lab Press, New York, 2001 Search PubMed.
- P. Blanco and S. Wiegand, J. Phys. Chem. B, 2010, 114, 2807–2813 CrossRef CAS.
- J. K. G. Dhont, S. Wiegand, S. Duhr and D. Braun, Langmuir, 2007, 23, 1674–1683 CrossRef CAS.
- E. Verwey, J. Overbeek and J. Overbeek, Theory of the Stability of Lyophobic Colloids, Dover Publications, 1999 Search PubMed.
- L. Song, U. S. Kim, J. Wilcoxon and J. M. Schurr, Biopolymers, 1991, 31, 547–567 CrossRef CAS.
- P. Holmqvist, D. Kleshchanok and P. R. Lang, Langmuir, 2007, 23, 12010–12015 CrossRef CAS.
- J. Buitenhuis, Langmuir, 2012, 28, 13354–13363 CrossRef CAS.
- G. S. Manning, Berichte der Bunsengesellschaft für physikalische Chemie, 1996, 100, 909–922 CrossRef CAS.
- G. S. Manning, J. Phys. Chem. B, 2007, 111, 8554–8559 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2013 |
