Attenuated short wavelength buckling and force propagation in a biopolymer-reinforced rod
W. L.
Shan
ab,
Z.
Chen
c,
C. P.
Broedersz
d,
A. A.
Gumaste
b,
W. O.
Soboyejo
ab and
C. P.
Brangwynne
*e
aThe Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
bPrinceton Institute for the Science and Technology of Materials, Princeton University, Princeton, NJ 08544, USA
cDepartment of Biomedical Engineering, Washington University in St. Louis, St. Louis, USA
dLewis-Sigler Institute for Integrative Genomics and the Department of Physics, Princeton University, Princeton, NJ 08544, USA
eThe Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08544, USA. E-mail: cbrangwy@princeton.edu
First published on 16th October 2012
Abstract
We investigate short wavelength buckling of a thin elastic rod embedded in an elastic gelatin biopolymer network. Using a combination of micro-mechanical testing, microscopic imaging, as well as theory, we show that the buckling penetration depth can be tuned by varying the mechanical properties of the rod and the rod–gel interface. Prior models have predicted a decay length that is dependent on the nonlinear material response of the embedding media. Here we identify a regime where the decay length is governed by the ratio of the bending rigidity of the rod and the linear elastic response of the medium, and show that our experiments are in good quantitative agreement with such a linear model.
Mechanical instabilities such as buckling are manifested in many synthetic and natural systems. These phenomena range from wrinkling viscoelastic films1–5 and morphing of multi-stable structures6 to structuring of intestinal epithelia7 and compression of cytoskeletal biopolymers in living cells.8–10 For a slender rod which is axially compressed, Euler buckling occurs at a critical force, fc. Below this threshold, the rod experiences pure axial compression; as the force increases beyond the threshold, the rod enters a regime in which the total deformation energy is smaller if the rod bends according to a buckling mode with the longest possible wavelength, λ = 2L, where L is the length of the rod. However, if the rod is embedded in an elastic medium, its deformation energy must also be accounted for. Specifically, the presence of an elastic medium with a shear modulus, G, can reduce the buckling wavelength; the competition between the energy of a rod with bending rigidity κ and the elastic energy in the medium due to lateral deflections of the rod results in a buckling wavelength according to, λ ∼ (κ/G)1/4.11 The surrounding medium not only strongly reduces the buckling wavelength, but also increases the critical buckling force threshold. This mechanical reinforcement has important applications in fiber composite materials,12–14 and plays a key role in structural reinforcement of microtubules within living cells.8
Within cells, it was found that this reinforced buckling behavior only extends a finite range away from the site of force application.8 This decay in the buckling profile reflects a length scale for the range of force propagation along the rod, which has important implications for mechano-chemical signal transduction.15 Prior theoretical studies have predicted such a decay length scale for the buckling profile, but suggested the need for an embedding medium that exhibits substantial nonlinear elastic behavior.9 While strain-stiffening elastic behavior is common to many biopolymeric materials16–18 and may thus be relevant for reinforced buckling in living cells, controlled experimental studies of this effect are lacking. It is thus unclear if such nonlinear properties are a prerequisite for stress attenuation, and whether nonlinearities will govern this behavior under typical physiological strains within cells. Indeed, even ignoring the complex biological context of the cellular cytoplasm, the underlying physics of attenuated short-wavelength buckling, and the parameters that set the extent of force transmission, remain poorly understood.
Here, we elucidate the physics of short-wavelength attenuated buckling using a model system consisting of a slender rod embedded in an elastic biopolymeric gelatin medium. We find that the surrounding elastic medium gives rise to short wavelength buckling behavior, which is attenuated away from the site of force application. Using a numerical approach, we elucidate how this system is controlled through a combination of the linear longitudinal elastic coupling between the rod and the medium, and the bending rigidity of the rod. Furthermore, we show that for embedding media with strongly nonlinear behavior, the system can cross over to a regime in which the decay length is controlled by the nonlinear response of the medium,9 as may be relevant for strongly strain-stiffening materials.16–18 However, we use custom micromechanical measurements to show that, in our system, the linear elastic response of the medium dominates and is sufficient to quantitatively account for the observed buckling attenuation. To test the robustness of this model, we vary the rod diameter, and the degree of the longitudinal coupling, and obtain good agreement with analytical predictions. These results suggest a novel mechanism through which the range of force propagation can be tuned, which may have implications for stress propagation in living cells, and suggest new design principles for biologically inspired materials.
Materials and methods
To investigate the buckling behavior of elastically reinforced rods, we use superelastic nitinol wires (55% nickel, 45% titanium) with diameters 203.2 μm and 355.6 μm obtained from Small Parts, Inc. (Amazon.com); the wires were straightened and annealed by the manufacturer per ASTM F2063. We determined the Young's modulus, E, of the nitinol wires using an Instron Microtester 5848 (Norwood, MA); at room temperature we obtained E = 60.8 ± 1.0 GPa (mean ± standard deviation, N = 4 samples). For the embedding medium, we use porcine gelatin (Sigma Aldrich) at a concentration of 20 g L−1. A solution of 10 g gelatin powder is dispersed into 500 mL deionized water at 80 °C and is shaken mildly until the powder is fully dissolved. We estimate the shear modulus of our gels to be G ≈ 0.64 kPa.19 The samples consist of nitinol wires of length L = 21.5 cm and coaxial graduated cylinders of roughly the same length filled with gelatin solution, as shown in Fig. 1a. The samples are quickly cooled to, and held at 5 °C for 12–24 hours to allow for gelling; upon gelation, the gelatin becomes firmly attached to the walls of the cylinder. Since the mechanical properties of gelatin are sensitive to temperature history,19 the buckling samples were first exposed to room temperature for ∼5 hours. The embedded rod was compressed from one end by applying a concentrated force through a slender metallic adaptor with tip diameter slightly larger than the rod diameter, while the rod is supported at the other end. Compression is increased at a displacement rate ∼0.1 mm s−1 using a manually controlled micromanipulator incorporated in a home-built micro-testing setup. We use a Panasonic HD digital cameral (DMC-FZ100) to obtain digital images. Images are subsequently analyzed using custom image analysis algorithms developed in Matlab.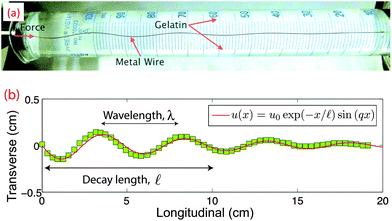 | ||
| Fig. 1 (a) Image of the experimental setup showing a compressed wire embedded in gelatin. (b) The deformation profile of the compressed wire in panel a, showing both short wavelength buckling and a decay length together with fit, as described in the main text. | ||
In order to probe the longitudinal coupling between the wire and the surrounding gelatin, pulling tests using the Instron Microtester 5848 were performed at a displacement rate of 0.1 mm s−1. In “rupturing” experiments, we reduce the as-prepared longitudinal coupling by pulling the wire to rupture the rod–gelatin interface completely. To investigate the microscopic details of the rod–gelatin interface, buckling samples were made which included dispersed microbeads with a 2 μm diameter, prepared within transparent polystyrene cuvettes (1.5 cm × 1.5 cm × 6 cm, Fisher Scientific). These samples were mounted onto a Nikon TE300 widefield fluorescence microscope equipped with a QImaging Retiga camera, driven by Slidebook software. During acquisition of time-lapse movies, the wire within the cuvette was pulled using an Eppendorf micromanipulator which was fixed to the exposed end of the wire. Particle Imaging Velocimetry image autocorrelation analysis was then performed using JPIV.20
Results and discussion
To evaluate the mechanical response and buckling profile of the rod in our system, we compress the rod by a longitudinal displacement of ∼1 mm at the free end. Consistent with previous studies,8 this elastically reinforced rod buckles at a reduced wavelength, and also adopts a profile for the transverse displacement that decays away from the site of compressive force application, as shown in Fig. 1a and b. We find that the transverse displacement, u(x), of the buckled rod is well described byu(x) = u0exp(−x/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )sin(qx), )sin(qx), | (1) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the decay length and q is related to the buckling wavelength through λ = 2π/q. For a rod diameter d = 203.2 μm, we obtain λ = 4.4 ± 0.3 cm and
is the decay length and q is related to the buckling wavelength through λ = 2π/q. For a rod diameter d = 203.2 μm, we obtain λ = 4.4 ± 0.3 cm and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 4.5 ± 0.4 cm (N = 14) (Fig. 2).
= 4.5 ± 0.4 cm (N = 14) (Fig. 2).
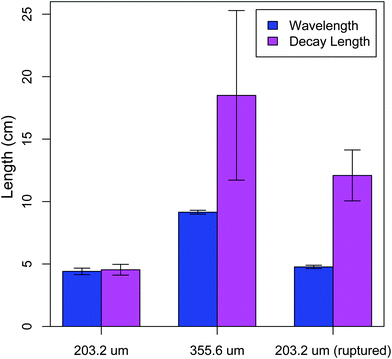 | ||
| Fig. 2 The buckling wavelength and decay length as determined from fitting the buckling profile. The samples include wires with diameters 203.2 μm and 355.6 μm with unperturbed and perturbed interfaces. The interface is ruptured by pulling the wire out of the gelatin under a tensile load until the load vanishes. | ||
To investigate how the buckling profile depends on the bending rigidity of the wire, we vary its diameter, d. For a rod diameter d = 355.6 μm, we obtain λ = 9.2 ± 0.2 cm, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 18.5 ± 6.8 cm (N = 6) (Fig. 2), implying that both characteristic length scales depend on the bending rigidity of the rod. The wavelength increase compared with that of a smaller diameter wire is roughly consistent with λ ∼ κ1/4 ∼ d, as described in prior work.9,11 However, the model in ref. 9 predicts a decay length that is controlled by the nonlinear elastic properties of the medium, which have not been varied in this experiment, even though the decay length increases roughly four-fold. Indeed, the biopolymeric gelatin used in these experiments as an embedding medium is only weakly nonlinear, calling into question this physical picture of the attenuation mechanism for these experiments.
= 18.5 ± 6.8 cm (N = 6) (Fig. 2), implying that both characteristic length scales depend on the bending rigidity of the rod. The wavelength increase compared with that of a smaller diameter wire is roughly consistent with λ ∼ κ1/4 ∼ d, as described in prior work.9,11 However, the model in ref. 9 predicts a decay length that is controlled by the nonlinear elastic properties of the medium, which have not been varied in this experiment, even though the decay length increases roughly four-fold. Indeed, the biopolymeric gelatin used in these experiments as an embedding medium is only weakly nonlinear, calling into question this physical picture of the attenuation mechanism for these experiments.
To provide insight into the origin of the buckling profile observed here, we develop a model that assumes only linear elasticity for the embedding medium. The energy functional for small rod deflections may be written as
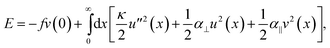 | (2) |
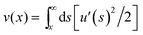 is the longitudinal displacement of an inextensible rod. The elastic coupling parameters α⊥ and α‖ are controlled by the dimensions of the rod and the gel's elasticity. For a straight rod of length L, diameter d with perfect coupling to an elastic medium: α⊥ = 4πG/ln(2L/d) and α‖ = α⊥/2.8,21 A similar model has been used to describe the behavior of microtubule biopolymers embedded in the cellular cytoskeleton;9 however, here we have not included a nonlinear response for the elastic medium. Motivated by the experimental finding that such constrained buckling is well-fit by eqn (1), we adopt this form as a variational ansatz for the buckling profile. This analysis yields a buckling wavelength, λ = 2π/(α⊥/κ)1/4 and a buckling force threshold, fc = 2(κα⊥)1/2—both independent of α‖—consistent with prior work.8,9,11 The predicted wavelengths, 5.2 cm and 9.0 cm, for the smaller and larger diameter wire, respectively, are in good agreement with the measured values (4.4 cm and 9.2 cm).
is the longitudinal displacement of an inextensible rod. The elastic coupling parameters α⊥ and α‖ are controlled by the dimensions of the rod and the gel's elasticity. For a straight rod of length L, diameter d with perfect coupling to an elastic medium: α⊥ = 4πG/ln(2L/d) and α‖ = α⊥/2.8,21 A similar model has been used to describe the behavior of microtubule biopolymers embedded in the cellular cytoskeleton;9 however, here we have not included a nonlinear response for the elastic medium. Motivated by the experimental finding that such constrained buckling is well-fit by eqn (1), we adopt this form as a variational ansatz for the buckling profile. This analysis yields a buckling wavelength, λ = 2π/(α⊥/κ)1/4 and a buckling force threshold, fc = 2(κα⊥)1/2—both independent of α‖—consistent with prior work.8,9,11 The predicted wavelengths, 5.2 cm and 9.0 cm, for the smaller and larger diameter wire, respectively, are in good agreement with the measured values (4.4 cm and 9.2 cm).
The decay length, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , characterizes the range of force propagation in the rod. To investigate the origins of the decay length and to understand how this model differs from previous work, we turn to a numerical approach to solve the model as described by eqn (2). We use a standard conjugate gradient method22 to minimize the energy functional and fit a decaying exponential to the envelope of the numerically obtained buckling profiles. We find that the decay length scales as
, characterizes the range of force propagation in the rod. To investigate the origins of the decay length and to understand how this model differs from previous work, we turn to a numerical approach to solve the model as described by eqn (2). We use a standard conjugate gradient method22 to minimize the energy functional and fit a decaying exponential to the envelope of the numerically obtained buckling profiles. We find that the decay length scales as ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∼ (κ/α∥)1/4, as shown in Fig. 3. This contrasts with a model previously described,9 that includes a nonlinear elastic response for the medium and predicts
∼ (κ/α∥)1/4, as shown in Fig. 3. This contrasts with a model previously described,9 that includes a nonlinear elastic response for the medium and predicts ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∼ (β/α∥)1/2, where β is the coupling constant for the nonlinear elastic energy,
∼ (β/α∥)1/2, where β is the coupling constant for the nonlinear elastic energy, 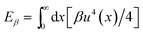 ; we confirmed that by including this term in our model, for large β the scaling of the decay length crosses over to a regime where
; we confirmed that by including this term in our model, for large β the scaling of the decay length crosses over to a regime where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∼ α−1/2∥.
∼ α−1/2∥.
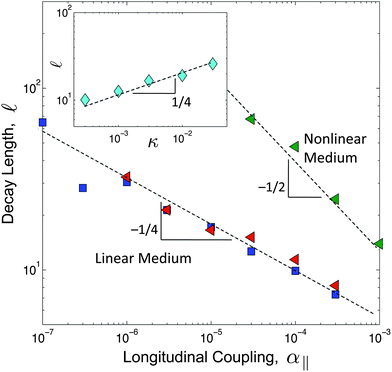 | ||
Fig. 3 Numerical results of the decay length as a function of the longitudinal coupling parameter, α‖. The decay length is determined by fitting a decaying exponential to the envelope of the buckling profile. We used chains of length L = 100![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, where the discretization scale is set as 0, where the discretization scale is set as ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 = 1 and the energy scale is set such that κ = 0.1. The different datasets correspond to β = 0 (blue squares), β = 0.1 (red triangles) and β = 1 (green triangles). Both κ and α⊥ = 5 × 10−3 have been held fixed. The inset shows the decay length as a function of κ, where the energy scale has been chosen such that α⊥ = 5 × 10−6. The parameters α‖ = 2.5 × 10−6 and β = 0, have been held fixed. 0 = 1 and the energy scale is set such that κ = 0.1. The different datasets correspond to β = 0 (blue squares), β = 0.1 (red triangles) and β = 1 (green triangles). Both κ and α⊥ = 5 × 10−3 have been held fixed. The inset shows the decay length as a function of κ, where the energy scale has been chosen such that α⊥ = 5 × 10−6. The parameters α‖ = 2.5 × 10−6 and β = 0, have been held fixed. | ||
From the data in Fig. 2, it is clear that the decay length scale depends not only on the degree of longitudinal coupling between the rod and the medium, but also on the wire diameter, consistent with the linear model described in eqn (2). However, the range over which these parameters need to be varied to verify the numerical predictions (Fig. 3) is not experimentally feasible. Instead, we sought to directly test the predicted force–compression profile of the linear medium model, which differs from the nonlinear medium model where β controls the force extension behavior.9 In the limit q![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≫ 1,23 the force profile
≫ 1,23 the force profile 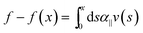 reduces to
reduces to
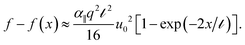 | (3) |
Importantly, this relationship suggest that the rod will only buckle over a distance ∼![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) measured from the point at which the load is imposed, beyond which the force falls below threshold such that f(
measured from the point at which the load is imposed, beyond which the force falls below threshold such that f(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) ≈ fc. This implies the following force–displacement relationships24
) ≈ fc. This implies the following force–displacement relationships24
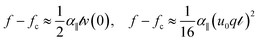 | (4) |
To test this prediction, we sought to measure α‖, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , and the force–compression profile in a series of independent experiments. We first measured α‖ using a pulling experiment in which a tensile force is applied at one end of the rod. This force–extension measurement indicates only weak strain-stiffening behavior of the medium at large rod displacements, as depicted in Fig. 4a. From this force–extension curve we obtain α‖ = 1.05 ± 0.12 kPa (N = 5) and 0.94 ± 0.02 kPa (N = 5) for the 203.2 μm and 355.6 μm thick wires, respectively; consistent with the expected weak logarithmic dependence of α‖ on the rod diameter, these values for α‖ are very similar. To directly visualize the mechanical coupling between the rod and the gelatin, we imaged the deformation profile within the surrounding medium using microscopic tracking of fluorescence probe particles embedded in the gelatin. Upon pulling or pushing the rod from one end, we find that the deformation of the medium follows the longitudinal movement of the rod, confirming tight elastic coupling between the rod and the medium (Fig. 4c).
, and the force–compression profile in a series of independent experiments. We first measured α‖ using a pulling experiment in which a tensile force is applied at one end of the rod. This force–extension measurement indicates only weak strain-stiffening behavior of the medium at large rod displacements, as depicted in Fig. 4a. From this force–extension curve we obtain α‖ = 1.05 ± 0.12 kPa (N = 5) and 0.94 ± 0.02 kPa (N = 5) for the 203.2 μm and 355.6 μm thick wires, respectively; consistent with the expected weak logarithmic dependence of α‖ on the rod diameter, these values for α‖ are very similar. To directly visualize the mechanical coupling between the rod and the gelatin, we imaged the deformation profile within the surrounding medium using microscopic tracking of fluorescence probe particles embedded in the gelatin. Upon pulling or pushing the rod from one end, we find that the deformation of the medium follows the longitudinal movement of the rod, confirming tight elastic coupling between the rod and the medium (Fig. 4c).
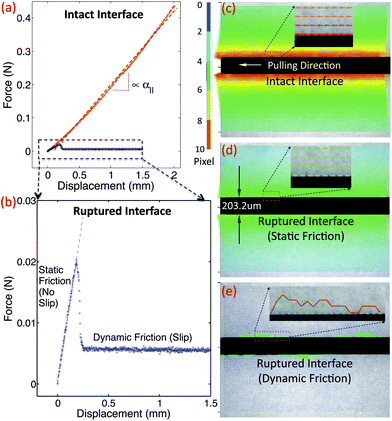 | ||
| Fig. 4 (a) Pulling load vs. displacement curve for as-prepared samples shows a linear longitudinal coupling (red). (b) Pulling load vs. displacement curve after interface rupture shows static and dynamic friction regimes. (c) The axis-symmetric displacement field before interface rupture, is similar to (d) the displacement field of the interface-ruptured rod before slip. (e) Once the pulling load exceeds the limit of static friction, the motion follows a stick-and-slip behavior along the interface, leaving traces of asperities moving together with the wire. | ||
To verify the dependence of α‖ on the mechanical coupling between the rod and the surrounding gelatin, we ruptured the rod–gelatin interface using large longitudinal wire displacements. After relaxing the wire to its original rest position, we studied the rod–gelatin interface using microscopic displacement mapping, as above. Somewhat surprisingly, we found that for small displacements, the gelatin appears to have firmly re-attached to the rod (Fig. 4d). The corresponding micro-testing results showed a reduced, yet nonzero, initial linear part in the force–displacement curve (Fig. 4b), with α‖ = 0.54 ± 0.03 kPa (N = 6) (wire diameter 203.2 μm); these data indicate a static friction regime for small displacement/strain. In contrast, fluorescence imaging revealed that at larger displacements, the rod decouples from the surrounding gelatin (Fig. 4e); here, we observe asperities along the unevenly ruptured rod–gelatin interface, which appear to contribute to the no-slip coupling observed under small displacement. Corresponding microtesting experiments show that for these large displacements, the load dropped to a level just above zero, reflecting a dynamic friction regime.
When we compressed and buckled these interface-ruptured rods, we still observed a finite decay length, which was approximately 2-fold larger than that found for the unperturbed interface, consistent with a decreased, but non-zero, value for α‖ (Fig. 2). To confirm that the microscopically observed asperities (as in Fig. 4e) dominate this remaining longitudinal coupling and, thus, the decay length, we wiped the surface of the interface-ruptured rod clean before the buckling experiment and observed a significantly increased decay length with large variation (data not shown). However, in all cases the wavelength was nearly identical (Fig. 2), suggesting that α⊥ remains essentially unchanged after rupture along the longitudinal direction, with or without surface asperities. These experiments show that the longitudinal mechanical response can be decoupled from the transverse mechanical response to tune the decay length.
These microtesting experiments show that the nonlinear material response of gelatin is weak (Fig. 4a). This suggests that the linear model described above, which only takes the contribution of the longitudinal mechanical coupling embodied in the linear modulus α‖, may be sufficient to account for the observed buckling attenuation. Using these precise measurements of the varied longitudinal coupling coefficient, α‖, we test this hypothesis using the predicted load–displacement behavior in the buckled regime (eqn (4)). The excess force beyond threshold, f − fc, is determined as a function of the longitudinal displacement, v(0), of the loaded end of the wire. These experiments are performed for the two different wire diameters, and show an approximately linear behavior, as depicted in Fig. 5. Importantly, the experimentally measured slope (f − fc)/v(0), should correspond to 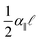 , which can be determined independently from pulling experiments (α‖) and by fitting the buckling profile (
, which can be determined independently from pulling experiments (α‖) and by fitting the buckling profile (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). We find excellent agreement between this prediction and the mechanical measurements, as shown in the inset of Fig. 5. This provides strong evidence that the buckling profile and mechanical behavior is well described by a model that includes only linear elastic behavior for the embedding medium.
). We find excellent agreement between this prediction and the mechanical measurements, as shown in the inset of Fig. 5. This provides strong evidence that the buckling profile and mechanical behavior is well described by a model that includes only linear elastic behavior for the embedding medium.
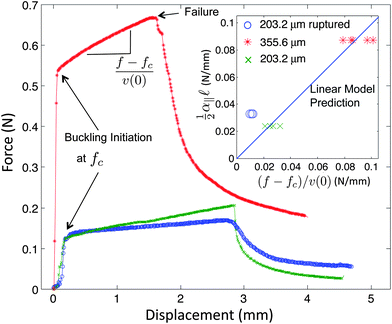 | ||
| Fig. 5 Load–displacement curves for buckling of nitinol wires with different diameters and longitudinal couplings. These curves all show three distinct deformation regimes: axial compression, short wavelength buckling, and catastrophic failure. The inset shows that the linear buckling slopes measured in micro-testing experiments are confirmed with predictions from eqn (4) for unperturbed cases with different wire diameters. However, wires with ruptured interfaces do not fit well if α‖ is interpreted as the linear slope of static friction. This shows that the effective α‖ is much lower than the static friction slope since the threshold for static friction has been exceeded and dynamic friction becomes relevant. | ||
Interestingly, rods with a pre-ruptured interface were less well-described by this model (inset of Fig. 5). By using α‖ from the initial slope in the static friction regime (Fig. 4e), the predicted decay length (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∼ 4.07 cm) was much smaller than the observed value of 12.09 ± 2.04 cm (N = 8). The effective value for α‖ ∼ 0.182 kPa determined from eqn (4), is thus lower than that determined from the static friction regime, α‖ = 0.54 kPa; this suggests that for this special case, the rod is not in a pure static friction regime during buckling. Consistent with this, the displacement threshold for static friction (∼250 μm, Fig. 4e) is much smaller than the maximum longitudinal displacement that occurs during buckling (∼2 mm, Fig. 5). Thus, although the buckling of rods with a perfect no-slip interface are well-described by the linear model, it appears to break down in the presence of more complicated stick–slip interfacial behavior.
∼ 4.07 cm) was much smaller than the observed value of 12.09 ± 2.04 cm (N = 8). The effective value for α‖ ∼ 0.182 kPa determined from eqn (4), is thus lower than that determined from the static friction regime, α‖ = 0.54 kPa; this suggests that for this special case, the rod is not in a pure static friction regime during buckling. Consistent with this, the displacement threshold for static friction (∼250 μm, Fig. 4e) is much smaller than the maximum longitudinal displacement that occurs during buckling (∼2 mm, Fig. 5). Thus, although the buckling of rods with a perfect no-slip interface are well-described by the linear model, it appears to break down in the presence of more complicated stick–slip interfacial behavior.
In conclusion, we have employed a combination of theoretical and experimental approaches to study the buckling behavior and force propagation of thin rods reinforced by a biopolymer matrix. We find that we can quantitatively account for the attenuated buckling behavior of thin rods reinforced by gelatin with a model that describes the no-slip coupling between the rod and medium within a linear framework; in contrast with previous work identifying a regime in which the decay length is controlled by the nonlinear response of the medium,9 here the decay length is controlled only by the linear longitudinal coupling to the medium and the rod's bending rigidity. We also identify a dynamic behavior where the rod and the gel are partially uncoupled and effective nonlinearities emerge from apparent stick–slip behavior at the interface, which appears to reflect a rich and more complex dynamical behavior of the microstructured interface. Future work will build on these results to understand the wrinkling and folding of elastic rods and plates,3–5,25,26 and may provide novel design principles for bio-inspired materials with applications in microfabrication and stretchable electronics.26,27
We thank Jesse Silverberg, Christopher Henley, Itai Cohen, Fred Mackintosh, and Moumita Das for helpful discussions. This work was supported in part by American Academy of Mechanics Founder's Award from the Robert M. and Mary Haythornthwaite Foundation (Z.C.), Society in Science – Branco Weiss fellowship, administered by ETH Zurich (Z.C.), a Lewis-Sigler fellowship (Ch.B.), and a Searle Scholar Award (Cl.B.).
References
- M. A. Biot, Proc. R. Soc. London, Ser. A, 1957, 242, 444–454 CrossRef CAS.
- L. Pocivavsek, R. Dellsy, A. Kern, S. Johnson, B. Lin, K. Y. C. Lee and E. Cerda, Science, 2008, 320, 912 CrossRef CAS.
- P. M. Reis, F. Corson, A. Boudaoud and B. Roman, Phys. Rev. Lett., 2009, 103, 045501 CrossRef CAS.
- J. Huang, B. Davidovitch, C. D. Santangelo, T. P. Russell and N. Menon, Phys. Rev. Lett., 2010, 105, 038302 Search PubMed.
- D. P. Holmes and A. J. Crosby, Phys. Rev. Lett., 2010, 105, 038303 CrossRef.
- Z. Chen, Q. Guo, C. Majidi, W. Chen, D. J. Srolovitz and M. P. Haataja, Phys. Rev. Lett., 2012, 109, 114302 Search PubMed.
- E. Hannezo, J. Prost and J. F. Joanny, Phys. Rev. Lett., 2011, 107, 078104 Search PubMed.
- C. P. Brangwynne, F. C. MacKintosh, S. Kumar, L. Mahadevan, N. Geisse, K. K. Parker, D. E. Ingber and D. A. Weitz, J. Cell Biol., 2006, 173, 733–741 CrossRef CAS.
- M. Das, A. J. Levine and F. C. MacKintosh, Europhys. Lett., 2008, 84, 18003 CrossRef.
- T. Li, J. Biomech., 2008, 41, 1711–1729 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Pergamon Press, Oxford, 1986 Search PubMed.
- M. Das and F. C. MacKintosh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061906 Search PubMed.
- B. Rosen, Fibre Composite Materials, Am Soc Metals, Metals Park, 1965, pp. 37–45 Search PubMed.
- X. Martinez and S. Oller, Arch. Comput. Meth. Eng., 2009, 16(4), 357–397 Search PubMed.
- S. Hu, J. Chen, B. Fabry, Y. Numaguchi, A. Gouldstone, D. E. Ingber, J. J. Fredberg, J. P. Butler and N. Wang, Am. J. Physiol., 2003, 285, C1082–C1090 CAS.
- M. L. Gardel, J. H. Shin, F. C. MacKintosh, L. Mahadevan, P. Matsudaira and D. A. Weitz, Science, 2004, 304, 1301 CrossRef CAS.
- C. Storm, J. J. Pastore, F. C. MacKintosh, T. C. Lubensky and P. A. Janmey, Nature, 2005, 435, 191–194 CrossRef CAS.
- B. Wagner, R. Tharmann, I. Haase, M. Fischer and A. R. Bausch, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13974 CrossRef CAS.
- J. D. Ferry, J. Am. Chem. Soc., 1950, 72(8), 3746–3752 Search PubMed.
- http://www.jpiv.vennemann-online.de/index.html .
- A. J. Levine, T. B. Liverpool and F. C. MacKintosh, Mobility of extended bodies in viscous films and membranes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 021503 CrossRef.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in C: The Art of Scientific Computing, Cambridge University Press, New York, NY, USA, 2nd edn, 1992 Search PubMed.
- As a consistency check, we confirmed that this assumption is valid for all experiments discussed here.
- For small deflections, v(0) ≈
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (qu0)2/8.
(qu0)2/8. - B. Audoly, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011605 CrossRef CAS.
- P. Kim, M. Abkarian and H. A. Stone, Nat. Mater., 2011, 10, 952–957 CrossRef CAS.
- J. A. Rogers, T. Someya and Y. G. Huang, Science, 2010, 327, 1603–1607 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2013 |
