Characterizing illusions of competence in introductory chemistry students
Samuel
Pazicni
* and
Christopher F.
Bauer
Department of Chemistry, University of New Hampshire, Durham, New Hampshire, USA. E-mail: sam.pazicni@unh.edu
First published on 14th October 2013
Abstract
The Dunning–Kruger effect is a cognitive bias that plagues a particular population of students – the unskilled. This population suffers from illusory competence, as determined by inaccurate ratings of their own ability/performance. These mistakenly high self-ratings (i.e. “illusions of competence”) are typically explained by a metacognitive deficiency of the unskilled – they simply can't recognize their own mistakes. This work, involving more than a thousand students, nine course sections, and sampling multiple time points over a semester, established the Dunning–Kruger effect as a robust phenomenon in university-level introductory chemistry. Using a combination of graphical analyses and hierarchical linear modeling, we confirmed that low-performing students tend to overestimate their own performance while high-performing students tend to underestimate their performance. We also observed a clear difference between female and male students with regard to these miscalibrations. Lastly, we demonstrated that student miscalibrations are invariant over time, a result that has profound implications for the types of instructor feedback conventionally provided in introductory chemistry courses.
Introduction
The fool doth think he is wise, but the wiseman knows himself to be a fool. (As You Like It, Act V:Sc. 1, line 30–31).Those of us who teach introductory chemistry courses are well aware that many students have a poor sense of their own ability, fail to engage early in the semester, underestimate the intellectual investment necessary, encounter a poor result on a first test, fail to act effectively on the resulting feedback, and spiral to an unsatisfactory outcome. This negative experience undoubtedly contributes to the exodus of students from STEM programs after only one year (or even one semester) of study.
We argue that a trigger for this lack of success is an illusion of competence. The initial misperception of ability is a well-documented social psychological phenomenon called the Dunning–Kruger effect (Kruger and Dunning, 1999; Ehrlinger and Dunning, 2003; Dunning, 2006a, 2006b). Specifically, students who perform very poorly in class grossly overestimate their relative standing and exam scores. Furthermore, lacking awareness of poor performance suggests that these students are not in a good position for taking corrective steps to improve. They don't know—and they don't know that they don't know. In other words, theses students lack metacognitive self-awareness about their weak understanding of chemistry and how to learn it. In this study, we demonstrate that the Dunning–Kruger phenomenon applies robustly to students in a typical university-level introductory chemistry (i.e. “General Chemistry”), track the progress of self-evaluation over a semester, explore the possibility of differences across student characteristics, and provide insight regarding what we as instructors might do to help students plagued by illusions of competence.
Background and theory
Interest in human self-evaluation has a long history in philosophy: “Know thyself” has attributions going back to the Greek philosophers and earlier. Self-evaluation has also received substantial attention in psychology and social psychology research, particularly in the last decade. Development of an understanding of the Dunning–Kruger effect has followed several lines of inquiry. Dunning and co-workers, in an evolving set of studies, have explored the phenomenon in predominantly clinical and non-academic settings to establish its nature and to identify the potential psychological and social mechanisms at work. They report the following important features of the phenomenon:• It occurs for a broad array of skills and knowledge, including: humor, logical reasoning, grammar (Kruger and Dunning, 1999); psychology exam performance, geography (Ehrlinger and Dunning, 2003); vocabulary, visual search tasks, ability to critique scientific research (Caputo and Dunning, 2005); class exams, debate performance, gun safety (Ehrlinger et al., 2008).
• Low-performing students show evidence of lacking or not engaging with metacognitive strategies that should adjust their self-perception (Kruger and Dunning, 1999; Dunning et al., 2004; Ehrlinger et al., 2008).
• Metacognitive training shows some sign of helping students better calibrate themselves (Kruger and Dunning, 1999, 2002).
• High-performing students lack other-awareness: they think that peers are smarter than they. When feedback is provided, however, they correct this negative self-perception (Kruger and Dunning, 1999, 2002).
• What one already believes about one's abilities in a particular field determines performance predictions rather than one's first hand experience with a task (Ehrlinger and Dunning, 2003; Crichter and Dunning, 2009). Women may underestimate performance even when they perform the same as men because they thought less of their ability (Ehrlinger and Dunning, 2003).
• Errors of omission (failure to explore alternative reasons for performance failures) create a bias in favor of perceived competence (Caputo and Dunning, 2005; Crichter and Dunning, 2009).
Dunning's claims have not been without challenge regarding the validity and etiology of the phenomenon. Krueger and Mueller (2002) and Ackerman et al. (2002) argued that the phenomenon is a statistical artifact of unreliable measures of ability (regression to the mean), as well as an example of people invoking the “better than average” heuristic in interpersonal comparisons. This criticism has been refuted convincingly by Dunning's group (Kruger and Dunning, 2002; Ehrlinger et al., 2008) and others (Mattern et al., 2010; Freund and Kasten, 2012). Thus, the Dunning–Kruger effect seems to be a real and pervasive human phenomenon (Dunning et al., 2003; Dunning, 2006a, 2006b, 2011). Ackerman and co-workers (Ackerman et al., 2002; Ackerman and Wolman, 2007), believing that the Dunning–Kruger argument shows an overly narrow and pessimistic picture of human intelligence, convinced off-the street participants to spend more than five hours responding to a broad set of surveys of cognitive abilities, reading characteristics, knowledge tests, and their confidence therein. Correlations suggested that individuals are fairly well calibrated in their perceptions of their understanding, although the authors (Ackerman et al., 2002) reported that business majors had the largest illusions of competence (i.e. an overestimated self-report when compared to objective knowledge). Self-estimates were most accurate regarding spatial ability, less so with math ability, and even less so with verbal ability. Self-estimates of content knowledge declined after experiencing content-area tests. Apparently, familiarity does breed contempt. The assessments used to estimate ability each consisted of six multiple-choice items from released Advanced Placement and College Level Experience Program tests. This population and setting are very different from the authentic classroom learning/assessment setting of our study.
The etiology of the Dunning–Kruger phenomenon has also been actively explored over the past decade. It is one example from a large literature on human self-comparison (Chambers and Windschitl, 2004). Many studies propose motivation as the source of biased judgments. Motivational arguments involve conscious and unconscious protection of self-image, e.g. dissonance reduction. Humans want to see themselves as knowledgeable and competent, and will respond in a way to minimize the perception of seeming the opposite (Blanton et al., 2001). Simply stated, inflating one's competency beliefs (employing the “better than average” heuristic), or downplaying/filtering the comparison population (“cherry-picking” data to compare one's self), makes us feel better about ourselves. Chambers and Windschitl (2004) in contrast posit that biased judgment is not just about affect but also about limitations on cognitive information processing: (1) egocentrism (self-relevant information given more weight), (2) focalism (target of question draws attention resources), (3) ill-defined comparison group, (4) ill-defined standard for judgment. In all of these cases, the information one considers or the bases for comparison are not all cognitively activated; thus, some piece of relevant information is not available when the judgment is made. Ehrlinger et al. (2008) provide evidence that the miscalibration phenomenon may not be caused simply by the motivation to be perceived well. When accountability to peers was manipulated experimentally, there was no difference in results. Furthermore, external incentives to encourage honest self-assessment (e.g. $100 reward) did not result in improved accuracy. Additional studies from this group (Ehrlinger and Dunning, 2003; Crichter and Dunning, 2009) support the idea that people base their self-perception on previously conceived beliefs about their skill and knowledge (a “top-down” perspective) and not necessarily on concrete experiences with using that skill and knowledge on a task (“bottom-up” cues). These authors manipulated belief by describing a common task as measuring either abstract reasoning ability (which subjects believed they possessed) or computer programming ability (which subjects believed they did not possess). They demonstrated that informing subjects of this distinction before the task affected their performance evaluation (inflated when they believed they were capable), but not if they were informed after doing the task (and before assessing performance).
Most of Dunning's work has been in non-academic settings. However, he has written about the implications of his work for education (Dunning et al., 2004), arguing for the importance of developing metacognitive awareness and skill, and for engaging peers in the process of assessment. Very few real classrooms have been studied and practically no rigorous investigations have occurred in the context of STEM education, reaffirming the value of the current study. In the last decade, only two educational psychology research groups contributed to publication threads concerning real classrooms. Hacker et al. (2000), in a single undergraduate educational psychology class, confirmed the miscalibration phenomenon and that prior beliefs concerning ability (but not prior performance) influence prediction accuracy. Bol et al. (2005) showed that neither self-calibration accuracy nor course performance improved with overt practice in making multiple self-judgments during the course of an education class. Providing opportunity for reflection led to a slight decline in calibration accuracy that was reversed by course point incentives to evaluate oneself fairly (Hacker et al., 2008). We note that the results of this study may have been affected by a ceiling effect in exam scores. Providing guidelines for reflection within a social group enhanced predictive accuracy for students in a high school biology course (Bol et al., 2012), confirming the potential beneficial role of peers. Nietfeld et al. (2006), again in a single undergraduate educational psychology class, tested the value of extensive self-monitoring and end-of-class exercises and discussion. A path analysis showed that this intervention had a significant effect on class performance, calibration, and self-efficacy (although inspection of the survey items suggests self-concept would be a better description). A similar improvement was found for fifth graders regarding reading comprehension (Huff and Nietfeld, 2009) when they were taught how to monitor comprehension and performance. Their confidence and calibrations improved, but not their reading comprehension.
These clinical and classroom studies suggest that whether feedback works to change calibration or performance depends on a complicated set of factors that have not yet been clearly delineated. Kitsantas and Zimmerman (2006) studied changes in dart-throwing performance by college students. Graphing the success rate and gradually increasing the standard of performance both improved self-efficacy and satisfaction with performance. It is notable that the control group in this study (who were not given the task of graphing nor were challenged by performance standards) did not spontaneously do anything on their own to monitor their performance. This suggests that effective self-monitoring may not be automatically engaged when performance results are received. Another study of German fifth graders working on orders of operation in mathematics (Labuhn et al., 2010) demonstrated that verbally-delivered information about standards of performance had no effect on performance, but that structured feedback helped ameliorate miscalibration issues (but did not improve performance). Another line of investigation explores counterfactual thinking in response to performance feedback, i.e. “If I had done X differently, my exam score would have been better” (Epstude and Roese, 2008; Petrocelli et al., 2012). There is disagreement, however, about whether generation of counterfactuals supports or inhibits improvement in academic performance. Regardless, the process of positing explanations for oneself may engage either or both of the motivational or informational processes described above.
In a very few recent cases, the Dunning–Kruger effect has been observed in chemistry learning environments. Potgieter et al. (2010) used prior performance in math and physics, and the extent of overconfidence regarding a chemistry pre-test to build a logistic regression model to predict likelihood of failing a first-semester chemistry course. They demonstrated 76% accuracy for this model for low-performing students. Bell and Volckmann (2011) compared student confidence in their understanding of specific topics at the end of a general chemistry course (using a Bloom-taxonomy-based knowledge survey) with their actual knowledge on the final exam. Their results confirmed the illusions of competence experienced by low performing students. Both of these chemistry studies relied on single point-in-time assessments.
Scope of this study
This contribution is the largest reported study of the Dunning–Kruger effect involving authentic classroom settings and assessments, and the first longitudinal study in STEM. The data set includes three separate measurements from over 1500 students in nine different General Chemistry course sections. This contrasts with the aforementioned chemistry studies by Potgieter et al. (2010) and Bell and Volckmann (2011) in which self-evaluations were done at single points in time before or after a single course. Because our data involve multiple time points, we can test hypotheses regarding change of self-assessment over time. Given previous evidence for differences between female and male students (Lundeberg et al., 1994; Ehrlinger and Dunning, 2003), we also investigated how sex influenced student performance perceptions and influenced change in these perceptions over time.Method
Research setting and student population
Student data were collected from a General Chemistry course over four years at a 4-year public research university with high research activity in the northeastern United States. This course is the first of a required two-semester sequence taken predominately by students in the physical sciences (about 10%), health sciences (about 20%), and biological sciences (about 60%). Topics covered in this course included chemical nomenclature, stoichiometry, solution chemistry, gases, thermochemistry, atomic theory, chemical bonding, and molecular structure. About 70% of the students were first-year students. The overall population consisted of 65% female and 35% male students. During each year of data collection, three or four lecture sections each enrolling 150–220 students were scheduled. The course involved either three fifty-minute or two eighty-minute lecture periods weekly along with a weekly three-hour hands-on laboratory. During this study, two instructors organized the lecture periods using a hybrid lecture/small group discussion approach. In some lecture sections, student response technology (“clickers”) was used. The text for the course was consistent across all semesters of data collection. Computer-based homework assignments were required, but different vendors were used over the period of data collection. In each class, three exams were given. Course exams required written problem solving and short answer essays graded with partial credit, and some multiple-choice questions. Exam means ranged from 49–70% raw score. Students were given their exams along with information on how to translate raw score to a grade. Information on how to interpret the scale and exam results were transmitted verbally in class by the instructor and were posted to the course website. In many ways, the course content, structure, and expectations were fairly representative of General Chemistry as it is taught in the United States.Data collection
A sheet of paper was attached to the last page of each of the three course exams. Written there were instructions directing students to “Estimate your ability in the subject of chemistry relative to the average student in this class by circling a percentile ranking.” A horizontal number line was presented from 1 (labeled with “I'm at the very bottom”) to 99 (labeled with “I'm at the very top”) in increments of 5. The median “50” was labeled “I'm exactly at the average”. Thus, students were asked to describe their level of understanding of chemistry in reference to the class population (i.e. predict their own percentile ranking). This is exactly the same procedure as used by Ehrlinger et al. (2008). Students were rewarded course bonus points for completing this self-evaluation page. Additional instructions indicated to students that this information would be separated from their exam and would not be consulted during grading. Once exams were graded, each student's exam score was converted to a percentile ranking. Thus, sets of (at most) three perceived/actual performance rankings for each student comprised the data set for this study.Data analysis and results
Graphical examination of data
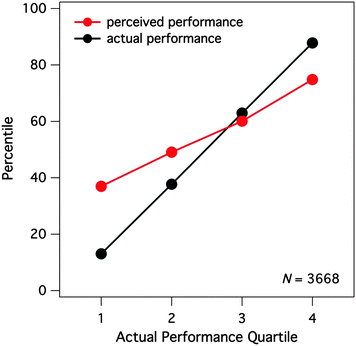
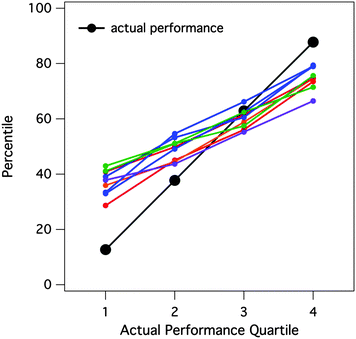
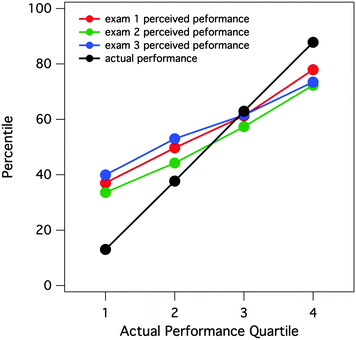
To gain insight into trends within our data prior to rigorous statistical treatment, we pooled perceived exam score/actual exam score pairs over all examination events and all nine classes. This resulted in 3668 perceived/actual score pairs, which we used to explore general trends within the data. First, we observed a clear average Dunning–Kruger effect occurring in this General Chemistry course (Fig. 1). In this figure, we have divided students based on their actual performance on exams, from the lowest 25% of performers to the highest 25%. As the figure illustrates, students in the lowest quartile greatly overestimated their performance on exams. Whereas their performance actually put them in the 15th percentile, their perceptions were placed in roughly the 40th percentile. In addition, students in the highest quartile slightly underestimated their performance on exams. While the students in this quartile performed at roughly the 90th percentile, their perceptions were placed in the 75th percentile. The high-performing students tended to underestimate their own performance less than the low-performing students overestimated their own performance. When this plot of perceived vs. actual percentile rankings is decomposed by class (Fig. 2), we observed that the Dunning–Kruger effect was consistent across all of the general chemistry classes in which data were collected.When this plot of perceived vs. actual percentile rankings is decomposed by examination event, we observe that the Dunning–Kruger effect is largely invariant over the course of the semester. Fig. 3 illustrates that the illusions of competence inherent in the lowest performing students persist over time from the first exam of the semester through the third exam. In fact, the students in the lowest-performing quartile appeared to be increasingly overestimating their actual performance as time passes. This preliminary analysis, however, only illustrated the stability of student perceptions over time as a function of quartile binning; it is not meant to suggest that the same students persisted in the same quartiles bins over all three exams. Subsequent analyses will more fully explore individual student change over time.
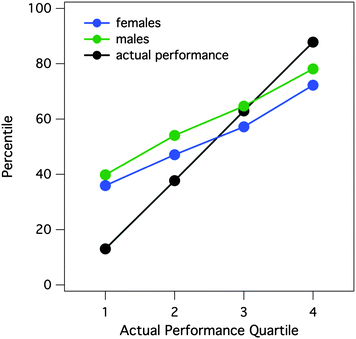
We also tailored this analysis to probe for differences between female and male students with regard to the overall Dunning–Kruger effect. Fig. 4 illustrates that even though the Dunning–Kruger effect was consistent for both sexes (i.e. students in the lowest quartile overestimated their performance while students in the highest quartile underestimated their performance), there is a clear sex difference. On average, male students tended to have a higher perception of their performance (regardless of whether they were a low- or a high-performing student) than females students. The difference in perception between male and female students was consistent across quartiles of performance, although the gap between sexes was smallest in the lowest quartile.
The miscalibration index
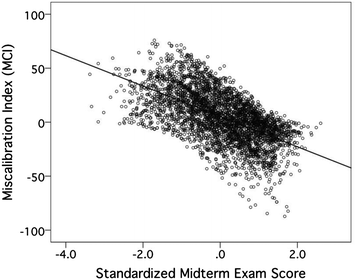
To quantify the Dunning–Kruger effect, we defined the difference between student's perceived exam percentile ranking and the student's actual percentile ranking as the miscalibration index (MCI) for the exam. A positive MCI therefore corresponded to an overestimation of performance, while a negative MCI corresponded to an underestimation. To validate the MCI as a quantitative measure of the Dunning–Kruger effect, we calculated Pearson correlations between students' MCIs and associated standardized exam scores. Standardized scores were used to control for the fact that, while exam content was consistent across the nine general chemistry classes in this study, exam questions and associated point allocations differed from semester to semester. Fig. 5 presents a scatter plot of MCI versus standardized midterm exam score, using data pooled over all classes and all exams. A clear relationship existed—students who performed poorly on exams tended to overestimate their performance (i.e. have positive MCIs), while students who performed well on exams tended to underestimate their performance (i.e. have negative MCIs). The Pearson correlation (two-tailed) between MCI and standardized exam score was r = −0.587, a strong relationship according to qualitative guidelines for interpreting the Pearson r (Cohen, 1988). This relationship between MCI and exam performance was consistent across exams (exam 1: r = −0.569, p < 0.001, n = 1263; exam 2: r = −0.560, p < 0.001, n = 1173; exam 3: r = −0.636, p < 0.001, n = 1232) and across sexes (females: r = −0.601, p < 0.001, n = 2322; males: −0.592, p < 0.001, n = 1209). Thus the MCI was a valid quantitative representation of the Dunning–Kruger effect.Hierarchical linear modeling of MCI over time
To investigate more rigorously how students' perceptions change over time and what factors may influence this phenomenon, a hierarchical linear model (HLM) was used (Raudenbush and Bryk, 2002). The data collected in this study were nested at different levels. At the top level, there were nine general chemistry classes; at the next level, there were a particular set of students within each class; and at the bottom level, three MCIs were calculated for each student. Because MCIs were nested within students, and students within classes, a typical regression would be violating assumptions of independence. As students repeatedly assessed their own performance over the course of this study, those repeated responses were not independent of one another. Also, since students in a particular class experienced only one type of class environment and were asked to judge their performance relative to that particular set of peers, the responses they gave as a result of being in the same class were not independent. Consider a set of MCIs from one class that is offset from those in another class because of some uncontrolled and unmeasured factor—this scenario would inflate the variance of the MCIs as a whole and make it harder to find the effect of any independent variable. Hierarchical linear modeling takes these issues into account, as these analyses estimate the variance associated with student/class differences in MCI and group differences in associations between predictors (sex, exam performance) and MCI. HLMs have become an important tool for investigating nested data in discipline-centered science education research, e.g. for students nested within physics classrooms (Tai and Sadler, 2001; Lawrenz et al., 2009), or for analyzing multiple measures of chemistry performance over time (Lewis and Lewis, 2008; Pyburn et al., 2013).| Description | Frequency | Percent (%) |
|---|---|---|
| Students with 3 MCI values | 910 | 59.3 |
| Students with 2 MCI values | 382 | 24.9 |
| Students with 1 MCI value | 174 | 11.3 |
| Students with no MCI data | 69 | 4.5 |
| MCI | Standardized exam means | |
|---|---|---|
| N | 3521 | 1408 |
| Mean | 4.78 | 0.027 |
| Standard deviation | 22.98 | 0.984 |
| Skewness | 0.079 (std. error = 0.041) | −0.267 (std. error = 0.065) |
| Excess kurtosis | −0.037 (std. error = 0.083) | −0.439 (std. error = 0.130) |
The extent to which assumptions of independence were violated in our nested data was evaluated by comparing the variance intrinsic to a particular level to the total variance in the data set. This ratio is known as the intraclass correlation, ρ (Raudenbush and Bryk, 2002, p. 36). Large intraclass correlations imply that the assumption of independence has been violated; i.e., that an HLM is more appropriate than a simple regression for analyzing the data. The intraclass correlation for the second level (between-students, ρ = 0.39) was large, indicating that including students as a random second-level unit was a valid choice. However, the intraclass correlation for the third level (between-classrooms, ρ = 0.01) was small, indicating that including classes as a random third-level unit would provide no clear advantage (i.e. there was no significant variability between the nine general chemistry classes used in this study, consistent with Fig. 2). Given that the variation in MCI values between classes was negligible, we revised our hypothesized model and employed a two-level HLM to analyze these data. This HLM was described by the following equations:
Level 1: within student
MCIij = π0j + π1j (time) + eij
Level 2: between students
π 0j = β00 + β01 (sex) + β02 (ExamAvg) + r0j
π 1j = β10 + β11 (sex) + β12 (ExamAvg) + r1j
At level one, MCIij was the miscalibration index corresponding to the perceived performance and actual performance on midterm exam i for student j; “time” was an ordinal variable that spanned from 0 (representing the first exam) to 2 (representing the third exam); π0j, the intercept, was the initial status (i.e. the first MCI) for student j; and π1j was the slope corresponding to the change in MCI over time. Deviations of individual MCI values for student j from π0j are represented by eij. Level-2 equations described the effect of student-level parameters (sex and mean exam performance) on MCI and the change in MCI over time. The equations were constructed to predict the intercept and slope of the level-1 equation from “sex” (a dichotomous dummy variable that was coded “0” for males and “1” for females) and “ExamAvg” (the mean exam score for student j, standardized to the grand mean of the student j's class). The mean initial status across all students is represented by β00, and the student-level effects of sex and mean exam performance on this initial status are given by β01 and β02, respectively. The mean rate of MCI change over time across all students is given by β10, and the student-level effects of sex and mean exam performance on this rate are given by β11 and β12, respectively. Deviation of student j's mean MCI from the overall grand mean is given by r0j. Finally, deviation of student j's rate of change from the overall mean rate is given by r1j.
| Fixed effect | Estimate | Standard error | Approx. df | t | p |
|---|---|---|---|---|---|
| Intercept, β00 | 7.21 | 0.941 | 3087 | 7.662 | <0.001 |
| Sex, β01 | −3.94 | 1.161 | 3072 | −3.392 | <0.001 |
| Mean exam performance, β02 | −10.55 | 0.560 | 3047 | −18.860 | <0.001 |
| Fixed effect | Estimate | Standard error | Approx. df | t | p |
|---|---|---|---|---|---|
| Intercept, β10 | 0.923 | 0.641 | 2408 | 1.440 | 0.150 |
| Sex, β11 | −0.286 | 0.789 | 2388 | −0.362 | 0.718 |
| Mean exam performance, β12 | −0.156 | 0.384 | 2392 | −0.407 | 0.684 |
Discussion and implications
The results presented here using multiple General Chemistry classes and a large set of students confirm and extend the observation of the Dunning–Kruger effect to the STEM college classroom environment. We found the general effect to be consistent across nine different classes—students who demonstrated low performance substantially overestimated what they knew, and those with high performance underestimated, but to a lesser degree. We observed that the perceptions of female students were less inflated than those of male students, consistent with prior work. We have also demonstrated robustly that students' perceptions were stagnant over time.The major implication of our findings is that student perceptions of their own performance in a course do not appear to be influenced by the feedback traditionally provided. In our research scenario, the main performance feedback mechanisms included exams and online homework assignments, both of which were graded and returned directly to students for review. We conjecture that instructors prefer to believe a large mismatch between a student's perceived performance and the student's actual performance (e.g. perceiving to be “average” while actually scoring in the 15th percentile) is a major impetus for change. This, however, does not appear to be the case. Students who harbored illusions of competence (i.e. who overestimated) on the first exam tended to do so throughout the semester; course feedback failed to lead these students toward more accurate self-insight. This observation is consistent with Crichter and Dunning's finding (2009) that concrete experiences with the task itself (so called “bottom-up” experiences) will not displace “top-down” preconceived notions concerning one's ability at the task.
We previously mentioned challenges to the validity of the Dunning–Kruger phenomenon and that these criticisms were convincingly refuted (Kruger and Dunning, 2002; Ehrlinger et al., 2008). One can ask whether our data and setting provided similar protections. The first criticism of the Dunning–Kruger effect was that low reliability in the measures of perceived ability would create the phenomenon as a statistical artifact via regression to the mean. Ehrlinger et al. (2008) refuted this criticism using test–retest data with correlations of 0.5. While we cannot estimate internal consistency and reliability for the measure of perceived ability used here, the measure was identical to that used in previous studies of the Dunning–Kruger effect. We can report, however, that perceived ability versus actual exam percentiles correlated more strongly than r = 0.50 (r = 0.60–0.66, p < 0.001) in our research scenario. A second criticism was that overestimation is more likely when assessments are perceived as too easy. While we did not directly survey students' perceptions regarding the difficulty of the midterm exams used in this study, we can report that the grand mean for midterm exams used in this study was 60.9% (SD = 5.95). This moderate exam average suggests a typical and not-too-easy level of challenge. In addition, the means of student exam self-ratings ranged from 41.5 to 62.1, meaning that students, on average, believed that they had performed better than only 40–60% of the class. If the midterm exams used here were perceived by students to be “easy”, average student self-ratings would have likely been much higher. A third criticism is that students may not be motivated to respond accurately regarding their ability. This criticism has been refuted by studies that investigated the effect of incentives (e.g. money) on calibration accuracy (Ehrlinger et al., 2008). For the present work, we asked students to comment on the reason for their rating. About 90% of participants did so, suggesting that they were sufficiently motivated by the prompt to give more than a perfunctory answer. Therefore, we feel confident that our data and design are providing valid information.
It is tempting to muse whether the quantification of students' performance miscalibrations presented here are overly precise. After all, miscalibration by a few points is far less meaningful in the context of a real course than gross miscalibrations such as a student believing he has passed an exam when, in fact, he has failed the exam. So, a practical question to ask in light of the data presented here is whether the illusions of competence possessed by low-skilled students are large enough to bring about pass/fail misjudgments. Our HLM results can be used to address this question. Let us consider the students whose exams scores were more than one standard deviation below the exam means. The classroom means of the midterm exams analyzed in this study ranged from 49.2% to 70.4%; subtracting associated standard deviations from these means yields a range of 29.8% to 51.4%—failing scores, by the standards of most instructors. Thus, exam scores one standard deviation below the mean are a reasonable approximation of “failing” in our research scenario. These failing scores corresponded to a mean percentile ranking of 17.4 (SD = 2.14). What is considered a “passing” exam score varies from instructor to instructor. For the sake of this argument, let a passing exam score be defined as >50%, which corresponds to a mean percentile ranking above 30.6 (SD = 10.9) on the midterm exams used in this study. The discussion of results in Table 3 reveal that, on average, students performing one standard deviation below an exam mean overestimate their performance by ∼16 points, assuming equal populations of men and women. Thus, students in our study who failed exams (ranking at approximately the 17th percentile) tended to provide self-rankings sixteen points higher (∼33rd percentile), which are more consistent with passing. Granted, surveying the pass/fail beliefs of students would provide more direct insight into this particular issue. However, the more quantitative work presented here highlights well the gross extent to which low-skilled students overestimate their own performance, consistent with pass/fail misjudgments.
Our suggestions for instructional intervention pertain most importantly to the students in the low performance/high self-perception category. The combination of doing poorly and being unaware of how poorly is not an advantageous position for a student to be in during the first semester of University study. There is some evidence that providing metacognitive training may help student calibrate themselves better (with the hope that doing so will motivate them to act to improve) (Kruger and Dunning, 1999; Hacker et al., 2000, 2008; Bol et al., 2005, 2012; Nietfeld et al., 2006; Huff and Nietfeld, 2009; Labuhn et al., 2010; Bercher, 2012; Ryvkin et al., 2012). For example, Bol et al. (2012) showed that calibration practice using guidelines improved accuracy; this improvement was intensified when participants practiced calibration in groups. Nietfeld et al. (2006) demonstrated the positive influence of metacognitive monitoring (using simple end-of-class worksheets) on student performance calibration. Further recommendations from Dunning et al. (2004) include:
• reviewing one's past performance, which has been shown to lead to better self-assessments of a variety of skills, including the interview skills of medical students (Ward et al., 2003) and student performance in a clinical dietitian course (Cochrane and Spears, 1980).
• benchmarking, i.e. comparing one's performance against that of others. A noteworthy study by Farh and Dobbins (1989) showed that students proofreading essays became better calibrated to their own ability after being presented with other students' editing efforts. This result by Farh and Dobbins and overall recommendation by Dunning suggests an additional benefit for incorporating classroom activities like Calibrated Peer Review (Russell, 2004) or writing-to-teach (Vázquez et al., 2012), which incorporate peer-review of writing in chemistry courses.
It was also been suggested that peer predictions of achievement are often more accurate than self-predictions because a peer is more likely to downgrade one's aspirations and place more emphasis on one's past performance when making a judgment (Helzer and Dunning, 2012). This finding may have interesting implications for peer-based activities that have gained popularity in introductory chemistry, such as Process-Oriented Guided Inquiry Learning (POGIL) and Peer-Led Team Learning (PLTL). For example, peer interactions facilitated by these methods may indirectly provide students with achievement predictions external to the self. Further work, however, will be necessary to determine if methods like POGIL or PLTL have effects on assuaging students' illusions of competence.
Lastly, is it important to note that being overconfident may not necessarily be detrimental. Self-efficacy is a significant component of motivation, and so higher efficacy (even if misplaced) may sustain motivation to put in the effort that ultimately leads to greater success. Mattern et al. (2010) replicated the Dunning–Kruger effect using data from hundreds of thousands of students who took the SAT, comparing Math Section scores with a survey question about perceived math ability. They also obtained data regarding student persistence and graduation from college. Using hierarchical logistic regression, they demonstrated that students with higher self-estimates of ability had a slightly higher chance of persisting to the fourth year of college, of graduating, and of having a higher grade point average. In some cases, low performing over-estimators did just as well as higher performing students who underestimated themselves. This result suggests that classroom interventions aimed at helping low-performing students to recognize their illusions of competence should also simultaneously provide mechanisms for addressing deficits.
References
- Ackerman P. L., Beier M. E. and Bowen K. R., (2002), What we really know about our abilities and our knowledge, Pers. Indiv. Differ., 33, 587–605.
- Ackerman P. L. and Wolman S. D., (2007), Determinants and validity of self-estimates of abilities and self-concept measures, J. Exp. Psychol: Applied, 13(2), 57–78..
- Bell P. and Volckmann D., (2011), Knowledge Surveys in General Chemistry: Confidence, Overconfidence, and Performance, J. Chem. Educ., 88(11), 1469–1476.
- Bercher D. A., (2012), Self-monitoring tools and student academic success: when perception matches reality, J. Coll. Sci. Teach., 41(5), 26–32.
- Blanton H., Pelham B. W., DeHart T. and Carvallo M., (2001), Overconfidence as dissonance reduction, J. Exp. Soc. Psychol., 37(5), 373–385.
- Bol L., Hacker D. J., O'Shea P. and Allen D., (2005), The influence of overt practice, achievement level, and explanatory style on calibration accuracy and performance, J. Exp. Educ., 73(4), 269–290.
- Bol L., Hacker D. J., Walck C. C. and Nunnery J. A., (2012), The effects of individual or group guidelines on the calibration accuracy and achievement of high school biology students, Contemp. Educ. Psychol., 37(4), 280–287.
- Caputo D. and Dunning D., (2005), What you don't know: the role played by errors of omission in imperfect self-assessments, J. Exp. Soc. Psychol., 41(5), 488–505.
- Chambers J. R. and Windschitl P. D., (2004), Biases in social comparative judgments: the role of nonmotivated factors in above-average and comparative-optimism effects, Psychol. Bull., 130(5), 813–838.
- Cochrane S. B. and Spears M. C., (1980), Self-assessment and instructor's ratings: a comparison, J. Am. Diet. Assoc., 76, 253–255.
- Cohen J., (1988), Statistical power analysis for the behavioral sciences, 2nd edn, Hillsdale, NJ: Lawrence Erlbaum Associates.
- Cohen J., Cohen P., West S. G. and Aiken L. S., (2003), Applied multiple regression/correlation analysis for the behavioral sciences, 3rd edn, Mahwah, NJ: Lawrence Erlbaum Associates.
- Crichter C. R. and Dunning D., (2009), How chronic self-views influence (and mislead) self-assessments of task performance: self-views shape bottom-up experiences with the task, J. Pers. Soc. Psychol., 97(6), 931–945.
- Dunning D., (2006a), Strangers to ourselves? Psychologist, 19(10), 600–603.
- Dunning D., (2006b), Not knowing thyself, Chronicle of Higher Education: The Chronicle Review, 52(35), B24.
- Dunning D., (2011), The Dunning-Kruger effect: on being ignorant of one's own ignorance, in Olson K. M. and Zanna M. P. (ed.), Advances in Experimental Social Psychology, Orlando, FL: Academic Press, vol. 44, pp. 247–296.
- Dunning D., Heath C. and Suls J. M., (2004), Flawed self-assessment: implications for health, education, and the workplace, Psychol. Sci. Publ. Interest, 5(3), 69–106.
- Dunning D., Johnson K., Ehrlinger J. and Kruger J., (2003), Why people fail to recognize their own incompetence, Curr. Dir. Psychol. Sci., 12(3), 83–87.
- Ehrlinger J. and Dunning D., (2003), How chronic self-views influence (and potentially mislead) estimates of performance, J. Pers. Soc. Psychol., 84(1), 5–17.
- Ehrlinger J., Johnson K., Banner M., Dunning D. and Kruger J., (2008), Why the unskilled are unaware: further explorations of (absent) self-insight among the incompetent, Organ. Behav. Hum. Decis. Process., 105(1), 98–121.
- Epstude K. and Roese N. J., (2008), The functional theory of counterfactual thinking, Pers. Soc. Psychol. Rev., 12(2), 168–192.
- Farh J. L. and Dobbins G. H., (1989), Effects of comparative performance information on the accuracy of self-ratings and agreement between self- and supervisor ratings, J. Appl. Psychol., 74, 606–610.
- Freund P. A. and Kasten N., (2012), How smart do you think you are? A meta-analysis on the validity of self-estimates of cognitive ability, Psychol. Bull., 138(2), 296–321.
- Hacker D. J., Bol L. and Bahbahani K., (2008), Explaining calibration accuracy in classroom contexts: the effects of incentives, reflection, and explanatory style, Metacogn. Learn., 3(2), 101–121.
- Hacker D. J., Bol L., Horgan D. D. and Rakow E. A., (2000), Test prediction and performance in a classroom context, J. Educ. Psychol., 92(1), 160–170.
- Helzer E. G. and Dunning D., (2012), Why and when peer prediction is superior to self-prediction: the weight given to future aspiration versus past achievement, J. Pers. Soc. Psychol., 103(1), 38–53.
- Huff J. D. and Nietfeld J. L., (2009), Using strategy instruction and confidence judgments to improve metacognitive monitoring, Metacogn. Learn., 4, 161–176.
- Kitsantas A. and Zimmerman B. J., (2006), Enhancing self-regulation of practice: the influence of graphing and self-evaluative standards, Metacogn. Learn., 1(3), 201–212.
- Krueger J. and Mueller R. A., (2002), Unskilled, unaware, or both? The better-than-average heuristic and statistical regression predict errors in estimates of own performance, J. Pers. Soc. Psychol., 82(2), 180–188.
- Kruger J. and Dunning D., (1999), Unskilled and unaware of it: how difficulties in recognizing one's own incompetence lead to inflated self-assessments, J. Pers. Soc. Psychol., 77(6), 1121–1134.
- Kruger J. and Dunning D., (2002), Unskilled and unaware – but why? A reply to Krueger and Mueller (2002), J. Pers. Soc. Psychol., 82(2), 189–192.
- Labuhn A. S., Zimmerman B. J. and Hasselhorn M., (2010), Enhancing students' self-regulation and mathematics performance: the influence of feedback and self-evaluative standards, Metacogn. Learn., 5(2), 173–194.
- Lawrenz F., Wood N. B., Kirchhoff A., Kim N. K. and Eisenkraft A., (2009), Variables affecting physics achievement, J. Res. Sci. Teach., 46, 961–976.
- Lewis S. E. and Lewis J. E., (2008), Seeking effectiveness and equity in a large college chemistry course: an HLM investigation of peer-led guided inquiry, J. Res. Sci. Teach., 45, 794–811.
- Lundeberg M. A., Fox P. W. and Punćochaŕ J., (1994), Highly confident but wrong: gender differences and similarities in confidence judgments, J. Educ. Psychol., 86(1), 114–121.
- Mattern K. D., Burrus J. and Shaw E., (2010), When both the skilled and unskilled are unaware: consequences for academic performance, Self Identity, 9(2), 129–141.
- Nietfeld J. L., Cao L. and Osborne J. W., (2006), The effect of distributed monitoring exercises and feedback on performance, monitoring accuracy, and self-efficacy, Metacogn. Learn., 1, 159–179.
- Petrocelli J. V., Seta C. E., Seta J. J. and Prince L. B., (2012), “If only I could stop generating counterfactual thoughts”: when counterfactual thinking interferes with academic performance, J. Exp. Soc. Psychol., 48(5), 1117–1123.
- Potgieter M., Ackermann M. and Fletcher L., (2010), Inaccuracy of self-evaluation as additional variable for prediction of students at risk of failing first-year chemistry, Chem. Educ. Res. Pract., 11(1), 17–24.
- Pyburn D. T., Pazicni S., Benassi V. A. and Tappin, E. E., (2013), Assessing the relation between language comprehension and performance in general chemistry, Chem. Educ. Res. Pract., 14, 524–541.
- Raudenbush S. W. and Bryk A. S., (2002), Hierarchical linear models: applications and data analysis methods, 2nd edn, Thousand Oaks, CA: Sage.
- Russell A. A., (2004), Calibrated Peer Review: A Writing and Critical-Thinking Instructional Tool, Invention and Impact: Building Excellence in Undergraduate Science, Technology, Engineering and Mathematics (STEM) Education, Washington, DC: AAAS, pp. 67–71.
- Ryvkin D., Krajc M. and Ortmann A., (2012), Are the unskilled doomed to remain unaware? J. Econ. Psychol., 33(5), 1012–1031.
- Tabachnick B. G. and Fidell L. S., (2013), Using Multivariate Statistics, 6th edn, Boston, MA: Pearson.
- Tai R. H. and Sadler P. M., (2001), Gender differences in introductory undergraduate physics performance: University physics versus college physics in the USA, Int. J. Sci. Educ., 23, 1017–1037.
- Vázquez A. V., McLoughlin K., Sabbagh M., Runkle A. C., Simon J., Coppola B. P. and Pazicni S., (2012), Writing-to-teach: a new pedagogical approach to elicit explanative writing in undergraduate chemistry students, J. Chem. Educ., 89, 1025–1031.
- Ward M., MacRae H., Schlachta C., Mamazz J., Poulin E., Reznick R. and Regehr G., (2003), Resident self-assessment of operative performance, Am. J. Surg., 1985(6), 521–524.
| This journal is © The Royal Society of Chemistry 2014 |