Edge-, width- and strain-dependent semiconductor–metal transition in SnSe nanoribbons

Abstract

First-principles calculations were employed to explore the electronic properties of SnSe nanoribbons. Our results showed that a semiconductor–metal or metal–semiconductor transition can be realized in SnSe nanoribbons by controlling the edge shape, width parameter and different levels of strain. It was found that the transition always occurs in SnSe nanoribbons with a zigzag edge (ZNR). With the width parameter of ZNRs less than 8, their optimized structures are perfect (P-structures) without any Sn–Se bond breaking and the electronic calculations demonstrate they display a metallic character. However, the structures became deformed (D-structures) with some Sn–Se bond rupture when tensile strain was applied, accompanied by the transition occurring from metal to indirect band gap semiconductors. On the other hand, compressive strain cannot induce the metal–semiconductor transition as ZNRs still keep their P-structures. With the width parameter greater than or equal to 8, ZNRs change to D-structure exhibiting a semiconductive feature at equilibrium state. The semiconductor–metal transition cannot be induced through applying tensile strain while a certain extent of compressive strain can trigger it. The localized–delocalized partial charge distribution of the conduction band minimum near the strained domains can be used to explain the metal–semiconductor or semiconductor–metal transition in SnSe ZNRs. Our results suggest that the SnSe ZNRs have potential applications in nanoelectromechanical sensors and switches, which will promote further experimental investigations on SnSe and other fascinating graphene-like metal chalcogenides.

---

1. Introduction

As we know, 1-dimensional (1D) nanostructures such as nanorods, nanotubes, nanowires, nanoribbons, and nanobelts have shown novel properties due to the low dimensionality and quantum confinement effect. The most representative example is graphene nanoribbons which have been found to possess unusual magnetic properties¹ and versatile electronic structures² in the absence of any impurities. Recently, other types of material with graphene-like structures, i.e., BN,³ MoS₂,⁴ ZnS⁵ and ZnO⁶ have received extensive attention. Compared to graphene with a zero band gap, the electronic properties of these graphene-like materials are more likely to be modulated. It was shown that graphene-like 1D nanoribbons exhibit different magnetic properties and band structures depending on the edge structure, width parameter, defects and doping as well as the external field, etc., and that these properties are totally different to their bulk structures.^3–8

For example, by using first-principles calculations, Li et al.⁴ found that MoS₂ ZNRs are ferromagnetic metals irrespective of the ribbon width and thickness. However, MoS₂ nanoribbons with an armchair edge (MoS₂ ANRs) are nonmagnetic and semiconducting, and their energy gaps depend on the width parameters. Lu et al.⁷ showed that strain can greatly affect the electronic and magnetic properties of MoS₂ monolayers, bilayers, nanoribbons and nanotubes. Theoretical investigations of Ma et al.⁸ on VX₂ (X = S, Se) monolayers indicated that VX₂ monolayers are ferromagnetic and that the magnetic moments can increase rapidly with the increase of isotropic strain from −5% to 5%. With different percentages of hydrogenation, the BN zigzag nanoribbons present various electronic and magnetic properties, which endows BN nanomaterials with many potential applications in novel integrated functional nanodevices.⁹ Inorganic nanoribbons (such as BN, AlN, GaN, SiC and ZnO) with unpassivated zigzag edges can lead to spin-splitting of energy bands, and possible structural reconstruction at unpassivated edges can greatly affect their electronic properties.¹⁰

IV–VI group semiconductors, such as SnS_x and SnSe_x (x = 1, 2), have layered graphene-like structures.^11–13 Owing to their interesting electronic and optical properties, they have attracted considerable attention in both experimental and theoretical fields.^14–20 As a typical IV–VI group semiconductor, SnSe belongs to the orthorhombic crystal system which resembles a distorted NaCl structure. The indirect band gap of 0.90 and direct band gap of 1.30 eV of SnSe¹⁷ happens to fall within the range of 1.0 to 1.5 eV, which is the best band gap scope for solar cells, leading to widespread interest in the research of its potential applications for optical devices.^21–23 As an earth-abundant and environmentally friendly material, the majority of research involved in SnSe has mainly focused on its synthesis and properties.^{13,17,18,21–26} Since little literature concerns SnSe 1D nanostructures, especially the modulation of the electronic structures, in this work, the difference in the electronic properties of 1D SnSe with the variation of edge shape, width and strain were systematically explored by theoretical means. Our results showed that all the nanoribbons are nonmagnetic. Among these, ANRs are semiconductors, and their electronic structures are less sensitive to their geometries. Interestingly, ZNRs exhibit diverse electronic properties: a metal–semiconductor transition can be triggered when the width parameter reaches a critical point of 8. As for one specific ZNR, the metal–semiconductor or semiconductor–metal transition can be realized by applying different uniaxial strain.

2. Computational details

Our first-principles calculations are based on density functional theory (DFT) using the projector-augmented plane wave (PAW)²⁷ method to model the ion–electron interaction as implemented in the Vienna ab initio simulation package (VASP).^28–30 In all calculations, generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE)^31,32 functional and a 300 eV energy cutoff for plane-wave basis set was adopted. The 1D Brillouin zone sampling for geometry optimizations was carried out using a 7 Monkhost–Pack³³ k-points grid. During the computation of electronic band structures, 21 k-points were used. Energy cutoff and k-point settings are proven to be sufficient for achieving converged results (see Table S1 in ESI†). The convergence threshold was 10⁻⁵ eV for energy and 10⁻² eV Å⁻¹ for force.

SnSe nanoribbons were constructed by cutting from a single layer of SnSe (100) with the desired widths and edges. In order to simulate infinitely long nanoribbon systems, we used a 1-D periodic boundary condition (PBC) along the growth direction of the nanoribbons. To avoid interaction between the nanoribbons, the periodically repeated supercells we constructed here were large enough to ensure that the vacuum space was at least 10 Å. For all the nanoribbons, both spin-unpolarized and spin-polarized calculations were performed to determine the ground state. Our results showed that all of them are nonmagnetic, as revealed by the lower energy of the spin-unpolarized computation, thus only spin-unpolarized results were presented in this work.

3. Results and discussion

3.1 Bulk SnSe

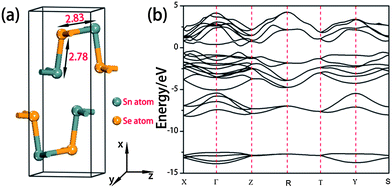
It is necessary to optimize the structure of bulk SnSe first because the structures of the SnSe nanoribbons used in this paper were cut from it. The optimized lattice parameters are a = 11.68 Å, b = 4.23 Å, and c = 4.50 Å (Fig. 1a), which are in good agreement with the experimental values (a = 11.55 Å, b = 4.16 Å, and c = 4.45 Å).¹⁸ The Sn–Se bond lengths, 2.78 and 2.83 Å (Fig. 1a), are slightly longer than the values (2.74 and 2.79 Å) reported in ref. 17. The calculated electronic structure demonstrates that bulk SnSe is a semiconductor with an indirect band gap of 0.78 eV (Fig. 1b), which is smaller than the experimental value (about 1.0 eV).³⁴ This deviation is caused by the fact that the DFT–PBE method tends to underestimate the band gap.⁷

Fig. 1 The geometry (a) and electronic structure (b) of bulk SnSe.

3.2 Zigzag and armchair edges of SnSe nanoribbons with different widths

To investigate the effect of the edge shape on the electronic properties of SnSe nanoribbons, two different edges of terminations, named zigzag and armchair, were constructed, as shown in Fig. 2. The width parameters are defined according to the previous convention of graphene nanoribbons.^35–37 In this work, ZNRs with a width (N_Z) from 5 to 10 and ANRs with a width (N_A) from 9 to 14 were selected to investigate the effect of the width parameter on the electronic properties.

Fig. 2 The structures of SnSe zigzag (left panel) and armchair (right panel) nanoribbons before relaxation, and the definitions of the width parameters.

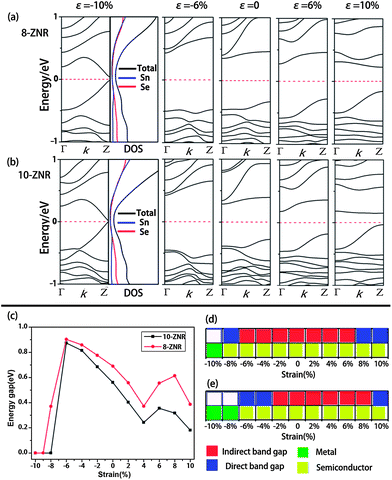
Interestingly, the ZNRs present two types of structure after full relaxation with the variation of the width parameters: i.e., perfect structures (denoted as P-structures hereafter) without any bond breaking when the width parameter is less than 8 (Fig. 3a) and deformed structures (D-structures) with some Sn–Se bond rupture when the width parameter is greater than or equal to 8 (Fig. 3b). For both types of structures, the Sn–Se bond lengths are in the range of 2.76–2.86 Å, which are close to the ones in the bulk SnSe. For the broken domains, the Sn–Se distances elongate to more than 3.00 Å. The different geometries of SnSe nanoribbons give rise to the distinct electronic structures. As illustrated in Fig. 3c, the ZNRs with P-structures are proven to be metals because there are electronic states which cross the Fermi level, while the ZNRs with D-structures display a typical semiconductor character as the Fermi level is located within the limits of the forbidden band. Scrutinizing the band structures shown in Fig. 3c, we can see that the bottom of the conduction band is located at the Γ point (ΓL) and the valence band edge is located at the Z point (ZH), which indicates an indirect gap character. With the increase in width, the point of ZH shifts upward while the ΓL point shifts downwards, leading to the energy gaps decreasing from 0.69 to 0.61 and 0.56 eV as the width parameters increase from 8 to 9 and 10 (Fig. 3c).

Fig. 3 Two types of structure of SnSe ZNRs after full relaxation: (a) P-structure when N_Z < 8 and (b) D-structure when N_Z ≥ 8. The electronic structures of ZNRs with 5 ≤ N_Z ≤ 10 are displayed in (c).

To gain further understanding of the physical origin of the electronic properties dependent on structure, the partial density of states (PDOS) of SnSe ZNRs were calculated. Here we only chose 7- and 8-ZNR as representative examples, as the metal–semiconductor transition occurs when the critical width of 8 is reached. As seen in Fig. 4a, for 7-ZNR, the coupling between the Sn atom s and p orbitals and the Se p orbital contributes to both the valance band maximum (VBM) and conduction band minimum (CBM). For 8-ZNR, although the VBM is contributed to by the same coupling as seen in 7-ZNR, the CBM composition is different. The main difference is the lack of Sn atom s orbital contribution (Fig. 4b). This is in accordance with the analysis of the partial charge distribution of VBM and CBM, which will be discussed later.

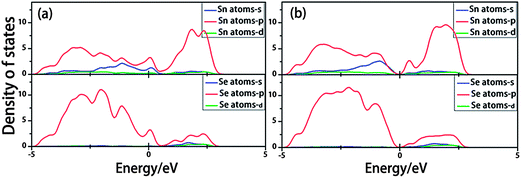Fig. 4 The partial density of states (PDOS) of 7-ZNR (a) and 8-ZNR (b). The blue, red and green lines represent the s, p and d orbitals, respectively.

For another type of nanoribbon with armchair edges, they all display D-structures as the edge atoms are split from the inner sites after geometry optimization, irrespective of the width parameter (Fig. 5a and b). The Sn–Se bond lengths vary in a wider range of 2.67–2.95 Å compared to those in ZNRs and the distances for the broken Sn–Se bonds are greater than 3.10 Å. Electronic structure calculations showed that these ANRs are semiconductors with indirect band gaps (Fig. 5c), and the energy gaps slightly decrease with the increase of width (Fig. 5d).

Fig. 5 The structure of 10-ANR with top view (a) and side view (b). The electronic structures of ANRs with 9 ≤ N_A ≤ 14, and the energy gaps as a function of ribbon width are shown in (c) and (d), respectively.

3.3 Effect of strain on the SnSe ZNRs

Here, the effect of strain on ZNRs was only investigated based on two considerations. First of all, the electronic properties of ANRs are less sensitive to the difference in the geometries. Secondly, our test calculations showed that they are also insensitive to the strain, which is distinct from graphene ANRs³⁸ whose energy gaps are strongly dependent on the strain. The 5-, 7-ZNRs with P-structures and the 8-, 10-ZNRs with D-structures were chosen as examples.

As demonstrated above, SnSe ZNRs with P-structures are metals (N_Z < 8). When subjected to a uniaxial tensile strain, they change to D-structures immediately, even with small strain (ε = 2%, Fig. 6a). Likewise, the electronic properties are highly sensitive to the structures. As presented in Fig. 6b, accompanied by the geometry change from the P- to D-structure, tensile strain triggers the transition from metal to indirect semiconductor. To further confirm that the electronic properties can be tuned by the strain, the band structures of 5- and 7-ZNRs under different levels of strain (ε = −10%, −5%, 5% and 10%, negative/positive value denotes compressive/tensile strain) were calculated in Fig. 6c and d, respectively. The band structures of 5- and 7-ZNRs at the equilibrium state were also illustrated as references. It can be seen that under tensile strain, ZNRs show a D-structure, and display a semi-conductive feature. On the contrary, a P-structure is maintained and metallic properties are always unchanged under compressive strain. Combining these results with those obtained in Section 3.2, we suggest that there is strong correlation between structure and the electronic properties for ZNRs, that is, the P-structure and D-structure correspond to metal and semiconductor, respectively.

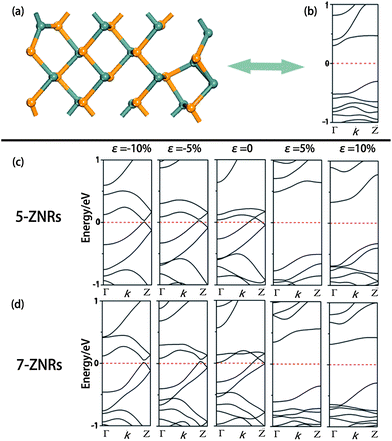Fig. 6 The geometry (a) and electronic structure of 7-ZNR under 2% tensile strain (b). The electronic structures of 5- and 7-ZNR under different strains are shown in (c) and (d), respectively.

In Fig. 7a, the variation of energy gaps of 5- and 7-ZNRs as a function of tensile strain was depicted. It was shown that the energy gap variation does not monotonously change with the strain. It increases first and reaches the highest value of 1.00 eV at ε = 4% for 5-ZNR, then decreases with the increase of tensile strain. As for 7-ZNR, the effect of tensile strain on the energy gap is similar to 5-ZNR with the exception of 4%, where it is a local minimum value.

Fig. 7 The plot of the energy gaps as a function of tensile strain for 5- and 7-ZNR (a). The PDOS of 7-ZNR under the strain of −5% and 5% are shown in (b) and (c), and the blue, red, green lines represent s, p, d orbitals, respectively.

In Fig. 7b and c, the PDOS of 7-ZNR under the strain of −5% and 5%, respectively, are shown to understand the phenomenon of the metal–semiconductor transition. The PDOS of 7-ZNR at the equilibrium state can refer to Fig. 4a. Just as we described in Section 3.2, the different composition of CBM would account for this transition. It is contributed to by the coupling between the Sn atom s and p orbitals and the Se atom p orbital for 7-ZNR at the equilibrium state or under −5% compressive strain, however, it originates mostly from the Sn p orbital with a weaker contribution from the Se p orbital under 5% tensile strain. Different contributions to the CBM leading to the change of band gap has been reported in monolayer MoS₂ under strain conditions.⁷

For D-structure ZNRs at the equilibrium state, they are indirect band gap semiconductors. When uniaxial tensile strain was applied, both 8- and 10-ZNRs kept their semi-conductive properties (Fig. 8a and b). The energy gap does not monotonously change with the tensile strain (Fig. 8c) because a local minimum value at ε = 4% was also observed as found in 7-ZNR. From Fig. 8a and b, we can see that the tensile strain gradually shifts upward and downward from the energy point of ZH and ZL, respectively. As a result, 8-ZNR transforms to a direct semiconductor when the strain increases to 8% (10% for 10-ZNR). Since an indirect semiconductor will largely constrain the application of SnSe ZNRs to optical devices, the indirect–direct-gap crossover would increase luminescence quantum efficiency,³⁹ which suggests their potential use for photostable markers and sensors in probing nanoscale dimensions. On the other hand, a compressive strain can induce the semiconductor–metal transition. The energy gaps increase monotonously with the increase of compressive strain firstly, and under a certain strain degree, the energy gap begins to decrease. As seen in Fig. 8a, the inflection point appears at the strain of −6% which is where both 8- and 10-ZNRs have the widest energy gap (0.90 and 0.87 eV for 8- and 10-ZNRs, respectively). With continued increase in the strain, the energy gap reduces sharply and becomes metallic at ε = −9% and −10% for 8-ZNR and 10-ZNR, respectively (Fig. 8a and b). Conclusively, as shown in Fig. 8d and e, the indirect–direct-gap the indirect–direct-gap crossover semiconductor and metal–semiconductor transitions can be engineered by applying different strains, indicating that they may be applied to optical devices, electromechanical sensors and switches.

Fig. 8 The electronic structures of 8- and 10-ZNR under various strains (a and b), energy gaps as a function of strains (c), and summative schemes describing the indirect–direct-gap crossover and metal–semiconductor or semiconductor–metal transition by applying different strains ((d) for 10-ZNR and (e) for 8-ZNR).

Above, we demonstrated that the metal–semiconductor or semiconductor–metal transition can be induced by controlling the zigzag edge width as well as the level of strain. In order to gain more insight into this transition in SnSe nanoribbons, we calculated the partial charge density distribution of the VBM and CBM as shown in Fig. 9. In analogy to the PDOS analysis, the main difference between metal and semiconductor derives from the CBM. As seen in Fig. 9, the charge of the VBM is basically delocalized over the whole structure, while the charge of the CBM is more likely to localize at the edge of the SnSe ZNRs. Under tensile strain, the band gap of 7-ZNR opens up. The metal–semiconductor transition originates from a redistribution of the CBM charge where it is mainly located at the edge near the strained ZNRs (Fig. 9a and b). Comparing the charge distribution between the 7- and 8-ZNRs at the equilibrium state, the metal–semiconductor transition can also be attributed to the localized charge of the CBM near the strained domains (Fig. 9a and c). Under a −10% compressive strain of 8-ZNR, the charges will gradually assemble at the other side of the edge where there are no broken Sn–Se bonds (Fig. 9c and d), thus the localized–delocalized partial charge distribution of the CBM near the strained ZNRs results in the gap closing, and the semiconductor–metal transition occurs. In general, the partial charge distribution of the CBM can explain the change of band structures with different width and strain very well.

Fig. 9 Partial charge density distribution of 7-ZNR at the equilibrium state (a) and under 5% tensile strain (b), 8-ZNR at equilibrium state (c) and under −10% compressive strain (d). The isosurface value is set to be 0.001 e Å⁻³.

3.4 Stability of the SnSe nanoribbons

Finally, we would like to comment on the relative stability of these nanoribbons as this is important for the possibility of experimental realizations. Binding energy per SnSe unit (E_b) is defined as E_b = (nE_Sn + nE_Se − E_NRs)/n, where E_Sn, E_Se, and E_NRs are the energies of the Sn, Se, and SnSe nanoribbons, respectively, n is the number of Sn or Se atoms. As shown in Fig. 10, E_b increases monotonously with increasing width for both types of ribbon, indicating that the wider the ribbon is, the more stable it will be. ANRs are more stable than ZNRs of a similar width. As the width increases, the stabilities of them remain close to each other (the binding energy difference is less than 0.1 eV at 25 Å). While applying different levels of strain, our calculation results showed that the binding energies varied in the narrow range of 0.06 eV (0.06 for 5-ZNR, 0.04 for 7-ZNR, 0.05 for 8-ZNR and 0.06 eV for 10-ZNR). Therefore, the binding strength depends insensitively on the strain, providing flexible and reversible tunability by stretching or compressing the SnSe nanoribbons. In view of these small binding energy differences, we expect that there will be further experimental efforts to prepare these nanoribbons.

Fig. 10 Binding energy of ZNRs and ANRs as a function of the width.

4. Conclusion

In summary, our first-principles calculations disclosed that the electronic properties of SnSe nanoribbons can be tailored by the edge shape, the width of the ribbons and the uniaxial strain. It was found that a semiconductor–metal or metal–semiconductor transition can be triggered through altering the width parameter or applying tensile/compressive strain in SnSe zigzag nanoribbons. Combining the PDOS and partial charge density analysis, we showed that the different composition and charge redistribution of the CBM would account for the metal–semiconductor or semiconductor–metal transition. Our theoretical results on the one hand, will help to further experimental and theoretical work in connection with SnSe, and on the other hand, will provide a guide to the potential applications in optical and nanoelectromechanical devices.

Acknowledgements

This work was supported by the National Younger Natural Science Foundation of China no. 21203001, Natural Science Foundation of Anhui Province no. 1208085QB37 and Doctoral Scientific Research Funding of Anhui Normal University.

References

1. K. Nakada, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter, 1996, 54, 17954.
2. Y.-W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347.
3. C.-H. Park and S. G. Louie, Nano Lett., 2008, 8, 2200.
4. Y. Li, Z. Zhou, S. Zhang and Z. Chen, J. Am. Chem. Soc., 2008, 130, 16739.
5. S. Zhang and J. Ma, J. Phys. Chem. C, 2011, 115, 4466.
6. A. R. Botello-Mendez, F. Lopez-Urias, M. Terrones and H. Terrones, Nano Lett., 2008, 8, 1562.
7. P. Lu, X. Wu, W. Guo and X. C. Zeng, Phys. Chem. Chem. Phys., 2012, 14, 13035.
8. Y. Ma, Y. Dai, M. Guo, C. Niu, Y. Zhu and B. Huang, ACS Nano, 2012, 6, 1695.
9. W. Chen, Y. Li, G. Yu, C.-Z. Li, S. B. Zhang, Z. Zhou and Z. Chen, J. Am. Chem. Soc., 2010, 132, 1699.
10. M. Wu, X. Wu, Y. Pei and X. C. Zeng, Nano Res., 2011, 4, 233.
11. J. W. Seo, J. T. Jang, S. W. Park, C. Kim, B. Park and J. Cheon, Adv. Mater., 2008, 20, 4269.
12. J. Choi, J. Jin, I. G. Jung, J. M. Kim, H. J. Kim and S. U. Son, Chem. Commun., 2011, 47, 5241.
13. M. Parenteau and C. Carlone, Phys. Rev. B: Condens. Matter, 1990, 41, 5227.
14. X. Yu, J. Zhu, Y. Zhang, J. Weng, L. Hu and S. Dai, Chem. Commun., 2012, 48, 3324.
15. X. He and H. Shen, Phys. B, 2012, 407, 1146.
16. L. Makinistian and E. Albanesi, Phys. Status Solidi B, 2009, 246, 183.
17. I. Lefebvre, M. Szymanski, J. Olivier-Fourcade and J. Jumas, Phys. Rev. B: Condens. Matter, 1998, 58, 1896.
18. M. A. Franzman, C. W. Schlenker, M. E. Thompson and R. L. Brutchey, J. Am. Chem. Soc., 2010, 132, 4060.
19. L. Li, Z. Chen, Y. Hu, X. Wang, T. Zhang, W. Chen and Q. Wang, J. Am. Chem. Soc., 2013, 135, 1213.
20. L. Huang, Y. Yu, C. Li and L. Cao, J. Phys. Chem. C, 2013, 117, 6469.
21. S. Liu, X. Guo, M. Li, W. H. Zhang, X. Liu and C. Li, Angew. Chem., Int. Ed., 2011, 50, 12050.
22. P. D. Antunez, J. J. Buckley and R. L. Brutchey, Nanoscale, 2011, 3, 2399.
23. W. J. Baumgardner, J. J. Choi, Y.-F. Lim and T. Hanrath, J. Am. Chem. Soc., 2010, 132, 9519.
24. B. Pejova and A. Tanuševski, J. Phys. Chem. C, 2008, 112, 3525.
25. B. Pejova and I. Grozdanov, Thin Solid Films, 2007, 515, 5203.
26. B. Subramanian, C. Sanjeeviraja and M. Jayachandran, J. Cryst. Growth, 2002, 234, 421.
27. P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953.
28. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 47, 558.
29. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1994, 49, 14251.
30. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169.
31. J. P. Perdew, J. Chevary, S. Vosko, K. A. Jackson, M. R. Pederson, D. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter, 1992, 46, 6671.
32. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter, 1992, 45, 13244.
33. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter, 1976, 13, 5188.
34. B. Subramanian, T. Mahalingam, C. Sanjeeviraja, M. Jayachandran and M. J. Chockalingam, Thin Solid Films, 1999, 357, 119.
35. V. Barone, O. Hod and G. E. Scuseria, Nano Lett., 2006, 6, 2748.
36. L. Yang, C.-H. Park, Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2007, 99, 186801.
37. T. Kawai, Y. Miyamoto, O. Sugino and Y. Koga, Phys. Rev. B: Condens. Matter, 2000, 62, R16349.
38. L. Sun, Q. Li, H. Ren, H. Su, Q. Shi and J. Yang, J. Chem. Phys., 2008, 129, 074704.
39. Y. Ma, Y. Dai, M. Guo, C. Niu, J. Lu and B. Huang, Phys. Chem. Chem. Phys., 2011, 13, 15546.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ra45724a

---