DOI:
10.1039/C2NR32226A
(Paper)
Nanoscale, 2013,
5, 200-208
Spin-dependent thermoelectric effects in graphene-based spin valves
Received
10th August 2012
, Accepted 15th October 2012
First published on 23rd October 2012
Abstract
Using first-principles calculations combined with non-equilibrium Green's function (NEGF), we investigate spin-dependent thermoelectric effects in a spin valve which consists of zigzag graphene nanoribbon (ZGNR) electrodes with different magnetic configurations. We find that electron transport properties in the ZGNR-based spin valve are strongly dependent on the magnetic configurations. As a result, with a temperature bias, thermally-induced currents can be controlled by switching the magnetic configurations, indicating a thermal magnetoresistance (MR) effect. Moreover, based on the linear response assumption, our study shows that the remarkably different Seebeck coefficients in the various magnetic configurations lead to a very large and controllable magneto Seebeck ratio. In addition, we evaluate thermoelectric properties, such as the power factor, electron thermal conductance and figure of merit (ZT), of the ZGNR-based spin valve. Our results indicate that the power factor and the electron thermal conductance are strongly related to the transmission gap and electron–hole symmetry of the transmission spectrum. Moreover, the value of ZT can reach 0.15 at room temperature without considering phonon scattering. In addition, we investigate the thermally-controlled magnetic distributions in the ZGNR-based spin valve and find that the magnetic distribution, especially the local magnetic moment around the Ni atom, is strongly related to the thermal bias. The very large, multi-valued and controllable thermal magnetoresistance and Seebeck effects indicate the strong potential of ZGNR-based spin valves for extremely low-power consuming spin caloritronics applications. The thermally-controlled magnetic moment in the ZGNR-based spin valve indicates its possible applications for information storage.
Introduction
Spin caloritronics, a novel and rich research field combining investigations in spin, charge and heat transport in materials,1 has attracted a lot of attention. Recently, the research pace of spin caloritronics has been greatly accelerated by the breakthrough discovery of spin Seebeck effect in magnetic metals, insulators and semiconductors.2–4 The spin Seebeck effect demonstrates that spin currents can be induced by a temperature bias in a uniform ferromagnetic material. Moreover, spin currents can be converted to spin voltages by the inverse spin Hall effect. The long-range spin Seebeck effect is beyond the traditional spin caloritronics concept proposed by Johnson and Silsbee.1 Recently, Uchida et al. and Huang et al. presented their experimental results about the spin Seebeck effect in ferromagnetic thin films (NiFe alloy).5,6 They concluded that substrates play a crucial role and the measured spin voltage originates from spin pumping.5,6 Besides uniform ferromagnetic materials, spin caloritronic effects in spin valves and magnetic tunnel junctions (MTJs) have recently attracted considerable interest.7–9 For instance, Breton et al. reported that thermally-induced spin currents can be injected from a ferromagnet into silicon with a temperature bias. At the same time, Walter et al. observed magneto-Seebeck effects in a MgO-based MTJ in which a large change in the Seebeck coefficient was achieved when the magnetization of ferromagnetic electrodes was switched from a parallel to an antiparallel configuration. Unlike the spin Seebeck effect in ferromagnetic materials, the experimental results for magnetic spin valves and MTJs can be explained by the standard thermoelectric model proposed by Johnson and Silsbee.1 Therefore, in magnetic spin valves and MTJs, the term magneto-Seebeck effect is used to distinguish the phenomena from the spin Seebeck effect observed in uniform ferromagnetic materials. This experimental progress has greatly motivated theoretical investigations on the spin thermoelectric properties of magnetic systems. For example, Seebeck coefficients as a function of temperature and relative angle between the two magnetizations of magnetic layers in Co/MgO/Co MTJ has been studied based on the ballistic transport assumption.10 Besides that, thermal spin transfer torques have been predicted to cause magnetization reversal in Fe/MgO/Fe MTJs with a small temperature difference (∼10 K), indicating a strong potential for thermally-induced high-frequency generation.11
Graphene nanoribbon (GNR) based spin valves have been experimentally demonstrated to show a large magnetoresistance (GMR) effect.12 Theoretically, a very large MR ratio in zigzag GNR (ZGNR) spin valves has been predicted,13 and it is caused by a sufficiently strong magnetic field which can drive the spin-polarized edge states in ZGNRs from antiferromagnetic to ferromagnetic coupling, resulting in a phase transition from the ground state to the magnetized state. While increasing the temperature may destroy the spin ordering and lead to the spin disordered and unpolarized state, magnetic anisotropy effect can be exploited to protect the spin ordering.13–15 Therefore, depending on the external conditions, ZGNRs in finite temperature may be in the ground state, spin disordered state or magnetized state.13–15 Controlling these different electronic states in ZGNRs offers ZGNR-based spin valves with flexible magnetic configurations, enabling the design of spin transistors and spin logic devices.16,17 Furthermore, ZGNRs have been predicted to possess high thermal conductivity, allowing faster heat transfer and heat management.18–21 Recently, thermally-induced currents and MR effects in magnetized ZGNRs and ZGNR-based heterostructures have been studied.22,23 However, an investigation into thermally-induced magnetoresistance (MR) and magneto-Seebeck (MS) effects in ZGNR-based spin valves is still lacking. In this work, using first principles calculations, we firstly investigate the spin-dependent transmission spectra of a ZGNR-based spin valve under different magnetic configurations ([MS, MD]). The schematic of the ZGNR-based spin valve is shown in Fig. 1, in which MS and MD represent the magnetization of ZGNR in the source and the drain, respectively. Next, the Landauer formula is implemented to study thermally-induced currents, which is driven by a temperature difference (TSD = TS − TD) between the source (TS) and the drain (TD). We find that the thermally-induced current is strongly dependent on the magnetic configurations and the temperature difference of the ZGNR-based spin valve. In addition, based on the linear response approximation, we find that the Seebeck coefficient can also be controlled by the magnetic configurations, indicating the simultaneous existence of MS and MR effects in the ZGNR-based spin valve. Moreover, both the MS and the MR ratios are remarkably high and show multi-values due to the diverse magnetic configurations. These interesting properties may be implemented for realizing multi-resistance storage systems or multi-logic systems. Additionally, we study the thermoelectric properties of ZGNR-based spin valve and find that the figure of merit (ZT) can reach 0.15 at room temperature, which might be further enhanced by considering phonon scattering in the magnetic ZGNR spin valves. Lastly, we investigate the thermally-controlled magnetic distributions in the antiparallel ZGNR-based spin valve when a Ni atom is absorbed on the edge of ZGNR. We find that the magnetic distribution, especially the local magnetic moment around the Ni atom, is strongly related to the thermal bias, indicating possible applications for information storage.
![A schematic illustration of a ZGNR-based thermal spin valve. The width of ZGNR is 1.36 nm, that is, 6ZGNR with six carbon dimers. A temperature difference TSD = TS − TD is applied on the spin valve. TS, TD, MS and MD represent the source temperature, the drain temperature, the source magnetization and the drain magnetization, respectively. The magnetic configuration of the spin valve is represented by [MS, MD]. MS, MD can take the value of 0 (spin disorder state), 1 (spin-up polarization), −1 (spin-down polarization) and GS (ground state). A back gate voltage can be implemented to control the chemical potential of ZGNR spin valve.](/image/article/2013/NR/c2nr32226a/c2nr32226a-f1.gif) |
| | Fig. 1 A schematic illustration of a ZGNR-based thermal spin valve. The width of ZGNR is 1.36 nm, that is, 6ZGNR with six carbon dimers. A temperature difference TSD = TS − TD is applied on the spin valve. TS, TD, MS and MD represent the source temperature, the drain temperature, the source magnetization and the drain magnetization, respectively. The magnetic configuration of the spin valve is represented by [MS, MD]. MS, MD can take the value of 0 (spin disorder state), 1 (spin-up polarization), −1 (spin-down polarization) and GS (ground state). A back gate voltage can be implemented to control the chemical potential of ZGNR spin valve. | |
Methodology
Due to the long spin diffusion length and weak electron–phonon coupling in graphene,24 the coherent transport of spin polarized electrons is assumed in this work. In other words, two-channel (spin-up and spin-down) circuit theory in spintronics can be applied to study the magneto thermoelectric properties of the ZGNR-based spin valve. We calculate the spin-dependent transmission spectra (T↑(E) and T↓(E)) at zero temperature using the ATK package.25,26 The graphene nanoribbons in our studies are terminated with hydrogen atoms to saturate dangling bonds at the edges of ZGNRs. The vacuum layers between two sheets along the transversal directions were 15 Å in order to minimize the artificial Coulomb interaction between the components in two neighboring systems. The local density approximation (LDA) is adopted for exchange and correlation functional,27 and pseudopotentials generated with LDA are adopted to describe the interaction between ions and electrons. Moreover, atomic orbitals are built up with the double-δ polarized (DZP) basis set. A mesh cutoff energy of 150 Ry is used to define the real-space grid on which the Poisson equation is solved, and a mesh of 1 × 1 × 100 based on the Monkhorst-Pack scheme is used for k-point sampling in the first Brillouin zone. Contour integration is carried out in the imaginary plane to obtain the density matrix from the Green's function. We use 30 contour points, with a lower energy binding of 3 Ry in the contour diagram. The NEGF-DFT self-consistency is controlled by a numerical tolerance of 10−5 eV. The retarded Green's function GR(E) is obtained by:28where H is the Hamiltonian of the scattering region and Σ = ΣS + ΣD is the total self-energy which describes the effect of the source and drain electrodes. Then, transmission can be computed by the following equation for the non-interaction system:| | ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (E) = Tr[ΓSGRΓD(GR)+] (E) = Tr[ΓSGRΓD(GR)+] | (2) |
| | | ΓS,D = i[ΣS,D − Σ†S,D] | (3) |
The function Γ describes the line-width broadening resulting from the coupling of the scattering region to the electrodes.
At finite temperature, we assume that the electronic properties of ZGNRs could be controlled by some external means, and thus are stable against variations in temperature.13–15 Therefore, the spin-dependent electronic transmission spectra of ZGNR-based spin valves are independent of the temperature, and the effect of temperature only appears in the Fermi-distribution function for calculating the thermally-induced currents based on the Landauer formula:
| | 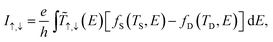 | (4) |
where
fS and
fD are the Fermi-distribution functions for the source and the drain, respectively. Utilizing the linear response assumption
i.e.,
TS ≈
TD,
18,29 we also calculate the Seebeck coefficient (
S), power factor (
pf), electron conductance (
G), electron thermal conductance (
κe) and figure of merit (
ZT) using the following equations
| | 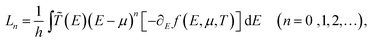 | (5) |
| | 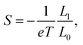 | (6) |
| | 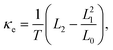 | (9) |
| | 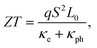 | (10) |
where
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif)
(
E) =
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ↑
↑(
E) +
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ↓
↓(
E) is the total electron transmission,
q is the electronic charge and
κph is the phonon thermal conductance obtained from
ref. 21.
It should be noted that the choice of electrodes may affect the performance of the proposed device. Normally, a mixing metal–graphene interface is used for current injection and detection. The efficiency of a metal–graphene contact can be affected by the connection geometry and the interaction between metal and graphene. For example, the Schottky barriers, suppressed and asymmetric conductance due to the metal–graphene contact have been discussed.30–34 In this work, we use ZGNRs as the electrodes. The requirement of a metal–graphene contact for current generation can be removed because this thermoelectric device relies on a thermal bias. Even though a metal–graphene contact as a detecting electrode is required, this current-meter mode operates under zero-electric bias. In this condition, Guo et al. have recently reported that electronic properties of ZGNRs are preserved when ZGNRs are deposited on s-dominated metals, such as Au, Ni, and Cu.35 Therefore, the choice of s-dominated metal electrodes guarantees the validity of our conclusion. In addition, because ZGNRs possess edge states with a large density of states near the Fermi level, the overlap of wave functions between metal contacts and the edge states means that completely transparent transmissions of electrons from ZGNRs into the metal are possible.36
Results and discussion
Thermally-induced magnetoresistance effect
Depending on external conditions, ZGNRs in finite temperature may be in the ground state (GS) or the spin disorder state (0 state).14,15 Moreover, ZGNRs can be magnetized by applying an external magnetic field,13 and the magnetization of the ZGNR electrodes can be set to 1 (spin-up polarization), or −1 (spin-down polarization). Therefore, the magnetic configuration of the spin valve is represented by [MS, MD], in which MS and MD can be 1, −1, 0 or GS. We simulate these different electronic states by setting up the initial scaled spin-dependent electron density 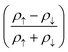 for DFT calculations. For example, as the spin disordered state is spin unpolarized, the initial scaled spin-dependent electron density for all atoms is set to zero. Fig. 2(a) shows the spin-dependent electron transmission spectra for the magnetic configurations of [1,1], [1,−1], [1,GS], [GS,GS]. It can be found that the electron transmission is closely related to the magnetic configuration of the left and right electrodes. It has been studied that for an even number of zigzag chains, such as 6ZGNR in our study, the π and π* orbitals have mismatching parity, resulting in a transmission gap under an electrical bias.13,37 However, under a temperature bias, the parity mismatch in a uniform even-numbered ZGNR, such as in the [0,0], [1,1] and [GS,GS] magnetic configurations, is absent since the electrons with the same energy posses the same parity at the source and drain electrodes. Furthermore, the parity mismatch can affect the spin-dependent transmission gap in the ZGNRs spin valve with [1,−1], [1,0] and [1,GS] magnetic configurations. Based on these electron transmission spectra and using the Landauer formula,27 thermally-induced currents are calculated as a function of the temperature difference between the source and the drain under different magnetic configurations. As shown in Fig. 2(b), the amplitudes of thermally-induced currents for both spin-up electrons and spin-down electrons increase linearly firstly and then saturates at a certain value. The detailed mechanism to generate thermally-induced currents in ZGNRs can be found in ref. 22. Since electrons with energy above (below) the Fermi energy contribute to the electron (hole) current, the amplitude of saturated current strongly depends on the electron–hole symmetry in the transmission spectrum because that the electron current and the hole current flow in opposite directions. For example, the most symmetric transmission spectrum for spin-down electrons is found in the [1,GS] configuration, where transmission increases from 0 to 1 at two symmetric energy points, that is, E − EF0 = 0.18 eV and E − EF0 = −0.18 eV. As a result, this highly symmetric electron transmission spectrum gives rise to a very small negative spin-down current as shown in the left panel of Fig. 2(b). Although there is a transmission peak for spin-up electrons within the energy range of −0.3 eV < E − EF0 < −0.24 eV, this transmission peak has little effect on breaking the electron–hole transmission symmetry due to the fact that the transmission peak is far from the Fermi energy and the Fermi distribution function decays exponentially with the energy. Thus, as shown in the right panel of Fig. 2(b), only a small positive spin-up current flows from the source to the drain in the [1,GS] configuration. Because the spin-up current and the spin-down current in the [1,GS] configuration flow in opposite directions with similar amplitude, the net thermally-induced current in the [1,GS] configuration approximates to zero, as shown in Fig. 2(c), displaying the smallest thermally-induced current compared to the other magnetic configurations. The [1,−1] configuration shows the maximum thermally-induced current, i.e. the minimum resistance. Therefore, it is implemented as a reference for defining the MR ratio:
for DFT calculations. For example, as the spin disordered state is spin unpolarized, the initial scaled spin-dependent electron density for all atoms is set to zero. Fig. 2(a) shows the spin-dependent electron transmission spectra for the magnetic configurations of [1,1], [1,−1], [1,GS], [GS,GS]. It can be found that the electron transmission is closely related to the magnetic configuration of the left and right electrodes. It has been studied that for an even number of zigzag chains, such as 6ZGNR in our study, the π and π* orbitals have mismatching parity, resulting in a transmission gap under an electrical bias.13,37 However, under a temperature bias, the parity mismatch in a uniform even-numbered ZGNR, such as in the [0,0], [1,1] and [GS,GS] magnetic configurations, is absent since the electrons with the same energy posses the same parity at the source and drain electrodes. Furthermore, the parity mismatch can affect the spin-dependent transmission gap in the ZGNRs spin valve with [1,−1], [1,0] and [1,GS] magnetic configurations. Based on these electron transmission spectra and using the Landauer formula,27 thermally-induced currents are calculated as a function of the temperature difference between the source and the drain under different magnetic configurations. As shown in Fig. 2(b), the amplitudes of thermally-induced currents for both spin-up electrons and spin-down electrons increase linearly firstly and then saturates at a certain value. The detailed mechanism to generate thermally-induced currents in ZGNRs can be found in ref. 22. Since electrons with energy above (below) the Fermi energy contribute to the electron (hole) current, the amplitude of saturated current strongly depends on the electron–hole symmetry in the transmission spectrum because that the electron current and the hole current flow in opposite directions. For example, the most symmetric transmission spectrum for spin-down electrons is found in the [1,GS] configuration, where transmission increases from 0 to 1 at two symmetric energy points, that is, E − EF0 = 0.18 eV and E − EF0 = −0.18 eV. As a result, this highly symmetric electron transmission spectrum gives rise to a very small negative spin-down current as shown in the left panel of Fig. 2(b). Although there is a transmission peak for spin-up electrons within the energy range of −0.3 eV < E − EF0 < −0.24 eV, this transmission peak has little effect on breaking the electron–hole transmission symmetry due to the fact that the transmission peak is far from the Fermi energy and the Fermi distribution function decays exponentially with the energy. Thus, as shown in the right panel of Fig. 2(b), only a small positive spin-up current flows from the source to the drain in the [1,GS] configuration. Because the spin-up current and the spin-down current in the [1,GS] configuration flow in opposite directions with similar amplitude, the net thermally-induced current in the [1,GS] configuration approximates to zero, as shown in Fig. 2(c), displaying the smallest thermally-induced current compared to the other magnetic configurations. The [1,−1] configuration shows the maximum thermally-induced current, i.e. the minimum resistance. Therefore, it is implemented as a reference for defining the MR ratio:| | 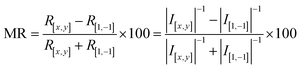 | (11) |
where [x,y] includes [1,1], [1,GS], and [GS,GS]. Depending on the final magnetic configurations, the MR ratio (see Fig. 2(d)) as a function of TSD may decrease or increase as the temperature difference increases. Switching the magnetic configuration from [1,−1] to [1,GS] provides the maximum MR ratio, which can be as high as 93%. Next, we further investigate the MR effect in the ZGNR spin valve with one or two electrodes in spin disorder states. Fig. 3(a) shows the spin-dependent transmission spectra for the [1,0] and [0,0] configurations. The transmission spectra for spin-up electrons and spin-down electrons in the [0,0] configuration are degenerate and highly symmetric, leading to a small thermally-induced spin-up (spin-down) current shown in Fig. 3(b). Compared to the [0,0] configuration, the thermally-induced spin-up and spin-down currents can be remarkably enhanced in the [1,0] configuration, due to the electron–hole asymmetry, as shown in Fig. 3(a). Fig. 3(c) displays the total thermal induced currents, indicating that the thermal resistance can be greatly increased by removing the magnetic field which is applied to the source electrode. Therefore, a large MR value can be obtained. As shown in Fig. 3(d), the MR ratio calculated from 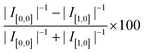 can reach 92% at TSD = 20 K. However, this MR ratio decreases with increasing the temperature difference because of the slow increase of I[0,0].
can reach 92% at TSD = 20 K. However, this MR ratio decreases with increasing the temperature difference because of the slow increase of I[0,0].
![(a) Spin-dependent transmission spectra in the [1,1], [1,−1], [1,GS] and [GS,GS] magnetic configurations of the ZGNR spin valve. EF0 represents the equilibrium Fermi energy when VG = 0. (b) Left (right) panel: current–TSD curves for spin-up (down) electrons in the [1,1], [1,−1], [1,GS], [GS,GS] configurations of ZGNR (TS = 400 K). (c) The net thermally-induced currents as a function of TSD in [1,1], [1,−1], [1,GS], [GS,GS] configurations of ZGNR. (d) The MR ratio as a function of TSD in three types of transition of the magnetic configurations.](/image/article/2013/NR/c2nr32226a/c2nr32226a-f2.gif) |
| | Fig. 2 (a) Spin-dependent transmission spectra in the [1,1], [1,−1], [1,GS] and [GS,GS] magnetic configurations of the ZGNR spin valve. EF0 represents the equilibrium Fermi energy when VG = 0. (b) Left (right) panel: current–TSD curves for spin-up (down) electrons in the [1,1], [1,−1], [1,GS], [GS,GS] configurations of ZGNR (TS = 400 K). (c) The net thermally-induced currents as a function of TSD in [1,1], [1,−1], [1,GS], [GS,GS] configurations of ZGNR. (d) The MR ratio as a function of TSD in three types of transition of the magnetic configurations. | |
![(a) Spin-dependent transmission spectra for spin-up electrons and spin-down electrons in the [1,0] and [0,0] configuration of ZGNR. (b) Current–TSD curves for spin-up and spin-down electrons in the [1,0] and [0,0] configuration (TS = 400 K). (c) The net thermally-induced currents as a function of TSD in the [1,0] and [0,0] configurations of ZGNR. (d) The MR ratio as a function of TSD in the transition from [1,0] to [0,0].](/image/article/2013/NR/c2nr32226a/c2nr32226a-f3.gif) |
| | Fig. 3 (a) Spin-dependent transmission spectra for spin-up electrons and spin-down electrons in the [1,0] and [0,0] configuration of ZGNR. (b) Current–TSD curves for spin-up and spin-down electrons in the [1,0] and [0,0] configuration (TS = 400 K). (c) The net thermally-induced currents as a function of TSD in the [1,0] and [0,0] configurations of ZGNR. (d) The MR ratio as a function of TSD in the transition from [1,0] to [0,0]. | |
Magneto-Seebeck effect
Next, we investigate the magneto-Seebeck effect in the ZGNR-based spin valve. When an electron current is induced by a temperature difference, a heat current can be generated simultaneously because every electron carries energy. The heat current can be converted to a thermopower voltage under open circuit conditions. Therefore, the thermopower or Seebeck coefficient (S) is used to characterize the relationship between an induced thermoelectric voltage and a temperature difference. As shown in Fig. 4(a), the Seebeck coefficient of the ZGNR-based spin valve displays a remarkable difference between different magnetic configurations. The spin valve with the magnetic configuration of [1,1] shows the minimum Seebeck coefficient, which approximates to zero when the chemical potential is within the range of −0.1 eV < μ < 0.3 eV, in which μ = 0 corresponds to the equilibrium Fermi energy (EF0) when VG = 0. The spin valve with the magnetic configuration of [0,0] or [1,0] shows a slightly enhanced Seebeck coefficient compared to that of the [1,1] configuration. A significantly increased Seebeck coefficient, a thousand times larger than that of the [1,1] configuration, can be found in the spin valve with magnetic configurations of [1,−1], [1,GS] and [GS,GS]. Interestingly, the Seebeck coefficient in all these three configurations shows sinusoidal-like variation with the chemical potential, in which S < 0, S = 0 and S > 0 correspond to electron conducting, electron–hole symmetry and hole-conducting, respectively. Moreover, the Seebeck coefficient in the ZGNR-based spin valve can reach 500 μV K−1. This value is much larger than that of graphene, which is less than 100 μV K−1.38 In order to understand the mechanism behind the Seebeck coefficient, we plot −T(E)∂Ef(E) as a function of energy in Fig. 4(b). According to eqn (6), S is determined by the transmission-weighted average value of the energy (E − μ).7 Moreover, at the center of mass of −T(E)∂Ef(E), the Seebeck coefficient is equal to zero. Therefore, as shown in Fig. 4(b), the Seebeck coefficient in the [0,0], [1,0] and [1,1] configurations is equal to zero at the Fermi energy due to the fact that −T(E)∂Ef(E) is highly symmetric with respect to the Fermi energy. On the other hand, the highly asymmetric function of −T(E)∂Ef(E) in the [1,−1], [1,GS] and [GS,GS] configuration gives rise to a zero Seebeck coefficient (ZSC) which is far away from the Fermi energy. Furthermore, the maximum |S| occurs when the chemical potential is several kBT away from the location of ZSC (LZSC), where the electron-transmission-weighted average value of (E − μ) is maximized and the highest electron–hole asymmetry is established. The higher |LZSC| increases the magnitude of |Smax| because the conducting electrons have much larger energy (E − μ) when the electron–hole symmetry is broken near the |LZSC|. As a consequence, the Seebeck coefficient in the [1,−1], [1,GS] and [GS,GS] configurations is much higher than that in the [0,0], [1,0] and [1,1] configurations, c.f., Fig. 4(a). Therefore, to obtain a large Seebeck coefficient, a strong asymmetric −T(E)∂Ef(E) with higher |LZSC| is favorable. Interestingly, the strong dependence of the Seebeck coefficient on the magnetic configurations indicates the existence of the magneto Seebeck effect in the ZGNR-based spin valve. We use the [1,1] configuration as a reference (initial magnetic configuration) and define the magneto Seebeck (MS) ratio as| | | MS = (S[x,y] − S[1,1])/(S[x,y]+S[1,1]) × 100 | (12) |
where [x,y] includes the [1,−1], [1,0], [0,0], [1,GS] and [GS,GS] configurations. As shown in Fig. 4(c), the calculated MS ratio in the vicinity of μ = 0 approximates to 100% when the magnetic configuration is changed from [1,1] to any other configurations. Moreover, the MS ratio in the spin valve with final magnetic configuration of [1,−1], [1,GS] or [GS,GS] keeps constant (∼100%) when the chemical potential is varied within a wide range of −0.1 eV < E − EF < 0.15 eV. We also use the [GS,GS] configuration as an example to study the temperature influence on the Seebeck coefficient. As shown in Fig. 5(a), the LZSC is stable against the temperature variation. This can be understood from −T(E)∂Ef(E) shown in Fig. 5(b), which indicates that increasing the temperature can symmetrically broaden −T(E)∂Ef(E) and thus leads to a robust LZSC. However, the maximum |S| decreases with increasing temperature. This can be attributed to the large transmission gap (∼0.38 eV as shown in Fig. 2(a)) in the [GS,GS] configuration. A high enough temperature is required to broaden the Fermi distribution so that electrons with energy beyond the transmission gap can contribute to the transport. Otherwise, at low temperature, the ZGNR-based spin valve in the [GS,GS] configuration can be regarded as an insulator, in which a very high Seebeck coefficient can be expected because the Seebeck coefficient is generally inversely proportional to the carrier density. Similar result of enhancement in thermopower of GNRs with a transmission gap has been discussed by Ouyang et al.18 Their work has shown that the thermopower is found to be approximately inversely proportional to the temperature.18 In addition to the magneto-Seebeck effect in the ZGNR-based spin valve, the magneto-Peltier effect, an inverse process to the magneto-Seebeck effect, can also be exploited to convert an electric voltage into a temperature difference for refrigerating applications. As a consequence of the Onsager reciprocity, the relation between the Seebeck and Peltier coefficients is Π = ST. Therefore, the above results for the magneto-Seebeck effect can be extended to the magneto-Peltier effect, indicating its potential applications as an on-chip cooler for cheap and fast spot cooling for ZGNR-based nano-circuits.
![(a) The Seebeck coefficient as a function of chemical potential for different magnetic configurations of ZGNR-based spin valves; μ = 0 corresponds to the equilibrium Fermi energy (EF0) when VG = 0. (b) The normalized integrand −T(E)∂Ef(E) as a function of energy for different magnetic configurations of the ZGNR-based spin valve. The integrands are normalized by 70.4939, 17.6424, 0.1039, 19.3346, 0.095 and 0.1061 for the [0,0], [1,0], [1,−1], [1,1], [1,GS] and [GS,GS] magnetic configurations, respectively. (c) The magneto-Seebeck ratio as a function of chemical potential when the magnetic configuration of the spin valve is changed from [1,1] to the other configurations.](/image/article/2013/NR/c2nr32226a/c2nr32226a-f4.gif) |
| | Fig. 4 (a) The Seebeck coefficient as a function of chemical potential for different magnetic configurations of ZGNR-based spin valves; μ = 0 corresponds to the equilibrium Fermi energy (EF0) when VG = 0. (b) The normalized integrand −T(E)∂Ef(E) as a function of energy for different magnetic configurations of the ZGNR-based spin valve. The integrands are normalized by 70.4939, 17.6424, 0.1039, 19.3346, 0.095 and 0.1061 for the [0,0], [1,0], [1,−1], [1,1], [1,GS] and [GS,GS] magnetic configurations, respectively. (c) The magneto-Seebeck ratio as a function of chemical potential when the magnetic configuration of the spin valve is changed from [1,1] to the other configurations. | |
![(a) The Seebeck coefficient as a function of chemical potential for ZGNR-based spin valve in the [GS,GS] magnetic configuration with different temperatures. (b) The normalized integrand −T(E)∂Ef(E) as a function of energy for different magnetic configurations of the ZGNR-based spin valve in the [GS,GS] magnetic configuration with different temperatures. The integrands are normalized by 6.3475 × 10−7, 0.1061, 0.9382, 2.0782 and 0.1061 for T = 100, 300, 500 and 700 K, respectively.](/image/article/2013/NR/c2nr32226a/c2nr32226a-f5.gif) |
| | Fig. 5 (a) The Seebeck coefficient as a function of chemical potential for ZGNR-based spin valve in the [GS,GS] magnetic configuration with different temperatures. (b) The normalized integrand −T(E)∂Ef(E) as a function of energy for different magnetic configurations of the ZGNR-based spin valve in the [GS,GS] magnetic configuration with different temperatures. The integrands are normalized by 6.3475 × 10−7, 0.1061, 0.9382, 2.0782 and 0.1061 for T = 100, 300, 500 and 700 K, respectively. | |
Power factor, electron thermal conductance and ZT of the graphene-based spin valve
Next, we explore the thermoelectric properties of the ZGNR-based spin valve. As shown in Fig. 6(a), the calculated power factor (pf) in all magnetic configurations shows a double peak pattern due to the competition between S2 and the electronic conductance G. In general, a larger electronic conductance is accompanied by a smaller S2. Therefore, the maximum power factor, calculated by multiplying S2 and G, is obtained when the energy is close to the edge of the transmission gaps in the [1,−1], [1,GS], [GS,GS] and [1,0] magnetic configurations. A larger transmission gap gives rise to a wider spacing between the two peaks of pf. In the [0,0] and [1,1] configurations, because of the extremely small Seebeck coefficient shown in Fig. 4(a), the value of the power factor is approximately zero. Furthermore, we investigate the electronic contribution to the thermal conductance (κe). As shown in Fig. 6(b), a zero κe platform is found in the ZGNR-based spin valve with a magnetic configuration of [1,−1], [1,GS] or [GS,GS]. Zero κe indicates the system behaves as an electrical insulator due to the fact that the temperature (300 K or 26 meV) is not large enough to broaden the Fermi distribution of electrons in order to cover the transmission gap (∼35 meV), thus no carriers contribute to the electron transport. Comparatively, the smaller transmission gap in the [1,0] configuration is overwhelmed by the broadening of the Fermi distribution, leading to the disappearance of the zero κe platform. The κe follows a similar trend with S2G in the [0,0] and [1,1] configurations, in which the transmission gap is absent and L2 calculated by eqn (5) has little dependence on the chemical potential. Besides, we estimate the figure of merit (ZT) of the ZGNR-based spin valve. The phonon thermal conductance (κph) of ZGNRs in the ground state has been calculated in ref. 21. We assume that the phonon conductance (1.8 nW K−1 for 6-ZGNR) keeps constant upon varying the magnetic configuration of the spin valve because the thermal conductance is determined by lattice dynamics, which may be insensitive to the magnetic states of ZGNRs if inelastic scattering can be ignored. By tuning the chemical potential, the highest ZT, which is close to 0.16 at room temperature, can be achieved in the [GS,GS] magnetic configuration. It can be seen that κe is much less than κph, indicating that the thermal conductivity in ZGNR-based spin valves are mainly due to phonons. In order to accurately estimate κph, a detailed study on the phonon transport in different magnetic states of ZGNRs in the presence of inelastic scatterings due to the magnon–phonon and electron–phonon interactions is necessary. As a result of the inelastic scattering, κph may be reduced, and thus ZT of the ZGNR-based spin valve could be further enhanced.
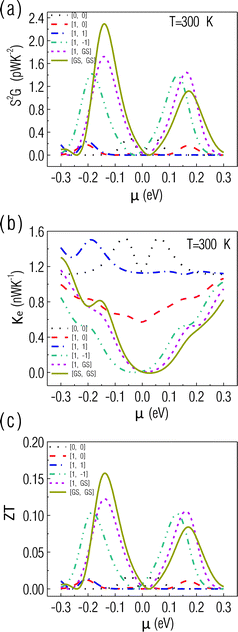 |
| | Fig. 6 (a) Power factor (pf), (b) electron thermal conductance (κe) and (c) figure of merit (ZT) as a function of chemical potential for the ZGNR-based spin valve in different magnetic configurations at room temperature. | |
Finally, we would like to note that the calculated results might be affected by the width of ZGNRs, which can change the electron and phonon transmission properties and further affect the thermoelectric performance. However, the typical electronic properties of ZGNRs, such as an antiferromagnetic coupling ground state and a spin-dependent band splitting in magnetized ZGNRs, are not affected by their widths. Therefore, our work offers a qualitative analysis on the thermoelectric effects of ZGNR spin valves.
Thermally-controlled magnetic distributions in the ZGNR-based spin valve
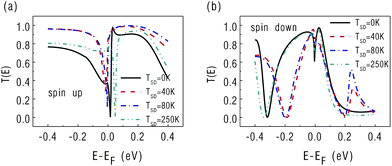
Controlling magnetic moments of impurities distributed in the scattering region has been proposed to be an effective way for storing information in a spin valve.39 In this work, we investigate the possibility of thermal control over magnetic distributions in the ZGNR-based spin valve. As shown in Fig. 7(a), this spin valve is in the antiparallel configuration and with a Ni atom absorbed on one edge of ZGNR.40 As shown in Fig. 7(b), when a Ni atom is absorbed at the edge of ZGNR, the transmission gap for the spin value in the antiparallel configuration disappears, indicating the removal of spin-selective rule.13 Next, we study the effects of the thermally-induced spin current on the magnetic moment around the Ni atom and find that the magnetic moment can be effectively controlled by the thermally-induced spin current. The magnetic moment of the Ni atom is determined by the number of its unpaired electrons, and thus it is affected by the flowing of conducting electrons, which tune the occupation of the electron orbital in the Ni atom. Fig. 8 (a) and (b) show the distribution of the magnetic moment in the scattering region with a temperature bias of TSD = 0 and 40 K, respectively. The edge carbon atoms on the left (right) side of the ZGNR show strong spin-up (down) polarization due to their coupling with the electrodes. As shown in Fig. 8(a), without any bias, the absorbed Ni atom in the ZGNR carries a magnetic moment around −0.01 μB. This value is much smaller than that of an isolated Ni atom, which can be as large as 2 μB. The quenching of the Ni magnetic moment in the ZGNR indicates the strong coupling, or charge transfer, between the Ni atom and its surroundings. Interestingly, as shown in Fig. 8(b), the thermally-induced current can considerably restore the magnetic moment of the Ni atom, which can be enhanced greatly to 1 μB by applying a thermal bias of TSD = 40 K. A bias of 80 K gives a very similar result. Therefore, despite the strong coupling between the Ni atom and its surroundings, the injected spin currents try to alight the Ni magnetic moment to its original value. However, further increasing of the thermal bias to TSD = 250 K gives rise to almost the same magnetic distribution in ZGNR as that of TSD = 0 K. This is due to the reciprocal determinism between the injected spin currents and the Ni magnetic moment. Furthermore, the similar behavior can be found in the spin-dependent transmission spectra. In principle, the spin-dependent transmission through the scattering region is strongly dependent on the electronic behaviors in the scattering region which is closely related to the magnetic moment of the Ni atom. As shown in Fig. 9, the spin-dependent transmission spectra at TSD = 40 K and TSD = 80 K are almost overlapped, and this similarity can also be observed for TSD = 0 K and TSD = 250 K, indicating the similar magnetic distribution in these two cases.
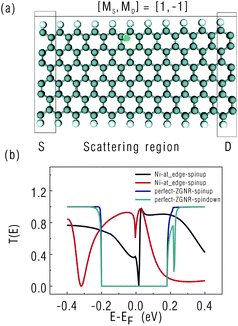 |
| | Fig. 7 (a) Schematic of the ZGNR-based spin valve in the antiparallel configuration and with a Ni atom absorbed on the edge. (b) Spin-dependent transmission spectra for the spin valve with or without Ni atom absorbed on the edge. | |
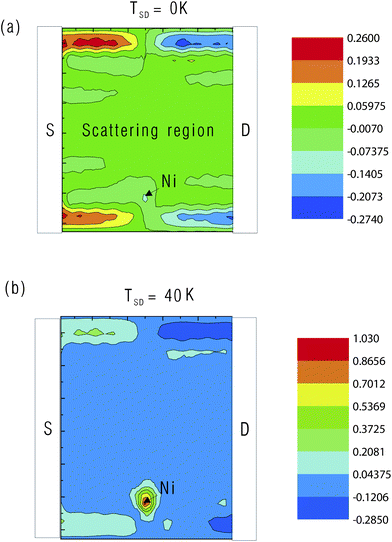 |
| | Fig. 8 (a) Spatial magnetic moment in the scattering region when a temperature bias of TSD = 0 K is applied to the spin valve shown in Fig. 7(a); TS = 300 K. The edges of ZGNR show strong polarization. The magnetic moment in the Ni atom is −0.01 μB. (b) Spatial magnetic moment in the scattering region when a temperature bias of TSD = 40 K is applied to the spin valve. The edges of ZGNR show the same polarization as in (a). The magnetic moment in the Ni atom is 1 μB. | |
Conclusions
In summary, we have investigated the spin caloritronic properties of a ZGNR-based spin valve using first principles calculations combined with the NEGF approach. We find that electronic transmissions through the ZGNR-based spin valve can be controlled by magnetic configurations. The electron–hole symmetry in the transmission spectrum is strongly affected by the various magnetic configurations of the spin valve. As a consequence, the thermally-induced current, which is closely related to the electron–hole symmetry, can be tuned by the magnetic configuration of the spin valve. This result indicates an interesting, thermally-induced and multi-valued magnetoresistance effect. In addition, we investigate the dependence of Seebeck coefficient on the magnetic configurations of the ZGNR spin valve. Similar to the thermally-induced magnetoresistance effect, we find that the Seebeck coefficient is strongly related to the magnetic configurations, indicating a magneto-Seebeck effect. Moreover, both the MR and MS ratios show remarkably high values and can be controlled by the temperature and chemical potentials of the spin valve. The unique thermal MR and MS effects indicate strong potentials for graphene-based spin valves in digital storages and logic operations in spin caloritronic circuits. Besides that, we study the thermoelectric properties of the ZGNR-based spin valve by evaluating several important thermoelectric parameters, including the power factor, electron thermal conductance and figure of merit. Our results show that these parameters are strongly affected by the transmission gap and the electron–hole symmetry of the transmission spectra. Moreover, we find that the figure of merit of the spin valve can reach 0.16 at room temperature, indicating its promising potential for thermal-to-electric energy conversion.
In addition, we study the thermally-controlled magnetic distributions in the ZGNR-based spin valve and find that the polarization of the Ni atom is related to the amount of flowing electrons, and thus controlled by the thermal bias. A possible application of this interesting effect may be a memory device where information is “written” in the form of an impurity spin polarization and “read” through its influence on the terminal current.39
Acknowledgements
We thank Dr E. Cuansing for the helpful discussion. The computations were performed on the cluster of Computational Nanoelectronics and Nano-device Laboratory, National University of Singapore. This work was supported in part by the Ministry of Education of Singapore under Grant R263000578112.
References
- M. Johnson and R. Silsbee, Phys. Rev. B, 1987, 35, 4959 CrossRef.
- C. M. Jaworski, J. Yang, S. Mack, D. D. Awschalom, J. P. Heremans and R. C. Myers, Nat. Mater., 2010, 9, 898 CrossRef CAS.
- K. Uchida, J. Xiao, H. Adachi, J. Ohe, S. Takahashi, J. Ieda, T. Ota, Y. Kajiwara, H. Umezawa, H. Kawai, G. E. W. Bauer, S. Maekawa and E. Saitoh, Nat. Mater., 2010, 9, 894 CrossRef CAS.
- K. Uchida, S. Takahashi, K. Harii, J. Ieda, W. Koshibae, K. Ando, S. Maekawa and E. Saitoh, Nature, 2008, 455, 778 CrossRef CAS.
- K. Uchida, H. Adachi, T. An, T. Ota, M. Toda, B. Hillebrands, S. Maekawa and E. Saitoh, Nat. Mater., 2011, 10, 737 CrossRef CAS.
- S. Y. Huang, W. G. Wang, S. F. Lee, J. Kwo and C. L. Chien, Phys. Rev. Lett., 2011, 107, 216604 CrossRef CAS.
- M. Walter, J. Walowski, V. Zbarsky, M. Muenzenberg, M. Schaefers, D. Ebke, G. Reiss, A. Thomas, P. Peretzki, M. Seibt, J. S. Moodera, M. Czerner, M. Bachmann and C. Heiliger, Nat. Mater., 2011, 10, 742 CrossRef CAS.
- J.-C. Le Breton, S. Sharma, H. Saito, S. Yuasa and R. Jansen, Nature, 2011, 475, 82 CrossRef CAS.
- N. Liebing, S. Serrano-Guisan, K. Rott, G. Reiss, J. Langer, B. Ocker and H. W. Schumacher, Phys. Rev. Lett., 2011, 107, 177201 CrossRef CAS.
- M. Czerner, M. Bachmann and C. Heiliger, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 132405 CrossRef.
- X. T. Jia, K. Xia and G. E. W. Bauer, Phys. Rev. Lett., 2011, 107, 176603 CrossRef.
- J. Bai, R. Cheng, F. Xiu, L. Liao, M. Wang, A. Shailos, K. L. Wang, Y. Huang and X. Duan, Nat. Nanotechnol., 2010, 5, 655 CrossRef CAS.
- W. Y. Kim and K. S. Kim, Nat. Nanotechnol., 2008, 3, 408 CrossRef CAS.
- O. V. Yazyev and M. I. Katsnelson, Phys. Rev. Lett., 2008, 100, 047209 CrossRef.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803 CrossRef.
- M. Zeng, L. Shen, H. Su, C. Zhang and Y. P. Feng, Appl. Phys. Lett., 2011, 98, 092110 CrossRef.
- M. Zeng, L. Shen, M. Zhou, C. Zhang and Y. Feng, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115427 CrossRef.
- Y. Ouyang and J. Guo, Appl. Phys. Lett., 2009, 94, 263107 CrossRef.
- J.-W. Jiang, B.-S. Wang and J.-S. Wang, Appl. Phys. Lett., 2011, 98, 113114 CrossRef.
- W. Huang, J.-S. Wang and G. Liang, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045410 CrossRef.
- Z. W. Tan, J.-S. Wang and C. K. Gan, Nano Lett., 2011, 11, 214 CrossRef CAS.
- M. Zeng, Y. Feng and G. Liang, Nano Lett., 2011, 11, 1369 CrossRef CAS.
- M. Zeng, Y. Feng and G. Liang, Appl. Phys. Lett., 2011, 99, 123114 CrossRef.
- N. Tombros, C. Jozsa, M. Popinciuc, H. T. Jonkman and B. J. van Wees, Nature, 2007, 448, 571 CrossRef CAS.
- M. Brandbyge, J. Mozos, P. Ordejon, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
- J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245407 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter, 1992, 45, 13244 CrossRef.
-
S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge University Press, UK, 1997 Search PubMed.
- U. Sivan and Y. Imry, Phys. Rev. B, 1986, 33, 551 CrossRef CAS.
- W. Y. Kim and K. S. Kim, Acc. Chem. Res., 2010, 43, 111 CrossRef CAS.
- Y. Cho, W. Y. Kim and K. S. Kim, J. Phys. Chem. A, 2009, 113, 4100 CrossRef CAS.
- Y. Cho, Y. C. Choi and K. S. Kim, J. Phys. Chem. C, 2011, 115, 6019 CAS.
- S. Hong, Y. Yoon and J. Guo, Appl. Phys. Lett., 2008, 92, 083107 CrossRef.
- G. Seol and J. Guo, Appl. Phys. Lett., 2012, 100, 063108 CrossRef.
- J. Chen, M. Vanin, Y. Hu and H. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075146 CrossRef.
- S. Krompiewski, Acta Phys. Pol., A, 2012, 121, 1216 CAS.
- Z. Li, H. Qian, J. Wu, B.-L. Gu and W. Duan, Phys. Rev. Lett., 2008, 100, 206802 CrossRef.
- Y. M. Zuev, W. Chang and P. Kim, Phys. Rev. Lett., 2009, 102, 096807 CrossRef.
-
S. Datta, 2008, Arxiv preprint arXiv:0802.2067.
- R. C. Longo, J. Carrete and L. J. Gallego, Phys. Rev. B, 2011, 83, 235415 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2013 |
Click here to see how this site uses Cookies. View our privacy policy here. ![A schematic illustration of a ZGNR-based thermal spin valve. The width of ZGNR is 1.36 nm, that is, 6ZGNR with six carbon dimers. A temperature difference TSD = TS − TD is applied on the spin valve. TS, TD, MS and MD represent the source temperature, the drain temperature, the source magnetization and the drain magnetization, respectively. The magnetic configuration of the spin valve is represented by [MS, MD]. MS, MD can take the value of 0 (spin disorder state), 1 (spin-up polarization), −1 (spin-down polarization) and GS (ground state). A back gate voltage can be implemented to control the chemical potential of ZGNR spin valve.](/image/article/2013/NR/c2nr32226a/c2nr32226a-f1.gif)
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (E) = Tr[ΓSGRΓD(GR)+]
(E) = Tr[ΓSGRΓD(GR)+]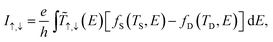
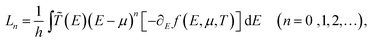
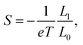
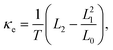
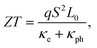
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (E) =
(E) = ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ↑(E) +
↑(E) + ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ↓(E) is the total electron transmission, q is the electronic charge and κph is the phonon thermal conductance obtained from ref. 21.
↓(E) is the total electron transmission, q is the electronic charge and κph is the phonon thermal conductance obtained from ref. 21.
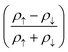 for DFT calculations. For example, as the spin disordered state is spin unpolarized, the initial scaled spin-dependent electron density for all atoms is set to zero. Fig. 2(a) shows the spin-dependent electron transmission spectra for the magnetic configurations of [1,1], [1,−1], [1,GS], [GS,GS]. It can be found that the electron transmission is closely related to the magnetic configuration of the left and right electrodes. It has been studied that for an even number of zigzag chains, such as 6ZGNR in our study, the π and π* orbitals have mismatching parity, resulting in a transmission gap under an electrical bias.13,37 However, under a temperature bias, the parity mismatch in a uniform even-numbered ZGNR, such as in the [0,0], [1,1] and [GS,GS] magnetic configurations, is absent since the electrons with the same energy posses the same parity at the source and drain electrodes. Furthermore, the parity mismatch can affect the spin-dependent transmission gap in the ZGNRs spin valve with [1,−1], [1,0] and [1,GS] magnetic configurations. Based on these electron transmission spectra and using the Landauer formula,27 thermally-induced currents are calculated as a function of the temperature difference between the source and the drain under different magnetic configurations. As shown in Fig. 2(b), the amplitudes of thermally-induced currents for both spin-up electrons and spin-down electrons increase linearly firstly and then saturates at a certain value. The detailed mechanism to generate thermally-induced currents in ZGNRs can be found in ref. 22. Since electrons with energy above (below) the Fermi energy contribute to the electron (hole) current, the amplitude of saturated current strongly depends on the electron–hole symmetry in the transmission spectrum because that the electron current and the hole current flow in opposite directions. For example, the most symmetric transmission spectrum for spin-down electrons is found in the [1,GS] configuration, where transmission increases from 0 to 1 at two symmetric energy points, that is, E − EF0 = 0.18 eV and E − EF0 = −0.18 eV. As a result, this highly symmetric electron transmission spectrum gives rise to a very small negative spin-down current as shown in the left panel of Fig. 2(b). Although there is a transmission peak for spin-up electrons within the energy range of −0.3 eV < E − EF0 < −0.24 eV, this transmission peak has little effect on breaking the electron–hole transmission symmetry due to the fact that the transmission peak is far from the Fermi energy and the Fermi distribution function decays exponentially with the energy. Thus, as shown in the right panel of Fig. 2(b), only a small positive spin-up current flows from the source to the drain in the [1,GS] configuration. Because the spin-up current and the spin-down current in the [1,GS] configuration flow in opposite directions with similar amplitude, the net thermally-induced current in the [1,GS] configuration approximates to zero, as shown in Fig. 2(c), displaying the smallest thermally-induced current compared to the other magnetic configurations. The [1,−1] configuration shows the maximum thermally-induced current, i.e. the minimum resistance. Therefore, it is implemented as a reference for defining the MR ratio:
for DFT calculations. For example, as the spin disordered state is spin unpolarized, the initial scaled spin-dependent electron density for all atoms is set to zero. Fig. 2(a) shows the spin-dependent electron transmission spectra for the magnetic configurations of [1,1], [1,−1], [1,GS], [GS,GS]. It can be found that the electron transmission is closely related to the magnetic configuration of the left and right electrodes. It has been studied that for an even number of zigzag chains, such as 6ZGNR in our study, the π and π* orbitals have mismatching parity, resulting in a transmission gap under an electrical bias.13,37 However, under a temperature bias, the parity mismatch in a uniform even-numbered ZGNR, such as in the [0,0], [1,1] and [GS,GS] magnetic configurations, is absent since the electrons with the same energy posses the same parity at the source and drain electrodes. Furthermore, the parity mismatch can affect the spin-dependent transmission gap in the ZGNRs spin valve with [1,−1], [1,0] and [1,GS] magnetic configurations. Based on these electron transmission spectra and using the Landauer formula,27 thermally-induced currents are calculated as a function of the temperature difference between the source and the drain under different magnetic configurations. As shown in Fig. 2(b), the amplitudes of thermally-induced currents for both spin-up electrons and spin-down electrons increase linearly firstly and then saturates at a certain value. The detailed mechanism to generate thermally-induced currents in ZGNRs can be found in ref. 22. Since electrons with energy above (below) the Fermi energy contribute to the electron (hole) current, the amplitude of saturated current strongly depends on the electron–hole symmetry in the transmission spectrum because that the electron current and the hole current flow in opposite directions. For example, the most symmetric transmission spectrum for spin-down electrons is found in the [1,GS] configuration, where transmission increases from 0 to 1 at two symmetric energy points, that is, E − EF0 = 0.18 eV and E − EF0 = −0.18 eV. As a result, this highly symmetric electron transmission spectrum gives rise to a very small negative spin-down current as shown in the left panel of Fig. 2(b). Although there is a transmission peak for spin-up electrons within the energy range of −0.3 eV < E − EF0 < −0.24 eV, this transmission peak has little effect on breaking the electron–hole transmission symmetry due to the fact that the transmission peak is far from the Fermi energy and the Fermi distribution function decays exponentially with the energy. Thus, as shown in the right panel of Fig. 2(b), only a small positive spin-up current flows from the source to the drain in the [1,GS] configuration. Because the spin-up current and the spin-down current in the [1,GS] configuration flow in opposite directions with similar amplitude, the net thermally-induced current in the [1,GS] configuration approximates to zero, as shown in Fig. 2(c), displaying the smallest thermally-induced current compared to the other magnetic configurations. The [1,−1] configuration shows the maximum thermally-induced current, i.e. the minimum resistance. Therefore, it is implemented as a reference for defining the MR ratio: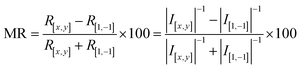
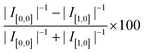 can reach 92% at TSD = 20 K. However, this MR ratio decreases with increasing the temperature difference because of the slow increase of I[0,0].
can reach 92% at TSD = 20 K. However, this MR ratio decreases with increasing the temperature difference because of the slow increase of I[0,0].
![(a) Spin-dependent transmission spectra in the [1,1], [1,−1], [1,GS] and [GS,GS] magnetic configurations of the ZGNR spin valve. EF0 represents the equilibrium Fermi energy when VG = 0. (b) Left (right) panel: current–TSD curves for spin-up (down) electrons in the [1,1], [1,−1], [1,GS], [GS,GS] configurations of ZGNR (TS = 400 K). (c) The net thermally-induced currents as a function of TSD in [1,1], [1,−1], [1,GS], [GS,GS] configurations of ZGNR. (d) The MR ratio as a function of TSD in three types of transition of the magnetic configurations.](/image/article/2013/NR/c2nr32226a/c2nr32226a-f2.gif)
![(a) Spin-dependent transmission spectra for spin-up electrons and spin-down electrons in the [1,0] and [0,0] configuration of ZGNR. (b) Current–TSD curves for spin-up and spin-down electrons in the [1,0] and [0,0] configuration (TS = 400 K). (c) The net thermally-induced currents as a function of TSD in the [1,0] and [0,0] configurations of ZGNR. (d) The MR ratio as a function of TSD in the transition from [1,0] to [0,0].](/image/article/2013/NR/c2nr32226a/c2nr32226a-f3.gif)
![(a) The Seebeck coefficient as a function of chemical potential for different magnetic configurations of ZGNR-based spin valves; μ = 0 corresponds to the equilibrium Fermi energy (EF0) when VG = 0. (b) The normalized integrand −T(E)∂Ef(E) as a function of energy for different magnetic configurations of the ZGNR-based spin valve. The integrands are normalized by 70.4939, 17.6424, 0.1039, 19.3346, 0.095 and 0.1061 for the [0,0], [1,0], [1,−1], [1,1], [1,GS] and [GS,GS] magnetic configurations, respectively. (c) The magneto-Seebeck ratio as a function of chemical potential when the magnetic configuration of the spin valve is changed from [1,1] to the other configurations.](/image/article/2013/NR/c2nr32226a/c2nr32226a-f4.gif)
![(a) The Seebeck coefficient as a function of chemical potential for ZGNR-based spin valve in the [GS,GS] magnetic configuration with different temperatures. (b) The normalized integrand −T(E)∂Ef(E) as a function of energy for different magnetic configurations of the ZGNR-based spin valve in the [GS,GS] magnetic configuration with different temperatures. The integrands are normalized by 6.3475 × 10−7, 0.1061, 0.9382, 2.0782 and 0.1061 for T = 100, 300, 500 and 700 K, respectively.](/image/article/2013/NR/c2nr32226a/c2nr32226a-f5.gif)