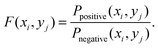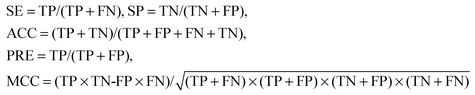De novo prediction of RNA–protein interactions from sequence information†
Ying
Wang‡
ab,
Xiaowei
Chen‡
c,
Zhi-Ping
Liu‡
d,
Qiang
Huang
b,
Yong
Wang
b,
Derong
Xu
c,
Xiang-Sun
Zhang
*b,
Runsheng
Chen
*c and
Luonan
Chen
*d
aSchool of Science, Dalian Jiaotong University, Dalian 116028, China
bNational Center for Mathematics and Interdisciplinary Sciences, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China. E-mail: zxs@amt.ac.cn
cLaboratory of Bioinformatics and Noncoding RNA, Institute of Biophysics, Chinese Academy of Sciences, Beijing 100101, China. E-mail: crs@sun5.ibp.ac.cn
dKey Laboratory of Systems Biology, SIBS-Novo Nordisk Translational Research Centre for PreDiabetes, Shanghai Institutes for Biological Sciences, Chinese Academy of Sciences, Shanghai 200031, China. E-mail: lnchen@sibs.ac.cn
First published on 11th October 2012
Abstract
Protein–RNA interactions are fundamentally important in understanding cellular processes. In particular, non-coding RNA–protein interactions play an important role to facilitate biological functions in signalling, transcriptional regulation, and even the progression of complex diseases. However, experimental determination of protein–RNA interactions remains time-consuming and labour-intensive. Here, we develop a novel extended naïve-Bayes-classifier for de novo prediction of protein–RNA interactions, only using protein and RNA sequence information. Specifically, we first collect a set of known protein–RNA interactions as gold-standard positives and extract sequence-based features to represent each protein–RNA pair. To fill the gap between high dimensional features and scarcity of gold-standard positives, we select effective features by cutting a likelihood ratio score, which not only reduces the computational complexity but also allows transparent feature integration during prediction. An extended naïve Bayes classifier is then constructed using these effective features to train a protein–RNA interaction prediction model. Numerical experiments show that our method can achieve the prediction accuracy of 0.77 even though only a small number of protein–RNA interaction data are available. In particular, we demonstrate that the extended naïve-Bayes-classifier is superior to the naïve-Bayes-classifier by fully considering the dependences among features. Importantly, we conduct ncRNA pull-down experiments to validate the predicted novel protein–RNA interactions and identify the interacting proteins of sbRNA CeN72 in C. elegans, which further demonstrates the effectiveness of our method.
Introduction
Proteins–RNA interactions have diverse functions within the cell. It has been shown to play essential roles in various biological processes, such as protein synthesis,1–3 gene expression,4,5 RNA processing,6–8 viral replication, cellular defence and developmental regulation.9,10 Furthermore, it is also important to understand the principle of protein–RNA interactions when selecting activators and inhibitors in rational drug design. However, at present, the protein–RNA interaction mechanisms are still poorly understood in contrast to those of protein–protein interactions and protein–DNA interactions. In recent years, rapid advances in genomic and proteomic techniques have generated tremendous amount of DNA and protein sequences. Great progress has been made in terms of predicting protein–DNA interactions and protein–protein interactions.11–13 However, insufficient attention has been paid to the prediction of protein–RNA interactions due to the lack of experimental data.Fortunately, the recently accumulated protein–RNA experimental data make it possible to analyze the characteristics of RNA binding and identify protein–RNA interactions. For instance, some researchers have analyzed and discussed the structural and chemical characteristics of RNA binding residues,14–18 and have compared those proteins that bind different functional classes of RNA targets.17 Jones et al.14 analyzed RNA–protein interactions at a structure level, mainly based on chemical and physical properties of RNA-binding residues and the distribution of atom–atom contacts in the complexes. Ellis et al.18 presented a statistical analysis of the large-scale dataset of protein–RNA complexes and made a comparison of properties for binding residues bound to different functional classes of RNA. On the other hand, there have been other literatures for analyzing and discussing protein–RNA interactions from structural, functional, and other aspects.19,20
Some methods synthetically analyzed the dominating factors for determining protein–RNA interactions in allusion to different groups of data.15–17 Most of the existing works on protein–RNA interactions focus on the analysis and discussion of protein–RNA complexes. Recently, computational approaches with regard to protein–RNA interactions have been proposed but they are mainly presented to predict either RNA-binding sites based on protein information21–28 or RNA-binding proteins,29–31 rather than the prediction of protein–RNA interactions. For example, Han et al.30 proposed an SVM-based machine learning method to distinguish the RNA-binding from non-RNA-binding proteins utilizing protein primary sequences. To date, the prediction of the RNA–protein binding residues has been extensively studied, but there have been few works for protein–RNA interaction prediction,32–34 which is essential to reconstruct the protein–RNA relevant network. Pancaldi and Bahler32 used more than 100 different properties of mRNA and protein to construct features to make predictions by RF and SVM classifiers. The method has many limits for the present data. Muppirala et al.33 also employed RF and SVM classifiers to predict protein–RNA interactions. In addition, Bellucci et al.34 utilized several kinds of physicochemical properties of protein and RNA to analyze and predict the interaction properties for individual residues.
The fact that there are many functional large non-coding RNAs (ncRNAs) inside cells drives the recent studies to explore the functional diversity and mechanistic role of these large ncRNAs. The precise mechanism by which ncRNAs function remains poorly understood. One urgent task is to explore the interaction between ncRNAs and proteins. The functional importance of many ncRNA-protein interactions for correct transcriptional regulation has been demonstrated in small scale experiments. For example, several ncRNAs were discovered to be required for the correct localization of chromatin proteins to genomic DNA targets. Thus, it is in pressing need to computationally predict ncRNA–protein interaction in a large scale manner. Importantly, long non-protein-coding RNAs (lncRNAs) are a novel class of RNA molecules that exhibit rising interest within the research community in recent years. These interactions are known to be closely related to the progression of complex diseases, and their function reaches from signaling, different ways of cellular modifications to scaffolding functions. In this study, we will particularly focus on non-coding RNA–protein (including lncRNA–protein) interaction prediction.
Computational approaches for predicting protein–RNA interactions by using small training data have become highly desirable. In particular, there is an urgent need for presenting a computational method to predict protein–RNA interaction based only on the primary sequences of RNA and protein. Hence, we aim to develop a new machine learning based method to distinguish protein–RNA interaction pairs from non-protein–RNA interaction pairs. Specifically to meet the challenge of small number of experimental data on protein–RNA interactions, we proposed a new Bayesian classifier to efficiently predict protein–RNA interactions based on supervised learning. We presented two kinds of Bayesian classification methods to identify protein–RNA interactions. One is a Naive Bayesian (NB) classification method, and the other is an Extended Naive Bayesian (ENB) classification method. Both of them just use primary sequences of RNA and protein as input, without requiring any structure-derived information. We show that the NB classifier is a fast and effective learning approach for predicting protein–RNA interactions, which follows the assumption of the independence between the features. On the other hand, the ENB classifier takes the feature dependency into account, and thus is able to offer the accurate prediction with correlated features. Numerical experiments show that our method achieved the prediction accuracy of 0.77 even although we currently used only small number of protein–RNA interaction pairs to train the classifiers. We demonstrated that our classifier performs better than other machine-learning-based models for predicting protein–RNA interactions. To verify the computational prediction on unknown protein–RNA interactions, we conducted non-coding RNA pull-down experiments for sbRNA CeN72 in C. elegans, which further validated the effectiveness of our method.
Materials and methods
Collecting data
Three non-redundant datasets of protein–RNA interactions were extracted from the databases PRIDB and NPInter. PRIDB is a database of protein–RNA interfaces calculated from protein–RNA complexes in PDB.36 We constructed a positive sample set RPI2241, which composes 2241 experimentally validated protein–RNA pairs.33 RPI369 is a subsection of RPI2241 by excluding all protein–RNA interaction pairs with ribosomal proteins or ribosomal RNAs in various organisms.33 Here, the dataset RPI369 is also taken into account. Moreover, a dataset of non-coding RNA and protein (protein–ncRNA) interaction pairs was extracted from our NPInter database (http://www.bioinfo.org.cn/NPInter), which is a complete database covering eight category functional interactions between noncoding RNAs (except tRNAs and rRNAs) and proteins related biomacromolecules (proteins, mRNAs and genomic DNAs) in six model organisms, i.e., Caenorhabditis elegans, Drosophila melanogaster, Escherichia coli, Homo sapiens, Mus musculus and Saccharomyces cerevisiae. At present, NPInter covers the largest number of experimentally verified protein–ncRNA interaction data. We selected the protein–ncRNA physical interactions in it. Totally, 367 pairs of the ncRNA and protein sequences were collected as positive samples, which are shown in Table S1 (ESI†). From the two datasets RPI369 and RPI2241, we individually constructed approximate negative sample sets with twice number of pairs by randomly pairing the RNA and protein sequences after removing the pairs existed in the positive sample sets. Due to the limitation of protein–RNA interaction data in NPInter, all pairs of protein–ncRNA interactions from the six organisms were used as positive samples (with the conservative assumption of the interacting molecular pairs). Up till now, there are no definite negative samples of ncRNA–protein interactions are available. To generate a negative sample set, for each organism, the protein–ncRNA pairs from the positive set were shuffled by randomly reordering the protein while keeping the RNA fixed. The random negative sample sets may contain a small fraction of false negative samples, which can affect prediction performances. In our computations, we select a negative sample set which can perform better in the training.Constructing a feature vector from sequences
The construction of a feature vector for each pair of protein–RNA was based only on composition information of the primary sequences. Protein properties contributed to protein classification showed that amino acid composition and hydrophobicity have important effect on the interaction of a protein with other biomolecules, such as protein and RNA.30 Furthermore, the dynamics of protein–RNA interfaces further proved the significant effect of charges and polarity.20 Since the backbone of RNA is negatively charged, charge and polarity are expected to be particularly important features for the binding of a protein with its RNA-substrate. Apparently, one method cannot focus solely on charges and polarity to discover how RNA–protein recognition occurs.37 Some analyses of the classification of RNA-binding residues suggest that RNA-binding residues have a prominent tendency towards the amino acid with certain properties.28,37The 20 amino acid residues were categorized into seven classes according to their physicochemical properties, and then the dimensions of the vector space were dramatically reduced, thereby overcoming the overfitting problem.35 The conjoint triad was proposed to express the properties of one amino acid and its vicinal amino acids.35 In this work, we employed the similar strategies to encode the residues. Different from that in the protein–protein interaction, 20 amino acid residues were classified into four classes {‘DE’}, {‘HRK’}, {‘CGNQSTY’}, and {‘AFILMPVW’} according to their charge and polarity of side chains in the protein–RNA interaction.26,30 To consider one amino acid and its vicinal amino acids, the definition of a conjoint triad is employed to denote a unit of three continuous amino acids.35 Accordingly, all the triads can be classified into 4 × 4 × 4 classes. For any two triads, if the residues in the corresponding positions belong to the same class, then the two triads are thought to be one class of triads. The latter ‘triads’ refer to one class of triads.
We mainly used three descriptors for a pair of protein and RNA sequence. From the biological perspective, these features indicate their interaction propensity. First is the composition of amino acid triads. One class of triads corresponds to one feature, and hence there are 4 × 4 × 4 features of triads. Triad composition is calculated by implementing the normalized frequency of the triads in the protein sequence.35 Second is the composition of k-nucleotide acids (simply k-NAs). k-NAs refer to a unit of k continuous nucleotide acids. k-NAs composition is calculated in the same way as the triad composition. Third is the composition of triads and k-NAs combination. The interaction of RNA and protein might be mainly attributed to the interaction of amino acid residues and nucleotide acid residues from the biochemical viewpoint. Thus, the combination of triads and k-NAs is also presented as a kind of feature descriptor. Totally, the features for the three descriptors are 4k + 4 × 4 × 4 + 4 × 4 × 4 × 4k in all. There might be some overlaps in these features to some extent. All the features are combined to form the feature vector, which is approximately a 4 × 4 × 4 × 4k dimensional vector. A high dimensional feature vector has resulted in high computational complexity. However, a small number of features may suffice to represent their relationship with RNA–protein interaction. To overcome the difficulty, a feature selection method was proposed to decrease the dimension of the feature vector and extract valuable features, which is described in the next section.
NB classifier and ENB classifier
We developed two classifiers, i.e., NB classifier and ENB classifier, to distinguish protein–RNA interaction pairs from non-protein–RNA interaction pairs. The NB method assumes the independence of attributes, which greatly reduces the complexity of the classifier and improves the reliability of the estimated parameters in particular when the dimensionality of the input is much higher comparing to the size of the available training set. However, if the features adopted in the classifier are highly correlated, the ENB model is more efficient.Construction of an NB classification model
This score measures the enrichment of combination (xi, yj) in the positive relative to negative samples. In essence the above score is the likelihood ratio scores, which can be regarded as a measure of the usefulness of single combination feature (xi, yj). A likelihood ratio score much larger than 1 indicates that the feature is a good predictor for protein–RNA interaction. Likewise, a likelihood ratio score less than 1 indicates that the evidence is anti-predictive for protein–RNA interaction. Likelihood ratios of different features are directly comparable. According to the measured F(xi, yj), the enriched features can be extracted from all the features. Fig. 1 shows that 500 features are extracted from all the 4 × 4 × 4 × 43 = 4096 features when k = 3.
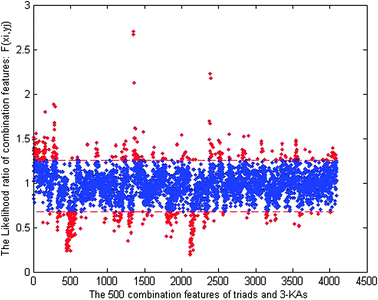 | ||
| Fig. 1 Selecting predictive features by thresholding the likelihood ratio based score. The 500 features (red points) were selected from all the 4096 triads and 3-KAs combination features (red points and blue points) for k = 3. The red points refer to the 500 selected features from all the combination features. The red points above the first dash line indicate the features enriched in the positive samples, and those below the second dash line indicate the features enriched in the negative samples. | ||
In Fig. 1, the horizontal axis corresponds to 4096 combination features, and the vertical axis corresponds to the score of the likelihood ratio for each feature. The two dashed lines divide all the features into three subsections, i.e. those above the first line denote the features enriched in the positive sample set, and those below the second line denote the features enriched in the negative sample set. The extracted 500 features are these enriched features discriminatively in the positive and negative sample sets. All of these features are available in Tables S2 and S3 (ESI†). We observed that the extracted features by feature selection scheme showed significant preferences for different classes of amino acid residues in the positive samples and negative samples, which implies that the prominent residues in the positive samples have significant tendency to basic and polar amino acids, and those in the negative samples have main tendency to acidic and non-polar residues. This was expected when the overall negative charge of RNA is considered.
The NB classifier classifies the samples according to the probability ratio:
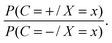 | (1) |
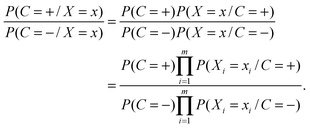 | (2) |
Construction of an ENB model
Given a pair of hypothetical RNA and protein sequences, as shown in Table 1, there are two classes of triads {ARR}, {RRK, RKR, KRR, RRR} and two 2-nucleotide features {UA}, {UU}. The amino acid residues ‘R’ and ‘K’ in the above triads fall into one class of amino acids, whereas residue ‘A’ falls into another class in the four classes of residues. From above, it is obvious that the residues in the first position of ‘ARR’ and ‘RRK’ belong to different classes, hence the two triads ‘ARR’ and ‘RRK’ belong to different classes of triads. If the residues in the corresponding positions belong to the same class respectively, the two triads are defined as one class of triads. For example, the four triads in the second brace belong to one class of triads due to the residues in the corresponding positions coming from the same class. The triads–2-NAs combinations correspond to four features, namely {ARR-UA}, {RRK-UA, RKR-UA, KRR-UA, RRR-UA}, {ARR-UU} and {RRK-UU, RKR-UU, KRR-UU, RRR-UU}. The above ones included in one brace belong to one combination feature. For the first two combination features {ARR-UA} and {RRK-UA, RKR-UA, KRR-UA, RRR-UA}, only two elements in the first position belong to different classes, and two elements in the remaining four positions belong to the same class, thereby the degree of similarity between the two features is computed as (5 − 1)/5 = 0.8. Similarly, the similarity degree of {ARR-UA} and {RRK-UU, RKR-UU, KRR-UU, RRR-UU} is (5 − 2)/5 = 0.6. The more similar features are, the stronger the correlation between them is. The similar features might have similar function, and hence they are deemed to belong to one kind of feature. In the above example, the similarity degree achieves 0.8, that shows that the two features are more similar, and then the two features are combined into a new group of combination feature {ARR-UA, RRK-UA, RKR-UA, KRR-UA, RRR-UA}.
| Amino acid sequence → A R R K R R R R R R K |
| Nucleotide acid sequence → U U U U A |
| Two kinds of triads: {ARR}, {RRK, RKR, KRR, RRR} |
| Two 2-nucleotide acids: {UA}, {UU}{UA}, {UU} |
Given the high computational complexity and a small scale training data, it is impossible to learn the optimal Bayesian network structure from training data. In this paper, we rely on prior knowledge to pre-determine the Bayesian network structure.
To determine the Bayesian network structure, we maximally utilize the available correlation relationships among features and meanwhile maximize the number of conditional independencies among features. We recombine the selected features in the NB model into a group of new features by clustering based on the correlation between them. Suppose there exist k non-overlapping groups of the total m features, i.e., G1,G2,⋯,Gk, Gi ∩ Gj = ∅, ∀ i,j. We use naïve Bayes to integrate features in group level, where two groups of sequence features are assumed to be conditionally independent given protein–RNA interaction. In this case, the likelihood ratio of the combined groups is equal to the product of the likelihood ratios for an individual group. The feature integration inside each individual group is achieved via a full Bayesian Network, where none of the features are conditionally independent. In this case, we estimate all possible combinations of features values. The structure is then fixed during training and testing. This way, the computational complexity of the problem is dramatically reduced, and only a small training set is required.
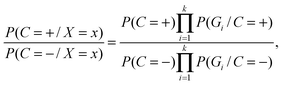 | (3) |
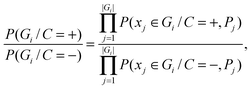 | (4) |
As an example, we assume X = (x1,x2,x3,x4) to denote a 4-dimensional feature vector corresponding to four features. And only the features related to x2 and x3 have strong correlation. Due to the correlation between the two features, the formula (1) can be computed in the following way.
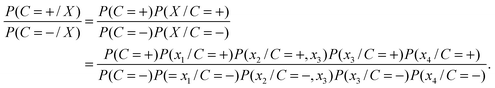 | (5) |
Performance evaluation
The performance of the NB classifier and the ENB classifier was evaluated by 10-fold cross validation experiments. In our experiments, the cross validation is performed for ten times and the average results are used. The threshold θ was empirically determined to provide an optimal correlation coefficient on the sample set. The performance of two classifiers was completely measured by the following parameters: SE (sensitivity), SP (specificity), ACC (overall accuracy), PRE (precision) and MCC (Matthew's correlation coefficient). They are commonly denoted as:where TP stands for true positives, TN for true negatives, FP for false positives, and FN for false negatives. SP and SE measure how well the binary classifier recognizes negative and positive samples, respectively. As a rule, SP decreases when a predictor's SE increases. The threshold θ can be tuned to increase the specificity at the expense of the sensitivity. With inevitable loss of information, a complementary measure of the predicted performance MCC41 is a more meaningful measure than SP and SE for comparing the different classifiers. Furthermore, overall accuracy (ACC) is given to show how well a classifier distinguishes all true samples (including true positives and true negatives). A perfect prediction achieves 100% ACC, and a random prediction achieves only 50% ACC. Compared to SE, PRE is given to further indicate the prediction accuracy of true positives.
In addition to the above measures, we also used the receiver operating characteristic (ROC) curve42 and area under the ROC curve (AUC)43 to assess the performance of NB and ENB classifiers. The different thresholds of probability are used to plot the ROC curve, by which we can visualize how the thresholds change SE and SP. AUC calculates the area under an ROC curve and its range of change is between 0 and 1. The maximum value 1 represents a perfect prediction. For a random guess, the value of AUC is close to 0.5. To further test the ability of NB and ENB classifiers to predict ncRNA–protein interactions, we also utilized the RPI369 and the RPI2241 as the training sample set, and the NPInter dataset as the testing sample set. We trained the two classifiers on the RPI369 and RPI2241 datasets, and independently tested the prediction performance of the two classifiers on the NPInter dataset, respectively.
ncRNA pull-down experiment
We validated our de novo prediction of protein–ncRNA interactions in the worm by an ncRNA pull-down experiment. The mix-stage N2 (wild type) worms were harvested and washed three times using an M9 buffer. Nuclear extracts were isolated with NE-PER Nuclear Protein Extraction Kit (Thermo Scientific). The RNA pull-down experiments were performed as previously described.38,39 Biotin-labeled full-length CeN-72 ncRNA44 and its antisense (negative control) were treated with the Biotin RNA Labeling Mix (Roche) and T7 and Sp6 RNA polymerase (Stratagene). Biotinylated RNAs were treated with 400 U mL−1 RNase-free DNase I and purified with TRIzol (Invitrogen). Blocked with 20 μg avidin (Roche) at 4 °C for 10 min and then incubated with 10 μL of Dynabeads® M-280 Streptavidin (Invitrogen) in lysis buffer (50 mM HEPES, pH 7.4, 10 mM MgCl2, 100 mM NaCl, 1 mM dithiothreitol, 0.1%Triton X-100, 10% glycerol, RNase inhibitor, protease inhibitor (Roche)). Then the nuclear extracts (0.1 mg) were added into the RNA–beads mixture mentioned above and incubated at 4 °C for 1 h. The resultant RNA–protein complexes were separated using MagRack 6 (GE Healthcare) for 3 min at 4 °C. Wash with 20 bed volumes of lysis buffer five times for 5 min each at 4 °C, boiled in SDS buffer and subjected to SDS-PAGE gel electrophoresis and Mass Spectrometry.40Results and discussion
The results for the NB classifier
In our experiments, the threshold θ was selected to maximize the correlation coefficient on the sample set. k Denotes the number of conjoint nucleotide acids for RNA sequences. Upon computation and comparison, the better results are obtained for k = 3. There are 64 × 43 triads–3-NAs combination features in all. There are more or less 1/2, 1/4 and 1/8 features selected for constructing a feature vector by feature selection. The average results of three sample sets are shown in Table 2. From Table 2, we found that the overall accuracy correlates positively with the number of selected features mostly. When the number of selected features increases to one half of all the features or even less, the higher overall accuracy is achieved. For example, the overall accuracy for three sample sets reaches 0.74, 0.77 and 0.76, respectively, when the number of features increases to one half of all features or even less. However, when the number of selected features increases to a certain degree, the overall accuracy then increases very slowly or even decreases. It is therefore concluded that feature selection process not only picks up the advantageous features and excludes the redundant ones, but also greatly improves the computational efficiency.| Sample set | # Of selected features | ACC | SE | SP | PRE | MCC |
|---|---|---|---|---|---|---|
| NPInter | 500 | 0.7432 | 0.4262 | 0.9016 | 0.6842 | 0.3810 |
| 1000 | 0.7423 | 0.3552 | 0.9358 | 0.7345 | 0.3730 | |
| 2000 | 0.7368 | 0.3333 | 0.9385 | 0.7305 | 0.3569 | |
| RPI369 | 500 | 0.7326 | 0.3089 | 0.9444 | 0.7355 | 0.3442 |
| 1000 | 0.7498 | 0.3659 | 0.9417 | 0.7584 | 0.3947 | |
| 2000 | 0.7715 | 0.3821 | 0.9661 | 0.8494 | 0.4598 | |
| RPI2241 | 500 | 0.7378 | 0.4496 | 0.8819 | 0.6556 | 0.3721 |
| 1000 | 0.7326 | 0.4174 | 0.8902 | 0.6552 | 0.3545 | |
| 2000 | 0.7574 | 0.4429 | 0.9147 | 0.7220 | 0.4180 |
In our computations, we found that the SE of prediction is mostly at a low level of 40%, compared to the level of 90% for SP. The lower prediction accuracy for positive samples is very likely resulted from the limiting positive samples. Few samples in a positive set tend to be less adequate in representing all kinds of positive samples, which might partially contribute to inaccurate prediction by the supervised learning. The fact that the sample data come from multiple different organisms likely makes it more difficult for a statistical classification system to unambiguously predict the interaction of RNA and protein, which is another possible reason for low accuracy for the positives. But, with the further accumulation of experimental data for protein–RNA interactions, this problem can be considerably alleviated in future. The sensitivity can be increased at the expense of a decrease in specificity by varying the threshold of classification θ. The change trend of SE and SP can be obviously seen in the ROC curve shown in Fig. 2.
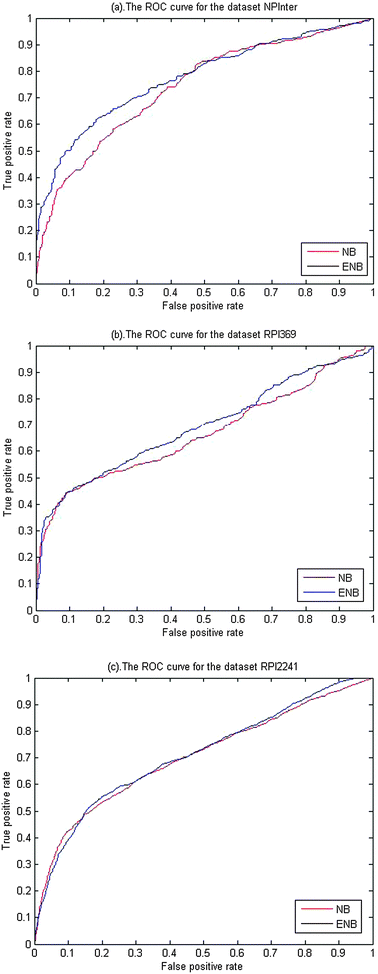 | ||
| Fig. 2 (a)–(c) indicate the ROC curves of the prediction results obtained from an NB classifier and an ENB classifier, separately in NPInter, RPI369 and RPI224. The blue dash line denotes the ROC curve from the NB classifier and the red solid line denotes the ROC curve from the ENB classifier. | ||
On this non-redundant dataset of RNA–protein interactions, the NB classifier performs well by only utilizing the primary sequence information. With the parameter k = 3 and the number of extracted features reaching 2000, the NB classifier achieved an overall accuracy of 0.74, 0.77 and 0.76, with a correlation coefficient of 0.36, 0.46 and 0.42, a specificity of 0.94, 0.97 and 0.92, and a precision of 0.73, 0.85 and 0.72 for NPInter, RPI369 and RPI2241 dataset, respectively.
The results for the ENB classifier
The same three sample sets were used to train the ENB classifier, and the results were shown in Table 3. Based on above feature selection, 1000 features are firstly extracted. Then a new group of features are constructed by clustering the extracted features. The ‘Cluster’ in Table 3 denotes the number of new feature groups obtained. Table 3 provided the results of the ENB classifier with the cluster threshold c = 0.2. The threshold recombines the extracted features into less than 500 groups of new features when k = 3. The ENB classifier obtained the ACC of 0.78, 0.75 and 0.74 for NPInter, RPI369 and RPI2241, with SP of 0.93, 0.95 and 0.92, PRE of 0.77, 0.78 and 0.70, and MCC of 0.47, 0.40 and 0.37.| Sample set | # Of selected features | Cluster | ACC | SE | SP | PRE | MCC |
|---|---|---|---|---|---|---|---|
| NPInter | 1000 | 91 | 0.7760 | 0.4728 | 0.9277 | 0.7656 | 0.4668 |
| RPI369 | 1000 | 465 | 0.7500 | 0.3497 | 0.9500 | 0.7772 | 0.3955 |
| RPI2241 | 1000 | 386 | 0.7403 | 0.3889 | 0.9158 | 0.6980 | 0.3693 |
Comparison studies
Upon comparison of Tables 2 and 3, the ENB classifier performed as good as or better than the NB classifier overall. In NPInter, RPI369 and RPI2241, the average overall accuracy obtained from ENB classifier was 0.78, 0.75 and 0.74 individually, compared to 0.74, 0.75 and 0.73 for the NB classifier when the number of selected features is 1000. In addition, the dimension of a feature vector in the ENB classifier decreases to at most 500 by clustering. The ENB classifier can achieve better prediction performance, and at the same time decrease the computational complexity.The computational results (data not shown) from the two classifying models indicate that the overall accuracy has improved in a way when k is from 2 to 3, but less improved or even declined when k is from 3 to 4. The best performance was obtained with k = 3. The similar change in accuracy for the two classifiers seems to conclude that the length of nucleotide acids has effects on the prediction of protein–RNA interaction, and that 3-nucleotide acid feature may be deemed as a functional unit in the interaction event. Moreover, we also constructed a balanced dataset with equal number of positive samples and negative samples. The prediction results on this dataset are shown in Table S4 (ESI†). We found that it is slightly different from those of Tables 2 and 3. For example, the overall accuracies have decreased obviously when the number of training samples decreased. The results also provided evidence for the importance of the number of the training samples.
Fig. 2(a)–(c) shows the ROC curves of the prediction results by the NB classifier, and the ENB classifier in NPInter, RPI369 and RPI224, respectively. From the figures, we observed that the ROC curve of the ENB classifier is slightly higher than that of the NB classifier for the RPI369 and the NPInter. For the RPI2241, two ROC curves have nearly the identical change. The trivial change of ROC curves indicates the two classifiers have similar prediction performance on the whole. However, the computational complexity for the NB classifier has increased more promptly with the increase of sample data compared to the ENB classifier. Namely, the ENB model is more efficient than the NB model meanwhile keeping the better prediction performance. The AUC of the ENB classifier achieved ∼0.78, ∼0.68, ∼0.72, compared to ∼0.74, ∼0.64, ∼0.71 for the NPInter, the RPI369 and the RPI2241.
All of the computational results demonstrate that our ENB classifier not only considers the correlation between features, but also yields a significant improvement in computational efficiency over the NB classifier. In NB, we employed a feature selection process to extract important features distinguishing protein–RNA interactions from non-interactions. Compared to NB, the relationship of these features are considered simultaneously in ENB. It will have large applicable scope because there is no assumption of the dependency and redundancy in these features. The competitive results of the NB with feature selection and ENB also provided evidence for the importance of feature relationship in the prediction. Our presented feature selection scheme and extended NB classification will also shed light on other similar researches.
The results for predicting ncRNA–protein interactions
To explore the effectiveness of the classifiers, we evaluated our method in predicting ncRNA–protein interaction networks derived from the NPInter data. As we know, the NPInter dataset is a dataset without ribosomal sequences. We first trained our classifiers on the RPI369 dataset (not to include any pairs from ribosomes), and then trained them on the RPI2241 dataset (to include ribosomal sequence pairs). In this experiment, a training sample set was constructed by the above method. And only 500 features were selected for prediction by feature selection method. The probability ratio threshold for prediction was 1. For a pair of ncRNA–protein sequences from the NPInter dataset, the probability ratio more than 1 shows that they are predicted to interact.In our method, we encoded proteins and RNAs only by sequence-based information. Compared to the limited structure information available, the easy availability of sequence information will benefit the flexibility and applicability of our method in the prediction. One research direction is to evaluate the potential improvement of prediction accuracy by employing more valuable information.
Tables 4 and 5 show the prediction results for the NB classifier and the ENB classifier on the NPInter dataset. In our prediction, we separately computed the number of correctly predicted ncRNA–protein pairs for different organisms that were shown in the two tables. The results showed that our ENB model predicted more accurate for the Drosophila melanogaster, Mus musculus and Saccharomyces cerevisiae than the other organisms for the two training sets RPI369 and RPI2241. The results indicate that ENB method out-performed NB method when trained whether on the RPI369 or the RPI2241 dataset. Concretely, when trained on the RPI369 dataset, the ENB classifier achieved an accuracy of ∼67%, compared to ∼62% for the NB classifier. And when trained on the RPI2241dataset, the ENB classifier achieved an accuracy of ∼79%, compared to ∼66% for the NB classifier. The prediction results further proved the effectiveness and efficiency of our proposed ENB method.
| Organism | Total RNA–protein pairs | Pairs predicted by NB classifier (%) | Pairs predicted by ENB classifier (%) |
|---|---|---|---|
| Caenorhabditis elegans | 3 | 3(100%) | 1(33%) |
| Drosophila melanogaster | 26 | 13(50%) | 19(74%) |
| Escherichia coli | 25 | 13(52%) | 17(68%) |
| Homo sapiens | 148 | 93(63%) | 77(52%) |
| Mus musculus | 46 | 30(65%) | 40(87%) |
| Saccharomyces cerevisiae | 119 | 76(64%) | 89(75%) |
| Total | 367 | 228(62%) | 243(67%) |
| Organism | Total RNA–protein pairs | Pairs predicted by NB classifier (%) | Pairs predicted by ENB classifier (%) |
|---|---|---|---|
| Caenorhabditis elegans | 3 | 1(33%) | 1(33%) |
| Drosophila melanogaster | 26 | 23(88%) | 25(96%) |
| Escherichia coli | 25 | 12(48%) | 15(60%) |
| Homo sapiens | 148 | 84(57%) | 91(62%) |
| Mus musculus | 46 | 28(61%) | 37(80%) |
| Saccharomyces cerevisiae | 119 | 94(79%) | 118(99%) |
| Total | 367 | 242(66%) | 287(79%) |
Prediction and experimental validation of protein–ncRNA interactions in worms
After training our predictor on the available RPI369 and RPI2241 datasets, we predicted the protein–ncRNA interactions in worms, respectively. As described above, the features selected in our predictor were constructed only based on available sequence information, without any other information. We collected a group of worm proteins and ncRNAs, and encoded them into the described features according to our proposed method, from which the interacting status can be predicted by the trained predictor.We selected 30 ncRNAs (17 sbRNAs and 13 snlRNAs) and 759 proteins to predict interactions in worms.44 The list of these proteins were shown in Table S5 (ESI†). For the nc11 (sbRNA CeN72) in C. elegans, we predicted 115 pairs of interactions when trained on the RPI369 and 207 pairs of interactions on the RPI2241, which were shown in Tables S6 and S7 (ESI†), respectively. To verify our prediction results, we performed the ncRNA pull-down experiments to identify the interacting proteins of sbRNA CeN72 in C. elegans. The detailed experimental steps are described in Materials and methods. Our biological experiments were repeated for 7 times, and 51 proteins were identified to interact with CeN72. We found that 7 predicted interacting proteins on the RPI369 (O44572, P41937, P49041, P52013, Q18943, Q20140 and Q93615) and 10 ones on the RPI2241 (P27639, P34460, P34690, P41937, P49405, P52013, P91306, Q18625, Q18885 and Q22508) were verified in the experiments. The detailed information of these proteins was listed in Table S5 (ESI†). The 7 predicted interacting proteins on the RPI 369 were from different protein families and had low sequence similarity. And the 10 proteins on the RPI2241 had low sequence identity, except P34690 and P41937, which were both members of the tubulin family. The results of the wet experiment provided evidence for the effectiveness of our method of de novo prediction of protein–RNA interaction only by sequence information.
Conclusions
In this paper, we presented a novel naïve Bayes based method for predicting protein–RNA interactions, and further validated the predictions by biological experiments. Specifically, the NB classifier assumes the independence of all features with a simple computational procedure, and the ENB classifier takes the dependence between features into account with much lower computational complexity. For ENB, we first chose effective features by filtering unreliable ones, then compressed the dimension of feature vectors to reduce the computational complexity, and further constructed the ENB classifier to infer protein–RNA interactions. The computational results show that the ENB classifier is superior to the NB classifier in effectiveness and efficiency. Clearly, the accuracy for the two classifiers is expected to be improved significantly when there are more training data of protein and RNA interactions. In other words, we believe that our model is able to achieve a higher accuracy in the prediction when substantial experimental data are available in the near future. Although the feature selection method was also constructed by selecting the effective features and removing the redundant ones, a great challenge is to how to further reduce the computational complexity without sacrificing the loss of information.To meet the challenge of a small set of well-constructed gold-standard dataset for ncRNA–protein interaction, we utilized graphical models such as Bayesian networks45,46 to capture the pattern in the training data. Specifically we adopted a transparent feature integration strategy which is especially important in our case, where the gold-standard data are scarce. Our extended naive Bayesian network structure is pre-chosen by carefully selecting predictive features and considering their possible conditional dependence relationships. As a major advantage, we only need to learn Bayesian network parameters during training. In addition, our method is particularly suitable for predicting long non-coding RNA–protein interactions. The longer the RNA sequence is, the more accurate the feature importance and correlation estimation are. In this case, the parameters in the Bayesian network can be reasonably estimated using the small set of gold-standard positive data. This fact enables our method to study functional roles for long non-coding RNAs, a novel class of RNA molecules, that exhibit rising interest within the research community in recent years.47,48
Funding
This work was supported by the Knowledge Innovation Program of CAS with Grant no. KSCX2-EW-R-01 (R.C. and L.C.). This work was also supported by NSFC under Grant nos. 91029301 (L.C.), 61134013 (L.C.), 31100949 (Z.P.L.), 11201045 (C.L.), 61171007 (Yo.W.) and 11131009 (X.S.Z.), the Chief Scientist Program of SIBS of CAS with Grant no. 2009CSP002 (L.C.), the Knowledge Innovation Program of SIBS of CAS with Grant no. 2011KIP203 (Z.P.L.), National Center for Mathematics and Interdisciplinary Sciences of CAS (L.C. and Z.P.L.), Shanghai NSF under Grant no. 11ZR1443100 (Z.P.L.), and Japan (JSPS) FIRST Program initiated by CSTP (L.C.), the Education Department Science Foundation of Liaoning Province of China with Grant no. L2011068 (Y.W.).Acknowledgements
We thank the members of Xiang-Sun Zhang's research group, Luonan Chen's lab for constructive discussions and Runsheng Chen's lab for experimental preparation. L.C., R.C. and X.S.Z. initialized and supervised the project. Y.W., Z.P.L. and Yo.W. discussed and designed the computational framework; Y.W. and Q.H. performed the calculations; R.C., X.C., D.X. designed and performed the experimental validation. Y.W., Z.P.L, Yo.W., X.S.Z., R.C. and L.C. wrote the paper. All authors read and approved the manuscript.Notes and references
- D. Moras, Curr. Opin. Struct. Biol., 1992, 2, 138–142 CrossRef.
- P. B. Moore, Annu. Rev. Biophys. Biomol. Struct., 1998, 27, 35–58 CrossRef CAS.
- V. Ramakrishnan and S. W. White, Trends Biochem. Sci., 1998, 23, 208–212 CrossRef CAS.
- H. Siomi and G. Dreyfuss, Curr. Opin. Genet. Dev., 1997, 7, 345–353 CrossRef CAS.
- J. Mata, S. Marguerat and J. Bahler, Trends Biochem. Sci., 2005, 30, 506–514 CrossRef CAS.
- R. Singh, Gene Expression, 2002, 10, 79–92 CAS.
- G. Varani and K. Nagai, Annu. Rev. Biophys. Biomol. Struct., 1998, 27, 407–445 CrossRef CAS.
- D. N. Frank and N. R. Pace, Annu. Rev. Biochem., 1998, 67, 153–180 CrossRef CAS.
- K. B. Hall, Curr. Opin. Struct. Biol., 2002, 12, 283–288 CrossRef CAS.
- B. Tian, P. C. Bevilacqua, A. Diegelman-Parente and M. B. Mathews, Nat. Rev. Mol. Cell Biol., 2004, 5, 1013–1023 CrossRef CAS.
- N. Luscomb, R. Laskowski and J. Thornton, Nucleic Acids Res., 2001, 29, 2860–2874 CrossRef.
- S. Jones, P. van Heyningen, H. Berman and J. Thornton, J. Mol. Biol., 1999, 287, 877–896 CrossRef CAS.
- K. Nadassy, S. Wodak and J. Janin, Biochemistry, 1999, 38, 1999–2017 CrossRef CAS.
- S. Jones, D. Daley, N. Luscombe, H. Berman and J. Thornton, Nucleic Acids Res., 2001, 29, 943–954 CrossRef CAS.
- M. Treger and E. Westhof, J. Mol. Recognit., 2001, 14, 199–214 CrossRef CAS.
- E. Jeong, H. Kim, S. Lee and K. Han, Mol. Cells, 2003, 16, 161–167 CAS.
- J. Allers and Y. Shamoo, J. Mol. Biol., 2001, 311, 75–86 CrossRef CAS.
- J. J. Ellis, M. Broom and S. Jones, Proteins, 2007, 66, 903–911 CrossRef CAS.
- S. D. Auweter, F. C. Oberstrass and F. H.-T. Allain, Nucleic Acids Res., 2006, 34, 4943–4959 CrossRef CAS.
- T. Hermann and E. Westhof, Nat. Struct. Biol., 1999, 6, 540–544 CrossRef CAS.
- E. Jeong, I. F. Chung and S. Miyano, Genome Inf., 2004, 15, 105–116 CAS.
- M. Terribilini, J. D. MSander, J. H. Lee, P. Zaback, R. L. Jernigan, V. Honavar and D. Dobbs, Nucleic Acids Res., 2007, 35, W578–W584 CrossRef.
- L. Wang and S. J. Brown, Nucleic Acids Res., 2006, 34, W243–W248 CrossRef CAS.
- Y. Wang, Z. Xue, G. Shen and J. Xu, Amino Acids, 2008, 35, 295–302 CrossRef CAS.
- M. Kumar, M. M. Gromiha and G. P. Raghava, Proteins, 2008, 71, 189–194 CrossRef CAS.
- C. W. Cheng, E. C. Su, J. K. Hwang, T. Y. Sung and W. L. Hsu, BMC Bioinf., 2008, 9(Suppl. 12), S6 CrossRef.
- Y. Murakami, R. V. Spriggs, H. Nakamural and S. Jones, Nucleic Acids Res., 2010, 38, W412–416 CrossRef CAS.
- Z. P. Liu, L. Y. Wu, Y. Wang, X. S. Zhang and L. Chen, Bioinformatics, 2010, 26, 1616–1622 CrossRef CAS.
- Y. D. Cai and S. L. Lin, Biochim. Biophys. Acta, 2003, 1648, 127–133 CrossRef CAS.
- L. Y. Han, C. Z. Cai, S. Lo, M. C. Chung and Y. Z Chen, RNA, 2004, 10, 355–368 CrossRef CAS.
- X. Yu, J. Cao, Y. Cai, T. Shi and Y. Li, J. Theor. Biol., 2006, 240, 175–184 CrossRef CAS.
- V. Pancaldi and J. Bahler, Nucleic Acids Res., 2011, 39, 5826–5836 CrossRef CAS.
- U. K. Muppirala, V. G. Honavar and D. Dobbs, BMC Bioinf., 2011, 12, 489 CrossRef CAS.
- M. Bellucci, F. Agostini, M. Masin and G. G. Tartaglia, Nat. Methods, 2011, 8, 444–445 CrossRef CAS.
- J. Shen, J. Zhang, X. Luo, W. Zhu, K. Q. Yu, K. X. Chen, Y. X. Li and H. Jiang, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 4337–4341 CrossRef CAS.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS.
- M. Terribilini, J. H. Lee, C. Yan, R. L. Jernigan, V. Honavar and D. Dobbs, RNA, 2006, 12, 1450–1462 CrossRef CAS.
- O. Gozani, J. G. Patton and R. Reed, EMBO J., 1994, 13, 3356–3367 CAS.
- J. L. Rinn, M. Kertesz, J. K. Wang, S. L. Squazzo, X. Xu, S. A. Brugmann, L. H. Goodnough, J. A. Helms, P. J. Farnham, E. Segal and H. Y. Chang, Cell, 2007, 129, 1311–1323 CrossRef CAS.
- A. Shevchenko, M. Wilm, O. Vorm, O. N. Jensen, A. V. Podtelejnikov, G. Neubauer, A. Shevchenko, P. Mortensen and M. Mann, Biochem. Soc. Trans., 1996, 24, 893–896 CAS.
- B. W. Matthews, Biochim. Biophys. Acta, 1975, 405, 442–451 CrossRef CAS.
- J. A. Swets, Science, 1988, 240, 1285–1293 CAS.
- A. P. Bradley, Pattern Recogn., 1997, 30, 1145–1159 CrossRef.
- W. Deng, Genome Res., 2005, 16, 20–29 CrossRef.
- Y. Wang, X. S. Zhang and Y. Xia, Nucleic Acids Res., 2009, 37, 5943–5958 CrossRef CAS.
- R. Jansen, H. Yu, D. Greenbaum, Y. Kluger, N. J. Krogan, S. Chung, A. Emili, M. Snyder, J. F. Greenblatt and M. Gerstein, Science, 2003, 302, 449–453 CrossRef CAS.
- T. R. Mercer, M. E. Dinger and J. S. Mattick, Nat. Rev. Genet., 2009, 10, 155–159 CrossRef CAS.
- J. A. Goodrich and J. F. Kugel, Nat. Rev. Mol. Cell Biol., 2006, 7, 612–616 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2mb25292a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2013 |