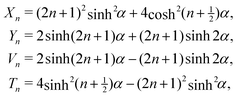Microfluidic ultralow interfacial tensiometry with magnetic particles
Scott S. H.
Tsai†
ab,
Jason S.
Wexler
b,
Jiandi
Wan‡
b and
Howard A.
Stone
*b
aSchool of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA
bDepartment of Mechanical and Aerospace Engineering, Princeton University, NJ 08544, USA. E-mail: hastone@princeton.edu
First published on 5th October 2012
Abstract
We describe a technique that measures ultralow interfacial tensions using paramagnetic spheres in a co-flow microfluidic device designed with a magnetic section. Our method involves tuning the distance between the co-flowing interface and the magnet's center, and observing the behavior of the spheres as they approach the liquid–liquid interface–the particles either pass through or are trapped by the interface. Using threshold values of the magnet-to-interface distance, we make estimates of the two-fluid interfacial tension. We demonstrate the effectiveness of this technique for measuring very low interfacial tensions, O(10−6–10−5) N m−1, by testing solutions of different surfactant concentrations, and we show that our results are comparable with measurements made using a spinning drop tensiometer.
1 Introduction
Ordinary oil–water solutions have interfacial tensions O(10−3) N m−1. However, there are also solutions that have interfacial tensions 1,000 times, or more, smaller. Such ultralow interfacial tensions occur in a range of different applications. For example, in enhanced oil recovery, residual oil that is trapped in reservoir pores can be dislodged when injected surfactant solutions cause interfacial tensions in the mixture to drop below O(10−5) N m−1.1–3 Phase separated colloid-polymer solutions, which have applications in the food industry for generating emulsions,4 have interfacial tensions in the ultralow range.5 Also, certain classes of surfactants are added to oil–water mixtures to produce very low interfacial tensions, in the range of O(10−7–10−5) N m−1, to make microemulsions.6 In addition, all-aqueous polymer solutions, with reported interfacial tensions O(10−4) N m−1 are used to create water-in-water droplets in microchannels and have potential benefits to drug delivery.7Despite the utility of these fluid systems, quantifying ultralow interfacial tensions practically and accurately is challenging. Traditional force tensiometry methods such as the Wilhelmy Plate and Du Noüy Ring are not suitable because of difficulties resolving the small forces experienced by the probes at the interfaces.8 Measuring very low interfacial tensions using the spinning drop method is also not ideal since the droplets equilibrate very slowly, making it challenging to extract an equilibrium value.9 The variety of techniques being proposed, including the breaking thread method,9 the laser interface manipulation method,8 the method of measuring static profiles near single walls,10 the method of visual observation of thermal capillary waves,11 and the method of deforming emulsion drops with optical tweezers12 suggest that a simple way to measure ultralow interfacial tensions is desirable.
Here we describe a method for measuring ultralow interfacial tensions by applying external magnetic fields to paramagnetic spheres in a microfluidic co-flow. Our approach has the distinct advantage of reducing the amount of reagents required, as well as the possibility of integration into lab-on-a-chip devices. Although microfluidic tensiometers have been demonstrated before,13–16 all such devices have been developed for measuring typical O(10−3) N m−1 interfacial tensions. Our technique is designed for measuring ultralow interfacial tensions. Specifically, we obtain estimates of the interfacial tension by determining whether and how paramagnetic spheres break through the interface between co-flowing fluids.
2 Experimental
Our microfluidic interfacial tensiometer is similar in design to a device for conformal coating of particles that we described previously.17 Polydimethylsiloxane (PDMS, Sylgard 184 silicone elastomer kit, Dow Corning, Midland, MI, USA) was patterned using standard soft-lithography techniques18 and then bonded to a glass microscope slide (Dow Corning, Midland, MI, USA) via plasma pretreatment. All channels have a constant height dc = 50 μm, and the co-flowing region has a width wc = 380 μm. Fig. 1(a) shows a schematic of paramagnetic beads suspended in the aqueous phase, entering the microfluidic device through the bead inlet, and centered, with a flow-focusing design, by the same fluid flowing through the inlet for the buffer phase. The beads (Sigma Aldrich, St. Louis, MI, USA) in our experiments have radii a = 2.5 μm and are suspended in the aqueous phase at 0.02 vol%.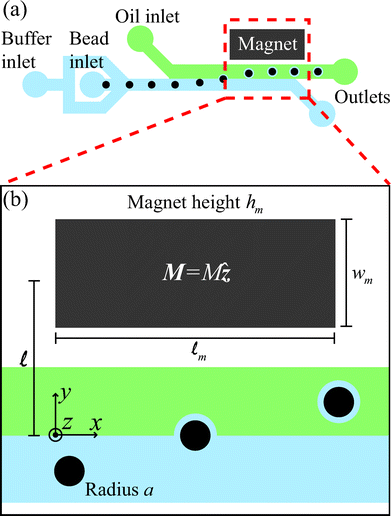 | ||
| Fig. 1 (a) A schematic diagram of the microfluidic tensiometer with a co-flow geometry, where the aqueous solution flows through the buffer inlet to center the beads, which are supplied through another inlet. Dodecane with 10 wt% Span 80 flows through the oil inlet. The permanent magnet draws paramagnetic beads towards, and possibly through, the two-fluid interface. (b) A magnified view of the region of influence of the magnet shows the geometric length scales of the system as well as the magnetization direction of the magnet, M = Mẑ. | ||
The non-aqueous (oil) solution enters through a side inlet to form a co-flow with the aqueous fluid and the beads. The non-aqueous solution consists of dodecane with 10 wt% sorbitan monooleate surfactant (Span 80), while the aqueous solution is a mixture of deionized water with sodium dodecyl sulfate (SDS) concentrations varying from 4–20 mM. Shum et al.19 reported interfacial tensions γ ≈ (10−6–10−5) N m−1 for similar mixtures, by spinning drop tensiometry. In our experiments, 25 wt% glycerol is added to the aqueous solution to more closely match the viscosities of the aqueous (μa) and non-aqueous (μna) phases, which are μa = 1.8 and μna = 2.7 mPa s, respectively.
A single flat neodymium iron boron magnet (K. J. Magnetics, Jamison, PA, USA), with magnetization M = 106 A m−1 and dimensions ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m × wm × hm = 9.5 × 4.8 × 1.6 mm, is placed adjacent to the microchannel, with the magnetization direction oriented through the thickness (Fig. 1(b)). A slot is cut in the PDMS next to the channel prior to bonding to the glass slide to allow close placement of the permanent magnet.
m × wm × hm = 9.5 × 4.8 × 1.6 mm, is placed adjacent to the microchannel, with the magnetization direction oriented through the thickness (Fig. 1(b)). A slot is cut in the PDMS next to the channel prior to bonding to the glass slide to allow close placement of the permanent magnet.
The perpendicular distance, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , between the magnet center and the fluid-fluid interface in the microchannel (see Fig. 1(b)) is controlled by carefully adjusting the magnet's position with an antimagnetic tweezer (Sigma Aldrich, St. Louis, MI, USA). This distance is further fine-tuned by controlling the relative flow rates of the two co-flowing phases. Constant flow-rate syringe pumps (Harvard Apparatus, Holliston, MA, USA) provide the flow to each inlet, and the total flow rate in the system is always maintained at 8 μL min−1.
, between the magnet center and the fluid-fluid interface in the microchannel (see Fig. 1(b)) is controlled by carefully adjusting the magnet's position with an antimagnetic tweezer (Sigma Aldrich, St. Louis, MI, USA). This distance is further fine-tuned by controlling the relative flow rates of the two co-flowing phases. Constant flow-rate syringe pumps (Harvard Apparatus, Holliston, MA, USA) provide the flow to each inlet, and the total flow rate in the system is always maintained at 8 μL min−1.
The experiments are imaged using bright-field microscopy (Leica Microsystems, Wetzlar, Germany) with 10× and 20× objectives and a high-speed camera (Vision Research, Wayne, NJ, USA). We use ImageJ software to measure the distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and track the particles in the microchannel.
and track the particles in the microchannel.
In separate control experiments, we measure interfacial tensions using a Krüss SITE100 spinning drop tensiometer, and follow standard operating procedures. As described later, these measurements give values for the interfacial tension that are comparable to the estimates obtained with our new particle and co-flow approach.
3 Results and discussions
3.1 The passage or trapping of paramagnetic spheres
In our experiments, paramagnetic beads follow streamlines in the aqueous phase until they reach the region of influence of the magnetic field, where they are pulled transverse to the flow and towards the two-phase interface. Two outcomes are observed as the particles approach the interface. Fig. 2(a) and 2(b) depict the two cases in a time-series of experimental images, at 5 ms intervals, of 2.5 μm radius paramagnetic spheres either passing through (Fig. 2(a)) or getting trapped (Fig. 2(b)) by the interface. The two different results arise from an imbalance of magnetic and interfacial forces on the particles. When the ratio of magnetic to interfacial forces is sufficiently high, the spheres pass through the interface. Fig. 2(c) and 2(d) show the positions of particles plotted against time, respectively, in the axial and normal directions, for the case where the aqueous and non-aqueous phases are 8 mM SDS and 25 wt% glycerol in water and 10 wt% Span 80 in dodecane. Here the reference time t = 0 is chosen as the instant when the particles reach the interface.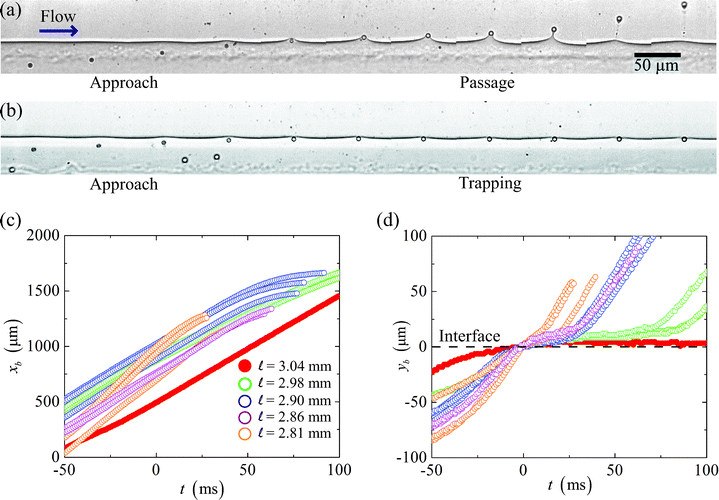 | ||
Fig. 2 (a–b) A time-series of images taken at intervals of 5 ms shows 2.5 μm radius paramagnetic spheres, in a solution of 8 mM SDS in water with 25 wt% glycerol, approaching a fluid-fluid interface. The spheres (a) deform and pass through the interface into a solution of 10 wt% Span 80 in dodecane, or (b) become trapped at the two-fluid interface when the magnetic force is not strong enough to pull the spheres through the interface. Plots of particle positions in the directions (c) of the flow and (d) perpendicular to the flow versus time. In the flow direction, the particles move at approximately constant speeds even as they cross the interface (at t = 0 ms), until they slow down as they approach the channel wall. In the perpendicular direction, when the distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) between the fluid-fluid interface and the magnet center is above a critical value, the spheres stop passing through the interface and remain trapped in the aqueous phase. between the fluid-fluid interface and the magnet center is above a critical value, the spheres stop passing through the interface and remain trapped in the aqueous phase. | ||
We observe that the speed of the particles in the flow direction (Fig. 2(c)) is approximately constant even as the particles are being pulled through the interface, which indicates that the spheres are following the bulk fluid flow, and that the speed of the two co-flowing solutions have equilibrated to an average speed, uo, upstream from the location of our measurements. The particles only slow down as they approach the channel wall next to the permanent magnet. Thus, from a Lagrangian perspective, we can approximate the particles as moving only perpendicular to the fluid-fluid interface.
In the perpendicular direction (Fig. 2(d)), we observe that in the case ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3.04 mm, the particle we track does not pass through the interface; rather it remains at the interface upon contact. For lower values of the magnet distance
= 3.04 mm, the particle we track does not pass through the interface; rather it remains at the interface upon contact. For lower values of the magnet distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) the other particles we follow eventually pass through the interface. We also note that smaller values of the length
the other particles we follow eventually pass through the interface. We also note that smaller values of the length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) result in more rapid deformation of the interface and a more prompt passage.
result in more rapid deformation of the interface and a more prompt passage.
3.2 The magnetic field and particle trajectories
Due to the spatial variations of the magnetic field, varying the magnet-to-interface distance![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) changes the force that acts on the paramagnetic spheres. In order to quantify the magnetic force, we describe here detailed calculations of the magnetic field H. Also, we calculate particle trajectories in an attempt to obtain a value for the particles' magnetic susceptibility χ, which is not a known quantity a priori and is different from one batch to another during manufacturing.20,21
changes the force that acts on the paramagnetic spheres. In order to quantify the magnetic force, we describe here detailed calculations of the magnetic field H. Also, we calculate particle trajectories in an attempt to obtain a value for the particles' magnetic susceptibility χ, which is not a known quantity a priori and is different from one batch to another during manufacturing.20,21
The origin of our coordinate system is the middle of the microchannel, parallel to the front edge of the permanent magnet, as depicted in Fig. 1(b). In our calculations, we non-dimensionalize all length scales, time scales, and the magnetic field via
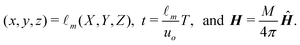 | (1) |
We obtain the full analytical solution to the magnetic field generated by the magnet with dimensions ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m × wm × hm and magnetization M = Mẑ using the approach described previously.22 Since the final expression is lengthy, and shows that the magnetic field is a function of the magnet's geometry, magnetization, and position relative to the origin, we will simply write the dimensionless expression as
m × wm × hm and magnetization M = Mẑ using the approach described previously.22 Since the final expression is lengthy, and shows that the magnetic field is a function of the magnet's geometry, magnetization, and position relative to the origin, we will simply write the dimensionless expression as
| Ĥ = f(X, Y, Z, Wm, Hm, Dc, L), | (2) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , all non-dimensionalized by
, all non-dimensionalized by ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m.
m.
Next, to obtain the particle trajectories we balance the most significant force contributions acting on the particles, which based on arguments proposed in the magnetophoresis literature, are magnetic and hydrodynamic forces.22,23 The magnetic force on a particle is given by22–24
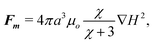 | (3) |
| Fd = 6πaηa(u − v), | (4) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) is the velocity of the flow. We first model the trajectory by assuming that the two-fluid interface is absent, then modify the model to account for the presence of the interface. Without consideration of the interface, and neglecting inertia, we can take the force balance Fm + Fd = 0 and obtain the velocity of the particle in the aqueous phase,
is the velocity of the flow. We first model the trajectory by assuming that the two-fluid interface is absent, then modify the model to account for the presence of the interface. Without consideration of the interface, and neglecting inertia, we can take the force balance Fm + Fd = 0 and obtain the velocity of the particle in the aqueous phase, 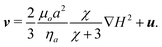 | (5) |
The particle's trajectory in dimensionless form is
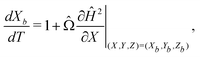 | (6) |
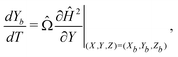 | (7) |
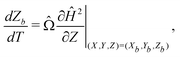 | (8) |
![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) is defined to be consistent with parameters previously used,22
is defined to be consistent with parameters previously used,22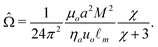 | (9) |
We can make scaling and physical arguments to further simplify eqn (6) and (8). Fig. 3(a), which plots 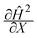 against the spatial positions X and Y, depicts large gradients at the magnet corners (X = 0 and X = 1). The large gradients decay quickly away from the corners. We can exploit the decay of the magnetic field gradient and the small parameter
against the spatial positions X and Y, depicts large gradients at the magnet corners (X = 0 and X = 1). The large gradients decay quickly away from the corners. We can exploit the decay of the magnetic field gradient and the small parameter ![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) = O(10−3) in our system and write
= O(10−3) in our system and write 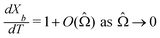 (see also Fig. 3(b)). This approximation agrees with experimental observations of constant particle speeds in the flow direction (Fig. 2(c)). We also make the assumption in our model that the beads remain in the mid-plane of the depth of the channel and that the vertical component of the magnetic force on the beads is negligible,
(see also Fig. 3(b)). This approximation agrees with experimental observations of constant particle speeds in the flow direction (Fig. 2(c)). We also make the assumption in our model that the beads remain in the mid-plane of the depth of the channel and that the vertical component of the magnetic force on the beads is negligible, 
 | ||
Fig. 3 (a) A three-dimensional plot of the flow-directed gradient of the squared magnetic field,  , is shown for the region of the microfluidic channel that is influenced by the applied magnetic field. The magnitude of the gradient decays away from the magnet corners, such that when (b) the speed , is shown for the region of the microfluidic channel that is influenced by the applied magnetic field. The magnitude of the gradient decays away from the magnet corners, such that when (b) the speed  is calculated at Y = 0, the speed can be reduced to is calculated at Y = 0, the speed can be reduced to 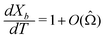 as as ![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) becomes asymptotically small. (c) A three-dimensional plot of the gradient of the squared magnetic field perpendicular to the flow, becomes asymptotically small. (c) A three-dimensional plot of the gradient of the squared magnetic field perpendicular to the flow, 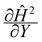 , shows that the field gradient is strongest in the region adjacent to the magnet and its strength decreases with the distance away from the magnet. , shows that the field gradient is strongest in the region adjacent to the magnet and its strength decreases with the distance away from the magnet. | ||
To take into account the presence of a fluid-fluid interface, we make use of the classical result of spheres settling towards an undeformable viscous fluid-fluid interface, as described by Brenner25 and Bart.26 As a sphere approaches a viscous two-fluid interface, the Stokes drag acting on the sphere is modified by a correction factor λ,
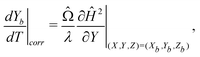 | (10) |
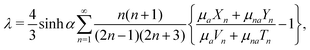 | (11) |
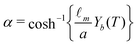 | (12) |
With a fitting parameter χ, we numerically solve eqn (7) and (10) for L = 0.305 and L = 0.315 and compare with our experimental results in Fig. 4(a) and 4(b). The models agree with the experimental data until the particles reach the interface. Very close to the interface, the particles' trajectories follow the results of the modified model that accounts for the interface (eqn (10)). As expected, the modified model fails to capture the dynamics of the trajectory at the fluid-fluid interface since it assumes an undeformed interface, while in reality the interface is deformed by the spheres. We find the best fit of the magnetic susceptibility χ ≈ 8 × 10−3.
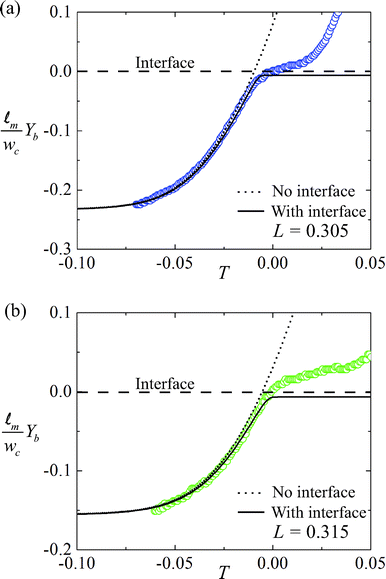 | ||
| Fig. 4 The approach of paramagnetic spheres towards the fluid-fluid interface for cases where (a) L = 0.305 and (b) L = 0.315. Circles represent experimental data. The dotted line represents numerical results of particle trajectory without considering the fluid-fluid interface. The solid lines are the trajectory model taking into account the two-fluid interface. The experimental values agree well with the theory. Deviations are observed very close to the fluid-fluid interface as expected since the model assumes an undeformed interface, while in reality the spheres deform and pass through the interface. The trajectories are used to calibrate for χ, the magnetic susceptibility of the 2.5 μm radius beads, and we find χ ≈ 8 × 10−3. | ||
3.3 Application to interfacial tensiometry
We take advantage of the dependence on L of the particles' passage or trapping at the interface to design a microfluidic tensiometer. Fig. 5 shows our measurements as we varied the concentration of SDS in the water from 4–20 mM, while maintaining 25 wt% glycerol. The non-aqueous solution is 10 wt% Span 80 in dodecane. Solid circles (•) are the instances where the particles are trapped by the interface and empty circles (○) represent their passage. We observe that for lower concentrations of SDS in the aqueous solution, L, the magnet's dimensionless distance from the fluid-fluid interface has to be smaller for the spheres to pass through the interface. As SDS concentration is increased, the cross-over distance for particle passage increases nearly monotonically.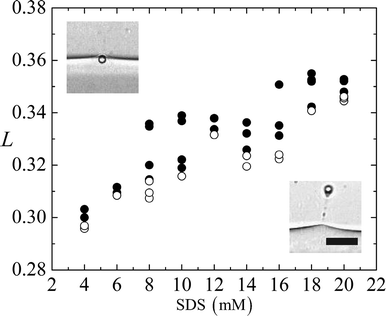 | ||
| Fig. 5 The interface-to-magnet distance L plotted against the SDS concentration in the aqueous phase. Solid circles (•) represent experiments where the beads experience lower magnetic force and cannot overcome the interfacial tension between the two liquid phases. Empty circles (○) represent beads that break through the interface. Scale bar 20 μm. | ||
For each experiment of different SDS concentration, we take the pair of data points closest to the cross-over from trapping to passage, and numerically calculate the magnetic forces (eqn (3)) in the direction perpendicular to the interface, corresponding to the average values of L. We then take a force balance on a single sphere at the two-phase interface (see Fig. 6(a)), 2πaγsinθ ≈ Fm, where θ denotes the angle of the interface, measured from the horizontal line that intersects the center of the particle.
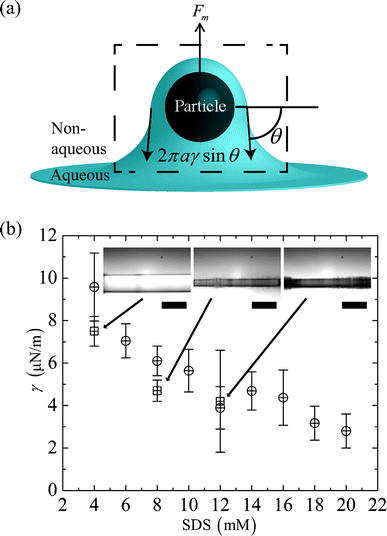 | ||
| Fig. 6 (a) A schematic diagram that illustrates the force balance on a particle at the two fluid interface. (b) The average dimensionless distance L of a pair of data points closest to the cross-over threshold is used to calculate the magnetic field gradient and estimate the interfacial tension γ viaeqn (13). γ is plotted as SDS concentration is increased from 4–20 mM. Results from microfluidic (⊕) and spinning drop (⊞) experiments are shown in the figure. The inset shows images from spinning drop experiments for different SDS concentrations in the aqueous phase. Scale bar 5 mm. | ||
We assume that during the interfacial deformation, the maximum value of sinθ ≈ 1, and that the interaction (if any) between the surface of the particle and the surfactants is minimal and contained within the force balance. Thus we find
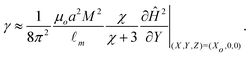 | (13) |
The magnetic field gradient 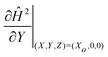 is evaluated at Xo = 0 and 0.5 for the pair of threshold dimensionless distance L to obtain the range of interfacial tensions for each set of experimental solutions. Median interfacial tension values (⊕) are plotted in Fig. 6(b) and the error bars indicate the range. The results from spinning drop tensiometry experiments (⊞), where non-aqueous phase droplets are immersed in the aqueous phase, are also plotted in Fig. 6(b).
is evaluated at Xo = 0 and 0.5 for the pair of threshold dimensionless distance L to obtain the range of interfacial tensions for each set of experimental solutions. Median interfacial tension values (⊕) are plotted in Fig. 6(b) and the error bars indicate the range. The results from spinning drop tensiometry experiments (⊞), where non-aqueous phase droplets are immersed in the aqueous phase, are also plotted in Fig. 6(b).
We find good agreement between the two techniques in the range of 4–12 mM SDS in the aqueous phase. However, the spinning drop measurements become very difficult at above 8 mM SDS in the aqueous phase as microemulsions appear in the mixture and obstruct the images of the drops (see inset of Fig. 6(b)). We are also unable to study the time dependence of the spinning drop measurements because of the tendency of the drops to shift in position over time. These challenges further convince us of the value of our magnetic microfluidic tensiometry technique.
We find that all of the solutions we test using the microfluidic tensiometer result in interfacial tensions of O(10−6–10−5) N m−1 and that the interfacial tension γ decreases as the SDS concentration in water increases. Below SDS concentration of 4 mM in water, we are unable to pull any particles through the fluid-fluid interface, which indicates that the upper limit of our interfacial tension measurements is set by how much magnetic force can be applied to the particles.
4 Conclusions
In this paper, we exploit the balance of magnetic and interfacial forces on paramagnetic spheres at fluid-fluid interfaces to measure ultralow interfacial tensions. The device we developed has a co-flow microchannel with an adjacent permanent magnet that provides the magnetic field. In experiments, we observe the existence of a critical dimensionless distance L, between the magnet's center and the fluid-fluid interface, below which paramagnetic spheres can pass through the interface.Using a mathematical model, we calculate the magnetic force that acts on paramagnetic spheres corresponding to the threshold dimensionless distance L, and estimate the interfacial tension between the co-flowing fluids by balancing magnetic and interfacial forces on the spheres. We also vary the surfactant concentration in the aqueous fluid to demonstrate that the microfluidic tensiometer can measure a range of interfacial tensions, from O(10−6–10−5) N m−1. We validate the effectiveness of our interfacial tension measurement technique by comparing our results with measurements from a spinning drop tensiometer and obtain good agreement.
The ability to measure very low interfacial tensions is challenging, but also relevant to different applications. We present a microfluidic ultralow interfacial tensiometer that simplifies and miniaturizes the measurement of interfacial tensions so that only small fluid samples are necessary. The approach we demonstrate should also allow for the interfacial tension measurement of other two-fluid systems such as phase-separated colloid-polymer solutions and all-aqueous polymer solutions.
Acknowledgements
We are grateful for financial support of this research from the NSF (Grant No. NSF-CBET-0961081) and we acknowledge I. M. Griffiths, M. Roche, P. H. Trinh and H. C. Shum for helpful discussions. We also thank V. Normand and K. Rong of Firmenich International for access to their spinning drop tensiometer.References
- J. J. Taber, Soc. Pet. Eng. J., 1969, 9, 3–12 CAS.
- H. Kunieda and K. Shinoda, J. Colloid Interface Sci., 1980, 75, 601–606 CrossRef CAS.
- M. J. Rosen, H. Z. Wang, P. P. Shen and Y. Y. Zhu, Langmuir, 2005, 21, 749–3756 CrossRef.
- D. G. A. L. Aarts, R. P. A. Dullens and H. N. W. Lekkerkerker, New J. Phys., 2005, 7, 40 CrossRef.
- H. N. W. Lekkerkerker, V. W. A. de Villeneuve, J. W. J. de Folter, Schmidt, Y. Hennequin, D. Bonn, J. O. Indekeu and D. G. A. L. Aarts, Eur. Phys. J. B, 2008, 64, 341–347 CrossRef CAS.
- A. L. Marquez, G. G. Palazolo and J. R. Wagner, Colloid Polym. Sci., 2007, 285, 1119–1128 CAS.
- I. Ziemecka, V. van Steijn, G. J. M. Koper, M. T. Kreutzer and J. H. van Esch, Soft Matter, 2011, 7, 9878–9880 RSC.
- S. Mitani and K. Sakai, Phys. Rev. E, 2002, 66, 031604 CrossRef.
- E. H. A. de Hoog and H. N. W. Lekkerkerker, J. Phys. Chem. B, 1999, 103, 5274–5279 CrossRef CAS.
- D. G. A. L. Aarts, J. H. van der Wiel and H. N. W. Lekkerkerker, J. Phys.: Condens. Matter, 2003, 15, S245–S250 CrossRef CAS.
- D. G. A. L. Aarts, M. Schmidt and H. N. W. Lekkerkerker, Science, 2004, 304, 847–850 CrossRef CAS.
- A. D. Ward, M. G. Berry, C. D. Mellor and C. D. Bain, Chem. Commun., 2006, 4515–4517 RSC.
- J. T. Cabral and S. D. Hudson, Lab Chip, 2006, 6, 427–436 RSC.
- A. G. Banpurkar, K. P. Nichols and F. Mugele, Langmuir, 2008, 24, 10549–10551 CrossRef CAS.
- J. H. Xu, S. W. Li, W. J. Lan and G. S. Luo, Langmuir, 2008, 24, 11287–11292 CrossRef CAS.
- S. W. Li, J. H. Xu, Y. J. Wang and G. S. Luo, J. Colloid Interface Sci., 2009, 331, 127–131 CrossRef CAS.
- S. S. H. Tsai, J. S. Wexler, J. D. Wan and H. A. Stone, Appl. Phys. Lett., 2011, 99, 153509 CrossRef.
- J. R. Anderson, D. T. Chiu, R. J. Jackman, O. Cherniavskaya, J. C. Mc-Donald, H. K. Wu, S. H. Whitesides and G. M. Whitesides, Anal. Chem., 2000, 72, 3158–3164 CrossRef CAS.
- H. C. Shum, A. Sauret, A. Fernandez-Nieves, H. A. Stone and D. A. Weitz, Phys. Fluids, 2010, 22, 082002 CrossRef.
- N. Pamme and A. Manz, Anal. Chem., 2004, 76, 7250–7256 CrossRef CAS.
- G. Fonnum, C. Johansson, A. Molteberg, S. Morup and E. Aksnes, J. Magn. Magn. Mater., 2005, 293, 41–47 CrossRef CAS.
- S. S. H. Tsai, I. M. Griffiths and H. A. Stone, Lab Chip, 2011, 11, 2577–2582 RSC.
- A. Sinha, R. Ganguly, A. K. De and I. K. Puri, Phys. Fluids, 2007, 19, 117102 CrossRef.
- C. Mikkelsen and H. Bruus, Lab Chip, 2005, 5, 1293–1297 RSC.
- H. Brenner, Chem. Eng. Sci., 1961, 16, 242–251 CrossRef CAS.
- E. Bart, Chem. Eng. Sci., 1968, 23, 193–210 CrossRef.
Footnotes |
| † Present address: Department of Mechanical and Industrial Engineering, Ryerson University, Toronto, ON, M5B 2K3, Canada. |
| ‡ Present address: Microsystems Engineering, Rochester Institute of Technology, Rochester, NY, 14623, USA. |
| This journal is © The Royal Society of Chemistry 2013 |