Effect of structural properties on catalytic performance in citral selective hydrogenation over carbon–titania composite supported Pd catalyst
Jie
Zhu
*ab,
Mingshi
Li
a,
Mohong
Lu
a and
Jianjun
Zhu
a
aSchool of Petrochemical Engineering, Changzhou University, Changzhou 213164, China. E-mail: zhujie_bit@yahoo.com.cn; Fax: +86-519-86334598; Tel: +86-519-86334597
bState Key Lab of Chemical Resource Engineering, Beijing 100029, China
First published on 6th November 2012
Abstract
A novel C/TiO2 composite supported palladium catalyst (Pd/C/TiO2) was prepared. The effects of the structural properties on the catalytic performance in citral hydrogenation were estimated from calculations and compared with a commercial activated carbon supported palladium catalyst (Pd/AC). The results showed that although the reaction rate was comparatively low over Pd/C/TiO2, which took approximately 24 h to reach 90% citral conversion, fourfold the time of Pd/AC, the selectivity for citronellal in citral hydrogenation remained high (approximately 85%) at the same citral conversion, while decreasing to 40% over Pd/AC. The comparatively lower reaction rate over Pd/C/TiO2 was attributed to the fewer surface Pd sites (3.94 μmol g−1 per cat) than on Pd/AC (12.2 μmol g−1 per cat). Further calculations discovered similar initial turnover frequency values over the two catalysts (approximately 0.1 s−1), which implied that citral hydrogenation is structure-insensitive over Pd catalysts and that crystallite size effects have little influence on the differences in the kinetics between the two catalysts. The high selectivity for citronellal over Pd/C/TiO2 was due to the negligible internal diffusion limitation inside the catalyst, which was proved by calculating the Weisz–Prater numbers (less than 0.3 of each reactant). In contrast, the pore structures, mainly composed of micro pores, caused serious internal diffusion limitation over Pd/AC, which finally led to the increase of the selectivity to the deeply hydrogenated product, 3,7-dimethyloctanol.
1. Introduction
Catalytic hydrogenation is one of the key processes in fine chemical industries. The properties of hydrogenation products can be significantly affected by the activity and structure of the employed catalyst. In heterogeneous catalysis, how to eliminate the mass transfer limitations inside the catalyst particles, thereafter gathering the intermediate products with high selectivity, has increasingly attracted researchers' attentions. For example, citral, a typical α,β-unsaturated aldehyde, is usually selected as a model molecule in that there are three sites of hydrogenation: a conjugate double bond (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), a carbonyl group (C
C), a carbonyl group (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and an isolated double bond (C
O) and an isolated double bond (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C). The selective hydrogenation of citral is a rather complex reaction network involving 6–8 important intermediates and a number of series-parallel reactions. Since palladium catalysts are very active in the hydrogenation of a C
C). The selective hydrogenation of citral is a rather complex reaction network involving 6–8 important intermediates and a number of series-parallel reactions. Since palladium catalysts are very active in the hydrogenation of a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond,1 citral is easily hydrogenated to citronellal on these catalysts, followed by deep hydrogenation to citronellol and finally to 3,7-dimethyloctan-1-ol (Fig. 1) due to the slow internal diffusion inside the micropores of the catalysts.2 Several systematic studies on citral selective hydrogenation have been reported. These studies covered some important aspects such as active metals3–6 and catalyst supports.7–9 Specifically, Yilmaz et al.7 reported the highest selectivity (90%) for citronellal at complete conversion of citral over a Pd/natural zeolite with particle sizes between 100 and 400 mesh, which was explained by the active metal properties and the absence of significant internal diffusion limitations.
C bond,1 citral is easily hydrogenated to citronellal on these catalysts, followed by deep hydrogenation to citronellol and finally to 3,7-dimethyloctan-1-ol (Fig. 1) due to the slow internal diffusion inside the micropores of the catalysts.2 Several systematic studies on citral selective hydrogenation have been reported. These studies covered some important aspects such as active metals3–6 and catalyst supports.7–9 Specifically, Yilmaz et al.7 reported the highest selectivity (90%) for citronellal at complete conversion of citral over a Pd/natural zeolite with particle sizes between 100 and 400 mesh, which was explained by the active metal properties and the absence of significant internal diffusion limitations.
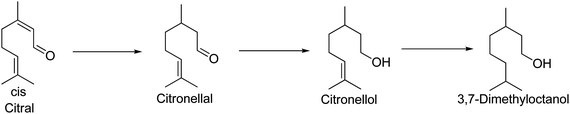 | ||
| Fig. 1 Consecutive reaction scheme of citral hydrogenation. | ||
Although the effects of internal diffusion limitations can be reduced in microscopic powdered catalyst particles, the powdered catalysts have to be separated from the products at the end of reaction via a costly filtration step, which can lead to the loss of catalysts and cause serious environmental problems.10 These disadvantages restrict the industrial applications of the powdered catalysts.
In recent years, many studies on macro-structured supports and their prepared catalysts have been launched for the purpose of resolving the disadvantages of the powdered catalysts employed in catalytic reactors, especially in fixed-bed ones. Some progresses have been published in which a few formed catalysts have been successfully developed using materials such as alumina,11,12 silica,13,14 monolith,15 nickel foam16 and graphite felt17 as the supports.
Currently, some studies which evaluate the mass transfer effects in catalytic reactions, especially internal diffusion over formed catalysts, have increasingly become the focus of researchers' attention. As the process is scaled up, the conditions are shifted from kinetically controlled to diffusion controlled. Therefore, increasing the catalyst particle size would affect the activity and selectivity. Zhu et al.18 studied the internal diffusion process in irregular A301 catalyst particles in ammonia synthesis and calculated the internal diffusion effectiveness factors based on a multi-component diffusion reaction model. The calculation result was verified to coincide with the experimental test. Aumo et al.19 studied the kinetics and mass transfer effects for the complex three-phase hydrogenation in large Ni/alumina catalyst pellets. The model accurately described the behavior of the system and it can be used for studies on reaction intensification. Zhang et al.20 and Chen et al.21 investigated the effects of the internal diffusions on the hydrogenation of 4-carboxybenzaldehyde (4-CBA) over a Pd/activated carbon catalyst and F-T synthesis over a Co/ZrO2 catalyst, respectively. The results indicated that the size of the catalyst had significant effects on the performances of the two catalytic reactions and some methods could be utilized to reduce the effects of internal diffusion, such as expanding the pore diameters of the supports, increasing the active compositions deposited on the outside surface of the catalysts and reducing the sizes of the catalyst particles as well.
To evaluate the presence or absence of pore diffusion limitations inside the catalysts, a Weisz–Prater criterion22 (or a Thiele modulus) is usually introduced in a calculation. Vannice et al.23 studied the effect of the solvent on the liquid-phase hydrogenation of citral over a Pt/SiO2 catalyst and numerous tests using the Weisz–Prater criterion verified that all the data for each solvent were obtained in the regime of kinetic control. Simmons et al.24 also studied enantioselective hydrogenation of dimethyl itaconate with an immobilised rhodium–duphos complex in a recirculating fixed-bed reactor. By calculating the value of the Thiele modulus, the employing catalyst was proven to not be subject to internal diffusion limitation.
Compared with the traditional supports, such as activated carbon, alumina, silica and monolith, TiO2 possesses several prominent advantages, including high chemical resistance to acidic or basic media as well as high mechanical strength. Carbon nanofiber (CNF) has increasingly become one of the hottest research points in catalysis in recent years due to its unique structure and exceptional catalytic performance. Jung et al.25 synthesized a CNF supported Pt catalyst (Pt/CNF) with the colloidal microwave process (CMP) and applied it in the hydrogenation of cinnamaldehyde. The result revealed the higher selectivity for cinnamyl alcohol. The enhanced allyl alcohol selectivity over the nanocatalysts compared to Pt/Al2O3 or Pt/C is often explained by the π-electron transfer from the graphite layers to the metal particle. In spite of some advantages in selective hydrogenation over CNF supported catalysts, it is difficult to prepare the CNFs to be used in a fixed-bed reactor.
In this work, we reported a novel macro-structured catalyst support based on a carbon nanofiber-titanium composite material, named C/TiO2. The composite was employed to synthesize a palladium catalyst (Pd/C/TiO2) and its catalytic performance was evaluated in the selective hydrogenation of citral. The effect of the structural properties of Pd/C/TiO2 on the catalytic hydrogenation performance was evaluated in this work through theoretical calculations. The result was compared to that of a commercial catalyst, i.e., activated carbon supported palladium (Pd/AC), to investigate the potential of Pd/C/TiO2 for commercial applications.
2. Experimental
2.1 Synthesis and characterizations of Pd/C/TiO2
The TiO2 (Sinopec Yangzi, China, φ 2 × 6 mm; 18 m2 g−1) was used as the host in this study to prepare a C/TiO2 composite material. Specifically, TiO2 was impregnated with an aqueous solution of a mixture of Ni(NO3)2·6H2O and Cu(NO3)2·3H2O (A.R, Sinopharm, China), in which the nickel loadings were kept fixed at 6 wt%. The molar ratio of Ni to Cu in the solution was varied within the range of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The samples were dried overnight at 393 K prior to calcinations at 773 K for 2 h. After they were reduced in a tube at 873 K in a stream of N2–H2 (80
1. The samples were dried overnight at 393 K prior to calcinations at 773 K for 2 h. After they were reduced in a tube at 873 K in a stream of N2–H2 (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20) (99.999%, Wuxi Tianhong, China) for 3 h, bimetallic Ni–Cu/TiO2 was obtained. Methane (99.999%, Wuxi Tianhong, China) was then passed through the tube to decompose at 873 K for 5 h. After refluxing in concentrated HNO3 at 393 K for 60 min to remove any exposed nickel and copper metal particles, the composite C/TiO2 supports were finally synthesized.
20) (99.999%, Wuxi Tianhong, China) for 3 h, bimetallic Ni–Cu/TiO2 was obtained. Methane (99.999%, Wuxi Tianhong, China) was then passed through the tube to decompose at 873 K for 5 h. After refluxing in concentrated HNO3 at 393 K for 60 min to remove any exposed nickel and copper metal particles, the composite C/TiO2 supports were finally synthesized.
The composite C/TiO2 was employed to support a Pd catalyst, i.e. Pd/C/TiO2.The as-synthesized C/TiO2 was then impregnated with an aqueous solution of PdCl2 (0.5 wt% Pd loading) (Pd ≥ 59%, Sinopharm, China) and stirred continuously for 6 h. The resulting sample was dried overnight at 393 K and stored in a desiccator. After reducing at 493 K in a stream of N2–H2 (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20) for 2 h, the Pd/C/TiO2 catalyst was finally prepared.
20) for 2 h, the Pd/C/TiO2 catalyst was finally prepared.
The as-prepared Pd/C/TiO2 was characterized to test the textural and structural properties. The BET surface area and the average pore diameter of the catalyst were calculated from the nitrogen adsorption isotherm obtained at 77 K using an ASAP 2010 sorptometer (Micromeritics). The palladium contents over the catalysts were determined by Vista-AX inductively coupled plasma atomic emission spectrometry (ICP-AES). Scanning electron images and element distributions were recorded using a JEOL JSM-6360 LA scanning electron microscope. The morphologies and the properties of the palladium particles on the catalysts were obtained with JEM-2100 transmission electron microscopy (TEM). A commercial activated carbon supported palladium catalyst (Pd loading 0.5 wt%, irregular particles, φ ≈ 3 mm, 810 m2 g−1, Sinopec Yangzi, China), named Pd/AC, was tested under the same conditions for comparison.
2.2 Estimation of the catalytic performance on Pd/C/TiO2
The catalytic performance on Pd/C/TiO2 was evaluated in the selective hydrogenation of citral and the result was compared to that of commercial Pd/AC. The experiments to reveal the intrinsic hydrogenation kinetics were carried out in a 100 ml pressurized autoclave. By dispersing approximately 1.0 g of the catalysts (2 wt%) into a total mass of 50 g of an isopropanol (A.R, Sinopharm, China) solution of citral (5 wt%, A.R, Sinopharm, China), the autoclave was sufficiently flushed with nitrogen flow and the following hydrogen to remove dissolved oxygen. The reaction commenced by switching the stirring to 1000 rpm, which was verified to be sufficient to exclude external diffusion. The experiments were conducted at 353 K and 3 MPa total pressure, which was maintained by continuously injecting hydrogen into the reactor. Small amounts of reaction samples were withdrawn from the reactor at different reaction times and analyzed by gas chromatography (VARIAN CP3800) equipped with an FID detector and HP-5 capillary column using nitrogen as a carrier gas.3. Results and discussion
3.1 Structural properties of Pd/C/TiO2
As described in the Experimental section, the preparation of Pd/C/TiO2 in this study employed a C/TiO2 composite as the catalyst support, which was synthesized by depositing carbon over TiO2. The structural properties of Pd/C/TiO2 were characterized and the results were compared with those of commercial Pd/AC, as shown in Fig. 2–5. | ||
| Fig. 2 The profile and morphology of the Pd/C/TiO2 catalyst: (a) the profile of Pd/C/TiO2; (b) the SEM image of the surface of Pd/C/TiO2; (c) the SEM image of the cross section of Pd/C/TiO2. | ||
 | ||
| Fig. 3 The profile and morphology of the commercial Pd/AC catalyst: (a) the profile of Pd/AC; (b) the SEM image of the surface of Pd/AC. | ||
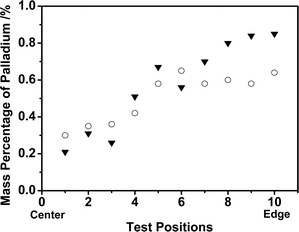 | ||
| Fig. 4 The palladium distributions in the of the Pd/C/TiO2 and Pd/AC catalysts: ▼ Palladium in Pd/C/TiO2; ○ Palladium in Pd/AC. | ||
 | ||
| Fig. 5 TEM images of Pd/C/TiO2 (a) and Pd/AC (b). | ||
Based on Fig. 2a, a Pd/C/TiO2 particle has a cylinder shaped profile with an average length of approximately 3.0 mm and diameter of 1.0 mm. The surface of the catalyst covered a significant amount of CNFs with diameters of 50–80 nm (Fig. 2b). They intertwined with each other to form pore structures. The thickness of the deposition layer can be identified from an SEM image of the catalyst section in Fig. 2c, i.e., 1.5–2.0 μm. In comparison, the commercial Pd/AC particle has an irregularly shaped profile with an average size of 3.0 mm (Fig. 3a), whose surface is smoother than that of a Pd/C/TiO2 particle (Fig. 3b). It is noted that, on the surface of Pd/AC, some small substrates conglutinate (Fig. 3b), which might be some fragments produced in the process of Pd/AC preparation.
In order to analyze the palladium distribution in the catalyst, 10 positions with the same spacing distance were assigned from the center to the edge of the catalyst section. The mass percentage of palladium was tested in each position and the results revealed some information on the two catalysts (Fig. 4). The mass percentage of palladium in Pd/C/TiO2 increased with the distance to the center of the catalyst. More active palladium sites in the exterior part of the catalyst than the interior would facilitate the catalytic reaction occurrence mainly on or near the exterior part of the catalyst. The same tendency in Pd distribution was found in Pd/AC.
The sizes and dispersions of the palladium particles on the catalysts could also be obtained from the TEM images (Fig. 5). Palladium particles in Pd/AC possess small sizes (average size 4.7 nm) compared with that of Pd/C/TiO2 (average size 14.5 nm). Based on the hemispherical model of metal particles on the surface of the catalyst, palladium dispersions in Pd/AC and Pd/C/TiO2 were calculated to be 25.88% and 8.39%, respectively. The high palladium dispersion in Pd/AC was attributed to its large BET surface area (810 m2 g−1), which was only 58 m2 g−1 for Pd/C/TiO2 (Table 2).
3.2 Catalytic performance on Pd/C/TiO2
In this study, the catalytic performance in citral hydrogenation over Pd/C/TiO2 was evaluated and the result was compared to that of the commercial Pd/AC catalyst. Citral conversions and product distributions over the two catalysts are shown in Fig. 6 and 7.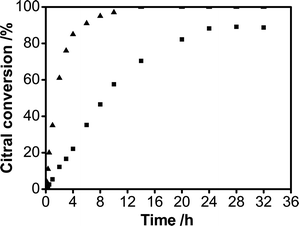 | ||
| Fig. 6 Citral conversion versus reaction time in citral hydrogenation over Pd/C/TiO2 (■) and commercial Pd/AC (▲). | ||
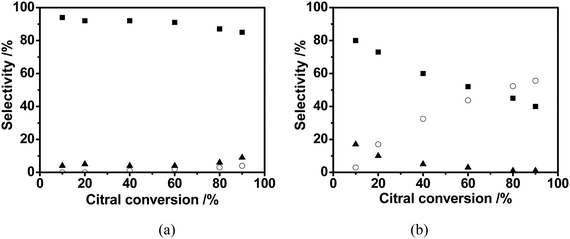 | ||
| Fig. 7 The product distribution versus citral conversion in citral hydrogenation over Pd/C/TiO2 (a) and commercial Pd/AC (b): ■ Citronellal; ▲ Citronellol; ○ 3,7-dimethyloctanol. | ||
Under the same reaction conditions, including the mass of the catalyst, Pd loading and the initial citral concentration, the reaction rate of citral hydrogenation on Pd/AC was much faster than that on Pd/C/TiO2. For example, the citral conversion over Pd/AC was 90% after 6 h, while it took nearly 24 h for Pd/C/TiO2, fourfold the time of the former catalyst, to reach the same conversion (Fig. 6). However, with the reaction continuing, the intermediate citronellal maintained the higher selectivity over Pd/C/TiO2 than that over Pd/AC. In particular, at a citral conversion of about 90%, the selectivity over Pd/C/TiO2 can be as high as 85% (Fig. 7a), being much higher than that over Pd/AC, 40% (Fig. 7b), while the selectivity to 3,7-dimethyloctanol, the final product in citral hydrogenation, climbed to approximately 55% at the same citral conversion over the Pd/AC catalyst (Fig. 7b).
The glaring discrepancy in the catalytic performance between Pd/AC and Pd/C/TiO2 could possibly be attributed to some factors, including the number of surface Pd sites, crystallite size effects as well as mass transfer limitations.24,26,27 Based on the Pd loadings and dispersions (Table 2), the molar number of surface Pd sites was calculated to be 12.2 μmol g−1 per cat on Pd/AC and 3.94 μmol g−1 per cat on Pd/C/TiO2. The high dispersion of Pd in Pd/AC (25.88%), due to its large BET surface area (810 m2 g−1), as shown in Table 2, led to more surface Pd sites on Pd/AC. This was the main reason for obtaining the comparatively higher reaction rate over Pd/AC than Pd/C/TiO2.
Next, the initial turnover frequency (TOF) for the catalyst was employed here to estimate the crystallite size effect on the catalytic performance. The TOF value might be calculated using eqn (1) at a citral conversion of approximately 10% because this initial reaction stage would ensure that the hydrogenation rate could not be affected by the changes in citral concentration.
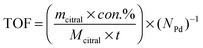 | (1) |
| Reactants and solvent | r (nm) | M (g mol−1) | ρ (g cm−3) | V b (m3 kmol−1) | χ | L vap (J kmol−1 × 107) | η (Pa s × 10−4) |
|---|---|---|---|---|---|---|---|
| Note:a Tyn–Calus method, Vb = 0.285, Vc1.048 (Vc: critical volume).b The solvent association parameter is taken as 1, since the citral and isopropanol are both non-polar.c Empirical expression of the viscosity of citral: lgη = 509.12 (T−1 − 3.42 × 10−3) − 3.0 (T: reaction temperature, K). | |||||||
| H2 | 0.12 | 2 | 0.0286 | ||||
| Citral | 0.39 | 152 | 0.780 | 0.171 | 1b | 4.55 | 5.01c |
| Isopropanol | 0.25 | 60 | 0.784 | 0.081 | 1b | 3.99 | 5.20 |
Fig. 6 shows that it took 20 min and 90 min to reach 10% citral conversions in the Pd/AC and Pd/C/TiO2 catalytic systems, respectively. Therefore, the initial TOF was calculated to be 0.11 s−1 for Pd/AC and 0.082 s−1 for Pd/C/TiO2. The similar initial TOFs in the 0.5 wt% Pd/AC and 0.5 wt% Pd/C/TiO2 catalytic systems implied that citral hydrogenation over Pd catalysts is structure-insensitive and that crystallite size effects are not expected to have a significant influence on the differences in the kinetics between the two catalysts. This result was in accordance with the study of Vannice et al.26 Therefore, the reaction rate and product distribution for citral hydrogenation in this study were presumed to be unaffected by crystallite size effects over the Pd/AC and Pd/C/TiO2 catalysts.
Finally, we focused on discussing the effect of mass transfer limitation, especially internal diffusion limitation, on citral selective hydrogenation over the two catalysts since the external particle mass transfer limitation was determined to be negligible in the earlier test when conducting the experiments at an agitation speed of 1000 rpm.
3.3 Modeling the internal diffusion behavior in the catalyst (Weisz–Prater criterion)
In a given catalytic system, the effect of the internal diffusion behavior of the substrates on the catalytic reactions could be estimated using the Weisz–Prater criterion (W–P criterion), expressed in eqn (2).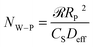 | (2) |
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) is the initial reaction rate, RP is the catalyst particle radius, Cs is the substrate concentration on the catalyst surface and Deff is the effective diffusivity of the substrate in the pores of the catalyst.
is the initial reaction rate, RP is the catalyst particle radius, Cs is the substrate concentration on the catalyst surface and Deff is the effective diffusivity of the substrate in the pores of the catalyst.
The W–P criterion asserted that if NW–P < 0.3, the rates for all the reactions with an order of 2 or less should have negligible mass transfer limitations, while a value of NW–P > 6 indicates definite diffusion control. If the W–P criterion gives a non-definitive value in the borderline region (between 0.3 and 6), additional calculations can be performed using the reactant concentrations and rates taken at different reaction times.23 In order to use the W–P criterion successfully, it is important to accurately determine the effective diffusivity of the reactant (Deff) and the initial reaction rate (![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ) in a given catalyst system.
) in a given catalyst system.
Prior to the calculation, we made two valid assumptions about the citral hydrogenation to simplify the computation process:
I. The intermediate products have the same physical properties as citral. The composition of the solution in the pores will change as the citral reacts but the intermediate products in this reaction are similar to citral in molecular size and configuration, so it is assumed that they have similar physical properties.
II. The physical properties of the liquid phase are essentially unchanged during the reaction. The initial concentration of citral in the reaction is calculated to be 2.0 mole percent, i.e., a dilute solution, and the products will exist in even smaller concentrations. Therefore, the physical properties of the liquid phase are assumed to be unchanged during the reaction, which would ensure that the effective diffusivity remains constant.
Seeing that the two assumptions mentioned above are reasonable for the practical reactions, the W–P criterion calculated using the initial reaction conditions is a satisfactory model to estimate the effect of internal diffusion behavior on citral hydrogenation.
Determining the Weisz–Prater criterion to evaluate the internal diffusion behavior is generally complicated for complex reactant (or solvent) molecules because their experimentally measured bulk diffusivities (Db) have rarely been reported. In a liquid-phase system, these parameters are needed to estimate the effective diffusivities (Deff) within the pore structure of the catalyst. The calculation of Db needs to determine the physical properties of the reactants as well as the solvent, including critical volume (Vc), pressure (P), density (ρ), viscosity (η) and vaporization enthalpy (Lvap). Once Db is known, Deff can be estimated. When combining Deff with a measured reaction rate (![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ), a known reactant concentration (Cs) and a determined value of the catalyst particle radius (RP), a Weisz–Prater (W–P) number can be finally calculated based on eqn (2).
), a known reactant concentration (Cs) and a determined value of the catalyst particle radius (RP), a Weisz–Prater (W–P) number can be finally calculated based on eqn (2).
Table 1 and 2 give some values which are needed in determining a W–P number. The data in Table 1 shows some physical properties of the reactants and solvent in the reaction system, which might be used in the calculation of bulk diffusivities. They were determined with methods derived from some handbooks.28–30Table 2 lists some properties of Pd/C/TiO2 and commercial Pd/AC, which were measured by catalyst characterization including density tests, nitrogen adsorption and TEM.
| Catalyst | 0.5% Pd/C/TiO2 | 0.5% Pd/AC | |
|---|---|---|---|
| Note:a The max length of the particle's cross section as the average size;b Based on the hemispherical model of metal particles on the surface of the catalyst. | |||
| Bulk properties | Bulk density of the catalyst, ρ (g cm−3) | 1.28 | 0.48 |
| Average radius of catalyst particle, Rp (cm) | 0.05a | 0.15a | |
| Textural properties | BET surface area, Stotal (m2 g−1) | 58 | 810 |
| Micro-pore area, Smicro (m2 g−1) | 2 | 720 | |
| Average pore radius, rp (nm) | 5.86 | 1.60 | |
| Palladium properties | Actual Pd loading (%) | 0.51 | 0.48 |
| Average Pd particle size (nm) | 10.8 | 4.7 | |
| Pd dispersion (%) | 8.39b | 25.88b | |
3.4 Estimation of the effective diffusivity (Deff) of the reactants in Pd/C/TiO2
In citral hydrogenation, there were two diffusing reactants, i.e., citral and hydrogen. They have different diffusivities in the reaction system due to their different physical and chemical properties. Therefore, it is necessary to calculate the effective diffusivities of each in the liquid-filled pores. Based on assumption I mentioned in Section 3.3, the intermediates in the pores have the same diffusivities as citral. So, the estimation of the intraparticle diffusion in citral hydrogenation needs to consider the diffusion behaviors of merely two reactants. | (3) |
The viscosity of the mixture (ηmixt) required in eqn (3) might be computed from the relationship in eqn (4):28
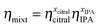 | (4) |
According to eqn (2), DH2,mixt is determined by the diffusivity of H2 in each solution of citral and isopropanol as well as the viscosity of each liquid.
Based on the method by Wilke and Chang,32 the diffusivity of a dilute gas solute in a liquid solvent (D1,2) could be expressed by eqn (5):
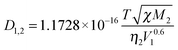 | (5) |
In this section, H2 was considered as the diffusing reactant and the diffusivity of H2 in citral or isopropanol can be estimated using eqn (5). The physical properties of citral and isopropanol (IPA) are listed in Table 1.
The diffusivities of H2 in citral and isopropanol were calculated to be 8.6 × 10−5 cm2 s−1 and 2 × 10−5 cm2 s−1 from eqn (5), respectively.
After the calculation of DH2,citral and DH2,IPA, the values were introduced into eqn (3). Thus, we solved the diffusivity of H2 in a citral/isopropanol binary liquid phase system, i.e., DH2,mixt = 6.34 × 10−5 cm2 s−1.
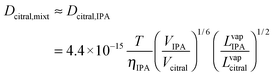 | (6) |
With the values of the parameters in Table 1, the value of Dcitral,mixt was computed to be 2.46 × 10−5 cm2 s−1.
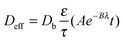 | (7) |
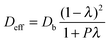 | (8) |
D H2,mixt and Dcitral,mixt, calculated in Sections 3.4.1 and 3.4.2, were then introduced in eqn (8) to estimate the effective diffusivities in the pores of the two catalysts.
To calculate the effective diffusivities, the structural properties of Pd/C/TiO2 and commercial Pd/AC which are required are listed in Table 2.
From the calculations, the effective diffusivity of the hydrogen and citral in the pores of Pd/C/TiO2 were: Deff/H2 = 4.59 × 10−5 cm2 s−1 and Deff/Citral = 1.03 × 10−5 cm2 s−1, while in commercial Pd/AC they were: D′eff/H2 = 2.44 × 10−5 cm2 s−1 and D′eff/Citral = 2.89 ×10−6 cm2 s−1.
3.5 Estimation of the Weisz–Prater criterion and its verification on the mass transfer behavior over Pd/C/TiO2
![[scr R, script letter R]](https://www.rsc.org/images/entities/b_char_e531.gif) ).
The initial global reaction rate (
).
The initial global reaction rate (![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ) on the catalyst could be estimated at the reaction stage of approximately 10% citral conversion and expressed in eqn (9):
) on the catalyst could be estimated at the reaction stage of approximately 10% citral conversion and expressed in eqn (9):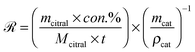 | (9) |
Since the parameters in the expression were all known, the maximum initial global reaction rate was calculated to be 1.18 μmol s−1 per cm3 cat for Pd/AC and 0.316 μmol s−1 per cm−3 cat for Pd/C/TiO2.
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) ), which are essential to calculate the Weisz–Prater number, have all been calculated in Sections 3.4 and 3.5.1. The surface concentration of citral (Cs,citral) could be determined using the mole fraction of citral in isopropanol at initial conditions, i.e., 2.558 × 10−4 mol−1 per cm3. Meanwhile, the surface concentration of H2 (Cs,H2) was given by the hydrogen solubility in isopropanol at 353 K and 3.0 MPa. Based on the study of Francesconi et al.,37 the surface concentration of H2 in this work was estimated to be 0.0111 mol%, i.e., approximately 1.47 × 10−4 mol per cm3, using the pressure–temperature (P–T) data obtained by curve fitting the experimental data. Therefore, the calculation of the W–P criterion for each reactant gives in Pd/C/TiO2, Nw–p,H2 = 0.11 < 0.3 and Nw–p,citral = 0.29 < 0.3 and in Pd/AC, N′w–p,H2 = 7.40 > 6 and N′w–p,Citral = 35.91 > 6. The calculated results infer that in the Pd/C/TiO2 catalytic system, NW–P for either reactant was less than 0.3, which satisfies the condition which ensures the elimination of significant internal diffusion limitations in citral hydrogenation in isopropanol. However, in the Pd/AC catalytic system, NW–P for each reactant was more than 6, which implies serious internal diffusion limitations of the reactants in Pd/AC. It is noted that in each catalytic system, the NW–P number for citral was higher than that for hydrogen, indicating a higher probability that the internal diffusion of citral, rather than hydrogen, would suppress the rate of reaction. This could be explained by the drastic differences in the molecular size of hydrogen and citral. Generally, the smaller the molecular size of the reactant, the more easily it diffuses inside the catalyst particles. Thus, the lower NW–P number of hydrogen, which suggests less internal diffusion limitation, is attributed to its smaller size compared to that of citral for a same type of catalyst.
), which are essential to calculate the Weisz–Prater number, have all been calculated in Sections 3.4 and 3.5.1. The surface concentration of citral (Cs,citral) could be determined using the mole fraction of citral in isopropanol at initial conditions, i.e., 2.558 × 10−4 mol−1 per cm3. Meanwhile, the surface concentration of H2 (Cs,H2) was given by the hydrogen solubility in isopropanol at 353 K and 3.0 MPa. Based on the study of Francesconi et al.,37 the surface concentration of H2 in this work was estimated to be 0.0111 mol%, i.e., approximately 1.47 × 10−4 mol per cm3, using the pressure–temperature (P–T) data obtained by curve fitting the experimental data. Therefore, the calculation of the W–P criterion for each reactant gives in Pd/C/TiO2, Nw–p,H2 = 0.11 < 0.3 and Nw–p,citral = 0.29 < 0.3 and in Pd/AC, N′w–p,H2 = 7.40 > 6 and N′w–p,Citral = 35.91 > 6. The calculated results infer that in the Pd/C/TiO2 catalytic system, NW–P for either reactant was less than 0.3, which satisfies the condition which ensures the elimination of significant internal diffusion limitations in citral hydrogenation in isopropanol. However, in the Pd/AC catalytic system, NW–P for each reactant was more than 6, which implies serious internal diffusion limitations of the reactants in Pd/AC. It is noted that in each catalytic system, the NW–P number for citral was higher than that for hydrogen, indicating a higher probability that the internal diffusion of citral, rather than hydrogen, would suppress the rate of reaction. This could be explained by the drastic differences in the molecular size of hydrogen and citral. Generally, the smaller the molecular size of the reactant, the more easily it diffuses inside the catalyst particles. Thus, the lower NW–P number of hydrogen, which suggests less internal diffusion limitation, is attributed to its smaller size compared to that of citral for a same type of catalyst.
The discrepancy in the product distributions is likely to be determined by the different structural properties of the two catalysts. As shown in Table 2, the pores of Pd/C/TiO2, with an average diameter 11.72 nm, are mainly composed of meso- and macropores. The micropore area of the catalyst occupies only 3.45% of the total surface area, whereas the distribution of numerous micropores in the interior part of Pd/AC with an average diameter 3.2 nm and the micropore area occupies approximately 88% of the total surface area.
The mechanism of the reaction was speculated to be that when the H2 and citral reactants diffused along the apertures in Pd/C/TiO2, they suffered less diffusion resistance due to the numerous meso- and macropores in the catalyst. Once citronellal, the intermediate product, was synthesized in the pores, it desorbed from the Pd crystal to the solution and easily diffused towards the outside of the pores, which meant there was little probability of hydrogenating deeply to citronellol or even 3,7-dimethyloctanol. However, when the reaction took place inside the Pd/AC catalyst, citronellal might have remained for a long time to be further hydrogenated to citronellol and 3,7-dimethyloctanol due to the serious diffusion limitations.
4. Conclusions
The catalytic performance of citral hydrogenation over Pd/C/TiO2 and Pd/AC was estimated from calculations. The comparatively lower reaction rate over Pd/C/TiO2 was attributed to fewer surface Pd sites (3.94 μmol g−1 per cat) than Pd/AC (12.2 μmol g−1 per cat). However, the similar initial TOF values over the two catalysts implied that citral hydrogenation is structure-insensitive over Pd catalysts and that crystallite size effects have little influence on the differences in the kinetics between the two catalysts. A Weisz–Prater criterion was employed to estimate the internal diffusion behavior of the reactants in the catalyst. The calculated results showed that the Weisz–Prater number of each reactant, including H2 and citral, was less than 0.3, which inferred the absence of internal diffusion limitations in Pd/C/TiO2. This proved the rationality of high citronellal selectivity (approximate 85%) at a citral conversion of 90% in citral hydrogenation over Pd/C/TiO2. Meso- and macropores, the dominant structures of the apertures in Pd/C/TiO2, resulted in the elimination of internal diffusion limitations in the catalyst. These results showed that the C/TiO2 composite, an effective catalyst support, has a wide application in multiphase catalytic reactions, especially those controlled by internal diffusion.Nomenclature
| C s | Concentration on the catalyst surface, mol cm−3 |
| D b | Bulk diffusivity, m2 s−1 |
| D eff | Effective diffusivity in the pores of the catalyst, m2 s−1 |
| L vap | Enthalpy of vaporization at the normal boiling point, J kmol−1 |
| M | Molecular weight, g mol−1 |
| m | The mass of the reactant, solvent or catalyst, g |
| N | The number of hygrogenation active sites, mol g−1 per cat |
| P | The fitting parameter in the expression of effective diffusivity |
| ρ | Density of the material, g cm−3 |
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) | Initial global reaction rate, mol s−1 per cm3 cat |
| R P | The catalyst particle radius, cm |
| r | Molecular radius or the average pore radius of the catalyst, nm |
| t | Reaction time, s |
| λ | The ratio of molecular radius to average pore radius of the catalyst, rmolecule/rpore |
| V | Molar volume at the normal boiling point, m3 kmol−1 |
| x | Mole fraction of the component in the solution, mol% |
| χ | Solvent association parameter |
| η | Viscosity of the liquid or the solution, Pa s |
Acknowledgements
This work is financially supported by the National Natural Science Foundation of China (grant no. 20976076) and the Natural Science Foundation of Changzhou (grant no. CE20115053). Financial support from the Priority Academic Program Development of Jiangsu Higher Education Institutions and State Key Lab of Chemical Resource Engineering (CRE-2011-C-106) is also acknowledged.References
- F. Delbecq and P. Sautet, J. Catal., 1995, 152, 217 CrossRef CAS.
- J. Álvarez-Rodríguez and A. Guerrero-Ruiz, Catal. Today, 2005, 107–108, 302 CrossRef.
- J. Álvarez-Rodríguez, I. Rodríguez-Ramos, A. Guerrero-Ruiz and A. Arcoya, Appl. Catal., A, 2011, 401, 56–64 CrossRef.
- A. Vicente, T. Ekou, G. Lafaye, C. Especel, P. Marécot and C. T. Williams, J. Catal., 2010, 275, 202 CrossRef CAS.
- A. Vicente, G. Lafaye, C. Especel, P. Marécot and C. T. Williams, J. Catal., 2011, 283, 133 CrossRef CAS.
- C. Caballero, J. Valencia, M. Barrera and A. Gil, Powder Technol., 2010, 203, 412 CrossRef CAS.
- S. Yilmaz, S. Ucar, L. Artok and H. Gulec, Appl. Catal., A, 2005, 287, 261 CrossRef CAS.
- J. Álvarez-Rodríguez, I. Rodríguez-Ramos, A. Guerrero-Ruiz, E. Gallegos-Suarez and A. Arcoya, Chem. Eng. J., 2012, 204–206, 169 CrossRef.
- T. Ekou, C. Especel and S. Royer, Catal. Today, 2011, 173, 44 CrossRef CAS.
- L. Kiwi-Minsker, I. Yuranov, V. Höller and A. Renken, Chem. Eng. Sci., 1999, 54, 4785 CrossRef CAS.
- P. L. Liu and L. Lefferts, Chem. Res. Appl., 2006, 18, 1077 CAS.
- W. L. Mi, Y. S. Lin, B. Q. Zhang and Y. D. Li, Mod. Chem. Ind., 2005, 25, 37 CAS.
- P. L. Liu and L. Lefferts, Chin. J. Chem. Eng., 2006, 14, 294 CrossRef CAS.
- Y. Yamada, Y. K. Hosono, N. Murakoshi, N. Higashi, H. Ichi-oka, T. Miyake, N. Ikenaga and T. Suzuki, Diamond Relat. Mater., 2006, 15, 1080 CrossRef CAS.
- X. Y. Chen, B. D. Gould and J. W. Schwank, Appl. Catal., A, 2009, 356, 137 CrossRef CAS.
- P. Tribolet and L. Kiwi-Minsker, Catal. Today, 2005, 105, 337 CrossRef CAS.
- P. Li, T. Li, J. H. Zhou, Z. J. Sui, Y. C. Dai, W. K. Yuan and D. Chen, Microporous Mesoporous Mater., 2006, 95, 1 CrossRef CAS.
- T. Li, M. S. Xu, B. C. Zhu and D. Y. Fang, J. Chem. Ind. Eng., 2002, 53, 1260 CrossRef CAS.
- J. Aumo, J. Wärnå, T. Salmi and D. Y. Murzin, Chem. Eng. Sci., 2006, 61, 814 CrossRef CAS.
- S. G. Zhang, J. H. Zhou, Z. J. Sui, X. G. Zhou and W. K. Yuan, Ind. Catal., 2008, 16, 60 CAS.
- C. B. Chen, J. G. Chen, K. G. Fang and Y. H. Sun, J. Fuel Chem. Technol., 2010, 38, 588 CAS.
- P. B. Weisz, Z. Phys. Chem., 1957, 11, 1 CrossRef CAS.
- S. Mukherjee and M. A. Vannice, J. Catal., 2006, 243, 108 CrossRef CAS.
- M. A. Al Herz, A. N. Tsoligkas, M. J. H. Simmons and J. Wood, Appl. Catal., A, 2011, 396, 148 CrossRef CAS.
- A. Jung, A. Jess, T. Schubert and W. Schütz, Appl. Catal., A, 2009, 362, 95 CrossRef CAS.
- U. K. Singh, M. N. Sysak and M. A. Vannice, J. Catal., 2000, 191, 181 CrossRef CAS.
- U. K. Singh and M. A. Vannice, J. Catal., 2001, 199, 73 CrossRef CAS.
- B. E. Poling, J. M. Prausnitz and J. P. O'Connell, The properties of gases and liquids, Chem. Ind. Press, Beijing, 5th edn, 2005 Search PubMed.
- N. L. Chen, Solvents Handbook, Chem. Ind. Press, Beijing, 3rd edn, 2002 Search PubMed.
- G. Q. Liu, L. X. Ma and J. Liu, Handbook of physical properties in chemistry & chemical engineering (Organic volume), Chem. Ind. Press, Beijing, 2002 Search PubMed.
- J. Leffler and H. T. Cullinan, Ind. Eng. Chem. Fundam., 1970, 9, 84 CAS.
- C. R. Wilke and P. Chang, AIChE J., 1955, 1, 264 CrossRef CAS.
- C. J. King, L. Hsueh and K. Mao, J. Chem. Eng. Data, 1965, 10, 348 CrossRef CAS.
- A. Chantong and F. E. Massoth, AIChE J., 1983, 29, 725 CrossRef CAS.
- M. Ternan, Can. J. Chem. Eng., 1987, 65, 244 CrossRef CAS.
- C. N. Satterfield, C. K. Colton and W. H. Pitcher, AIChE J., 1973, 19, 628 CrossRef CAS.
- J. Vicente, H. d'Angelo and A. Z. Francesconi, J. Chem. Eng. Data, 2001, 46, 671 CrossRef.
| This journal is © The Royal Society of Chemistry 2013 |
