H₂ dissociation over Ag/Al₂O₃: the first step in hydrogen assisted selective catalytic reduction of NO_x

Abstract

Hydrogen assisted selective catalytic reduction of NO_x over Ag/Al₂O₃ with either hydrocarbons or ammonia as reducing agents is an emerging technology for lean NO_x reduction. Herein, we present a density functional theory study of H₂ dissociation over a representative set of sites present on the Ag/Al₂O₃ catalyst. Whereas H₂ dissociation over supported Ag ions and oxidized Ag surfaces is found to be facile, dissociation over metallic Ag, defect free Al₂O₃ and alumina-supported Ag is associated with high barriers. The results are rationalized by analysis of the electronic structure.

---

1 Introduction

Silver supported on γ-alumina is a promising catalyst for selective catalytic reduction (SCR) of NO_x in the presence of excess oxygen when either hydrocarbons (HC) or ammonia (NH₃) is used as a reducing agent. Although experimental studies have clarified properties of the catalyst, several aspects remain elusive. Most fundamental is the uncertainty regarding the reaction paths and the sites over which the reactions occur. Numerous studies have shown that the silver phase, as well as the performance of the catalyst, is sensitive to the method of preparation^1–3 and amount of silver loading^4–6 (1–10%). In particular, it has been demonstrated that the catalyst should contain both large metallic particles and small clusters for an overall high activity. The presence of metallic silver is known to facilitate oxidation reactions, whereas Ag clusters are believed to enhance the selectivity towards NO_x reduction under lean conditions.⁷ The character of the Ag clusters is, however, not known and suggestions include charged silver clusters (Ag_n^δ+), metallic silver (Ag⁰),^4,8,9 oxidized silver (O–Ag),¹⁰ and silver aluminate.¹¹ The optimal loading for high NO_x conversion is reported to be ∼2 wt% Ag at which both a fair amount of small Ag species and large particles are formed.^12–16

It has been shown that a small amount of H₂ (<1.0%) in the feed gas lowers the temperature for NO_x conversion.^13,17,18 The role of hydrogen in the overall reaction is, however, unclear. Based on UV-vis spectroscopy during propane-SCR over Ag/Al₂O₃, Satsuma and co-workers¹⁹ reported a shift in the UV-spectra from that of Ag⁺ ions to one with signatures associated with small Ag clusters when hydrogen was added to the feed gas. Based on this observation, it was suggested that H₂ promotes agglomeration of Ag clusters from dispersed Ag cations. In a similar study, in situ infrared spectroscopy measurements indicated enhanced formation of HC-SCR intermediates, such as –NCO and acetate, when hydrogen was added to propane.²⁰ In addition, a volumetric NO_x adsorption study by Brosius et al.¹⁶ put forth that hydrogen may counteract catalyst poisoning by reduction of nitrates to nitrites. In order to clarify the role of hydrogen and ultimately improve the performance of Ag/Al₂O₃, it is desirable to understand the roles of the different sites in the catalyst. In particular, as a crucial reaction step in hydrogen assisted SCR should be H₂ dissociation, the character of the active sites for this reaction should be clarified.

In this report, we present a systematic theoretical investigation of the H₂ dissociation step over Ag/Al₂O₃. Energetic, structural, and electronic properties of hydrogen adsorption are discussed together with activation energies for dissociation over a representative set of sites on Ag/Al₂O₃.

In particular, we investigate H₂ dissociation over Ag(111), Ag(100), Ag(211), partially oxidized Ag(111), γ-Al₂O₃, Ag-doped Al₂O₃, and a model for a Ag–Al₂O₃ interface. It should be noted that Ag/Al₂O₃ is a catalyst where reactions probably take place on both the metal and the oxide phase. It has recently been demonstrated that the mere contact with a metal phase may alter the chemical properties of oxides.^21–23 One example is the activation of O₂ on MgO supported on Ag(100)^22,23 and the prediction of low temperature CO oxidation over this system.²²

2 Computational method

The Density Functional Theory (DFT) is used as implemented in the Dmol³ program with the gradient corrected exchange–correlation (xc) functional according to Perdew, Burke and Ernzerhof (PBE).²⁴ The one-electron, Kohn–Sham orbitals are expanded in a local numerical basis set where the basis functions are stored on a radial grid centered at each atom.^25–27 In particular, a so-called double numerical basis with polarization functions (dnp) is used for all atoms. The bases for hydrogen, oxygen, nitrogen, aluminum, and silver are [1s(H), 1s(H⁺), 2p(2⁺)], [1s2s2p(O), 2s2p(O²⁺), 3d(7⁺)], [1s2s2p(N), 2s2p(N²⁺), 3d(7⁺)], [1s2s2p3s3p(Al), 3s3p(Al²⁺), 3d(4⁺)], and [4s4p4d5s(Ag), 4d5s5p(Ag²⁺)], respectively. A real space cutoff of 5.0 Å is applied for all basis functions. Interaction between the valence electrons and the core of silver is described by a scalar relativistic pseudo potential.²⁸ The Kohn–Sham equations are solved self-consistently with an integration technique of weighted overlapping spheres located at each atomic center. The direct Coulomb potential is obtained by projection of the charge density onto angular-dependent weighting functions also centered at each atom. The Poisson equation can in this way be solved by integration in one dimension. A Fermi distribution smearing of 0.1 eV is used.

All slab calculations are performed with periodic boundary conditions where integration over the Brillouin zone is approximated by finite sampling. Ag bulk and Ag₂O bulk oxide are treated with a (10, 10, 10) mesh which corresponds to 500 unique k-points in the irreducible unit cell. Ag(111), Ag(211), and Ag₂O(111) surfaces are cut from the optimized bulk phases and modeled in (4 × 4), (2 × 1), and (2 × 2) surface cells, respectively. Four [Ag(111)] or five [Ag(211) and Ag₂O(111)] layered slabs are used to model the surfaces. The slabs are separated by at least 15 Å vacuum. The k-point sampling for Ag(111), Ag(211), and Ag₂O(111) is (6, 6, 1), (6, 8, 1), and (2, 2, 1), respectively. Structural optimization is performed until convergence criteria of 0.002 eV, 0.005 Å, and 0.002 eV Å⁻¹ are met for the total energy, the coordinates and gradients, respectively. The two bottom layers for the slabs are kept fixed during the geometry optimization.

γ-Alumina is a transitional alumina phase for which no unambiguous crystallographic data is available. This poses problems for atomistic calculations, and several models have been proposed over the years.^29–33 Here, the spinel structure designed by Digne and co-workers³⁴ is employed. The γ-alumina bulk is optimized using a (4, 2, 2) k-point sampling (4 unique k-points). From the optimized bulk structure, a surface is cut in the (100) crystallographic direction. Digne et al. termed this surface (110)³⁴ as it represents the (110) orientation in boehmite (an aluminum oxide hydroxide precursor of alumina).³⁴ Because this notation is generally used in the literature, it is adopted also here. The alumina slabs are modeled with eight atomic layers using a (1 × 1) surface cell.

In order to model an Al₂O₃(110) supported Ag Wulff-nanoparticle, a periodic geometry in two dimensions is used, where the particle is assumed to wet the surface.³⁵ The nanoparticle is based on three (100) layers with in total 21 Ag atoms (Fig. 1d). The three layers consist of 9, 6, 6 atoms, respectively. The particle is placed on the Al₂O₃(110) surface such as to form a one-dimensional rod, see Fig. 1d and e. During the geometry optimization, the Ag atoms close to the cell boundary are held fixed in the lateral (xy) direction in order to simulate the bulk of a nanometer sized particle. The particle is treated in a (1 × 2) surface cell of Al₂O₃(110). This leads to a lattice mismatch of ∼5% in the direction of the rod periodicity (x-direction).

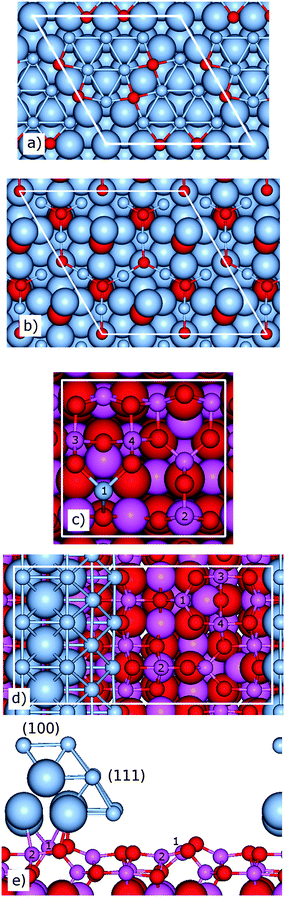Fig. 1 Ball and stick models of the (a) p(4 × 4)), (b) Ag₂O(111), (c) Ag@Al₂O₃(110)-b, (d) top and (e) side views of the Ag_NPM/Al₂O₃(110) structure. Small balls are chosen to highlight surface atoms. In (c), (1)–(4) indicate the positions of surface Al atoms on the bare Al₂O₃(110) surface. The (100) and (111) facets are indicated on the Ag_NPM in (d). Atomic color codes: blue (Ag), magenta (Al), and red (O). White lines indicate the surface cells.

The transition state (TS) of H₂ dissociation is estimated by a linear synchronous transit and quadratic synchronous transit (LST/QST) method.³⁶ LST is first used to bracket a maximum between the initial and the final geometries. Energy minimization of the obtained maximum is performed, upon which a first structure for the transition state is generated. Subsequently, QST is used for a finer optimization and the procedure is finished with a conjugate gradient minimization. The TS-search is performed until a value of 0.02 eV Å⁻¹ is reached for the largest elements of the gradients. The calculated transition state structures are confirmed by vibrational analysis. These are performed within the harmonic approximation by finite differences.

Adsorption energy for an adsorbate (X) is calculated according to:

E_ads(X) = E_X/S − E_S − E_X, (1)

where E_X/S is the total energy of the combined system (adsorbate and surface slab), E_S is the energy of the relaxed bare surface and E_X is the total energy of the optimized adsorbate in the gas-phase. Positive (negative) adsorption energies refer to endothermic (exothermic) adsorption. The surface energy Γ is calculated by:

Γ = (E_slab − NE_bulk)/2A (2)

where E_slab is the total energy of the slab, E_bulk is the total energy of the optimized bulk, N is the number of bulk units, and A is the surface area. A factor of two enters as the slab has two surfaces.

Possible basis set superposition errors (BSSE) have been estimated by calculations of gas-phase H₂ and OH using the counterpoise method.³⁷ The errors were found to be smaller than 0.005 eV.

3 Results

3.1 Reference systems

Calculations of a set of reference systems allow for evaluation of the computational approach. The Ag and Ag₂O lattice constants are calculated to be 4.19 and 4.88 Å, respectively. These results are in fair agreement with the experimental values of 4.08 and 4.73.³⁸ The calculated expansion is a known effect of the applied xc-functional.³⁹ The cohesive energy of Ag and the heat of formation for Ag₂O (with respect to Ag in the bulk and O₂ in the gas phase) are found to be 2.52 and 0.26 eV. The corresponding experimental values are 2.80 and 0.32 eV.³⁸ The lattice parameters of γ-Al₂O₃ are calculated to be a = 5.60 Å, b = 8.43 Å, c = 8.10 Å, and β = 90.56°. These values are in good agreement with previous reports where a = 5.59 Å, b = 8.41 Å, c = 8.07 Å, and β = 90.59.^34,40,41 The calculated (experimental) binding energy, bond length, and vibrational wavenumber⁴² of H₂ is 4.54 (4.52) eV, 0.75 (0.74) Å, and 4347 (4401) cm⁻¹. The corresponding values for O₂ are 6.10 (5.23) eV, 1.23 (1.21) Å, and 1574 (1580) cm⁻¹. The deviations from the experimental bond lengths and vibrational wavenumbers are generally small (within ∼2%). The large discrepancy of the O₂ binding energy is a well known effect of the xc-functional.²⁴

3.2 Model systems

As already mentioned, the active phase of Ag/Al₂O₃ for NO_x reduction is yet unsolved. Nevertheless, experiments show that Ag is present in the form of silver clusters (Ag_n^δ+), metallic silver (Ag⁰), and oxidized silver. It should be noted that despite a nominal silver content of 1–10%, most of the catalyst surface consists of bare alumina, which, in principle, could have sites available for H₂ dissociation. Here, different types of representative sites present in/on the catalyst are explored with respect to H₂ dissociation.

The presence of Ag⁰ on Ag/Al₂O₃ samples with high silver-loading has been reported in several studies.^2,3,11 It is probable that the metal particles largely exhibit low energy facets. Here, large Ag particles are modeled by Ag(111) facets to describe terraces and Ag(211) to describe model steps between facets. The two models are calculated to have surface energies of 0.050 and 0.055 eV/Ų, respectively. The values are within 5% of previous reports.⁴³

The Ag/Al₂O₃ catalyst operates under oxygen excess and it is probable that Ag to some extent is oxidized. As Ag(111) is the low energy facet, we consider oxidized Ag(111). Previous studies, based on scanning tunneling microscopy, surface X-ray diffraction, core level spectroscopy and density functional theory have reveled a p(4 × 4) surface reconstruction of Ag(111) upon oxygen adsorption.^44,45 The structure consists of a stoichiometric Ag₁₂O₆ ad-layer with two Ag₆ clusters positioned in either hcp or fcc hollow sites. The spacing between the hexamer sub-units provides sites for six O atoms (Fig. 1a).^44–46 This structure is hereafter denoted p(4 × 4).

To model the case of complete metal oxidation, an Ag₂O(111) surface (cut from Ag₂O bulk) with an O-termination (Fig. 1b) is considered. The structure is based on the work of Li and co-workers⁴⁷ where it was shown that growth of a silver oxide phase under increased oxygen pressure results in a structure similar to that of the Ag₂O(111) surface.

For γ-alumina, it has been shown that the predominant orientation is (110); it constitutes about 70–85% of the total surface area. The remaining 30–15% are believed to consist of the (100) orientation, with small patches of (111).^40,48,49 Here, only the (110) orientation is considered. The relaxed surface energy of a clean Al₂O₃(110) surface is calculated to be 0.105 eV Å⁻². The value is in good agreement with previous calculations of 0.097 eV Å⁻².³⁴ The clean Al₂O₃(110) surface displays surface Al atoms of two distinct types (Fig. 1c). One type originates from tetrahedral bulk alumina atoms and are 3-fold coordinated to oxygen atoms [Al_III (1)] on the surface. The second type of Al-atoms occupy octahedral positions in the bulk. These atoms have a 4-fold coordination on the surface and are present in three versions, namely Al_IV (2), Al_IV (3), and Al_IV (4).

Ag_n^δ+ clusters in the very small size regime (n < 10) have been suggested to be active sites for NO_x reduction and their presence in experimental samples has been documented.^{2,3,9,11,13,15} In order to model such sites, an Ag₁ cluster is embedded in the (1 × 1)-Al₂O₃(110) matrix at bulk and surface positions, respectively. However, as the bonding in alumina is ionic (with Al³⁺ cations and O²⁻ anions) modeling of such sites needs care. To remove the dangling bonds which are introduced by the Al to Ag substitution, the structures with Ag₁ are compensated by two hydrogen atoms at the bottom of the slab. This procedure compensates for the fact that Ag is monovalent whereas Al is trivalent and ensures that the band gap of the system is preserved.⁵⁰ Upon structural optimization, two particular low energy structures of Ag@Al₂O₃(110) are identified. The stable structure is found to be one where Ag₁ is in the position of a tetrahedral bulk alumina atom, located in the fourth atomic layer (Fig. S9, ESI†). In this position, the binding energy of Ag is found to be −1.32 eV with respect to Ag in the bulk phase.⁵¹ A second metastable structure is found where the Ag atom is in the surface layer of the alumina slab at the position of the Al_III atom (position 1). The binding energy is, in this case, calculated to be −1.13 eV where position (1) is preferred by 0.56, 0.83, and 0.83 eV over Ag₁ located in surface positions (2), (3), and (4), respectively. The two stable structures will be referred to as Ag@Al₂O₃(110)-a and Ag@Al₂O₃(110)-b.‡

To model the three phase boundary between a supported Ag nanoparticle, the alumina support and H₂ in gas phase, a rod of Ag is considered on Al₂O₃(110), see Fig. 1d. Short Al–Ag bond lengths (∼2.8 Å) are calculated to Al atoms at positions 1 and 2. The total adhesion energy of the rod is calculated to be −2.27 eV, with an average adhesion energy of −0.25 eV per Ag atom in contact with the Al₂O₃(110) surface (9 Ag atoms).⁵² The low adhesion is consistent with the minor structural relaxation observed for the rod upon geometry optimization. Below, the model will be referred to as Ag_NPM/Al₂O₃(110) (NPM = nanoparticle model).

3.3 Molecular and dissociated adsorption of H₂

Molecular adsorption of H₂ on Ag surfaces has been studied extensively^53–56 and it has been concluded that dissociation over low index surfaces is a slightly endothermic and activated process. The results for molecular and dissociated adsorption are presented in Table 1. The relaxed structures are used as initial and final configurations in the transition state searches. All structures are shown in the ESI.†

Table 1 Results for molecular (H₂) and dissociated (2H) adsorption on the considered surfaces. E_ads is the average binding energy per H atom, with respect to H₂ in the gas phase, d_H–H is the internal bond length of H₂ and d_H–S is the bond length to the closest surface site (S = O, Al, Ag). Energies are reported in eV, whereas bond-lengths are given in Å

Molecular adsorption
	Eads(H2)	dH–H	Position	dH–S
Ag(111)	−0.02	0.76	Atop Ag	3.70
Ag(211)	−0.04	0.75	Atop step Ag	3.40
p(4 × 4)	−0.05	0.75	Atop side Ag	3.34
Ag2O(111)	−0.05	0.75	Bridge Ag–O	2.75
Al2O3(110)	−0.26	0.76	Atop AlIII	2.15
Ag@Al2O3(110)-a	−0.27	0.76	Atop AlIII	2.13
Ag@Al2O3(110)-b	—	—	—	—
AgNPM/Al2O3(110)	−0.19	0.76	Aside AgNPM	2.06

---

Dissociative adsorption
	Eads(2H)	Position	dH–S
Ag(111)	+0.21	Fcc	1.94/1.94
Ag(211)	+0.26	Bridge	1.82/2.01
p(4 × 4)	−1.20	2 OH groups	0.98/0.98
Ag2O(111)	−0.92	2 OH groups	0.98/0.98
Al2O3(110)	−0.58	H–AlIII/OH group	1.58/1.02
Ag@Al2O3(110)-a	−0.65	H–AlIII/OH group	1.58/1.04
Ag@Al2O3(110)-b	−2.23	2 OH groups	0.98/0.98
AgNPM/Al2O3(110)	−0.60	H–AlIII/OH group	1.60/1.03

---

H₂ is calculated to be physisorbed in atop positions on both Ag(111) and Ag(211) where the internal bond length of adsorbed H₂ (d_H–H) is calculated to be 0.76 and 0.75 Å, respectively. The bond lengths between H₂ and the surfaces are calculated to be long (>3.0 Å). In fact, as this interaction could include dispersive contributions, the adsorption energies and the molecular-surface distances should not be regarded as very accurate within the present computational approach. It should also be noted that the potential energy surface is flat at large distances between the molecule and the metal.

Upon H₂ dissociation on Ag(111), the two H atoms are calculated to occupy 3-fold fcc positions (see Fig. 2a), with an endothermic adsorption energy [E_ads(2H)] of +0.21 eV per H atom with respect to H₂ in the gas-phase. The fcc position is calculated to be preferred by 0.04 and 0.51 eV (per H atom) over the hcp and atop configurations, respectively. (The bridge position is for Ag(111) not a minimum on the potential energy surface.) The average distance for the two H atoms to their neighboring Ag atoms is calculated to be 1.94 Å. On the (211) surface, the preferred adsorption sites for the two H are bridge positions, one on the step and the other between a step and a (111) atom (see ESI†). The average adsorption energy, per H atom on (211), is calculated to be +0.26 eV and the corresponding bond lengths are 1.82 and 2.01 Å for the step and adjacent Ag(111) adsorption sites, respectively. The adsorption energies, geometries and general trends are in good agreement with previous experimental^53,54 and theoretical^55,56 reports.

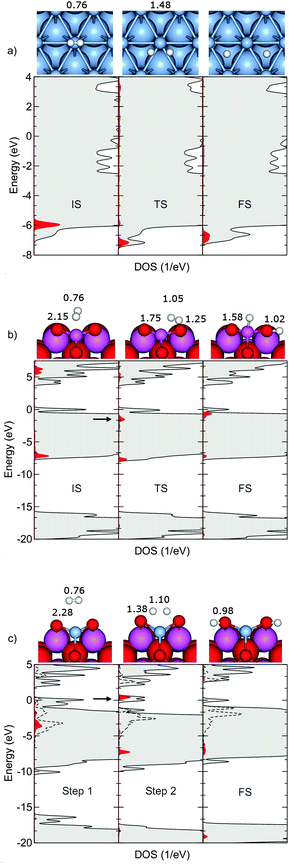Fig. 2 Electronic density of states (gray) for the initial (IS), transition state (TS), and final (FS) structures (shown as insets) of H₂ dissociation over Ag(111) (a), and Al₂O₃(110) (b). In the case of Ag@Al₂O₃(110)-b (c) the DOS is presented for the structures used during a constrained TS-search. 0 eV corresponds to the Fermi energy and projections are made on H-states (red) and Ag-states (broken lines). The arrows indicate the anti-bonding states. Structures are reported with selected bond lengths (given in Å). The presented bond lengths refer to the H–H and H–S (S = O, Al, Ag) distances, respectively.

Similar to the low index silver surfaces, molecular adsorption on both oxidized surfaces, p(4 × 4) and Ag₂O(111), displays low adsorption energies, −0.05 and −0.05 eV, respectively. In the ground state structure of H₂ on p(4 × 4), H₂ is located atop a side atom in the Ag₆ unit with a long (>3.30 Å) distance to the surface (see ESI†). The internal H–H distance is calculated to be similar to the gas phase distance of 0.75 Å. The same situation applies for H₂ on Ag₂O(111); H₂ adopts a bridge configuration between an Ag and O atom, and the nearest H₂–O and H₂–Ag distances are calculated to be 2.75 and 3.19 Å, respectively. Unlike the Ag metal surfaces, atomic adsorption, with subsequent OH formation, over the p(4 × 4) and Ag₂O(111) is calculated to be exothermic. The average H adsorption energy (per atom) and H–O bond length for p(4 × 4) (Ag₂O(111)) are calculated to be −1.20 (−0.92) eV and 0.98 (0.98) Å, respectively. Upon OH formation, both surfaces experience minor surface relaxation, where subsurface oxygen is displaced in order to form an OH group (see ESI†). By use of a planewave implementation of DFT, Mohammad and co-workers⁵⁶ have reported similar results for H₂ dissociation over a p(2 × 1)-O/Ag(110) missing row structure.

Turning to the Al₂O₃(110) surface, H₂ is weakly adsorbed at the Al_III site. This site (1) is preferred over sites (2), (3), and (4) by 0.14, 0.24, and 0.24 eV, respectively. At (1), H₂ is located 2.15 Å from the Al_III atom and the internal H–H bond is 0.76 Å (Fig. 2b). The adsorption energy is calculated to be −0.26 eV with respect to H₂ in the gas phase. In the case of dissociated adsorption, the stable conformation has one H atom bound to Al_III (d_H–Al = 1.58 Å), and an OH group formed with a nearby oxygen (d_H–O = 1.02 Å), see Fig. 2b. This configuration is 1.73 eV more stable than a structure with two OH groups on the surface and a consequence of electron pairing where the Al–H unit (formally +2) matches the formation of the OH group (formally −1). This configuration ensures that a band-gap is preserved with no unpaired electrons. The dissociated H₂ molecule is preferred by −0.93 eV with respect to the molecular state.

If Al₂O₃(110) is doped with silver in the bulk [Ag@Al₂O₃(110)-a], our calculations indicate minor geometry and energy effects on molecular and dissociated H₂ adsorption. Similar to the bare alumina surface, the site (1) is preferred with an adsorption energy of −0.27 eV and H–H internal bond length of 0.76 Å. The H₂ molecule is in this case located atop the Al_III atom at a distance of 2.13 Å. Upon dissociation, electron pairing results in the formation of a H–Al and OH group pair with an average binding energy and bond lengths of −0.65 eV and 1.58/1.04 Å, respectively. However, if the doping Ag ion is placed in the surface layer [Ag@Al₂O₃(110)-b], no minimum is found on the potential energy surface for molecular H₂ adsorption close to the Ag atom. Instead, OH groups are formed with an average adsorption energy of −2.23 eV and O–H bonds of 0.98 Å. It should be noted that energy minimum for molecular adsorption on the doped surface exists over the Al_IV sites (2–4). In these cases, the adsorption energies are calculated to be −0.14 (2), −0.04 (3) and −0.04 eV (4), respectively.

In order to explore possible effects of the metal/oxide interface, dissociation is considered at the perimeter of the supported Ag nanoparticle. Here, the metal/oxide interface as well as edges between the (111) and (100) facets on the Ag nanoparticle are investigated.⁵⁷ In the stable configuration, H₂ is weakly adsorbed at the metal/oxide interface, with an E_ads of −0.19 eV and a H–H distance of 0.76 Å. The hydrogen molecule is found 2.06 Å from the Al₂O₃(110) surface (near the Al_III atom) and >3.20 Å from the nanoparticle edge. Upon dissociation, the low energy structure resembles the one over the bare Al₂O₃(110) surface; an Al–H and an O–H group formed with an average binding energy of −0.60 eV. The bond-lengths are calculated to be 1.60 and 1.03 Å, respectively, where dissociation is preferred by −1.02 eV with respect to the molecular H₂ state. A configuration with two OH groups is also found to be a minima on the potential energy surface. However, it is calculated to be a metastable structure, +1.83 eV above the ground state. Moreover, a second metastable structure with an OH group and a hydrogen adsorbed in a 3-folded position on the Ag nanoparticle is found to be +2.01 eV over the low energy geometry. Notably, the two structures are not stable with respect to H₂ in the gas-phase. The effect of the considered metal/oxide interface seems to be of minor importance as molecular and dissociative adsorption processes display energetics (and geometries) similar to that of the bare alumina surface. Hence, it is reasonable to assume that adsorption of atomic H is a result of electron pairing rather than stabilization through charge transfer from the adsorbates to the metal/oxide interface.^21–23,58 Based on the similarities in molecular and dissociated adsorption-energies and -geometries, the transition state barrier for H₂ dissociation over the Ag nanoparticle is not considered.

3.4 H₂ dissociation

Transition state (TS) calculations were performed in order to evaluate the dissociation barriers. All barriers were calculated with respect to the molecularly adsorbed state of H₂, i.e. they are intrinsic barriers. As expected, H₂ dissociation over Ag(111) and Ag (211) is an activated process. The barriers are calculated to be 1.55 and 1.33 eV, respectively (see Table 2). In the transition state, the H–H distances are 1.48 and 1.49 Å. On (111), dissociation occurs slightly on the side of an Ag surface atom, whereby the two H atoms assume adjacent fcc positions (see Fig. 2a). In the TS, the H–Ag distance is calculated to be 1.76 Å. Dissociation on (211) occurs over an Ag atom in the step, where one hydrogen is found in a bridge configuration with H–Ag distances of 1.82 and 1.94 Å and the second hydrogen is located 1.69 Å atop a neighboring Ag atom. The TS for Ag(211) is close to the final configuration.

Table 2 Calculated intrinsic TS barriers (eV) and H–H bond-lengths (Å) at the TS

	ETS	dH–H
Ag(111)	1.55	1.48
Ag(211)	1.33	1.49
p(4 × 4)	0.37	0.96
Ag2O(111)	1.04	1.12
Al2O3(110)	0.68	1.05
Ag@Al2O3(110)-a	0.69	1.04

---

On p(4 × 4), the H₂ molecule dissociates over an Ag atom located on the side of the Ag₆ sub-unit. The process to form two OH groups is strongly exothermic with an activation barrier of 0.37 eV. The TS is associated with breaking of the H–H bond where the H–H distance is calculated to be 0.96 Å. Here, one H atom is located 1.28 Å from a surface O atom and the second H is located 1.97 Å from an adjacent silver atom. A similar process was recently observed by use of X-ray photoemission spectroscopy and DFT calculations during CO dosage over p(4 × 4);⁵⁹ carbonates were formed with low barriers. In both cases, oxidation reactions lead to a formal reduction of the oxidized silver surface.

Dissociation of H₂ over the silver bulk oxide turns out to be markedly different as compared to the oxidized surface. Dissociation is an activated process with a barrier of 1.04 eV. In the TS, the two H atoms are separated by 1.12 Å and located 1.15 and 2.25 Å over neighboring oxygen and silver atoms, respectively.

Over the Al₂O₃(110) surface, the H₂ dissociation proceeds with a barrier of 0.68 eV. The reaction takes place over the Al_III site where the H–H, H–O, and H–Al distances at the TS are calculated to be 1.05, 1.25 and 1.75 Å respectively (see Fig. 2b). Doping the alumina in the bulk phase displays similar energetics. Here [Ag@Al₂O₃(110)-a], the TS also occurs over the Al_III site with a barrier of 0.69 eV and H–H, H–O, and H–Al distances of 1.04, 1.25, and 1.74 Å. As already mentioned, H₂ dissociates without any barrier on Ag@Al₂O₃(110)-b and forms two OH groups on the surface. The overall reaction is in this case exothermic by −4.47 eV with respect to H₂ in the gas phase. (Each O–H bond has a binding energy of 4.51 eV with respect to atomic hydrogen which could be compared with the O–H bond strength in the water molecule which is calculated to be 5.03 eV.)

In the literature, it has been speculated that removal of surface nitrates (NO₃⁻ on Al₂O₃) could occur via an Eley–Rideal process.⁶⁰ In particular, it was suggested that H₂ dissociation takes place directly over NO₃⁻ species. Here we estimate the direct H₂ dissociation over NO₃⁻ on Al₂O₃(110) to be in the range of the H₂ binding energy (∼4.5 eV). Thus, this process is unlikely and reduction of nitrates to nitrites with H₂ should be ascribed to a Langmuir–Hinshelwood mechanism.

3.5 Analysis of electronic structure

Adsorption of H₂ on metal surfaces has been thoroughly studied in the literature.⁶¹ As a H₂ molecule approaches a metal surface, the H–H σ bonding orbital experiences a Pauli repulsion with respect to s-derived states in the metal. If a vacancy exist in the d-band near the Fermi energy, a lower repulsion and barrier for dissociation can be obtained by a transfer of charge from s- to d-derived states.⁶² For a selected set of systems, the total density of states (DOS) together with the projection onto atomic H and Ag (PDOS) are shown in Fig. 2a–c. The DOS and PDOS are calculated for the corresponding initial state (IS), transition state (TS), and final state (FS), respectively. As no activation barrier exists for Ag@Al₂O₃(110)-b, the IS and TS results correspond to constrained calculations where the two hydrogen atoms are placed at 2.0 Å and 0.8 Å above the surface plane, respectively.

On Ag(111), the molecular bonding state (1σ) in the initial state is found at ∼6 eV below the Fermi energy (located at 0 eV), see Fig. 2a. At the transition state, H₂ interacts more strongly with the metal and the anti-bonding combination between σ and the metal states can be observed as a broad resonance (Fig. 2a TS). As both the bonding and anti-bonding σ-metal states are located below the Fermi level, the H₂ molecule experiences a repulsion towards the surface, which yields a high barrier for dissociation.

On the bare Al₂O₃(110) surface, the molecular σ and σ* states are initially located at −7.30 eV below and +6.2 eV above the Fermi energy, respectively. In the transition state, the σ state has split into one that is bonding and one that is anti-bonding with respect to the surface states. The bonding combination is slightly stabilized with respect to the IS, whereas the antibonding combination is located at about −1.9 eV below the Fermi energy.

If Al₂O₃(110) is doped with Ag ions, substrate–adsorbate states are formed without repulsion. The atomic Ag d-state is broadened when the atom is put in the alumina surface and spans a region between −5 and 0 eV. The broadening of the H₂ derived states is also substantial, and takes place already at large distances between the molecule and the surface. When H₂ approaches the surface (Step 2), the DOS displays formation of substrate–adsorbate states where the bonding state is located at ∼−7.5 eV. In this case, the anti-bonding σ-surface state (arrow in Fig. 2c, Step 2) is located above the Fermi energy (∼1 eV). Finally (FS), OH formation leads to states at ∼−18 eV below the Fermi energy. In the final state, the broadening of the Ag d-state is somewhat reduced.

4 Discussion and conclusions

We have performed first principle DFT calculations to elucidate H₂ dissociation over a silver promoted γ-alumina catalyst. This reaction is a crucial step in hydrogen assisted SCR of NO_x. Mapping the dissociation and adsorption sites of hydrogen species is one step to understand the “H₂ effect” and identify active sites for the SCR process. Our results show that dissociation over bare alumina or metallic Ag is associated with substantial activation barriers. Low barriers are instead calculated over Ag-ions and partially oxidized silver.

Acknowledgements

Support from the Swedish Research Council and the Swedish Foundation for Strategic Research is gratefully acknowledged. The Competence Centre for Catalysis is hosted by Chalmers University of Technology and financially supported by the Swedish Energy Agency and the member companies AB Volvo, Volvo Car Corporation, Scania CV AB, Haldor Topsoe A/S, and The Swedish Space Agency. The calculations were performed at C3SE (Göteborg).

References

1. E. Seker, J. Cavataio, E. Gulari, P. Lorpongpaiboon and S. Osuwan, Appl. Catal., A, 1999, 183, 121.
2. K. Shimizu, J. Shibata, H. Yoshida, A. Satsuma and T. Hattori, Appl. Catal., B, 2001, 30, 151.
3. H. Kannisto, H. H. Ingelsten and M. Skoglundh, J. Mol. Catal. A: Chem., 2009, 302, 86.
4. K. Bethke and H. Kung, J. Catal., 1997, 172, 93.
5. F. C. Meunier, J. P. Breen, V. Zuzaniuk, M. Olsson and J. R. H. Ross, J. Catal., 1999, 187, 493.
6. H. He and Y. Yu, Catal. Today, 2005, 100, 37.
7. A. Hellman and H. Grönbeck, Phys. Rev. Lett., 2008, 100, 116801.
8. M. Richter, U. Bentrup, R. Eckelt, M. Schneider, M. M. Pohl and R. Fricke, Appl. Catal., B, 2004, 51, 261.
9. K. Shimizu and A. Satsuma, Phys. Chem. Chem. Phys., 2006, 8, 2677.
10. N. Bion, J. Saussey, M. Haneda and M. Daturi, J. Catal., 2003, 217, 47.
11. N. Bogdanchikova, F. C. Meunier, M. Avalos-Borja, J. P. Breen and A. Pestryakov, Appl. Catal., B, 2002, 36, 287.
12. K. Eränen, L.-E. Lindfors, F. Klingstedt and D. Y. Murzin, J. Catal., 2003, 219, 25.
13. P. Sazama, L. Čapek, H. Drobná, Z. Sobalík, J. Dědeček, K. Arve and B. Wichterlová, J. Catal., 2005, 232, 302.
14. B. Wichterlová, P. Sazama, P. J. Breen, R. Burch, C. J. Hill, L. Čapek and Z. Sobalík, J. Catal., 2002, 235, 195.
15. J. P. Breen, R. Burch, C. Hardacre and C. J. Hill, J. Phys. Chem. B, 2005, 109, 4805.
16. R. Brosius, K. Arve, M. H. Groothaert and J. A. Martens, J. Catal., 2005, 231, 344.
17. S. Satokawa, Chem. Lett., 2000, 294.
18. J. Shibata, Y. Takada, A. Shichi, S. Satokawa, A. Satsuma and T. Hattori, J. Catal., 2004, 222, 368.
19. A. Satsuma, A. Wada, Y. Shinozaki and T. Hattori, Stud. Surf. Sci. Catal., 2002, 145, 235.
20. S. Satokawa, J. Shibata, K. Shimizu, A. Satsuma and T. Hattori, Appl. Catal., B, 2003, 42, 179.
21. H. Grönbeck, J. Phys. Chem. B, 2006, 110, 11977.
22. A. Hellman, S. Klacar and H. Grönbeck, J. Am. Chem. Soc., 2009, 113, 16636.
23. Y. Sun, L. Giordano, J. Goniakowski, M. Lewandowski, Z.-H. Qin, C. Noguera, S. Shaikhutdinov, G. Pacchioni and H.-J. Freund, Angew. Chem., Int. Ed., 2010, 49, 4418.
24. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
25. B. Delley, J. Chem. Phys., 1990, 92, 508.
26. B. Delley, J. Chem. Phys., 2000, 113, 7756.
27. We have used DMol, version 4.0.
28. B. Delley, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155125.
29. H. Knözinger and P. Ratnasamy, Catal. Rev.: Sci. Eng., 1978, 17, 31.
30. M. B. Fleicher, L. O. Golender and M. V. Shimanskaya, J. Chem. Soc., Faraday Trans., 1991, 87, 745.
31. J. Fernández-Sanz, H. Rabaâ, F. M. Poveda, A. M. Máeques and C. J. Calzado, Int. J. Quantum Chem., 1998, 70, 359.
32. K. Sohlberg, S. J. Pennycook and S. T. Pantelides, J. Am. Chem. Soc., 1999, 121, 10999.
33. A. Ionescu, A. Allouche, J. P. Aycard, M. Rajzmann and F. Hutschka, J. Phys. Chem. B, 2002, 106, 9359.
34. M. Digne, P. Sautet, P. Raybaud, P. Euzen and H. Toulhoat, J. Catal., 2002, 211, 1.
35. L. M. Molina and B. Hammer, Phys. Rev. Lett., 2003, 90, 206102.
36. T. A. Halgren and W. N. Lipscomb, Chem. Phys. Lett., 1977, 49, 225.
37. S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
38. D. R. Lide, Handbook of Chemistry and Physics, CRC Press, Inc., 71st edn, 1990–1991.
39. M. Körling and J. Häglund, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13293.
40. M. Digne, P. Sautet, P. Raybaud, P. Euzen and H. Toulhoat, J. Catal., 2004, 226, 54.
41. Z. Liu, L. Ma and A. S. M. Junaid, J. Phys. Chem. C, 2010, 114, 4445.
42. Vibrational analysis was performed by calculating numerical derivatives with finite differences.
43. N. Seriani and F. Mittendorf, J. Phys.: Condens. Matter, 2008, 20, 184023.
44. J. Schnadt, A. Michaelides, J. Knudsen, R. T. Vang, K. Reuter, E. Lægsgaard, M. Scheffler and F. Besenbacher, Phys. Rev. Lett., 2006, 96, 146101.
45. M. Schmidt, A. Reicho, A. Stierle, I. Costina, J. Klikovits, P. Kostelnik, O. Dubay, G. Kresse, J. Gustafson, E. Lundgren, J. N. Andersen, H. Dosch and P. Varga, Phys. Rev. Lett., 2006, 96, 146102.
46. S. Klacar, A. Hellman, I. Panas and H. Grönbeck, J. Phys. Chem. C, 2010, 114, 12610.
47. W. Li, C. Stampfl and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 045408.
48. J. P. Beaufils and Y. Barbaux, J. Chem. Phys., 1981, 78, 347.
49. P. Nortier, P. Fourre, A. B. Mohammed-Saad, O. Saur and J. C. Lavalley, Appl. Catal., 1990, 61, 141.
50. This reflects the experimental situation where dangling bonds will be saturated by, for example, hydroxyl groups.
51. The Ag binding energy was calculated by: 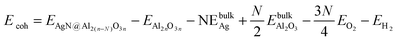where E_{AgN@Al2(n−N)O3n} is the calculated total energy of the system with N Ag ions in the alumina matrix, E_Al2nO3n is the total energy of a geometry optimized bare alumina (110) surface containing n Al₃O₂ units, and E^bulk_Ag is the total energy per Ag atom in the silver bulk, 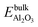is the total energy of a geometry optimized alumina bulk, E_O2 and E_H2 are the total energies of O₂ and H₂ in the gas phase, respectively.
52. The value could be compared to −2.34 eV which is the adsorption energy of an Ag atom at the Al₂O₃ surface with a vacancy [Ag@Al₂O₃(110)-b], calculated with respect to an Ag atom in the gas phase and the Al₂O₃(110) structure with a vacancy at the position of the Ag atom.
53. K. Christmann, Surf. Sci. Rep., 1988, 9, 1.
54. G. Lee and E. W. Plummer, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 7250.
55. C. Mijoule and V. Russier, Surf. Sci., 1991, 254, 329.
56. A. B. Mohammad, K. H. Lim, I. V. Yudanov, K. M. Neyman and N. Rösch, Phys. Chem. Chem. Phys., 2007, 9, 1247.
57. As the Ag nanoparticle is modeled with a three layer Ag(100) structure, H₂ dissociation over terrace Ag(100) was investigated for completeness. H₂ is calculated to be weakly physisorbed (−0.02 eV), in a bridge position. The internal bond length of adsorbed H₂ is calculated to be 0.75 Å where the H–Ag bond lengths are long (>3.0 Å). When dissociated, the two H atoms occupy 4-fold positions. The average binding energy and Ag–H bond lengths are +0.37 eV and 2.13 Å, respectively. The transition state barrier is calculated to be +1.44 eV with respect to molecular H₂ adsorption. In the TS, the H–H distance is 1.42 Å.
58. K. Honkala, A. Hellman and H. Grönbeck, J. Phys. Chem. C, 2010, 114, 7070.
59. J. Knudsen, N. M. Martins, E. Grånäs, S. Blomberg, J. Gustafson, J. N. Andersen, E. Lundgren, S. Klacar, A. Hellman and H. Grönbeck, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 115430.
60. D. Creaser, H. Kannisto, J. Sjöblom and H. H. Ingelsten, Appl. Catal., B, 2009, 90, 18.
61. I. Chorkendorff and J. W. Niemantsverdriet, Concepts of Modern Catalysis and Kinetics, Wiley-VCH, Weinheim, 2nd edn, 2007.
62. J. Harris and S. Andersson, Phys. Rev. Lett., 1985, 55, 1583.

---

Footnotes

† Electronic supplementary information (ESI) available: Atomic structures of all considered models. See DOI: 10.1039/c2cy20343j

‡ Because of the large difference of ionic sites of Ag⁺ and Al³⁺, the structures with embedded Ag are strained. To estimate the degree of strain, the -a and -b structures were considered in (2 × 2) surface cells. With the large cell, the binding energies for a and b were calculated to be −1.64 and −1.73 eV, respectively.

---