 Open Access Article
Open Access ArticleFundamental and overtone vibrational spectroscopy, enthalpy of hydrogen bond formation and equilibrium constant determination of the methanol–dimethylamine complex†
Lin
Du
,
Kasper
Mackeprang
and
Henrik G.
Kjaergaard
*
Department of Chemistry, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen Ø, Denmark. E-mail: hgk@chem.ku.dk; Fax: +45-35320322; Tel: +45-35320334
First published on 8th May 2013
Abstract
We have measured gas phase vibrational spectra of the bimolecular complex formed between methanol (MeOH) and dimethylamine (DMA) up to about 9800 cm−1. In addition to the strong fundamental OH-stretching transition we have also detected the weak second overtone NH-stretching transition. The spectra of the complex are obtained by spectral subtraction of the monomer spectra from spectra recorded for the mixture. For comparison, we also measured the fundamental OH-stretching transition in the bimolecular complex between MeOH and trimethylamine (TMA). The enthalpies of hydrogen bond formation (ΔH) for the MeOH–DMA and MeOH–TMA complexes have been determined by measurements of the fundamental OH-stretching transition in the temperature range from 298 to 358 K. The enthalpy of formation is found to be −35.8 ± 3.9 and −38.2 ± 3.3 kJ mol−1 for MeOH–DMA and MeOH–TMA, respectively, in the 298 to 358 K region. The equilibrium constant (Kp) for the formation of the MeOH–DMA complex has been determined from the measured and calculated transition intensities of the OH-stretching fundamental transition and the NH-stretching second overtone transition. The transition intensities were calculated using an anharmonic oscillator local mode model with dipole moment and potential energy curves calculated using explicitly correlated coupled cluster methods. The equilibrium constant for formation of the MeOH–DMA complex was determined to be 0.2 ± 0.1 atm−1, corresponding to a ΔG value of about 4.0 kJ mol−1.
1. Introduction
Hydrogen bonding is involved in many chemical and biological processes in nature.1–6 The investigation of the role of hydrogen bonded molecular complexes in the Earth's atmosphere is of significant interest in atmospheric chemistry, in terms of both radiative transfer and aerosol formation and growth.1,4,5,7,8 Among the atmospherically relevant compounds, amines are unique in their acid-neutralizing capacity. Amines have recently been proposed as possible stabilizers of binary pre-nucleation clusters, which are important for aerosol formation.9–14 Amines, such as dimethylamine (DMA) and trimethylamine (TMA), are good examples of strong hydrogen bond acceptors15 and methanol (MeOH) is a good hydrogen bond donor.16–21 Thus, methanol–amine complexes have been studied frequently.19,22–30Vibrational spectroscopy is one of the most useful experimental tools in the study of hydrogen bonded clusters.31–39 Molecular complexes can be identified by new ro-vibronic bands that are not present in the spectra of the monomers.5,8,31–33,40 There have been several infrared spectroscopic studies of methanol–amine systems reported in the literature. The infrared spectroscopic results of methanol–amine systems show the usual hydrogen bond characteristics, with a wavenumber redshift and an intensity enhancement of the OH-stretching fundamental transition.40,41 Both these characteristics facilitate the detection of these complexes in the gas phase. The gas phase mixtures between MeOH and amines were first measured in the IR region by Millen and Zabicky.22,23 They concluded that the strongest complex among them is formed between MeOH and TMA. Ginn and Wood examined the far-IR (FIR) absorption of a gas phase MeOH–TMA complex and found a band at 142.6 cm−1 and assigned it to the hydrogen bond vibration.24 The OH-stretching fundamental transition frequencies of methanol with ammonia and several amines were measured in the IR region and substantial frequency shifts of the OH-stretching fundamental transitions upon complexation were reported.25,26 Tan et al. measured the rotational transitions of the MeOH–TMA complex using Fourier transform microwave spectroscopy and found a nearly linear hydrogen bonded structure with an intermolecular hydrogen bond distance (O–H⋯N) of 1.92 Å.29
Due to the low abundance of the complexes and the weaker intensity of overtone and combination vibrations in the near-IR (NIR) region, the number of NIR spectroscopic studies of hydrogen bonded complexes is limited. The available NIR studies of hydrogen bonded complexes are mostly carried out either at very low temperatures,36,42–46 or in organic solutions,47–51 conditions that are less relevant to the atmosphere. Recently, gas phase NIR spectra of the hydrogen bonded complex MeOH–TMA were recorded to about 6500 cm−1.19 Besides the OH-stretching fundamental transition, a combination transition of the MeOH–TMA complex involving one quantum of OH-stretching and one quantum of predominantly in-plane COH bending (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH + δCOH) was observed and the much less intense first OH-stretching overtone transition was tentatively assigned in the NIR region. So far, no higher overtone gas phase transitions have been observed for methanol–amine complexes. In this work, in addition to the fundamental transitions we have detected the second NH-stretching overtone in the MeOH–DMA complex.
OH + δCOH) was observed and the much less intense first OH-stretching overtone transition was tentatively assigned in the NIR region. So far, no higher overtone gas phase transitions have been observed for methanol–amine complexes. In this work, in addition to the fundamental transitions we have detected the second NH-stretching overtone in the MeOH–DMA complex.
The importance of hydrogen bonded complexes is well known.8,52 However, few atmospheric models incorporate them because little is known about their thermodynamic properties, such as their enthalpy for hydrogen bond formation (ΔH) and Gibbs free energy of complexation (ΔG) or equilibrium constants of complexation (Kp). The latter ΔG or Kp is necessary to determine the atmospheric abundance of these complexes. In the gas phase, the Kp values for hydrogen bonded complexes are typically small. Perhaps the most studied atmospherically relevant complex, a water dimer, has a Kp value of about 0.05 atm−1,53,54 which indicates that it is a weak hydrogen bonded complex. The methanol–amine systems are likely somewhat more strongly bound than the water dimer. Previously, the ΔH and Kp were estimated for MeOH–DMA and MeOH–TMA based on pressure, volume, temperature studies,27 and MeOH–TMA also by IR spectroscopy.28 The enthalpy for hydrogen bond formation was found to be −25.9 kJ mol−1 and −28.9 kJ mol−1 for MeOH–DMA and MeOH–TMA, respectively, and it was suggested that the wavenumber redshift of the transition was correlated with ΔH. The equilibrium constant at 298 K was determined to be 0.6 atm−1 and 0.85 atm−1 for MeOH–DMA and MeOH–TMA, respectively.27
In this work, we have measured the temperature dependence of the fundamental OH-stretching transitions and used this to determine the enthalpy of complexation (ΔH) for MeOH–DMA and MeOH–TMA in the temperature range from 298 K to 358 K. The complexes can be quantified by the integrated area of certain absorption bands in gas phase IR/NIR spectra, provided the intensity of these bands is known.19,31,33,37–39 We have used a combination of measured and calculated transition intensities of the fundamental OH-stretching transition and the second NH-stretching overtone to determine the equilibrium constant of complexation for MeOH–DMA. Quantum chemical calculations of the MeOH–DMA and MeOH–TMA complexes and their monomers were performed to help interpreting the spectra. The geometry and interaction energies for the complexes are calculated with the explicitly correlated CCSD(T)-F12a method with the associated VDZ-F12 basis set.55 Results of this method have previously been found to be in good agreement with results obtained using much larger basis sets using conventional CCSD(T) theory and where possible with experiment.38,56–60 The OH- and NH-stretching transition wavenumbers and intensities for the complexes and monomers were calculated with an anharmonic oscillator local mode model.61–65
2. Experimental section
MeOH (Aldrich anhydrous, 99.8%) was degassed with freeze–pump–thaw cycles on a vacuum line before use. DMA (Aldrich, anhydrous, 99+%) and TMA (Aldrich, anhydrous, 99%) were used without any further purification. The IR spectra were recorded at 1.0 cm−1 resolution with a Vertex 70 FTIR spectrometer (Bruker) fitted with a CaF2 beam splitter. A liquid nitrogen cooled MCT detector and an InGaAs detector were used to measure the fundamental and overtone transitions, respectively. Both MIR and NIR light sources were used. The sample compartment and the optics of the spectrometer were purged with dry nitrogen gas to reduce the content of unwanted atmospheric interferents (H2O and CO2) inside the spectrometer. Several gas cells with different optical path lengths were used to measure the spectra. The fundamental transitions were recorded using a 10 cm cell equipped with KBr windows and the overtone transitions were recorded using a 4.8 m path length multi-reflection gas cell (Infrared Analysis, Inc) fitted with KCl windows. A heatable 2.4 m path length multi-reflection gas cell (Infrared Analysis, Inc) fitted KCl windows was used in the temperature dependent measurements. The compounds were led into the respective sample cells on a vacuum line; for more details, see ref. 37. Known pressures of DMA (or TMA) and MeOH vapors were mixed for at least one hour to ensure equilibrium. The OPUS program was used to perform spectral subtraction and band integration. The bands were fitted to Lorentzian functions to obtain the band center positions and full width at half maximum (fwhm).In the experiments, the gas adsorption of DMA (or TMA) on the cell wall before measurement was very slow (<2%) and neglected. However, the adsorption of MeOH on walls and its loss during the process of preparing the gas mixture was relatively larger. Therefore, a pressure “calibration” procedure was performed for MeOH. We measured a pure MeOH spectrum at a certain pressure (nominal) immediately after filling the vapor into the cell. In the spectral subtraction a weighting factor was applied to the pure MeOH spectrum, such that the MeOH transitions matched in regions where only MeOH absorbed. The product of the nominal MeOH pressure and the weighting factor is the “real” MeOH pressure in the cell. We have recorded the IR spectra of gas phase MeOH, TMA and a mixture of the two to verify previous results and to compare with our MeOH–DMA spectra. In the variable temperature experiments, the IR spectra were measured with the heatable cell in the temperature range between 298 and 358 K. The gas pressures were measured at room temperature and the ideal gas law used to obtain the gas pressure in the cell at the elevated temperatures. Before each measurement, we waited about 30 min for the gas in the cell to reach a stable temperature.
3. Theoretical section
Gaussian 09 (revision B.01) and Molpro (version 2010.1) were used to perform all the calculations.66,67 We have optimized the geometries of DMA, TMA, MeOH, MeOH–DMA and MeOH–TMA with the B3LYP, LC-wPBE, M06-2X, and wB97XD functionals with the aug-cc-pVTZ basis set. As suggested in our recent work, all DFT calculations were performed with Gaussian 09 using the “opt = verytight” and “int = ultrafine” options.38 Such calculation should provide reasonably good frequencies and thus good thermochemical corrections to the electronic energies for the hydrogen bonded complexes.38 We have, furthermore, optimized the geometries of the monomers and complexes with the explicitly correlated CCSD(T)-F12a/VDZ-F12 (F12) method in Molpro 2010.1. The CCSD(T)-F12 methods have been shown to give very accurate intermolecular distances and interaction energies of hydrogen bonded complexes.56 The optimization threshold criteria of the Molpro calculations were set to: energy = 1 × 10−7 a.u., gradient = 1 × 10−5 a.u., and step size = 1 × 10−5 a.u., and the global thresholds for single-point calculations were set to: energy = 1 × 10−8 a.u., orbital = 1 × 10−7 a.u., and coefficient = 1 × 10−7 a.u. Three stable conformers of the MeOH–DMA complex were identified by theoretical calculations. Frequencies were calculated with DFT methods for each stable conformer to ensure that a true minimum had been found. We have calculated the enthalpies and Gibbs free energies (ΔH298K and ΔG298K) of formation for the MeOH–DMA and MeOH–TMA complexes using standard statistical mechanics.7 Zero point vibrational energy (ZPVE) corrections for binding energies (BE) were obtained from unscaled DFT harmonic frequencies. The BE is defined as the energy of the complex minus that of the two monomers. The enthalpies and Gibbs free energies of formation are obtained with the DFT methods and with a combination of CCSD(T)-F12a/VDZ-F12 electronic energies and DFT harmonic frequencies and rotational constants. Similar to our previous calculations for the DMA–TMA complex,38 we did not correct the CCSD(T)-F12a/VDZ-F12 binding energies for basis set superposition error (BSSE) using the popular counterpoise (CP) approach.68 For a given basis set, the magnitude of BSSE obtained with explicitly correlated CCSD(T)-F12 calculations has been shown to be significantly smaller than the magnitude of BSSE obtained with conventional CCSD(T).56 Furthermore, with the F12 method, the CP corrected BE is in poorer agreement with the CCSD(T) complete basis set limit than non-CP corrected BE.56The OH- and NH-stretching transition wavenumbers and oscillator strengths for the MeOH–DMA complex and monomers were calculated with an anharmonic oscillator local mode model.61,62,69 Previously, the OH- and NH-stretching modes in a range of molecules have been well described by the local mode model of vibration (see for example, ref. 19, 57, 58 and 63). The F12 method has been found to give accurate XH-stretching fundamental and overtone transition wavenumbers and intensities.58 In the local mode model, we assume that the OH-stretching (and NH-stretching) vibrations can be described by a Morse oscillator, with the vibrational energy levels given by
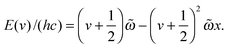 | (1) |
This expression can also be written as
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) v0/v = v0/v = ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) − (v + 1) − (v + 1)![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) x x | (2) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) v0 is the transition energy in cm−1 from v = 0 to v. The Morse oscillator frequency
v0 is the transition energy in cm−1 from v = 0 to v. The Morse oscillator frequency ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) and anharmonicity
and anharmonicity ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) x are found from the 2nd, 3rd, and 4th-order derivatives of the potential energy curve.63 The 13-point CCSD(T)-F12a/VDZ-F12 level potential energy curve is obtained by displacing the O–H bond from −0.30 to 0.30 Å in 0.05 Å steps around equilibrium bond length. The difference between the use of a Morse potential approximation for the potential and a full potential with a numeric solution of the 1D Schrodinger is at most a few wavenumbers.70,71 For the hydrogen bonded OH-stretching vibration in the water dimer the difference was less than 1 cm−1 and for the MeOH–DMA complex we find a difference of 6 cm−1. The dimensionless oscillator strength of a transition from the ground vibrational state to an excited vibrational state is calculated using the transition frequency and the transition dipole moment matrix.63,64,72 The transition dipole moment matrix can be expanded as a Taylor series in the OH-stretching displacement coordinate and we limit the expansion to 6th order terms. The dipole moment coefficients are found by fitting a 6th-order polynomial to a 13-point dipole moment function calculated by displacing the O–H bond from −0.30 to 0.30 Å in 0.05 Å steps around equilibrium bond length. The F12 dipole moment was calculated using the finite field approach with a field strength of 0.0001 a.u. The calculated dipoles and energies, obtained from the 13-point CCSD(T)-F12a/VDZ-F12 level calculation, are given in ESI.† More details of the theory method can be found in ref. 38 and 63.
x are found from the 2nd, 3rd, and 4th-order derivatives of the potential energy curve.63 The 13-point CCSD(T)-F12a/VDZ-F12 level potential energy curve is obtained by displacing the O–H bond from −0.30 to 0.30 Å in 0.05 Å steps around equilibrium bond length. The difference between the use of a Morse potential approximation for the potential and a full potential with a numeric solution of the 1D Schrodinger is at most a few wavenumbers.70,71 For the hydrogen bonded OH-stretching vibration in the water dimer the difference was less than 1 cm−1 and for the MeOH–DMA complex we find a difference of 6 cm−1. The dimensionless oscillator strength of a transition from the ground vibrational state to an excited vibrational state is calculated using the transition frequency and the transition dipole moment matrix.63,64,72 The transition dipole moment matrix can be expanded as a Taylor series in the OH-stretching displacement coordinate and we limit the expansion to 6th order terms. The dipole moment coefficients are found by fitting a 6th-order polynomial to a 13-point dipole moment function calculated by displacing the O–H bond from −0.30 to 0.30 Å in 0.05 Å steps around equilibrium bond length. The F12 dipole moment was calculated using the finite field approach with a field strength of 0.0001 a.u. The calculated dipoles and energies, obtained from the 13-point CCSD(T)-F12a/VDZ-F12 level calculation, are given in ESI.† More details of the theory method can be found in ref. 38 and 63.
4. Results and discussion
4.1. IR spectra
We have measured the spectra of the MeOH–DMA complex in the region from 1000 to 9800 cm−1. Bands associated with the OH-stretching Δv = 1, 2 and NH-stretching Δv = 2, 3 have been observed. In addition some combination bands were observed. A summary of the assignments of the fundamental and overtones of MeOH–DMA and MeOH–TMA are listed in Table 1.The spectrum of the MeOH–DMA complex in the OH-stretching fundamental transition ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH region was obtained by subtraction of individual spectra of 466 Torr DMA and 25 Torr MeOH, from the spectrum of their mixture and is shown in Fig. 1. The IR spectra of DMA, MeOH, and a mixture of the two gases recorded using a 10 cm path length cell before subtraction are given in ESI† (Fig. S1). Both DMA and its dimer exist at 466 Torr DMA, however, both can be successfully subtracted from the spectrum of the mixture.37 To check the reproducibility of the experiment, the spectra of the individual components and of the mixture were recorded at different pressure combinations. The resultant band obtained from the 131 Torr DMA and 17 Torr MeOH mixture is also shown in Fig. 1. The two spectra in Fig. 1 are very similar with the weaker signal from the 131 Torr DMA + 17 Torr MeOH mixture illustrating the smaller amount of complex formed. To further confirm the assignment, experiments with two other pressure combinations were carried out and the integrated area of the complex band is plotted against the product of the pressures of the two monomers (Fig. S2, ESI†). The results fit well with a linear fit indicating the formation of a 1
OH region was obtained by subtraction of individual spectra of 466 Torr DMA and 25 Torr MeOH, from the spectrum of their mixture and is shown in Fig. 1. The IR spectra of DMA, MeOH, and a mixture of the two gases recorded using a 10 cm path length cell before subtraction are given in ESI† (Fig. S1). Both DMA and its dimer exist at 466 Torr DMA, however, both can be successfully subtracted from the spectrum of the mixture.37 To check the reproducibility of the experiment, the spectra of the individual components and of the mixture were recorded at different pressure combinations. The resultant band obtained from the 131 Torr DMA and 17 Torr MeOH mixture is also shown in Fig. 1. The two spectra in Fig. 1 are very similar with the weaker signal from the 131 Torr DMA + 17 Torr MeOH mixture illustrating the smaller amount of complex formed. To further confirm the assignment, experiments with two other pressure combinations were carried out and the integrated area of the complex band is plotted against the product of the pressures of the two monomers (Fig. S2, ESI†). The results fit well with a linear fit indicating the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex.
1 complex.
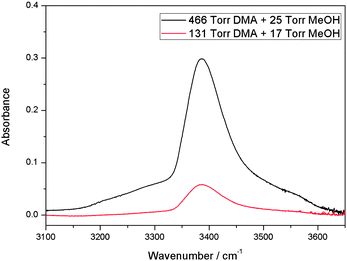 | ||
Fig. 1 The ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH transition of the MeOH–DMA complex obtained by spectral subtraction of 466 Torr DMA and 25 Torr MeOH from the mixture of the two gases (upper trace), and of 131 Torr DMA and 17 Torr MeOH from the mixture of the two gases (lower trace). All the spectra were recorded in a 10 cm path length cell using an MIR light source and an MCT detector at 300 ± 1 K. OH transition of the MeOH–DMA complex obtained by spectral subtraction of 466 Torr DMA and 25 Torr MeOH from the mixture of the two gases (upper trace), and of 131 Torr DMA and 17 Torr MeOH from the mixture of the two gases (lower trace). All the spectra were recorded in a 10 cm path length cell using an MIR light source and an MCT detector at 300 ± 1 K. | ||
The spectrum of MeOH–DMA demonstrates the formation of a hydrogen bonded complex in much the same way as for MeOH–TMA (Fig. S3, ESI†). According to experimental measurement in this work, the OH-stretching fundamental transition wavenumber of the MeOH–DMA and MeOH–TMA complexes are 3387 and 3355 cm−1, respectively. In order to obtain the frequency shift of the OH-stretching transition, we measured the room temperature (298 K) vapor phase fundamental and overtone spectra (ΔvOH = 1–4) of MeOH. These spectra are given in ESI† (Fig. S4). The OH-stretching transitions (ΔvOH = 1–4) of MeOH are observed at 3688, 7197, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 532, and 13
532, and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 701 cm−1, respectively. The red shift of the OH-stretching fundamental transition of the MeOH–DMA complex (301 cm−1) is smaller than the shift of the MeOH–TMA complex (333 cm−1). The red shift (Δ
701 cm−1, respectively. The red shift of the OH-stretching fundamental transition of the MeOH–DMA complex (301 cm−1) is smaller than the shift of the MeOH–TMA complex (333 cm−1). The red shift (Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) of the OH-stretching frequency is often used as a criterion of hydrogen bond strength, which would suggest that MeOH–DMA is a slightly weaker complex than MeOH–TMA.
) of the OH-stretching frequency is often used as a criterion of hydrogen bond strength, which would suggest that MeOH–DMA is a slightly weaker complex than MeOH–TMA.
Similar to MeOH–TMA, side bands of the OH-stretching fundamental transition also appear in the spectrum of the MeOH–DMA complex.19 The low frequency side band looks similar to the one observed in MeOH–TMA, however, the high frequency side band is not as well resolved as that in MeOH–TMA.19 For the MeOH–TMA complex, Ginn and Wood observed an absorption band in the far infrared spectrum at 142.6 cm−1,24 which is close to the observed frequency from the sum-and-difference (combination) band assignment. This band is a low-frequency inter-subunit hydrogen bond vibration band, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) σ. Because of the similarity of structures and spectra between the MeOH–DMA and MeOH–TMA complexes, we assign the side bands in the MeOH–DMA spectrum to be the combination bands (sum-and-difference bands). We fit this fundamental OH-stretching region to three bands (Fig. S5a, ESI†). Adding additional peaks would improve this fit to the observed spectrum (Fig. S5b, ESI†) and likely illustrate the existence of the two conformers with slightly different vibrational frequencies. However, without clear indication in the spectra such deconvolutions are not accurate. We found that the sum and difference bands are located at ∼3540 and ∼3240 cm−1, respectively. It suggests that the
σ. Because of the similarity of structures and spectra between the MeOH–DMA and MeOH–TMA complexes, we assign the side bands in the MeOH–DMA spectrum to be the combination bands (sum-and-difference bands). We fit this fundamental OH-stretching region to three bands (Fig. S5a, ESI†). Adding additional peaks would improve this fit to the observed spectrum (Fig. S5b, ESI†) and likely illustrate the existence of the two conformers with slightly different vibrational frequencies. However, without clear indication in the spectra such deconvolutions are not accurate. We found that the sum and difference bands are located at ∼3540 and ∼3240 cm−1, respectively. It suggests that the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) σ vibration band of MeOH–DMA is about 150 cm−1. The B3LYP/aug-cc-pVTZ calculated harmonic frequency of the
σ vibration band of MeOH–DMA is about 150 cm−1. The B3LYP/aug-cc-pVTZ calculated harmonic frequency of the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) σ vibration is 195 and 173 cm−1 for MeOH–DMA and MeOH–TMA, respectively (Tables S1 and S2, ESI†), which agrees reasonably well with the experimental values.
σ vibration is 195 and 173 cm−1 for MeOH–DMA and MeOH–TMA, respectively (Tables S1 and S2, ESI†), which agrees reasonably well with the experimental values.
We measured the gas phase spectra of 202 Torr DMA, 36 Torr MeOH, and a mixture of the two gases in a 4.8 m path length cell. The spectra in the range between 4650 and 5000 cm−1 are shown in Fig. S6 (ESI†). After spectral subtraction, the spectrum of the MeOH–DMA complex shows two bands in this region with band center located at 4797 and 4846 cm−1, respectively (Fig. S7, ESI†). For comparison, the spectrum of the MeOH–TMA complex was measured and is also shown in Fig. S7 (ESI†). The band position of the MeOH–TMA complex spectrum was determined to be 4827 cm−1. This band was assigned as the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH + δCOH transition of the complex,19 corresponding to a transition to a combination band with one quantum in the OH-stretching and the in-plane COH-bending modes, respectively. The corresponding combination
OH + δCOH transition of the complex,19 corresponding to a transition to a combination band with one quantum in the OH-stretching and the in-plane COH-bending modes, respectively. The corresponding combination ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH + δCOH transition in methanol is located at 5017 cm−1.19 The
OH + δCOH transition in methanol is located at 5017 cm−1.19 The ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH + δCOH transition of the MeOH–TMA complex is red shifted by ∼190 cm−1. In MeOH–DMA we find this transition split, probably due to a Fermi resonance, into two bands at 4797 and 4846 cm−1, respectively. The unperturbed
OH + δCOH transition of the MeOH–TMA complex is red shifted by ∼190 cm−1. In MeOH–DMA we find this transition split, probably due to a Fermi resonance, into two bands at 4797 and 4846 cm−1, respectively. The unperturbed ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH + δCOH transition of the MeOH–DMA complex is estimated at ∼4830 cm−1 similar to that found in MeOH–TMA.73 The redshift of these combination bands are significantly smaller than the redshift of the pure OH-stretching fundamental indicating a significant blueshift of the COH-bending mode. The blueshift for the in-plane COH-bending mode is a typical feature of forming a hydrogen bond, and a larger blue shift is expected for stronger hydrogen bonds.74,75
OH + δCOH transition of the MeOH–DMA complex is estimated at ∼4830 cm−1 similar to that found in MeOH–TMA.73 The redshift of these combination bands are significantly smaller than the redshift of the pure OH-stretching fundamental indicating a significant blueshift of the COH-bending mode. The blueshift for the in-plane COH-bending mode is a typical feature of forming a hydrogen bond, and a larger blue shift is expected for stronger hydrogen bonds.74,75
The MeOH–DMA spectrum in the first OH-stretching overtone (2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH) region was also measured (Fig. 2). Due to the strong first NH-stretching overtone transition (2
OH) region was also measured (Fig. 2). Due to the strong first NH-stretching overtone transition (2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH) of DMA, it is difficult to obtain a good spectrum of the MeOH–DMA complex between 6520 and 6700 cm−1. In the MeOH–DMA spectrum, four bands at 6207, 6341, 6504 and 6561 cm−1 were observed in our experiment. As seen in Fig. 2, the transition at 6504 cm−1 is much weaker and overlapped with the transition at 6561 cm−1. We tentatively assign the transition at 6561 cm−1 to be the 2
NH) of DMA, it is difficult to obtain a good spectrum of the MeOH–DMA complex between 6520 and 6700 cm−1. In the MeOH–DMA spectrum, four bands at 6207, 6341, 6504 and 6561 cm−1 were observed in our experiment. As seen in Fig. 2, the transition at 6504 cm−1 is much weaker and overlapped with the transition at 6561 cm−1. We tentatively assign the transition at 6561 cm−1 to be the 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH band and the 6504 cm−1 band to be the 2
NH band and the 6504 cm−1 band to be the 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH transition. The 2
OH transition. The 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH band has an fwhm of 52 cm−1 and its redshift relative to the NH-stretching first overtone in DMA is 30 cm−1. The redshift of the 2
NH band has an fwhm of 52 cm−1 and its redshift relative to the NH-stretching first overtone in DMA is 30 cm−1. The redshift of the 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH band of MeOH–DMA relative to methanol is 693 cm−1. We increased the pressures of the monomers to form more complex in the cell although this led to saturation in the NH-stretching region. The spectra of 146 Torr DMA, 48 Torr MeOH, and a mixture of the two gases recorded in a 4.8 m path length cell in the range between 6100 and 6520 cm−1 are shown in Fig. S8 (ESI†). The MeOH–DMA spectrum after spectral subtraction is compared with that of MeOH–TMA in Fig. S9 (ESI†). Due to the rotational structure in MeOH, the subtracted spectra between 6300 and 6350 cm−1 is not at as smooth as other regions. In agreement with the previous report,19 we observed three bands in this region of the MeOH–TMA spectrum at 6199, 6314, 6469 cm−1, respectively. We assign the band at 6469 cm−1 to the first OH-stretching overtone (2
OH band of MeOH–DMA relative to methanol is 693 cm−1. We increased the pressures of the monomers to form more complex in the cell although this led to saturation in the NH-stretching region. The spectra of 146 Torr DMA, 48 Torr MeOH, and a mixture of the two gases recorded in a 4.8 m path length cell in the range between 6100 and 6520 cm−1 are shown in Fig. S8 (ESI†). The MeOH–DMA spectrum after spectral subtraction is compared with that of MeOH–TMA in Fig. S9 (ESI†). Due to the rotational structure in MeOH, the subtracted spectra between 6300 and 6350 cm−1 is not at as smooth as other regions. In agreement with the previous report,19 we observed three bands in this region of the MeOH–TMA spectrum at 6199, 6314, 6469 cm−1, respectively. We assign the band at 6469 cm−1 to the first OH-stretching overtone (2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH) of MeOH–TMA. Its redshift relative to methanol is 728 cm−1, slightly larger than the redshift in MeOH–DMA. The bands at ∼6200 and 6300 cm−1 are likely combination bands, with the 6300 cm−1 tentatively assigned them to the 2
OH) of MeOH–TMA. Its redshift relative to methanol is 728 cm−1, slightly larger than the redshift in MeOH–DMA. The bands at ∼6200 and 6300 cm−1 are likely combination bands, with the 6300 cm−1 tentatively assigned them to the 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH transition of the complex coupling with the low-frequency hydrogen bond vibration
OH transition of the complex coupling with the low-frequency hydrogen bond vibration ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) σ, 2
σ, 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH −
OH − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) σ. Based on this the
σ. Based on this the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) σ transition would be ∼160 cm−1 in reasonable agreement with the observations in the fundamental region, the literature value and our calculations.
σ transition would be ∼160 cm−1 in reasonable agreement with the observations in the fundamental region, the literature value and our calculations.
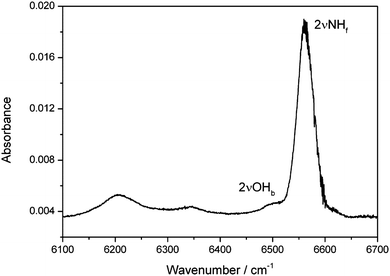 | ||
Fig. 2 The 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NHf and 2 NHf and 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OHb bands of the MeOH–DMA complex obtained by spectral subtraction of 27 Torr DMA and 27 Torr MeOH from the mixture of the two gases. The spectra were recorded in a 4.8 m path length cell using an NIR light source and an InGaAs detector at 297 K. OHb bands of the MeOH–DMA complex obtained by spectral subtraction of 27 Torr DMA and 27 Torr MeOH from the mixture of the two gases. The spectra were recorded in a 4.8 m path length cell using an NIR light source and an InGaAs detector at 297 K. | ||
We have also observed a spectrum in the second NH-stretching overtone region that we assign to the MeOH–DMA complex. The measured spectra of 202 Torr DMA, 36 Torr MeOH, and a mixture of the two gases in the region between 9000 and 9800 cm−1 is shown in Fig. S10 (ESI†). It is apparent from the spectra that any possible absorption due to the complex is very weak. After spectral subtraction, two weak bands located at 9371 and 9618 cm−1 were identified (Fig. 3). Comparison of DMA, MeOH and of the MeOH–DMA complex spectra in the 9000–9800 cm−1 region are given in ESI† (Fig. S11). In order to check the reproducibility of these two bands, three more pressure combinations of DMA and MeOH were used. The integrated absorbance of the band at 9618 cm−1 was plotted as a function of the product of the DMA and MeOH pressures (Fig. S12, ESI†). It confirms that this band comes from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 MeOH–DMA complex. The fwhm of the 3
1 MeOH–DMA complex. The fwhm of the 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH band in the complex is measured to be 61 cm−1. Unfortunately, the band at 9371 cm−1 is too weak to measure the integrated absorbance accurately. However, we can clearly see that the band area is smaller at lower pressures, which partially confirms that it comes also from the complex. We have tentatively assigned the 9618 cm−1 band to be 3
NH band in the complex is measured to be 61 cm−1. Unfortunately, the band at 9371 cm−1 is too weak to measure the integrated absorbance accurately. However, we can clearly see that the band area is smaller at lower pressures, which partially confirms that it comes also from the complex. We have tentatively assigned the 9618 cm−1 band to be 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH transition and the 9371 cm−1 band as a hot band combination of a low frequency methyl torsion with a wavenumber of ∼247 cm−1 with the 3
NH transition and the 9371 cm−1 band as a hot band combination of a low frequency methyl torsion with a wavenumber of ∼247 cm−1 with the 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH transition. The B3LYP/aug-cc-pVTZ calculated normal mode harmonic frequency of the methyl torsion in MeOH–DMA is 221 cm−1 (Table S1, ESI†), which support this assignment. In the spectrum of the DMA monomer (Fig. S10, ESI†), two bands located at 9656 and 9410 cm−1 are observed in the 9000–9800 cm−1 region.57 Similar to the complex, we assign the 9656 cm−1 band to the 3
NH transition. The B3LYP/aug-cc-pVTZ calculated normal mode harmonic frequency of the methyl torsion in MeOH–DMA is 221 cm−1 (Table S1, ESI†), which support this assignment. In the spectrum of the DMA monomer (Fig. S10, ESI†), two bands located at 9656 and 9410 cm−1 are observed in the 9000–9800 cm−1 region.57 Similar to the complex, we assign the 9656 cm−1 band to the 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH transition of DMA and the 9410 cm−1 band to a hot band combination of a low frequency methyl torsion with a wavenumber of ∼246 cm−1 with the 3
NH transition of DMA and the 9410 cm−1 band to a hot band combination of a low frequency methyl torsion with a wavenumber of ∼246 cm−1 with the 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH transition.57 The B3LYP/aug-cc-pVTZ calculated normal mode harmonic frequency of the methyl torsion in DMA is 226 cm−1,57 which support our assignment of the 9410 cm−1 band. It is not possible to record spectra with even higher vapor pressures of the two gases because the 3
NH transition.57 The B3LYP/aug-cc-pVTZ calculated normal mode harmonic frequency of the methyl torsion in DMA is 226 cm−1,57 which support our assignment of the 9410 cm−1 band. It is not possible to record spectra with even higher vapor pressures of the two gases because the 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH transition of DMA will be too strong and saturate the detector.
NH transition of DMA will be too strong and saturate the detector.
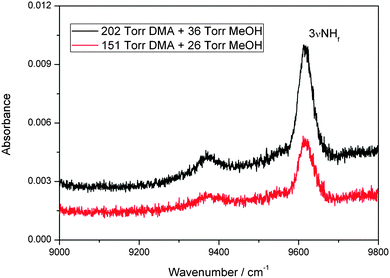 | ||
Fig. 3 The 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH band of the MeOH–DMA complex obtained by spectral subtraction of 202 Torr DMA and 36 Torr MeOH from the mixture of the two gases (upper trace), and of 151 Torr DMA and 26 Torr MeOH from the mixture of the two gases (lower trace). The spectra were recorded in a 4.8 m path length cell using an NIR light source and an InGaAs detector at 297 K. NH band of the MeOH–DMA complex obtained by spectral subtraction of 202 Torr DMA and 36 Torr MeOH from the mixture of the two gases (upper trace), and of 151 Torr DMA and 26 Torr MeOH from the mixture of the two gases (lower trace). The spectra were recorded in a 4.8 m path length cell using an NIR light source and an InGaAs detector at 297 K. | ||
4.2. Calculated geometry and interaction energy
In an ideal hydrogen bonded complex, the hydrogen bond angle is expected to be 180°.40 The MeOH–TMA complex has CS symmetry and the hydrogen bond angle (O–H⋯N angle) is nearly linear.29 Due to steric repulsion from the methyl group in methanol, the symmetry axis of the TMA subunit was measured to tilt by 5.5° with respect to the N–H bond.29 In the MeOH–DMA complex, the methyl group in the methanol subunit can rotate about the O–H⋯N hydrogen bond and more conformers are possible. Furthermore, there is also the possibility of the N–H bond in DMA being the hydrogen donor (N–H⋯O bond) although the O atom is a weaker acceptor than the N atom.15 Several initial structures based on above mentioned possibilities were optimized with different levels of theory. Harmonic vibrational frequencies were calculated with the DFT methods to confirm that all structures were true minima. Three stable conformers of the MeOH–DMA complex were located and further optimized with the CCSD(T)-F12a/VDZ-F12 method. For comparison, the MeOH–TMA and MeOH–MeOH complexes were optimized with the same methods. The structures of the stable MeOH–DMA complex conformers (A, B and C), together with that of the MeOH–TMA and MeOH–MeOH complexes are shown in Fig. 4 and the most interesting geometric parameters related to hydrogen bonding are listed in Table 2. All three MeOH–DMA conformers have CS symmetry and in conformers A and B the methyl group unit can rotate along the O–N axis. This property is very similar to the DMA dimer, in which the DMA unit can rotate relatively freely about the N⋯N axis.37 In the MeOH–TMA complex, the intermolecular hydrogen bond distance R(OHb⋯N) was determined to be 1.92 Å.29 The F12 calculated value at the equilibrium geometry (Re) is 1.88 Å, in good agreement with the experimental value, with the difference likely due to vibrational averaging. In conformers A and B of MeOH–DMA, and MeOH–TMA, the deviation of the hydrogen bond from linearity is 13.7°, 6.5° and 0.6°, respectively. In comparison the value in DMA–DMA and DMA–TMA is 26.9° and 26.3°, respectively,38 which shows the DMA–DMA and DMA–TMA complexes are significantly weaker, as expected since amines are not strong hydrogen donors.15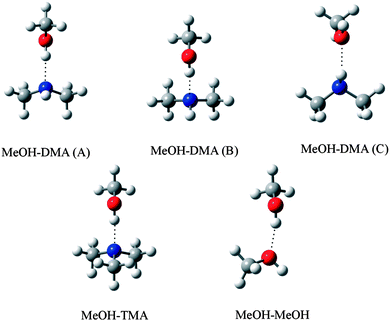 | ||
| Fig. 4 Optimized structure of MeOH–DMA (conformers A, B and C), MeOH–TMA and MeOH–MeOH complexes. | ||
| Complex | R(OH) | Δr(OH)a | R(NH) | Δr(NH)b | R(HB)c | θ(HB)d |
|---|---|---|---|---|---|---|
| a Change in the OH bond length upon complexation, Rcomplex − RMeOH. b Change in the NH bond length upon complexation, Rcomplex − RDMA. c The intermolecular hydrogen bond distance, i.e., R(OHb⋯N) for A, B, and MeOH–TMA, R(NHb⋯O) for C, and R(OHb⋯O) for MeOH–MeOH. d The intermolecular hydrogen bond angle, i.e., θ(OHb⋯N) for A, B, and MeOH–TMA, θ(NHb⋯O) for C, and θ(OHb⋯O) for MeOH–MeOH. e Data are for the hydrogen bonded OHb. | ||||||
| MeOH–DMA (A) | 0.9746 | 0.0163 | 1.0123 | 0.0003 | 1.8879 | 166.3 |
| MeOH–DMA (B) | 0.9745 | 0.0161 | 1.0128 | 0.0008 | 1.9060 | 173.5 |
| MeOH–DMA (C) | 0.9584 | 0.00004 | 1.0135 | 0.0014 | 2.1400 | 150.9 |
| MeOH–TMA | 0.9761 | 0.0178 | 1.8781 | 179.4 | ||
| MeOH–MeOH | 0.9654e | 0.0070e | 1.8987 | 168.3 | ||
The CCSD(T)-F12a/VDZ-F12 method have been found to give binding energies for small complexes that are in good agreement with CCSD(T) results at the complete basis set limit.56 In order to find the most stable conformer of the MeOH–DMA complex, we calculated the binding energy (BE), enthalpy of formation (ΔH298K) and Gibbs free energy of formation (ΔG298K) of the three structures with different methods and show the results in Table 3, Tables S3 and S4 (ESI†). The comparative results for MeOH–TMA and MeOH–MeOH are given in Table 4 and Table S5 (ESI†), respectively. The calculated BE, ΔH298K and ΔG298K values of conformers A and B of the MeOH–DMA complex are very similar (differ by less than 1 kJ mol−1) with all methods used and these two conformers are significantly more strongly bound than conformer C (by about 20 kJ mol−1), which is not expected to be present in any significant quantities at ambient temperature. The BE of the MeOH–TMA complex is about 1 kJ mol−1 smaller than that of the MeOH–DMA complex, which suggests that the hydrogen bond in MeOH–TMA is slightly stronger than in MeOH–DMA. The ΔH298K and ΔG298K values of MeOH–TMA are also slightly smaller than the corresponding values for conformer A and B of MeOH–DMA. This difference in hydrogen bond strength is reflected in the difference in the OH-stretching vibrational frequencies observed for MeOH–TMA and MeOH–DMA. In comparison, as seen from Table S5 (ESI†), the MeOH dimer (MeOH–MeOH) is not as strongly bound compared to the methanol–amine complexes (about 10 kJ mol−1 higher BE) and is not expected to affect our spectra.
| B3LYP/aug-cc-pVTZ | LC-wPBE/aug-cc-pVTZ | M06-2X/aug-cc-pVTZ | wB97XD/aug-cc-pVTZ | CCSD(T)-F12a/VDZ-F12 | |
|---|---|---|---|---|---|
| a All energies are given in kJ mol−1, and all Kp given in atm−1. b Calculated using the CCSD(T)-F12a/VDZ-F12 optimized electronic energies and the DFT thermal correction. | |||||
| BE | −26.7 | −27.4 | −33.8 | −35.2 | −33.7 |
| BE(ZPVE) | −20.8 | −21.6 | −28.1 | −29.0 | |
| BE(ZPVE)b | −27.8 | −27.9 | −27.9 | −27.4 | |
| ΔH298K | −19.8 | −20.6 | −27.3 | −28.3 | |
ΔH298K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
−26.8 | −26.9 | −27.1 | −26.7 | |
| ΔG298K | 10.6 | 10.3 | 7.3 | 5.5 | |
ΔG298K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
3.6 | 4.0 | 7.5 | 7.1 | |
| K p | 1.4 × 10−2 | 1.6 × 10−2 | 5.3 × 10−2 | 1.1 × 10−1 | |
K
p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
2.4 × 10−1 | 2.0 × 10−1 | 5.0 × 10−2 | 5.7 × 10−2 | |
| B3LYP/aug-cc-pVTZ | LC-wPBE/aug-cc-pVTZ | M06-2X/aug-cc-pVTZ | wB97XD/aug-cc-pVTZ | CCSD(T)-F12a/VDZ-F12 | |
|---|---|---|---|---|---|
| a All energies are given in kJ mol−1, and all Kp given in atm−1. b Calculated using the CCSD(T)-F12a/VDZ-F12 optimized electronic energies and the DFT thermal correction. | |||||
| BE | −25.3 | −26.8 | −33.0 | −36.2 | −34.5 |
| BE(ZPVE) | −19.7 | −21.4 | −28.2 | −30.7 | |
| BE(ZPVE)b | −28.9 | −29.1 | −29.7 | −28.9 | |
| ΔH298K | −18.6 | −20.2 | −26.9 | −29.5 | |
ΔH298K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
−27.7 | −27.9 | −28.4 | −27.8 | |
| ΔG298K | 11.4 | 8.6 | 3.2 | 0.6 | |
ΔG298K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
2.2 | 0.9 | 1.7 | 2.3 | |
| K p | 1.0 × 10−2 | 3.1 × 10−2 | 2.7 × 10−1 | 7.9 × 10−1 | |
K
p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
4.1 × 10−1 | 6.8 × 10−1 | 5.0 × 10−1 | 4.0 × 10−1 | |
4.3. Calculated OH- and NH-stretching transitions
The wavenumbers and intensities of OH- and NH-stretching in the MeOH–DMA (A) and MeOH–TMA complexes calculated with an anharmonic oscillator local mode model and CCSD(T)-F12a/VDZ-F12 parameters are presented in Tables 5 and 6, respectively, and those of the monomers in Table 7. The calculated results for MeOH–DMA (B and C) and those for MeOH–MeOH are given in Tables S6–S8 (ESI†). The calculated vibrational transitions for the A and B conformers of MeOH–DMA are very similar both for the fundamental OH-stretching and second NH-stretching overtone transitions. The difference in calculated intensity is minimal and the difference in wavenumber is about 10 cm−1. The differences between our experimental and calculated wavenumbers of the ΔvOH = 1 transition for MeOH–DMA is 105 cm−1, much larger than expected with explicitly correlated coupled cluster parameters.63 This simple local mode model has been found to model the hydrogen bonded OH-stretching frequencies worse compared with the free stretching modes. The corresponding differences for the ΔvOH = 1 transition are 117 cm−1 for the slightly strongly bound MeOH–TMA and about 35 cm−1 for the more weakly bound water dimer.70,76 Further examples can be found for hydrogen bonded NH-stretching transitions. In the DMA–DMA and DMA–TMA complexes, the differences between experimental observation and calculations of NH-stretching fundamental transitions are 47 and 43 cm−1, respectively.38 This shows that the errors in calculated hydrogen bonded XH-stretching frequencies are larger for stronger complexes. The reason for the discrepancy seems to be the larger anharmonic coupling of vibrations in stronger complexes.76 Coupling to lower frequency modes has been found to explain much of this difference for the water dimer. There is also a small error from using the Morse potential in the local mode calculations rather than the full numeric potential, however this error is only a few wavenumbers for the fundamental transition.70 In addition, our experiments were carried out at room temperature, which also affects the discrepancy between the calculated values for isolated molecules at T = 0 K.31,32 For comparison, the calculated harmonic OH- and NH-stretching wavenumbers and intensities of MeOH, DMA and MeOH–DMA (A) with various DFT methods are given in Table S9 (ESI†). As expected, the harmonic frequencies (which include the harmonic part of the coupling) are in poor agreement with the experimental measured values, however, the frequency shifts are slightly better than frequency shifts calculated with our anharmonic local mode model, and the intensity of the ΔvOH = 1 transition in the complex is very similar with the two approaches, which is important for the determination of the complex abundance (vide infra).| Δv | OHb | NHf | ||||||
|---|---|---|---|---|---|---|---|---|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) /cm−1 /cm−1 |
Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) /cm−1 /cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
f OHb | f OHb/fM |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) /cm−1 /cm−1 |
Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) /cm−1 /cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
f NHf | f NHf/fM | |
a Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = = ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) MeOH − MeOH − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OHb.
b Δ OHb.
b Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = = ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) DMA − DMA − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NHf. NHf.
|
||||||||
| 1 | 3282 | 411 | 1.8 × 10−4 | 51.4 | 3383 | −1 | 2.8 × 10−8 | 0.5 |
| 2 | 6317 | 896 | 7.6 × 10−8 | 0.1 | 6613 | −2 | 3.4 × 10−7 | 1.0 |
| 3 | 9105 | 1455 | 2.2 × 10−9 | 0.1 | 9690 | −5 | 1.8 × 10−8 | 0.9 |
| 4 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 646 646 |
2087 | 3.2 × 10−10 | 0.2 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 615 615 |
−10 | 8.6 × 10−10 | 0.8 |
| 5 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 940 |
2794 | 2.7 × 10−10 | 2.5 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 387 387 |
−15 | 6.2 × 10−11 | 0.8 |
| Δv | NH-stretching in DMA | OH-stretching in MeOH | ||
|---|---|---|---|---|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) /cm−1 /cm−1 |
f |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) /cm−1 /cm−1 |
f | |
| 1 | 3382 | 5.4 × 10−8 | 3693 | 3.6 × 10−6 |
| 2 | 6611 | 3.7 × 10−7 | 7213 | 6.0 × 10−7 |
| 3 | 9685 | 2.1 × 10−8 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 559 559 |
2.4 × 10−8 |
| 4 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605 605 |
1.1 × 10−9 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 733 |
1.4 × 10−9 |
| 5 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 372 372 |
7.7 × 10−11 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 733 |
1.1 × 10−10 |
Compared to the observed XH-stretching wavenumbers, the calculated results for DMA and MeOH showed good agreement. The largest differences between experimental determination and calculations of Δv = 1–4 transitions for DMA and MeOH are 29 and 32 cm−1, respectively. The differences between experimental observation and calculation of ΔvNH = 2 and 3 for MeOH–DMA are 52 and 72 cm−1, respectively. Even though this is still a “free” NH bond in the complex, the calculated values are not as good as for the isolated DMA molecule.
The NH-stretching fundamental transition in MeOH–DMA is expected around 3380 cm−1. However, it is overlapped with the OH-stretching fundamental transition and ∼6000 times weaker and not observed. In contrast, the calculated intensity of the ΔvNH = 2 and 3 transitions are 4 and 8 times stronger than the ΔvOH = 2 and 3 transitions, respectively, and the corresponding NH- and OH-stretching overtone transitions are more separated and we have observed these. The calculated relative intensity between the NH- and OH-stretching first overtone transitions agrees with experimental results as seen in Fig. 2 and Table 5. The NH-stretching transition shows, similar to DMA, that the first overtone is stronger than the fundamental transition.57
The OH-stretching fundamental transition intensity of the MeOH–DMA and MeOH–TMA complexes are calculated to be 51 and 61 times stronger than that of methanol. The intensity increase of ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) XH is considered to be a criterion for hydrogen bonding.40 The first overtone transition is usually weaker than the fundamental transition and since the amount of complex in the mixture is small these overtones are very difficult to observe. In the water dimer, the first overtone of the OHb-stretching transitions was predicted theoretically to be very weak and has only been observed in Ne matrix experiments.77,78 In addition, these hydrogen bonded OHb-stretching transitions have been suggested to be wider than non-hydrogen bonded transitions, which further complicates their detection.72,79,80
XH is considered to be a criterion for hydrogen bonding.40 The first overtone transition is usually weaker than the fundamental transition and since the amount of complex in the mixture is small these overtones are very difficult to observe. In the water dimer, the first overtone of the OHb-stretching transitions was predicted theoretically to be very weak and has only been observed in Ne matrix experiments.77,78 In addition, these hydrogen bonded OHb-stretching transitions have been suggested to be wider than non-hydrogen bonded transitions, which further complicates their detection.72,79,80
We present the observed and calculated XH-stretching local mode parameters of DMA, MeOH, MeOH–DMA and MeOH–TMA in Table 8. The observed values were obtained from a fit of the experimentally determined OH- and NH-stretching wavenumbers (Table 1) to eqn (2). The observed local mode parameters for MeOH–DMA and MeOH–TMA are only obtained from two points and thus have no uncertainty and should be considered only as a check on the calculated parameters. For the OH-stretching of the MeOH unit, it is clear that ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) decrease and
decrease and ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) x increase upon complexation with the amines as expected for hydrogen bonding.19
x increase upon complexation with the amines as expected for hydrogen bonding.19
| DMA | MeOH | MeOH–DMA (A) | MeOH–TMA | |||
|---|---|---|---|---|---|---|
| NHa | OHb | OHb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
NHf![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
OHb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
||
| a From ref. 57. b Obtained from the Birge–Sponer fit of the measured XH-stretching transitions in Table 1. c Calculated using the CCSD(T)-F12a/VDZ-F12 method. | ||||||
| Observed |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif)
|
3522.83 | 3862.23 | 3657.0 | 3429.5 | 3596.0 |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) x x
|
75.33 | 87.61 | 135.0 | 74.5 | 120.5 | |
| Calculatedc |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif)
|
3536.22 | 3866.14 | 3528.87 | 3535.31 | 3495.60 |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) x x
|
76.98 | 86.58 | 123.49 | 76.32 | 128.65 | |
4.4. Equilibrium constant
The complexation between MeOH and DMA is an equilibrium process.| MeOH + DMA ↔ MeOH–DMA | (3) |
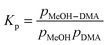 | (4) |
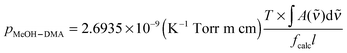 | (5) |
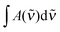 is in cm−1, T is the temperature in K, and fcalc is the calculated oscillator strength. This method has been used to successfully determine Kp for other complexes.31,33,37,38
is in cm−1, T is the temperature in K, and fcalc is the calculated oscillator strength. This method has been used to successfully determine Kp for other complexes.31,33,37,38
The OH-stretching fundamental transition ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH for the MeOH–DMA complex is not well separated from its side bands, therefore we cannot precisely measure the integrated absorbance of the
OH for the MeOH–DMA complex is not well separated from its side bands, therefore we cannot precisely measure the integrated absorbance of the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH band itself. However, the contribution from the side bands to the integrated absorbance is quite small compared to the OH-stretching transition and most of the intensity of these side bands
OH band itself. However, the contribution from the side bands to the integrated absorbance is quite small compared to the OH-stretching transition and most of the intensity of these side bands ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH ±
OH ± ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) σ, is likely to originate from the pure OH-stretching transition. Thus, we use the full band as the experimental intensity of the OH-stretching fundamental transition. The calculated oscillator strength of the OH-stretching fundamental transition in MeOH–DMA is 1.8 × 10−4 with the local mode method and F12 parameters. This same oscillator strength is obtained for conformer B, and thus the accurate abundance of each of these will not affect the result. This value is in good agreement with the intensities calculated using the harmonic approach and the various DFT methods (Table S9, ESI†). Measurements of absolute intensities of hydrogen bonded complexes are very sparse. In the water dimer, the intensity calculated using a similar local mode approach and using a harmonic oscillator approach is approximately a factor of 2 larger than the intensity obtained using VPT2 calculations.76 The VPT2 calculation is a full dimensional anharmonic normal mode calculation, which for the water dimer was found to give good agreement with absolute intensities calculated from He droplet experiments.76,82 VPT2 calculations for larger complexes are currently not possible. A larger calculated intensity would lead to an underestimation of the Kp value.
σ, is likely to originate from the pure OH-stretching transition. Thus, we use the full band as the experimental intensity of the OH-stretching fundamental transition. The calculated oscillator strength of the OH-stretching fundamental transition in MeOH–DMA is 1.8 × 10−4 with the local mode method and F12 parameters. This same oscillator strength is obtained for conformer B, and thus the accurate abundance of each of these will not affect the result. This value is in good agreement with the intensities calculated using the harmonic approach and the various DFT methods (Table S9, ESI†). Measurements of absolute intensities of hydrogen bonded complexes are very sparse. In the water dimer, the intensity calculated using a similar local mode approach and using a harmonic oscillator approach is approximately a factor of 2 larger than the intensity obtained using VPT2 calculations.76 The VPT2 calculation is a full dimensional anharmonic normal mode calculation, which for the water dimer was found to give good agreement with absolute intensities calculated from He droplet experiments.76,82 VPT2 calculations for larger complexes are currently not possible. A larger calculated intensity would lead to an underestimation of the Kp value.
A plot of pMeOH–DMA determined from eqn (5) with the F12 oscillator strength against pMeOH × pDMA is shown in Fig. 5. From the slope of the least square fitting, the equilibrium constant Kp is determined to be 0.11 atm−1 at the temperature of 300 ± 1 K. If we assume that the intensity of the OH-stretching fundamental transition is overestimated by a factor of two, similar to the water dimer, we get a Kp value of 0.22 atm−1 from this experiment. This is much larger than the equilibrium constants of DMA–DMA and DMA–TMA, which were 1.7 × 10−3 atm−1 determined with the same approach.38 These Kp values show, not surprisingly, that the MeOH–DMA complex is a much stronger hydrogen bonded complex than amine complexes.
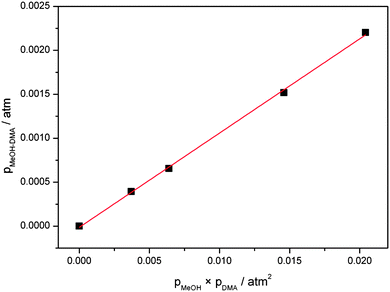 | ||
| Fig. 5 Plot of pMeOH–DMA against pMeOH × pDMA. pMeOH–DMA are determined from the experimental and theoretical fundamental OH-stretching transition intensities. | ||
In our spectra, we also clearly observe the NHf-stretching second overtone transition (3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NHf) with an intensity that allows us to determine the Kp value as well. However, we expect a larger uncertainty on the absorbance measurements as the signal is weaker. In principle oscillator strengths of the higher overtones are more difficult to calculate, however this is compensated by the more accurate calculation of intensities for bonds not involved in hydrogen bonding. The anharmonic oscillator local mode calculated intensity with the F12 parameters, for the NH-stretching second overtone 3
NHf) with an intensity that allows us to determine the Kp value as well. However, we expect a larger uncertainty on the absorbance measurements as the signal is weaker. In principle oscillator strengths of the higher overtones are more difficult to calculate, however this is compensated by the more accurate calculation of intensities for bonds not involved in hydrogen bonding. The anharmonic oscillator local mode calculated intensity with the F12 parameters, for the NH-stretching second overtone 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH in DMA were found to be within 20% of the experimental intensity.57 The oscillator strength used for the 3
NH in DMA were found to be within 20% of the experimental intensity.57 The oscillator strength used for the 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NHf transition in MeOH–DMA is 1.8 × 10−8 (Table 5, F12 method), and the plot of pMeOH–DMA against pMeOH × pDMA is given in Fig. S13 (ESI†). From the 3
NHf transition in MeOH–DMA is 1.8 × 10−8 (Table 5, F12 method), and the plot of pMeOH–DMA against pMeOH × pDMA is given in Fig. S13 (ESI†). From the 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NHf band, the equilibrium constant Kp is determined to be 0.19 atm−1 at 297 K, in reasonable agreement with the Kp value determined from the
NHf band, the equilibrium constant Kp is determined to be 0.19 atm−1 at 297 K, in reasonable agreement with the Kp value determined from the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH band.
OH band.
The largest error in our experiment is the calculated intensities, which we believe is about a factor of two higher for the fundamental transition and has an error of about 20% for the second NH-stretching overtone. The experimental errors are mainly in the pressure measurements and in the determination of the areas. The uncertainty of the pressure gauges is 5% and 15% for pressures larger and smaller than ca. 80 Torr, respectively. Based on these results we estimate the Kp value for the MeOH–DMA complex to be 0.2 atm−1 at 298 K, with an error of less than 0.1 atm−1. Our present value is significantly smaller than the previously determined value of 0.6 atm−1.27
We have also estimated Kp purely from our ab initio and DFT calculations.7 The combination of F12 single point energies and B3LYP/aug-cc-pVTZ or wB97XD/aug-cc-pVTZ thermal corrections have previously been shown to predict well the Kp of other hydrogen bonded complexes.38 We obtained a Kp value of 0.24 atm−1 for the MeOH–DMA complex at 298 K with a combination of F12 electronic energies and B3LYP/aug-cc-pVTZ harmonic frequencies and rotational constants and 0.057 atm−1 with the combination of F12 and wB97XD/aug-cc-pVTZ methods.7 Both these values as well as the values obtained with thermal corrections using the other two DFT methods, LC-wPBE/aug-cc-pVTZ and M06-2X/aug-cc-pVTZ, are in reasonable agreement with our experimentally determined value (Table 3).
4.5. Enthalpy of hydrogen bond formation
If we assume that the enthalpy of the complexation reaction of the MeOH–DMA and MeOH–TMA complexes is independent of temperature and we keep the vapor pressures of the corresponding monomers constant, we can rewrite the van't Hoff equation as: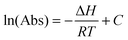 | (6) |
With our 2.4 m path length heatable cell, we recorded the IR spectra of the MeOH–DMA and MeOH–TMA complexes in the temperature range from 298 to 358 K in steps of 10 K to determine the enthalpy of hydrogen bond formation for the two complexes. Before each spectral subtraction, the spectra of DMA, MeOH and the mixture of them were measured separately at the same elevated temperature. The pressure of DMA and MeOH should be kept constant for all the temperature dependent measurements. We have used the ideal gas law to determine the filling pressure in order to obtain the constant pressures of the monomers at elevated temperatures. The amount of complex in the mixture is very small and therefore the contribution from the complex to the total pressure is neglected. In the mixture of 466 Torr DMA and 25 Torr MeOH, the partial pressure of the MeOH–DMA complex is calculated to be 1.7 Torr. The enthalpy determination of the MeOH–TMA complexation reaction was performed with the same method. We used a mixture of 64 Torr DMA and 22 Torr MeOH (pressure at room temperature) for the measurements with the MeOH–DMA complex, and 32 Torr TMA and 22 Torr MeOH for the measurements with the MeOH–TMA complex. A summary of the details of MeOH–DMA and MeOH–TMA experiments are given in Tables S10 and S11 (ESI†), respectively. The temperature dependence of the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH band of the MeOH–DMA and MeOH–TMA complexes are shown in Fig. 6 and 7, respectively. The area of these bands decreases with increasing temperature, which nicely illustrate the decrease of Kp with temperature.
OH band of the MeOH–DMA and MeOH–TMA complexes are shown in Fig. 6 and 7, respectively. The area of these bands decreases with increasing temperature, which nicely illustrate the decrease of Kp with temperature.
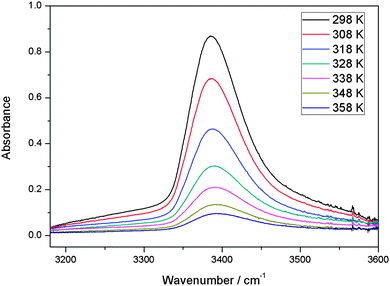 | ||
Fig. 6 The temperature dependence of the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH band in MeOH–DMA complex. A path length of 2.4 m was used. At a given temperature, the spectrum was obtained by subtracting the spectra of 64 Torr DMA and 22 Torr MeOH from the mixture of the two gases. OH band in MeOH–DMA complex. A path length of 2.4 m was used. At a given temperature, the spectrum was obtained by subtracting the spectra of 64 Torr DMA and 22 Torr MeOH from the mixture of the two gases. | ||
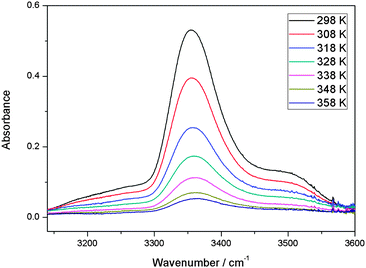 | ||
Fig. 7 The temperature dependence of the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH band in MeOH–TMA complex. A path length of 2.4 m was used. At a given temperature, the spectrum was obtained by subtracting the spectra of 32 Torr TMA and 22 Torr MeOH from the mixture of the two gases. OH band in MeOH–TMA complex. A path length of 2.4 m was used. At a given temperature, the spectrum was obtained by subtracting the spectra of 32 Torr TMA and 22 Torr MeOH from the mixture of the two gases. | ||
The linear least-square fit of the van't Hoff equation to the data for MeOH–DMA and MeOH–TMA is shown in Fig. 8. Based on the slopes of the plots in Fig. 8, the enthalpy of hydrogen bond formation for MeOH–DMA and MeOH–TMA in the temperature range of 298 and 358 K is determined to be −35.8 ± 3.9 and −38.2 ± 3.3 kJ mol−1, respectively. The lower enthalpy of MeOH–TMA compared to MeOH–DMA indicates that the hydrogen bonding in the MeOH–TMA complex is a bit stronger than that in MeOH–DMA, as expected. A summary of the experimentally determined ΔH values of the MeOH–DMA and MeOH–TMA complexes are listed in Table 9. There was only one previous report for MeOH–DMA by pressure measurements, but several measurements for MeOH–TMA with different methods. Our calculated values with the mix of F12 electronic energy and DFT thermal corrections give ΔH (298 K) of about −27 kJ mol−1 and −28 kJ mol−1 for MeOH–DMA and MeOH–TMA, respectively. Comparison of values from the literature and this work indicate that the enthalpy is not constant over a temperature range from 283 to 358 K for the two complexes. The enthalpy of hydrogen bond formation, as derived from the slope in Fig. 8, clearly changes with temperature. The enthalpy becomes more negative with increasing temperature. Our experimental values are clearly higher than our calculated values and the literature values as would be expected by our higher temperatures. More detailed studies are required to further understand the temperature dependence of the heat of formation of the two complexes.
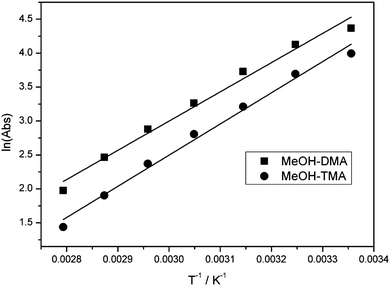 | ||
Fig. 8 The linear least-square fitting of the van't Hoff equation plot of the MeOH–DMA and MeOH–TMA complexes. Both bands were integrated in the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH band region between 3192 and 3580 cm−1. OH band region between 3192 and 3580 cm−1. | ||
| Complex | Method | Temperature range/K | −ΔH/kJ mol−1 |
|---|---|---|---|
| a From ref. 27. b From ref. 28. | |||
| MeOH–DMA | Pressure measurementsa | 298 | 25.9 ± 1.0 |
| This work, IR | 298–358 | 35.8 ± 3.9 | |
| MeOH–TMA | Pressure measurementsa | 298 | 28.9 ± 1.0 |
| IRb | 283–319 | 29.7 ± 0.8 | |
| Pressure measurementsb | 283–319 | 31.4 ± 1.3 | |
| This work, IR | 298–358 | 38.2 ± 3.3 | |
5. Conclusions
We have measured gas phase vibrational spectra of the hydrogen bonded bimolecular complex formed between methanol (MeOH) and dimethylamine (DMA) up to about 9800 cm−1. We have observed the fundamental and overtone transitions (Δv = 1 and 2) of the hydrogen bonded OHb-stretching vibration and the overtone transitions (Δv = 2 and 3) of the non-hydrogen bonded NHf-stretching vibration. The assignment of the spectra was facilitated by comparison with spectra of the bimolecular complex between MeOH and trimethylamine (TMA) and theoretical calculations. The room temperature equilibrium constant Kp of MeOH–DMA complexation has been determined by combining the experimentally measured and theoretically calculated OHb-stretching fundamental and NHf-stretching second overtone oscillator strengths. The OHb- and NHf-stretching transitions in MeOH–DMA were calculated with the anharmonic oscillator local mode model. The equilibrium constant for formation of the MeOH–DMA complex was determined to be 0.2 ± 0.1 atm−1, corresponding to a ΔG value of about 4.0 kJ mol−1. Ab initio calculated ΔG values, obtained from a DFT thermal correction combined with an explicitly correlated coupled cluster electronic energy, provides a good estimate of the measured Kp or ΔG value.Acknowledgements
We are grateful to Anna Schou Hansen for helpful discussions. We thank The Danish Council for Independent Research – Natural Sciences and the Danish Center for Scientific Computing (DCSC) for funding.References
- S. Aloisio and J. S. Francisco, Acc. Chem. Res., 2000, 33, 825–830 CrossRef CAS.
- V. Vaida, J. Chem. Phys., 2011, 135, 020901 CrossRef.
- V. Vaida, H. G. Kjaergaard and K. J. Feierabend, Int. Rev. Phys. Chem., 2003, 22, 203–219 CrossRef CAS.
- W. Klemperer and V. Vaida, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10584–10588 CrossRef CAS.
- H. G. Kjaergaard, T. W. Robinson, D. L. Howard, J. S. Daniel, J. E. Headrick and V. Vaida, J. Phys. Chem. A, 2003, 107, 10680–10686 CrossRef CAS.
- S. Melandri, Phys. Chem. Chem. Phys., 2011, 13, 13901–13911 RSC.
- V. Vaida and J. E. Headrick, J. Phys. Chem. A, 2000, 104, 5401–5412 CrossRef CAS.
- V. Vaida, J. S. Daniel, H. G. Kjaergaard, L. M. Goss and A. F. Tuck, Q. J. R. Meteorol. Soc., 2001, 127, 1627–1643 CrossRef.
- T. Kurten, V. Loukonen, H. Vehkamaki and M. Kulmala, Atmos. Chem. Phys., 2008, 8, 4095–4103 CrossRef CAS.
- A. B. Nadykto, F. Q. Yu, M. V. Jakovleva, J. Herb and Y. S. Xu, Entropy, 2011, 13, 554–569 CrossRef CAS.
- X. L. Ge, A. S. Wexler and S. L. Clegg, Atmos. Environ., 2011, 45, 524–546 CrossRef CAS.
- X. L. Ge, A. S. Wexler and S. L. Clegg, Atmos. Environ., 2011, 45, 561–577 CrossRef CAS.
- M. Kulmala, J. Kontkanen, H. Junninen, K. Lehtipalo, H. E. Manninen, T. Nieminen, T. Petaja, M. Sipila, S. Schobesberger, P. Rantala, A. Franchin, T. Jokinen, E. Jarvinen, M. Aijala, J. Kangasluoma, J. Hakala, P. P. Aalto, P. Paasonen, J. Mikkila, J. Vanhanen, J. Aalto, H. Hakola, U. Makkonen, T. Ruuskanen, R. L. Mauldin, J. Duplissy, H. Vehkamaki, J. Back, A. Kortelainen, I. Riipinen, T. Kurten, M. V. Johnston, J. N. Smith, M. Ehn, T. F. Mentel, K. E. J. Lehtinen, A. Laaksonen, V. M. Kerminen and D. R. Worsnop, Science, 2013, 339, 943–946 CrossRef CAS.
- J. N. Smith, K. C. Barsanti, H. R. Friedli, M. Ehn, M. Kulmala, D. R. Collins, J. H. Scheckman, B. J. Williams and P. H. McMurry, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6634–6639 CrossRef CAS.
- C. A. Hunter, Angew. Chem., Int. Ed., 2004, 43, 5310–5324 CrossRef CAS.
- E. E. Fileti and S. Canuto, Int. J. Quantum Chem., 2005, 104, 808–815 CrossRef CAS.
- K. V. J. Jose, S. R. Gadre, K. Sundararajan and K. S. Viswanathan, J. Chem. Phys., 2007, 127, 104501 CrossRef.
- G. Piani, M. Pasquini, I. Lopez-Tocon, G. Pietraperzia, M. Becucci and E. Castellucci, Chem. Phys., 2006, 330, 138–145 CrossRef CAS.
- D. L. Howard and H. G. Kjaergaard, J. Phys. Chem. A, 2006, 110, 9597–9601 CrossRef CAS.
- R. W. Larsen, P. Zielke and M. A. Suhm, J. Chem. Phys., 2007, 126, 194307 CrossRef.
- M. Nedic, T. N. Wassermann, R. W. Larsen and M. A. Suhm, Phys. Chem. Chem. Phys., 2011, 13, 14050–14063 RSC.
- D. J. Millen and J. Zabicky, Nature, 1962, 196, 889–890 CrossRef CAS.
- D. J. Millen and J. Zabicky, J. Chem. Soc., 1965, 3080–3085 RSC.
- S. G. W. Ginn and J. L. Wood, Nature, 1963, 200, 467–468 CrossRef CAS.
- L. Aladhami and D. J. Millen, Nature, 1966, 211, 1291 CrossRef CAS.
- M. A. Hussein and D. J. Millen, J. Chem. Soc., Faraday Trans. 2, 1974, 70, 685–692 RSC.
- D. J. Millen and G. W. Mines, J. Chem. Soc., Faraday Trans. 2, 1974, 70, 693–699 RSC.
- M. Fild, M. F. Swiniars and R. R. Holmes, Inorg. Chem., 1970, 9, 839–843 CrossRef CAS.
- X. Q. Tan, I. I. Ioannou, K. B. Foltz and R. L. Kuczkowski, J. Mol. Spectrosc., 1996, 177, 181–193 CrossRef CAS.
- T. A. Iskanderov, Y. M. Kimelfeld and E. M. Smirnova, Chem. Phys., 1987, 112, 379–386 CrossRef CAS.
- M. Hippler, J. Chem. Phys., 2007, 127, 084306 CrossRef.
- M. Hippler, S. Hesse and M. A. Suhm, Phys. Chem. Chem. Phys., 2010, 12, 13555–13565 RSC.
- S. Chung and M. Hippler, J. Chem. Phys., 2006, 124, 214316 CrossRef.
- J. J. J. Dom, B. Michielsen, B. U. W. Maes, W. A. Herrebout and B. J. Van der Veken, Chem. Phys. Lett., 2009, 469, 85–89 CrossRef CAS.
- J. J. J. Dom, B. J. van der Veken, B. Michielsen, S. Jacobs, Z. F. Xue, S. Hesse, H. M. Loritz, M. A. Suhm and W. A. Herrebout, Phys. Chem. Chem. Phys., 2011, 13, 14142–14152 RSC.
- B. Michielsen, W. A. Herrebout and B. J. van der Veken, ChemPhysChem, 2008, 9, 1693–1701 CrossRef CAS.
- L. Du and H. G. Kjaergaard, J. Phys. Chem. A, 2011, 115, 12097–12104 CrossRef CAS.
- L. Du, J. R. Lane and H. G. Kjaergaard, J. Chem. Phys., 2012, 136, 184305 CrossRef.
- D. L. Howard and H. G. Kjaergaard, Phys. Chem. Chem. Phys., 2008, 10, 4113–4118 RSC.
- E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1637–1641 CrossRef CAS.
- E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1619–1637 CrossRef CAS.
- W. A. Herrebout, S. N. Delanoye, B. U. W. Maes and B. J. van der Veken, J. Phys. Chem. A, 2006, 110, 13759–13768 CrossRef CAS.
- K. S. Rutkowski, W. A. Herrebout, S. M. Melikova, B. J. van der Veken and A. Koll, Chem. Phys., 2008, 354, 71–79 CrossRef CAS.
- K. S. Rutkowski, P. Rodziewicz, S. M. Melikova, W. A. Herrebout, B. J. van der Veken and A. Koll, Chem. Phys., 2005, 313, 225–243 CrossRef CAS.
- T. Scharge, D. Luckhaus and M. A. Suhm, Chem. Phys., 2008, 346, 167–175 CrossRef CAS.
- B. Michielsen, W. A. Herrebout and B. J. van der Veken, ChemPhysChem, 2007, 8, 1188–1198 CrossRef CAS.
- M. A. Czarnecki and D. Wojtkow, J. Phys. Chem. A, 2004, 108, 2411–2417 CrossRef CAS.
- D. Wojtkow and M. A. Czarnecki, J. Phys. Chem. A, 2005, 109, 8218–8224 CrossRef CAS.
- D. Wojtkow and M. A. Czarnecki, J. Phys. Chem. A, 2006, 110, 10552–10557 CrossRef CAS.
- Y. Futami, Y. Ozaki, Y. Hamada and M. J. Wojcik, J. Phys. Chem. A, 2011, 115, 1194–1198 CrossRef CAS.
- T. Gonjo, Y. Futami, Y. Morisawa, M. J. Wojcik and Y. Ozaki, J. Phys. Chem. A, 2011, 115, 9845–9853 CrossRef CAS.
- I. V. Ptashnik, K. M. Smith, K. P. Shine and D. A. Newnham, Q. J. R. Meteorol. Soc., 2004, 130, 2391–2408 CrossRef.
- R. W. Larsen, F. M. Nicolaisen and H. G. Kjaergaard, unpublished.
- C. Leforestier, K. Szalewicz and A. van der Avoird, J. Chem. Phys., 2012, 137, 014305 CrossRef.
- D. P. Tew, W. Klopper, C. Neiss and C. Hattig, Phys. Chem. Chem. Phys., 2007, 9, 1921–1930 RSC.
- J. R. Lane and H. G. Kjaergaard, J. Chem. Phys., 2009, 131, 034307 CrossRef.
- B. J. Miller, L. Du, T. J. Steel, A. J. Paul, A. H. Sodergren, J. R. Lane, B. R. Henry and H. G. Kjaergaard, J. Phys. Chem. A, 2012, 116, 290–296 CrossRef CAS.
- J. R. Lane and H. G. Kjaergaard, J. Chem. Phys., 2010, 132, 174304 CrossRef.
- B. J. Miller, J. R. Lane and H. G. Kjaergaard, Phys. Chem. Chem. Phys., 2011, 13, 14183–14193 RSC.
- E. Salli, T. Salmi and L. Halonen, J. Phys. Chem. A, 2011, 115, 11594–11605 CrossRef CAS.
- B. R. Henry, Acc. Chem. Res., 1977, 10, 207–213 CrossRef CAS.
- B. R. Henry, Acc. Chem. Res., 1987, 20, 429–435 CrossRef CAS.
- D. L. Howard, P. Jorgensen and H. G. Kjaergaard, J. Am. Chem. Soc., 2005, 127, 17096–17103 CrossRef CAS.
- D. L. Howard, T. W. Robinson, A. E. Fraser and H. G. Kjaergaard, Phys. Chem. Chem. Phys., 2004, 6, 719–724 RSC.
- B. I. Niefer, H. G. Kjaergaard and B. R. Henry, J. Chem. Phys., 1993, 99, 5682–5700 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision B.01), Wallingford, CT, 2010 Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and A. Wolf, MOLPRO, version 2010.1, 2010 Search PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- B. R. Henry and H. G. Kjaergaard, Can. J. Chem., 2002, 80, 1635–1642 CrossRef CAS.
- D. P. Schofield, J. R. Lane and H. G. Kjaergaard, J. Phys. Chem. A, 2007, 111, 567–572 CrossRef CAS.
- M. Yekutiel, J. R. Lane, P. Gupta and H. G. Kjaergaard, J. Phys. Chem. A, 2010, 114, 7544–7552 CrossRef CAS.
- D. L. Howard and H. G. Kjaergaard, J. Phys. Chem. A, 2006, 110, 10245–10250 CrossRef CAS.
- D. L. Howard and H. G. Kjaergaard, J. Chem. Phys., 2004, 121, 136–140 CrossRef CAS.
- A. V. Stuart and G. Sutherland, J. Chem. Phys., 1956, 24, 559–570 CrossRef CAS.
- M. Asselin and C. Sandorey, Can. J. Chem., 1971, 49, 1539–1544 CrossRef CAS.
- H. G. Kjaergaard, A. L. Garden, G. M. Chaban, R. B. Gerber, D. A. Matthews and J. F. Stanton, J. Phys. Chem. A, 2008, 112, 4324–4335 CrossRef CAS.
- G. R. Low and H. G. Kjaergaard, J. Chem. Phys., 1999, 110, 9104–9115 CrossRef CAS.
- Y. Bouteiller and J. P. Perchard, Chem. Phys., 2004, 305, 1–12 CrossRef CAS.
- A. L. Garden, L. Halonen and H. G. Kjaergaard, J. Phys. Chem. A, 2008, 112, 7439–7447 CrossRef CAS.
- K. L. Plath, K. Takahashi, R. T. Skodje and V. Vaida, J. Phys. Chem. A, 2009, 113, 7294–7303 CrossRef CAS.
- P. W. Atkins and R. S. Friedman, Molecular Quantum Mechanics, Oxford University Press, Oxford, 1997 Search PubMed.
- M. N. Slipchenko, K. E. Kuyanov, B. G. Sartakov and A. F. Vilesov, J. Chem. Phys., 2006, 124, 241101 CrossRef.
Footnote |
† Electronic supplementary information (ESI) available: Spectra of DMA, MeOH, and a mixture of the two gases recorded in different regions; integrated absorbance of the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH and 3 OH and 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH bands in the MeOH–DMA complex as a function of the product of the MeOH and DMA pressures; comparison of MeOH–DMA and MeOH–TMA spectra at the NH bands in the MeOH–DMA complex as a function of the product of the MeOH and DMA pressures; comparison of MeOH–DMA and MeOH–TMA spectra at the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH, OH, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH + δCOH and 2 OH + δCOH and 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH regions; deconvolution fitting of the OH regions; deconvolution fitting of the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH band of MeOH–DMA; room temperature (298 K) vapor phase spectra of MeOH in the ΔvOH = 1–4 regions; comparison of DMA, MeOH and the MeOH–DMA spectra in the 3 OH band of MeOH–DMA; room temperature (298 K) vapor phase spectra of MeOH in the ΔvOH = 1–4 regions; comparison of DMA, MeOH and the MeOH–DMA spectra in the 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH region; a plot of pMeOH–DMA against pMeOH × pDMA (pMeOH–DMA are derived from the 3 NH region; a plot of pMeOH–DMA against pMeOH × pDMA (pMeOH–DMA are derived from the 3![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) NH absorbance); calculated frequencies and intensities for MeOH, DMA, MeOH–DMA (A, B and C) and MeOH–TMA using a harmonic oscillator model at the B3LYP/aug-cc-pVTZ level; calculated energies and Kp at 298 K for MeOH–DMA (B and C) and MeOH–MeOH; calculated OH- and NH-stretching wavenumbers and intensities of MeOH–DMA (B and C) and MeOH–MeOH complexes using a local mode method at the CCSD(T)-F12a/VDZ-F12 level; calculated harmonic OH- and NH-stretching wavenumbers and intensities of MeOH, DMA and MeOH–DMA (A) using DFT methods; experimental details for MeOH–DMA and MeOH–TMA measurements; calculated dipoles and energies for OH- and NH-displacement in MeOH, DMA and MeOH–DMA (A) for local mode model calculations. See DOI: 10.1039/c3cp50243k NH absorbance); calculated frequencies and intensities for MeOH, DMA, MeOH–DMA (A, B and C) and MeOH–TMA using a harmonic oscillator model at the B3LYP/aug-cc-pVTZ level; calculated energies and Kp at 298 K for MeOH–DMA (B and C) and MeOH–MeOH; calculated OH- and NH-stretching wavenumbers and intensities of MeOH–DMA (B and C) and MeOH–MeOH complexes using a local mode method at the CCSD(T)-F12a/VDZ-F12 level; calculated harmonic OH- and NH-stretching wavenumbers and intensities of MeOH, DMA and MeOH–DMA (A) using DFT methods; experimental details for MeOH–DMA and MeOH–TMA measurements; calculated dipoles and energies for OH- and NH-displacement in MeOH, DMA and MeOH–DMA (A) for local mode model calculations. See DOI: 10.1039/c3cp50243k |
| This journal is © the Owner Societies 2013 |
