Restricted active space spin-flip (RAS-SF) with arbitrary number of spin-flips
Franziska
Bell
ab,
Paul M.
Zimmerman
ab,
David
Casanova
c,
Matthew
Goldey
ab and
Martin
Head-Gordon
*bd
aDepartment of Chemistry, University of California, Berkeley, California 94720, USA
bChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
cDepartament de Quimica Fisica and Institut de Quimica Teorica i Computacional (IQTCUB) Universitat de Barcelona, Marti i Franques 1–11, 08028 Barcelona, Spain
dDepartment of Chemistry, University of California, Berkeley, California 94720, USA. E-mail: m_headgordon@berkeley.edu; Fax: 0015106431255; Tel: 0015106425957
First published on 7th November 2012
Abstract
The restricted active space spin-flip (RAS-SF) approach is a multistate, spin-complete, variational and size consistent method applicable to systems featuring electronic (near-)degeneracies. In contrast to CASSCF it does not involve orbital optimizations and so avoids issues such as root-flipping and state averaging. This also makes RAS-SF calculations roughly 100–1000 times faster. In this paper RAS-SF method is extended to include variable orbital active spaces and three or more spin-flips, which allows the study of polynuclear metal systems, triple bond dissociations and organic polyradicals featuring more than four unpaired electrons. Benchmark calculations on such systems are carried out and comparison to other wave-function based, multi-reference methods, such as CASSCF and DMRG yield very good agreement, provided that the same active space is employed. Where experimental values are available, RAS-SF is found to substantially underestimate the exchange coupling constants, if the minimal active space is chosen. However, the correct ground state is always obtained. Not surprisingly, inclusion of bridge orbitals into the active space can cause the magnitude of the coupling constants to increase substantially. Importantly, the ratio of exchange couplings in related systems is in much better agreement with experiment than the magnitude of the coupling. Nevertheless, the results indicate the need for the inclusion of dynamic correlation to obtain better accuracy in minimal active spaces.
1 Introduction
The most common electronic structure of molecules is when there is an appreciable gap between nominally filled and nominally empty molecular orbitals (MOs). In this case a single electron configuration of doubly occupied MOs is the correct zero order picture, and corrections, either by perturbation theory or coupled cluster theory1–3 account for the secondary effects of electron correlation. However, electronic degeneracy or near-degeneracy of the nominally occupied and virtual orbitals is nonetheless widely encountered in chemistry. Examples include bond dissociations, radicals and metal complexes.(Near-)degeneracies lead to wavefunctions in which several determinants contribute considerably, rather than just one configuration. Since most electronic structure methods are based on a single reference, systems featuring (near-)degeneracies have been posing considerable challenges. Furthermore, another important consequence of near-degeneracy of occupied and virtual MOs is that there are very low-lying excited states. Treating both the ground state and low-lying excited states in a balanced way is another challenge for electronic structure theory. Problems in this category are often said to exhibit strong electron correlations.
One of the simplest examples of electronic degeneracy is the dissociation of a σ bond, such as the hydrogen molecule, H2. At equilibrium, the (σ)2 configuration describes the wavefunction almost exclusively, whereas at the dissociation limit, the antibonding orbital, σ*, is now degenerate and the (σ*)2 configuration carries equal weight. Therefore, as the bond length increases, a minimum of two configurations need to be included to adequately describe the wavefunction. Alternatively, spin-unrestriction may be employed. This results in improved energies over a single-determinant spin-restricted approach. However, often considerable spin-contamination and unreliable wave-function properties can be encountered, particularly for excited states.4
In the past, multi-reference wavefunctions, such as the complete-active-space self-consistent-field (CASSCF)5,6 theory have been employed to overcome the challenges of single-determinant approaches. CASSCF, however, suffers from several issues that hinders its application to complex, strongly correlated molecules. Firstly, the method scales exponentially with the active space size. Therefore only calculations involving small active spaces (less than 17 orbitals) can be carried out to date. Secondly, the problem of optimizing the active orbitals is often poorly convergent and computationally demanding. Other commonly encountered issues in CASSCF calculations include the intruder state problem7,8 and the need for state-averaging,9,10 when multiple states are sought.
Despite these limitations, CASSCF can be viewed as the appropriate simplified Schrödinger equation to solve for the zero-order wavefunction in strongly correlated molecules. Therefore there is growing interest in tractable approximations to CASSCF, of which we will discuss a few of the current alternatives. Perhaps the simplest is the Restricted Active Space (RAS)5,11–13 approach in which some excitations are discarded. Like most approximate configuration interaction (CI) methods, it is not size-consistent, although useful results can be obtained when it is carefully applied. Coupled-cluster approximations to CASSCF are under active development, based on a single reference (e.g. valence orbital optimized coupled-cluster (VOO-CC),14–16 and their local variants, including perfect pairing (PP),17,18 perfect quadruples (PQ),18,19 and perfect hextuples (PH)18,20), as well as true multi-reference coupled-cluster (MR-CC) methods.21–24 The density matrix renormalization group (DMRG),25–32 as well as reduced density matrix methods33–38 are other novel alternatives.
Recently, a family of methods based on the spin-flip (SF) approach39–45 has been introduced to address the issue of electronic degeneracy. In this theory, a high-spin wavefunction is chosen as the reference. By contrast with the low-spin wavefunction, the high-spin wavefunction can be chosen to be mainly single-reference in character at any nuclear distance. Through spin-flipping, complex multi-configurational states of lower spin multiplicity can be accessed. Therefore these methods are able to address many multi-reference problems, while retaining the theoretical simplicity and computational speed of single reference approaches. Spin-flip versions of both CI4,43,46,47 and CC42,48,49 methods have been successfully developed. At the single spin-flip level, these methods are widely used. Here, biradicaloid singlet ground and excited states are accessed via a high-spin triplet reference. Double spin-flip approaches, where a quintet reference is used to access strongly correlated singlet and triplet states, have also been implemented.44
While the above SF methods have wavefunctions that are strictly truncated by excitation level (e.g. SF-CIS, EOM-SF-CCSD, etc.), an alternative CI-based version based on the RAS concept, termed RAS-SF, has been recently introduced.45 RAS-SF allows, in principle, excitations of any number of electrons in the half-occupied orbitals of the high-spin reference (the “RAS-II” space) as well as single excitations into RAS-II from lower doubly occupied MOs (“RAS-I”, which are also known as hole excitations) or single excitations from RAS-II into higher empty MOs (“RAS-III”, also referred to as particle excitations). In practice, however, the maximum number of spin flips in RAS-SF was restricted to two. At the level of two spin-flips (RAS-2SF), very encouraging results were obtained for large tetraradicaloids.45
Our work extends the number of possible spin flips and allows for a variable orbital active space. This has the exciting potential to provide accurate, spin-pure, wavefunction-based results in many areas that were inaccessible so far, such as large polyradicals, three or more bond dissociation processes, as well as bi- or polynuclear-metal systems, which are of importance in biology, catalysis50 and materials science.51 Due to their size, studies of such complexes have been limited to calculations involving density functional theory (DFT), which cannot properly describe strong electron correlation. Organic polyradicals have found great interest as potential magnetic materials52–56 or conductors,57–61 with the advantage of tunability by altering substituents and the potential of solubility in organic media.
In this paper several binuclear metal complexes, bond dissociation processes as well as organic polyradicals will be studied. The RAS-SF results are compared to experimental values, other wavefunction-based, multi-reference methods, such as DMRG, CASSCF, and CASPT2, as well as broken-symmetry DFT.
2 Theory
Our extension to the SF family is based on the formulation of the restricted active space spin-flip method by Casanova and Head-Gordon.45 Writing the expansion for the general excitation operator![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) in terms of hole, particle, hole-particle, etc., excitations allows the SF method to be formulated in the framework of a restricted active space configuration interaction (RAS-CI) method.
in terms of hole, particle, hole-particle, etc., excitations allows the SF method to be formulated in the framework of a restricted active space configuration interaction (RAS-CI) method. | (1) |
 | ||
| Fig. 1 Orbital subspaces in the RAS-SF approach. Adapted from ref. 45. | ||
In order to have linear scaling outside the active space (RAS-I and III) and ensure size intensivity, only single h and p excitations are included in this method. In contrast to MCSCF and CASSCF methods, no orbital optimization is performed in the SF approach, eliminating orbital optimization problems such as root-flipping and the need for state averaging. As discussed in the introduction, high-spin ROHF orbitals can be chosen to yield a satisfactory reference. In addition, the inclusion of hole and particle excitations, respectively, provides state-specific orbital relaxation to a first approximation.
2.1 FCI in the active space, A (RAS-II)
As mentioned above, all possible excitations are generated in the active space, A (RAS-II in Fig. 1), which results in a FCI problem in this orbital subspace. In our implementation, the FCI technique by Olsen et al. was used.12 This was found to be more efficient than the algorithm proposed by Knowles and Handy62 as it avoids the resolution of identity and therefore the need to generate all possible double excitations. Furthermore, the operation count of the Olsen algorithm is favorable for small active spaces, as is the case here. Both of these factors outweigh the computational speed-up resulting from matrix–matrix multiplications in the Handy–Knowles algorithm compared to the vector-matrix approach used by Olsen and co-workers. The α and β strings are generated using the algorithm proposed by Ruedenberg et al.,63 which was slightly modified to account for hole and particle contributions from the RAS-I and III spaces. The guess vector for the Davidson algorithm is generated by diagonalizing the RAS-II space, and if memory permits hole and particle excitations are also included. Algorithmic details and computational timings for the general implementation of the RAS-SF method presented here will be given elsewhere.642.2 Properties of RAS-SF
As discussed in previous work,45 RAS-SF features many of the desirable properties that an electronic structure theory ought to have. It is multistate, spin-complete, variational, size consistent, and orbital invariant within the RAS subspaces. The size-consistency/intensivity property for a fixed number of spin-flips is particularly special and reflects the fact that RAS-SF is constructed analogously to CIS, another rare example of a truncated CI model that is size-consistent. It is also worth mentioning that the RAS-SF method mainly captures static correlation and lacks dynamical correlation. Extensions to recover dynamical correlation would be highly desirable.3 Computational details
All calculations have been carried out using a developer's version of Q-Chem 3.0.65 For computational speed-up resolution-of-the-identity (RI) integrals66,67 have been used. All RAS-SF calculations were carried out using a restricted open shell (ROHF) high-spin reference. Unless indicated, all electrons were included (no frozen core or frozen virtual spaces were employed). For metal complexes, single point calculations at the X-ray crystal geometries have been carried out to determine the exchange coupling constants, as is typical for such calculations.4 Results and discussion
4.1 Bond dissociation
The ability to perform more than two spin flips allows bond dissociation processes of three or more bonds to be described. Fig. 2 shows the dissociation curve for the N2 molecule. Comparison with CASSCF(6,6) calculations68 show extremely good agreement with RAS-SF(6,6) results. In order to understand the effect of orbitals on RAS-SF, numerical results based on restricted singlet and septet references are shown, respectively. Interestingly, both guesses yield similar results. However, only the ROHF orbitals dissociate to the correct limit of two nitrogen atoms.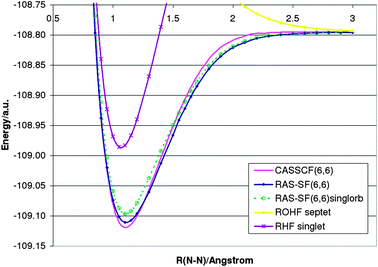 | ||
| Fig. 2 Dissociation curve for the N2 molecule (cc-pVTZ). | ||
4.2 Binuclear metal complexes
When properties of transition metal complexes are studied, the exchange coupling between different sites is a sought after quantity. To extract this quantity, typically, data obtained from neutron diffraction, Raman spectroscopy, magnetic susceptibility and electron paramagnetic resonance measurements is fitted to the model Heisenberg-Dirac-Van Vleck spin-only Hamilitonian, which takes the form69–71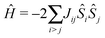 | (2) |
From a theoretical point of view, a balanced description of ground and excited states is required to determine Jij accurately. Most wavefunction methods that would be suitable for these types of problems are computationally too expensive given the size of typical bi- or polynuclear metal complexes. Therefore, density-functional theory (DFT) is typically used to compute the exchange couplings. In this approach, broken symmetry solutions enter the equations to account for states that exhibit multideterminantal character. However, there may be artifacts due to the approximate nature of the exchange-correlation functionals, and indeed several different expressions are used to extract the magnetic coupling parameters.73–77 An alternative approach, based on constrained DFT has recently been shown to be successful in predicting exchange coupling constants in a number of binuclear metal complexes.78
In the remainder of this section and in the following section coupling constants for several binuclear metal complexes and excitation energies for various organic polyradicals will be computed using the RAS-SF method and compared to experimental, DFT and CASSCF results.
![Binuclear Cr(iii)–Cr(iii) complex, [Cr2(NH3)10(OH)]5+.](/image/article/2013/CP/c2cp43293e/c2cp43293e-f3.gif) | ||
| Fig. 3 Binuclear Cr(III)–Cr(III) complex, [Cr2(NH3)10(OH)]5+. | ||
| Expt.79 | −15.8 |
|---|---|
| RAS-SF(6,6)/6-31G* | −3.6 |
| RAS-SF(8,8)/6-31G* | −3.8 |
| RAS-SF(6,6)/TZVP/6-31G* | −3.9 |
| RAS-SF(6,6)/TZVP/6-31G*/6-31+G* on O | −3.9 |
| RAS-SF(6,8)/TZVP/6-31G*/6-31+G* on O | −7.9 |
| RAS-SF(8,7)/TZVP/6-31G*/6-31+G* on O | −4.4 |
| RAS-SF(6,10)/TZVP/6-31G*/6-31+G* on O | −7.8 |
| RAS-SF(8,9)/TZVP/6-31G*/6-31+G* on O | −8.4 |
We also tested the adequacy of the size of the RAS-II space. It turns out that inclusion of orbitals affiliated with the linker are essential for a balanced treatment of antiferromagnetic versus ferromagnetic states. Omission of such orbitals is expected to bias the results against antiferromagnetic states. Since the active space employed so far is (6,6), this could explain why the antiferromagnetic exchange coupling constant is underestimated. One way to resolve this issue is to expand the active space to include the relevant linker orbitals. A related solution is to introduce dynamic correlation while retaining the original active space size. Since the latter method is not yet available, we tested various different active space sizes, which were chosen based on the high-spin ROHF reference orbitals. As can be seen from Table 1, inclusion of some linker orbitals causes the magnitude of the coupling constant to increase substantially and for the (8,9) active space its value is more than doubled compared to the (6,6) active space.
| Expt.82 | −225 |
|---|---|
| RAS-SF(6,6)/TZVP/6-31G*/6-31+G* on O | −66 |
| RAS-SF(6,9)/TZVP/6-31G*/6-31+G* on O | −88 |
![Binuclear Cr(iii)–Cr(iii) complex, [Cr2(NH3)10(O)]4+.](/image/article/2013/CP/c2cp43293e/c2cp43293e-f4.gif) | ||
| Fig. 4 Binuclear Cr(III)–Cr(III) complex, [Cr2(NH3)10(O)]4+. | ||
4.3 Organic polyradicals
High-spin organic polyradicals have gained considerable interest as they may lead to novel magnetic materials.52–56 Both intra- as well as intermolecular spin coupling have been pursued, with the former providing a more promising route.54,55,83 In attempts to form extended intramolecular high-spin systems, one-dimensional poly(m-phenylenecarbenes) and two-dimensional branched carbenes (Fig. 7) have been synthesized, which are all found experimentally to exhibit high-spin ground states.84–87 Typically the m-phenylene moiety is used as a linker as it is one of the strongest ferromagnetic coupling units. The exchange coupling, Jij, between the the spin sites, as introduced in eqn (2) is one of the important properties to be determined in such systems, as it will gauge their applicability as magnetic materials.![Singly occupied orbitals of [Cr2(NH3)10(O)]4+ used for (6,6) active space.](/image/article/2013/CP/c2cp43293e/c2cp43293e-f5.gif) | ||
| Fig. 5 Singly occupied orbitals of [Cr2(NH3)10(O)]4+ used for (6,6) active space. | ||
However, the minimum energy geometry for these carbenes deviates strongly from idealized C2v symmetry, which was applied for computational savings in previous studies, and the comparative calculations reported above. Any deviation from planarity is expected to affect the extent of electronic delocalization and thus the exchange coupling, i.e. the relative energies of the various spin states (Fig. 6). We therefore also carried out RAS-SF calculations on re-optimized structures (UB3LYP/6-31G*) of linear carbenes n = 1–5 (Fig. 7), which will be referred to as C1 structures. Since the RAS-SF, CASSCF and DMRG results for the C2v structures agreed very well, we expect the RAS-SF results for the C1 structures to yield very similar results to these other methods with greater computational ease. Relative RAS-SF energies and selected UB3LYP geometric parameters are shown in Tables 4–7. The dihedral angles given are those spanned by two adjacent benzene moieties and the carbene unit and the angles refer to the angles in the carbene unit.
![Doubly occupied orbitals of [Cr2(NH3)10(O)]4+used for (6,9) active space.](/image/article/2013/CP/c2cp43293e/c2cp43293e-f6.gif) | ||
| Fig. 6 Doubly occupied orbitals of [Cr2(NH3)10(O)]4+used for (6,9) active space. | ||
 | ||
| Fig. 7 One- and two-dimensional carbenes. (n = 1–5, m = 3,6,9). | ||
| Geometry (S) | 0 | 0 | 1 | 1 |
|---|---|---|---|---|
| Point Group | C 1 | C 2v | C 1 | C 2v |
| Dihedral (°) | 35 | 0 | 27 | 0 |
| Angle (°) | 119 | 126 | 142 | 147 |
| States (S) | ||||
| 1 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0 | 3.76 | 6.70 | 21.8 | 25.8 |
| Geometry (S) | 0 | 0 | 1 | 1 | 2 | 2 |
|---|---|---|---|---|---|---|
| Point Group | C 1 | C 2v | C 1 | C 2v | C 1 | C 2v |
| Dihedral1 (°) | −33 | 0 | −34 | 0 | −31 | 0 |
| Dihedral2 (°) | 37 | 0 | 27 | 0 | 26 | 0 |
| Angle1 (°) | 119 | 126 | 119 | 136 | 143 | 147 |
| Angle2 (°) | 119 | 126 | 142 | 136 | 143 | 147 |
| States (S) | ||||||
| 2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | 0.78 | — | 1.04 | — | 1.62 | 1.68 |
| 0 | 1.37 | — | 1.75 | — | 2.60 | 2.70 |
| Geometry (S) | 0 | 1 | 2 | 3 | 3 |
|---|---|---|---|---|---|
| Point Group | C 1 | C 1 | C 1 | C 1 | C 2v |
| Dihedral1 (°) | −33 | −34 | −34 | −31 | 0 |
| Dihedral2 (°) | 35 | 29 | 30 | 29 | 0 |
| Dihedral3 (°) | −37 | −38 | −26 | −26 | 0 |
| Angle1 (°) | 119 | 129 | 143 | 143 | 147 |
| Angle2 (°) | 119 | 143 | 143 | 143 | 147 |
| Angle3 (°) | 119 | 129 | 143 | 143 | 147 |
| States (S) | |||||
| 3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.40 | 0.60 | 0.70 | 0.79 | 0.85 |
| 1 | 0.81 | 1.23 | 1.41 | 1.61 | 1.72 |
| 2 | 1.27 | 1.84 | 2.18 | 2.41 | 2.39 |
| 1 | 1.33 | 1.92 | 2.30 | 2.50 | 2.56 |
| 0 | 1.42 | 2.42 | 2.86 | 3.17 | 3.47 |
| 1 | 2.09 | 3.17 | 3.78 | 4.17 | 4.43 |
| RAS-SF | UB3LYP | UBP86 | ||
|---|---|---|---|---|
| Point group | C 1 | C 2v | C 1 | C 1 |
| Dihedral1 (°) | −24 | 0 | −24 | −24 |
| Dihedral2 (°) | 20 | 0 | 20 | 20 |
| Dihedral3 (°) | −23 | 0 | −23 | −23 |
| Dihedral4 (°) | −20 | 0 | −20 | −20 |
| Angle (°) | 138 | 141 | 138 | 138 |
| States (S) | ||||
| 4 | 0.00 | 0.00 | 0.00(20.2) | 0.00(20.1) |
| 3 | 0.48 | 0.73 | 18.6(12.2) | 5.98(13.0) |
| 2 | 0.99 | 1.00 | 48.9(6.2) | 13.8(7.8) |
| 1 | 1.12 | 1.54 | 44.5(3.8) | 6.61(5.0) |
| 3 | 1.21 | 1.61 | — | — |
| 0 | 1.42 | 1.95 | 30.5(3.5) | 2.82(4.1) |
| 2 | 1.46 | 1.98 | — | — |
Geometric parameters between the C2v and C1 structures of the same spin multiplicity are considerably different (Tables 4–7). The dihedral angles, which are restricted to 0° in the C2v structures, relax to 27–37° in the C1 geometries. This allows the angles around the carbene moiety to be smaller in the case of the C1 structures. Despite these geometric differences, the relative energies between the spin states differ by at most 4 kcal mol−1. However, for longer carbenes, where the energy gaps are very small, this can cause the energy difference to be overestimated by a factor of 2.5. In general, the C2v geometries overestimate the coupling between the units as the planarity maximizes the interaction between the π system of the carbene units and the benzene rings.
The large decrease in vertical singlet-triplet gap on going from n = 1 (Table 4) to more extended carbene chains (Tables 5–7) is likely because in n = 1 the singlet state can only be formed by pairing the two electrons on the same carbene moiety, whereas for, e.g. n = 2 the singlet state can be obtained from coupling two triplet carbene units. This would be consistent with the observation88 that the low-spin states in extended carbene systems feature considerable multi-reference character and that single-reference methods obtain a similar vertical singlet-triplet energy gap for n = 1, but overestimate the spin-gaps betwen highest-spin and singlet states greatly for larger n.
Finally, for n = 3 and n = 4 we also compared our RAS-SF results to two density functionals (UB3LYP and UBP86). Values for n = 3 are given in Tables 8 and 9, and for n = 4 in Table 7. The energy gaps predicted by UB3LYP and UBP86 are considerably larger than those obtained from RAS-SF studies. The relative energies computed by DFT are also found to be much more sensitive towards geometrical changes. In some cases this causes even the ordering of the spin states to switch. Noteworthy is also, that BP86 features considerable spin contamination, for the lower spin multiplicities. Furthermore, the two density functionals, when compared to each other, yield substantially different results. For example, the singlet-septet energy gaps for the S = 3 geometry are 35.4 and 9.63 kcal mol−1 for UB3LYP and UBP86, respectively (Tables 8 and 9), and for n = 4, UBP86 predicts a completely different ordering of the spin states compared to RAS-SF and UB3LYP (Table 7). This highlights the need for a method that can reliably predict spin state energies and is systematically improvable.
| Geometry (S) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| States (S) | ||||
| 3 | 0.00(12.2) | 0.00(12.2) | 0.00(12.2) | 0.00(12.2) |
| 2 | 1.06(6.1) | 2.17(6.9) | 7.90(6.1) | 11.59(7.1) |
| 1 | −2.38(2.2) | 16.15(2.1) | 15.26(3.0) | 17.98(3.9) |
| 0 | −8.10(1.0) | 7.24(2.8) | 12.21(3.0) | 7.69(3.1) |
| Geometry (S) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| States (S) | ||||
| 3 | 0.00(12.1) | 0.00(12.1) | 0.00(12.1) | 0.00(12.1) |
| 2 | −0.80(6.0) | 1.40(6.8) | 1.37(6.8) | 6.03(7.0) |
| 1 | −7.56(3.0) | 2.81(3.5) | 7.46(3.7) | 3.65(4.1) |
| 0 | −6.96(0.0) | 13.5(2.2) | 18.17(2.5) | 9.63(3.0) |
4.3.2.1 Polycarbene m = 3. Branched systems such as the two-dimensional carbenes (Fig. 7) and Closs-radicals, which will be discussed in the next section, are of interest, as the broken-symmetry DFT approaches are not applicable to such systems. Table 10 lists the relative energies obtained from RAS-SF(6,6) calculations for the two-dimensional polycarbene with m = 3, Fig. 7. The relative energies are found to be quite insensitive towards geometrical changes. In accordance with experimental findings, the ground state is predicted to be a septet. The other spin states lie in close proximity, indicating weak coupling between the spin centers. Comparison to UB3LYP calculations shows that RAS-SF again tends to predict considerably smaller energy gaps, although the ordering of the spin states is predicted to be the same for both methods.
| RAS-SF(6,6) | UB3LYP | ||||
|---|---|---|---|---|---|
| Geometry (S) | 0 | 1 | 2 | 3 | 3(〈S2〉) |
| States (S) | |||||
| 3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00(12.2) |
| 2 | 0.60 | 1.35 | 1.50 | 1.94 | 6.66(7.1) |
| 2 | 0.97 | 1.74 | 2.16 | 2.33 | — |
| 1 | 1.68 | 2.75 | 3.16 | 4.02 | 13.69(3.9) |
| 1 | 1.72 | 3.03 | 3.50 | 4.04 | — |
| 1 | 2.08 | 3.25 | 4.00 | 4.41 | — |
| 0 | 2.32 | 3.75 | 4.46 | 5.22 | 35.4(2.8) |
4.3.2.2 Catenated closs radicals. Recently three diradicals were linked via a 1,3,5-trimethylbenzene moiety (1) shown in Fig. 8.89 The high stability of species (1) at low temperatures (77 K) with a septet ground state makes it a very promising candidate for a molecular magnet. Calculations using DFT and UHF on the model systems shown in Fig. 990 explored the relative stability of ring-closed compared to the nearly-planar open structures. However, no calculations on the excited states of species (1) have been performed.
 | ||
| Fig. 8 Catenated Closs Radicals, (1). | ||
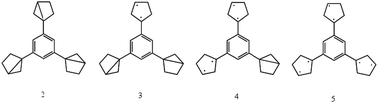 | ||
| Fig. 9 Model systems used in90 to study relative stabilities of catenated Closs radicals. | ||
Since the septet is experimentally found to be prevalent, we investigated the energy differences between the various spin states for the S = 3 geometry, which are related to the spin-coupling within each molecule. Since the phenyl groups are expected to affect the stability of the high-spin states considerably as they allow delocalization over the π system, calculations were carried out on the full system (Fig. 8). As in the previous part, RAS(6,6), UB3LYP, UBP86 and UHF calculations were studied. As can be seen from Table 11, all methods predict the septet state to be the ground state, in accordance with experimental findings. However, as was already observed in other examples, RAS-SF predicts substantially smaller energy differences between the various spin states compared to the density functionals under consideration. The singlet-septet gap, for example, is 0.86, 72.2, and 6.13 kcal mol−1 for RAS-SF(6,6), UB3LYP, and UBP86, respectively (Table 11). However, the two functionals again vary considerably in their predictions and show considerable spin contamination in lower spin states. We believe that the minimal (6,6) active space used in the RAS-SF calculations may result in an underestimation of the relative energies of the spin states. Inclusion of the 3 π orbitals from the central benzene moiety into the RAS-II space is expected to result in stronger coupling between the three biradical units.
| States (S) | RAS-SF(6,6) | UB3LYP | UBP86 | UHF |
|---|---|---|---|---|
| 3 | 0.00 | 0.00(12.1) | 0.00(12.1) | 0.00(14.4) |
| 2 | 0.22 | 0.08(7.2) | 0.10(7.1) | 25.0(9.3) |
| 2 | 0.22 | — | — | — |
| 2 | 0.45 | — | — | — |
| 1 | 0.50 | 9.30(4.1) | 0.20(4.1) | 25.5(6.2) |
| 1 | 0.51 | — | — | — |
| 1 | 0.72 | — | — | — |
| 0 | 0.86 | 0.36(3.2) | 6.13(3.0) | 0.46(5.5) |
5 Conclusions
Benchmark calculations on a triple bond dissociation, various binuclear metal systems, and organic polyradicals were carried out using a new implementation of the restricted active space spin-flip (RAS-SF) method, which allows for variable orbital active spaces and the study of systems requiring three or more spin-flips. Relative to CASSCF, RAS-SF calculations are roughly 100–1000 times faster as orbital optimization is avoided.Comparison of RAS-SF to other wave-function based, multi-reference methods, such as CASSCF and DMRG yielded very good agreement, provided that the same active space was employed. Although the ordering of the spin states is typically found to be the same, UB3LYP and UBP86 are found to consistently predict considerably larger energy gaps than RAS-SF. However, it has to be noted that the two functionals differ substantially in their predictions when compared to one another.
Where experimental values are available, RAS-SF is found to underestimate the energy gaps (and thus exchange coupling constants) by a factor of 4 to 8, if the minimal active space is chosen. However, the correct ground state was always obtained, and furthermore, the ratio of exchange couplings in related systems (e.g. [Cr2(NH3)10(O)]4+vs. [Cr2(NH3)10(OH)]5+) is in much better agreement with experiment than the magnitude of the coupling. We found the RAS-SF results to be relatively insensitive towards the choice of basis set on the metal and ligand atoms and the presence of counterions.
Not surprisingly, inclusion of bridge orbitals into the active space is crucial for a balanced description of antiferromagnetic versus ferromagnetic states, and can cause the magnitude of the coupling constants to more than double, when compared to the minimal active space, which only includes the d electrons. Inclusion of the π orbitals of bridging benzene rings is also expected to have a similar effect on the energy gaps of the organic polyradicals under consideration, albeit smaller in magnitude, as concluded from CASSCF and CASPT2 data for the linear poly(m-phenylenecarbene) series.
The results reported here demonstrate the applicability of the open-ended RAS-SF implementation to large system with complex electron correlation and low-lying excited states. Perhaps not surprisingly they also reveal the need for a tractable dynamic correlation correction to obtain better accuracy in a minimal active space. Inclusion of dynamic correlation could be achieved for example via perturbation theory or, through a Jastrow factor,91 as is practice in Quantum Monte Carlo methods. Such an extension to the RAS-SF approach utilizing perturbation theory is currently underway in our group.
Acknowledgements
Support for this work was provided through the Scientific Discovery through Advanced Computing (SciDAC) program funded by the U.S. Department of Energy, Office of Science, Advanced Scientific Computing Research, and Basic Energy Sciences.References
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- R. J. Bartlett, in Theory and Applications of Computational Chemistry: The First Forty Years, Elsevier, Amsterdam, 2005, pp. 1191–1221 Search PubMed.
- J. Paldus, in Theory and Applications of Computational Chemistry: The First Forty Years, Elsevier, Amsterdam, 2005, pp. 115–147 Search PubMed.
- J. S. Sears, C. D. Sherrill and A. I. Krylov, J. Chem. Phys., 2003, 118, 9084–9094 CrossRef CAS.
- B. O. Roos, In Ab Initio Methods in Quantum Chemistry, 1987, vol. 2, p. 399 Search PubMed.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, J. Phys. Chem., 1980, 48, 157 CAS.
- J. Paldus, P. Piecuch and B. Jeziorski, Phys. Rev. A, 1993, 47, 2738 CrossRef CAS.
- P. Piecuch and J. Paldus, Phys. Rev. A, 1994, 49, 3479 CrossRef CAS.
- K. K. Docken and J. Hinze, J. Chem. Phys., 1972, 57, 4928 CrossRef CAS.
- K. Ruedenberg, L. M. Cheung and S. T. Elbert, Int. J. Quantum Chem., 1979, 16, 1069 CrossRef CAS.
- I. Shavitt, in Modern Theoretical Chemistry, Plenum, New York, 1977, vol. 3, p. 189 Search PubMed.
- J. Olsen, B. O. Roos, P. Jorgensen and H. J. A. Jensen, J. Chem. Phys., 1988, 89, 2185–2192 CrossRef CAS.
- P.-A. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477 CrossRef CAS.
- C. D. Sherrill, A. I. Krylov, E. F. C. Byrd and M. Head-Gordon, J. Chem. Phys., 1998, 109, 4171 CrossRef CAS.
- A. I. Krylov, C. D. Sherrill, E. F. C. Byrd and M. Head-Gordon, J. Chem. Phys., 1998, 109, 10669 CrossRef CAS.
- A. I. Krylov, C. D. Sherrill and M. Head-Gordon, J. Chem. Phys., 2000, 113, 6509 CrossRef CAS.
- J. Cullen, Chem. Phys., 1996, 202, 217–229 CrossRef CAS.
- J. Parkhill and M. Head-Gordon, J. Chem. Phys., 2010, 133, 124102 CrossRef.
- J. Parkhill, K. Lawler and M. Head-Gordon, J. Chem. Phys., 2009, 130, 084101 CrossRef.
- J. Parkhill and M. Head-Gordon, J. Chem. Phys., 2010, 133, 024103 CrossRef.
- X. Li and J. Paldus, J. Chem. Phys., 2003, 119, 5320 CrossRef CAS.
- J. Pittner, J. Chem. Phys., 2003, 118, 10876 CrossRef CAS.
- F. A. Evangelista, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 2006, 125, 154113 CrossRef.
- F. A. Evangelista, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 2006, 127, 024102 CrossRef.
- S. R. White, Phys. Rev. Lett., 1992, 69, 2863 CrossRef.
- S. R. White, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10345 CrossRef CAS.
- G. K.-L. Chan and D. Zgid, Annu. Rep. Comput. Chem., 2009, 5, 149 CrossRef CAS.
- G. K.-L. Chan, J. J. Dorando, D. Ghosh, J. Hachmann and E. Neuscamman, An introduction to the density matrix renormalization group ansatz in quantum chemistry, In Frontiers in Quantum Systems in Chemistry and Physics, Springer, New York, 2008 Search PubMed.
- U. Schöllwock, Rev. Mod. Phys., 2005, 77, 259–315 CrossRef.
- G. K.-L. Chan and M. Head-Gordon, J. Chem. Phys., 2002, 116, 4462 CrossRef CAS.
- K. A. Hallberg, Adv. Phys., 2006, 55, 477–526 CrossRef CAS.
- S. R. White and R. L. Martin, J. Chem. Phys., 1999, 110, 4127 CrossRef CAS.
- D. A. Mazziotti, Acc. Chem. Res., 2006, 39, 207 CrossRef CAS.
- A. J. Coleman and V. I. Yukalov, Reduced Density Matrices: Coulson's Challenge, Springer-Verlag, New York, 2000 Search PubMed.
- A. J. Coleman, in Density Matrices and Density Functionals, Proceedings of the A. John Coleman Symposium, Reidel, Dordrecht, 1987 Search PubMed.
- W. B. McRae and E. R. Davidson, J. Math. Phys., 1972, 13, 1527 CrossRef.
- R. M. Erdahl, Int. J. Quantum Chem., 1978, 13, 697 CrossRef.
- J. K. Percus, Int. J. Quantum Chem., 1978, 13, 89 CrossRef CAS.
- A. Krylov, Acc. Chem. Res., 2006, 39, 83 CrossRef CAS.
- J. S. Sears, C. D. Sherrill and A. I. Krylov, J. Chem. Phys., 2003, 118, 9084 CrossRef CAS.
- S. V. Levchenko and A. I. Krylov, J. Chem. Phys., 2003, 118, 9084 CrossRef.
- S. V. Levchenko and A. I. Krylov, J. Chem. Phys., 2004, 120, 175 CrossRef CAS.
- D. Casanova and M. Head-Gordon, J. Chem. Phys., 2008, 129, 064104 CrossRef.
- D. Casanova, L. V. Slipchenko, A. I. Krylov and M. Head-Gordon, J. Chem. Phys., 2009, 130, 044103 CrossRef.
- D. Casanova and M. Head-Gordon, Phys. Chem. Chem. Phys., 2009, 11, 9779 RSC.
- A. I. Krylov and C. D. Sherrill, J. Chem. Phys., 2002, 116, 3194 CrossRef CAS.
- A. I. Krylov, Chem. Phys. Lett., 2001, 350, 522 CrossRef CAS.
- A. I. Krylov, Chem. Phys. Lett., 2001, 338, 375 CrossRef CAS.
- L. V. Slipchenko and A. I. Krylov, J. Chem. Phys., 2005, 123, 84107 CrossRef.
- M. T. Pope and A. Muller, Angew. Chem., Int. Ed. Engl., 1991, 30, 34 CrossRef.
- Molecular Magnetism: From Molecular Assemblies to the Devices, ed. E. Coronado, P. Delhaes, D. Gatteschi and J. S. Miller, Kluwer Academic Publishers, 1995, vol. 321 Search PubMed.
- D. A. Dougherty, Acc. Chem. Res., 1991, 24, 88–94 CrossRef CAS.
- H. Iwamura and N. Koga, Acc. Chem. Res., 1993, 26, 346–351 CrossRef CAS.
- A. Rajca, Chem. Rev., 1994, 94, 871–893 CrossRef CAS.
- J. S. Miller and A. Epstein, Angew. Chem., Int. Ed. Engl., 1994, 106, 385–418 CrossRef.
- M. Baumgarten and K. Mullen, Top. Curr. Chem., 1994, 169, 1–104 CrossRef CAS.
- S. Pedersen, J. L. Herek and A. H. Zewail, Science, 1994, 266, 1359–1364 CAS.
- Conjugated polymers and Related Materials, ed. B. R. W. R. Salaneck and I. Lundstrm, Oxford, New York, 1993 Search PubMed.
- T. A. Albright, J. K. Burdett and M.-H. Whangbo, Orbital Interactions in Chemistry, Wiley-Interscience, New York, 1985 Search PubMed.
- L. A. Bumm, J. J. Arnold, M. T. Cygan, T. D. Dunbar, T. P. Burgin, L. Jones II, D. L. Allara, J. M. Tour and P. S. Weiss, Science, 1996, 271, 1705–1707 CAS.
- M.-H. Whangbo, In Extended Linear Chain Compounds, Plenum, New York, 1982 Search PubMed.
- P. Knowles and N. Handy, Chem. Phys. Lett., 1984, 111, 315–321 CrossRef CAS.
- J. Ivanic and K. Ruedenberg, Theoretical Chemistry Accounts: Theory, Computation, and Modeling (Theoretica Chimica Acta), 2001, 106, 339–351 CAS.
- P. M. Zimmerman, F. Bell, M. Goldey, A. T. Bell and M. Head-Gordon, J. Chem. Phys., 2012, 137, 164110 CrossRef.
- Y. Shao, et al. , Phys. Chem. Chem. Phys., 2006, 8, 3172–3191 RSC.
- M. Feyereisen, G. Fitzgerald and A. Komornicki, Chem. Phys. Lett., 1993, 208, 359 CrossRef CAS.
- O. Vahtras, J. E. Almlof and M. W. Feyereisen, Chem. Phys. Lett., 1993, 213, 514 CrossRef CAS.
- T. Tsuchimochi, T. M. Henderson, G. E. Scuseria and A. Savin, J. Chem. Phys., 2010, 133, 134108 CrossRef.
- W. Heisenberg, Z. Phys., 1928, 49, 619 CrossRef CAS.
- P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1929, 123, 714 CrossRef CAS.
- J. H. Van Vleck, The Theory of Electric and Magnetic Susceptibilities, Oxford U.P., Oxford, 1932 Search PubMed.
- J. B. Goodenough, Magnetism and the Chemical Bond, Wiley, New York, 1963 Search PubMed.
- E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391 CrossRef CAS.
- L. Noodleman and J. J. G. Norman, J. Chem. Phys., 1979, 70, 4903 CrossRef CAS.
- R. Caballol, O. Castell, F. Illas, P. R. De, I. Moreira and J.-P. Malrieu, J. Phys. Chem. A, 1997, 101, 7860 CrossRef CAS.
- J.-M. Mouesca, J. Chem. Phys., 2000, 113, 10505 CrossRef CAS.
- T. Soda, Y. Kitagawa, T. Onishi, Y. Tkaano, Y. Shigeta, H. Nagao, Y. Yoshioka and K. Yamaguchi, Chem. Phys. Lett., 2000, 319, 223 CrossRef CAS.
- I. Rudra, Q. Wu and T. Van Voorhis, J. Chem. Phys., 2006, 124, 024103 CrossRef.
- J. T. Veal, D. Y. Jeter, J. C. Hempel, R. P. Eckberg, W. E. Hatfield and D. J. Hodgson, Inorg. Chem., 1973, 12, 2928 CrossRef CAS.
- P. Harris, H. Birkedal, S. Larsen and H. U. Güdel, Acta Crystallogr., Sect. B, 1997, 53, 795–802 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- E. Pedersen, Acta Chem. Scand., 1972, 26, 333 CrossRef CAS.
- H. Iwamura, Adv. Phys. Org. Chem., 1990, 26, 179 CrossRef CAS.
- Y. Teki, T. Takui and K. Itoh, J. Am. Chem. Soc., 1983, 105, 3722–3723 CrossRef CAS.
- T. Sugawara, S. Bandow, K. Kimura and H. Iwamura, J. Am. Chem. Soc., 1984, 106, 6449–6450 CrossRef CAS.
- Y. Teki, T. Takui, H. Yagi, K. Itoh and H. Iwamura, J. Chem. Phys., 1985, 83, 539 CrossRef CAS.
- T. Sugawara, S. Bandow, K. K. H. Iwamura and K. Itoh, J. Am. Chem. Soc., 1986, 108, 368–371 CrossRef CAS.
- W. Mizumaki, Y. Kurashige and T. Yanai, J. Chem. Phys., 2010, 133, 091101 CrossRef.
- W. Adam, M. Baumgarten and W. Maas, J. Am. Chem. Soc., 2000, 122, 6735 CrossRef CAS.
- M. S. Schuurman, C. Pak and H. F. Schaefer, J. Chem. Phys., 2002, 117, 7147 CrossRef CAS.
- C. J. Umrigar, J. Toulouse, C. Filippi, S. Sorella and R. G. Hennig, Phys. Rev. Lett., 2007, 98, 110201 CrossRef CAS.
| This journal is © the Owner Societies 2013 |
