Effect of sodium chloride on the structure and stability of spider silk's N-terminal protein domain

Abstract

A spider's ability to store silk protein solutions at high concentration is believed to be related to the protein's terminal domains. It has been suggested that a shift in salt concentration and pH can have a significant influence on the assembly process. Based on experimental data, a model has been proposed in which the N-terminal domain exists as a monomer during storage and assembles into a homodimer upon spinning. Here we perform a systematic computational study using atomistic, coarse-grained and well-tempered metadynamics simulation to understand how the NaCl concentration in the solution affects the N-terminal domain of the silk protein. Our results show that a high salt concentration, as found during storage, weakens key salt bridges between the monomers, inducing a loss in bond energy by 28.6% in a single salt bridge. As a result, dimer formation is less likely as 35.5% less energy is required to unfold the dimer by mechanical force. Conversely, homodimer formation appears to be more likely at low salt concentrations as the salt bridge stays at the lower energy state. The link between salt concentration, structure and stability of the N-terminal domain provides a possible molecular mechanism that prevents premature fiber formation during storage.

---

Introduction

Spider dragline silk stands out due to its exceptional mechanical properties such as high toughness and strength.^1,2 Nano-confined assemblies of hydrogen bonds have been proposed to yield this high mechanical performance,^3,4 maintain biodegradability and allow energy-efficient assembly of the material. In this sense, the in vivo fiber assembly of silk may inspire polymer processing towards a low-energy polymer fiber formation.⁵ Dragline silk mainly consists of major ampullate spidroin 1 and 2. A highly repetitive core region, which is linked to the mechanical behavior of silk, makes up most of the spidroin, while the terminal domains are non-repetitive and related to the silk assembly process.^6,7 Before the major ampullate spidroin (MaSp) is drawn on demand into a fiber at ambient temperature, it is stored in a highly concentrated form in aqueous solution in the major ampullate gland.⁸ The production of silk strands is triggered by various processing variables, such as shear force, solvent removal and dope composition, that each impacts MaSp differently.^8–10 The terminal domains of MaSp react to changes in the solvent conditions,^11–14 primarily from a shift from a strong presence of sodium chloride and near neutral conditions in the gland, to predominantly potassium and phosphate ions at slight acidic conditions in the spinning duct.⁹

Specifically, the N-terminal domain of MaSp plays a critical role in delaying aggregation at neutral pH.¹¹ At pH values of around 6, the N-terminal domain is found as a homodimer, while at high salt concentration and neutral pH it is found as a monomer.^13–15 Several models based on these experimental observations have been proposed to describe the role of the terminal domains in the spinning process. Hagn et al.¹³ proposed a model where the spidroin is stored in micelles with the terminal domains at the surface. The N-terminal domain is thought to be present as a monomer while stored and later assembled into a homodimer in the spinning duct (see Fig. 1a). However, the way in which the solvent conditions govern the formation process of the silk homodimer is not clear. This prevents understanding of how spiders manage to store the silk in a liquid crystalline phase and transition it into strong fibers during spinning.

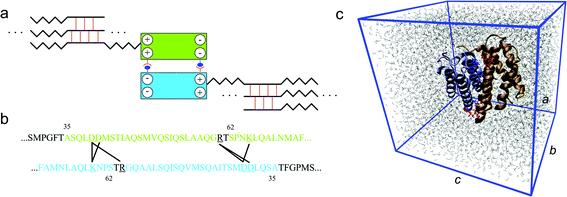Fig. 1 Role of the N-terminal domain in the silk assembly process. Panel a: schematic figure (not drawn to scale) of the association of the two monomers to form a dimer, which helps the alignment of the spidroins and leads to very long spidroin strands. The two blocks represent the homodimer that is also depicted in panel c. The zigzag line stands for the semi-amorphous region that alternates with β-sheet crystal forming parts, which connect different strands to a network. Panel b: the relevant domain within each of the monomer to form salt bridges. A black line connects the two amino acids involved in a salt bridge. These salt bridges are identified during the equilibrium molecular dynamic simulation using the length criterion. Panel c: simulation unit cell of the atomic structure of the homodimer of the N-terminal domain at equilibrium in aqueous conditions. The two monomers are depicted in different colors and each of them consists of five α-helices. The charged residues at the dimer interface are shown in red (for monomer 1) and blue (for monomer 2), in detail. The periodic box is given by the blue frame with lattice constants a, b and c in different directions. Water molecules are depicted by gray lines.

It is difficult for experimental studies to capture the details of certain molecular interactions. Computational approaches may give complementary insights into the detailed mechanisms of the events partially exposed by experimental observations. For example, Wallace and Shen¹⁶ have investigated the effect of pH on the pK_a values of the N-terminal domain using constant pH molecular dynamics. They revealed that glutamine residues are ionized at elevated pH and as a consequence, water molecules enter the interface between the monomers and reduce the dimer stability. However, so far there has been no computational study that explains how the dimer interface is affected by high salt concentration, which is a condition essential for silk storage.^13,14 Here we use molecular dynamics simulations to elucidate the effect of sodium and chloride ions on the N-terminal domain and compare our results to experimental studies. The analysis on the molecular scale allows us to investigate the biophysical mechanism involved in destabilizing the homodimer. We focus on the mechanical stability of the assembled homodimer, and investigate the adhesion energy between the interfaces at two different salt conditions. Our results reveal how salt weakens the dimer bonding and alters its molecular conformation to prevent premature fiber formation while stored in the gland, which is consistent with experimental observations.

Materials and methods

Crystal structure of the N-terminal domain and molecular simulation setup

The crystal structure of the N-terminal domain from the spider Euprosthenops australis has been determined by X-ray crystallography with 1.7 Å resolution by Askarieh et al.¹¹ and is obtained from the Protein Data Bank (PDB identification code 3LR2). The initial structure is equilibrated in a solvent environment modeled by explicit TIP3P water molecules¹⁷ using full-atomistic molecular dynamics. The molecular simulations are carried out using the CHARMM27 force field¹⁸ and TIP3P water model¹⁷ with the NAMD2.8 simulation package.¹⁹ We use a time step of 2 fs to simulate an isothermal–isobaric ensemble (NPT) at a temperature of T = 300 K and pressure of P = 1 atm using a Langevin-piston barostat and a friction coefficient of γ = 5 ps⁻¹. We apply periodic boundary conditions in all directions and use the Particle Mesh Ewald method with 1 Å grid size to efficiently account for the full electrostatics. The simulated system is a rectangular unit cell with its size of 64 Å × 61 Å × 70 Å (a × b × c as shown in Fig. 1c). This edge length is chosen large enough to accommodate the protein structure. The minimum distance between mirroring structures is beyond 15 Å, which is the cutoff length of the van der Waals interaction. We neutralize the system by controlling the number of cations and anions added to the system. We equilibrate the homodimer separately for 20 ns at two different conditions. The environment of the spider's spinning gland is represented by a NaCl concentration of 0.5 M NaCl solution, while the absence of NaCl in the spinning duct is modeled by a water box containing no salt. The two conditions are chosen to align with recent experiments that examined the influence of salt on the N-terminal domain.^13,14 During the equilibration process we monitor the root-mean-square deviation (RMSD, as shown in Fig. S1 in the ESI†) and the length of each cross-monomer salt bridge. A salt bridge is defined when the nitrogen and oxygen atoms of the charged residues pairs get closer than 4 Å during the equilibration.²⁰

Well-tempered metadynamics method

Free-energy calculations are carried out using the well-tempered metadynamics algorithm²¹ implemented in the PLUMED1.3²² external plugin for the NAMD2.8 package. This method enhances the sampling speed in simulations by adding bias potentials during the simulation and has the advantage of ensuring convergence of the energy landscape without requiring an initial estimate. We chose the biased collective variable to be the distance between the center of mass of NH₃ of Lys65 (in monomer 1) and COO of Asp40 (in monomer 2). The simulations are run with an initial configuration of the equilibrated homodimer obtained after equilibration for 20 ns. Other parameters include the enhanced temperature of 1500 K where the collective variable is sampled, and Gaussian hills with a width of 0.35 Å are added to bias the energy of the collective variable at a rate of 0.1 kcal mol⁻¹ for every 2 ps, corresponding to a deposition rate of 0.05 kcal mol⁻¹ ps⁻¹. Each of the well-tempered metadynamics runs is 10 ns long and the convergence is confirmed (as shown in Fig. S2 in the ESI†).

Coarse-grained model with MARTINI force field

Additionally, we carried out an equilibration and tensile test of the molecular structure using the residue-based coarse-grained MARTINI force field in explicit water. This allows us to explore the stability of the homodimer at time-scales of several hundreds of nanoseconds, and larger length-scales.^23,24 The initial coarse-grained geometry is generated from the full atomistic model of the homodimer (after the equilibration process, as shown in Fig. 1c). Each amino acid is represented by one to five beads, one of which is the backbone bead that is generated from the coordinate of the residue backbone and the rest of which are side-chain beads that are generated from the coordinate of the residue side chain. Every four water molecules are represented by a bead. The coarse-grained system includes 3585 particles (503 for the protein plus 3082 for water molecules), while the corresponding full atomistic system includes 40 635 particles (3652 for the protein plus 36 984 for water molecules). We note that 59 ions (sodium plus chloride) are included in the system for the 0.5 M solution while 9 ions (sodium) are included as the counter ion for the non-salt solution. We use a 20 fs time step in this coarse-grained model, and apply the same ensemble (NPT) with the same constant temperature (300 K) and pressure (1 atm) as in the full atomistic model during the 200 ns equilibration phase. We ensure that the structures are fully equilibrated in different solutions by computing the RMSD of the structure and the potential energy (as shown in Fig. S3 and S4 in the ESI†), as well as the length of each of the salt bridge; each of which converges before 200 ns equilibration.

Steered molecular dynamics: mechanical analysis

The simulations of the response of the homodimer under mechanical force are carried out with the steered molecular dynamics (SMD) method.²⁵ The backbone bead at the C-terminal of one monomer is tethered to a spring with a force constant of 10 kcal mol⁻¹ Å⁻², being pulled in a constant rate, while the C-terminal of the other monomer is fixed. The pulling force is recorded versus the position of the tether point. The simulations are carried out at a pulling velocity of 0.1 m s⁻¹. It is noted that for this pulling rate, the simulation time reaches 400 ns before the two monomers completely break apart. We record the force–displacement curve during the SMD simulation and compare the breaking force and external work for the homodimer in different solutions.

Results and discussion

We equilibrate the crystal structure of the N-terminal domain of E. australis (with PDB identification code 3LR2) via full-atomistic classic molecular dynamics simulations for 20 ns at two different solvent conditions, one non-salt and one with 0.5 M sodium chloride. The salt conditions resemble the storage conditions in the spider's gland and match experiments that investigated the salt influence on the N-terminal domain.^13–15 For non-salt conditions we align with the experiments that use a 10 mM or 20 mM phosphate buffer,^13,14 although in vivo there are potassium and phosphate ions prevalent in the spinning duct.⁹ The concentration of the phosphate buffer used in the experiments is so low that we neglect to use the buffer in our simulations.

After running the simulation for 20 ns, there is no significant change in the structure, as the RMSD stays within 1.9 Å for the non-salt conditions and within 2.9 Å for the salt conditions. The equilibrated structure for both solvent conditions maintains a homodimer composed of two monomers, each as a bundle of five α-helices, as illustrated in Fig. 1c. The RMSD of the homodimer in both solutions converges by the end of those calculations, indicating that both structures reach their equilibrated states within the current setup of the simulations (as shown in Fig. S1†).

For both conditions there are six residue pairs found to have the capacity to form intermolecular salt bridges to stabilize the dimer as shown in Fig. 1b and c. Those six residue pairs include:

• Lys65(monomer 1)–Asp40(monomer 2) named SB1,

• Arg60(monomer 1)–Asp40(monomer 2) named SB2,

• Arg60(monomer 1)–Asp39(monomer 2) named SB3,

• Asp40(monomer 1)–Lys65(monomer 2) named SB4,

• Asp39(monomer 1)–Arg60(monomer 2) named SB5,

• Asp39(monomer 1)–Lys65(monomer 2) named SB6.

All residues that are involved in forming intermolecular salt bridges are located on helix 2 and helix 3 of each subunit. This observation is in agreement with the concept reported by Jaudzems et al.²⁶ that the two subunits dimerize via these two helices. It is interesting that SB4 and SB5 are in a symmetric position with regards to SB1 and SB3, respectively. We keep a record of the length of the six salt bridges and statistically summarize the result in Fig. 2a. We find that SB1 and SB4 have the shortest length among all the salt bridges in both non-salt and salt conditions, indicating that it is the strongest interaction to stabilize the dimer. We find more evidence of the importance of SB1 and SB4, as shown in Fig. 2b, which shows that the distance between Lys65 and Asp40 (for SB1 and SB4) are permanently closer than 4 Å for all conditions and always form salt bridges with conserved length. We propose that these salt bridges represent the most relevant interactions to stabilize the two monomers since the rest of the salt bridges fluctuate more in length and maintain larger distances.

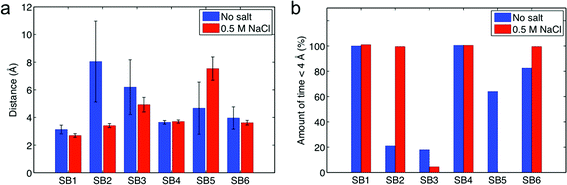Fig. 2 Distances between charged residues of the two molecules that are able to form intermolecular salt bridges. Data is taken from the last 10 ns equilibration of the all-atom model. Panel a: mean distance with standard deviation under salt and non-salt conditions. Panel b: amount of time the residue pair has been in an effective salt bridge state (distance ≤ 4 Å).

There is no direct evidence to show a difference in the stability of the homodimer in different solvent conditions via this classic molecular dynamics simulation. This issue most likely arises because the interaction between the two monomers is too strong and thermal fluctuations have no significant effect on the structure stability during the limited sampling time. To extend the sampling time we coarse-grain the model with a Martini force field to gain access to longer time scales. The coarse-grained model, as illustrated in Fig. 3, is set up based on the coordinates of each residue of the equilibrated atomic structure, and it preserves the secondary structure information as well as the non-bonded interactions between the residue pairs of the full atomic model.

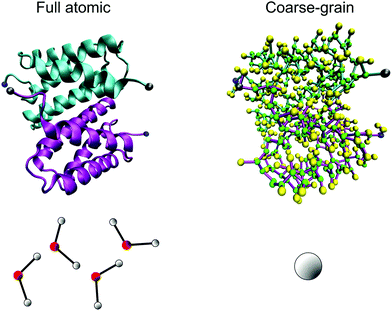Fig. 3 Coarse-grained representation of the N-terminal dimer model. By replacing the full atomistic representation (on left) of the protein and water with a residue-based bead model (on right, where several beads reflect one amino acid), much longer time-scales can be reached. In the coarse-grained model, the backbone is represented by a green bead and the side chain is represented by yellow beads. We highlight the N-terminal and C-terminal of each monomer by coloring them in blue and gray, respectively. Four water molecules are represented by a single bead in the coarse-grained model.

We equilibrate the coarse-grained model for 200 ns to ensure the structure is at equilibrium (convergence of RMSD as shown in Fig. S3† and potential energy as shown in Fig. S4 in the ESI†). Additionally, we monitor the fluctuations of the distance of each salt bridge as shown in Fig. 4a and b under non-salt conditions and salt conditions, respectively. During the longer sampling time for the non-salt conditions, all salt bridges have conserved lengths between 6 and 8 Å during the equilibration, as shown in Fig. 4a. However, these salt bridges under salt conditions behave significantly differently, as shown in Fig. 4b, especially SB2, SB3, and SB6, which fluctuate most significantly. We statistically summarize those results in Fig. 4c and find that all the salt bridges under salt conditions get longer than their counterparts under non-salt conditions; however, the extension is not as significant for SB1, SB4 and SB5. Moreover, SB1 and SB4 represent salt bridges with less fluctuation than all the others in the two solvent conditions, which agrees with the observation in full atomic simulations. It is noted that the distances for the salt bridges are much larger than the criterion we use in the full atomistic model (≤4 Å) because the coarse-grain scheme decreases the number of particles in the model, making the network sparser and thus leading to the increased salt bridge distance. A salt bridge of ∼4 Å in the full atomistic model yields to ∼8 Å once the model is converted to the coarse-grained form. We thereby increase the criterion to 8 Å to estimate the amount of time that each salt bridge is in effect, as shown in Fig. 4d, where it is seen that under salt conditions almost all charged residue pairs remain in equilibrium the majority of the time at a distance to each other that does not meet the criterion of a salt bridge.

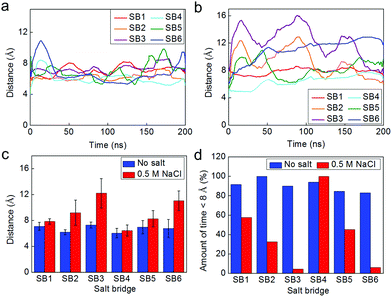Fig. 4 Fluctuation of the salt bridges within the dimer during the equilibrium at time-scales of hundreds of nanoseconds simulated by the coarse-grained model. Panel a/b: fluctuations of the distance between the mass center of the two amino acids involved in each of the salt bridge in non-salt condition (panel a) and for the solution with 0.5 M NaCl (panel b). Panel c: statistical result (average ± standard deviation) for the distance of each of the salt bridge during the 200 ns equilibrium. Panel d: amount of time the residue pair has been in an effective salt bridge state (<8 Å for the coarse-grained model).

It is interesting to note that the solvent effect on the distance of salt bridges has a pattern, as depicted in Fig. 4c and d (SB3 > SB2 > SB1 and SB6 > SB5 > SB4). We believe that this pattern can be explained by considering that the salt condition not only destabilizes each single salt bridge but also alters the overall conformation of the dimer, as illustrated in Fig. 5a. We establish an end-to-end vector in each monomer and measure the angle between the two in forming the dimer. This angle is initially the same for the dimer in both solvent conditions but deviates from its original value during equilibration. The angle of the dimer under salt solution becomes much smaller than the angle of the dimer in non-salt conditions, as shown in Fig. 5b. This difference is statistically significant during the last half of the equilibration process, as shown in Fig. 5c, which means the salt solution is quite effective at altering the conformation of the homodimer. Also, the fluctuation of the measured angle is higher for the salt condition. This result provides evidence that the dimer under salt conditions is free to move while the non-salt conditions lead to a fixed, more aligned position. Landreh et al.¹⁴ suggested a similar pH dependent mechanism where the dimer is able to rotate around the dimer interface at neutral pH (storing conditions) and undergoes an electrostatic locking after a pH-drop as present in the spinning duct.

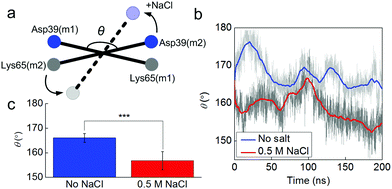Fig. 5 Fluctuations of the angle between two monomers in different solvent conditions. Panel a: schematic figure of the angle between the two monomers, which is measured by the angle θ between two vectors as Asp39(m1)–Lys65(m1) and Asp39(m2)–Lys65(m2). Panel b: fluctuations of the angle θ as a function of the simulation time. Panel c: average and standard deviation of θ for different solvent conditions between 100 and 200 ns in the simulation as shown. We use 10 ns as the window to average θ and then perform the t-test for the 10 datasets, the resultant t-value = 8.5 and P = 0.00001, which suggests that the effect of salt on the overall dimer conformation is highly significant.

We further test the effect of salt by stretching the dimer via the SMD method in both solvent conditions. This method is similar to the tapping mode for atomic force microscopy in avoiding any direct force that instantly breaks the structure, and is thus promising to reveal a relation between mechanical and microstructural properties of proteins.²⁵ The tensile tests, as shown in Fig. 6a, focus on the mechanical function of the N-terminal. They clearly show how strong the assembly of the two monomers is and how much energy is required to break the dimer. We apply force to the C-terminal of each monomer because it connects to the long MaSP strand that is subject to shear force during silk assembly. This test makes it clear how stable the two monomers are when they are subjected to force, which arises from the silk protein strands under shear deformation. The pulling rate in our simulation is 0.1 m s⁻¹, inspired by native spinning conditions. For instance, the vertical fall of a spider leads to a physiological spinning rate ranging from 0.05 to 1.30 m s⁻¹ (while the native spinning rate during web building can be lower, at ∼0.02 m s⁻¹).^27–29 The results summarized in Fig. 6 show how a dimer under tension responds differently in different solvents. It is shown in Fig. 6a that for both the cases two α-helices of each monomer unfold from the bundle before the complete breaking of the dimer. This corresponds to the first two major force peaks. The third force peak corresponds to the dimer breaking apart, as shown in Fig. 6b. It is noted that we only consider the major force peaks since the noisy peaks are caused by the oscillation of the spring applied in the SMD method to avoid large impact forces. Before breaking, there are more water molecules and ions observed at the interface of the dimer under salt conditions, yielding to the larger salt-bridge distance before breaking, as shown in Fig. 6d. The force for breaking apart of the dimer under salt conditions reaches 266 pN at a smaller extension level (415 Å versus 506 Å) and is 31.0% smaller than the breaking force obtained under non-salt conditions (383 pN). We extract the external energy applied to unfold the dimer by integrating the area below the force-extension curve, as shown in Fig. 6c. The difference between those two energies is 35.5%, which only applies to the final stage before the dimer breaks apart, indicating that the salt conditions destabilize the interaction at the interface between the two monomers. The average distance of the six salt bridges during stretching, as summarized in Fig. 6d, clearly shows that salt conditions increases the salt bridge distance during the entire pulling process, making this interaction between the two monomers more vulnerable to the external force (or thermal fluctuations). We also point out that the simulation focuses primarily on fundamental questions at the microscopic scale. We are exploring the application of coarser models to investigate silk assembly at the macroscopic level.

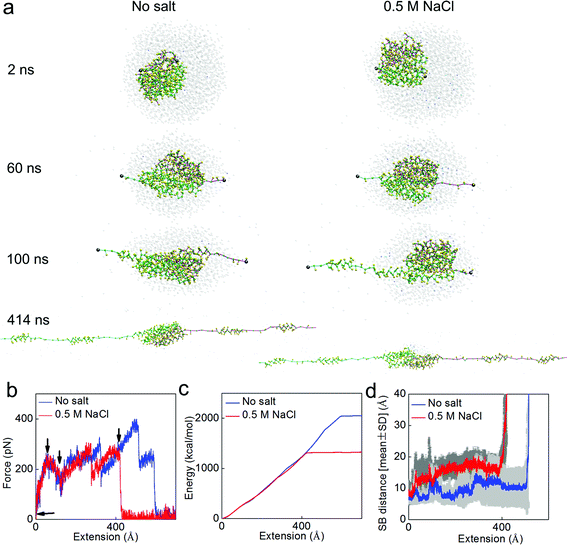Fig. 6 Simulation snapshots for the deformation and mechanical response analysis during pulling apart of the dimer. Panel a: simulation snapshots taken as the applied extension is increased up to 400 Å. Panel b: force–extension curve of the dimer under stretching with a rate of 0.1 m s⁻¹. Each of the arrows in this panel points to places where the corresponding snapshot in Panel a is taken. Panel c: external energy applied to break the structure as a function of the extension, as the amount of area integrated below the force–extension curve. Panel d: the statistic result (average ± standard deviation for every 20 ps) of the distances of all the salt bridges (SB1–SB6) during the extension process. It is noted that the salt conditions make the dimer easier to break apart by breaking the salt bridges.

Finally, we carry out well-tempered metadynamics simulations for the full atomistic model to elucidate how a change in the salt conditions leads to a decrease in the strength of the salt bridge. Metadynamics allows us to sample a much longer time-scale than would be accessible with standard molecular dynamics. We focus on the interaction strength of SB1, as shown in Fig. 7a because it is shown to be the most relevant salt bridge at the interface to connect the two monomers within the dimer (Fig. 2 and 4). The free energy landscape as a function of the distance of SB1 is computed, and we find that the depth of the energy well keeps increasing as more bias potentials are added and it converges to the actual free-energy landscape before the end of the simulation (as shown in Fig. S2†). We compare the free-energy results obtained in different solvent conditions. It is shown in Fig. 7b that for high salt conditions, the initial structure is trapped in a local minimum at 4 Å, while the global energy minimum is shifted to a distance at around 5 Å. This increased distance is not counted as a salt bridge anymore, which explains the reason we obtain fewer salt bridges in the salt condition. Moreover, the height of the energy barrier for SB1 under salt conditions to cross before breaking apart is 10 kcal mol⁻¹, which is 28.6% smaller than the energy barrier obtained for non-salt conditions. This energy difference agrees well with the difference in the tensile force and external energy to unfold the entire dimer (as discussed above). This salt bridge interaction is much larger than the van der Waals interaction (∼1 kcal mol⁻¹) but much smaller than the covalent bond (∼60 kcal mol⁻¹) and a little stronger than the hydrogen bond (9 kcal mol⁻¹). This explains why this interaction can affect the overall conformation of the dimer and act as a reversible switch to prevent or facilitate the assembly of spider silks. We believe that sodium chloride shields the electrostatic interactions between charged residues and thereby inhibits the formation of intermolecular salt bridges. Further investigation of additional collective variables would lead to a clearer picture of the free energy landscape between the charged residues at the dimer interface. Especially the inclusion of other charged residues that might have an effect on the residues of SB1 (Lys65 and Asp40) would be interesting. A likely candidate is the proximate Asp39 residue, as well as the Glu84 residue from the same subunit that is believed to form a “handshake interaction” with Asp40.¹¹

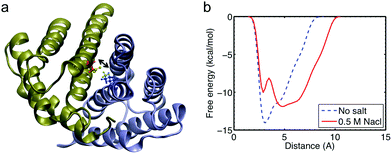Fig. 7 The salt bridge pair SB1 Lys65(m1)–Asp40(m2), analysis with more detail. Panel a: visualization of the N-terminal domain with pertaining residues in more detail. The biased variable is the distance between NH₃ of Lys65 and COO of Asp40 that is depicted in green. Panel b: free energy profile of the distance between Lys65(monomer 1) and Asp40(monomer 2) with and without sodium chloride.

The energy landscape revealed by well-tempered metadynamics simulation in explicit solvent conditions provides an accurate description of how a single salt bridge at the interface between two monomers reacts toward the state with lower free energy. The initial structure in salt conditions is trapped at a merely local energy minimum, as shown in Fig. 7b, while the global energy minimum is reached at a longer distance between monomers. This fundamental mechanism causes the conformation change in the dimer, as illustrated in Fig. 5. The existence of the energy barrier (∼1.5 kcal mol⁻¹) between the initial state and the state with a lower free energy and longer distance explains the difficulty of observing overall conformation change in classic molecular dynamics simulations with the full atomistic model for several tens of nanoseconds. The time span to observe an overall structure change can be theoretically estimated by τ₀exp[ΔG/(k_BT)], based on the Bell model,³⁰ where τ₀ ≈ 0.1 ps is the reciprocal of a natural frequency of solids, ΔG = 6 × 1.5 kcal mol⁻¹ is the total energy to cross for overall conformation change, k_B represents the Boltzmann constant and T = 300 K is the sampling temperature. It shows that at least 300 ns are necessary for an overall conformation change. This explains why the overall structure change can only be observed in the simulation with the coarse-grained model over a long time duration.

Our results demonstrate that an increased concentration of sodium chloride is important in destabilizing the homodimer. This confirms the experimental results that with a higher salt concentration, the shift from monomeric state to the dimer state takes place at lower pH values. This has been seen in pull-down experiments¹⁵ and electrospray-ionization mass spectrometry experiments.¹⁴ Divalent cations were found to destabilize the dimer state even further.¹⁵ This effect is in contrast to the role that ions play to build a bridge to crosslink protein molecules. For example, the calcium and magnesium ions (2⁺) in vimentin crosslink the tail domain and make the protein network more stable;³¹ ferric ions (3⁺) can stabilize many polymers into a highly crosslinked form.³² While other fibrillar molecules such as collagen and hard keratin provide strong intermolecular bonding through disulfide bonds,^33,34 dragline silk strands also form disulfide bonds at the C-terminal,¹² but feature tunable bonding at the N-terminal controlled by the chemical and mechanical environment during the spinning process. This makes a reorientation of strands at the beginning of the spinning process possible, and might prevent premature assembly.

Conclusion

In this study, we modeled the dimer of the spider silk N-terminal domain in explicit solvent with different salt conditions. We use both an atomistic model and a coarse-grained model to understand the effect of salt on mechanical stability and the associated underlying molecular mechanisms from different perspectives. Recent experimental evidence has shown that a lower salt concentration facilitates the formation of the dimers, whereas higher salt concentration favors formation of the monomers.^13–15 These findings could be explained with the decreasing salt bridge strength for higher salt concentration. Furthermore, we detect a conformational change upon increasing ionic strength. This allows the monomers to rotate freely; an effect that also has been experimentally found to be linked to the pH.¹⁴ Our result implies that the interaction between the two monomers is tunable by altering the salt concentration. The crucial point for understanding silk fiber formation is that MaSp, which mainly consists of repetitive poly-Ala-rich and Gly-rich segments, quickly aggregates when passing the spinning duct without prior aggregation in the gland (which would be fatal for a spider). Here, our study confirms that salt concentration is an important issue that strongly affects the physiological function of the solvent during the assembly process of spider silk fibers, together with the pH-value, as suggested in earlier works.^11,13–16 The understanding of these key mechanisms may help us improve synthetic silk spinning processes, which have not yet been able to fully mimic the remarkable material properties of natural silk. Often, the protein concentration used in synthetic approaches has to be significantly lower than seen in nature, owing to solubility problems. This and other related issues might partly explain the differences found when comparing synthetic silk to natural spider silk.^35,36 Some recently reported spinning devices are capable of mimicking the pH-drop^35,36 and changes in ion concentrations,³⁶ and point in the right direction of including appropriate solvent conditions in the synthetic spinning process. The insights reported here may help to improve the design of these processes, based on a close integration of experiment and modeling.³⁷

Acknowledgements

We acknowledge support from NIH (NIH/U01 EB014976), NSF (CMMI-0642545), AFOSR (FA9550-11-1-0199) and ONR (N000141010562), as well as the German National Academic Foundation (Studienstiftung des deutschen Volkes) (G. G.) and Dr Jürgen-Ulderup-Foundation (G. G.).

References

1. I. Agnarsson, M. Kuntner and T. A. Blackledge, Bioprospecting finds the toughest biological material: extraordinary silk from a giant riverine orb spider, PLoS ONE, 2010, 5(9), e11234.
2. F. G. Omenetto and D. L. Kaplan, New Opportunities for an Ancient Material, Science, 2010, 329(5991), 528–531.
3. S. Keten and M. J. Buehler, Geometric confinement governs the rupture strength of H-bond assemblies at a critical length scale, Nano Lett., 2008, 8(2), 743–748.
4. Z. Qin and M. J. Buehler, Cooperative deformation of hydrogen bonds in beta-strands and beta-sheet nanocrystals, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82(6), 061906.
5. C. Holland, F. Vollrath, A. J. Ryan and O. O. Mykhaylyk, Silk and synthetic polymers: reconciling 100 degrees of separation, Adv. Mater., 2012, 24(1), 105–109.
6. L. Eisoldt, C. Thamm and T. Scheibel, Review the role of terminal domains during storage and assembly of spider silk proteins, Biopolymers, 2012, 97(6), 355–361.
7. M. Hedhammar, A. Rising, S. Grip, A. S. Martinez, K. Nordling, C. Casals, M. Stark and J. Johansson, Structural properties of recombinant nonrepetitive and repetitive parts of major ampullate spidroin 1 from euprosthenops australis: implications for fiber formation, Biochemistry, 2008, 47(11), 3407–3417.
8. X. Chen, D. P. Knight and F. Vollrath, Rheological characterization of Nephila spidroin solution, Biomacromolecules, 2002, 3(4), 644–648.
9. D. P. Knight and F. Vollrath, Changes in element composition along the spinning duct in a Nephila spider, Naturwissenschaften, 2001, 88(4), 179–182.
10. C. W. P. Foo, E. Bini, J. Hensman, D. P. Knight, R. V. Lewis and D. L. Kaplan, Role of pH and charge on silk protein assembly in insects and spiders, Appl. Phys. A: Mater. Sci. Process., 2006, 82(2), 223–233.
11. G. Askarieh, M. Hedhammar, K. Nordling, A. Saenz, C. Casals, A. Rising, J. Johansson and S. D. Knight, Self-assembly of spider silk proteins is controlled by a pH-sensitive relay, Nature, 2010, 465(7295), 236–238.
12. F. Hagn, L. Eisoldt, J. G. Hardy, C. Vendrely, M. Coles, T. Scheibel and H. Kessler, A conserved spider silk domain acts as a molecular switch that controls fibre assembly, Nature, 2010, 465(7295), 239–242.
13. F. Hagn, C. Thamm, T. Scheibel and H. Kessler, pH-Dependent dimerization and salt-dependent stabilization of the N-terminal domain of spider dragline silk-implications for fiber formation, Angew. Chem., Int. Ed., 2011, 50(1), 310–313.
14. M. Landreh, G. Askarieh, K. Nordling, M. Hedhammar, A. Rising, C. Casals, J. Astorga-Wells, G. Alvelius, S. D. Knight, J. Johansson, H. Jornvall and T. Bergman, A pH-dependent dimer lock in spider silk protein, J. Mol. Biol., 2010, 404(2), 328–336.
15. W. A. Gaines, M. G. Sehorn and W. R. Marcotte, Spidroin N-terminal domain promotes a pH-dependent association of silk proteins during self-assembly, J. Biol. Chem., 2010, 285(52), 40745–40753.
16. J. A. Wallace and J. K. Shen, Unraveling a trap-and-trigger mechanism in the pH-sensitive self-assembly of spider silk proteins, J. Phys. Chem. Lett., 2012, 3(5), 658–662.
17. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79(2), 926–935.
18. A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, All-atom empirical potential for molecular modeling and dynamics studies of proteins, J. Phys. Chem. B, 1998, 102(18), 3586–3616.
19. M. T. Nelson, W. Humphrey, A. Gursoy, A. Dalke, L. V. Kale, R. D. Skeel and K. Schulten, NAMD: a parallel, object oriented molecular dynamics program, Int. J. High Perform. Comput. Appl., 1996, 10(4), 251–268.
20. D. J. Barlow and J. M. Thornton, Ion-pairs in proteins, J. Mol. Biol., 1983, 168(4), 867–885.
21. A. Barducci, G. Bussi and M. Parrinello, Well-tempered metadynamics: a smoothly converging and tunable free-energy method, Phys. Rev. Lett., 2008, 100(2), 020603.
22. M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, PLUMED: a portable plugin for free-energy calculations with molecular dynamics, Comput. Phys. Commun., 2009, 180(10), 1961–1972.
23. L. Monticelli, S. K. Kandasamy, X. Periole, R. G. Larson, D. P. Tieleman and S. J. Marrink, The MARTINI coarse-grained force field: extension to proteins, J. Chem. Theory Comput., 2008, 4(5), 819–834.
24. Z. Qin, L. Kreplak and M. J. Buehler, Hierarchical structure controls nanomechanical properties of vimentin intermediate filaments, PLoS ONE, 2009, 4(10), e7294.
25. M. Sotomayor and K. Schulten, Single-molecule experiments in vitro and in silico, Science, 2007, 316(5828), 1144–1148.
26. K. Jaudzems, G. Askarieh, M. Landreh, K. Nordling, M. Hedhammar, H. Jörnvall, A. Rising, S. D. Knight and J. Johansson, pH-Dependent dimerization of spider silk N-terminal domain requires relocation of a wedged tryptophan side chain, J. Mol. Biol., 2012, 422(4), 477–487.
27. D. N. Breslauer, L. P. Lee and S. J. Muller, Simulation of flow in the silk gland, Biomacromolecules, 2009, 10(1), 49–57.
28. C. S. Ortlepp and J. M. Gosline, Consequences of forced silking, Biomacromolecules, 2004, 5(3), 727–731.
29. F. Vollrath, B. Madsen and Z. Z. Shao, The effect of spinning conditions on the mechanics of a spider's dragline silk, Proc. R. Soc. London, Ser. B, 2001, 268(1483), 2339–2346.
30. G. I. Bell, Models for the specific adhesion of cells to cells, Science, 1978, 200(4342), 618–627.
31. Y. C. Lin, C. P. Broedersz, A. C. Rowat, T. Wedig, H. Herrmann, F. C. MacKintosh and D. A. Weitz, Divalent cations crosslink vimentin intermediate filament tail domains to regulate network mechanics, J. Mol. Biol., 2010, 399(4), 637–644.
32. M. J. Harrington, A. Masic, N. Holten-Andersen, J. H. Waite and P. Fratzl, Iron-clad fibers: a metal-based biological strategy for hard flexible coatings, Science, 2010, 328(5975), 216–220.
33. S. Keten, C. C. Chou, A. C. T. van Duin and M. J. Buehler, Tunable nanomechanics of protein disulfide bonds in redox microenvironments, J. Mech. Behav. Biomed. Mater., 2012, 5(1), 32–40.
34. M. J. Buehler, Nature designs tough collagen: explaining the nanostructure of collagen fibrils, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(33), 12285–12290.
35. M. E. Kinahan, E. Filippidi, S. Koster, X. Hu, H. M. Evans, T. Pfohl, D. L. Kaplan and J. Wong, Tunable silk: using microfluidics to fabricate silk fibers with controllable properties, Biomacromolecules, 2011, 12(5), 1504–1511.
36. S. Rammensee, U. Slotta, T. Scheibel and A. R. Bausch, Assembly mechanism of recombinant spider silk proteins, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(18), 6590–6595.
37. J. Y. Wong, J. McDonald, M. Taylor-Pinney, D. I. Spivak, D. L. Kaplan and M. J. Buehler, Materials by design: merging proteins and music, Nano Today, 2012, 7(6), 488–495.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2bm00140c

‡ These authors contributed equally to this work.

---