Retention in continuous two-dimensional thermal field-flow fractionation: comparison of experimental results with theory
Pertti
Vastamäki
*ad,
P. Stephen
Williams
b,
Matti
Jussila
a,
Michel
Martin
c and
Marja-Liisa
Riekkola
a
aLaboratory of Analytical Chemistry, Department of Chemistry, University of Helsinki, P.O. Box 55, FIN-00014, Finland. E-mail: pertti.vastamaki@vtt.fi; Fax: +358 20 722 4374
bCambrian Technologies Inc., 1772 Saratoga Avenue, Cleveland, OH 44109, USA
cÉcole Supérieure de Physique et de Chimie Industrielles, Laboratoire de Physique et Mécanique des Milieux Hétérogènes (PMMH, UMR 7636 CNRS, ESPCI-ParisTech, Université Pierre et Marie Curie, Université Paris-Diderot), 10 rue Vauquelin, 75231 Paris Cedex 05, France
dVTT Technical Research Centre of Finland, P.O.Box 1000, FIN-02044 VTT, Finland
First published on 8th October 2013
Abstract
A theoretical and experimental study of continuous two-dimensional thermal field-flow fractionation (2D-ThFFF) is presented. Separation takes place in radial flow between two closely spaced discs, one of which is heated and the other cooled in order to maintain a temperature gradient across the channel. The cooled disc, which serves as the accumulation wall, is rotated relative to the other to create a shear component to the fluid flow. Under the influence of the thermal gradient and flow components, the sample components spiral outwards along different paths to the outer rim of the channel to be collected. The general principle of operation is described and an approximate theoretical model formulated for predicting the outlet position for the path of each sample component. The influence of the principal operational parameters, such as radial and angular flow rates and thermal gradient, on the deflection angle of the sample trajectory is investigated. Fractionation is demonstrated for polystyrene polymer standards in a binary solvent consisting of cyclohexane and ethylbenzene. Experimental results are compared with theoretical predictions.
Introduction
Field-flow fractionation (FFF) is an elution technique for fractionation and characterization of macromolecular, colloidal, and particulate materials. Since 1966 when Giddings introduced the principle of FFF,1 the technique has matured into a family of different sub-techniques that are established nowadays as routine analytical tools for a wide range of industrial, biological, biomedical, and environmental applications.2–4 A common feature of almost all the FFF techniques is a non-uniform laminar eluent fluid flow in a thin channel, across which a field is applied perpendicular to the direction of flow. The applied field drives dissolved polymer molecules or suspended particles toward one of the channel walls. The increase in the concentration of the analytes close to the wall is opposed by ordinary diffusion, with the result that steady state distributions are established. Depending on the physicochemical properties of the sample components and their interactions with the field, analytes of different molecular masses or particle sizes establish steady state distributions of different thicknesses adjacent to the wall. These steady state distributions are dynamic, in that polymer molecules or particles constantly exchange positions within the zone thickness. The molecules in a thin zone will therefore sample slow fluid velocities close to the wall while those in a thicker zone will sample faster fluid velocities as well as those close to the wall. The sample components are consequently eluted along the channel with velocities dependent on their zone thicknesses.5The common fields employed in FFF are gravitation and centrifugation (together being referred to as sedimentation), displacement by a cross-channel flow component, thermal gradient, and electrical and magnetic fields. FFF, as it was conceived1 and generally still implemented, is a batchwise analytical and characterization technique. The mechanism does not lend itself to larger samples (greater than, say, 50 or 100 μL), and FFF in its conventional form is not suitable for preparative separations. The same may be said of other separation techniques, such as chromatography and electrophoresis. There has been some success in simply up-scaling liquid chromatographic separations, of course, but approaches have also been developed to adapt these techniques for continuous operation, as described below. In the present work we present an adaptation of thermal FFF for continuous operation.
Continuous two-dimensional separations
There have been many examples of continuous, two-dimensional separations described in the literature. Wankat6,7 described the relationship between one-dimensional, time-dependent separations and two-dimensional, steady state (continuous) separations. The continuous two-dimensional separations usually involve a selective displacement of sample components in one direction and a non-selective displacement in an orthogonal direction. Giddings8,9 pointed out that the second displacement need not be non-selective, but it is necessary that a second, selective displacement must not be strongly correlated with the first. In fact, it is necessary only that the two selective displacements have sufficiently different selectivities.Different kinds of continuous separation methods have been developed. Examples of continuous electrophoresis methods are continuous two-dimensional electrophoresis,10 and continuous free-flow electrophoresis.11 Continuous separation is achieved in the dipole magnetic fractionator (DMF)12–14 using a field-flow configuration identical to that of continuous free-flow electrophoresis. Turina et al.15 described a continuous two-dimensional gas–liquid chromatographic apparatus, but only preliminary experiments were carried out. Giddings16 described in theory a continuous annular gas chromatograph. Sussman and co-workers17–19 have developed an approach to continuous two-dimensional gas chromatography using radial flow between two closely spaced glass plates. The method was referred to as continuous disc chromatography or continuous surface chromatography. Continuous two-dimensional liquid chromatographic separations have been carried out in annular packed columns.20–22 Another important implementation of continuous two-dimensional separation is that of split-flow thin channel (SPLITT) fractionation, invented by Giddings,23 and developed further with several designs.24–26
Continuous two-dimensional FFF
Giddings27 considered the various possible configurations for incorporation of FFF into two-dimensional separations, including those that may be operated in continuous mode. He pointed out that, for continuous operation, FFF methods may be combined with a field-induced displacement perpendicular to the FFF displacement, as in the case of the continuous steric FFF,28,29 where the selectivities of the longitudinal migration (steric FFF) and the lateral migration (sedimentation) are different. He also mentioned that the combination of normal mode sedimentation FFF with transverse sedimentation, which could be implemented using a sedimentation FFF channel tilted with respect to the axis of rotation, should exhibit a selectivity of 5 with respect to particle diameter and a selectivity of 2 with respect to density difference between particles and carrier fluid. Ivory et al.30 assembled a similar two-dimensional sedimentation FFF device. They constructed a channel that had a wedge-shaped cross-section. However, experiments using a clear Plexiglas channel and dye injection showed convective instabilities at only 200 rpm that they attributed to Coriolis effects coupled with flow. They suggested that these instabilities might be eliminated by reducing channel thickness, increasing flow velocity, and restricting rotation rate. They concluded that further studies were necessary.Giddings27 also pointed out that continuous two-dimensional FFF could be achieved by combining FFF with either a bulk displacement or a flow displacement perpendicular to the FFF displacement. In order to realize selective deflection for continuous fractionation using a flow at right angles to the FFF displacement, it would be required that the flow profiles in the two directions are different (for example, Poiseuille and electro-osmotic flows). He suggested that if FFF was carried out in an annular channel (with a radial field), then continuous operation could be achieved by rotation of the channel as in continuous annular chromatography. He also suggested that continuous FFF could be carried out using radial flow between rotating discs. This is the same configuration as rotating disc chromatography. A rotating disc gravitational FFF was constructed in the Giddings laboratory with separation to be carried out in the steric mode. The operation of the system was not successful. It is possible that secondary flow patterns may have interfered with separation in this device also. It would probably be advantageous to have a stationary channel, and rotate the sample inlet port and the outlet ports around the channel.
Continuous two-dimensional thermal FFF
Continuous two-dimensional thermal field-flow fractionation (2D-ThFFF) is a relatively new technique for continuous fractionation of macromolecules and particles. In our previous publications31,32 we introduced the general concept of the method and included preliminary results of its application to continuous fractionation of polystyrene samples according to their molecular masses. In addition, retention was shown to be dependent on field strength and flow conditions of the carrier in two dimensions.32The system is similar in some aspects to those of continuous disc chromatography17–19 and rotating disc gravitational FFF.27 The carrier stream flows from a central inlet in the heated upper wall to 23 outlets spaced at equal intervals around the perimeter of the disc-shaped channel. Collection syringes are installed at the channel outlets and the flow maintained by suction at the syringes. The carrier reservoir supplying the central inlet is pressurized to reduce the tendency for bubble formation. In addition to a parabolic flow profile established in the radial direction, a shear-driven flow component is generated in the angular direction by slowly rotating the cooled lower channel wall. A continuous sample stream is introduced at a second inlet in the upper wall at a point close to the center of the channel. The sample components are subjected to two orthogonal displacement mechanisms: selective field-flow fractionation in the radial direction, and a flow displacement in the angular direction that has a relatively small selectivity, provided it is the accumulation wall that rotates. The combination of these simultaneously acting mechanisms underlies the two-dimensional continuous fractionation.8,27,33 The sample components are separated by these two displacements into continuous filaments that strike off at different angles over the 2D surface. The separated components are then collected at different locations around the perimeter of the channel. The superposition of shear flow onto the radial flow may help to suppress secondary flow disturbances, but this aspect is yet to be explored.
Theoretical equations have been formulated to examine the capability of the new method for analytical and preparative applications. These will aid in the selection of experimental conditions for optimal performance. A full theoretical treatment would be capable of predicting the deflection of a sample component trajectory and its lateral dispersion to each side of its path. Such a full theoretical characterization of the 2D-ThFFF operation will be required for further development of instrument configuration, channel structure, and operative practice. Our previous experimental work,33 where the 2D-ThFFF system was shown capable of almost baseline continuous fractionation of two standard polymers of different molar masses, will support these further developments. The starting point for the theoretical model is presented in this paper and predicts the paths and outlet positions for sample components. The theory is based on that of thermal field-flow fractionation,34–37 and classical fluid dynamics assumptions. The objective of this study was to formulate these basic theoretical equations and to examine the agreement between theory and experiment by introducing polystyrene standards of different molar masses and of narrow molar mass distribution.
Theory
An approximate theoretical model for predicting the trajectory of a sample component zone, and angular displacement of its elution point from the initial point of introduction is derived below. The model is based on the following assumptions:(1) The radial fluid velocity profile is assumed to be parabolic. The small departure from the parabolic profile, caused by variation of viscosity with temperature across the channel thickness, can easily be taken into account by using the corrected equation for retention ratio already developed.38
(2) It is assumed that there is a simple shear flow in the angular direction. (Variation in viscosity will also influence the flow profile in the angular direction.)
(3) The concentration profile for each sample component is assumed to be exponential across the channel thickness.
(4) The sample flow rate is assumed to be negligibly small in comparison to the radial carrier flow rate.
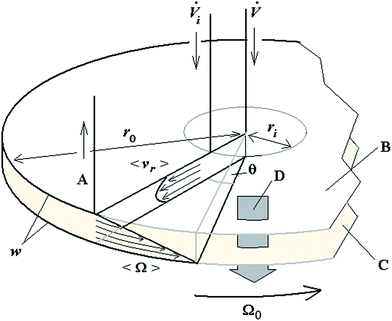
A schematic of the 2D-ThFFF system, along with the flow components and geometrical parameters, is illustrated in Fig. 1.
Derivation for retained components
Given these assumptions, the mean radial fluid velocity component 〈vr〉 as a function of radial distance r from the axis is given by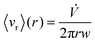 | (1) |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) is the total carrier flow rate and w the channel thickness. The average rate at which a retained zone changes its radial position is then given by
is the total carrier flow rate and w the channel thickness. The average rate at which a retained zone changes its radial position is then given by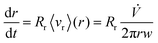 | (2) |
| Rr = 6λ(coth(1/2λ) − 2λ) ≈ 6λ(1 − 2λ) | (3) |
For λ of 0.170, the accurate expression for Rr yields a value of 0.679, corresponding to rather poor retention, yet the approximate expression on the right of eqn (3) gives a result of 0.673. The error is less than 0.9% at this point, and falls rapidly with reduction of λ.
Similarly, the rate at which a retained zone changes its angular position is
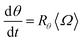 | (4) |
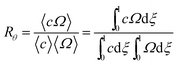 | (5) |
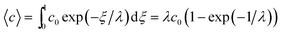 | (6) |
The angular velocity profile is given as
| Ω = Ω0(1 − ξ) | (7) |
| Ω = Ω0ξ | (8) |
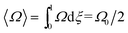 | (9) |
The respective equations for Ω (eqn (7) and (8)) are substituted into the equation
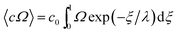 | (10) |
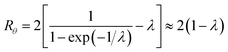 | (11) |
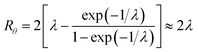 | (12) |
At the retention level considered in relation to eqn (3), where λ = 0.170, the accurate Rθ given by eqn (11) is 1.666, and the approximate form of the equation is in error by less than 0.4%. At the same level of retention, the approximate form of eqn (12) is in error by almost 1.7%.
Note that Rθ approaches a constant value of 2 at high retention, if the accumulation wall rotates. This is consistent with the requirement that orthogonal selectivities differ. The angular selectivity in this case approaches zero, and rotational migration is non-selective. This is not the case for a static accumulation wall. Angular selectivity for a static accumulation wall approaches that for radial migration, so that overall selectivity approaches zero and no separation is possible.
Dividing eqn (2) by eqn (4) gives, with eqn (9)
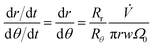 | (13) |
The zone trajectory is given by rearranging eqn (13) and integrating from the initial radial distance ri and zero angle to radial distance r at angle θ:
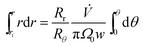 | (14) |
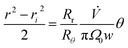 | (15) |
The final angle θr at the time of elution tr is given by
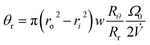 | (16) |
We can replace π(ro2 – ri2)w by the effective void volume of the channel V0, and write eqn (16) in the form
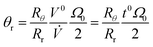 | (17) |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) .
.
Derivation for non-retained components
The non-retained elution angle, θ0, is obtained by setting Rr = Rθ = 1 in eqn (17)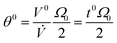 | (18) |
Hence, the θr/θ0 ratio is equal to Rθ/Rr, and using the high retention limits for these retention ratios we obtain for a rotating accumulation wall:
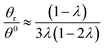 | (19) |
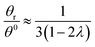 | (20) |
At λ = 0.170, eqn (19) is in error by just over 0.5%; it predicts a ratio of 2.466 as opposed to the true ratio of 2.453. At the same level of retention, eqn (20) predicts a ratio of 0.505 while the true ratio is 0.493; the error is 2.5%.
It is interesting to note that the elution angle is larger than the non-retained elution angle if accumulation occurs at the rotating wall while it is smaller for a static accumulation wall. This provides a means to determine the status of this accumulation wall, and hence the sign of the Soret coefficient (at least, when θr is smaller than 2π). Furthermore, for a rotating accumulation wall, the selectivity with respect to λ is given by
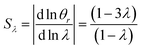 | (21) |
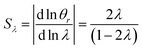 | (22) |
The selectivity for a rotating accumulation wall approaches unity for strong retention, whereas selectivity approaches zero for a stationary accumulation wall. It is therefore obvious that the accumulation wall must rotate with respect to the sample introduction port and the collection ports if a separation is to be achieved.
Experimental
Continuous 2D-ThFFF instrumentation
The continuous 2D-ThFFF instrument, presented in detail previously,31 consisted of an in-house constructed fractionation channel, a microflow pump (Micro Feeder Model MF-2, Azumadenki Kogyo, Tokyo, Japan) with an HPLC syringe of 500 μL for sample introduction, an electrically driven fraction collection unit, an electric motor for rotating the lower (cold) channel wall, and an electric heating cartridge (max. 700 W) installed into the upper wall. The diameter of the disk-shaped fractionation space was 135 mm. The carrier was introduced at the center of the channel and the sample at a port located 17 mm from the center. Fractions were collected at 23 collection ports equally spaced around the circumference of the channel. A channel thickness of 125 μm was selected as it was previously observed that larger thicknesses gave rise to greater broadening.32 Rotation speeds of the accumulation wall of 0.016, 0.024, 0.032, and 0.040 rpm were used. The carrier flow rate was 9.6 or 12.0 μL min−1 at each outlet, corresponding to a total flow rate of 221 or 276 μL min−1, respectively. The sample introduction flow rate was either 1.25 or 2.50 μL min−1, the latter being used at a higher ΔT and faster rotation rates. This was to ensure the collection of sufficient sample for determination of the relative concentration by conventional ThFFF at a higher number of collection ports. It was previously found that the sample introduction rate did not significantly affect the band broadening.32 Experiments were performed without a temperature gradient, ΔT = 0 K, and with ΔT values between 10 K and 21 K across the channel. A ΔT value of 21 K represents the highest practical temperature gradient for the prototype instrument, when using a channel thickness of 125 μm. The cold wall temperature Tc was dependent on the flow rate and the temperature of the circulating tap water used for cooling the cold wall. For a ΔT value of 0 K, the instrument was operated at room temperature without cooling water circulating through the lower wall.Analytical ThFFF instrumentation
The conventional ThFFF system has been described in our earlier publication,31 and it was used to determine sample concentrations in each of the collected 2D-ThFFF fractions. The retention parameter λ for each polystyrene sample was predicted from the data processed during our previous work.32 The ThFFF system consisted of an HPLC pump (PU-2080; Jasco Corp., Tokyo, Japan), a UV detector (SP8450; Spectra Physics Inc., San Jose, CA, USA) with a detection wavelength of 254 nm, two valves for injection and bypass (C6W: Valco Instrument Co., Inc., Houston, USA), and an in-house constructed ThFFF channel (45 cm × 2 cm × 125 μm). The injection volume was 10 μL and the flow rate of the carrier 150 μL min−1. Various thermal gradients ΔT across the channel thickness were used. For determination of λ vs. 1/ΔT plots for each polymer, ΔT values varied between 16 K and 70 K, depending on the sample. For determination of PS concentrations in each collected fraction, ΔT value was 80 K for the sample PS 51k, 25 K for PS 520k, and 15 K for PS 1000k, respectively.Reagents
Three polymer samples were used for determining the elution angles at the circumference of the channel. The samples were polystyrene standards PS 51k, PS 520k, and PS 1000k with molar masses Mw of 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da (Waters Associates, Framingham, MA, USA), 520
000 Da (Waters Associates, Framingham, MA, USA), 520![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da (Polymer Laboratories Ltd, UK), and 1
000 Da (Polymer Laboratories Ltd, UK), and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da (Polymer Laboratories Ltd, UK). Polydispersities of the standards were 1.03 (PS 51k), 1.05 (PS 520k), and 1.03 (PS 1000k), respectively. Concentrations in terms of % (w/w) of the continuously injected samples were 0.38% (PS 51k), 0.40% (PS 520k), and 0.41% (PS 1000k), respectively. For the mixture of two samples, PS 51k and PS 1000k, the concentrations were 0.41% and 0.45%, respectively. A binary solvent consisting of 75% analytical-grade cyclohexane (Merck KGaS, Darmstadt, Germany) and 25% reagent-grade ethyl benzene (Sigma-Aldrich GmbH, Steinheim, Germany) was used as a carrier for the continuous 2D-ThFFF runs. HPLC-grade tetrahydrofuran (Labscan Ltd, Dublin, Ireland) was used as the carrier fluid in the analytical ThFFF channel. The sample molar masses were selected for the study based on their sufficiently good solubility and sufficiently high retention under the applied temperature gradients.
000 Da (Polymer Laboratories Ltd, UK). Polydispersities of the standards were 1.03 (PS 51k), 1.05 (PS 520k), and 1.03 (PS 1000k), respectively. Concentrations in terms of % (w/w) of the continuously injected samples were 0.38% (PS 51k), 0.40% (PS 520k), and 0.41% (PS 1000k), respectively. For the mixture of two samples, PS 51k and PS 1000k, the concentrations were 0.41% and 0.45%, respectively. A binary solvent consisting of 75% analytical-grade cyclohexane (Merck KGaS, Darmstadt, Germany) and 25% reagent-grade ethyl benzene (Sigma-Aldrich GmbH, Steinheim, Germany) was used as a carrier for the continuous 2D-ThFFF runs. HPLC-grade tetrahydrofuran (Labscan Ltd, Dublin, Ireland) was used as the carrier fluid in the analytical ThFFF channel. The sample molar masses were selected for the study based on their sufficiently good solubility and sufficiently high retention under the applied temperature gradients.
Continuous fractionation procedure
Before continuous injection of the sample, all run conditions were properly adjusted and stabilized. The temperature gradient across the channel was measured regularly with two thermistors installed into the vicinity of the two wall surfaces. Because one wall was rotating, the relative positions of the two thermistors changed during the fractionation. For runs where a temperature gradient was applied, the temperature of each of the walls was measured, whereas when no gradient was applied, the room temperature was assumed to apply inside the channel. The temperatures were measured every 10 minutes to determine the mean thermal gradient for each run. The sample introduction was initiated only when steady state conditions were achieved.After the continuous 2D-ThFFF run, the collected samples from the syringes, containing equal amounts of the binary carrier, were transferred to test tubes and evaporated to dryness. A small amount of tetrahydrofuran (100 μL) was added to each test tube to dissolve the polymer fractions. The same solvent was used as a carrier in the analytical ThFFF instrument. Relative concentrations of the polymer in each fraction were calculated from the peak areas of the fractograms.
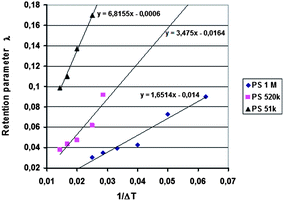
Runs were carried out using two different temperature gradients and also without a temperature gradient, and the outlet positions determined for the different samples. In addition, four rotation rates of the accumulation wall and two radial flow rates of the carrier were applied. Other run conditions were kept constant. The first series of the runs was performed without an applied temperature gradient for the determination of the outlet positions of a non-retained sample. The theoretical non-retained elution angles were calculated using eqn (18) and these were compared with the experimental results. The runs were repeated using an applied temperature gradient, and as previously, the elution angles for retained samples were determined. The predicted elution angles were calculated using eqn (17) with retention parameters λ predicted from the retention data obtained in our previous work using the analytical ThFFF instrument.32 The λ values were predicted using the plots of λ vs. 1/ΔT (see Fig. 2), and it was assumed that the thicknesses of the analytical and continuous FFF channels were identical.
Results and discussion
The results of the analytical ThFFF experiments are plotted in Fig. 2 in the form of λ versus 1/ΔT together with the linear regression fits to the data for each polymer standard.It was shown in our previous work that the 2D-ThFFF method is suitable for continuous fractionation of lipophilic polymers under the influence of a thermal gradient.31,32 In this study, new experimental results, together with some from our previous work, have been compared with predictions of the theoretical retention model described in the previous section. The method is rather complex due to the number of relevant parameters. In this work we have examined the influence of the molar mass of the sample, the angular rotation rate and radial flow rate of the carrier on the deflection of the sample zone. The parameters affecting deviations from the theory, such as angular broadening of the deflected sample zone, the effect of the temperature of the lower wall, and the lack of relaxation time, have also been discussed.
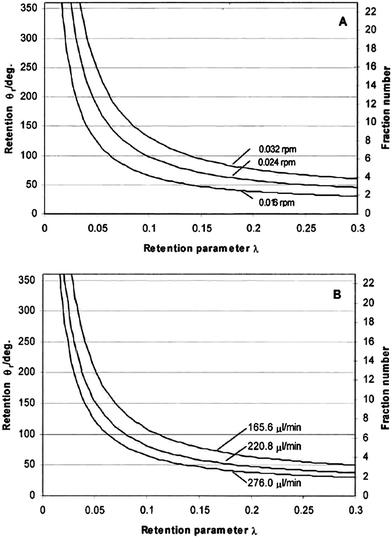
Fig. 3 shows the theoretically predicted (by eqn (3), (11) and (17)) dependence of elution angle (θr) on the dimensionless retention parameter λ, for (A) different rotation rates Ω0 of the accumulation wall at a fixed radial flow rate, and for (B) different radial flow rates ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) at a fixed rotation rate. It was assumed that the rotating cold wall was the accumulation wall, and therefore eqn (3), (11), and (17) were assumed to apply. From these curves it is clear that the elution angle is predicted to increase with decrease of λ or radial flow rate, or with increase of angular velocity of the cold wall. These findings are, in fact, in good agreement with the experimental results described below.
at a fixed rotation rate. It was assumed that the rotating cold wall was the accumulation wall, and therefore eqn (3), (11), and (17) were assumed to apply. From these curves it is clear that the elution angle is predicted to increase with decrease of λ or radial flow rate, or with increase of angular velocity of the cold wall. These findings are, in fact, in good agreement with the experimental results described below.
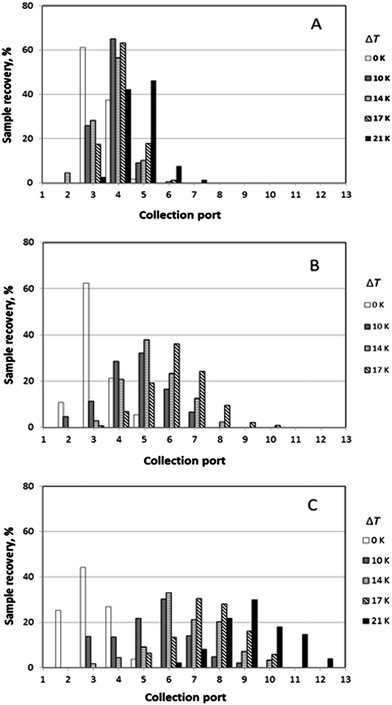
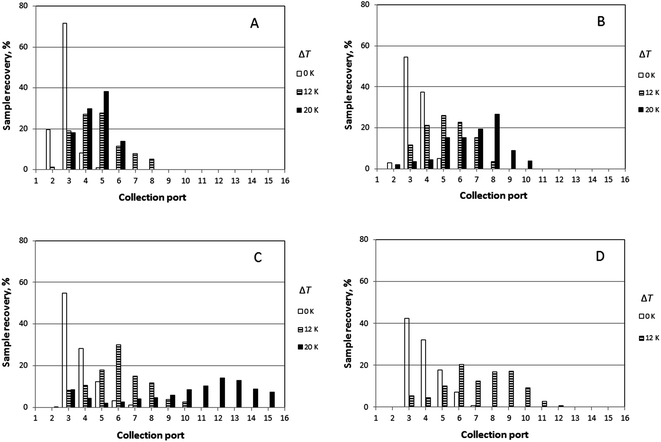
It was generally the case that a polymer sample was eluted over several collection ports at the channel periphery. The result of a given run can thus be reported by plotting the fractional recovery of the polymer collected at each port. Results obtained for a set of experiments performed using the three individual polystyrene samples under conditions of five different temperature gradients (0, 10, 14, 17 and 21 K) are shown in Fig. 4. A fixed carrier flow rate ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) of 221 μL min−1, and a fixed angular velocity of the accumulation wall Ω0 of 0.024 rpm were used in these experiments. In Fig. 4A–C the fractional recoveries of the polymers are plotted as functions of the different outlet port numbers. For each run, the mean elution angle is computed according to (360°/23)(Σ(i − 1) φi), where φi is the fractional recovery of the polymer collected at port i, port number 1 being aligned with the sample introduction port, the sum extending from i = 1 to i = 23, the number of ports. These mean angles are expressed as elution angles θr if a temperature gradient is applied and as θ0 if no gradient is applied. The theoretically predicted and the experimentally observed mean elution angles together with their percentage errors are listed in Table 1. The theoretically predicted elution angles were calculated by means of eqn (16) using the accurate forms of eqn (3) and (11) in all cases.
of 221 μL min−1, and a fixed angular velocity of the accumulation wall Ω0 of 0.024 rpm were used in these experiments. In Fig. 4A–C the fractional recoveries of the polymers are plotted as functions of the different outlet port numbers. For each run, the mean elution angle is computed according to (360°/23)(Σ(i − 1) φi), where φi is the fractional recovery of the polymer collected at port i, port number 1 being aligned with the sample introduction port, the sum extending from i = 1 to i = 23, the number of ports. These mean angles are expressed as elution angles θr if a temperature gradient is applied and as θ0 if no gradient is applied. The theoretically predicted and the experimentally observed mean elution angles together with their percentage errors are listed in Table 1. The theoretically predicted elution angles were calculated by means of eqn (16) using the accurate forms of eqn (3) and (11) in all cases.
| Sample | PS 51k | PS 520k | PS 1000k | |
|---|---|---|---|---|
| ΔT = 0 K | θ 0 (exp) | 38° | 36° | 33° |
| θ 0 (theory) | 32.8° | 32.8° | 32.8° | |
| % error | 15% | 11% | −0.3% | |
| θ 0/Ω0 min (exp) | 4.4 | 4.2 | 3.8 | |
| ΔT = 10 K | θ r (exp) | 44° | 57° | 69° |
| θ r (theory) | 42.0° | 54.1° | 87.9° | |
| % error | 5.6% | 5.3% | −22% | |
| θ r/θ0 (exp) | 1.2 | 1.6 | 2.1 | |
| θ r/θ0 (theory) | 1.3 | 1.6 | 2.7 | |
| ΔT = 14 K | θ r (exp) | 43° | 67° | 90° |
| θ r (theory) | 46.3° | 65.5° | 119° | |
| % error | −7.5% | 2.5% | −25% | |
| θ r/θ0 (exp) | 1.1 | 1.8 | 2.7 | |
| θ r/θ0 (theory) | 1.4 | 2.0 | 3.6 | |
| ΔT = 17 K | θ r (exp) | 47° | 81° | 100° |
| θ r (theory) | 49.8° | 75.0° | 145° | |
| % error | −4.9% | 8.1% | −30% | |
| θ r/θ0 (exp) | 1.3 | 2.2 | 3.1 | |
| θ r/θ0 (theory) | 1.5 | 2.3 | 4.4 | |
| ΔT = 21 K | θ r (exp) | 57° | — | 129° |
| θ r (theory) | 54.6° | 88.8° | 182° | |
| % error | 4.0% | — | −29% | |
| θ r/θ0 (exp) | 1.5 | — | 3.9 | |
| θ r/θ0 (theory) | 1.7 | 2.7 | 5.5 | |
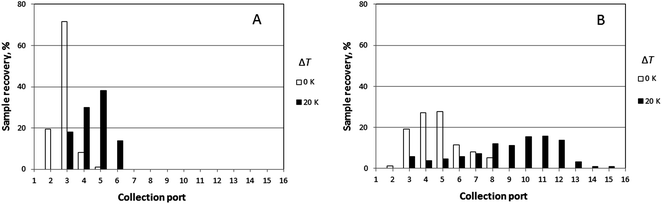
Experimental results obtained for the sample PS 1000k carried out at four different rotation rates (0.016, 0.024, 0.032, and 0.040 rpm) and three different temperature gradients (ΔT = 0, 12, and 20 K), and a fixed carrier flow rate (![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) = 276 μL min−1) are shown in Fig. 5. The results for the mean elution angles are reported in Table 2, again compared with theoretically predicted values.
= 276 μL min−1) are shown in Fig. 5. The results for the mean elution angles are reported in Table 2, again compared with theoretically predicted values.
| Ω 0 (rpm) | 0.016 | 0.024 | 0.032 | 0.040 | |
|---|---|---|---|---|---|
| ΔT = 0 K | θ 0 (exp) | 29° | 38° | 42° | 46° |
| θ 0 (theory) | 17.5° | 26.3° | 35.1° | 43.8° | |
| % error | 67% | 46% | 19% | 4.4% | |
| θ 0/Ω0 min (exp) | 5.1 | 4.4 | 3.6 | 3.2 | |
| ΔT = 12 K | θ r (exp) | 58° | 66° | 78° | 97° |
| θ r (theory) | 55.0° | 82.5° | 110° | 138° | |
| % error | 6% | −20% | −29% | −29% | |
| θ r/θ0 (exp) | 2.0 | 1.7 | 1.9 | 2.1 | |
| θ r/θ0 (theory) | 3.1 | 3.1 | 3.1 | 3.1 | |
| ΔT = 20 K | θ r (exp) | 55° | 90° | 144° | — |
| θ r (theory) | 92.0° | 138° | 184° | 230° | |
| % error | −41% | −35% | −22% | — | |
| θ r/θ0 (exp) | 1.9 | 2.3 | 3.4 | — | |
| θ r/θ0 (theory) | 5.2 | 5.2 | 5.2 | 5.2 |
Similarly, elution profiles for PS 1000k obtained at a fixed rotation rate (0.016 rpm), but at two different carrier flow rates (276 and 221 μL min−1) and two temperature gradients (ΔT = 0 and 20 K) are shown in Fig. 6. Experimentally observed mean elution angles are compared with theoretical predictions in Table 3.
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif)
|
(μL min−1) | 276 | 221 |
|---|---|---|---|
| ΔT = 0 K | θ 0 (exp) | 29° | 59° |
| θ 0 (theory) | 17.5° | 21.9° | |
| % error | 67% | 170% | |
| ΔT = 20 K | θ r (exp) | 55° | 124° |
| θ r (theory) | 92.0° | 115° | |
| % error | −41% | 8.0% | |
| θ r/θ0 (exp) | 1.9 | 2.1 | |
| θ r/θ0 (theory) | 5.2 | 5.2 |
Confirmation of accumulation wall
The lowest channel flow rate employed for the experimental results shown in Fig. 4–6 is 221 μL min−1. The channel void volume, calculated from the radius of the sample inlet point (17 mm from the center) to the periphery, is nominally 1.68 mL. It follows that the longest void time t0 may be calculated as 7.60 min. The highest retention time would be given by the sample of highest molecular mass (PS 1000k) run under conditions of the lowest flow rate and highest temperature gradient (ΔT = 21 K). The value for λ predicted for this 21 K-gradient is obtainable from Fig. 2, and is found to be 0.0646. The longest expected retention time tr is then calculated using eqn (3) for the corresponding Rr (= 0.338). The time, calculated as tr = t0/Rr, is therefore 22.5 min. The fastest rotation rate for the cold wall used in the experiments is 0.040 rpm, and 22.5 min is not sufficient time for a single, complete rotation. It can therefore be assumed that θr cannot exceed 2π for any of the experiments, whether the stationary hot or the rotating cold wall serves as the accumulation wall.The identity of the accumulation wall may be obtained from Fig. 4–6. Fig. 4, for example, shows that θr increases with increase of either ΔT or the molecular mass of the sample, and therefore, with decrease of λ. This is consistent with eqn (19) and inconsistent with eqn (20). It follows that the cold wall must serve as the accumulation wall. The increase of θr for PS 1000k with ΔT in Fig. 5 and 6 also indicates that the cold wall is the accumulation wall. In fact, if the accumulation wall was the stationary hot wall eqn (20) would predict θr to be smaller than θ0, which is not the case for any of the results shown in Fig. 4–6.
This observation indicates that the thermal diffusion-induced migration of polystyrene dissolved in a binary ethylbenzene–cyclohexane solvent mixture acts to drive molecules from warmer to colder regions, as has been observed for polystyrene in either pure ethylbenzene38 or pure tetrahydrofuran.39 A molecular theory of thermal diffusion in liquids has not yet been developed. Neither the values nor the signs of thermal diffusion coefficients may be predicted. Experimental determination of the coefficients is required, and continuous 2D-ThFFF appears to be a convenient alternative to existing methods for the investigation of the phenomenon.
Comparison of experimental results with theoretical predictions
When the field is applied, the experimental mean elution angles, θr(exp), are seen to be smaller than the theoretical values θr (theory) in almost all cases, the exception being for ΔT = 12 K and Ω0 = 0.016 rpm. As the temperature drop is increased from 0 K to 12 K, then to 20 K, whatever the rotation rate, the distribution of the polymer along the exit ports becomes wider and shifted toward larger port numbers, as expected for samples accumulating at the rotating wall. For ΔT = 12 K, the relative error between experimental and theoretical values of θr tends to increase with the rotation rate. For ΔT = 20 K, the relative error decreases with increasing rotation rate. The experimental θr/θ0 ratios are all smaller than the theoretical values. According to eqn (19), these values should only depend on λ and be equal to 3.1 and 5.2 for ΔT = 12 K and 20 K, respectively.
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) leads to an increase in the time spent in the channel and thus to an increased deflection induced by the rotation of one plate. Whatever the carrier flow rate, the experimental value of θ0 (exp) is larger than expected, the more so for the lower flow rate. However, while the experimental elution angle θr (exp) is lower than the theoretical angle when
leads to an increase in the time spent in the channel and thus to an increased deflection induced by the rotation of one plate. Whatever the carrier flow rate, the experimental value of θ0 (exp) is larger than expected, the more so for the lower flow rate. However, while the experimental elution angle θr (exp) is lower than the theoretical angle when ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) = 276 μL min−1, it is observed to be slightly larger than theoretically expected when
= 276 μL min−1, it is observed to be slightly larger than theoretically expected when ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) = 221 μL min−1. Still, for both flow rates, the experimental θr/θ0 ratio is seen to be smaller than theoretically expected.
= 221 μL min−1. Still, for both flow rates, the experimental θr/θ0 ratio is seen to be smaller than theoretically expected.
Additional effects not accounted for in the modeling
If the general qualitative trends observed in elution behavior when operational parameters are changed one by one are generally with the theoretical expectation, relatively significant quantitative differences are noticed between experimental and theoretical values. In order to unravel the origins of these differences, we discuss in the following some of the effects, not accounted for in the modeling, which could affect the operation of the 2D-ThFFF system.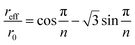 | (23) |
For n = 23, this gives reff/ro = 0.755. The effective void volume, V0eff, of the 2D-ThFFF system to be used in eqn (17) and (18) instead of V0 is then equal to 0.91 mL instead of 1.68 mL. The corresponding reductions in θ0 and θr are thus significant (46%). This is because the radial flow decreases with increasing distances from the channel center, thus the polymer spends more time in traveling a given radial distance near the channel edge than near the center. This however should not affect the θr/θ0 ratio. If the effective channel radius must be correctly determined in order to obtain accurate retention parameters, the fact that it is smaller than the channel radius can clearly not explain why experimental θ0 are larger than expected.
Furthermore, for the computation of the mean deflection angle, whatever the angular position at which a streamline reaches the periphery of the channel, or even the effective radius, it is set to the value of the angular position of the nearest exit port. This introduces a bias which limits the accuracy of the determination of the mean elution angles θ0 and θr.
The above estimations of the effects of the number of ports and of the sample flow rate are based on highly simplified assumptions. A detailed fluid mechanical study of the system would help to get a more precise description of the effects. Additional hydrodynamic effects may be encountered if the sample viscosity is initially significantly different from that of the carrier liquid.
Conclusions
The comparison of the experimental results for fractionation of polystyrene samples under various operating conditions with predictions of a theoretical model of continuous 2D-ThFFF was valuable. The trends in θ0 and θr are qualitatively in agreement with predictions of the model, but there are significant differences between the experimental results and the model predictions. The theoretical model could be refined to take into account sample relaxation under flow conditions; the stop-flow procedure is, of course, not compatible with continuous operation. As mentioned above, the present model assumes that the sample is already relaxed at the start of migration, and this assumption may contribute to some of the discrepancies between theory and experiment. The dispersion of sample materials in radial and angular directions could also be incorporated.The instrumental limitations, such as rather low maximum temperature gradient, the limited number (23 at present) of collection ports, and non-continuous fraction collection due to the limited volume of the syringes, restrict the full-scale operation and extension of the technique to lower molar mass applications. However, the temperature gradients applied in this work resulted in the retention of PS 1000k with Rr < 0.5 for ΔT ≥ 14 K, which allowed the effect of field strength on the continuous fractionation to be demonstrated.
In spite of the fact that there were significant discrepancies between predicted and experimental θr, it may be seen from Table 1 that with the current system PS 51k and PS 1000k would be quite well separated from one another on a continuous basis at ΔT of 17 K. With ΔT of 20 K the separation would be even better. The theoretical model presented here will provide guidelines for future interpretation and optimization of separations in continuous 2D-ThFFF. It constitutes a first step in the modeling of the system and it suggests that there may be flow disturbances caused by non-uniform w and/or ΔT in the current system. These are design and construction issues that can be addressed in future instruments. With improved instrumentation, the extension of the model to account for relaxation and dispersion phenomena will be the natural next step.
Symbols
| c | Concentration |
| c 0 | Concentration at the accumulation wall |
| r | Radial distance |
| r i | Radial distance of the sample inlet |
| r o | Outlet radius |
| r eff | Effective channel radius |
| R | Retention ratio |
| R r | Retention ratio in the radial direction |
| R θ | Angular retention ratio |
| t | Time |
| t 0 | Void time (V0/![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ) ) |
| T | Absolute temperature |
| T c | Cold wall temperature |
| ΔT | Thermal difference between channel walls |
| V 0 | Effective void volume of the channel |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif)
| Carrier fluid flow rate (total) |
| 〈vr〉 | Mean radial fluid velocity |
| w | Channel thickness |
| x | Distance from the accumulation wall |
| λ | Dimensionless retention parameter |
| ξ | Reduced distance from accumulation wall (=x/w) |
| θ | Angular displacement |
| θ r | Final elution angle |
| θ 0 | Non-retained elution angle |
| φ i | Fractional recovery of the polymer collected at port i |
| Ω | Angular fluid velocity |
| 〈Ω〉 | Mean angular fluid velocity |
| Ω 0 | Angular velocity of the rotating wall |
References
- J. C. Giddings, Sep. Sci., 1966, 1, 123 CrossRef.
- J. C. Giddings, Science, 1993, 260, 1456 CAS.
- M. E. Schimpf, Trends Polym. Sci., 1996, 4, 114 CAS.
- L. J. Gimbert, K. N. Andrew, P. M. Haygarth and P. J. Worsfold, Trends Anal. Chem., 2003, 22, 615 CrossRef CAS.
- J. C. Giddings, M. N. Myers, G.-C. Lin and M. Martin, J. Chromatogr., 1977, 142, 23 CrossRef CAS.
- P. C. Wankat, AIChE J., 1977, 23, 859 CrossRef CAS.
- P. C. Wankat, Sep. Sci. Technol., 1984, 19, 801 CrossRef CAS.
- J. C. Giddings, Anal. Chem., 1984, 56, 1258A CrossRef CAS.
- J. C. Giddings, in Unified Separation Science, John Wiley & Sons, Inc., New York, NY, 1991, pp. 112–140 Search PubMed.
- H. H. Strain and J. C. Sullivan, Anal. Chem., 1951, 23, 816 CrossRef CAS.
- A. C. Arcus, A. E. McKinnon, J. N. Livesey, W. S. Metcalf, S. Vaughan and R. B. Keey, J. Chromatogr., A, 1980, 202, 157 CrossRef CAS.
- M. Zborowski, L. R. Moore, S. Reddy, G.-H. Chen, L. Sun and J. J. Chalmers, ASAIO J., 1996, 42, 666 CrossRef PubMed.
- L. R. Moore, M. Zborowski, L. Sun and J. J. Chalmers, J. Biochem. Biophys. Methods, 1998, 37, 11 CrossRef CAS.
- T. Schneider, L. R. Moore, Y. Jing, S. Haam, P. S. Williams, A. J. Fleischman, S. Roy, J. J. Chalmers and M. Zborowski, J. Biochem. Biophys. Methods, 2006, 68, 1 CrossRef CAS PubMed.
- S. Turina, V. Krajovan and T. Kostomaj, Fresenius' J. Anal. Chem., 1962, 189, 100 CrossRef CAS.
- J. C. Giddings, Anal. Chem., 1962, 34, 37 CrossRef CAS.
- M. V. Sussman and C. C. Huang, Science, 1967, 156, 974 CAS.
- M. V. Sussman, K. N. Astill, R. Rombach, A. Cerullo and S. S. Chen, Ind. Eng. Chem. Fundam., 1972, 11, 181 CAS.
- M. V. Sussman, K. N. Astill and R. N. S. Rathore, J. Chromatogr. Sci., 1974, 12, 91 CrossRef CAS PubMed.
- C. D. Scott, R. D. Spence and W. G. Sisson, J. Chromatogr., 1976, 126, 381 CrossRef CAS.
- M. Goto and S. Goto, J. Chem. Eng. Jpn., 1987, 20, 598 CrossRef CAS.
- A. Uretschläger and A. Jungbauer, Bioprocess Biosyst. Eng., 2002, 25, 129 CrossRef PubMed.
- J. C. Giddings, Sep. Sci. Technol., 1985, 20, 749 CrossRef CAS.
- Y. Gao, M. N. Myers, B. N. Barman and J. C. Giddings, Part. Sci. Technol., 1991, 9, 105 CrossRef CAS.
- S. R. Springston, M. N. Myers and J. C. Giddings, Anal. Chem., 1987, 59, 344 CrossRef CAS.
- C. B. Fuh, M. N. Myers and J. C. Giddings, Ind. Eng. Chem. Res., 1994, 33, 355 CrossRef CAS.
- J. C. Giddings, J. Chromatogr., 1990, 504, 247 CrossRef CAS.
- M. N. Myers and J. C. Giddings, Powder Technol., 1979, 23, 15 CrossRef CAS.
- M. R. Schure, M. N. Myers, K. D. Caldwell, C. Byron, K. P. Chan and J. C. Giddings, Environ. Sci. Technol., 1985, 19, 686 CrossRef CAS PubMed.
- C. F. Ivory, M. Gilmartin, W. A. Gobie, C. A. McDonald and R. L. Zollars, Biotechnol. Prog., 1995, 11, 21 CrossRef CAS.
- P. Vastamäki, M. Jussila and M.-L. Riekkola, Sep. Sci. Technol., 2001, 36, 2535 CrossRef PubMed.
- P. Vastamäki, M. Jussila and M.-L. Riekkola, Analyst, 2003, 128, 1243 RSC.
- P. Vastamäki, M. Jussila and M.-L. Riekkola, Analyst, 2005, 130, 427 RSC.
- G. E. Thompson, M. N. Myers and J. C. Giddings, Anal. Chem., 1969, 41, 1219 CrossRef CAS.
- M. E. Hovingh, G. H. Thompson and J. C. Giddings, Anal. Chem., 1970, 42, 195 CrossRef CAS.
- M. Martin and R. Reynaud, Anal. Chem., 1980, 52, 2293 CrossRef CAS.
- J. C. Giddings, M. Martin and M. N. Myers, J. Chromatogr., 1978, 158, 419 CrossRef CAS.
- J. C. Giddings, M. Martin and M. N. Myers, Sep. Sci. Technol., 1979, 14, 611 CrossRef CAS.
- M. Martin, B.-R. Min and M. H. Moon, J. Chromatogr., A, 1997, 788, 121 CrossRef CAS.
- C. A. Rue and M. E. Schimpf, Anal. Chem., 1994, 66, 4054 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |