Foam drainage study during plateau border mineralisation

Abstract

We investigate the drainage of a foaming solution during inorganic polycondensation by macroscopic measurements and local observations. We reveal an original mineralisation mechanism starting from Plateau border interfaces. This slow process is not able to counteract the destabilizing effects of foam drainage and we therefore propose a new strategy in which mineralisation is assisted by a biopolymer.

---

Hierarchical porous solids (HPS) combining several porous networks covering a wide range of pore size (from Å to μm) occur widely in nature and are interesting in an ever expanding range of applications such as bioactive frameworks, electrodes, filters or even catalysts.¹ Among different routes,¹ the confinement of sol–gel reactions (soft chemical reactions) in the continuous phase of liquid foams appears to be low cost and effective routes to elaborate inorganic HPS, with macropore size higher than 50 μm, in a tailored manner.^2,3 The topology and dimension of the macroporous networks can be varied^1–3 by a tight control over the complex fluid structure which is determined by the liquid fraction and the bubble size. In this issue, a typical strategy consists first in the preparation of a well defined foam pattern obtained for instance by injecting the calibrated gas bubble in a foaming solution and wetting from above the growing foam at constant flow rate (forced drainage conditions) to control the foam liquid fraction. Then, an extended inorganic network can be formed in the liquid continuous phase via in situflocculation of preformed particles or via the polymerisation of molecular precursors leading to materials with specific characteristics detailed elsewere.^2,3 Finally, a solid foam transcription is obtained after solvent removal. Well defined HPS can be obtained as monoliths after about 2–3 days of free drainage and drying under ambient conditions when gelification results from preformed colloids assembly.² A mechanism of jamming at low flow rate has been recently proposed to account for this increased stability.⁵ In contrast, the polymerisation approach does not prevent foam collapse after a short time under free drainage conditions thus requiring a lyophilisation step to overcome this problem.³ This behaviour seems to be independent of the nature of the inorganic monomer (SiO₂ and TiO₂) or the catalytic route (one-step or two-step) but closely related to the drainage dynamic since solid emulsions can be easily obtained by combining polymerisation and drying under ambient conditions.⁴ Addressing this problem appears as a corner stone challenge in the field of HPS due to the high degree of control that can be obtained on mesoporous network architecture via molecular approaches in contrast with approaches based on preformed nanoparticles.⁶ Our present communication attempts to answer the following questions: (i) how does inorganic polycondensation develop at the local scale under forced drainage conditions? (ii) Why does this kind of system collapse under free drainage conditions? (iii) How can we overcome this problem? To this end, we present macroscopic drainage measurements and in situ visualisations of mineralisation taking place at one Plateau border submitted to drainage. To the best of our knowledge, the interplay between drainage and inorganic polycondensation has never been studied in the past. Nonetheless, without this basic knowledge the drying process could probably not be simplified and the origin of the weak mechanical properties of such promising materials can be neither understood nor fully controlled. In this study, we consider 2 reference foams that we carefully studied in the past:^5,7 (i) a surfactant foam composed of trimethyl tetradecyl ammonium bromide (C₁₄H₂₉N(Br)(CH₃)₃) called TTAB, at C_TTAB = 10 CMC and (ii) a particulate foam composed of TTAB at 10 CMC with Ludox© HS 40 silica nanoparticles at C_SiO2 = 0.15 wt%. The typical inorganic polymer foam that we selected as a case study is an aqueous solution composed of tetraethyl orthosilicate (Si(OC₂H₅)₄, C_SiO2 = 0.15 wt%) and TTAB (C_TTAB = 10 CMC) at low pH (C_HCl = 2 M). Ethanol released as a reaction by-product after the hydrolysis and condensation of TEOS was evaporated before beginning the local drainage experiments. This kind of protocol has been developed to yield sol–gel materials where the only solvent present at the gelation point is water to limit the harmful effect of ethanol toward foam films stability. Moreover, hydrolysis ratio (molar ratio of water to alkoxy silicate) several times higher than in common sol–gel recipes was used to obtain weakly viscous solutions enabling the control of foam liquid fraction by forced drainage. For such hydrolysis ratio and pH, the first stage of polymerization leading to opened particles (fractal dimension ≈ 2) is favored while linking into chains then networks that extend throughout the liquid medium is hindered by the low poly-condensation kinetic (i.e.hydrolysis of the siloxane bonds) and the dilution effect.⁸ As a result the foaming solution is visibly composed of small polymeric aggregates after the evaporation stage. According to light scattering measurements (Fig. S1 of ESI†), these aggregates are polydisperse with apparent hydrodynamic diameters in the range 0.5–10 μm and a mean diameter around 4 μm. In the following, these polymeric aggregates obtained since the preparation of the foaming solution will be called primary particle (PP). To compare the macroscopic stability of the different foams we first studied their ageing dynamics in free drainage configuration. The foams are made in a cylindrical tube of height 7 cm and cross-sectional area 4.15 cm² by slowly injecting compressed air into the foaming solution (V_foam ≈ 14.9 cm³) through a glass disc with pore size in the range 10–16 μm. These foams are composed of bubbles with parietal diameter around 0.3 mm according to image analysis whatever the foaming solution under attention. Once the foam has filled the tube, the tube is closed and the foam is allowed to drain and collapse freely. To quantify the ageing dynamic of such mixed system we have recently shown⁵ that usual measurements based on conductimetry are not reliable, thus here we monitored independently the time evolution of the front heights associated with the water/foam and foam/air interfaces. The accurate detection of the different fronts was performed using periodic (Δt = 300 s) optical transmission measurements all along the sample height (Δh = 40 μm) with a Turbiscan© device as shown in Fig. 1.

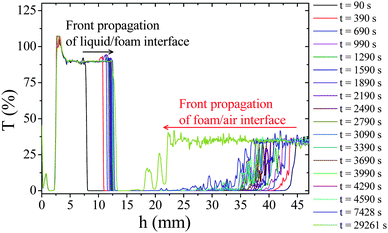Fig. 1 Evolution of the optical transmission (T) versus sample height (h) for a surfactant foam (TTAB at 10 CMC) at different times.

This evolution has three different origins. First, the volume of water in the foam decreases due to drainage. Liquid flows in the downward direction due to gravity leading to liquid fraction gradient. Second, the mean size of the bubble grows due to Ostwald ripening. The increase of the mean droplet size accelerates the drainage process. Third, some coalescence events occur at the top of the foam column. We recall that coalescence in foams in the absence of Ostwald ripening occurs below a critical liquid fraction.⁷ This critical liquid fraction is equal to 2 × 10⁻⁴ for a solution of TTAB at 10 CMC.⁷ Such a low liquid fraction may be achieved at the top of the foam due to drainage and water evaporation.⁹ We then deduce the evolution of the relative volume of water released from the foam and the relative volume of foam as a function of time. Fig. 2 shows that all the foams release water with a rate scaling of 1/t^α, with 0.3 ≤ α ≤ 0.5, until a final static equilibrium. This final value is increased by a factor of 3 when nanoparticles are present. In contrast, the kinetic of foam volume decrease seems to be faster for polymer foams than for surfactant and particulate foams. However, this effect is not very significant due to the experimental uncertainty arising from the determination of the foam/air interface by optical transmission measurements in the dry state (see Fig. 1c). In all cases the foam volume evolution is continuous as expected for such fine and wet foams. Fig. 3 shows bubble growth as a function of time for the three systems, indicating similar coarsening rates. The coarsening of such wet foams is dominated by Ostwald ripening rather than coalescence and theoretical evolutions are expected to be described by the following relation:

R(t)/R₀ = (1 + K₂t/2R²₀)^1/2 (1)

where R₀ is the initial bubble size. The characteristic constant K₂ can be expressed as: K₂ ≈ 2σDHν_mα(ε)/h, where σ ≈ 40 mN m⁻¹ is the surface tension of the solution, D ≈ 2 × 10⁻⁹ m² s⁻¹ is the diffusion coefficient of the gas in the liquid, H ≈ 6.4 × 10⁻⁶ mol m⁻³Pa⁻¹ is the Henry's law constant, ν_m ≈ 22.4 × 10⁻³ m³ mol⁻¹ is the ideal gas molar volume, α(ε) is a function of the liquid volume fraction,¹⁰ and h is the thin film thickness.

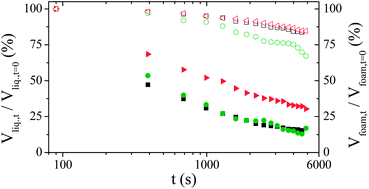Fig. 2 Time evolution of the relative liquid volume contained in the foam (full symbols) and of the relative foam volume (open symbols) in free drainage configuration at 25 °C for the reference foaming solution (TTAB 10 wt%, black squares) and foaming solutions containing either TEOS (green circles) or silica nanoparticles (red triangles).

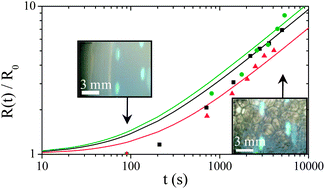Fig. 3 Time evolution of the relative parietal bubble radius determined by image analysis for the reference foaming solution (TTAB at 10 CMC, black squares) and foaming solutions containing either TEOS (green circles) or silica nanoparticles (red triangles). The lines correspond to the best adjustment of eqn (1) for the different data.

The above evolution law has been fitted for each set of data considering an average liquid fraction equal to ε ≈ 0.04, so that α(ε) ≈ 0.5,¹⁰ giving K₂ ≈ 4.32 × 10⁻¹⁰, 3.72 × 10⁻¹⁰ and 3.42 × 10⁻¹⁰ m² s⁻¹ for TTAB, TEOS and Ludox© respectively. The corresponding values deduced for the thin film thickness are respectively 30, 33 and 36 nm. Note that the slight increase in film thickness between TTAB and Ludox© can be attributed to the slightly larger liquid fraction of foam made with Ludox©. This range of values is consistent with results already published for solutions of pure surfactant¹¹ and suggests that inorganic additives are not present in foam films. It is in qualitative agreement with the systematic achievement of open porous network by the inorganic polycondensation approach³ and probably also for particulate approaches at low volume fraction.

These macroscopic measurements show that mineralisation occurs without significant modification of the macroscopic drainage kinetic and of the overall ageing dynamic whereas particulate foams containing the same silica content depict an improved stability compared to surfactant foams as already shown.

To get further insight into this puzzling interplay between drainage and mineralisation we performed direct visualisations at the Plateau border (Pb) scale, with the Plateau border apparatus¹² (PbA), since macroscopic drainage is mainly determined by liquid flow in Pb (Scheme 1).

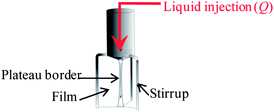Scheme 1 Schematic view of the experimental set-up used for the local flow observations. Adapted from ref. 12.

In brief, we recall that in a PbA (Scheme S1 of ESI†), a Pb and the three adjoining films are formed upon withdrawing a tripod from a reservoir containing the foaming solution and that liquid can be injected through the channel at a controlled flow rate, Q, corresponding to typical liquid velocities encountered during foam drainage. Pictures of the Pb cross-sections could be obtained during the experiment using a camera. We present in Fig. 4 a typical snapshot taken during Pb mineralisation at low flow rate Q = 20 μL min⁻¹.

Fig. 4 Photographs of a Plateau border during TEOS polycondensation with a constant liquid flow (Q = 20 μL min⁻¹) at different times: (a) 1 min, (b) 5 min and (c) 40 min. The scale bar represents 0.2 mm in (a) and (b).

The as-observed mechanism of Pb mineralisation can be described as a four step process. For clarity, the different steps discussed in the following are illustrated in Scheme 2.

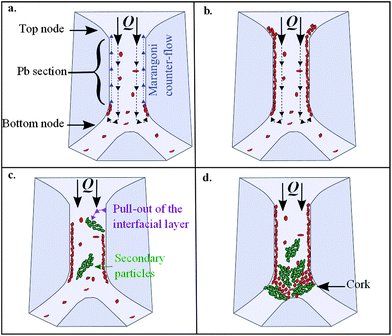Scheme 2 Tentative sketch of the 4 steps for Pb clogging during TEOS polycondensation: (a) formation of a polymer layer at Pb interfaces; (b) full coverage of Pb interfaces and thickening of the layer; (c) formation of SP by pull-out of the layer from the interface; (d) cork formation.

Step 1. At first, one observes preformed “primary” particles (PPs) flowing in the Pb bulk. The majority of these particles crossover the whole Pb along the length without noticeable displacement perpendicular to the flow direction. When PP gets to the bottom node, a small fraction of PP is brought against the Pb interface where they come “to be stored” in the course of time (Fig. 4a–c). According to this scenario, an interfacial polymeric layer, with an open structure, results from individual PP aggregation. The adhesion seems to be ‘irreversible’ as long as the adsorbed PPs are weakly sheared by the bulk flow. In this respect, PP can be described as amphiphilic species.

Step 2. Then, the interfacial layer formed at the bottom of Pb is slowly carried along the Pb interface toward the top node by surface counter-currents. This ascension process is much slower than bulk velocity and is probably driven by the Gibbs–Marangoni effect.¹³ When the layer reaches the top of Pb interface, the counter-current vanishes thus promoting layer thickening and densification. At the end of this second step the Pb interface is covered by a polymeric layer composed of PP.

Step 3. When the interfacial layer reaches a critical thickness, the shearing action exerted by the bulk flow pulls out, fully or partially, the layer from the interface. Thus, large polymeric objects come into the Pb bulk through this erosion process. Their typical size is ∼100 μm and they will be called secondary particles (SPs). At the end of step 3, PP and SP are present together in the Pb bulk.

Step 4. after about 40 min of forced drainage at low flow rate, corks with diameter equal to Pb section are progressively formed by successive adhesive collisions between SP themselves in the bottom node area. Once a cork appears the continuous aggregation of PP contributes to expend the structure of the cork to the whole Pb (Fig. 4d). It is interesting to mention that we never observe the above described stratification process and consequently the formation of cork at high flow rate.

This local mechanism is in qualitative agreement with our macroscopic measurements concerning the dynamic of ageing. Indeed, the slow growth of the inorganic network localised at Pb interfaces does not influence the bulk flow and thus drainage for a long time. Our local observations also indicate that inorganic entities are almost absent in the foam films in agreement with the macroscopic measurements concerning the foam volume and the bubble size evolution. This process may also explain why freeze drying is needed to realize solid foams via dilute solutions of molecular precursors since we show here that the mineralisation of the Pb is probably not completed at the time of their freezing. The small size of the final solid foams and their open porosity should be also a consequence of this incomplete and probably heterogeneous polymerisation state across the foam structure. However, more experiments are needed to fully transpose our local observations at the macroscale and notably to understand why the macroscopic measurements do not detect any effect on 2 h measurements while the clogging of single Pb occurs within 40 min? An answer may be that the time necessary for a measurable clogging effect at the scale of the whole foam channel network is strongly delayed compared to one channel due to the different orientations of Pb in real foam volume that must modify the stratification kinetic and the size distribution of the PP as a function of the foam altitude due to progressive adsorption of the smaller PP. One has also to consider the possible artifact arising from the flowing condition in the upper part of the PbA tripod with respect to real Pb.

As the reported mineralisation process is not able to counteract the destabilizing effects of foam drainage, we introduce an alternative strategy in which the mineralisation is assisted by a biopolymer that increases foam stability. To achieve the role of surfactant, thermo-gelator and mesostructuring agent we propose to use gelatin in place of classical molecular surfactants like TTAB. The interest of this kind of biopolymer toward the first two roles are already known. We briefly recall that gelatin gelation is thermoreversible with a sol state above T_gel consisting in a solution of single chains of denatured collagen whereas below T_gel, renaturation of the native triple helix forms a percolating network of helical segments connected by single strand coils. Concerning the last role, it is expected from recent studies¹⁴ that such biopolymer could act as template for producing mesoporosity in the wall of the inorganic monolith. To the best of our knowledge gelatin or other biopolymers were never used to realize these three roles simultaneously in the field of HPS elaboration. To validate this alternative we studied the ageing dynamic of gelatin foams (C_gelatin = 10 wt%) and gelatin foams containing TEOS in the course of polycondensation. The gelatin considered here was derived from porcine skin (T_gel ≈ 29 °C, M_w = 1 × 10⁵ g mol⁻¹) nicely provided by Rousselot. We performed measurements on foams prepared at 30 °C and quenched at T = 8 °C < T_gel for the measurements. The time evolution of the relative liquid volume contained in the foam and of the relative foam volume in free drainage configuration at 8 °C (see Fig. 5) indicate that the ageing dynamic is fully arrested from at most t = 400 s, with and without TEOS until several days.

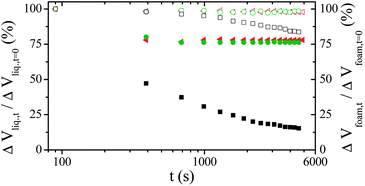Fig. 5 Time evolution of the relative liquid volume contained in the foam (full symbols) and of the relative foam volume (open symbols) in free drainage configuration at 8 °C for the reference foaming solution (TTAB, black squares) and foaming solutions containing either pure gelatin (green circles) or gelatin with TEOS (red triangles).

The present study has unveiled an unexpected mechanism of Pb mineralisation during drainage starting from a dilute solution of inorganic molecular precursors. By observations at the Pb scale, we have shown that polymerisation starts at the Pb interface until the formation of a thick coating that is then pulled-out by the shearing action of the bulk flow. Thus large particles appear in the bulk of Pb and promote Pb clogging by successive adhesive collisions in the bottom node area. This local mechanism is in qualitative agreement with the macroscopic ageing dynamic of the corresponding foams that is almost not affected by the polycondensation process. It may also explain why lyophilisation is often necessary to obtain well defined porous solid by the sol–gel approach starting from a dilute solution of inorganic precursors. As a green alternative to freeze drying and to usual synthetic surfactants, we propose to use a natural water-gelator like gelatin that could achieve the role of surfactant, thermo-gelator and mesostructuring agent.

Acknowledgements

We thank Dr Christelle Fritz (LPMDI, Marne-la-Vallée) for her assistance during PbA experiments.

Notes and references

1. (a) M. Scheffler and P. Colombo, Cellular Ceramics, Wiley, 2005; (b) S. Cox, D. Weaire and K. Brakke, Liquid Foams—Precursors for Solid Foams, Wiley, 2005; (c) A. R. Studart, U. T. Gonzenbach, I. Akartuna, E. Tervoort and L. J. Gauckler, J. Mater. Chem., 2007, 17, 3283; (d) R. Backov, Soft Matter, 2006, 2, 452.
2. (a) M. X. Wu, T. Fujiu and G. L. Messing, J. Non-Cryst. Solids, 1990, 121, 407; (b) G. T. Chandrappa, N. Steunou and J. Livage, Nature, 2002, 416, 702; (c) F. Carn, N. Steunou, J. Livage, A. Colin and R. Backov, Chem. Mater., 2005, 17, 644; (d) F. Carn, A. Derre, W. Nerri, O. Babot, H. Deleuze and R. Backov, New J. Chem., 2005, 29, 1346; (e) F. Carn, H. Saadaoui, P. Masse, S. Ravaine, B. Julian-Lopez, C. Sanchez, H. Deleuze, D. R. Talham and R. Backov, Langmuir, 2006, 22, 5469; (f) U. T. Gonzenbach, A. R. Studart, E. Tervoort and L. J. Gauckler, Angew. Chem., Int. Ed., 2006, 45, 3526; (g) R. M. Guillermic, A. Salonen, J. Emile and A. Saint-Jalmes, Soft Matter, 2009, 5, 4975; (h) S. Mishra and R. Mitra, J. Mater. Sci., 2010, 45, 4115.
3. (a) S. A. Bagshaw, Chem. Commun., 1999, 767; (b) F. Carn, A. Colin, M.-F. Achard, H. Deleuze, Z. Saadi and R. Backov, Adv. Mater., 2004, 16, 140; (c) F. Carn, A. Colin, M.-F. Achard, H. Deleuze, C. Sanchez and R. Backov, Adv. Mater., 2005, 17, 62; (d) F. Carn, M.-F. Achard, O. Babot, H. Deleuze, S. Reculusa and R. Backov, J. Mater. Chem., 2005, 15, 3887; (e) A. van der Net, A. Gryson, M. Ranft, F. Elias, C. Stubenrauch and W. Drenckhan, Colloids Surf., A, 2009, 346, 5.
4. (a) A. Imhof and D. J. Pine, Nature, 1997, 389, 948; (b) F. Carn, A. Colin, M.-F. Achard, H. Deleuze, E. Sellier, M. Birot and R. Backov, J. Mater. Chem., 2004, 14, 1370; (c) H. Zhang and A. I. Cooper, Soft Matter, 2005, 1, 107; (d) F. Carn, A. Colin, V. Schmitt, F. L. Calderon and R. Backov, Colloids Surf., A, 2005, 263, 341.
5. F. Carn, A. Colin, O. Pitois, M. Vignes-Adler and R. Backov, Langmuir, 2009, 25, 7847.
6. (a) L. Nicole, C. Boissiere, D. Grosso, A. Quach and C. Sanchez, J. Mater. Chem., 2005, 15, 3598; (b) C. Sanchez, P. Belleville, M. Popall and L. Nicole, Chem. Soc. Rev., 2011, 40, 696.
7. (a) V. Carrier and A. Colin, Langmuir, 2003, 19, 4535; (b) A. L. Biance, A. Delbos and O. Pitois, Phys. Rev. Lett., 2011, 106, 068301.
8. C. J. Brinker and G. W. Scherrer, in The Physics and Chemistry of Sol–Gel Processing, Academic, San Diego, 1990, pp. 97–233.
9. K. Malysa, Adv. Chem. Phys., 1992, 40, 37.
10. S. Hilgenfeldt, S. A. Koehler and H. A. Stone, Phys. Rev. Lett., 2001, 86, 4704.
11. A. Saint-Jalmes, M.-L. Peugeot, H. Ferraz and D. Langevin, Colloids Surf., A, 2005, 263, 219.
12. O. Pitois, C. Fritz and M. Vignes-Adler, J. Colloid Interface Sci., 2005, 282, 458.
13. O. Pitois, N. Louvet and F. Rouyer, Eur. Phys. J. E, 2009, 30, 27.
14. (a) G. L. Drisko, X. Wang and R. A. Caruso, Langmuir, 2011, 27, 2124; (b) Y.-C. Lin, C.-H. Hsu, H.-P. Lin, C.-Y. Tang and C.-Y. Lin, Chem. Lett., 2007, 36, 1258; (c) F. Carn, O. Durupthy, B. Fayolle, T. Coradin, G. Mosser, M. Schmutz, J. Maquet, J. Livage and N. Steunou, Chem. Mater., 2010, 22, 398.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c1sm06778h

---