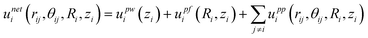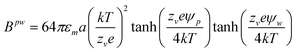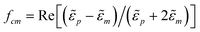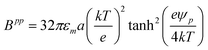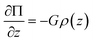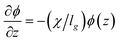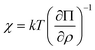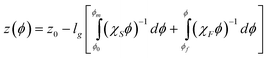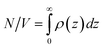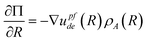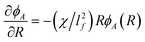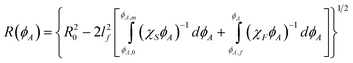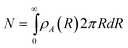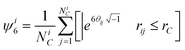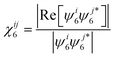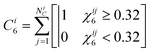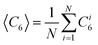DOI:
10.1039/C1SM06414B
(Paper)
Soft Matter, 2012,
8, 94-103
Electric field mediated assembly of three dimensional equilibrium colloidal crystals†
Received
24th July 2011
, Accepted 7th September 2011
First published on 7th October 2011
Abstract
We report confocal laser scanning microscopy (CLSM) measurements, Monte Carlo (MC) simulations, and an analytical model of the assembly of three dimensional (3D) equilibrium colloidal crystals within quadrupole electrodes on microscope cover slip surfaces. Micron sized fluorescent silica colloids in an index matching dimethylformamide (DMF) medium enable three dimensional CSLM imaging to measure particle coordinates. By matching density profiles from CSLM measurements and MC simulations, we obtain electrostatic, dipole–field, dipole–dipole, and gravitational potentials that accurately capture the three dimensional microstructure and morphology. We also report analytical density profiles with fluid–solid coexistence by balancing gravitational and electric field mediated compression against local osmotic pressure, which agree with CSLM and MC results. These results provide fundamental information on the assembly of three dimensional equilibrium colloidal crystals in the presence of multiple external fields and with coexisting inhomogeneous fluid and solid phases.
Introduction
Colloidal assembly provides the capability to produce microscopically structured materials for use in numerous traditional and emerging applications.1–3 The assembly of ordered colloidal materials, or colloidal crystals, has been proposed as an approach for scalable manufacturing of photonic and meta-materials with exotic electromagnetic properties.4 The primary limitation is assembling colloidal crystals with sufficiently low defect densities for these advanced material applications. Part of the problem with assembling low defect colloidal crystals is that most approaches involve strong interactions that produce highly non-equilibrium structures and irreversibly quench the final state. Because perfect colloidal crystals are the lowest free energy configurations for conditions where crystals should exist, non-equilibrium assembly processes are more likely to produce imperfections. For particle configurations that are irreversibly quenched, there is no way to repair defects.5,6
Several approaches have been developed to produce equilibrium colloidal crystals using tunable pair potentials to enable the possibility of reversible assembly and repairing defects. Methods employing tunable pair potentials include temperature dependent interactions mediated by DNA,7,8 non-adsorbing hydrogel particles,9,10 and binary solvents.11 However, such temperature dependent interactions rely on a global thermodynamic variable that does not easily allow for local manipulation and can also suffer from slow spatiotemporal transients. These potentials all involve relatively short range attractive interactions that cause crystallizationvia condensation and are susceptible to slow equilibration or dynamic arrest. While such tunable kT-scale (i.e. thermal energy scale) potentials show promise for creating equilibrium colloidal structures, they might be best implemented in conjunction with assistance from tunable external fields that provide additional control authority.
External fields such as shear,12,13 gravity,14,15 electric,16,17 magnetic,18,19 and optical20,21 fields have been used to manipulate colloidal crystal assembly processes with different advantages and disadvantages. For example, gravity is accessible but is not easily manipulated dynamically. Magnetic fields are more easily manipulated, but can involve complex apparatus and require magnetic particles. Shear can be easily controlled and does not require specific particle material properties, but dissipative fluid forces generally produce non-equilibrium configurations and multi-body hydrodynamic interactions can have complex connections to microstructures. Optical fields require the right combination of optical properties; no optical contrast between particles and media produces no net force, whereas too much contrast produces random scattering. Electric fields may offer the fewest limitations since they can be generated in numerous geometries and on different length scales via micro-fabrication, and can operate on static charge (electrophoresis) or electrically neutral materials by inducing dipoles (dielectrophoresis).
Electric fields have been used to manipulate colloidal crystallization in a number of ways. Low frequency AC and DC electric fields have been used to create 2D22,23 and 3D24,25 colloidal crystals, but the mechanisms controlling these processes are still not well understood.26 High frequency AC electric fields have been observed to assemble 2D16 and 3D17,27–29 colloidal crystals. Many of these studies relate microstructures to particle and field potentials in a qualitative manner, although several quantify density profiles using continuum models.30 More recently, equilibrium 2D colloidal crystals formed in high frequency AC electric fields have been related to frequency and amplitude dependent kT-scale dipole–field and dipole–dipole potentials using inverse MC methods.31–33 Also of relevance to the present work, colloids have previously been shown to assemble into 3D crystalline configurations in quadrupole electrodes where gravity is also significant,34,35 but these studies reported primarily qualitative observations.
In the present work, we use CSLM to measure the reversible equilibrium assembly of finite sized 3D colloidal crystals in a coplanar quadrupole electrode where gravity acts normal to the plane containing the electrode (see Fig. 1 and 2). Index matching 1.5 micron silica colloids in DMF enables 3D CSLM imaging while still allowing for electrostatic particle–particle and particle–surface repulsion and induced dipole–dipole and dipole–field interactions in 1MHz AC fields. Using functional forms for potentials measured in our previous work,15,31–33 we obtain quantitative agreement between measured microstructure and morphology with MC simulations and analytical predictions. Our findings demonstrate how kT-scale interactions between particles, the underlying surface, and multiple fields (i.e. gravity, electric) lead to the formation of reversible, equilibrium 3D colloidal crystals. This fundamental understanding provides the basis to quantitatively design, control, and optimize reversible colloidal crystal assembly processes with the goal of creating defect free microstructured materials.
 |
| | Fig. 1
CSLM images and MC renderings of 1.5 μm fluorescent SiO2 colloids in DMF medium displaying 3D hemispherical morphology with crystalline interior and thin fluid surface layer in quadrupole electrode at 10 V and 1 MHz. Supplemental movies show the dynamic equilibrium nature of this structure from several 3D views (i.e. spatial scan through XY slices, temporal scan of XZ slice, rotated view, “temporal” XZ rendering from MC simulation). (A) Projected view of 3D CSLM XYZ stack, and cross sectional view from 2D CSLM XZ slice. (B) Projected view and cross sectional renderings of 3D MC simulation of experiment in A. Details of matching experiments and simulations described in text. An 8-bit white-blue color scheme indicates 〈C6〉 values for each particle between 0–6 as computed using eqn (32)–(35). (C) Projected view of 3D CSLM XYZ stack rotated through 360° to illustrate 3D microstructure and morphology. | |
 |
| | Fig. 2 Co-planar thin gold film quadrupole electrode on a cover slip with a PDMS O-ring. (A) Top view photograph of device showing connections to function generator. (B) Side view rendering of device. (C) Zoom in rendering of colloidal crystal assembly in quadrupole device. (D) Contour plot of electric field in eqn (7) with linear spectrum scale from E/E0 = 0 to E/E0 = 3. | |
Theory
Interaction potentials
For concentrated colloidal particles in a non-uniform electric field near a planar wall surface, the net potential energy for particle i, as a function of particle–particle separation, rij, and orientation, θij, elevation above the wall, zi, and radial distance from the quadrupole center, Ri, is given by,| |  | (1) |
The particle–wall interaction in the limit of negligible van der Waals includes only electrostatic interactions given by,36
| | | upwe(z) = Bpwexp[−κ(z − a)] | (2) |
| | 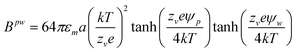 | (3) |
where
κ−1 is the Debye length,
εm is the medium dielectric constant,
k is Boltzmann's constant,
T is absolute temperature,
e is the charge of an electron,
zv is the electrolyte valence, and
ψp and
ψw are the particle and wall electrostatic surface potentials.
The net particle–field interaction includes the gravitational potential energy and the interaction of induced dipoles with electric field gradients as,
| | | upf(R, z) = upfg(z) + upfde(R) | (4) |
where the gravitational potential energy is given by,
where
G = (4/3)πa
3(
ρp −
ρm)g is the buoyant particle weight,
ρp and
ρm are the particle and medium densities, and
g is acceleration due to gravity. The interaction of an induced dipole with a non-uniform electric field for the geometry in
Fig. 2 is,
37| | | upfde(R) = −2kTλfϕf−1cmE*(R)2 | (6) |
where
fϕ is a volume fraction,
ϕ, dependent modification of the local electric field,
31,33,38 and
E*(
R) is the electric field in the central portion of quadrupole electrodes given by,
39| | | E*(R) = E(R)/E0 = 4d−1gR | (7) |
where
E0 = 0.5
Vpp/
dg,
Vpp is the applied peak-to-peak voltage,
dg is the distance between electrodes, and
λ is the relative dipolar and Brownian energies given by,
38and
fcm is the Clausius–Mosotti factor given as,
| | 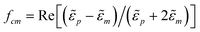 | (9) |
The net particle pair interaction as the sum of an electrostatic interaction due to electrostatic surface charge and a dipole–dipole interaction due to an applied electric field as,
| | | upp(rij, θij, Ri) = uppe(rij) + uppd(rij, θij, Ri) | (10) |
where the potential between colloids with thin electrostatic double layers (
κa ≫ 1) is,
36| | | uppe(rij) = Bppexp[−κ(rij − 2a)] | (11) |
where
Bpp is,
| | 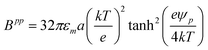 | (12) |
and the dipolar interaction in concentrated, quasi-two dimensional dispersions is,
38| | | uppd(rij, θij, Ri) = −kTλfϕfωP2(cosθij)(2a/rij)3E*(Ri)2 | (13) |
where
P2(cos
θij) is the second Legendre polynomial.
Field mediated equilibrium density profiles
For the geometry in Fig. 1 and 2 where gravity is oriented normal to the substrate, a differential change in osmotic pressure, Π, with a differential change in elevation, z, is given as,| | 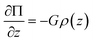 | (14) |
where ρ(z) is the local particle volumetric number density. This expression can be rearranged with the use of a couple definitions as,15| | 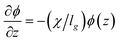 | (15) |
where lg = kT/G is a characteristic length scale, χ is a reduced osmotic compressibility given by,| | 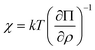 | (16) |
and ϕ(z) is the local particle volume fraction given by,
Eqn (15) can then be integrated to relate z and ϕ using the fluid, χF, and solid, χS, reduced osmotic compressibilities as,
| | 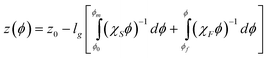 | (18) |
where
eqn (18) can be plotted as
ϕ(
z) curves,
z0 and
ϕ0 are a reference elevation and concentration, and
ϕ0 is obtained by constraining area under each density profile to give the total number of particles per volume,
N/
V, as,
40| | 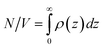 | (19) |
The χ values can be obtained for effective hard sphere fluids and solids using the osmotic pressure for hard sphere colloids given by,36
where the hard sphere fluid compressibility factor for concentrations from infinite dilution up to the freezing transition,
ϕf = 0.494, is given as,
41| | | ZHS,F(ϕ) = (1 + ϕ + ϕ2 − ϕ3)(1 − ϕ)−3 | (21) |
and the hard sphere, solid compressibility factor for concentrations from the melting transition,
ϕm = 0.545, up to close packing,
ϕcp = 0.74, is given as,
42| | | ZS = 2.6 + 0.13β + 0.18β2 − 1.1β3 + 2.8β4 − 2.9β5 + 1.1β6 + (12 − 3β)/β | (22) |
where
β = 4(1 −
ϕ/
ϕcp).
With regard to electric field mediated interactions for the geometry in Fig. 1 and 2, the electric field gradients are significant parallel to the substrate and radially from the quadrupole center. In this case, a differential change in Π with a differential change in R is given as,
| | 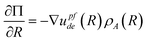 | (23) |
where
ρA is the number of particles per area in a 2D analysis. This can be rearranged with substitutions as,
| | 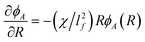 | (24) |
where
lf is a characteristic length scale for the quadrupole field in
eqn (7) given by,
| | | lf = dg(fcm/64λfϕ)1/2 | (25) |
and
ϕA(
z) is the local particle area fraction given by,
Eqn (24) can then be integrated to relate R and ϕ using the fluid, χF, and solid, χS, reduced osmotic compressibilities as,
| | 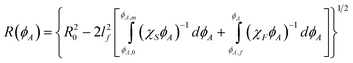 | (27) |
where
eqn (27) can be plotted as
ϕ(
R) curves,
R0 and
ϕA,0 are a reference radial position and concentration, and
ϕA,0 is obtained by constraining area under each density profile to give the correct total number of particles as,
40| | 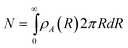 | (28) |
The χ values can be obtained for effective hard disk fluids and solids using the osmotic pressure for hard disk colloids given by,36
where the hard disk fluid compressibility factor for concentrations from infinite dilution up to the freezing transition,
ϕA,f = 0.69,
43 is given as,
44| | | ZHD,F(ϕA) = (1 + ϕ2A/8)(1 − ϕA)−2 | (30) |
and the hard disk, solid compressibility factor for concentrations from the melting transition,
ϕA,m = 0.716,
43 up to close packing,
ϕA,cp = 0.907, is given as,
45| | | ZHD,S = 2α−1 + 0.67α + 1.9 | (31) |
where
α =
ϕA,cp/
ϕA − 1.
45
Crystallinity order parameter
The crystallinity order parameter, 〈C6〉, is defined as the average number of crystalline nearest neighbors around each particle in an ensemble. The number of coordinated neighbors, NCi, to particle i are all particles j within a coordination radius, rC. Identification of crystalline near neighbors is based on a six-fold bond orientational order parameter for particle i, ψ6i, given by,46| | 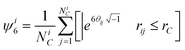 | (32) |
which is used to determine crystalline connectivity, χ6ij, between particle i and neighboring particles j as,47| |  | (33) |
where ψ6j* is the complex conjugate of ψ6j. The number of crystalline near neighbors, C6i, for particle i is,9| |  | (34) |
which is based on a criterion that a connection between particles i and j only be considered crystalline for χ6ij > 0.32.47 The value of 〈C6〉 is the average over all particles in an ensemble as,| |  | (35) |
Materials and methods
Electrodes and particles
Coplanar quadrupole gold film electrodes were patterned on glass microscope cover slips (50 mm × 24 mm × ∼150 μm, Corning) that were washed with acetone (Sigma-Aldrich), KOH (Sigma-Aldrich), and deionized water prior to patterning. The hyperbolic quadrupole electrodes were fabricated by spin coating photoresist (SU-8, Microchem) onto microscope cover slips, UV exposure through a chrome photomask, and physical vapor deposition of a 10nm chromium adhesive layer and a 40 nm gold layer. The photoresist liftoff was accomplished with agitation in 1165 Remover (Shipley). The electrode tips are separated by 100 μm (Fig. 2a, c). Nominal 1.5μm fluorescent SiO2 colloids (Kisker Biotech) were dispersed in n-dimethylformaldehyde (DMF) (Sigma-Aldrich) for index matching and allowed to sediment for 30 min in a polydimethylsiloxane (PDMS) (Dow Chemical) batch cell (1 mm high × 5 mm diameter) sealed with a cover slip (Corning). The coplanar quadrupole electrodes were connected in series with a function generator (Agilent, 33220A).
CLSM experiments were performed using an inverted microscope (Zeiss) with a mounted Zeiss LSM 5 Pascal Scanner and an oil immersion objective (63× magnification, 1.45 numerical aperture). The excitation source was a 488 nm line on a 500 mW argon ion laser. Vertical scan images were collected in a fast mode (∼3 s to scan 50 μm) at 1024 × 718 pixels with pixel dimensions of 52 × 52 nm2. Horizontal scans were collected at 1024 × 1024 pixels with pixel dimensions of 52 × 52 nm2. Reconstructed 3D images were produced from XYZ stacks with the same horizontal scan resolution as all other images and 160 nm spacing of 150 slices. Density profiles were determined by averaging temporal scan data in 100 successive images. Particle locations were located in 2D slices using standard algorithms coded in FORTRAN.
Simulation experiments
Particle configurations were simulated using a canonical MC code adapted from Allen and Tildesley.48 The simulation employed periodic boundary conditions and a cutoff of the long range dipolar potential at 5a, which is much less than half the simulation box size (equal to the electrode spacing dg). 2D MC simulations were initialized using experimental configurations. 3D MC simulations were initialized by stacking equilibrated 2D configurations aligned at their centers of mass, with HCP registry, and layer spacing based on effective particle dimensions (i.e. (24/9)0.5aeff). All simulations included image resolution limiting effects and polydispersity for realistic comparison with experiments.49,50 2D simulations were given a half million steps to equilibrate (ensured by monitoring potential energy and density profiles) followed by half-million steps for collecting particle coordinates. 3D simulations were given twenty thousand steps to relax before data collection. Simulated histograms were constructed using the same protocol used to construct experimental density profiles.
Results and discussion
Equilibrium colloidal crystals in quadrupolar fields
Fig. 1 shows CSLM images and MC simulation renderings of an equilibrium 3D colloidal crystal assembled into a hemispherical morphology in a high-frequency, inhomogeneous AC electric field within a quadrupole electrode. Supplemental movies show the dynamic equilibrium nature of this structure from several 3D views (i.e. spatial scan through XY slices, temporal scan of XZ slice, rotated view, “temporal” XZ rendering from MC simulation). The material system consists of 1.5 micron fluorescent SiO2 colloids dispersed in DMF with no added electrolyte. The SiO2 colloids and cover slip refractive indices are sufficiently close to the DMF medium to enable 3D CSLM imaging and minimize van der Waals attraction. For the equilibrium structure in Fig. 1, a 1MHz, 10V peak-to-peak voltage was applied to the quadrupole electrode (Fig. 2). The DMF dielectric constant is reduced compared to water, which increases the Debye length, decreases surface charge and potential via reduced dissociation, and shifts the frequency dependence of high-frequency electrokinetic phenomena.
Before reporting a quantitative analysis, we first qualitatively discuss the relevant interactions leading to the microstructure and morphology observed in Fig. 1. The total interaction includes a number of competing interactions between colloids, surfaces, and external fields. In the absence of the applied electric field, the 1.5 micron silica colloids experience electrostatic particle–particle and particle–surface interactions. Gravity is the sole external field when the electric field is not applied and is sufficiently strong to confine colloids within a quasi-2D monolayer near the underlying substrate, or in other words, prevents colloids from moving over top each other.51 Before application of the field, the local lateral concentration is not affected by van der Waals interactions with the underlying glass or metal film surfaces.52
With application of the spatially inhomogeneous AC electric field, the gravitational interaction remains the same, but dipoles induced on colloids are attracted to each other and interact with electric field gradients.31 For the material and field properties in our measurements, induced dipoles experience a minimum potential energy at the electric field minimum, which is in the center of the quadrupole electrode (Fig. 2). We refer to this as the dipole–field interaction (eqn (6)). To make the connection to a well-known related phenomenon, the dipole–field interaction is the same conservative force that leads to induced dipole transport from high to low fields, which is called “negative dielectrophoresis”. We are not concerned with transport in this work, but rather the balance of conservative forces that leads to the assembly of the equilibrium structure in Fig. 1. For the case in Fig. 1, the dipole–field interaction is comparable to gravity, which causes particles to be compressed into 3D configurations in contrast to their initially uncompressed quasi-2D state in the absence of the field.
Once many dipoles are located at the electric field minimum, they are also attracted to each other. The dipole–dipole attraction between colloids has been show to produce a body-centered-tetragonal microstructure as the lowest potential energy configuration in uniform electric fields.53 In the present work, we are interested in the lowest free energy configuration that is formed in the presence of gravity and a non-uniform electric field near a surface.
Experimental and simulated density profiles
A quantitative description of the interactions leading to the microstructure and morphology in Fig. 1 should include all particle–particle, particle–surface, and particle–field interactions. To avoid any approximations and include all potentials, we employ Monte Carlo (MC) simulations using dipole–dipole and dipole–field potentials previously identified to be accurate on the kT-scale for quasi-2D concentrated colloids confined at an electric field minimum between parallel electrodes in aqueous media.31–33 These previous direct measurements provide a good foundation for modeling interactions in the present case despite the different media, geometry, and dimensionality.
To quantitatively match the CSLM measured microstructure and morphology to MC simulated results, a number of spatial distribution functions are compared in Fig. 3. Fig. 3a shows for both CSLM and 2D MC results the radial distribution function, g(r) = ρ(r)/ρb, averaged over all particles within specified elevation ranges that correspond to layers formed parallel to the wall (that are crystalline at low elevations and fluid at the highest elevation). From Fig. 3a, the effective radius, aeff, is taken as 0.875μm based on the location of the first peak in the radial distribution function of the first layer. Fig. 3b shows radially dependent effective volume fraction profiles, ϕeff(R) = (4/3)πaeff3ρ(R), from CSLM experiments and 2D MC simulations. Radial density profiles are smoothed by fitting sigmoidal curves and converted to effective volume fractions or area fractions using eqn (17) and (26) with aeff in place of a.
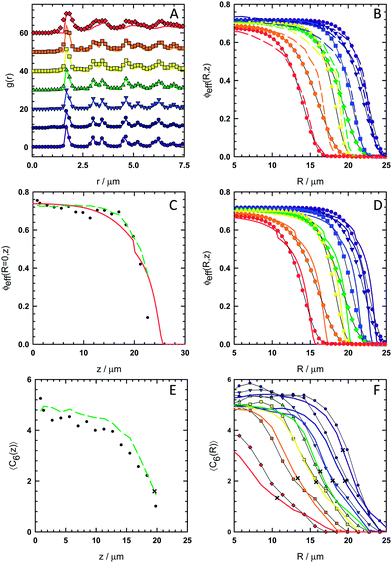 |
| | Fig. 3 Spatial distribution functions to characterize microstructure and morphology in experiments, simulations, and theory for the conditions in Fig. 1. (A) 2D radial distribution functions averaged over all particles in layers parallel to the microscope slide in seven alternating layers starting with first layer closest to microscope slide (spectrum color scale from violet to red) from CSLM images (points) and 2D MC simulations (lines). (B) Angular averaged radially dependent effective volume fraction within 2D layers with origin at quadrupole center from CSLM images (points) and 2D MC simulations (lines) with same color scheme as A. (C) Elevation dependent effective volume fraction at the quadrupole center from CSLM (points), 3D MC simulations (dashed line), and analysis using eqn (14)–(22) (solid line). (D) Same plot as B with CSLM data (points) and analysis using eqn (23)–(31) (line). (E) Elevation dependent crystallinity order parameter averaged over all particles within layers parallel to microscope slide from CSLM (points) and 3D MC simulations (line). “x”'s correspond to fluid–solid transition from analytical predictions. (F) Angular averaged radially dependent crystallinity order parameter averaged within 2D layers with origin at quadrupole center from CSLM images (points) and 3D MC simulations (lines) with same color scheme as A. | |
We began by matching 2D MC simulations with density profiles (i.e. g(r) and ϕeff(R)) within individual crystalline layers. The analytical form of all potentials in the MC simulations were fixed to those described in the theory section (i.e.eqn (1)–(13)) and our previous papers on electric field mediated colloidal interactions31–33 and sedimentation equilibria.15Table 1 summarizes all input parameters. The number of particles in each simulation was determined from the area under each experimental curve (i.e.eqn (19), (28)).
Table 1 Parameters used in potentials for MC simulations and analysis in eqn (14)–(31). Parameters were determined from: (a) particle manufacturer, (b) first peak in g(r)'s in Fig. 3a, (c) literature value,55 (d) previous CSLM measurements in DMF,15 (e) literature value,56 (f) function generator readout, (g) microscope measurement, (h) literature value,57 (i) fit in MC simulations
| Parameter |
Value |
|
a/nma |
750 |
| aeff(nm)b |
875 |
|
εm/ε0c |
36.4 |
| κ−1 (nm)d |
28.9 |
|
ψp = ψw(mV)d |
−40 |
|
εp/ε0e |
3.8 |
|
σm (μS m−1)c |
0.34 |
| Vpp (V)f |
10 |
|
dg (μm)g |
93 |
|
ρp (g cm−3)d |
1.75 |
|
ρm (g cm−3)h |
0.95 |
|
fϕi |
0.76 |
The sole adjustable parameter to obtain agreement between the CSLM measurements and MC simulations in Fig. 1 is a correction, fϕ, to the dipole–dipole and dipole field interactions in eqn (6) and (13). This correction accounts for how the local electric field is modified by the presence of dielectric particles, which in principle also depends on particle configuration,38 but is dominated by concentration.31 The best fit constant was fϕ = 0.76, which is consistent with previous measurements and the expectation that fϕ < 1 based on relatively high core particle volume fractions (e.g. ϕ = (a/aeff)3ϕeff = (750 nm/875 nm)3(0.74) = 0.47 at center of the first layer).
The agreement between measured and simulated 2D density profiles is good in Fig. 3. In particular, in Fig. 3a both CSLM and MC results display a distinctive split in the second peak of g(r) indicative of crystalline order in every layer up to ∼21 μm (the 13th layer in our analysis in Fig. 3). Above ∼21 μm, the particles remain within distinct layers under gravitational confinement but the lateral structure within layers is fluid. In Fig. 3b, the radial density profiles, ϕeff(R), show good agreement at all elevations between CSLM and MC results.
To assess whether the procedure using 2D MC simulations in Fig. 3a and 3b produce potentials that accurately capture the 3D behavior of the equilibrium hemisphere, we next performed 3D MC simulations. Fig. 3c shows average elevation dependent effective particle volume fraction, ϕeff(z) = (4/3)πaeff3ρ(z), evaluated at the center of the hemisphere (R = 0) from CSLM experiments and 3D MC simulations. This 3D MC simulation used the same potentials and number of particles in each layers as the 2D MC simulations, but was initialized using a hexagonal close packed (i.e. ABAB…) crystal with a layer spacing of (24/9)0.5aeff = 1.43 μm using aeff obtained from the 2D g(r)s in Fig. 3a. After the hemisphere surface melted during equilibration, the elevation dependent density profile in the center of the simulated 3D hemisphere was in excellent agreement with experimental CSLM results as shown in Fig. 3c. The average equilibrated layer spacing in the CSLM measurements and 3D MC simulations were 1.53 μm and 1.39 μm. These are within the diffraction limit of each other and the predicted layer spacing, which indicates good agreement within the resolution of our measurements.
Experimental and analytical density profiles
We also compare measurements with predictions based on the analytical models in eqn (14)–(31). This analysis employs the local density approximation, which assumes the average local thermodynamic properties within the equilibrium microstructure depend only on the local density (and vice versa). Using this approximation in conjunction with effective hard sphere or hard disk particle dimensions (from g(r)s in Fig. 3a), equations of state can be used to determine spatially varying density profiles. In addition to the CSLM and MC results in Fig. 3c, a curve for ϕeff(z) evaluated at the hemisphere center (R = 0) was computed by balancing gravitational compression against the hard sphere osmotic pressure for fluid and solid phases (eqn (14)–(22)). Fig. 3d shows ϕeff(R) within each layer from CSLM experiments similar to Fig. 3b but now in comparison to the analytical model in eqn (23)–(31). In Fig. 3d, the model is based on balancing the radially varying electric field in the dipole–field potential against the 2D hard disk osmotic pressure for fluid and solid phases within each layer.
These calculations follow the methods outlined in our previous paper on sedimentation equilibria,15 although we provide some additional details. The total number of particles was conserved by constraining the area under each experimental and analytical curve to be the same using eqn (19) and (28). The curves were fit to data by adjusting the density at reference positions (i.e. either z = 0 or R = 0) to match the value from CSLM experiments while still conserving the area under the curves. The same parameters obtained in the MC analysis in Table 1 were used for computing the analytical curves in Fig. 3c and 3d. For plotting purposes, 2D area fractions are converted into effective volume fractions in Fig. 3d using the same aeff.
In all cases, the models predict density profiles in excellent agreement with both CSLM experiments and MC simulations. While the CSLM and MC density profiles are not of sufficiently high resolution to distinguish the fluid–solid boundaries in Fig. 3c and 3d, the profiles clearly follow each other quite closely at nearly all coordinates. The main discrepancy is that the radially dependent analytical profiles in Fig. 3d end more abruptly than the experimental and simulated profiles. In contrast, the elevation dependent analytical profile in Fig. 3c is somewhat more extended than the measured and simulated results.
The small systematic biases in regions where the density profiles vanish at the hemisphere periphery could arise from simplifying assumptions. The hard disk and hard sphere equations of state are approximate for the soft electrostatic repulsion (κa ≈ 25). The analytical model assumes dipole–dipole interactions produce no net interaction (i.e. dipole–dipole interactions average to zero) in bulk, isotropic, crystalline configurations,30 which might be appropriate in the hemisphere crystalline interior17 but not for the inhomogeneous fluid layer on the hemisphere surface where the density profile vanishes over dimensions comparable to the particle size.54 A single average correction to the electric field (i.e. fϕ in eqn (6))38 rather than a local concentration dependent17 parameter is also approximate and expected to work best in the hemisphere interior. The analytical electric field model (eqn (7)) is less accurate away from the electrode center and does not take into account fabrication non-uniformities (e.g. roughness, irregular shape). The overall good agreement between experiments, simulations, and the analytical curves generally validates these simplifying assumptions.
Experimental and simulated crystallinity profiles
The agreement between CSLM measured structure and 3D MC simulations was further assessed by measuring spatial distributions of crystalline order in Fig. 3 and through direct visual comparisons in Fig. 4. Fig. 3e and 3f show elevation and radial distributions of crystalline order as characterized by 〈C6〉 (computed using eqn (32)–(35)) from CSLM experiments and MC simulations. Fig. 3e shows the average elevation dependent 〈C6〉, which is the average number of crystalline particles around each particle averaged over all particles within an elevation range (i.e. crystalline and fluid layers parallel to the substrate). Fig. 3f reports the radial dependence of 〈C6〉 averaged over all angles and for all particles within each elevation range. Points represent experimental data extracted from CSLM measured particle centers, and lines correspond to 3D MC simulation results. Although 〈C6〉 was not considered as part of the process of matching spatial density profiles and MC simulations, good agreement is observed between all 〈C6〉 profiles in CSLM experiments and 3D MC simulations.
 |
| | Fig. 4
CSLM
XY images (1st, 3rd rows) and 3D MC renderings (2nd, 4th rows) of alternating layers in 3D colloidal assemblyvs. elevations for the conditions in Fig. 1. Rendering color scale is the same as in Fig. 1B. Highest to lowest elevations are shown from left to right, top to bottom. | |
Based on a comparison of the elevation dependent density and 〈C6〉 profiles in Fig. 3c and 3e, significant crystallinity is observed in the first thirteen layers up to a height of ∼21 μm, beyond which little order is seen (the density profile in Fig. 3c continues beyond the 〈C6〉 profile in Fig. 3e). A comparison of the radial profiles in Fig. 3d and 3f show a similar effect with density persisting beyond 〈C6〉 profiles in each case, which indicates a several micron thick fluid layer on the hemisphere surface. The fluid layer becomes thinner near the base of the hemisphere where the radial extent is the greatest and stronger dipole–field interactions are encountered based on the dependence in eqn (6) and (7).
Points in Fig. 3e and 3f mark the locations of the fluid–solid transitions from the analytical models in Fig. 3c and 3d, which all occur around 〈C6〉 ≈ 2. Although the analytical model is not capable of predicting spatial dependence of crystalline order, it is interesting to note the correlation between 〈C6〉 values at the spatial position of fluid–solid coexistence in each case. The agreement between both density and 〈C6〉 profiles in Fig. 3 indicates the quantitative connection between the reported potentials and the observed inhomogeneous coexisting solid–fluid microstructure and hemispherical morphology.
As final confirmation of the agreement between simulations and experiments, Fig. 4 shows CLSM images and rendering from 3D MC simulations. Several layers in the experiments contain defects including point defects caused either by the absence of particles or presence of doublets and line defects where particles did not hexagonally pack. Experiments are also likely to contain stacking faults that are not present in the simulations. Simulations were started from perfect crystal configurations, which they retain in contrast to the experiments. While differing degrees of crystallinity in Fig. 4 indicate kinetic differences between experiments and simulations, the same local microstructure (or phase) is obtained in each case.
The morphology of several of the bottom layers also show slight distortion toward a square shape, which probably results from the quadrupolar field shape that is not captured by the angular independent field used in eqn (7). This also probably accounts for some of the variations in the density profile edges in Fig. 3d. Despite these small difference, the agreement between the CSLM images and MC renderings in Fig. 4 is good and not surprising based on the agreement in Fig. 3. In any case, the visual comparison provides a final check on the analysis and shows a couple small differences due to polycrystallinity and overall morphology.
Experimental and simulated morphology vs. applied voltage
To show the broader applicability of our results to different applied fields, Fig. 5 shows CSLM measurements and MC simulation results at different voltages and a 1 MHz frequency (lower frequencies could also be used to reduce the compressive dipole–field interaction32,33). Specifically, Fig. 5 shows the microstructural and morphological evolution captured by CLSM XZ scans and MC simulations as the field strength decreases from 8 V to 2 V in 2 V increments. In general, the agreement between experiment and simulations is excellent further validating the models presented in this work for capturing the 3D assembly of colloidal crystals in inhomogeneous electric fields.
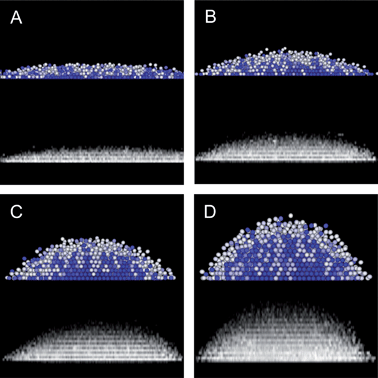 |
| | Fig. 5
CSLM projection of XYZ stack and 3D MC renderings of microstructure and morphology changes with decreasing voltages from the 10V case discussed in Fig. 1, 3, and 4 for (A) 2V, (B) 4V, (C) 6V, and (D) 8V. Rendering color scale is the same as in Fig. 1B. | |
We do not perform an extensive quantitative analysis for each voltage as we did for the 10 V case in Fig. 3, but discuss qualitative features that emerge. Experiments and simulations both show that height decreases as the dipole–field interactions weaken with decreasing field strength. This results from gravitational compression dominating a decreasing electric field mediated inward radial compression. Along with the decreasing height, particles escape the quadrupole at the bottom peripheral edge of the hemisphere. For applied voltages less than 1 V, the 1.5 micron SiO2 colloids form sub-monolayer fluid configurations, similar to our previous measurements of 2D structures between parallel electrodes.31,33 The hemispherical morphology and height arise from a balance of a radial force concentrating particles into the quadrupole center with sufficient pressure to overcome the gravitational energy penalty associated with forming layers normal to the substrate.
In addition to the field dependent morphological changes captured in Fig. 5, these results also show how the inhomogeneous microstructure depends on the applied field. From 8 V down to 4 V, the microstructures all correspond to crystalline layers within the hemisphere center. The central crystal is encased within a thin fluid-phase layer where the density profile vanishes in both the normal and radial directions. At 2 V, a multi-layered inhomogeneous fluid is observed not unlike sedimentation equilibrium profiles with insufficient pressure to induce crystallization.15 As a result, tuning the field amplitude and number of particles within the quadrupole can be used to control the resulting 3D crystal size, morphology, and microstructure.
Conclusions
We demonstrated the assembly of a 3D equilibrium colloidal crystal within an inhomogeneous electric field formed by a coplanar quadrupole electrode on a cover slip. By using an index matching non-aqueous medium and fluorescent silica colloids, CSLM was used to quantitatively measure the three dimensional particle coordinates to quantify the resulting microstructure and morphology. By matching CSLM measured density profiles and spatial distributions with MC simulations, our results confirm the electrostatic, dipole–field, and dipole–dipole potentials used in our analysis. We also report analytical predictions of density profiles and spatially varying fluid–solid coexistence in agreement with CSLM and MC results. These analytical results show that density profiles within layers parallel to the substrate can modeled as two dimensional hard disks compressed by radially varying electric fields, whereas the density normal to the substrate can be modeled as gravitational compression of hard spheres. Simulations also captured dynamic equilibrium microstructures and morphologies for varying applied electric fields, providing further confirmation of the models developed in this work. By measuring and modeling the equilibrium assembly of 3D colloidal crystals, our findings provide a basis to quantitatively design, control, and optimize assembly processes in similar configurations.
Acknowledgements
We acknowledge financial support provided by the National Science Foundation through a Cyber Enabled Discovery and Innovation grant (CMMI-0835549) and an unsolicited grant (CBET-0932973), and the Air Force Office of Scientific Research (FA9550-08-1-0329).
References
- O. D. Velev and S. Gupta, Adv. Mater., 2009, 21, 1897–1905 CrossRef CAS.
- M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, ACS Nano, 2010, 4, 3591–3605 CrossRef CAS.
- F. Li, D. P. Josephson and A. Stein, Angew. Chem., Int. Ed., 2011, 50, 360–388 CrossRef CAS.
- K. A. Arpin, A. Mihi, H. T. Johnson, A. J. Baca, J. A. Rogers, J. A. Lewis and P. V. Braun, Adv. Mater., 2010, 22, 1084–1101 CrossRef CAS.
- M. A. Bevan, J. A. Lewis, P. V. Braun and P. Wiltzius, Langmuir, 2004, 20, 7045–7052 CrossRef CAS.
- W. Lee, A. Chan, M. A. Bevan, J. A. Lewis and P. V. Braun, Langmuir, 2004, 20, 5262–5270 CrossRef CAS.
- P. L. Biancaniello, A. J. Kim and J. C. Crocker, Phys. Rev. Lett., 2005, 94, 058302 CrossRef.
- A. J. Kim, R. Scarlett, P. L. Biancaniello, T. Sinno and J. C. Crocker, Nat. Mater., 2009, 8, 52–55 CrossRef CAS.
- G. E. Fernandes, D. J. Beltran-Villegas and M. A. Bevan, Langmuir, 2008, 24, 10776–10785 CrossRef CAS.
- G. E. Fernandes, D. J. Beltran-Villegas and M. A. Bevan, J. Chem. Phys., 2009, 131, 134705 CrossRef.
- F. Soyka, O. Zvyagolskaya, C. Hertlein, L. Helden and C. Bechinger, Phys. Rev. Lett., 2008, 101, 208301 CrossRef.
-
B. J. Ackerson, Shear induced order and shear processing of model hard sphere suspensions, SOR, 1990 Search PubMed.
- T. Solomon and M. J. Solomon, Journal of Chemical Physics, 2006, 124, 10 Search PubMed.
- K. E. Davis, W. B. Russel and W. J. Glantschnig, Science, 1989, 245, 507–510 CAS.
- R. E. Beckham and M. A. Bevan, J. Chem. Phys., 2007, 127, 164708 CrossRef.
- S. O. Lumsdon, E. W. Kaler and O. D. Velev, Langmuir, 2004, 20, 2108–2116 CrossRef CAS.
- M. T. Sullivan, K. Zhao, A. D. Hollingsworth, R. H. Austin, W. B. Russel and P. M. Chaikin, Phys. Rev. Lett., 2006, 96, 015703 CrossRef CAS.
- L. E. Helseth, H. Z. Wen, R. W. Hansen, T. H. Johansen, P. Heinig and T. M. Fischer, Langmuir, 2004, 20, 7323–7332 CrossRef CAS.
- R. Haghgooie, C. Li and P. S. Doyle, Langmuir, 2006, 22, 3601–3605 CrossRef CAS.
- P. T. Korda and D. G. Grier, J. Chem. Phys., 2001, 114, 7570–7573 CrossRef CAS.
-
D. L. J. Vossen, M. A. Plaisier and A.v. Blaaderen, Colloidal crystallization induced by optical gradient forces exerted by optical tweezers, SPIE, 2004 Search PubMed.
- M. Giersig and P. Mulvaney, Langmuir, 1993, 9, 3408–3413 CrossRef CAS.
- M. Trau, S. Sankaran, D. A. Saville and I. A. Aksay, Nature, 1995, 374, 437–439 CrossRef CAS.
- A. L. Rogach, N. A. Kotov, D. S. Koktysh, J. W. Ostrander and G. A. Ragoisha, Chem. Mater., 2000, 12, 2721–2726 CrossRef CAS.
- T. Gong, D. T. Wu and D. W. M. Marr, Langmuir, 2003, 19, 5967–5970 CrossRef CAS.
- D. C. Prieve, P. J. Sides and C. L. Wirth, Curr. Opin. Colloid Interface Sci., 2010, 15, 160–174 CrossRef CAS.
- U. Dassanayake, S. Fraden and A.v. Blaaderen, J. Chem. Phys., 2000, 112, 3851–3858 CrossRef CAS.
- A. Yethiraj and A.v. Blaaderen, Nature, 2003, 421, 513–517 CrossRef CAS.
- M. E. Leunissen, M. T. Sullivan, P. M. Chaikin and A. van Blaaderen, J. Chem. Phys., 2008, 128, 164508–164511 CrossRef.
- B. Khusid and A. Acrivos, Phys. Rev. E, 1996, 54, 5428 CrossRef CAS.
- J. J. Juarez and M. A. Bevan, J. Chem. Phys., 2009, 131, 134704 CrossRef.
- J. J. Juarez, J. Cui, B. Liu and M. A. Bevan, Langmuir, 2011, 27, 9211–9218 CAS.
- J. J. Juarez, B. Liu, J. Cui and M. A. Bevan, Langmuir, 2011, 27, 9219–9226 CAS.
- A. Docoslis and P. Alexandridis, Electrophoresis, 2002, 23, 2174–2183 CrossRef CAS.
- M. Abe, M. Orita, H. Yamazaki, S. Tsukamoto, Y. Teshima, T. Sakai, T. Ohkubo, N. Momozawa and H. Sakai, Langmuir, 2004, 20, 5046–5051 CrossRef CAS.
-
W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge University Press, New York, 1989 Search PubMed.
- T. B. Jones and M. Washizu, J. Electrost., 1994, 33, 199–212 CrossRef.
- P. M. Adriani and A. P. Gast, Phys. Fluids, 1988, 31, 2757–2768 CrossRef CAS.
- Y. Huang and R. Pethig, Meas. Sci. Technol., 1991, 2, 1142–1146 CrossRef CAS.
-
T. L. Hill, Statistical mechanics: principles and selected applications, Dover Publications, New York, 1987 Search PubMed.
- N. F. Carnahan and K. E. Starling, J. Chem. Phys., 1969, 51, 635 CrossRef CAS.
- K. R. Hall, J. Chem. Phys., 1972, 57, 2252–2254 CrossRef CAS.
- T. M. Truskett, S. Torquato, S. Sastry, P. G. Debenedetti and F. H. Stillinger, Phys. Rev. E, 1998, 58, 3083–3088 CrossRef CAS.
- D. Henderson, Mol. Phys., 1977, 34, 301–315 CrossRef CAS.
- B. J. Alder, W. G. Hoover and D. A. Young, J. Chem. Phys., 1968, 49, 3688–3696 CrossRef CAS.
- D. R. Nelson and B. I. Halperin, Phys. Rev. B, 1979, 19, 2457–2484 CrossRef CAS.
- S. van Teeffelen, C. N. Likos and H. Lowen, Phys. Rev. Lett., 2008, 100, 108302–108304 CrossRef.
-
M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford Science, New York, 1987 Search PubMed.
- T. O. Pangburn and M. A. Bevan, J. Chem. Phys., 2005, 123, 174904 CrossRef.
- T. O. Pangburn and M. A. Bevan, J. Chem. Phys., 2006, 124, 054712 CrossRef.
- H.-J. Wu, T. O. Pangburn, R. E. Beckham and M. A. Bevan, Langmuir, 2005, 21, 9879–9888 CrossRef CAS.
- H.-J. Wu, W. N. Everett, S. G. Anekal and M. A. Bevan, Langmuir, 2006, 22, 6826–6836 CrossRef CAS.
- R. Tao and J. M. Sun, Phys. Rev. Lett., 1991, 67, 398 CrossRef.
- N. Li, H. D. Newman, M. Valera, I. Saika-Voivod and A. Yethiraj, Soft Matter, 2010, 6, 876–880 RSC.
- G. Macfie, R. G. Compton and H. R. Corti, J. Chem. Eng. Data, 2001, 46, 1300–1304 CrossRef CAS.
-
D. R. Lide, ed., CRC Handbook of Chemistry and Physics, CRC Press, New York, 2000 Search PubMed.
- P. S. Nikam and S. J. Kharat, J. Chem. Eng. Data, 2005, 50, 455–459 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Supplemental Videos: CSLM xyt.avi (3.87 MB) CSLM measured XY slices show individual layers from bottom to top. CSLM xzt.avi (3.39 MB) CSLM measured XZ slice shows cross-sectional view of hemisphere. MC xzt.avi (2.10 MB) MC simulated XZ rending shows cross-sectional view of hemisphere. CSLM rotate.avi (2.98 MB) CSLM measured XY stack rendered as 3D rotating view. See DOI: 10.1039/c1sm06414b |
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here.