Does size matter? Elasticity of compressed suspensions of colloidal- and granular-scale microgels†
Paul
Menut‡
ab,
Sebastian
Seiffert‡
acd,
Joris
Sprakel
ae and
David A.
Weitz
*a
aHarvard University, School of Engineering and Applied Sciences and Department of Physics, 29 Oxford Street, Cambridge, MA 02138, USA. E-mail: weitz@seas.harvard.edu
bUMR IATE, SupAgro, INRA, CIRAD, UM2, 2plViala, 34060, Montpellier, France
cHelmholtz Zentrum Berlin, F-I2 Soft Matter and Functional Materials, Hahn-Meitner-Platz 1, D-14109, Berlin, Germany
dFU Berlin, Institute of Chemistry and Biochemistry, Takustr.3, D-14195, Berlin, Germany
eLaboratory of Physical Chemistry and Colloid Science, Wageningen University, Dreijenplein 6, 6703 HB, Wageningen, The Netherlands
First published on 21st October 2011
Abstract
We investigate the mechanics of dense packing of very small, colloidal-scale, and larger, granular-scale microgel particles. At low particle concentration, thermally induced Brownian motion of the particles is important for the colloidal-scale systems; in contrast, such Brownian motion is irrelevant at particle packing fractions beyond jamming. As a consequence, colloidal and granular systems behave very similarly under these conditions. At sufficiently high compression of the microgel particles, their polymeric nature sets the scale of the osmotic pressure and shear modulus of the whole packing, in direct analogy with macroscopic, continuous polymer gels. This observation suggests that the particulate nature of microgels is inconsequential for their linear elasticity in a highly packed state. In contrast, the particulate nature of the microgels does become essential when the packed suspensions are forced to yield and flow; here, the differences between colloidal- and granular-scale particles are marked.
1 Introduction
Microgels are particles composed of a cross-linked polymer network swollen with solvent.1 In contrast to colloids that are composed of incompressible and undeformable solids, microgels can be both compressed and deformed to a degree that is determined by their internal cross-link density.2 As a result, they can be packed to effective volume fractions much greater than the random close packing limit for hard spheres.3 At such packing, the particles become trapped in cages formed by their neighbors; this leads to an apparent glass transition into a jammed state. Nonetheless, even at these high particle volume fractions, thermally activated particle rearrangements still exist,4 allowing the system to accommodate stresses applied from outside. However, the precise nature of these particle rearrangements in jammed microgel packing remains elusive, precluding a full understanding of their properties. Moreover, it is difficult to disentangle effects of internal properties of the particles, such as their deformability and compressibility, and properties of their surfaces that influence inter-particle interactions.5 An effective means to distinguish these effects is to compare the behavior of small, colloidal-scale, and larger, granular-scale microgels.Here we explore the rheology of both colloidal- and granular-scale microgel particles to reveal how important purely thermal events are in governing the elasticity of microgel suspensions. We find that the linear elasticity and the osmotic pressure show identical scaling for both colloidal- and granular-scale microgel suspensions. In contrast, when the dense suspensions are forced to yield and flow, colloidal systems behave significantly different from their granular counterparts. The flow curves of the colloidal particles can be collapsed by rescaling with an effective relaxation time, while the data for the granular-scale particles cannot be collapsed, since these suspensions do not exhibit any zero-shear relaxation due to their non-Brownian character.
2 Experimental
2.1 Microgel preparation by precipitation polymerization
Three different batches of colloidal-scale microgel particles consisting of poly(N-isopropylacrylamide-co-acrylic acid) (p(NIPAAm-co-AAc)) are synthesized by precipitation polymerization.6 For this purpose, a mixture of N-isopropylacrylamide (NIPAAm, Acros Organics), acrylic acid (AAc, Fluka), and N,N′-methylenebisacrylamide (BIS, Sigma) is dissolved in 800 mL of deionized water. The total amount of these reagents is held constant at 8 g (95 wt% NIPAAm and 5 wt% AAc), whereas the relative amounts of cross-linker studied include 0.1, 1, and 10 wt% relative to the monomer; this allows us to vary the stiffness of the microgels. The solution is heated and maintained at 70 °C and mixed under nitrogen flow for 30 minutes. After complete dissolution of all compounds, an initiator mixture composed of 800 mg of ammonium and potassium persulfate (50/50, w/w) is added under continuous agitation, leading to immediate initiation of the polymerization. Due to precipitation of the growing polymer chains, the solution becomes turbid after a few minutes. After 3 h, the reaction is quenched and the suspension gently cooled. Some coagulum that is formed during the reaction is removed by filtration. At ambient temperature, below the lower critical solution temperature (LCST) of the copolymer, the microgel particles are swollen, as evidenced by low solution turbidity. While the suspensions of very soft particles become translucid, those of highly cross-linked microgels appear milky.To remove unreacted compounds, the particles are purified by dialysis against deionized water for 5 days (SpectraPor regenerated cellulose membrane, MWCO 12–14 kDa); during the dialysis, successive heating–cooling cycles are used to induce particle collapse and re-swelling. Finally, the particle suspensions are dialyzed against phosphate buffer (pH = 8.5 at 20 mM) for two days. Suspending the particles in this buffer at slightly basic pH ensures purely repulsive interactions between the microgel particles,7 and the relatively high ionic strength ensures that electrostatic repulsion is short ranged. The average particle diameter, measured in dilute solution by dynamic light scattering, is (2 ± 0.5) μm at 4 °C in phosphate buffer.
2.2 Microgel preparation by droplet-based microfluidics
Granular-scale microgel particles with sizes between 100 and 400 μm are synthesized using monodisperse emulsion templates formed with microfluidic devices. Both flow-focusing glass microcapillary devices and cross-junction microchannels stamped into polydimethylsiloxane (PDMS) elastomers are employed; the production and working principle of these microfluidic devices are detailed elsewhere.8,9For the production of p(NIPAAm-co-AAc) microgels, monomer solutions are emulsified in glass microcapillary devices with a tip diameter of 120 μm. These solutions contain a total of 100 g L−1 of NIPAAm (Acros Organics), AAc (Fluka), and BIS (Sigma), along with 2 g L−1 of ammonium persulfate in water. Again, the composition of the monomer mixture is varied to produce particles of different stiffness, using a constant amount of 5 wt% of AAc and a cross-linker concentration of either 1 or 10 wt%. The continuous phase for the microfluidic emulsification is a mixture of kerosene (99 vol%) and N,N,N′,N′-tetramethylethylenediamine (TEMED, 1 vol%), containing 80 g L−1 of surfactant PGPR90 (Danisco). Pumping these fluids into the microfluidic device with volume flow rates of 1.2 mL h−1 for the continuous and 0.4 mL h−1 for the dispersed phase leads to the formation of ∼130-μm droplets of the aqueous phase dispersed in the continuous hydrocarbon phase. The flow rates are adjusted with syringe pumps (Harvard Apparatus PhD 2000), and analytical glass syringes (Hamilton Gastight) and polyethylene tubing (Scientific Commodities) are used for fluid supply. To monitor the droplet formation, the microfluidic devices are operated on an optical microscope equipped with a digital camera with a fast shutter that creates a strobing effect (Sony XCD-V50).
Once formed, TEMED penetrates into the droplets from the continuous phase, triggering a free-radical cross-linking copolymerization of the monomers which gels the drops. To complete this reaction, the emulsion is stored at room temperature overnight, and the resultant microgels are transferred into plain water by removing the organic phase, washing them five times with isopropanol, three times with cold 1,4-dioxane, and five times with cold water, allowing the microgels to sediment between each of these washing steps.
To produce large amounts of such particles, which is a prerequisite for bulk rheology experiments, this experiment is repeated ten times, emulsifying approximately 5 mL of the monomer phase in 15 mL of the organic phase, respectively. This procedure yields ten stocks of p(NIPAAm-co-AAc) microgels which are stored in water or in phosphate buffer at 4 °C. Particle-size distributions are determined from optical micrographs of the particle suspensions, analyzed using ImageJ software. The particle size depends on both the solvent and the cross-link density: we find d = 210 μm in water and 150 μm in buffer (10% BIS), as well as d = 400 μm in water and 210 μm in buffer (1% BIS), all measured at 4 °C. The polydispersity of the particle size is approximately 5% for all batches.
In addition to the p(NIPAAm-co-AAc) microgels, polyacrylamide (pAAm) microgels are produced with a similar method: two different monomer solutions are emulsified in PDMS-based microfluidic channels with a rectangular cross-section and a uniform channel width and height of 100 μm, as illustrated in Fig. 1. These solutions contain a total of 100 g L−1 of acrylamide (Sigma) and BIS, along with 1 g L−1 of ammonium persulfate. Again, cross-linker concentrations of either 1 or 10 wt% are used. The continuous phase in these experiments is a fluorocarbon oil (HFE 7500, 3M) containing 1 vol% of TEMED and 18 g L−1 of the ammonium salt of surfactant Krytox 157 FSL (Dupont). The fluids are supplied with volume flow rates of 3.3 mL h−1 for the continuous and 1.3 mL h−1 for the dispersed phase. This leads to the formation of 100-μm droplets of the aqueous phase dispersed in the continuous fluorocarbon phase; gelation of these drops occurs overnight.
 | ||
| Fig. 1 Droplet-based microfluidic production of pAAm microgels. (A) A PDMS-based microfluidic device with a cross-junction channel is used to form monodisperse pre-microgel droplets of an aqueous solution of AAm, BIS, and APS. The continuous phase is a fluorocarbon oil that contains a surfactant and TEMED. Right after droplet formation, TEMED penetrates into the droplets and triggers their free-radical gelation. (B) Pre-microgel emulsion obtained from the experiment shown in panel (A). After complete gelation (12 hours at room temperature), the microgel particles are isolated from the oil phase and suspended in water, where they swell to their equilibrium size dependent on their degree of cross-linking. (C) Aqueous microgel suspension with particles cross-linked with 10% BIS. (D) Aqueous microgel suspension with particles cross-linked with 1% BIS. All micrographs are recorded at room temperature. The scale bar denotes 100 micrometres and applies to all panels. | ||
The resultant pAAm particles are consecutively washed with fluorocarbon oil containing 20 vol% of perfluorooctanol (Aldrich), plain fluorocarbon oil, hexane containing 1 wt% of surfactant Span 80 (Aldrich), plain hexane, water containing 0.1 wt% of surfactant Triton X (Aldrich), and plain water. Again, this experimental scheme is repeated ten times, emulsifying 8 mL of the monomer phase in 20 mL of the organic phase, respectively, yielding ten stocks of pAAm microgels which are stored in water at 20 °C. These particles have diameters of 120 μm (10% BIS) and 240 μm (1% BIS) at 20 °C, with a particle size polydispersity of about 5%.
2.3 Osmotic stress experiments
The mechanical properties of the microgel suspensions under isotropic compression are determined with osmotic stress experiments. Microgel suspensions are transferred into dialysis membranes (SpectraPor regenerated cellulose membrane, MWCO 12–14 kDa) and immersed in different solutions of polyethylene glycol (PEG, 20 kg mol−1) in phosphate buffer. The relationship between the PEG concentration and the resultant osmotic pressure has been calibrated previously.10 The microgel suspensions are osmotically stressed to a range of 1 to 200 kPa. After equilibration for one week, aliquots are withdrawn. The overall polymer concentration in the equilibrated sample is determined by measurement of the wet and dry weight after evaporation of all solvent.2.4 Shear rheology
Rheological measurements are performed on a stress-controlled rheometer (Anton Paar MCR 501) in a plate–plate geometry. We use roughened surfaces to prevent wall slip. This is necessary, since rheological measurements on microgel pastes can be dramatically affected by wall-slip on smooth surfaces when applying stresses close to and below the yield stress.11–13 These unwanted events are suppressed by the use of a rough geometry; we accomplish this by sandblasting both plates, which creates a roughness in the order of 50 μm. The effective suppression of wall-slip in our microgel systems is assessed by the absence of its usual signature in flow experiments: while progressively decreasing the shear rate, we observe a monotonic decrease of the shear stress until it reaches the sample yield stress, without any abrupt drop.12For accuracy, the gap between the plates must be large compared to the particle size; this prevents the use of a cone–plate geometry, in which the gap below the central truncation is much smaller than the granular-scale particles investigated in this work. For the colloidal-scale particles, a sufficient plate–plate distance is 0.5 mm. For the granular-scale systems we choose a gap of 1 mm due to constraints in sample volume; this is still approximately 10× the particle size for most cases. Frequency sweeps are performed from 0.05 to 100 rad s−1 at 1% strain, followed by strain sweeps from 0.1 to 1000% at a constant frequency of 1 rad s−1. Flow curves are obtained for shear rates ranging from 100 to 0.001 s−1. The measuring protocol is programmed such that only apparent steady-state data are obtained; this is achieved by keeping the shear rate constant until the variation in stress is smaller than 5% over a few seconds, which results in acquisition times from about 10 s (highest shear rate) to more than 50 s (lowest shear rate). For the p(NIPAAm-co-AAc) particles (colloidal- and granular-scale), these experiments are conducted at 4 °C to ensure good solvent quality for the thermo-sensitive p(NIPAAm-co-AAc) copolymer, while the pAAm particles (granular-scale only) are probed at 20 °C. In all cases, a solvent trap is used to avoid solvent evaporation. As colloidal suspensions of microgels show ageing,14 all suspensions are rejuvenated by strong shearing (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 50 s−1) for 60 s and left to relax for 15 minutes before commencing any measurement. This procedure eliminates any history dependence of the results.
= 50 s−1) for 60 s and left to relax for 15 minutes before commencing any measurement. This procedure eliminates any history dependence of the results.
3 Results and discussion
3.1 Equation of state
Upon compression of a suspension of microgels by equilibration against an external osmotic pressure, the particles are squeezed together and deform one another, as shown for colloidal-scale p(NIPAAm-co-AAc) microgels in Fig. 2, and for granular-scale polyacrylamide (pAAm) microgels in Fig. 3. Even though these microgels are sufficiently monodisperse to crystallize, the osmotic stress is increased so rapidly that ordered structures are precluded in both the colloidal- and the granular-scale systems. To monitor the deformation of the microgel particles in greater detail, we visualize the granular-scale particles by optical microscopy. With increasing compression, the extent of deformation of these particles increases, facets are formed between the particles, and their size decreases as the microgels expel solvent, as shown in Fig. 3. However, since the original particle volume is known and since the amount of polymer inside the microgels remains unchanged, the microgel packing fraction can be calculated. Alternatively, the overall polymer concentration in the suspensions can be taken as a measure of the particle packing fraction; we follow this approach. | ||
| Fig. 2 DIC micrograph of colloidal p(NIPAAm-co-AAc) microgels cross-linked with 10 wt% BIS upon compression with an external osmotic pressure of Π = 1.33 kPa. The scale bar denotes 10 micrometres. | ||
 | ||
| Fig. 3 Optical micrographs of pAAm microgel particles cross-linked with 1% BIS after exposure to different external osmotic pressures. All micrographs were recorded at room temperature. The scale bar denotes 200 micrometres and applies to all panels. | ||
As the polymer concentration first increases, we observe a sharp increase in the osmotic pressure; this is followed by a more gradual increase with a constant slope, as shown in Fig. 4. The polymer concentration at which the initial onset occurs increases with increasing cross-link density; however, both colloidal- and granular-scale microgel particles exhibit the same general behavior for a given cross-link density, despite the significant differences in their particle number densities, n. There is just a markedly stronger scattering in the data for the granular-scale systems, which we attribute to particle rearrangements that occur due to gravitational forces, for which the granular-scale systems are sensitive. Nevertheless, there is no evidence of a divergence or plateau in the osmotic pressure as the concentration continues to increase; this implies that the microgel particles behave differently from incompressible solid particles in a suspension, where the osmotic pressure diverges with increasing concentration,15 or liquid droplets in an emulsion, where the osmotic pressure reaches a plateau with increasing concentration.16
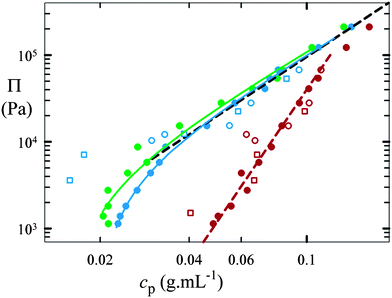 | ||
| Fig. 4 Osmotic pressure, Π, as a function of the polymer concentration, cp, in compressed microgel suspensions. Full symbols: colloidal-scale particles; empty symbols: granular-scale particles. Circles represent p(NIPAAm-co-AAc) microgels at cross-linker contents of 0.1 (green), 1 (blue), and 10 wt% (dark red); squares represent pAAm microgels at cross-linker contents of 1 (blue) and 10 wt% (dark red). The black dashed line represents the scaling prediction for an uncross-linked, semi-dilute polymer solution, Π ∼ cp9/4. The curved lines are calculated with the Flory–Rehner theory for macroscopic gels as detailed in the ESI†; they resemble the behavior of the 0.1 (green line) and 1% (blue line) cross-linked systems. However, this calculation fails for the 10% cross-linked data, which are represented by a power law (dashed dark red line) with an exponent of 5 instead. | ||
In the highly compressed regime, we observe that the osmotic pressure of each microgel suspension, both colloidal-scale and granular-scale, approaches an asymptotic power-law increase with polymer concentration, with an exponent close to 9/4, as illustrated by the dashed line in Fig. 4; this is exactly what is predicted for an uncross-linked, semi-dilute polymer solution.17,18 It thus appears that in this regime, the microgels are so strongly compressed that the chains in the polymer network behave as if they were fully relaxed in a semi-dilute solution. As a result, the osmotic pressure arises from mixing of the solvent and polymer alone, as it would in a semi-dilute solution. In contrast, at low particle concentration and therefore low compression, the systems deviate from this behavior, and an initial steep rise in the osmotic pressure is observed. This is due to the additional effect of internal elastic forces resulting from the network chain stretching, which balances the internal osmotic pressure from the polymer–solvent interaction.
Within this conceptual picture, we can describe the equation of state of the compressed microgel systems: just as in macroscopic, continuous polymer gels, the swelling and osmotic compressibility of compressed microgel suspensions can be described by the Flory–Rehner theory,19,20 which models the osmotic pressure of a gel as the sum of a mixing and an elastic component, Π = Πm + Πe, as detailed in the ESI†. In a good solvent, the polymer–solvent interactions are energetically favored, and the mixing term is always positive. The elastic term, however, opposes swelling: it is negative and gains significance with increasing network chain stretching, which is reduced by external compression of the microgels. As a result, this term plays an important role only in the initial steep part of the concentration-dependent osmotic pressure in Fig. 4.
The applicability of the Flory–Rehner theory to the microgel suspension is a consequence of the high degree of microgel compression: in a strongly compressed state, once the contact geometry of the suspension is fixed, the only way for the system to equilibrate with an externally applied pressure is to expel solvent; this is a direct analogy to the response of a macroscopic continuous gel to an external pressure. In contrast, a different situation is encountered upon dilution: in a dilute state, a macrogel will be fully swollen and cannot take up more solvent. For a microgel suspension, however, this is different, because even beyond full swelling of the microgel particles, the system can take up more solvent by breaking the packed microgel suspension into a suspension of isolated particles.
This concept does not include any arguments about the particle size. Hence, it describes the experimental results for both the colloidal-scale microgels and the granular-scale microgels. This can be understood by a calculation of the relevant stresses: the stress scale for deformation of a microgel particle is given by the modulus kBT/ξ3, with ξ the average mesh size of the polymer network. This is much larger than the osmotic pressure originating from collisions with neighboring particles, kBT/a3, with a the particle size. Hence, the equation of state of a microgel suspension is dominated by the microgel network elasticity, independent of the microgel size.
Only the behavior of very stiff particles, cross-linked with 10 wt% BIS, is different. We postulate that this deviation is due to failure of the ideal chain hypothesis for the short network strands in these microgels. Instead of following the Flory–Rehner prediction, these data are better represented by a power-law scaling of the osmotic pressure as a function of the polymer concentration. However, even though the behavior of these stiffer particles deviates from ideal rubber theory, there is again no difference in the behavior of colloidal-scale and granular-scale particles.
3.2 Shear elasticity
To explore whether macrogel-type behavior of compressed microgel suspensions is also observed in shear deformation, we probe these systems through oscillatory shear rheology at low deformation (1%). Frequency-dependent measurements on the colloidal-scale microgel suspensions show a nearly frequency-independent plateau in the storage modulus, G′, while the loss modulus, G′′, which is significantly smaller, exhibits a distinct minimum, as shown for a suspension of colloidal-scale p(NIPAAm-co-AAc) microgels cross-linked with 1 wt% BIS in Fig. 5a. This response, which has also been observed in other soft glassy materials,16,21,22 can be attributed to two competing processes: particle rearrangements, which become less important with increasing frequency, and viscous dissipation of the solvent which increases with frequency.16 The viscous loss of most soft glassy materials is large compared to the loss that originates from pure solvent viscosity. This difference can be explained by considering that particles can slip against each other. For randomly and loosely packed incompressible objects such as droplets in an emulsion, the loss modulus scales with ω1/2 at high frequencies.23 Despite the limited frequency-range investigated here, we observe that the less-packed colloidal-scale microgel suspensions apparently follow this behavior, whereas for the more concentrated systems, the loss modulus scales with ω with a smaller exponent at high frequencies (approximately 1/3). This suggests that the behavior of microgel suspensions is similar to that of emulsions only in the limit of low compression.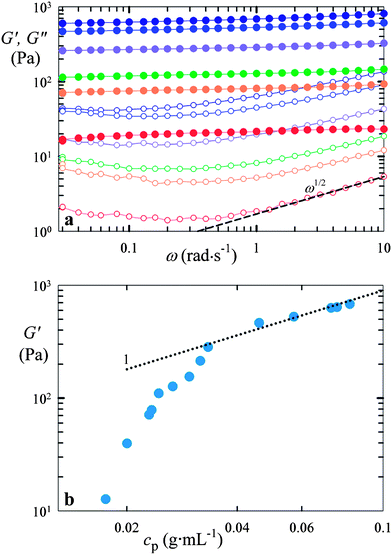 | ||
| Fig. 5 Rheological behavior of a suspension of colloidal-scale p(NIPAAm-co-AAc) microgels cross-linked with 1 wt% BIS. (a) Selected frequency sweeps of the elastic (G′, full symbols) and viscous (G′′, open symbols) part of the complex shear modulus at increasing particle compression, and hence, increasing polymer concentration (from bottom to top). The dashed line represents the power ½ scaling prediction. (b) G′ (ω = 1 rad s−1) as a function of the polymer concentration in the microgel suspension, cp. The dotted line represents a fit of the upper part of the dataset to the scaling prediction according to the theory of rubber elasticity, G ≈ G′ ∼ (cp/N) kBT.20 | ||
The plateau shear modulus, determined at a frequency of 1 rad s−1, increases with increasing polymer concentration, as shown for a suspension of colloidal-scale p(NIPAAm-co-AAc) microgels cross-linked with 1 wt% BIS in Fig. 5b. For a macroscopic, continuous gel, the theory of rubber elasticity predicts G = νkBT = C[Na/(MmN)]kBT,20 with ν the number density of elastically active chains, C the polymer concentration (in g m−3), Na the Avogadro number, Mm the monomer molecular weight (in g mol−1), and N the number of monomer units in each polymer chain between cross-links. By comparison with the microgel data, we find that both the colloidal- and granular-scale systems follow this macrogel-type behavior, showing linear scaling of G′ with C (or equivalently cp) at sufficiently high compression. From a linear fit of this high concentration regime, we determine the value of N. We find N = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 2200, and 250 for our soft, intermediate, and stiff p(NIPAAm-co-AAc) particles (Mm = 111 g mol−1), and N = 1560 and 390 for our intermediate and stiff pAAm particles (Mm = 71 g mol−1), respectively. Rescaling with N allows us to represent all the data on a single graph. Again, we find that dense systems of granular-scale particles exhibit the same behavior as suspensions composed of colloidal-scale particles, as shown in Fig. 6. Moreover, the behavior is independent of the specific chemistry of the microgels, because both p(NIPAAm-co-AAc) and pAAm display the same behavior.
000, 2200, and 250 for our soft, intermediate, and stiff p(NIPAAm-co-AAc) particles (Mm = 111 g mol−1), and N = 1560 and 390 for our intermediate and stiff pAAm particles (Mm = 71 g mol−1), respectively. Rescaling with N allows us to represent all the data on a single graph. Again, we find that dense systems of granular-scale particles exhibit the same behavior as suspensions composed of colloidal-scale particles, as shown in Fig. 6. Moreover, the behavior is independent of the specific chemistry of the microgels, because both p(NIPAAm-co-AAc) and pAAm display the same behavior.
 | ||
| Fig. 6 Elastic shear modulus of compressed microgel suspensions, G′(ω = 1 rad s−1), as a function of the polymer concentration, cp, normalized by the average length of the elastically active network chains, N. Full symbols: colloidal-scale particles of p(NIPAAm-co-AAc) at cross-linker contents of 0.1 (green), 1 (blue), and 10 wt% (dark red). Empty symbols: granular-scale particles of p(NIPAAm-co-AAc) (circles) and pAAm (squares) at cross-linker contents of 1 (blue) and 10 wt% (dark red). Data in the high concentration limit of each system follow the prediction from the theory of rubber elasticity, G ≈ G′ ∼ (cp/N) kBT,20 represented by the dashed line. | ||
Despite the analogy of this result to the macrogel-type behavior under osmotic compression, the shear elasticity of concentrated microgel suspensions is more complex: while macrogel-type behavior of the osmotic compressibility according to the Flory–Rehner prediction is found in the entire range of concentrations investigated here, the signature of a macroscopic polymer system is found only at high microgel compression in shear. The concentration at which macrogel-type behavior is first observed increases with the particle stiffness: it is 0.020, 0.033 and 0.082 g mL−1 for the soft, intermediate, and stiff microgels, respectively. Below this high level of compression, the shear properties of the compressed microgel suspensions do not resemble that of a macroscopic polymer gel. In contrast, the shear modulus increases steeply, unlike a macroscopic continuous gel, and instead, more analogous to a packing of emulsion droplets above the jamming transition.16 Thus, local slipping and sliding of the particles can accommodate the imposed shear strain, significantly reducing the mechanical energy required to accomplish a deformation; this results in a lower shear modulus and a higher viscous modulus. However, these local events are quenched by further compression. When the density of particles increases, the length scale of these cooperative local relaxation modes increases,4 and the mechanical energy required to induce such rearrangements increases, thereby decreasing their likelihood. At a certain level of compression, these local modes become so unfavorable that the entire material deforms affinely, and the correlation length reaches the order of the sample, such that there is no difference in the local versus global properties of the suspensions.
Our data also suggest that the softness of the particles plays a crucial role in these non-affine relaxation mechanisms. The initial steep rise of the shear modulus with concentration can be described by a power law (for greater clarity, lines are not shown in the graph in Fig. 6). For the softer particles, the increase of rigidity with concentration is much weaker than for stiffer particles, and the power-law exponent in G0′(cp) increases from 4.4 to 6.1 and 14 when going from soft to stiff colloidal particles. Again, this behavior is independent of particle size, as shown in Fig. 6.
3.3 Non-linear behavior
Macroscopic polymer gels can support only a limited deformation and break when the yield strain is exceeded. In contrast, this cannot be the case for suspensions of microgels, even though they behave as continuous polymer gels in the linear regime. The covalent bonds within each gel particle are orders of magnitude stronger than the physical interactions between the microgels. Yielding of a microgel suspension is therefore the result of the disruption of the contacts between particles, eventually resulting in a shear-melted, fluid-like state.24 This transition from a solid-like state at rest to a fluid-like state under flow can be probed by strain sweeps. In these experiments, both colloidal-scale and granular-scale systems exhibit the features of a soft glassy material:25,26 with increasing strain, the elastic modulus remains constant, ultimately decreasing when the material yields. Additionally, the loss modulus exhibits a peak when yielding occurs, reflecting the energy dissipation.Depending on the microgel concentration and cross-linking density, the magnitudes of the storage and loss moduli in these strain sweeps vary by more than three orders of magnitude, as shown for various colloidal-scale p(NIPAAm-co-AAc) microgel suspensions in Fig. 7a. Nevertheless, all these strain sweeps exhibit the same shape and can be superimposed by rescaling the storage modulus G′ by its plateau value G0′, the loss modulus G′′ by its maximum Gmax′′, and the strain γ by the yield strain γy, taken as the strain at the peak of the loss modulus; this yields a single master curve as shown in Fig. 7b. This result shows that the transition from a solid-like to a fluid-like state occurs in a similar fashion for all colloidal microgel suspensions, independent of their particle concentration and particle softness.
 | ||
| Fig. 7 G′ (full symbols) and G′′ (open symbols) of compressed microgel suspensions measured as a function of the deformation γ. Colors represent different degrees of microgel cross-linking: 0.1 (green), 1 (blue), and 10 wt% (dark red). (a) Data obtained from various samples of colloidal-scale particles with different cross-link densities and different levels of osmotic compression, chosen to cover a wide range of resultant suspension moduli. (b) Same curves after rescaling G′ by the plateau modulus G0′, G′′ by its maximum value for each curve, Gmax′′, and the strain by the yield strain defined as the strain at Gmax′′. (c) Similar data obtained for granular-scale particles consisting of pAAm (squares) and p(NIPAAm-co-AAc) (circles) after rescaling. | ||
For the granular-scale microgels we find a similar behavior, as shown in Fig. 7c. However, we observe differences between the granular-scale microgels of p(NIPAAm-co-AAc) and of pAAm, which we attribute to the frictional contribution to the viscous dissipation during yielding: if the microgel particles behave as a core structure covered by a shell of polymer brushes,5 the frictional forces might be more dependent on the quality of the polymer–solvent interaction, and thus on the microgel chemistry.27 Whereas colloidal-scale particles are still subjected to Brownian motion within their cages and maintain their individuality,5,28 granular-scale particles do not, which results in a greater polymer brush interpenetration of their shell.
The main parameter that characterizes a particulate system is the particle volume fraction. However, for soft microgels, this parameter does not account for particle compression. It is thus expedient to define a packing fraction ζ = nVd, where n is the number density of particles per unit volume and Vd is the volume of a fully swollen single particle in the dilute limit. The relation cp = ζ(Vd/mp) links ζ and cp; here, mp is the polymer weight contained in one particle. The ratio Vd/mp, also called particle voluminosity, is also a characteristic parameter of the system. For the colloidal-scale particles, we determine this quantity in the dilute regime (ζ < 0.25) by mapping the viscosity of dilute suspensions onto the Einstein–Bachelor relation.29 These viscosity measurements are performed in a double-gap Couette geometry on at least five suspensions of known polymer concentration. Determining the voluminosity of the particles from these experiments allows us to convert the polymer concentration into an effective packing fraction ζ. For the granular-scale particles, Vd can be derived from optical micrographs of the swollen particles. The voluminosity is obtained from the known volume and concentration of the pre-microgel droplets during the microfluidic particle synthesis, assuming that the monomers polymerize completely.
It appears that the yield strain of the colloidal-scale microgel suspensions increases with the packing fraction ζ, as illustrated in Fig. 8. Strong data scattering is observed for packing fractions below 3, possibly due to the non-deterministic nature of yielding in thermal systems. However, if observed on the whole range of ζ investigated, this trend suggests that the material is more resistant to yielding at high particle concentration. In this disordered packing, zones of lower mechanical rigidity will nucleate yield planes ultimately leading to flow. At low strain, these same defects are responsible for the ω1/2 scaling of the loss modulus at high frequencies seen in Fig. 5a.23
 | ||
| Fig. 8 Yield strain, γy, versus microgel packing fraction, ζ, for suspensions of colloidal- and granular-scale microgels. Full symbols: colloidal-scale particles of p(NIPAAm-co-AAc) at cross-linker contents of 0.1 (green), 1 (blue), and 10 wt% (dark red). Empty symbols: granular-scale particles of p(NIPAAm-co-AAc) (circles) and pAAm (squares) at cross-linker contents of 1 (blue) and 10 wt% (dark red). The dashed black line is a guide to the eye with a slope of 9. | ||
Close to the jamming transition, where the material is at the verge of mechanical instability, these slip planes are numerous, and the material yields at very low strain. As the packing fraction increases, the number of slip planes decreases and the yield strain increases. It appears that only the packing fraction is important in this argument, since a universal behavior is found irrespective of the microgel softness, as illustrated in Fig. 8. However, this behavior is again different for the granular-scale systems: while p(NIPAAm-co-AAc) shows significant elastic deformation before yielding, this is not the case for the pAAm microgels, which yield at lower deformations despite similar packing fractions. Again, this discrepancy suggests that in these granular-scale systems the extent of friction at the particle interfaces seems to play a significant role, and that this is dependent on the type of polymer used to form the microgels.
Upon yielding, the characteristic timescale is set by the competition between elastic restoring forces exerted by the surrounding particles, which scales with G0, and by interparticle friction. These properties can be probed in a steady-state flow experiment, in which the shear rate of a flowing paste is progressively reduced. Since flowing is a particularly out-of-equilibrium state, the properties of flowing microgel suspensions strongly depend on the experimental procedure used; hence, reaching a real steady state can be difficult. To account for this, each paste is first rejuvenated at a shear rate of 60 s−1 and then left to relax for 15 min. Then, a shear rate of 100 s−1 is imposed and progressively reduced in 50 successive steps to 0.001 s−1. For each step, we do not impose a constant waiting time, but let the rheometer reach a steady state before conducting the measurement. This ensures reproducible experiments, relatively close to a steady state on a reasonable timescale.
In a steady state, elastic restoring forces can be approximated by the plateau modulus, G0, while interparticle friction can be assimilated with the viscous drag flow that occurs in the thin film of solvent which separates the particles and therefore scales with the solvent viscosity.28 Consequently, it is possible to rescale all the flow curves using independently measured values of the shear modulus G0 and the yield stress σy. For the colloidal-scale systems, this rescaling gives a reasonable superposition of the original flow curves obtained at different packing fractions, yielding a single master curve, as shown for colloidal-scale p(NIPAAm-co-AAc) microgels cross-linked with 10 wt% BIS in Fig. 9a. In contrast, for the granular-scale systems, the zero-shear relaxation time is infinitely long due to the absence of Brownian motion of the particles, and thus a similar master curve cannot be obtained, as seen for granular-scale microgels with a similar composition in Fig. 9b. In addition, the yield stress estimated from the onset of flow at low shear rate differs from that determined on the same samples in an oscillatory amplitude sweep. This can again be attributed to the large size of the particles and reflects the importance of interparticle friction in these samples: in a static suspension of these particles, yielding involves the separation of their interpenetrated surficial polymer brushes. If these brushes are already disintegrated in a flowing system, the yield stress determined by progressively decreasing the stress on the flowing material is significantly lower than that determined by increasing the stress on the same material at rest.
 | ||
Fig. 9 Flow curves for microgel suspensions of p(NIPAAm-co-AAc) microgels cross-linked with 1 wt% BIS. The shear stress σ is rescaled by the yield stress σGmax′′, and the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) by the plateau modulus G0. (a) Colloidal-scale particles and (b) granular-scale particles. Suspensions compressed at increasing osmotic pressures are represented by different colors, from dark blue to blue-green. Insets: unrescaled curves. by the plateau modulus G0. (a) Colloidal-scale particles and (b) granular-scale particles. Suspensions compressed at increasing osmotic pressures are represented by different colors, from dark blue to blue-green. Insets: unrescaled curves. | ||
Conclusions
We have investigated the osmotic compressibility and shear deformation of dense packing of small, colloidal-scale microgel particles and compared their behavior to that of larger, granular-scale microgel particles. The mechanics of both systems exhibits a transition from a particulate suspension to a continuum macrogel as the particle concentration increases and the particles become deformed; as a result, densely compressed microgel suspensions behave as bulk polymer networks. This behavior is observed for both colloidal-scale and granular-scale microgels independent of their size; it is also independent of the type of polymer used to form the microgels. In contrast, the same microgel suspensions can flow if they are forced to yield; in this state, the particulate nature of the system governs its properties and the particle size and particle composition make a marked difference: colloidal-scale particles, which are still subject to Brownian motion even in a jammed state, remain separated from each other by a thin solvent layer; in contrast, granular-scale particles become interpenetrated due to the polymer brushes on their surfaces. Therefore, the interparticle friction controls the dynamics of the particle rearrangements and determines the flow properties. Thus, the flow curves of the two types of samples behave qualitatively differently.Acknowledgements
This work was supported by the NSF (DMR-1006546) and the Harvard MRSEC (DMR-0820484). PM thanks Agropolis Foundation for financial support. SS was a research fellow of the German Academy of Sciences Leopoldina (BMBF-LPD 9901/8-186) and is now a Liebig fellow of the Fund of the Chemical Industry (Germany). JS acknowledges the Netherlands Organization for Scientific Research (NWO) for funding.References
- W. Funke, O. Okay and B. Joos-Muller, Adv. Polym. Sci., 1998, 136, 139–234 CrossRef.
- D. M. Heyes and A. C. Branka, Soft Matter, 2009, 5, 2681–2685 RSC.
- A. Le Grand and G. Petekidis, Rheol. Acta, 2008, 47, 579–590 CrossRef CAS.
- D. A. Sessoms, I. Bischofberger, L. Cipelletti and V. Trappe, Philos. Trans. R. Soc., A, 2009, 367, 5013–5032 CrossRef CAS.
- F. Scheffold, P. Diaz-Leyva, M. Reufer, N. Ben Braham, I. Lynch and J. L. Harden, Phys. Rev. Lett., 2010, 104, 128304 CrossRef.
- K. Kratz, T. Hellweg and W. Eimer, Colloids Surf., A, 2000, 170, 137–149 CrossRef CAS.
- J. K. Cho, Z. Y. Meng, L. A. Lyon and V. Breedveld, Soft Matter, 2009, 5, 3599–3602 RSC.
- R. K. Shah, J. W. Kim, J. J. Agresti, D. A. Weitz and L. Y. Chu, Soft Matter, 2008, 4, 2303–2309 RSC.
- R. K. Shah, H. C. Shum, A. C. Rowat, D. Lee, J. J. Agresti, A. S. Utada, L. Y. Chu, J. W. Kim, A. Fernandez-Nieves, C. J. Martinez and D. A. Weitz, Mater. Today, 2008, 11, 18–27 CrossRef CAS.
- http://www.brocku.ca/researchers/peter_rand/osmotic/osfile.html .
- S. P. Meeker, R. T. Bonnecaze and M. Cloitre, J. Rheol., 2004, 48, 1295–1320 CrossRef CAS.
- S. P. Meeker, R. T. Bonnecaze and M. Cloitre, Phys. Rev. Lett., 2004, 92 Search PubMed.
- J. R. Seth, M. Cloitre and R. T. Bonnecazea, J. Rheol., 2008, 52, 1241–1268 CrossRef CAS.
- M. Cloitre, R. Borrega and L. Leibler, Phys. Rev. Lett., 2000, 85, 4819 CrossRef CAS.
- W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge University Press, Cambridge, UK, 1989 Search PubMed.
- T. G. Mason, J. Bibette and D. A. Weitz, Phys. Rev. Lett., 1995, 75, 2051–2054 CrossRef CAS.
- J. des Cloizeaux, J. Phys., 1975, 36, 281–291 CAS.
- P. G. de Gennes, Adv. Colloid Interface Sci., 1987, 27, 189–209 CrossRef CAS.
- P. J. Flory and J. Rehner, J. Chem. Phys., 1943, 11, 521–526 CrossRef CAS.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, NY, 1953 Search PubMed.
- T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 74, 1250–1253 CrossRef CAS.
- T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 75, 2770–2773 CrossRef CAS.
- A. J. Liu, S. Ramaswamy, T. G. Mason, H. Gang and D. A. Weitz, Phys. Rev. Lett., 1996, 76, 3017–3020 CrossRef CAS.
- T. Divoux, D. Tamarii, C. Barentin and S. Manneville, Phys. Rev. Lett., 2010, 104, 208301 CrossRef.
- V. Carrier and G. Petekidis, J. Rheol., 2009, 53, 245–273 CrossRef CAS.
- K. Miyazaki, H. M. Wyss, D. A. Weitz and D. R. Reichman, Europhys. Lett., 2006, 75, 915–921 CrossRef CAS.
- J. Klein, E. Kumacheva, D. Perahia, D. Mahalu and S. Warburg, Faraday Discuss., 1994, 98, 173–188 RSC.
- M. Cloitre, R. Borrega, F. Monti and L. Leibler, Phys. Rev. Lett., 2003, 90, 068303 CrossRef.
- H. Senff and W. Richtering, J. Chem. Phys., 1999, 111, 1705–1711 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c1sm06355c |
| ‡ Both authors contributed equally to this article. |
| This journal is © The Royal Society of Chemistry 2012 |
