Modeling the making and breaking of bonds as an elastic microcapsule moves over a compliant substrate
Egor A.
Maresov
a,
German V.
Kolmakov
b,
Victor V.
Yashin
a,
Krystyn J.
Van Vliet
c and
Anna C.
Balazs
*a
aChemical Engineering Department, University of Pittsburgh, Pittsburgh, PA 15261, USA
bDepartment of Physics, New York City College of Technology, City University of New York, Brooklyn, NY 11201, USA
cMaterials Science and Engineering Department, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 4th October 2011
Abstract
By integrating the lattice Boltzmann model for hydrodynamics, the lattice spring model for micromechanics of elastic solids, and the Bell model for bond formation and rupture, we examine the fluid driven motion of elastic microcapsules on compliant surfaces. The capsules, modeled as three-dimensional fluid-filled elastic shells, represent polymeric microcapsules or biological cells. We observed three regimes of capsule motion. Namely, the capsule rolls steadily along the substrate at a sufficiently high shear rate, it is stationary at a low shear rate, and exhibits an intermittent motion (saltation) at intermediate shear rates. At a given shear rate, the regime of capsule motion was found to depend on the substrate stiffness, and on the rate of rupture of the adhesive bonds. The capsule was observed to roll steadily on a sufficiently stiff substrate, and at a high rate of bond rupture. In the opposite limit of a soft substrate and low rate of bond rupture, the system was localized in the stationary regime. The findings provide guidelines for creating smart surfaces that could regulate the motion of the microcapsules.
1. Introduction
Polymeric microcapsules constitute ideal micro-carriers for a range of materials, from inks and flavorants, to cosmetics and drugs. These microcapsules permit the controlled release of the encapsulated species and thus, are useful in the food, chemical and pharmaceutical industries.1 In the vast majority of these applications, the utility of the capsules comes from their binding to substrates, and consequently, releasing the encapsulated species at these surfaces. For example, for the targeted delivery of drugs, dyes or flavorings, the capsules must bind to an interface in order to be effective. In this binding process, the mechanical compliance of both the capsule and the substrate can have a significant effect. For instance, the contact area between a compliant capsule and a surface will be greater than the contact area between a stiff capsule and that surface; hence, the more compliant capsule could be more effective in the delivery process. Similarly, a more compliant substrate can be more effective at binding the capsules and thus, improving the utility of the delivery device.Another important component in the technological uses of polymeric microcapsules1 (as well as other micro-carriers, such as liposomes2 and polymersomes3) is an imposed flow field; for example, blood flow plays a vital role in the effectiveness of microcapsules used for drug delivery. Thus, to enhance the efficacy of these micro-carriers, it becomes important to determine how the combined effects of the flow field, the compliance of the capsule, the elasticity of the substrate and binding interactions between the capsule and substrate contribute to the performance of the system. Given this number of critical variables, computational modeling provides an effective approach for pinpointing the factors that influence the system's behavior.
Herein, we take advantage of our recently developed hybrid “LBM/LSM” computational approach4–9 to model a microcapsule as a fluid-filled, elastic shell and simulate the effects of an external fluid on the motion of this capsule on a flexible substrate. In our hybrid approach, we integrate two mesoscopic lattice models, the lattice Boltzmann model (LBM) and the lattice spring model (LSM), which can be used to simulate the underlying processes that give rise to the appropriate continuum behavior. In particular, the fluid dynamics is captured via the LBM, which can be viewed as an efficient solver for the Navier–Stokes equation. More specifically, the LBM incorporates the mesoscopic physics of fluid “particles” propagating and colliding on a cubic lattice such that the averaged, long-wavelength properties of the system obey the desired Navier–Stokes equation.10
The behavior of the capsule's elastic shell is simulated using the LSM. In the LSM, an elastic material is modeled through a network of interconnected harmonic “springs”, which describe the interactions between neighboring sites. The mechanical properties of this material (e.g., the Young's modulus) can be expressed in terms of the spring constants of the harmonic springs and the spacing between the lattice sites. Notably, the large scale behavior of the resultant system can be mapped onto continuum elasticity theory.11
Our integrated LBM/LSM approach allows for a dynamic interaction between the elastic walls and the surrounding fluid. In other words, dynamically and interactively, the moving walls exert a force on the fluid and, in turn, the fluid reacts back on the walls. In this manner, we can model the complex fluid-structure interactions that occur at the boundaries between the fluid and the compliant surfaces (i.e., the capsule's elastic shell and the soft substrate). We have validated our three-dimensional (3D) LBM/LSM model by determining the drag force on a periodic array of spheres, as well as simulating the breathing mode oscillations of a single capsule.4 In both cases, the simulations showed quantitative agreement with analytical theory.4
In our previous LBM/LSM simulations of the motion of fluid-driven capsules on adhesive surfaces,4–9 we used the Morse potential to model the binding interactions between the capsule and substrate. Herein, we modify our approach by integrating the Bell model12 into the LBM/LSM to describe the formation and rupture of chemical bonds between the compliant capsule and soft substrate. The Bell model allows us to take into account the effect of an applied force (arising, for example, from an imposed flow) on the rupture of the bonds. Furthermore, we can ascribe a degree of chemical specificity to the bonds formed between the capsules and substrate. As detailed in the Methodology section, the rupture rate, kr, is an exponential function of the force applied to the bond between the capsule and the substrate. The rupture rate is also directly proportional to the off-rate constant, koff, which is an intrinsic characteristic of a chemical bond. By specifying the value of koff, we can ascribe a specific chemical character to the bond between the capsule and surface.
Notably, the Bell model has been used successfully to describe ligand-receptor interactions between biological interfaces. In particular, Hammer et al.13 have pioneered the use of the Bell model to simulate the dynamic interactions of leukocytes rolling on rigid surfaces and showed how the behavior of the leukocytes depended on the applied force and relevant rate constants. In the latter studies, the leukocytes were modeled as rigid spheres. More recently, researchers have modeled the leukocytes as compliant capsules.14,15 Nonetheless, in these different studies, the substrates were modeled as rigid surfaces.
To the best of our knowledge, the studies described herein constitute the first simulations of the interactions between mobile, compliant capsules and soft surfaces that interact through Bell bonds. These studies not only provide insight into the dynamic behavior of microcapsules on flexible substrates, but also can shed light on the factors that contribute to regulating the interactions between biological cells, such as leukocytes, and compliant interfaces. Below, we demonstrate that the compliance of the substrate can have a significant effect on the motion of the capsules. Furthermore, by examining the behavior of the system at different values of the shear rate, the Young's moduli of both the substrate and the capsule, and the chemical binding constants, we show that judicious choices in the parameter space allow one to either localize the capsule at a fixed site on the surface or drive the micro-carrier to roll along the interface. Given that different applications might necessitate different behavior, the findings provide guidelines for tailoring the system to exhibit the desired performance.
Below, we first describe our computational approach and then discuss our findings on the sensitivity of the dynamic behavior of the microcapsules to the properties of its local environment.
2. Methodology
2.1 Model
We use our hybrid LBM/LSM approach to simulate a fluid-filled, three-dimensional capsule, which is immersed in a host fluid and localized on a compliant substrate (Fig. 1). Due to an imposed shear flow, the capsule can be driven move along the substrate. The capsule's elastic, solid shell is modeled via the lattice spring model (LSM), which consists of a triangular network of harmonic springs connecting regularly spaced mass points, or nodes.4–9,11,16 The spring force Fs on node ri is equal to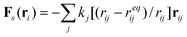 | (1) |
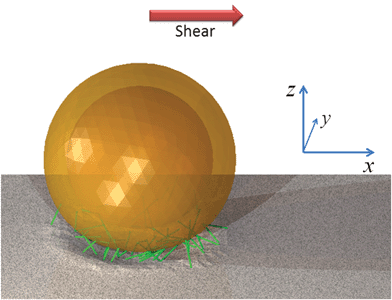 | ||
| Fig. 1 An elastic capsule adhered to a compliant substrate and surrounded by fluid with an imposed shear flow. The green lines represent the adhesive bonds formed between the capsule and substrate. | ||
The capsule's spherical shell is formed from three concentric layers of the LSM nodes. The layers were generated by triangulation of a sphere and each layer contains N = 642 nodes. The nodes within a layer are connected by springs along the edges of the triangles, and each node in a layer is connected by springs to several neighboring nodes in an adjacent layer. Hence, the shell contains a total of 14,724 springs. The distance between the layers of the shell is 1.5 ΔxLBM, where ΔxLBM is the spacing in the lattice Boltzmann model LBM (see below), so that the capsule thickness is h = 3 ΔxLBM. (The distance between the layers of the shell was chosen to be similar to the mean length of the springs within a layer to maintain the isotropic nature of the elastic properties.) The outer radius of the shell was taken to be R = 12.5 ΔxLBM.
All springs in the capsule have the same spring constant kcap, and the equilibrium length of a spring is equal to the distance between the two corresponding nodes in the undeformed state. Note that the springs can differ in their equilibrium length because they are used to model an intrinsically curved object (capsule). For small deformations, the LSM obeys linear elasticity theory and all the macroscopic elastic properties, such as the Young's modulus, shear modulus, bending rigidity, etc., are expressed in terms of the spring constants, nodal masses, and the lattice geometry.11,16,17 In particular, the Young's modulus of the capsule's shell can be estimated as Ecap ≈ 5kcap/2lcap,11 where lcap ≈ 1.94 ΔxLBM is the average equilibrium length of the springs. (We note that in order to avoid numerical fluctuations in the forces acting on the solid nodes,4,8,16 the respective LSM and LBM spacing should be chosen such that lcap ≥ ΔxLBM.)
The elastic substrate is modeled via a cubic lattice of LSM nodes, with the spacing between these nodes being ΔxLSM. The springs connect the nearest and next-nearest nodes and thus, have equilibrium lengths of ΔxLSM and 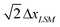 , respectively; the respective spring constants are ksub and ksub/2. The resulting Young's modulus of the substrate is Esub = 5ksub/2 ΔxLSM.11 We took ΔxLSM = ΔxLBM in the simulations.
, respectively; the respective spring constants are ksub and ksub/2. The resulting Young's modulus of the substrate is Esub = 5ksub/2 ΔxLSM.11 We took ΔxLSM = ΔxLBM in the simulations.
The dynamics of the host fluid and the fluid within the capsule are simulated using the lattice Boltzmann model (LBM). The LBM can be viewed as an efficient solver for the Navier–Stokes equation.10 Specifically, this lattice-based model consists of two processes: the propagation of fluid “particles” to neighboring lattice sites, and the subsequent collisions between particles when they reach a site. These fluid particles are representative of mesoscopic portions of the fluid, and are described by a particle distribution function fi(r,t), which characterizes the mass density of fluid particles at a lattice node r and time t propagating in the direction i with a constant velocity ci. The velocities ci in the ith direction are chosen so that fluid particles propagate from one lattice site to the next in exactly one LBM time step, ΔtLBM.
The time evolution of these distribution functions is governed by a discretized Boltzmann equation.10 To model the three-dimensional system, we use the 3DQ19 scheme, which involves a set of 19 particle velocity distribution functions at each node, and the single relaxation time approximation (the LBGK scheme).18 The hydrodynamic quantities of interest are the moments of the distribution function, i.e., the mass density ρ = ∑ifi, the momentum density j = ρu = ∑icifi, with u being the local fluid velocity, and the momentum flux Π = ∑icicifi.
In our LBM/LSM simulations, the fluid and solid phases interact through appropriate boundary conditions.4,5,16 In particular, the lattice spring nodes that are situated at the solid-fluid interface impose their velocities on the surrounding fluid; the velocities are transmitted through a linked bounce-back rule19 to those LBM distribution functions that intersect the moving solid boundary. In turn, the LSM nodes at the solid-fluid interface experience forces due to the fluid pressure and viscous stresses at that boundary. We calculate the latter force based on the momentum exchange between the LBM particle and the solid boundary, and then distribute this quantity as a load to the neighboring LS nodes. This scheme provides a means of implementing no-slip boundary conditions at the fluid-solid interface.
The capsule binds to the substrate through the formation of bonds that mimic the ligand-receptor interactions in biological systems. Each node on the capsule's outer surface can form a bond with each substrate node if the distance between the two nodes, r, is shorter than a certain cut-off radius, rcut. When the bond is formed, the interaction between the two nodes is described by the Hookean spring potential
| Ubond(r) = 1/2 κ(r − leq)2, | (2) |
| Us(r) = us exp(−r/ls) | (3) |
The bonds between the capsule and substrate can break and reform repeatedly. We utilize the Bell model12,13 to simulate the stochastic processes of bond rupture and reforming. The Bell model serves as a useful framework for describing the relationship between bond dissociation and force.21–23 The Bell model has been used widely to describe bonding interactions in various biological systems; for example, the model was utilized in characterizing the mechanical behavior of biological tissue,24 the unfolding of proteins,25 viral attachment,26,27 and adhesion of cells to surfaces.28–30 In the Bell model, the rupture rate constant, kr, is an exponential function of the force F applied to the bond, kr = koff exp(r0F/kBT). Here, koff is the rupture rate constant of an unstressed bond (the off-rate), the parameter r0 characterizes the sensitivity of the bond to stress, kB is the Boltzmann constant, and T is temperature. The force acting on a bond depends on the bond length, i.e., on the distance between the nodes, r, and is calculated by differentiating eqn (2) to obtain the following expression for the distance-dependent rate constant of rupture:
| kr(r) = koff exp[r0κ(r − leq)/kBT], | (4) |
The distance-dependent rate constant of bond reforming, kf(r), for a broken bond is determined from the principle of detailed balance as13
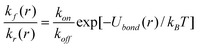 | (5) |
In the above equation, Ubond(r) is given by eqn (2), and kon is the rate constant of bond formation (the on-rate).
2.2 Model parameters
Typical radii of polyelectrolyte multilayer microcapsules are in the range of 0.5 to 10 μm.1,31 In our simulations, we assume the radius of capsule to be of R = 10 μm, so the LBM spacing corresponds to ΔxLBM = 0.8 μm since we take R = 12.5 ΔxLBM (see above). The LBM viscosity is given as μ = 1/6 Δx2LBMΔt−1LBM.10 We assume that in the dimensional units, the viscosity is equal to that of water at the room temperature, μ = 10−6 m2 s−1, so one time step of the LBM corresponds to ΔtLBM = 1.07 × 10−7 s.The fluid is located in a channel of thickness H = 45 ΔxLBM, which corresponds to the distance between the substrate and the top of the simulation box. The shear flow is generated by assigning a constant value to the fluid velocity in the X direction at the top LBM nodes; we refer to this as the wall velocity, Vw. The shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) was varied from 2 × 10−7 to 4 × 10−6 Δt−1LBM. A wall velocity of Vw = 1 × 10−4ΔxLBMΔt−1LBM corresponds to a shear rate of
was varied from 2 × 10−7 to 4 × 10−6 Δt−1LBM. A wall velocity of Vw = 1 × 10−4ΔxLBMΔt−1LBM corresponds to a shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = Vw/H = 2.2 × 10−6 Δt−1LBM, or 20.1 s−1 in the dimensional units, and a Reynolds number Re = RVw/μ = 7.5 × 10−3. In what follows, the shear rate 20.1 s−1 is taken as the reference value, and is denoted
= Vw/H = 2.2 × 10−6 Δt−1LBM, or 20.1 s−1 in the dimensional units, and a Reynolds number Re = RVw/μ = 7.5 × 10−3. In what follows, the shear rate 20.1 s−1 is taken as the reference value, and is denoted ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. It is worth noting that the value of
0. It is worth noting that the value of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = 20.1 s−1 lies within the range of shear rates used in experimental studies of capsules and biological cells; the latter range typically varies from 5 to 400 s−1.1
0 = 20.1 s−1 lies within the range of shear rates used in experimental studies of capsules and biological cells; the latter range typically varies from 5 to 400 s−1.1
It is convenient to characterize the rigidity of capsule by the dimensionless capillary number Ca = ρμVcap/Ecaph, where ρ and Vcap are the respective fluid density and capsule velocity. The capillary number Ca represents the relative importance of the viscous stress and the elastic stress on the capsule's shell. The capillary number for rigid, essentially non-deformable capsules6 is typically on the order of Ca < 10−3. Here, we use Ca ∼ 10−2, which corresponds to a capsule that is slightly deformable under a viscous stress. At the shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = 2.2 × 10−6 Δt−1LBM, the capillary number in our system is Ca = 2.05 × 10−2.
0 = 2.2 × 10−6 Δt−1LBM, the capillary number in our system is Ca = 2.05 × 10−2.
The rigidity of the substrate was taken to be considerably lower than that of the capsule. The relative substrate modulus E = Esub/Ecap was varied from 0.024 to 0.121.
The strength of the capsule-substrate adhesive interactions relative to the elastic stress in the capsule is controlled by the dimensionless parameter Φ = κN/Ecaph, where k is the bond spring constant and N is the total number of nodes on the shell surface. We set Φ = 0.62 in the simulations, so the adhesion strength was comparable to the elastic stresses in the capsule’s shell.4
The rate constant of bond rupture koff was varied from 3.3 × 10−6 to 1/6 × 10−4 Δt−1LBM. In the dimensional units of time, the latter value equals 156 s−1 and corresponds to a bond energy of 25 kBT, which is characteristic of some ligand-receptor interactions, such as avidin–iminobiotin,32 and for the thiol/disulfide exchange reaction.33 The value koff ∼ 102 s−1 is also characteristic of other biological binding interactions.34–36
In contrast to koff, the value of the on-rate kon is not as readily evident from experimental studies. It is usually taken to be one to four orders of magnitude greater than koff. For example, the value of kon = 35koff was used for interpreting the experimental data on the E-selectin/sLex pair.14 In our simulations, the rate constant of the bond formation was taken to be kon = 1 × 10−3 Δt−1LBM, so that the ratio kon/koff was in the range of 60 to 250.
2.3 Computer simulations
The LBM simulation box consisted of 70 × 40 × 46 nodes in the XYZ directions, respectively. The shear flow was generated by setting the X component of fluid velocity to a constant value of VW at the top LBM nodes. The boundary conditions for the LBM simulations were periodic in the X and Y directions. The mid-grid bounce back scheme was used to approximate the no-slip boundary conditions at the fluid-solid interface, as discussed above. The reversed propagation scheme was employed for the purpose of parallelization.37 We note that the forces and fluid velocities are averaged over two successive LBM steps to eliminate potential numerical instabilities in the simulations.38 (Other stabilization techniques can also be used to address this issue.39)The cubic lattice for modeling the elastic substrate via the LSM consisted of 72 × 42 × 9 nodes in the XYZ directions, respectively. The LSM lattice was shifted relative to the LBM nodes by ΔxLSM/2 in all three directions. The bottom nodes of the substrate lattice were fixed in space. The top nodes of the substrate were subject to the forces due to the hydrodynamic and substrate-capsule interactions. Free boundary conditions were applied to the LSM nodes of substrate at the vertical edges of the sample, so that these edges were allowed to move without specific constrictions. It is worth noting that the LSM lattice is sufficiently wide that the capsule remains far from the substrate's edges during the simulation.
Newton's equations of motion for the LSM nodes in the substrate and capsule were integrated numerically using the fourth order Runge–Kutta algorithm with the time step ΔtLBM.
The capsule and substrate interact though the chemical bonds, eqn (2), and the repulsive potential, eqn (3). Reshuffling of the Bell bonds was performed every time step of the LBM simulations. The probability of a connected bond to break and the probability of a broken bond to reform during the time step ΔtLBM were taken to be of the following forms:
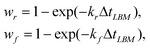 | (6) |
Each simulation run was initiated by establishing the equilibrium adhesion contact between the capsule and substrate for the given set of model parameters. For this purpose, the undeformed, spherical capsule was put into the quiescent fluid (i.e., the LBM and upper wall velocities were zero) close to the substrate so that the bonds could form. Due to this bond formation, the capsule moves toward the substrate. During the equilibration, the capsule assumes its equilibrium shape and the velocities of the capsule's center of mass and surrounding fluid gradually decrease. The shear flow was initiated by setting the velocity VW of the upper LBM nodes at the time tstart = 1.5 × 105 ΔtLBM, which is equivalent to 0.016 s (see Fig. 2). The total duration of a simulation run was 2 × 106 ΔtLBM, or 0.21 s in the dimensional units.
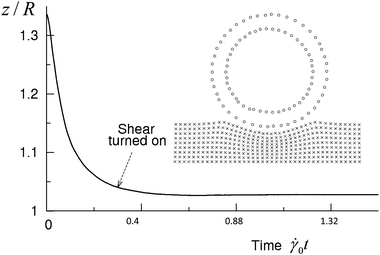 | ||
| Fig. 2 The vertical position of the capsule's shell center of mass as a function of time. The shear flow is imposed at tstart = 1.5 × 105 ΔtLBM. The inset shows the LSM nodes of the substrate and capsule (internal and external layers only) at tstart. | ||
Finally, the physical and the computational parameters of our model are summarized in Table 1.
| LBM | |
| Lattice spacing | ΔxLBM = 0.8 μm |
| Time step | ΔtLBM = 1.07 × 10−7 s |
| Simulation box | 70 × 40 × 46 (ΔxLBM)3 |
| Unperturbed height of channel | H = 45 ΔxLBM |
| Capillary number | Ca = ρμVcap/Ecaph ∼ 10−2 |
| Shear rate |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2 × 10−7–4 × 10−6 Δt−1LBM = 2 × 10−7–4 × 10−6 Δt−1LBM |
| Reference value |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = 2.2 × 10−6 Δt−1LBM ∼ 20.1 s−1
0 = 2.2 × 10−6 Δt−1LBM ∼ 20.1 s−1 |
| Reynolds number | Re = RVw/μ ∼ 10−3–10−2 |
| Kinematic viscosity | μ = (1/6) Δx2LBM Δt−1LBMμ = 10−6 m2 s−1 |
| LSM | |
| Mass of a node | m LSM |
| Capsule | |
| Radius | R = 12.5 ΔxLBM = 10 μm |
| Shell thickness | h = 3 ΔxLBM |
| Number of nodes (per each of 3 layers) | N = 642 |
| Average equilibrium spring length | l cap ≈ 1.94 ΔxLBM |
| Spring constant | k cap = 0.8 × 10−4–1.0 × 10−4mLSM Δt−2LBM |
| Substrate | |
| Lattice size | 72 × 42 × 9 (ΔxLBM)3 |
| Equilibrium spring length | ΔxLSM = ΔxLBM |
| Spring constant | k sub = 2 × 10−6–5 × 10−6mLSM Δt−2LBM |
| Relative stiffness (Young's modulus) | E = Esub/Ecap = 0.024–0.121 |
| Adhesion | |
| Bell bonds (eqn (4), 5) | |
| Off-rate of unstressed bonds |
k
off
= 3.3 × 10−6–1/6 × 10−4 Δt−1LBM = 1.5–7.6![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 0 |
| On-rate of unstressed bonds |
k
on
= 1 × 10−3 Δt−1LBM = 4.5 × 102![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 0 |
| Equilibrium length | l eq = 2 ΔxLBM |
| Spring constant | κ = 3 × 10−7mLSM Δt−2LBM |
| Sensitivity to strain | r 0 κ/kBT = 0.9 Δx−1LBM |
| Nonspecific repulsion (eqn (3)) | |
| Length | l s = 0.75 ΔxLBM |
| Respective strength | u s = 14.4 κΔx2LBM |
3. Results and discussion
3.1 Three regimes of capsule motion
The above computational model was used to investigate the dynamic behavior of the fluid-driven capsules for a range of shear rates. Via these simulations, we observed three distinct types of dynamic behavior, which are characterized in Fig. 3. In particular, the plots in Fig. 3a and 3b show the respective displacement and velocity of the capsule's center of mass as a function of time t for three values of shear rate (indicated in the figure); the interaction strength and rate of bond rupture are fixed at Φ = 0.62 and koff = 1.67 × 10−5 Δt−1LBM = 7.6![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, respectively. As seen in Fig. 3, for the lowest shear rate considered here,
0, respectively. As seen in Fig. 3, for the lowest shear rate considered here, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.10
= 0.10![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, the capsule is in the “stationary” state, i.e., the capsule's position does not change with time (Fig. 3a) and its velocity fluctuates near zero (Fig. 3b). For an intermediate value of shear rate,
0, the capsule is in the “stationary” state, i.e., the capsule's position does not change with time (Fig. 3a) and its velocity fluctuates near zero (Fig. 3b). For an intermediate value of shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.19
= 0.19![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, a capsule can exhibit a cycle of “stop and start” behavior, where the capsule is stationary for a period of time, but then is driven to move for a finite time by the imposed flow. This “stop-and-start” phenomenon, referred to as “saltation”, has been detected in experimental studies of leucocytes.40,41 Saltation was also observed in the computer simulations of capsules driven to move along a rigid surface by an imposed shear flow.15 It is important to recall that in contrast to the previous studies, we are modeling the rolling of capsules along a compliant substrate. Finally, at the sufficiently higher shear rate of
0, a capsule can exhibit a cycle of “stop and start” behavior, where the capsule is stationary for a period of time, but then is driven to move for a finite time by the imposed flow. This “stop-and-start” phenomenon, referred to as “saltation”, has been detected in experimental studies of leucocytes.40,41 Saltation was also observed in the computer simulations of capsules driven to move along a rigid surface by an imposed shear flow.15 It is important to recall that in contrast to the previous studies, we are modeling the rolling of capsules along a compliant substrate. Finally, at the sufficiently higher shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.6
= 0.6![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, the capsule moves continuously (i.e., travels from left to right in our simulation, with a steady increase in its x-coordinate), as shown in Fig. 3a. The velocity of the moving capsule fluctuates around some positive value (see Fig. 3b).
0, the capsule moves continuously (i.e., travels from left to right in our simulation, with a steady increase in its x-coordinate), as shown in Fig. 3a. The velocity of the moving capsule fluctuates around some positive value (see Fig. 3b).
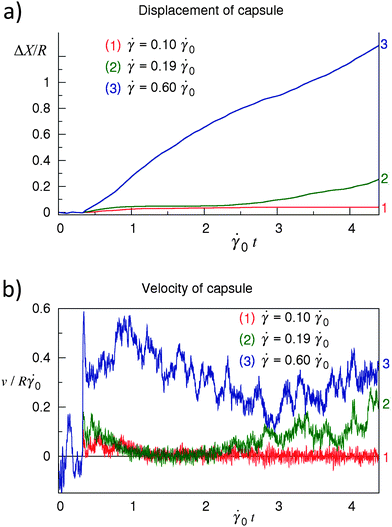 | ||
Fig. 3 The three regimes of the capsule's motion observed in the simulations. (a) Displacement of the capsule's shell center of mass as a function of time corresponding to (1) the stationary state at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.1 = 0.1![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, (2) the intermittent regime (saltation) at 0, (2) the intermittent regime (saltation) at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.19 = 0.19![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, (3) the steady rolling at 0, (3) the steady rolling at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.6 = 0.6![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. (b) Velocity of the capsule's shell center of mass along the trajectories shown in (a). Φ = 0.62, E = 0.061, koff/ 0. (b) Velocity of the capsule's shell center of mass along the trajectories shown in (a). Φ = 0.62, E = 0.061, koff/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = 7.6. 0 = 7.6. | ||
The continuously moving capsule undergoes a rolling motion on the substrate. Fig. 4 shows the velocity profiles vfluid and vcaps for the fluid and capsule, respectively, at t = 1.1 × 106 ΔtLBM or ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0t = 2.4, which corresponds to the middle of the simulation run. The fluid velocity profile vfluid(z) was obtained by averaging the x-component of the fluid velocity, vx(x,y,z), along nodes in the y-direction at x = 0 and a given value of z. To obtain vcaps(z), the x-component of the velocity of the capsule shell nodes was averaged over the nodes having the z-coordinate within the interval from z to z + ΔxLBM. As seen in Fig. 4, the capsule velocity vcaps is close to zero near the substrate surface at z = 0, and increases with an increase in z. The latter behavior of vcaps as a function of z indicates that the capsule is undergoing a rolling motion. It is worth noting that although the velocity of the capsule fluctuates in time (see Fig. 3b), the velocity of nodes is always close to zero near the substrate.
0t = 2.4, which corresponds to the middle of the simulation run. The fluid velocity profile vfluid(z) was obtained by averaging the x-component of the fluid velocity, vx(x,y,z), along nodes in the y-direction at x = 0 and a given value of z. To obtain vcaps(z), the x-component of the velocity of the capsule shell nodes was averaged over the nodes having the z-coordinate within the interval from z to z + ΔxLBM. As seen in Fig. 4, the capsule velocity vcaps is close to zero near the substrate surface at z = 0, and increases with an increase in z. The latter behavior of vcaps as a function of z indicates that the capsule is undergoing a rolling motion. It is worth noting that although the velocity of the capsule fluctuates in time (see Fig. 3b), the velocity of nodes is always close to zero near the substrate.
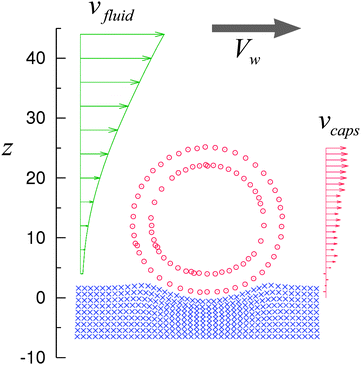 | ||
Fig. 4 The regime of steady rolling. The velocity profiles of fluid, vfluid, and capsule, vcaps, and the configuration of the capsule (circles) and substrate (crosses) correspond to the middle of the simulation run (3) in Fig. 3 at t = 1.1 × 106 ΔtLBM = 2.4![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −10. −10. | ||
Our simulations successfully reproduce the three dynamic regimes observed in experimental studies on living cells, namely, the “stationary”, “saltation” and “rolling” regimes.41 It is important to note that our simulations are capable of reproducing the stationary and saltation regimes because the capsule-substrate interactions are described by the Bell model, which mimics the formation of the ligand-receptor bonds.12,13 In contrast, if the energy-conserving Morse potential is used to model the capsule-substrate interactions, the capsule moves even under a weak shear flow; the capsule motion can, however, be arrested if the surfaces encompass chemical patterns or physical corrugations.4,7 Below, we show that a capsule interacting with a substrate via Bell bonds can remain stationary even on a chemically homogeneous, smooth surface provided that the latter substrate is sufficiently soft.
3.2 Effect of substrate compliance on the rolling motion of the capsule
By varying the relative rigidity of the substrate, E = Esub/Ecap, we found that the capsule is capable of rolling only on a sufficiently rigid substrate. Fig. 5 shows the mean velocity v of the capsule's center of mass (averaged over 1.5 million time steps) as a function of E at the shear rate of![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.15
= 0.15![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 and the two values of capsule rigidity of Φ1 = 0.62 (softer capsule) and Φ2 = 0.5 (stiffer capsule). Note that the substrate rigidity Esub was normalized by the respective value of Ecap. Each data point shown in Fig. 5 represents an average over three or four independent simulation runs. The error bars indicate the standard deviation of the mean velocity. Fig. 5 shows that the dynamic behavior of fluid-driven capsules depends critically on the substrate rigidity. Namely, at a given shear rate
0 and the two values of capsule rigidity of Φ1 = 0.62 (softer capsule) and Φ2 = 0.5 (stiffer capsule). Note that the substrate rigidity Esub was normalized by the respective value of Ecap. Each data point shown in Fig. 5 represents an average over three or four independent simulation runs. The error bars indicate the standard deviation of the mean velocity. Fig. 5 shows that the dynamic behavior of fluid-driven capsules depends critically on the substrate rigidity. Namely, at a given shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and capsule rigidity Φ, the capsule moves if the value of E exceeds some critical value Ecr, and is stationary if E < Ecr. The value of Ecr decreases with an increase in the capsule rigidity, i.e., stiffer capsules can move on softer substrates. For a relative substrate rigidity E within the range of 0.058 to 0.061, the stiffer capsule Φ2 = 0.5 moves while the softer capsule Φ1 = 0.62 is in the stationary state (Fig. 5). At 0.061 ≤ E ≤ 0.064, both of the capsules roll, but the stiffer capsule moves faster than the softer one. (It is worth noting that according to the Mann–Whitney–Wilcoxon test,42 the difference in the mean velocity values is significant at the level of 5% within the latter range of E.) Finally, at a higher substrate rigidity of E ≥ 0.07, both of the capsules move with the same velocity of ≈0.15
and capsule rigidity Φ, the capsule moves if the value of E exceeds some critical value Ecr, and is stationary if E < Ecr. The value of Ecr decreases with an increase in the capsule rigidity, i.e., stiffer capsules can move on softer substrates. For a relative substrate rigidity E within the range of 0.058 to 0.061, the stiffer capsule Φ2 = 0.5 moves while the softer capsule Φ1 = 0.62 is in the stationary state (Fig. 5). At 0.061 ≤ E ≤ 0.064, both of the capsules roll, but the stiffer capsule moves faster than the softer one. (It is worth noting that according to the Mann–Whitney–Wilcoxon test,42 the difference in the mean velocity values is significant at the level of 5% within the latter range of E.) Finally, at a higher substrate rigidity of E ≥ 0.07, both of the capsules move with the same velocity of ≈0.15![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0R, i.e., the velocity of the shear flow at the distance R from surface,
0R, i.e., the velocity of the shear flow at the distance R from surface, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) R.
R.
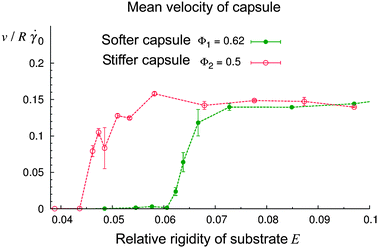 | ||
Fig. 5 Effect of the relative compliance of the substrate, E = Esub/Ecap, on the velocity of rolling motion of the capsule at the capsule rigidity of Φ1 = 0.62 (softer capsule) and Φ2 = 0.5 (stiffer capsule). The results shown were obtained at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.15 = 0.15![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 and koff/ 0 and koff/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = 7.6. The data points were obtained by averaging the velocity over the last three-fourths of the simulation time. 0 = 7.6. The data points were obtained by averaging the velocity over the last three-fourths of the simulation time. | ||
If a capsule is in the stationary state on a soft substrate, a sufficient increase in the shear rate can drive the capsule to roll. Fig. 6 shows a phase map of the rolling and stationary regimes in the coordinates E and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for a capsule of rigidity Φ = 0.62. In Fig. 6, the circles and crosses denote the rolling and stationary regimes, respectively. As can be seen, the rolling regime is located at higher shear rates than the stationary regime, and the boundary between the two regimes is a decreasing function of substrate rigidity E. Hence, a higher shear rate
for a capsule of rigidity Φ = 0.62. In Fig. 6, the circles and crosses denote the rolling and stationary regimes, respectively. As can be seen, the rolling regime is located at higher shear rates than the stationary regime, and the boundary between the two regimes is a decreasing function of substrate rigidity E. Hence, a higher shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is necessary to induce rolling on a soft substrate (low E) than on a stiff substrate.
is necessary to induce rolling on a soft substrate (low E) than on a stiff substrate.
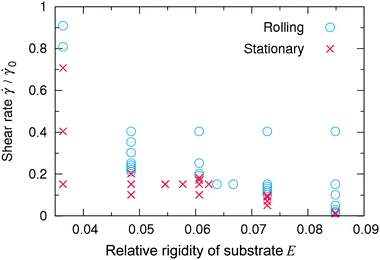 | ||
Fig. 6 Phase map of the rolling (circles) and stationary (crosses) regimes in the coordinates E and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) at Φ = 0.62 and koff/ at Φ = 0.62 and koff/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = 7.6. 0 = 7.6. | ||
The observed dependence of the dynamic behavior on the rigidity of both the capsule and substrate (Fig. 5 and 6) can be readily explained. Due to adhesion, both the capsule and substrate undergo a deformation (see Fig. 4). The more compliant the adherent surfaces are, the more adhesive bonds that are formed. As a result, a greater drag force is needed to break the bonds and drive the capsule to move. It is also clear that the motion of a capsule in shear flow should depend on how readily the capsule-surface bonds can be broken. The effect of the bond breakage rate is discussed in the next section.
3.3 Effect of the rate of bond breakage
Fig. 7a shows the trajectories of the capsule at values of the off-rate constant koff varying from 1.5![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 to 7.6
0 to 7.6![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0; the on-rate constant is fixed at kon = 10−3 Δt−1LBM = 450
0; the on-rate constant is fixed at kon = 10−3 Δt−1LBM = 450![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. To obtain the results presented in Fig. 7a, a capsule of rigidity Φ = 0.62 was driven by an imposed shear rate of
0. To obtain the results presented in Fig. 7a, a capsule of rigidity Φ = 0.62 was driven by an imposed shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.16
= 0.16![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 along a substrate of relative rigidity E = 0.073. The plot indicates that the dynamics of bond breakage and formation can affect the regime of capsule motion on this substrate. In particular, Fig. 7a shows that the capsule motion is stationary at a low rate constant of the bond breakage (curve 1), and that an increase in koff enables this capsule to roll on the surface (curves 2–5).43
0 along a substrate of relative rigidity E = 0.073. The plot indicates that the dynamics of bond breakage and formation can affect the regime of capsule motion on this substrate. In particular, Fig. 7a shows that the capsule motion is stationary at a low rate constant of the bond breakage (curve 1), and that an increase in koff enables this capsule to roll on the surface (curves 2–5).43
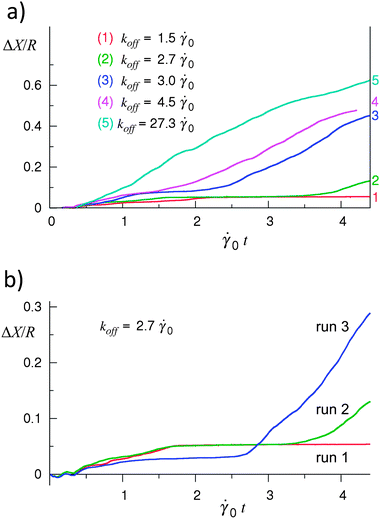 | ||
Fig. 7 Effect of the rate of bond breakage on the capsule's motion. (a) Displacement of the capsule's shell center of mass as a function of time at the values of koff indicated in the figure. Depending upon koff, the capsule exhibits the stationary state (curve 1), saltation (curves 2 and 3), or steady rolling (curves 4 and 5). (b) Irregularity of the capsule motion in the saltation regime: the behavior varies between different simulation runs. Φ = 0.62, E = 0.073, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.16 = 0.16![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. 0. | ||
It is important to note that the steady rolling motion was observed only in simulations involving sufficiently high breakage rates; in Fig. 7a, curves 4 and 5 correspond to the rolling regime. At intermediate values of koff, the capsule exhibits irregular motion during which the capsule stops and then, starts moving again, as in curves 2 and 3 in Fig. 7a. This is the characteristic feature of the saltation regime. For a fixed set of parameters, the behavior of the capsule varies between different simulation runs in the saltation regime as demonstrated in Fig. 7b, which shows the trajectories obtained in three simulation runs at koff = 2.7![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. Furthermore, an increase in koff does not necessarily result in a systematic increase in the velocity of the capsule in the saltation regime (not shown); this is in contrast to the behavior observed in the steady rolling regime.
0. Furthermore, an increase in koff does not necessarily result in a systematic increase in the velocity of the capsule in the saltation regime (not shown); this is in contrast to the behavior observed in the steady rolling regime.
The irregularity of capsule motion in the saltation regime is a manifestation of the fluctuations induced by the Bell bonds, which break and reform stochastically. At each time step in the simulations, there are from 5 × 103 to 1.5 × 104 bonds formed between the capsule and substrate; however, only a small fraction of these bonds affect the rolling of the capsule. The latter observation is evident from Fig. 8, which shows the probability of a bond to break as a function of the bond position at koff = 2.7![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. The bond breakage, which is necessary for the capsule to move, takes place predominantly at the rim of capsule-substrate contact area. Thus, only bonds located at the rim control the capsule rolling motion and cause the irregular dynamics in the saltation regime.
0. The bond breakage, which is necessary for the capsule to move, takes place predominantly at the rim of capsule-substrate contact area. Thus, only bonds located at the rim control the capsule rolling motion and cause the irregular dynamics in the saltation regime.
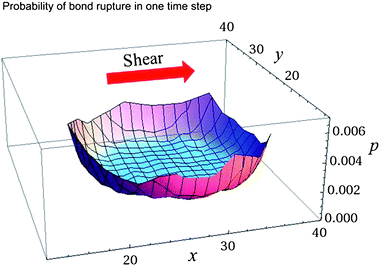 | ||
Fig. 8 The probability of a bond to break, wr (see eqn (6)), as a function of bond position at koff = 2.7![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0, Φ = 0.62, E = 0.073, 0, Φ = 0.62, E = 0.073, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.16 = 0.16![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. 0. | ||
Fig. 9 summarizes the results of the simulations at various values of koff and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , and the rigidities of the capsule and substrate of Φ = 0.62 and E = 0.073, respectively. In this figure, the symbols indicate a regime of motion observed at a specific pair of values koff and
, and the rigidities of the capsule and substrate of Φ = 0.62 and E = 0.073, respectively. In this figure, the symbols indicate a regime of motion observed at a specific pair of values koff and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . For each (koff,
. For each (koff, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) pair, we ran three simulations and each simulation was run for 2 × 106 time steps, which corresponds to approximately 0.21 s of real time (see Section 2.2). The regime was labeled as “rolling” if the capsule moved steadily without stopping until the end of each of the three runs, and cases where the capsule was initially immobile up to 106 time steps were included. The regime was labeled as “stationary” if by the end of each of the three runs the capsule velocity was zero, and the cases of initial saltation were included. The regime was labeled as “saltation” in all other cases. The plot in Fig. 9 indicates that an increase in the off-rate koff gives rise to a weaker capsule-substrate adhesion so that the capsule can move under lower shear rates.
) pair, we ran three simulations and each simulation was run for 2 × 106 time steps, which corresponds to approximately 0.21 s of real time (see Section 2.2). The regime was labeled as “rolling” if the capsule moved steadily without stopping until the end of each of the three runs, and cases where the capsule was initially immobile up to 106 time steps were included. The regime was labeled as “stationary” if by the end of each of the three runs the capsule velocity was zero, and the cases of initial saltation were included. The regime was labeled as “saltation” in all other cases. The plot in Fig. 9 indicates that an increase in the off-rate koff gives rise to a weaker capsule-substrate adhesion so that the capsule can move under lower shear rates.
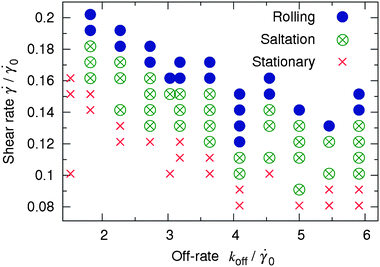 | ||
Fig. 9 Phase map of the stationary (crosses), saltation (crossed open circles), and rolling (solid disks) regimes of capsule motion in the coordinates koff and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) at Φ = 0.62 and E = 0.073. at Φ = 0.62 and E = 0.073. | ||
4. Conclusions
By integrating mesoscale computational approaches for modeling hydrodynamics, micromechanics, and adhesion, we investigated the fluid driven motion of an elastic microcapsule reversibly bound to a compliant surface. Our combined LBM/LSM approach captures the dynamic interaction between the elastic capsule, substrate, and surrounding fluid, which is subject to the external shear. The adhesion between the capsule's shell and the substrate was due to the formation of biomimetic, reversible bonds, which were described by the Bell model.Using this computational model, we observed three regimes of capsule motion. Namely, the capsule rolls steadily along the substrate at a sufficiently high shear rate, it is stationary at a low shear rate, and exhibits an intermittent motion (saltation) at intermediate shear rates. At a given shear rate, the regime of capsule motion was found to depend on the substrate stiffness, and on the rate of rupture of the adhesive bonds. The capsule was observed to roll steadily on a sufficiently stiff substrate, and at a high rate of bond rupture. In the opposite limit of a soft substrate and a low rate of bond rupture, the system was localized in the stationary regime.
Within the range of model parameters considered here, the saltation regime is most clearly distinguished through a variation of the rate of bond rupture. We demonstrated that the irregular capsule motion characteristic of saltation is due to the stochasticity in the processes of bond rupture and formation. The irregular saltation motion exists even at a high surface density of the adhesive bonds. The latter behavior is due to the fact that not all of the bonds contribute to the capsule's dynamics; rather, it is only the fraction of bonds situated at the rim of the contact area that is primarily responsible for the motion of the capsule.
One of the motivations for carrying out these studies was to demonstrate that the compliance of the substrate can play a critical role in the dynamic behavior of the capsules. As noted above, we observed that a sufficiently rigid substrate is necessary for the sustained fluid-driven motion of the capsules. In other words, even in an imposed flow field, the capsules can be made to remain stationary by tailoring the compliance of the substrate. The latter findings are particularly important when considering the release of species encased within the capsules; namely, soft surfaces will favor the release of the encapsulated species in a specific area, while more rigid substrates will enable the released species to be effectively spread over a large region of the surface. In applications where the surface rigidity is not a variable, our findings show that the values of koff and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) can be used to tailor the motion of the capsules. For example, for small koff values (which can be achieved by judicious choice of functional groups on the capsules and surface), the capsules can remain stationary on a relatively rigid surface for a range of shear rates and again, the micro-carriers can thus be induced to deliver their contents to specific locations on the substrate. We note that the latter considerations are particularly important for drug delivery applications. More generally, our findings can provide design rules for tailoring the efficacy of micro-carriers in transporting the encapsulated species to localized sites or broad regions on a substrate.
can be used to tailor the motion of the capsules. For example, for small koff values (which can be achieved by judicious choice of functional groups on the capsules and surface), the capsules can remain stationary on a relatively rigid surface for a range of shear rates and again, the micro-carriers can thus be induced to deliver their contents to specific locations on the substrate. We note that the latter considerations are particularly important for drug delivery applications. More generally, our findings can provide design rules for tailoring the efficacy of micro-carriers in transporting the encapsulated species to localized sites or broad regions on a substrate.
Acknowledgements
ACB gratefully acknowledges financial support from the DOE.References
- O. I. Vinogradova, J. Phys.: Condens. Matter, 2004, 16, R1105–R1134 CrossRef CAS.
- N. Maurer, D. B. Fenske and P. R. Cullis, Expert Opin. Biol. Ther., 2001, 1, 1–25 Search PubMed.
- B. M. Discher, Y.-Y. Won, D. S. Ege, J. C.-M. Lee, F. S. Bates, D. E. Discher and D. A. Hammer, Science, 1999, 284, 1143–1146 CrossRef.
- A. Alexeev, R. Verberg and A. C. Balazs, Macromolecules, 2005, 38, 10244–10260 CrossRef CAS.
- A. Alexeev, R. Verberg and A. C. Balazs, Phys. Rev. Lett., 2006, 96, 148103 CrossRef.
- A. Alexeev and A. C. Balazs, Soft Matter, 2007, 3, 1500–1505 RSC.
- A. Alexeev, R. Verberg and A. C. Balazs, Langmuir, 2007, 23, 983–987 CrossRef CAS.
- O. B. Usta, A. Alexeev and A. C. Balazs, Langmuir, 2007, 23, 10887–10890 CrossRef CAS.
- G. V. Kolmakov, R. Revanur, R. Tangirala, T. Emrick, T. P. Russell, A. J. Crosby and A. C. Balazs, ACS Nano, 2010, 4, 1115–1123 CrossRef CAS.
- S. Succi, The lattice Boltzmann equation for fluid dynamics and beyond, Oxford University Press, Oxford, 2001 Search PubMed.
- G. A. Buxton, C. M. Care and D. J. Cleaver, Modell. Simul. Mater. Sci. Eng., 2001, 9, 485–497 CrossRef.
- G. I. Bell, Science, 1978, 200, 618–627 CrossRef CAS.
- M. Dembo, D. C. Torney, K. Saxman and D. Hammer, Proc. R. Soc. London, Ser. B, 1988, 234, 55–83 CrossRef CAS.
- S. K. Bhatia, M. R. King and D. A. Hammer, Biophys. J., 2003, 84, 2671–2690 CrossRef CAS.
- V. Pappu and P. Bagchi, Comput. Biol. Med., 2008, 38, 738–753 CrossRef CAS.
- G. A. Buxton, R. Verberg, D. Jasnow and A. C. Balazs, Phys. Rev. E, 2005, 71, 056707–18 CrossRef.
- S. Duki, G. V. Kolmakov, V. V. Yashin, T. Kowalewski, K. Matyjaszewski and A. C. Balazs, J. Chem. Phys., 2011, 134(8), 084901 CrossRef.
- Y. H. Qian, D. D'Humières and P. Lallemand, Europhys. Lett., 1992, 17, 479–484 CrossRef.
- (a) R. Cornubert, D. D'Humieres and D. Levermore, Phys. D, 1991, 47, 241–259 CrossRef; (b) P. Lallemand and L.-S. Luo, Phys. Rev. E, 2000, 61, 6546–6562 Search PubMed.
- For the model parameters used in the simulations, we never approach the regime where overlapping is possible and thus, it is not necessary to use a potential that exhibits a divergence (as the separation distance approaches zero). Namely, the shear rates are sufficiently small that the distance between the capsule and the substrate nodes varies around its equilibrium value. Therefore, a description of the potential at distances much shorter than the latter equilibrium distance is not essential in our simulations.
- M. D. Ward, M. Dembo and D. A. Hammer, Biophys. J., 1994, 67, 2522–2534 CrossRef CAS.
- E. Evans and K. Ritchie, Biophys. J., 1997, 72, 1541–1555 CrossRef CAS.
- T. Strunz, K. Oroszlan, I. Schumakovitch, H.-J. Güntherodt and M. Hegner, Biophys. J., 2000, 79, 1206–1212 CrossRef CAS.
- M. J. Buehler, S. Keten and T. Ackbarow, Prog. Mater. Sci., 2008, 53, 1101–1241 CrossRef CAS.
- M. Rief, M. Gautel, F. Oesterhelt, J. M. Fernandez and H. E. Gaub, Science, 1997, 276, 1109–1112 CrossRef CAS.
- T. J. Wickham, R. R. Granados, H. A. Wood, D. A. Hammer and M. L. Shuler, Biophys. J., 1990, 58, 1501–1516 CrossRef CAS.
- B. Zhang, T. S. Lim, S. R. K. Vedula, A. Li, C. T. Lim and V. B. C. Tan, Biochemistry, 2010, 49, 1776–1786 CrossRef CAS.
- R. Alon, D. A. Hammer and T. A. Springer, Nature, 1995, 374, 539–542 CAS.
- M. R. King and D. A. Hammer, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 14919–15924 CrossRef CAS.
- L. S.-L. Cheung, X. Zheng, L. Wang, J. C. Baygents, R. Guzman, J. A. Schroeder, R. L. Heimark and Y. Zohar, J. Micromech. Microeng., 2011, 21, 054033 CrossRef.
- A. Fery, F. Dubreuil and H. Möhwald, New J. Phys., 2004, 6, 18 CrossRef.
- V. T. Moy, E.-L. Florin and H. E. Gaub, Science, 1994, 266, 257–259 CrossRef.
- A. P. Wiita, S. R. K. Ainavarapu, H. H. Huang and J. M. Fernandez, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7222–7227 CrossRef CAS.
- M. A. Hjortso and J. W. Roos (ed.), Cell adhesion: Fundamentals and Biotechnological Applications, Marcel Dekker, 1995 Search PubMed.
- C. Andersen, M. Jordy and R. Benz, J. Gen. Physiol., 1995, 105, 385–401 CrossRef CAS.
- M. A. Hachem, E. N. Karlsson, E. Bartonek-Roxå, S. Raghothama, P. J. Simpson, H. J. Gilbert, M. P. Williamson and O. Holst, Biochem. J., 2000, 345, 53–60 CrossRef.
- C. Obrecht, F. Kuznik, B. Tourancheau and J.-J. Roux, Comput. Math. Appl., 2011, 61(12), 3628–3638 CrossRef.
- A. J. C. Ladd, J. Fluid Mech., 1994, 271, 285–309 CAS.
- J. Latt and B. Chopard, Math. Comput. Simul., 2006, 72, 165–168 CrossRef.
- G. B. Zibari, M. F. Brown, D. L. Burney, N. Granger and J. C. McDonald, Transplant. Proc., 1998, 30, 2327–2330 CrossRef CAS.
- K.-C. Chang, D. F. J. Tees and D. A. Hammer, PNAS, 2000, 97, 11262–11267 CrossRef CAS.
- S. M. Ross, Introductory statistics, vol. 1, Elsevier Academic Press, 2005 Search PubMed.
- The number of breaking events during the time it takes the capsule to displace its own radius is a meaningful characteristic of the system; however, this parameter is well defined only in the steady rolling regime, which takes place at sufficiently high values of koff. Hence, to present the data in Fig. 7 and 9, we normalize koff using the reference shear rate
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0; the latter combination is well defined in all of the observed regimes.
0; the latter combination is well defined in all of the observed regimes.
| This journal is © The Royal Society of Chemistry 2012 |
