Students' understanding of mathematical expressions in physical chemistry contexts: An analysis using Sherin’s symbolic forms
Nicole
Becker
and
Marcy
Towns
Purdue University—Chemistry, 560 Oval Drive, Lafayette, Indiana 47907, USA. E-mail: mtowns@purdue.edu
First published on 8th March 2012
Abstract
Undergraduate physical chemistry courses require students to be proficient in calculus in order to develop an understanding of thermodynamics concepts. Here we present the findings of a study that examines student understanding of mathematical expressions, including partial derivative expressions, in two undergraduate physical chemistry courses. Students participated in think-aloud interviews and responded to a set of questions involving mixed second partial derivatives with either abstract symbols or thermodynamic variables. The findings describe students’ ability to transfer mathematics knowledge to chemistry problems and how students use symbolic forms described by Sherin (2001) to make sense of mathematical expressions in physical chemistry contexts.
Introduction
Mathematical inscriptions related to derivatives and integrals are a fundamental part of the language of physical chemistry. Consider, for instance, a type of mathematical relationship commonly encountered in a junior-level chemical thermodynamics course, the Maxwell Relations. Also referred to as the equality of mixed second partial derivatives of exact differentials, the Maxwell Relations provide a way to relate macroscopic observable quantities such as temperature and pressure to more abstract chemical properties such as entropy or Gibb's Energy (Fig. 1).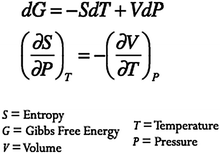 | ||
| Fig. 1 Gibbs Energy and corresponding Maxwell's Relation. | ||
The use of mathematical equations allows physical chemists to have a common language for inquiry (Kozma and Russell, 1997). Becoming fluent with mathematical representations is thus essential for the acquisition of expertise in chemistry (Kozma et al., 2000; Kozma and Russell, 1997). In the context of a physical chemistry course, students are commonly asked to use mathematical relationships, such as that shown in Fig. 1 to relate physical variables such as temperature and pressure to more abstract chemical constructs such as Gibbs Energy. Understanding of fundamental concepts in thermodynamics thus becomes tied to the student's ability to translate between mathematical equations and the macroscopic phenomena they represent. Students must become able to not only interpret symbolic expressions and perform mathematical manipulations but they must also develop an understanding of the physical significance of the symbolic representations. As instructors of chemistry, we hope that students become able to interpret and work with mathematical expressions such as this with understanding, not just to routinely apply algorithms and formulae. How do we as instructors help students make physical sense of mathematical expressions and to use them to predict and explain chemical behavior?
Research on the students' ability to translate mathematical equations and symbols into descriptions of the macroscopic system under study have not been extensively investigated in chemistry education research. The vast majority of studies related to thermodynamics have been done to document student difficulties and misconceptions in thermodynamics contexts and have taken place either in K-12 classrooms or introductory courses with few exceptions. Greenbowe and Meltzer's (2003) work focused on thermochemical concepts related to solution calorimetry. Jasien and Oberem (2002) focused on thermal equilibrium and energy transfer. Thomas and Schwenz's (1998) work focused on physical chemistry students' concepts of the first and second law of thermodynamics. These studies largely focused on conceptual understandings related to thermodynamics contents rather than difficulties tied to how students make physical sense from mathematics inscriptions in physical chemistry contexts.
If instructors of chemistry are to effectively facilitate students' reasoning with mathematical expressions in chemistry, more research that looks specifically at how students interpret and use mathematical inscriptions to reason about chemistry concepts is needed. The qualitative study described here aims to explore the role of students' interpretation of mathematical expressions and how their understanding of mathematical ideas informs their reasoning about physical chemistry constructs.
Literature background
Work in sociological studies on how natural phenomena are represented uses the term inscriptions to refer to representations including but not limited to narrative text, graphs, symbolic representations, and photographs (Latour and Woolgar, 1979; Roth and McGinn, 1998). Lunsford et al. (2007) contend that the more information an inscription summarizes, the more powerful it becomes, simultaneously becoming more abstract and less detailed. More abstract forms of inscription such as equations have less in common with the particular detailed natural phenomenon they represent and therefore are farther away from student experience.Many of the abstract equations students encounter in physical chemistry are quite distant from the natural phenomenon they represent. Perhaps because of this abstract nature, interpreting mathematical inscriptions and connecting them to information about macroscopic or microscopic systems has been shown to be quite challenging for students (Greenbowe and Meltzer, 2003; Hadfield and Wieman, 2010; Jasien and Oberem, 2002).
Some studies have focused on difficulties related to the ways in which students interpret and use mathematical expressions in thermodynamics contexts. Hadfield and Wieman (2010) examined student difficulties interpreting mathematical expressions related to the first law of thermodynamics. Participants were drawn from two classes of undergraduate chemistry student enrolled in the first semester physical chemistry, the content of which included thermodynamics and kinetics topics. Fifty-five students completed a two-parts survey; students selected true or false for a given statement, for instance “U = w + q” a change in the internal energy for a system can be the result of changes in heat and work; Second, participants were asked to write a response explaining their reasons for answering true or false. Eight additional students participated in interviews in which they were asked to think aloud as they reasoned about the survey questions.
Hadfield and Wieman found that students struggled to provide physically meaningful descriptions of how equations related to conservation and conversion of energy. For instance, one participant who selected true for the statement “the equation for work, 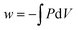 indicates how to calculate the quantity of work associated with specific changes in pressure in volume” (p. 752) responded that the statement represented conversion and conservation of energy and that pressure and volume in this equation represented different forms of energy. Even students who had performed well in the course based on end-of-semester grades selected answers based on recognition of the expressions or mathematical validity of the expressions rather than physical interpretations.
indicates how to calculate the quantity of work associated with specific changes in pressure in volume” (p. 752) responded that the statement represented conversion and conservation of energy and that pressure and volume in this equation represented different forms of energy. Even students who had performed well in the course based on end-of-semester grades selected answers based on recognition of the expressions or mathematical validity of the expressions rather than physical interpretations.
In another study related to how advanced undergraduate students reason about mathematical expressions in a physics context, Thompson et al. (2005) surveyed eight physics majors enrolled in an upper division thermal physics course to explore their understanding of mixed partial derivatives and the Maxwell relations. Students were asked to explain the difference between partial derivatives and total derivatives, and were asked to express their understanding of the math and physics related to the Maxwell relations as part of a survey prior to an examination; they also completed a question on the course final that dealt with the expansion of an elastic thin film. The responses of seven students to a written mathematical task involving partial derivatives and Clairaut's theorem and a roughly analogous task were compared. The authors found that many of the physics students struggled to interpret the expressions and relate mathematical representations into realistic scenarios. Two students expressed a belief that the Maxwell relationships were valid because both sides of the expression were equal to zero and relied on algebraic approaches to working with differential equations. Though five of the seven student interviewed could describe the physical meaning a partial derivative expression, all students had difficulties when asked to write a mathematical expression to represent physical scenario.
These findings suggest that even students who are successful according to course metrics, such final exam scores and course grades, may fail to correctly interpret and use mathematical inscriptions in new contexts, such as that of thermodynamics (Hadfield and Wieman 2010; Thompson et al., 2005). An understanding of science content does not always enable students to successfully relate prior mathematics knowledge to problem solving tasks.
Procedural and conceptual understanding of mathematical inscriptions
Similarly, a rigorous understanding of mathematics ideas does not always ensure that students will be able to successfully relate mathematical knowledge to science content. For example, Orton (1983a, 1983b) classified student errors related to the use of integration and differentiation in a cross age study (age 16 to 22) of British students and outlined three categories of common errors: structural errors were conceptual in nature; executive errors involved mistakes in procedure or operations; and arbitrary errors seemed to have no underlying cause. Orton found no strong connection between procedural errors in conceptual understanding of rate of change in university level calculus students' use of integrals or derivatives; some students were able to solve an integral even if they did not conceptualize integrals using a formally correct definition (i.e. integrals as the limit of a Riemann sum). In a similar study, Grundmeier et al. (2006) found that students who articulated sound definitions for integration did not necessarily demonstrate procedural fluency in applying mathematical resources.It has been suggested that such discrepancies between conceptual and procedural fluency may be the result of differing contextual clues in mathematics and science contexts (Cui et al., 2007; Rebello et al., 2005). In particular, it may be challenging for students to transfer mathematical understanding successfully to physics and chemistry contexts (Rebello et al., 2005). Though students' may possess understandings related to mathematics use they may fail to apply those resources if they focus on surface features such as notational differences (Hammer et al. 2005; Rebello Zollman and Allbaugh, 2005). Students who rely primarily on rote memory learning may be particularly vulnerable to this type of difficulty (Yeatts and Hundhausen, 1992). The question remains, exactly what resources do students draw upon to make sense of mathematical expressions in new contexts if they are unable to apply ‘correct’ mathematical understandings?
Symbolic forms and mathematical resources
In a qualitative study of how pairs of engineering majors wrote equations to represent physical scenarios and how they solved physics problems, Sherin (2001) observed that students repeatedly focused on symbol patterns in mathematical expressions, and that these patterns seemed to cue students' various aspects of prior knowledge related to mathematics. He suggested that students draw from a range of intuitive mathematical ideas deriving from patterns in symbolic representations, or symbolic forms, as they make sense of equations in physics. As Sherin described the relationship of symbolic forms to conceptual knowledge,Each symbolic form associates a simple conceptual schema with an arrangement of symbols in an equation. Because they possess these symbolic forms, students can take a conceptual understanding of some physics situation and express that understanding in an equation. Furthermore, they can look at an equation and understand it as a particular description of a physical system (p. 482).
For example, upon examining a physics equation, students may identify the following symbol pattern shown in Fig. 2. Here, using Sherin's shorthand notation, the boxes indicate unspecified quantities or variables. Students may associate this particular arrangement of terms with the idea of “a whole comprised of two or more parts” or “two components” (p. 491). Thus, Sherin referred to this pattern as a symbolic form he called “parts-of-a-whole”.
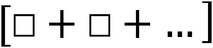 | ||
| Fig. 2 Sherin's (2001) parts of a whole symbolic form. | ||
It is important to note that symbolic forms represent intuitive ways of making sense of representations. Though Sherin postulates that they may be abstracted from students' experiences working with equations in math and science contexts to a certain extent, symbolic forms are not explicitly taught in most classroom contexts. Instead they represent a primitive way of how individuals make sense of mathematical expressions.
Some researchers have used Sherin's symbolic forms to account for students' mathematical thinking in physics contexts. Tuminaro (2004) examined how students solved problems in an algebra-based college-level introductory physics course using mathematical resources, that is cognitive knowledge elements related to students use of mathematics. He considered symbolic forms to be one type of resource used by students as they understand and use equations in physics. By analyzing video data of students' group problem solving activities for evidence of mathematical resource use, Tuminaro found that although students may possess mathematical resources they may not always use them in the context of physics problem solving. He suggested that how and when students' use mathematical resources depends on other factors such as how students frame problem contexts.
Though Sherin's original work focused on describing how students reason about algebraic expressions in the context of physics problem solving, the construct has more recently been used to describe how students use calculus resources in physics contexts. Meredith and Marrongelle (2008) explored how students use mathematics skills learned from introductory calculus courses in the context of electrostatics problems. They interviewed twelve students enrolled in either an integrated calculus/physics class or a traditional physics class (with co-enrollment in a calculus course) and they found that though some students possessed an understanding of when and where integration would be relevant and how to apply it, they did not always use mathematical resources appropriately in physics contexts. While Sherin's original work dealt only with algebraic forms, Meredith and Marrongelle (2008) described several symbolic forms including a “parts-of-a-whole” symbolic form, which students used to reason about calculus concepts such as integration and suggest that such symbolic forms may be a useful component of student reasoning about physics ideas. However, instructors must be aware of how these symbolic forms contribute to student reasoning in various contexts if they are to meaningfully facilitate student reasoning with such inscriptions.
Summary of literature
While there have been studies that describe students' approaches to interpreting and using mathematical inscriptions for problem solving in the mathematics and physics education research literature, few such studies in chemistry education have explored how advanced chemistry students reason about mathematical expressions in thermodynamics contexts. In order to improve student learning of thermodynamics, more work is needed that examine the ways in which students make sense of mathematical expressions in chemistry contexts. Our work contributes in this direction providing a description of how students make sense of partial derivative expressions in a chemistry context related to thermodynamics in terms of Sherin's symbolic forms. The following section outlines the theoretical perspective that guides this work.Methods
Theoretical perspective
For this study, we adopt Sherin's (2001) symbolic forms as a theoretical perspective that guides our interpretation of the data presented here. This theoretical perspective derives from a constructivist view of learning in that it looks specifically at what knowledge resources students possess, when that knowledge is activated, and under what circumstances (Redish, 2004).Sherin's perspective originates in diSessa's (1993) idea of intuitive knowledge elements related to mechanics of action in physics problems, known as phenomenological primitives. Sherin extended these intuitive ideas to include aspects of mathematical reasoning. The symbolic forms framework assumes a complex interaction between knowledge elements exists for any particular task, meaning that the ways in which students' activate knowledge resources in response to a particular task may be highly context-dependent.
Research questions
The goal of the qualitative study described here is to provide a rich description of how students reason about mathematical expressions in math and physical chemistry contexts. The following questions framed our design and analysis of this study:• What are physical chemistry students' understandings of partial derivatives in mathematical contexts?
• How do students apply their understanding of partial derivatives in mathematical and physical chemistry contexts?
From our preliminary data analysis, we noted that students focused on aspects of mathematical expressions other than what an expert might consider ‘correct’. To further explore this phenomenon, we added a third research question:
• What symbolic forms outlined by Sherin (2001) are used by students to make sense of mathematical expressions in mathematics and physical chemistry contexts?
The ways in which Sherin's (2001) symbolic forms framework are used in this study will be further described in the data analysis section of this paper.
Development of interview protocol
In order to explore students' understanding of partial derivatives in mathematics and physical chemistry contexts, we adapted a pen and paper survey developed by Thompson and colleagues (2005) for use as a semi-structured think aloud interview protocol. The interview question asked students to interpret mathematical expressions in analogous math and physical chemistry contexts. We added two additional open-ended interview questions that asked students to generate their own mathematical expressions in order to further explore the ways in which students represent physical situations using mathematical inscriptions. For these two questions, we selected problems in which students would likely be expected to represent change in variables using a derivative in a classroom context. Follow-up questions, which took the form of sample responses from a fictitious student, were used in cases where students were unable to come up with their own expressions.The protocol was piloted with five chemistry graduate students and four undergraduate students in order to refine interview questions. Two chemistry faculty members were also interviewed in order to gain feedback about the structure and wording of the protocol. In this paper, however, we discuss only those interview questions that informed the research questions outlined in the previous section. The interview protocol is shown in Fig. 3.
 | ||
| Fig. 3 Interview protocol. | ||
Participants and setting
The first classroom was a lecture section at a large research university in the Midwestern United States. The second was a small course using the Process Oriented Guided Inquiry (POGIL) approach at a comprehensive university in the Midwestern United States. Since 2003, the POGIL project has developed and disseminated curricular materials based on a student-centered model of learning. In the POGIL classroom observed in this study, students worked the majority of each class period on exercises from the POGIL workbooks. The instructor served as a facilitator of student learning rather than a lecturer; whole class discussions in this context generally involved students reporting out answers to workbook questions. A thorough description of POGIL settings is detailed by Moog and Spencer (2008).
| Participants | Year | Major | Semesters of mathematics | |
|---|---|---|---|---|
| POGIL class participants | Andrea | Junior (3rd) | Chemistry | 2 |
| Adam | Junior (3rd) | Chemistry | 1 | |
| Craig | Junior (3rd) | Chemistry and Math | 2 | |
| Marie | Junior (3rd) | Chemistry | 2 | |
| Melissa | Junior (3rd) | Chemistry | 2 | |
| Lecture class participants | David | Senior (5th yr) | Biochemistry | 3 |
| Jacob | Senior (4th year) | Aeronautical Engineering | 6 | |
| Nevah | Junior (3rd year) | Chemistry | 3 | |
| Taylor | Junior (3rd year) | Pharmacy | 3 | |
| Yang | 2nd year graduate | Nuclear Pharmacy | 2 |
Data collection
Interviews took place mid-semester after students had covered content related to total and partial derivatives as well as the Maxwell relations. Both classes covered units dealing with Maxwell relationships at least a week prior to the interviews. In the lecture section, students spent over a week working on manipulations based on the Maxwell relations in order to obtain expressions for coefficient of thermal expansion (αP), and similar relationships that could be expressed in terms of partial derivatives. In the POGIL class, students worked through one unit on the Maxwell relations prior to the interviews and had also previously discussed the equality of mixed second partial derivatives in a math review unit at the beginning of the semester.During the interviews, which lasted approximately 45 min on average, students were then asked to think aloud as they worked through a series of interview questions. Interview questions asked students to write or interpret a mathematical expression involving total or partial derivatives in math or thermodynamics contexts. Additional questions asked students to define terms such as partial derivative or total derivative.
Interviews were audio recorded and students' written work was collected at the end of the interview. The first author observed both classes for the duration of the semester and also served as a graduate teaching assistant for the large lecture course. Classroom observations focused on describing the examples related to partial derivatives in class and identifying contexts in which mathematical inscriptions were discussed.
Data analysis
As data collection was ongoing, all interviews were transcribed verbatim. In our initial analysis, transcripts of student responses were compared for each question and codes were assigned to indicate the students' approach to interpreting expressions and whether they understood the mathematical expression. As evidence of understanding, we looked for instances in which students could provide a physical interpretation or alternate descriptions of a symbolic expression. We examined data related to emerging themes as a whole to identify the common theme of ideas and compared student responses both within and across cases. Our approach to condensing theses initial codes into broader themes derives from Glasser and Strauss’s (1967) constant comparison approach, which advocates an ongoing comparison of data in order to refine of theoretical constructs derived from data analysis.Since our initial analysis did little to explain what students focused on when they did not apply correct mathematical understandings or physical interpretations of the systems, we adapted Sherin's (2001) symbolic forms as an analytical tool in order to better describe students' reasoning processes. In our second phase of analysis, we looked for evidence that students identified patterns in the mathematical expressions for which they associated some intuitive understandings and coded these instances using the type of symbolic form that was used. The code definitions and criteria for identification outlined by Sherin (2001) were used as a guide and we reinterpreted identification criteria as needed to fit our data set. For the symbolic forms analysis, we coded only those questions that asked students to interpret or produce a mathematical expression rather than the interview questions that asked students to define terms.
Inter-rater reliability for the symbolic forms analysis was established using two additional reviewers who coded one complete transcript representing a sample of 34 codes. The percent agreement between the two raters (who coded collaboratively) and the first author was 76.5%.
An overview of student responses to the interview protocol will be discussed in the following section.
Findings
Overview of student responses to interview questions
To set the context for our discussion of students' use of symbolic forms in interpreting and reasoning with mathematical expressions in thermodynamics contexts, we first provide an overview of student responses to the interview questions that were relevant to our research questions. Table 2 summarizes student responses to the interview questions.| Interview question | Summary of student responses (N = 10) |
|---|---|
| 1 | (6) Correct response f′(x) = −32x + c1 |
| (4) Incomplete or no written response | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| 2 | (4) Definition in terms of change; E.g. David: “how does R change when C changes, and when F changes, holding constant the other variable” |
| (4) Definition in terms of the process of finding the derivative. E.g. Marie: “Like take the derivative holding something constant then adding the other thing holding the other variable constant” | |
| (3) Definition as a sum of the partial derivatives; E.g. Adam: “Um, I think the total differential is the sum of the partial differentials” | |
| (1) No response | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| 3 | (6) A partial derivative is the result of taking the derivative of an expression while hold variables constant |
| (3) A partial derivatives represents change in a function in response to one variable only | |
| (1) All other partial derivatives in a total derivate expression become zero | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| 4 | (6) Indicated that 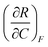 represents the change in R with respect to a change in C as F is held constant represents the change in R with respect to a change in C as F is held constant |
(3) Indicated that 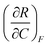 represents the partial derivative of R with respect to C when F is constant represents the partial derivative of R with respect to C when F is constant |
|
| (1) Noted relationship between total and partial derivatives. E.g. Marie: “Like a total differential, just part of it, holding something constant” | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| 5 | (3) Expression would be true only for certain types of functions (e.g. for thermodynamic functions only) |
| (2) Expression would be true only for particular values of F and C | |
| (3) Expression would always be true because of nature of operation (switching order in which partial derivatives are taken) | |
| (2) Expression would only be true when dC = 0 | |
| (1) Recalled from physical chemistry class that the expression should sometimes be true | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| 6 | (9) 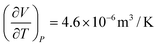 represents change in volume for a particular change in temperature with pressure held constant represents change in volume for a particular change in temperature with pressure held constant |
| (1) Indicated that the expression represented a ratio of volume to temperature at a specific temperature and volume | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| 7 | (9) Believed the sign of 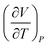 meant that volume increases as temperature increases meant that volume increases as temperature increases |
(1) Believed the negative sign in exponent of 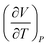 meant the value would decrease meant the value would decrease |
|
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| 8 | (2) Correct response of 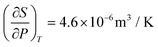 using an algebraic approach using an algebraic approach |
| (4) Correct response using a mnemonic device to recall Maxwell Relationships | |
| (2) Incorrect response, attempted substitution into expression for dC | |
| (1) No answer, not enough information | |
| (1) Answer will be 0 because pressure doesn’t influence entropy | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| 9 | (7) Correct expression 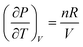 , using differentiation , using differentiation |
| (3) Incorrect response in terms of change between initial and final states | |
Overall, participants' responses to interview questions 1 through 4 suggested that the majority of participants could provide reasonable interpretations of the terms total and partial derivatives and offer an interpretation in terms of change for partial derivative expression such as 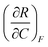 . The majority of students could also successfully write an expression for change in interview question 1.
. The majority of students could also successfully write an expression for change in interview question 1.
In the remaining interview questions, nearly all students could give an physical interpretation of change when asked to interpret mathematical expressions with thermodynamic variables such as 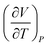 . However, interview questions that asked students to apply mathematical ideas rather than interpret or define mathematical constructs were met with more difficulty.
. However, interview questions that asked students to apply mathematical ideas rather than interpret or define mathematical constructs were met with more difficulty.
Interview questions 8 and 9, for instance, proved challenging for a number of students. These questions asked students to apply information they may have previously learned in mathematics or physical chemistry courses to write an expression for the described scenario. Students' approaches to these problems will be further discussed in the next section.
Students' ways of interpreting mathematical expressions
Rather than a straightforward application of prior knowledge, we observed that students used a variety of approaches to dealing with the mathematical expressions in the interview protocol. We found the notion of symbolic forms to be useful in explaining students' reasoning, especially when they appeared to struggle to interpret mathematical expressions. Sherin's (2001) original set of codes included a number of instances in which symbolic forms related to forces or similar influences were used in student reasoning. In our data set, we identified few such instances likely due to the nature of the content discussed by students in the interviews. Most symbolic forms used by participants related to dependence of terms, recognition of constant terms or coefficients, or proportionality of quantities. Five examples of symbolic forms that were identified in our data set are summarized in Table 3 (see Sherin, 2001 for complete list of codes used in original study).| Symbolic form | Symbol pattern | Definition |
|---|---|---|
| Dependence | […x…] | A whole depends on a quantity associated with an individual symbol; identification may include references such as “if x varies, then the whole must vary” |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Prop + |
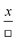
|
Directly proportional to a quantity, x, which appears as an individual symbol in the denominator; identification may include references such as “as X increases, then Y increases” |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Same amount | [□=□] | Two amounts, each associated with a side, are the same |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Coefficient | [x□] | A product of factors is broken into two parts and one part is identified with an individual symbol, the coefficient |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Ratio |
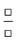
|
Comparison of a quantity in the numerator and denominator |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Symbol template key | ||
| […] | Expression in brackets corresponds to an entity in the schema | |
| x, y | Individual symbols | |
| □ | A term, or a group of terms | |
| … | Omitted parts of an expression that continue the pattern or are inconsequential | |
We also coded instances in which students recalled particular pieces of information or associated symbols such as 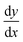 with change or the process of taking a derivative. Because of the nature of the content discussed here, symbolic forms other than those described by Sherin may be possible. However, our goal was not to identify new symbolic forms unique to this data set, but rather use the construct of symbolic forms to explain aspects of student reasoning as they discussed these expressions.
with change or the process of taking a derivative. Because of the nature of the content discussed here, symbolic forms other than those described by Sherin may be possible. However, our goal was not to identify new symbolic forms unique to this data set, but rather use the construct of symbolic forms to explain aspects of student reasoning as they discussed these expressions.
In total, we identified the use of ten symbolic forms similar to those described by Sherin (2001) in our data. A summary of the symbolic forms and the frequency with which they were used in participants' responses is shown in Table 4.
| Question | Symbolic form code | Number of participants |
|---|---|---|
| 1 | Dependence | 5 |
| Prop− | 2 | |
| No dependence | 1 | |
| 4 | Parts of a Whole | 2 |
| Dependence | 1 | |
| 5 | Same Amount | 6 |
| Dependence | 1 | |
| Cancelling | 1 | |
| Coefficient | 1 | |
| 6 | Dependence | 9 |
| Prop+ | 2 | |
| Ratio | 2 | |
| 7 | Prop+ | 8 |
| Prop− | 1 | |
| 8 | Same Amount | 3 |
| Ratio | 2 | |
| Competing Terms | 2 | |
| 9 | Coefficient | 5 |
| Prop + | 4 | |
| Same Amount | 2 | |
| Dependence | 2 |
The frequencies in Table 4 illustrate that a number of students used symbolic forms to reason about the mathematical expressions in the interview questions. These uses included both instances in which students arrived at correct and incorrect responses. In some instances, symbolic forms were used by students in conjunction with recalled prior knowledge to make sense of mathematical expressions. In other instances, the use of symbolic forms predominated.
In the next section we compare the responses of several students to interview questions 9 and 8 in order to illustrate the range of ways in which symbolic forms influenced students' reasoning. Two responses to question 9 given by Craig and Jacob were selected as they were information-rich cases in which both students used intuitive reasoning to arrive at a response for question 9; however, Craig used a combination of symbolic forms as well as recall to arrive at the correct answer while Jacob relied on intuitive reasoning to arrive at response that differed significantly from our experts' responses to the question. We then summarize the remaining participants' responses to question 9 in order to compare Craig and Jacob's approaches with the remainder of the participants, and we discuss possible reasons for students' varied use of symbolic forms in reasoning about mathematical expressions.
| Participant | Transcript | Symbolic form |
|---|---|---|
| Craig: | [reading] Write an expression for how the pressure of the container would change, er below, would change in the container were heated while the volume remains constant. | |
| Because you're increasing temperature, you're gonna get a corresponding increase in the pressure, because you're holding the volume constant. | Prop+; coefficient-constant | |
| Um, it and that just goes along with kind of what I was saying, the change in the pressure volume and you get a change in the nRT value, | Prop+ | |
| well, R is constant. | Coefficient-constant | |
| Actually, just write it all out, so you ended up with VdP plus PdV is equal to R, T dn I guess? Plus R ndT | Recall: Process of taking total derivative | |
| Since you're changing, uh heat and not the number of moles in the container since there's no chemical reaction going on you can just assume that's zero. | Recall: dX = 0 if X is constant | |
| And since the pressure's being held constant, er, not pressure, but since the volume's being held constant you can go ahead and destroy that equat, that portion. So VdP is equal to RndT. | Recall: dX = 0 if X is constant |
Here, Craig began by discussing general features of the expression, PV = nRT. After identifying which symbols represented constants, Craig found the total derivative of PV = nRT and then eliminated terms that involved change in a variable he identified as a constant, recalling that dx = 0 for a constant variable. His written response is shown in Fig. 4.
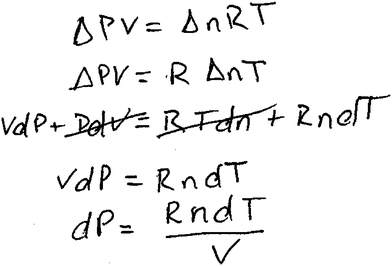 | ||
| Fig. 4 Craig's written response to interview question 9. | ||
His approach seemed guided by his recognition of symbolic forms that would help him construct an expression. Craig also used recalled information about the process of finding a total derivative and the idea that dx = 0 when x remains constant, in order to construct an appropriate response to this question that was similar to the experts' responses.
Interviewer: Ok. So what do you think a partial derivative is, the next question?
Jacob: A partial derivative is, it's not a stand-alone derivative. It's part of an overall differential equation.
Interviewer: Can you describe that a little bit more for me?
Jacob: Um, it's instead of being just one uh, uh er, partial derivative is like it's kind of like, it'd be like a system of derivatives. Where uh, the partial derivative's kind of treated like a variable in itself, it just happens to be a variable that changes. Well I guess that's what a variable is but, the variable is a differential, the rate of change of other variables. So the, instead of having a large expression of each rate of change, you can write it a partial derivative and make them simpler.
Later, when asked to clarify what he meant by taking a derivative he responded:
Jacob: It's a rate of change, er that's generally how I view it, there's multiple, uh, sub definitions of it, the tangent line or the slope of the curve. But usually I, when I use it it's usually a rate of change with respect to another variable like time or something.
Jacob offered multiple interpretations, both in terms of change of the slope of a line on a graph and as a rate of change with respect to another variable, suggesting an understanding of derivatives that is consistent with the various definitions of derivative described in the mathematics literature (Zandieh, 2000). Also, Jacob clearly associated derivatives with change. When asked to write an expression for how f(x) changes as x changes for the expression f(x) = − 16x2 + c1x + c2, he easily obtained the correct result, f′(x) = − 32x + c1, explaining that “usually if something changes you're talking about the derivative”.
In response to interview Question 9, however, Jacob did not immediately use a derivative in order to represent change. Instead, he wrote an expression comparing the pressure and temperature before and after a change had occurred in the container (response shown in Fig. 5).
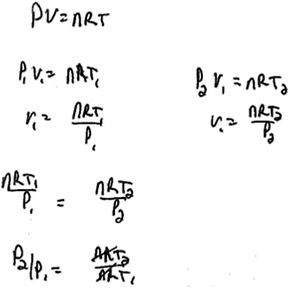 | ||
| Fig. 5 Jacob's written response to interview question 9. | ||
Like Craig, Jacob's reasoning seemed to be guided by several symbolic forms he recognized as relevant to mathematizing this scenario. The following transcript example (Table 6) illustrates the symbolic forms Jacob used to generate his solution.
| Participant | Transcript | Symbolic form |
|---|---|---|
| Jacob: | Uh, for how, how pressure of the container would change if the container were heated with constant volume? Ok. So we have constant volume, of a liter? So uh, I'm going to say, you have n moles of ideal gas, you've got PV = nRT. | Recall PV = nRT |
| um, so you can do P1V1 equals nRT1 as your initial condition, and your second condition is going to be P2 with the same V1 equals nRT2. And you can combine these equations setting them equal to the V1. | Same Amount | |
| That's just, (writing) so you have, nRT1 over P1 equals nRT2 over P2, so P2 over P1 um, is uh, nRT2 over nRT1 and then nR's cancel out and you get P2 over P1 is T2 over T1. | Cancelling-ratio | |
| So, if, since it's heated I'm guessing the T2 is greater than T1. So P2 over P1 would increase, meaning that P2 is greater than P1. | Ratio |
In asking this question, we were interested in how students would write expression for incremental change during a process. In particular, we were interested in whether they would use a derivative to represent change in this context, as might an expert. While Jacob's response correctly expressed the ratio between pressures and temperatures before and after the change, he did not use a derivative to represent this change.
In order to see if Jacob could relate derivatives to this context, the interviewer prompted Jacob to consider how to represent incremental change in pressure as the temperature was increasing.
Interviewer: What if I wanted to know, what are we looking for, what if I wanted to know how the pressure was changing somewhere in the middle. Like as the temperature's increasing. Is there an expression you could write to show that?
Jacob: Um, I'm going to say if you want to know something while it's changing there then you probably want a, some sort of a derivative or a differential equation. And I'm not entirely sure how to apply that to the ideal gas. I mean it would be something along the lines of dP, it's like dP equals uh, VdT. Where V is a constant, actually that'd be one over V dT. I think.
Jacob noted that a derivative would be appropriate and attempted to obtain a derivative for the expression PV = nRT. Though he was able to talk through how he would find a derivative (even outlining an approach by noting that a change in pressure could be represented as 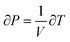 ), when he tried to write an expression for his reasoning, he substituted P2 − P1 in for ∂P and T2 − T1 for ∂T, resorting back to his initial reasoning about the initial and final states of the cylinder (Fig. 6).
), when he tried to write an expression for his reasoning, he substituted P2 − P1 in for ∂P and T2 − T1 for ∂T, resorting back to his initial reasoning about the initial and final states of the cylinder (Fig. 6).
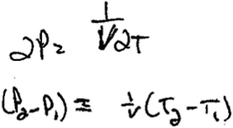 | ||
| Fig. 6 Jacob's written response to follow up question. | ||
We consider problems based on the ideal gas law in which students are expected to manipulate PV = nRT to be exceedingly common in this type of thermodynamics context. As instructors, it is likely that we view the PV = nRT relationship as a relatively simple mathematical expression and we may expect that our students will have little trouble expressing change using a partial or total derivative. However, as we've seen here, Jacob did not immediately invoke prior knowledge related to derivatives and instead relied on more intuitive understandings of symbolic forms to manipulate the expression PV = nRT to represent change between initial and final variables. Even after identifying that change could be expressed by a derivative in this context, he reverted back to his initial P2 − P1 notation in his final answer. His reasoning seemed to stem, at least in part, from a physically intuitive sense of the variables for temperature and pressure, and an association with patterns of symbol use, the symbolic forms we note in Table 6.
When students are asked to solve problems such as these, they must not only recall relevant information and apply it to the problem, but also must use mathematical tools and inscriptions in discipline-appropriate fashions in order to demonstrate a correct understanding (Airey and Linder, 2008). This means that students must be able to frame and approach problems in increasingly expert-like ways and use mathematical resources accordingly, not just in ways that seem intuitive and reasonable for the system under study. Though Jacob was able to produce an answer that seemed rational and that enabled him to predict variation in pressure with response to temperature, his response was not characteristic of what our expert participants would consider “correct”.
Overall for Question 9, seven of the ten students used derivatives correctly to respond to the question. The three students who answered incorrectly also relied on symbolic forms, especially those related to identifying constants (coefficient symbolic form) and proportionality relationships (prop+ symbolic form). The analysis of interview protocols for all ten students suggested that recognition of symbolic forms played a significant role in their reasoning. Especially when students did not arrive at a correct answer, it became evident that these more intuitive elements of reasoning guided students' approaches.
Participant responses to question 8
Interview question 8 also provided several instances in which students used recall or symbolic forms to reason about mathematical expression. Next, we discuss two examples of how students approached this question.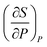 , but her approach to deriving this expression did not involve differentiation or prior knowledge related to the Maxwell Relations. Though Yang initially recalled having used the cross derivative relationship from her physical chemistry class, she could not articulate why the relationship was valid or whether it could applied in this context (Yang: “Seems uh, I used the cross…I used this dP as constant T, dV/dT as constant, oh no. I don't think so. That, these are not correct…). Instead, Yang set dG equal to 0 and then manipulated the expression algebraically to obtain her result. Her work is shown in Fig. 7.
, but her approach to deriving this expression did not involve differentiation or prior knowledge related to the Maxwell Relations. Though Yang initially recalled having used the cross derivative relationship from her physical chemistry class, she could not articulate why the relationship was valid or whether it could applied in this context (Yang: “Seems uh, I used the cross…I used this dP as constant T, dV/dT as constant, oh no. I don't think so. That, these are not correct…). Instead, Yang set dG equal to 0 and then manipulated the expression algebraically to obtain her result. Her work is shown in Fig. 7.
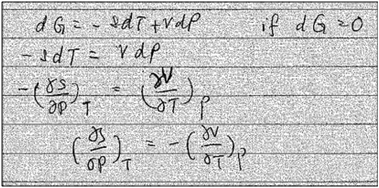 | ||
| Fig. 7 Yang's written response. | ||
Yang's reasoning seemed to stem from her recognition that she could obtain two partial derivatives set equal to one another when dG = 0. We coded this recognition as related to a symbolic form having to do with “same amount”. Also, she seemed to associate partial derivatives generally with a ratio of thermodynamic quantities, such as 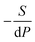 or
or 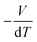 which suggests a recognition of a ratio symbolic form. She added partial derivative notation to the expression
which suggests a recognition of a ratio symbolic form. She added partial derivative notation to the expression 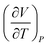 only at the end of the solution.
only at the end of the solution.
In this instance, Yang's intuitive ways of reasoning were productive in that they enabled her to begin making sense of the mathematical expression; her use of algebraic manipulation allowed her to obtain the desired relationship. However, in more complicated physical chemistry problems, functions become more complex. In such cases, a more sophisticated use of mathematics may be required and derivatives must be used to express change. Relying exclusively on recognition of symbolic forms and algebraic manipulation (as in Yang's case) may thus become considerably more problematic once students begin working with more complex mathematical expressions.
David: Yeah, so basically, choo, like that, (writes Fig. 8) I can switch up those uh, derivatives, and that's helpful because sometimes one of these expressions is easier to find experimentally than the other. In this case, well, that might be simpler to find out, but that would be simpler to go about finding. Finding out volume changes and temperature changes at constant pressure, you can more easily think of that and design an experiment than you can for finding changes in entropy versus pressure.
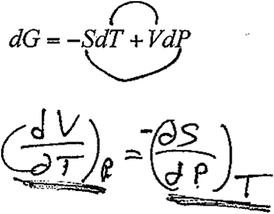 | ||
| Fig. 8 David's “outer-inner” mnemonic device. | ||
Here, David used what he referred to as the “outer-inner” mnemonic device to obtain the cross derivative relationship to obtain the expression 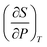 . David's depiction of this device and his written response is shown in Fig. 8.
. David's depiction of this device and his written response is shown in Fig. 8.
As he recalled the Maxwell relation, David discussed the importance of the Maxwell relations in physical chemistry, namely that they provide a way of relating macroscopic observable quantities to more abstract variables such as entropy. We considered this level of discussion to represent a more meaningful physical interpretation of the expression than other students who used this mnemonic device provided. However, when discussing interview question 4 on the mathematical basis of the cross derivative relationship, David was unable to articulate under what conditions the relationship would be valid. While mnemonic devices such the “arrow device” may be helpful for promoting recall, it is critical that they be tied to relevant information regarding under what circumstances they can be applied.
Discussion and implications
Here we've illustrated ways in which students used intuitive symbolic forms when reasoning about mathematical expressions in physical chemistry contexts. We noted that many participants centered their attempts to make sense of unfamiliar mathematical expressions on these symbolic forms similar to those described by Sherin (2001). In some instances, the use of these heuristics were able to provide students with a plausible, though not necessarily correct, responses to the interview questions, such as Jacob's case. We believe that Sherin's symbolic forms may prove a useful lens for examining student reasoning about mathematical expressions in chemistry contexts, particularly in instances where students seemingly fail to transfer calculus ideas that an expert might deem relevant.Regardless of whether students arrived at a correct or incorrect answer, the degree to which students relied on recall versus intuitive reasoning and symbolic forms varied widely. We believe that, in addition to students’ prior knowledge related to derivatives in physical chemistry contexts, students' framing of problem solving task may help explain why some students presented evidence of multiple symbolic forms when reasoning about the interview tasks, while some used few symbolic forms. Tuminaro (2004) suggested that the ways in which students approach problem solving in physics contexts was influenced not only by the mathematical resources students possessed, but also by their epistemological framing of the problem solving tasks. He described several “epistemic games,” which are characterized by particular problem-solving strategies that are considered legitimate for the particular epistemic game. For example the “Pattern Matching” epistemic game involved students recognizing a particular symbolic structure (for instance the ratio symbol template in Table 3) and trying to fill in the pattern with relevant quantities. Students who framed a problem-solving task as related to “Pattern Matching” less often sought to reconcile their solutions with qualitative reasoning and physical interpretations of the system at hand. We believe a similar research direction that examines how chemistry students construe their use of mathematics could be a productive direction for research that aims to explain how students approach mathematical problem solving in chemistry.
Meredith and Marrongelle (2008) note that when students are asked to use mathematics in science contexts such as physics, they seldom are able to recall and apply mathematics ideas in a straighforward fashion. They comment that.
Physics instructors often count on students to learn the requisite mathematics in their mathematics classes and expect them to effortlessly apply it in the physics context. But it is likely that such a transfer of skills does not happen as readily as we would hope because students must reinterpret mathematics in a physics context (p. 576).
Our account of student reasoning using partial derivatives in physical chemistry contexts suggests that much the same may be true in chemistry. To successfully reinterpret mathematics in new contexts, such as physical chemistry, students may need significant guidance from instructors.
One way to help instructors to better scaffold students’ use of mathematics in chemistry contexts may be to engage students in collaborative problem solving. For instructors of chemistry, observing students working together may offer instructors an opportunity to observe facets of students' reasoning that may not be made explicit from an examination of student homework and exams. Observing students’ difficulties as they occur may provide unique opportunities for instructors to give formative feedback that may help students develop a deeper understanding of content. Furthermore, such collaborative activity may provide students a space to negotiate understandings of concepts with their peers permitting them to make connections between symbolic representations and physical understandings (Towns and Grant, 1997).
Since there is a large overlap in content between related domains such as chemistry, physics, and mathematics, there is a critical need for effective communication between faculty if we are to better facilitate student meaning making with mathematical representations across domains. More work is needed that explores what resources students bring from mathematics courses, and how chemistry and physics instructors can aid students as they reinterpret mathematics in chemistry contexts.
Interdisciplinary approaches to thermodynamics and other highly mathematical science content may be one way to facilitate productive use of mathematical inscriptions in science contexts. One current curriculum development relevant to upper-division chemistry instructors is entitled “Creating a Common Thermodynamics.” This project aims to develop an interdisciplinary core curriculum for thermodynamics courses in biology, chemistry, and physics (Klymkowsky, 2011). Such approaches may be a potentially powerful way to transform the teaching and learning of thermodynamics.
Acknowledgements
This research is supported by the National Science Foundation under Grant No. 0817467 (CCLI). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. The authors gratefully acknowledge suggestions and comments from Dr Chris Rasmussen (San Diego State University) on the design of the interview protocol. We also thank Mrs Ashley Versprille and Ms Alena Moon for assisting with determining inter-rater reliability.References
- Airey J. and Linder C., (2008), A disciplinary discourse perspective on university science learning: Achieving fluency in a critical constellation of modes, J. Res. Sci. Teach., 46(1), 27–49.
- Cui L., Rebello N. S. and Bennett A. G., (2007), Assessing college students' transfer of learning from calculus to physics using non-traditional problems. Paper presented at the NARST 2007 Annual Meeting, New Orleans, LA.
- diSessa A. A., (1993), Toward and epistemology of physics, Cognit. Instruct., 10(2 and 3), 105–225.
- Greenbowe T. J. and Meltzer D. E., (2003), Student learning of thermochemical concepts in the context of solution calorimetry, Int. J. Sci. Educ., 25, 779–800.
- Grundmeier T. A., Hansen J. and Sousa E., (2006), An exploration of definition and procedural fluency in integral calculus, PRIMUS, 162178-191.
- Hadfield L. C. and Wieman C. E., (2010), Student interpretations of equations related to the first law of thermodynamics, J. Chem. Educ., 87, 750–755.
- Hammer D., Elby A., Scherr R. E. and Redish E. F., (2005), Resources, framing, and transfer. In J. P. Mestre (ed.), Transfer of learning from a modern multidisciplinary perspective. Greenwich, CT: Information Age Publishing.
- Jasien P. G. and Oberem G. E., (2002), Understanding of elementary concepts in heat and temperature among college students and K-12 teachers, J. Chem. Educ., 79, 889–895.
- Klymkowsky M. W., (2011), Collaborative Research: Creating a common thermodynamics: NSF TUES Type 2 Project (DUE 1122896).
- Kozma R. B., Chin C., Osborne J., Russell J. and Marx N., (2000), The role of representations and tools in the chemistry laboratory and their implications for chemistry learning, J. Learn. Sci., 9, 102–143.
- Kozma R. B. and Russell J., (1997), Multimedia and understanding: Expert and novice responses to different representations of chemical phenomena, J. Res. Sci. Teach., 34, 949–968.
- Latour B. and Woolgar S., (1979), Laboratory life: The construction of scientific facts. London: Sage.
- Lunsford E., Melear C. T., Roth W.-M. and Hickok L. G., (2007), Proliferation of inscriptions and transformations among preservice science teachers engaged in authentic science, J. Res. Sci. Teach., 44, 538–564.
- Meredith D. C. and Marrongelle K. A., (2008), How students use mathematical resources in an electrostatics context, Am. J. Phys., 76, 570–578.
- Moog R. S. and Spencer J. N., (2008), POGIL: An overview. In R. S. Moog & J. N. Spencer (ed.), Process Oriented Guided Inquiry Learning (POGIL). Washington, DC: American Chemical Society.
- Orton A., (1983a), Students' understanding of differentiation, Educ. Stud. Math., 14, 235–250.
- Orton A., (1983b), Students' understanding of integration, Educ. Stud. Math., 14, 1–18.
- Rebello N. S. Zollman D. A. and Allbaugh A. R., (2005), Dynamic Transfer: A perspective from physics education research. In J. P. Mestre (ed.), Transfer of learning from a modern multidisciplinary perspective. Greenwich, CT: Information Age Publishing.
- Redish E. F., (2004), A theoretical framework for physics education research: Modeling student thinking. In E. F. Redish and M. Vincentini (ed.), Research on physics education (pp. 1–63). Bologna/Amsterdam: Italian Physical Society/IOS Press.
- Roth W.-M. and McGinn M. K., (1998), Inscriptions: Towards a theory of representing as social practice, Rev. Educ. Res., 68, 35–59.
- Sherin B. L, (2001), How students understand physics equations, Cognit. Instruct., 19, 479–541.
- Thomas P. L. and Schwenz R. W, (1998), College physical chemistry students' conceptions of equilibrium and fundamental thermodynamics, J. Res. Sci. Teach., 35, 1151–1191.
- Thompson J. R., Bucy B. R. and Mountcastle, D. B., (2005), Assessing student understanding of partial derivatives in thermodynamics. Paper presented at the Physics Education Research Conference, Salt Lake City, UT.
- Towns M. H. and Grant E., (1997), “I believe I will go out of this class actually knowing something”: Cooperative learning activities in physical chemistry, J. Res. Sci. Teach., 34, 819–835.
- Tuminaro J., (2004), A cognitive framework for analyzing and describing introductory students' use and understanding of mathematics in physics. Unpublished Doctoral Dissertation, University of Maryland, College Park.
- Yeatts F. R. and Hundhausen J. R., (1992), Calculus and physics: Challenges at the interface, Am. J. Phys., 60, 716–721.
- Zandieh M. J., (2000), A theoretical framework for analyzing student understanding of the concept of derivative. In E. Dubinsky A. H. Shoenfeld. and J. Kaput (ed.), Research in collegiate mathematics education, IV (Vol. 8, pp. 103–127). Providence, RI: American Mathematical Society.
| This journal is © The Royal Society of Chemistry 2012 |
