Particle-impact nanoelectrochemistry: a Fickian model for nanoparticle transport

Abstract

The transport of nanoparticles to a substrate electrode for collision can be quantitatively described by a Fickian (i.e. diffusional) model both where the nanoparticles are oxidatively electrolysed at the electrode and where electrolysis of solution-phase species occurs on the surface of the impacting nanoparticles.

---

Introduction

The rapid progress made in the area of particle-impact nanoelectrochemistry has led to a realisation that it has the potential for wide-ranging applications from environmental monitoring to the synthesis of nano-architectures.^1–4 As the field develops the focus of study progresses from purely phenomenological observations to obtaining a theoretical understanding of the factors affecting the experimental results, notwithstanding that some effects may be nanoparticle specific in the sense of reflecting the chemical composition of the nanoparticle.

In response to the observation that a kinetic theory (i.e. ballistic) view of the nanoparticle-electrode encounter over-estimates collision frequencies by at least 3 orders of magnitude,⁵ we have adopted a Brownian motion view of the process: applying random walks to the electrodeposition onto impacting NPs,⁶ for example

Tl⁺(aq) + e⁻ → Tl@Ag(NP) (1)

and the destructive oxidation of metal NPs such as AgNPs,⁷

Ag(NP) − e⁻ → Ag⁺(aq) (2)

both of which yielded valuable insight into the factors that made the impacts visible on the experimental timescale. Very recently, we have proposed a purely Fickian interpretation of the impact frequencies of oxidative NP-electrode collisions as in (2), specifically for AgNPs and NiNPs, and obtained good agreement with experimental results.⁸

In this paper, we present further quantitative evidence that the NP transport is determined by diffusion and not kinetic theory, illustrated for the case of AgNP impacts showing that the frequencies of catalytically amplified spikes can be quantitatively explained by a diffusional model, for the case of hydrogen peroxide reduction on AgNPs, with no requirement for complex simulation. We have selected AgNPs as the test system for these studies because they are the most well-characterised nanoparticles using these techniques, as successive studies have used direct oxidative electrochemistry to obtain sizing, aggregation, and sticking probability data^2,9,10 as well as indirect surface chemistry such as electrodeposition,^11,12 and reduction of protons and adsorbed tag molecules.^13–15 Importantly for this study, their sticking coefficients (the proportion of collisions that result in adsorption) have been determined (s = 0.15) for collisions with carbon surfaces;¹⁰ such adsorption is important in that it creates the concentration gradient required for Fickian diffusion.

Experimental

Silver nanoparticles (AgNPs) were fabricated in-house using a literature method^16,17 of mean radius 13 nm. Chemicals were also obtained commercially from Sigma-Aldrich and used as received without further purification: hydrogen peroxide (30%), sodium dihydrogen citrate (NaC₆O₇H₇, >99.5%), hydrochloric acid (37%), and potassium chloride (>99.5% Riedel-de-Haan). All solutions were made using ultrapure water of resistivity not less than 18.2 MΩ.cm at 298 K (Millipore). The exact concentration of the stock hydrogen peroxide was determined via titration with dilute potassium permanganate.¹⁸

Experiments were conducted within a faraday cage using a μAutolab II (Metrohm-Autolab BV, Utrecht, Netherlands) and a three electrode arrangement. The working electrode used in this study was a carbon fibre microelectrode (BASi Inc, Stareton, Warks. UK) with a radius of 4.8 μm determined via electrochemical calibration. A saturated Ag/AgCl reference electrode was used, with a graphite rod as counter electrode. All experiments were conducted under an argon atmosphere.

Results & discussion

1. Direct electrochemistry of nanoparticles

The variation of impact frequency with temperature was investigated for the oxidation of AgNPs as in (2), as indicative of the mass transport of NPs. A solution of 10 mM citrate/90 mM KCl was placed into the electrochemical cell, which was surrounded by a heating coil to achieve thermal control. The electrode (4.8 μm radius carbon fibre) was potentiostatted at +0.30 V (vs. SCE) and an aliquot of AgNPs (mean radius 13 nm) added. At this potential and for NPs of the size studied, full oxidation of impacting AgNPs is expected.² The first experiment was conducted at 296 K. Several chronoamperometric profiles were recorded and oxidative current spikes were observed in all measurements (see for example²). Sufficient profiles were recorded to obtain several hundred impact spikes to provide a meaningful average frequency. The time period that these chronoamperograms were recorded over was limited to 10 min to minimise the effects of aggregation on the impact rate. This procedure was repeated at a range of temperatures (295–309 K), and the impact frequencies computed for each temperature.

If the transport of NPs to the electrode were diffusional, then it follows that impact frequency would be proportional to NP diffusion coefficient

f ∝ D (3)

and hence via the Stokes–Einstein equation, inversely proportional to solution viscosity

In this case, an Arrhenius-type analysis of the frequency vs. temperature data would be linear with activation energy equal to that of diffusion through water of 24.6 kJ mol⁻¹ (based on data taken from¹⁹). Fig. 1 shows a logarithmic plot of impact frequency against inverse temperature and good agreement is found with the expected activation energy of 24.6 kJ mol⁻¹.

Fig. 1 An Arrhenius plot of experimental data showing the dependence of impact frequency on temperature.

2. Indirect electrochemistry of nanoparticles

To investigate the dependence of impact frequency with time, a series of chronoamperograms for AgNP impacts were recorded as described in¹⁸ at 295 K in a solution of 2.8 mM H₂O₂ in 0.01 M HCl/0.3 M KCl with a carbon fibre microelectrode (radius 4.8 μm) potentiostatted at −0.90 V vs. SCE and several hundred reductive impact spikes recorded as the H₂O₂ present was electrolysed at the AgNP surface during the time in contact with the electrode.

H₂O₂(aq) + 2e⁻ + 2H⁺ → 2H₂O (5)

Between each chronoamperogram (duration 5 s), the solution was vigorously bubbled with argon to agitate the NP suspension and clean the electrode surface. Fig. 2 shows a typical chronoamperogram recorded and a plot of cumulative impacts (N) vs. time. In all cases, a rapid rise in the number of observed spikes occurs in approximately the first second of measurement followed by a marked levelling off towards a limiting value.

Fig. 2 (a) A typical chronoamperogram showing impact spikes, and (b) the associated plot of cumulative number of spikes versus time.

In previous work,⁸ assuming that all impacting nanoparticles are oxidatively destroyed in ‘direct’ mode, we have shown how the Shoup and Szabo expression for a current transient at a microdisk electrode of radius r_d, which is given by

I = 4nFCDr_df(τ) (6)

where

f(τ) = 0.1854 + 0.8863τ^−1/2 + 0.2146exp(0.7823τ^−1/2) (7)

and n is the number of electrons transferred, F is the Faraday constant, and normalised time τ = 4Dt/r_d², can be used to derive an expression for N

N = NACr_d³g(τ) (8)

where

g(τ) = τ + 1.437τ^1/2 + 6.57 × 10⁻²lnτ − 3.35 × 10⁻³τ⁻¹ + 3.43 × 10⁻³τ^−1/2 + 3.49 × 10⁻⁴τ^−3/2

Eqn (7) has been shown to be capable of accurately describing the frequency of NP impacts for the case of destructive impacts, that is, where the metal NP is exhaustively oxidised during the collision.⁸

We have previously determined the sticking coefficient, s, for AgNPs (of radii 13–45 nm) on carbon substrate electrodes and found that s was essentially independent of potential.⁹ We note that where a proportion of impacting NPs stick to the surface this provides a sink for the NPs and a concentration gradient for Fickian diffusion. To reflect this, eqn (7) in ‘indirect’ mode would be expressed as

N = N_ACsr_d³g(τ) (9)

For a surface coverage, θ, the rate of adsorption of impacting NPs will be given by

where k is a constant with dimensions of (no. of particles)⁻¹. This expression can be solved to yield

θ = 1 + Ce^−skN (11)

Considering the lower limit of θ namely that θ = 0 at N = 0, the integration constant, C, can be evaluated to be −1.

The rate of observable impacts, can then be expressed as

Substitution of (10) into (11) followed by direct integration, along with the condition that N_obs = 0 when N = 0 yields

Here, the parameter k reflects such factors that affect the effective free surface area for an incoming NP to impact and be voltammetrically observed such as:

(i) reduced effective free surface area due to the depletion zones established around each adsorbed NP, and (ii) increased effective free surface area due to the greater sticking probability of Ag on Ag (ca 0.70 at 293 K²⁰) than Ag on C, and hence the possibility of surface aggregation, and (iii) any effects of solution-based aggregation of the NPs. We therefore expect values of k to be specific to the composition of the NP and in some cases, its size.

To calculate the N_obsvs. t plots required for simple analysis of the data, it is recognised that although eqn (8) is continuous the impact phenomenon is intrinsically stochastic, as reflected in eqn (9)–(12). Therefore N_obs is calculated from integral values of N provided from eqn (8) and plotted against the times t at which N is an integer in (8).

Fig. 3 shows a selection of fits of eqn (12) with the value of k = 0.30 particle¹ compared to experimental data, with Fig. 4a showing data taken from a chronoamperometric scan performed within 100 s of ultrasonic dispersion of the AgNPs, and Fig. 4b data from a scan of 5 min later which shows no significant effects of aggregation on this timescale.

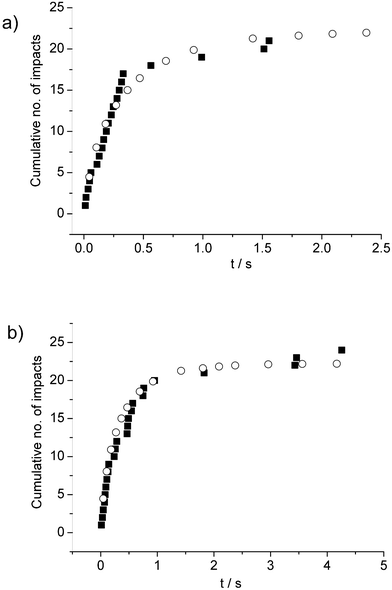Fig. 3 impacts versus time plots showing experiment data (■) compared to eqn (12) (○) for the known concentration of 55.9 pM and with k = 0.30 particle⁻¹ (see text) for chronoamperograms recorded (a) 100s and (b) 5 min after ultrasound-assisted dispersion of the NPs.

Conclusions

We have demonstrated that experimental observation of the frequencies of particle impacts as a function of both time and temperature can be quantitatively explained by diffusive transport of the nanoparticles to the electrode surface using a simple model. In the cases of both direct (i.e. destructive oxidation) and indirect (surface electrolysis of solution-phase H₂O₂) impacts there is a concentration gradient set up. In the former, the nanoparticle sink is provided by destruction of the NP itself at suitably oxidising potentials, that is

Ag(NP) − e⁻ → Ag⁺(aq)

as in (2), or in the case of the latter, the sink is provided by adsorption of the nanoparticles onto the electrode. A simple Fickian model to explain the frequency response for direct impacts was proposed in,⁸ with excellent agreement for the cases of aggregating (AgNPs) particles and non-aggregating (NiNPs) particles. We have now shown that the Fickian approach can also quantitatively explain the frequency of impacts for indirect impact processes for cases where there is a non-zero sticking probability of the nanoparticles with the electrode surface.

Acknowledgements

The authors thank the Leverhulme Trust for financial support.

References

1. N. V. Rees, Y.-G. Zhou and R. G. Compton, RSC Adv., 2012, 2, 379.
2. Y.-G. Zhou, N. V. Rees and R. G. Compton, Angew. Chem., Int. Ed., 2011, 50, 4219.
3. M. Giovanni and M. Pumera, Electroanalysis, 2012, 24, 615.
4. A. V. Korshunov and M. Heyrovsky', Electroanalysis, 2006, 18, 423.
5. A. J. Bard and X. Y. Xiao, J. Am. Chem. Soc., 2007, 129, 9610.
6. I. J. Cutress, N. V. Rees, Y. G. Zhou and R. G. Compton, Chem. Phys. Lett., 2011, 514, 58.
7. E. J. F. Dickinson, N. V. Rees and R. G. Compton, Chem. Phys. Lett., 2012, 528, 44.
8. E. J. E. Stuart, Y.-G. Zhou, N. V. Rees and R. G. Compton, RSC Adv., 2012, 2, 6879.
9. N. V. Rees, Y.-G. Zhou and R. G. Compton, ChemPhysChem, 2011, 12, 1645.
10. Y.-G. Zhou, N. V. Rees and R. G. Compton, Chem. Phys. Lett., 2011, 514, 291.
11. Y-G. Zhou, N. V. Rees and R. G. Compton, Chem. Phys. Lett., 2011, 511, 183.
12. Y-G. Zhou, N. V. Rees and R. G. Compton, ChemPhysChem, 2011, 12, 2085.
13. J. M. Kahk, N. V. Rees, J. Pillay, S. Vilakazi, R. Tshikhudo and R. G. Compton, Nanotoday, 2012, 7, 174.
14. Y-G. Zhou, N. V. Rees and R. G. Compton, Chem. Commun., 2012, 48, 2510.
15. N. V. Rees, Y.-G. Zhou and R. G. Compton, Chem. Phys. Lett., 2012, 525–526, 69.
16. A. Pyatenko, M. Yamaguchi and M. Suzuki, J. Phys. Chem. C, 2007, 111, 7910.
17. A. Pyatenko, M. Yamaguchi and M. Suzuki, J. Phys. Chem. B, 2005, 109, 2160.
18. E. J. E. Stuart, N. V. Rees and R. G. Compton, Chem. Phys. Lett., 2012, 531, 94.
19. CRC Handbook of Chemistry and Physics, 86th Edition, CRC Press, Boca Raton, FL, USA.
20. R. F. Benck, C. Crisco and H. L Spies, J. Vac. Sci. Technol., 1973, 10, 582.

---