Click-chemistry approach to azacycloalkene monosulfonyl diamines: synthesis and computational analysis of the reaction mechanism

Abstract

The cycloaddition reaction of the morpholino enamines of N-methylpiperidone and N-methyl tropinone with sulfonylazides was exploited, leading to a click-chemistry approach to uncommon azacycloalkene monosulfonyl diamines in good yields. A computational model for the key step decomposition of the triazoline intermediate was then realized by DFT calculations. The model explains the observed reaction outcome and leads to a new interpretation of the decomposition mechanism for 5-amino-1,2,3-triazolines.

---

Introduction

Vicinal diamines frequently appear as structural units in organic molecules of biological and medicinal interest, as well as in auxiliary groups or ligands for catalytic processes.¹ Moreover it was demonstrated that monotosylated diamine complexes of Ru(II) form highly enantioselective catalysts for ketone reductions.² In particular, our group is currently interested in synthetic methodologies to achieve novel sulfonamide derivatives which have been found useful as potential inhibitors of protein Rac1.³

For those reasons, in this paper we describe a facile and versatile synthetic method to obtain azacycloalkene-monosulfonyl-diamines from accessible starting materials.

Our group studied for a long time cycloaddition reactions and the subsequent rearrangement of the cycloadducts of aryl and sulfonyl azides with enamines of various aldehydes and linear or cyclic ketones.⁴ In particular, when sulfonyl azides were used, the primary unstable dihydrotriazole cycloadduct underwent a spontaneous transformation and two main products were obtained: 2-alkyl-sulfonylamidine 1 by nitrogen loss and C-5 substituent transposition and the sulfonylformamidine 2 by alkyl diazomethane loss (Scheme 1).

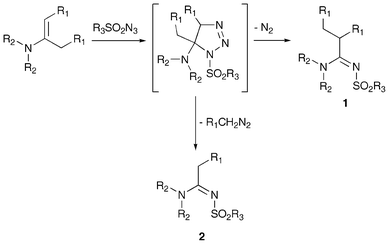Scheme 1 General reaction scheme for the cycloaddition of enamines with sulfonyl azides.

The obtained amidines were extensively used as syntones in heterocycle synthesis.⁵ Aiming to obtain new synthetically useful starting materials, a number of carbonylic compounds have been used. It is known that the nature of the starting carbonyl reactant appears to rule the outcome of the reaction, and cyclic ketones containing a nitrogen atom showed an unexpected behaviour.⁶ Consequently, one aim of this work was to thoroughly investigate the behaviour of alkylpiperidones and tropinones as the carbonylic reactant. Moreover, due to the peculiar regiochemical results herein obtained, an in-depth computational study of the reaction mechanism was performed. The results were in perfect agreement with the experiments and provided the evidence for a new interpretation of the mechanism of 5-amino-1,2,3-triazoline decomposition and rearrangement.

Results and discussion

Chemistry

The reaction between morpholino enamine of 1-methyl-4-piperidone 3 and tosyl azide 4a was initially investigated. By performing the reaction at room temperature in methylene dichloride as the solvent, we observed a rapid nitrogen development, but any attempt to isolate the components of the complex crude mixture failed. Indeed, the crude changed during the work-up procedures and subsequent chromatography purification gave discouraging results. The main evidence was the absence of expected amidine 1 or formamidine 2. Even by working at lower temperature, comparable results were obtained. However, starting from freshly distilled enamine in appropriate conditions of solvent and temperature (i.e. diethyl or diisopropyl ether, depending on the product's solubility, and 5–10 °C) the pure compound 5a precipitated from the solution and was isolable in good yields. This compound was stable for several days at room temperature and for several months at 0 °C. The structure of tosylamide 5a was deduced from the reported spectroscopic and spectrometric data. Indeed, the molecular weight supplied by mass analysis showed the loss of nitrogen and the ¹H NMR showed the presence of the tosyl group and two different multiplets corresponding to the morpholine moiety. The exchangeable proton, two methyl groups and complex multiplets in the aliphatic zone were also evident. ¹³C NMR spectra showed the presence of three methylene signals and two quaternary carbons at 129.0 and 126.0 δ in addition to the tosyl and morpholine signals. ¹H NMR spectra in CDCl₃ also showed a complex multiplet at 5.75–5.80 δ associated to enaminic CH of tautomer D (see Scheme 3). However, this characteristic multiplet disappeared by changing the NMR solvent to DMSO, suggesting a stabilization of the 5a form.

Encouraged by those interesting results, we drove to extend this scheme to other starting materials to verify the reaction trend and the repeatability of the results. The selected enamines were the morpholino enamines of 4-methylpiperidone 3 and of tropinone 6, while the chosen sulfonylazides were tosylazide 4a, p-nitrosofolylazide 4b, styrylsulfonylazide 4c, o-nitrosulfonylazide 4d and phenylmethanesulfonylazide 4e (Scheme 2).

Scheme 2 Reaction scheme for azacycloalkene-monosulfonyl-diamines 5 and 7. Reagents and contitions: (i) Et₂O (iPr₂O for 5b), 20 °C, 15 min.

In all cases the products were obtained in good yields in accordance with the proposed scheme. An in-depth study of NMR HSQC, COSY and NOESY spectra of 7d allowed us to unequivocally confirm the proposed structure. All signals were separable and identified in ¹H and ¹³C NMR at 500 and 125 MHz, respectively. So the nOe effect between NCH-1 at 3.49 δ and morpholino CH₂N at 2.55 δ confirmed the C2 position of morpholine. Another observation was useful to explain the reaction steps. When the ¹³C spectra of a concentrated solution of 7d (50 mg of 7d in 1 mL of CDCl₃) was recorded, the first 50 scans only showed signals associated with the imino form C (see Scheme 3). Instead the ¹³C spectra recorded after 10 h of sample preparation only showed signals associated with the enamino form 7. This fact suggested the imino form C as the initial reaction product, which subsequently tautomerizes (Scheme 3).

Scheme 3 Tautomeric forms of products 5, 7.

Computational investigation of the reaction mechanism

Save for a theoretical study for the proton-induced decomposition of 1,2,3-triazoline and 1-methyl-1,2,3-triazoline,⁷ to our knowledge no detailed theoretical studies for the thermal decomposition and rearrangement of 4- and 5-substituted triazolines have been reported in the literature. A well formulated mechanistic hypothesis, although not supported by theoretical calculations, for the decomposition of bicyclic triazolines obtained by the reaction of benzylazide with different enones has been proposed by Aubè and coworkers.⁸

Although the reported mechanism concerned bicyclic triazolines bearing an alkyl group at the 7a position, its generalization to the 7-morpholino substituted triazolines herein described, as depicted in Scheme 4, appears to be legitimate.

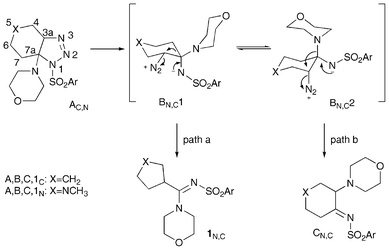Scheme 4 Stepwise mechanistic hypothesis for bicyclic 1,2,3 triazolines.

Indeed, the triazolines A, through an initial ring opening, could provide a zwitterion intermediate B which could evolve by either ring contraction (path a) or [1,2] shift of the morpholino group (path b) and consequent nitrogen loss. The zwitterion intermediate could exist in two different conformations, B1 and B2: while conformer B1 leads to 1–2 bond migration onto the leaving diazonium group in an antiperiplanar fashion, migration of the morpholino group in B2 onto the axial diazonium species results in formation of imine C which could tautomerize to 5 and D (see Scheme 3).

Previously reported decompositions of triazolines obtained by the reaction of tosylazide with 4-cyclohexenylmorpholine (X = CH₂),^4a only provided the ring contraction product 1 (path a). On the other hand, the herein reported reactions (X = NCH₃) only provided diamino products 5, 7 (or the corresponding C and D tautomers) deriving from the migration of the morpholino group (path b).

Starting from the results herein reported and considering our interest in modeling reaction mechanisms,⁹ we decided to perform a computational mechanistic study by means of Density Functional Theory (DFT). The mPW1B95 functional,¹⁰ coupled with the 6-31+G(d,p) basis set, was chosen for all calculations as in precedent works of our group it proved to be highly reliable when compared with other common functionals.^9d,e All calculations have been performed in the gas phase and in solution, where the solvent effect was considered for both geometry optimizations and Intrinsic Reaction Coordinates (IRCs) analyses by means of the conductor-like polarizable continuum model (CPCM) for diethyl ether.¹¹ Unless differently specified, the following discussion is referred to solution phase results.

The decomposition of triazolines A_N (from 1-methylpiperidin-4-one, hereafter referred as the “aza” model) and A_C (from cyclohexanone, hereafter referred as the “carbo” model), where Ar = Ph, were chosen as representative reaction models. The following discussion, unless differently specified, refers to both the “aza” and “carbo” models.

Starting from the mechanistic hypothesis of Scheme 4, we initially evaluated the difference in stability between zwitterion conformations B1 and B2 as their energy difference might be responsible for the observed outcome. However, for both the “aza” and “carbo” models, the B1 conformer was the most favored, being 2.3 and 3.1 kcal mol⁻¹ more stable, respectively.

This result suggests that the reaction outcome might be controlled at the transition state level, then the relative stability between transition states for paths a and b could rule the reaction outcome. For this reason, structures corresponding to triazolines A, zwitterions B and products 1 and C, were fully optimized. Starting from the most stable conformation of triazolines A, the location of the transition states (TSs) leading to zwitterions B was attempted by slightly lengthening the N1–N2 bond distances.

In both the “aza” and “carbo” models, the corresponding TS-A_N1 and TS-A_C1 presented N1–N2 and C3a–N3 (d1 and d2, accordingly to Fig. 1), bond distances both increased with respect to the corresponding distances in triazolines A (Δd1 = 1.066 Å, Δd2 = 0.400 Å and Δd1 = 1.043 Å, Δd2 = 0.382 Å for the “aza” and “carbo” models, respectively), thus suggesting that the nitrogen molecule might be eliminated in a concerted manner.

Fig. 1 Geometries for the “aza” and “carbo” model TSs. Selected distances are reported in Å, Wiberg bond indices calculated from NBO analysis are reported in parenthesis.

To confirm or refuse this hypothesis, an IRC analysis,¹² which locates the lowest energy path connecting reactants to TSs and TSs to products, was performed starting from TS-A_N1 and TS-A_C1. In both cases the IRC analyses confirmed the direct transformation of triazolines A into the final products 1 without the obtainment of any zwitterionic structure that could be considered a stationary point along the potential energy surface (PES) (Fig. 2).

Fig. 2 IRC analysis for the decomposition of triazoline A_C (“carbo” model) following path a. Geometries for selected points along the reaction energy path are also reported. Energies are calculated relatively to the most stable conformation of triazoline A_C.

This result gives weight to the hypothesis that triazolines might decompose through a pericyclic mechanism, involving a sigmatropic [1,2] shift of the alkyl (path a) or morpholino (path b) groups accompanied by nitrogen loss. The two different paths a and b would then originate from the conformations A1 or A2 of the corresponding triazoline, accordingly to Scheme 5.

Scheme 5 Proposed concerted reaction mechanism.

It should be noted that, analogously to what is observed for the hypothesized zwitterion intermediates, conformation A1 is always preferred for triazolines also (ΔG_A2−A1 = 3.2 and 1.1 kcal mol⁻¹ for “aza” and “carbo” models, respectively) and so the preference toward paths a or b should be exclusively determined at the transition state level. This hypothesis could be confirmed by locating the TSs involved in path b for both the “aza” and “carbo” models (TS-A_N2 and TS-A_C2, respectively). Activation energies should then favor path b in the former and path a in the latter model.

Both TS-A_N2 and TS-A_C2 were obtained from the corresponding triazolines A2 by lengthening the N1–N2 bond distance and the evaluation of the corresponding activation free energies (ΔΔG^‡_b−a = −1.1 and 2.2 kcal mol⁻¹ for the “aza” and “carbo” models, respectively, accordingly to Table 1) supported our thesis. As expected, a successive IRC analysis (Fig. 3 and Fig. S2, ESI‡) confirmed that the located TSs directly connect the triazoline reactants with the imino product C, providing further evidence of a concerted decomposition.

Fig. 3 Intrinsic Reaction Coordinate analysis for the decomposition of triazolines obtained from the enamines of 4-piperidone (“aza” model) or cyclohexanone (“carbo” model).

To provide a complete description of the reaction, the formation of triazolines A_N and A_C through the 1,3-dipolar cycloaddition of azide 3 with enamines 4_N and 4_C (for “aza” and “carbo” models, respectively) was initially modelled (see Fig. S3, ESI‡) and the complete reaction profiles are reported in Scheme 6.

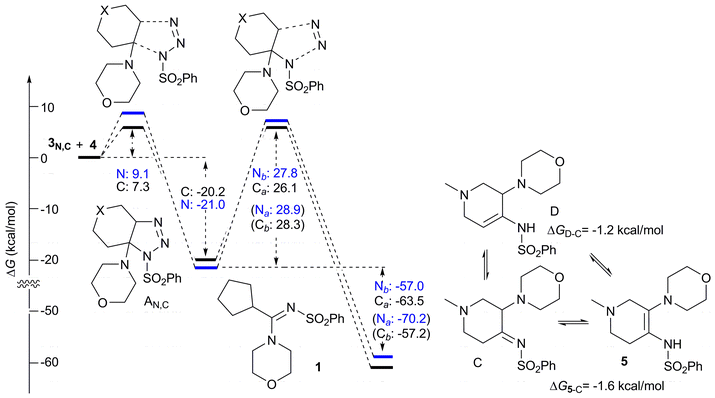Scheme 6 Complete reaction profiles for “carbo” (black) path a and “aza” (blue) path b. Free energy differences are calculated in solution (Et₂O) and reported in kcal mol⁻¹. Free energy differences for the unfavored “carbo” path b and “aza” path a are reported in parenthesis. Thermochemical corrections were obtained from vibrational analyses performed at 298.15 K, 1 atm.

For both the “aza” and “carbo” models, the reaction between enamines 3 and azide 4 occurs with rather low activation free energy barriers, with the reaction of 1-methyl-4-piperidone 3 being less favoured with respect to the carbocyclic analogue (9.1 and 7.3 kcal mol⁻¹, respectively) and leads to the corresponding triazolines with a free energy difference, with respect to isolated reagents, of −21.0 and −20.2 kcal mol⁻¹ for the “aza” and “carbo” models, respectively, this path being slightly advantagous over the reverse reaction in both cases. The reaction then proceeds through the triazoline decomposition, taking different routes for “carbo” and “aza” models, as described above. In both cases, quite large activation free energies are computed, suggesting that the triazoline might not immediately decompose. In the case of the herein reported compounds 5a–d and 7a–c,e, this is supported by the experimental observation that nitrogen starts to be released after about 2 min from the addition of the azide, while the reaction reaches completion in about 10 min. In both cases the triazoline decomposition is predicted to be quite exothermic, with free energy differences of −63.5 and −57.0 kcal mol⁻¹ for the “carbo” and “aza” models. For this latter reaction path, the imino form C, directly obtained from TS-A_N2, tautomerizes to the most stable enamino forms 5 (ΔG_5−C = −1.6 kcal mol⁻¹) and D (ΔG_D−C = −1.2 kcal mol⁻¹, see Scheme 6). While in Et₂O the enamino tautomer 5 prevails over D (ΔG_5−D = −0.4 kcal mol⁻¹), and exactly the opposite is predicted by performing the calculation in chloroform (ΔG_D−5 = −0.4 kcal mol⁻¹). These results suggest that both 5 and D enamino forms coexist and their equilibrium can be shifted to one or to the other depending on conditions.

The lower reaction free energy differences obtained for both the path a products (Scheme 6) are not surprising, as the triazoline decomposition is not reversible and a thermodynamic equilibrium between products is not possible. The outcome might then only be ruled by the energy differences between transition states, making the reaction proceed under exclusive kinetic control.

A further remark should be given on the comparison of activation and reaction free energies for paths a and b. While the energy difference between TS-A_C1 (“carbo” path a) and TS-A_C2 (“carbo” path b; ΔG_b−a = 2.2 kcal mol⁻¹) fully supports the isolation of 1 as the only product, the difference between TS-A_N2 (“aza” path b) and TS-A_N1 (“aza” path a; ΔG_b−a = 1.1 kcal mol⁻¹) appears to be too low to suggest the isolation of 5 as the only product. Indeed, according to the Arrhenius equation, the ratio between products 1_N and C_N, predicted from computed activation free energies as [1_N]/[C_N] = e^{(ΔG‡C−ΔG‡1)/RT}, is 16 : 84. Although we did not expect to exactly reproduce the complex experimental results by a computational method (the mean average errors of some among the most accurate theoretical methods in predicting activation energies for 1,3-dipolar cycloadditions spanned from 1.2 to 3.5 kcal mol^−1 13), it is true that 16% of compound 1_N should have been detected by NMR. However, it is also true that for all the reported reactions the principal product precipitated in the reaction mixture and was isolated in about 80% yield, while byproducts in the mother liquors were not isolable.

Finally, providing a rationale of the computed activation barriers for “aza” and “carbo” species has not been trivial. Our investigation started from two hypotheses on the role of N5, that is the stabilization of TS-A_N2 or the destabilization of TS-A_N1. Nevertheless, the visual inspection of TS geometries for paths a and b of both models evidenced only minor differences, suggesting that the observed outcome should not be ruled by one main reason (such as an evident difference in steric hindrance or the presence of hydrogen bonds at the TS level), but by the combination of different minor effects. For instance, Wiberg bond indices (BIs)¹⁴ were calculated via NBO¹⁵ analysis (see Fig. 1) for TS-A_C,N1,2. Indeed, the difference between BIs (Δ_BI) at the TS level can be taken as a measure of the synchronicity degree, the lower is Δ_BI, the higher is the synchronicity.^9e Such analysis showed that path b TSs were less synchronous than path a TSs, but a higher variation in synchronicity was observed when switching from TS-A_N1 (Δ_BI = 0.32) to TS-A_N2 (Δ_BI = 0.53) than from TS-A_C1 (Δ_BI = 0.33) to TS-A_C2 (Δ_BI = 0.45). This observation was also supported by the analysis of NBO charges on the leaving N₂ group (see Fig. S4, ESI‡), showing a higher cationic character in TS-A_N2 and TS-A_C2 (N₂ charge = 0.219 and 0.176, respectively), than in TS-A_N1 and TS-A_C1 (N₂ charge = 0.140 and 0.146, respectively).

The above data help in defining the chemical-physical variations induced by the replacement of the C5 with a nitrogen, but a further indication came from an Atom In Molecules (AIM)¹⁶ wavefunction analysis of TS-A_N1, -A_N2, -A_C1 and -A_C2, which by locating bond critical points (BCP) and corresponding bond paths (BP) allows a rigorous identification of those weak interactions that are otherwise difficult to evidence (Fig. 4). Indeed, in recently published studies AIM analysis has been found useful in characterizing TSs leading to competing reaction paths.¹⁷

Fig. 4 AIM analyses, molecular graphs and bond critical points (BCP) for TSs of path a (TS-A_N1 and TS-A_C1) and path b (TS-A_N2 and TS-A_C2). Bond paths are denoted by solid lines, BCPs are denoted by small red balls on the bond path. Weak interactions which differentiate “aza” and “carbo” models are evidenced by a black arrow. The values of ρ_b for selected BCP are reported in a.u.: BCP1, 0.0080; BCP2, 0.0076; BCP3, 0.0129; BCP4, 0.0109.

As reported in Fig. 4, our analyses show that the replacement of C5 with N5 induces both a destabilization of TS-A_N1 with respect to TS-A_C1, where BCP1 defines an additional weak attractive interaction between the SO₂ oxygen and the axial C6 hydrogen in the cyclohexane ring, as well as a stabilization of TS-A_N2, where BCP3 defines an additional weak attractive interaction between the SO₂ oxygen and the axial C7 hydrogen. Other differences can be observed between TS-A_N2 and TS-A_C2, that are the presence of a BCP between SO₂ and the CH next to the morpholine oxygen in TS-A_N2 (BCP2), not present in TS-A_C2, which is however characterized by an additional BCP between SO₂ and the equatorial C7 hydrogen in the cyclohexane ring. The values of ρ_b (Fig. 4), which are proportional to the strength of the interaction,¹⁸ at the selected BCPs are in line with values reported in previous work for an analogous weak interaction,¹⁷ and confirm a clear stabilization effect in TS-A_N2. As mentioned above, this analysis is intended to provide a rationale of the observed experimental outcome, but we cannot exclude that other reasons could concur in determining the computed activation barriers.

Seeking for an ultimate proof on the reliability of our theoretical findings, several attempts for locating transition states for a stepwise mechanism were also made by evaluating different levels of theory. However, in every case, TSs from zwitterions B1 and B2 to products 1 and C were actually located (TS-B_N,C1 and TS-B_N,C2, respectively, see ESI‡) but no TSs connecting triazoline A to zwitterion B were found.

In should be finally considered that the proposed mechanism is only possible if, at the reaction conditions, an equilibrium between conformations A1 and A2 might be established. Moreover, the required energy for the conversion between triazolines A1 and A2 should be lower than the reaction activation energy. In order to prove this, we realized a simple computational model based on the main scaffold of triazoline A, accordingly to Scheme 7. The activation energy for the conformational change between the most stable chair conformation and the boat intermediate was then calculated by locating the corresponding TSs (ΔG^‡ = 6.6 and 6.9 kcal mol⁻¹ for the chair 1 to boat transition and 7.5 and 5.0 kcal mol⁻¹ for the boat to chair 2 transition in the “aza” and “carbo” models, respectively), and was far below the activation energy required for the reaction to proceed via either path a or b (ΔG^‡ = 28.9 and 27.8 kcal mol⁻¹, respectively, for the “aza” model), confirming that an equilibrium between the two triazoline conformations is possible in the reaction conditions.

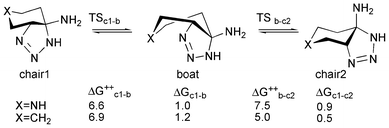Scheme 7 Chair–twisted boat–reversed chair equilibrium. Activation and reaction free energy differences are calculated in solution and reported in kcal mol⁻¹.

Conclusion

A series of new azacycloalkene monosulfonyl diamines 5 and 7 has been efficiently prepared trough a click-chemistry approach affording the desired products in good yields.

The key reaction step, consisting of the decomposition and rearrangement of the 1,2,3-triazoline intermediate, has been modeled and compared to the parent carbocyclic derivative, which only leads to the amidine product through the ring contraction mechanism. Contrarily to what is expected, the triazoline decomposition occurs in both cases in a concerted manner, directly leading to the final products. The reaction is predicted to be under kinetic control and the selectivity toward the diamino derivatives can be due to stabilising weak interactions at the TS level, as evidenced by AIM analyses.

Experimental

Theoretical calculations

Reactants 3_N, 3_C, 4, A_N1, A_N2, A_C1, A_C2, zwitterions B_N1, B_N2, B_C1, B_C2 and products 1_N, 1_C, C_N, C_C, 5_N and D_N were obtained from a conformational search performed in vacuum at the molecular mechanic level using the MMFF94x force field implemented in MOE,¹⁹ and subsequently optimized at the mPW1B95/6-31+G(d,p) level of theory.¹⁰ Transition states TS-3+4_N,C, TS-A_N1, A_N2, A_C1 and -A_C2 were then constructed and fully optimized at the same level of theory. Vibrational frequencies were computed at the same level of theory in order to define optimized geometries as minima (no imaginary frequencies) or TSs (a unique imaginary frequency corresponding to the vibrational stretching of the forming/breaking bonds) and to calculate zero-point and thermochemical corrections to electronic energies (1 atm, 298.15 K, unscaled frequencies). In order to verify that no other minima or TSs were present over the reaction path, IRC analyses¹² were performed at the mPW1B95/6-31+G(d,p) level starting from TS-A_N1,A_N2,A_C1 and -A_C2, and requesting the localization of 30 points along each direction of the reaction path (forward and reverse) with a step size of 0.2 amu^1/2 bohr. All calculations were performed in both the gas phase and in solution, using the CPCM solvent model for diethyl ether (and chloroform, for tautomeric forms C_N, 5_N and D_N),¹¹ as implemented in the Gaussian09 software package.²⁰ AIM analyses^16,18 were performed on the wavefunctions obtained from the CPCM-mPW1B95/6-31+G(d,p) optimized TS-A_N1,A_N2,A_C1 and -A_C2 geometries using the AIM2000 software.²¹

Chemistry

Mps were determined by a Büchi 510 (capillary) apparatus. IR was performed with Perkin–Elmer FT-IR ‘Spectrum One’ (KBr), NMR spectra, performed at 25 °C, were obtained with Bruker Advance 300, Bruker Advance 500 and Varian Gemini 200 spectrometers in CDCl₃. Low-resolution MS spectra were recorded with a Thermo-Finnigan LCQ ADVANTAGE AP electrospray/ion trap equipped instrument using a syringe pump device for the direct injection of sample solutions.

The synthesis of enamine 3a²² and 6²³ was previously described.

Synthesis of tosylamides 5 and 7

General Procedure: Enamine 3a and 6 (3 mmol) were dissolved in 20 mL of diethyl ether. The solution was cooled with a cold bath (5–10 °C) and azide 4a–e (3 mmol) was added. A plentiful extrication of gas was observed after 2 min. from the addition of azide and the reaction was ended in 10 min. (TLC ethyl acetate-cyclohexane 1 : 1). The abundant precipitate was filtered and dried in vacuum.

4-Methyl-N-(1-methyl-5-morpholino-1,2,3,6-tetrahydro-pyridin-4-yl)-benzensulfonamide (5a)

Yield 78%; white solid; mp 109–110 °C (from Et₂O). ν_max/cm⁻¹ 3435 and 3207 (NH). δ_H (200 MHz; CDCl₃, Me₄Si): = 2.24–2.31 (m, 5H, 2CH₂ + NH), 2.32 (s, 3H, CH₃–N), 2.39 (s, 3H, CH₃Ph), 2.45–2.49 (m, 4H, CH₂–N), 2.82–2.86 (m, 2H, CH₂–2), 5.62–5.68 (m, 1H, CH), 7.27 (d, J = 7.0 Hz, 2H, Ar–H), 7.70 (d, 7.0Hz, 2H, Ar–H) ppm. δ_C (50 MHz; CDCl₃) = 21.7(CH₃), 26.2(CH₂), 46.0(CH₃), 49.9(CH₂), 50.4(CH₂), 51.8(CH₂), 67.4(CH₂),126.0 (C), 127.1(CH), 129.0(C), 129.9(C), 137.4(C), 143(C). m/z 352 (M⁺). Found: C, 57.9; H, 7.3; N 11.8 calcd. for C₁₇H₂₅N₃O₃S C, 58.1; H,7.2; N, 11.9.

4-Nitro-N-(1-methyl-5-morpholino-1,2,3,6-tetrahydro-pyridin-4-yl)-benzensolfonamide (5b)

Yield 85%; pale yellow solid; mp 103–104 °C (from iPr₂O). ν_max/cm⁻¹ 3436 and 3283 (NH). δ_H (200 MHz; CDCl₃) = 2.24 (s, 3H, CH₃–N), 2.25–2.38 (m, 6H, 3CH_2-5+D), 2.40–3.08 (m, 3H, CH₂-2-₅ + CH₂-2_D + CH_D), 3.58–3.82 (m, 4H, 2CH₂O), 5.76–5.81 (m, 1H, CH-5_D), 8.06 (d, J = 7.0 Hz, 2H, Ar–H), 8.33 (d, J = 7.0 Hz, 2H, Ar–H) ppm. δ_H (200 MHz; DMSO) = 2.11 (s, CH₃–N), 2.10–2.38 (m, 5H, 2CH₂N + CH-3), 3.02–3.09 (m, 1H, CH-3), 3.25–3.63 (m, 8H, 2CH₂–O + 2CH₂–N), 8.06 (d, J = 7.0 Hz, 2H, Ar–H), 8.33 (d, J = 7.0 Hz, 2H, Ar–H), 8.68 (sb, 1H, NH) ppm. δ_C (50 MHz; CDCl₃, Me₄Si) = 26.0 (CH_2-5), 45.6 (CH_3-D), 45.7 (CH_3-5), 49.1 (CH_2-5), 50.0 (CH_2-5), 50.5 (CH_2-D), 51.6 (CH_2-5) 56.4 (CH_2-D), 57.6 (CH_2-D), 61.1 (CH-_D), 67.3 (CH_2-5+D), 110.7 (CH-_D), 124.5 (CH-_5+D), 125.1 (C-₅), 128.4 (CH-_5+D), 129.2 (C-_D), 129.9 (C-₅), 146.4 (C-_5+D), 150.4 (C-_5+D). m/z 383 (M⁺). Found: C, 50.0; H, 5.9; N 14.5 calcd. for C₁₆H₂₂N₄O₅S C, 50.2; H,5.8; N, 14.6

N-(1-Methyl-5-morpholino-1,2,5,6-tetrahydro-pyridin-4-yl)-2-phenylethenesolfonamide (5c)

Yield 83%; white solid; mp 108–109 °C (from Et₂O). ν_max/cm⁻¹ 3238 (NH). δ_H (200 MHz; CDCl₃, Me₄Si) = 2.34 (s, 3H, CH₃N), 2.24–2.78 (m, 6H, 3CH₂N), 2.82–3.05 (m, 2H, CH₂N), 3.24–3.38 (m, 1H, CH-3), 3.62–3.78 (m, 4H, CH₂O), 5.74–5.79 (m, 1H, CH-5), 7.82 (d, J = 15.63 Hz, 1H, CHSO₂), 7.38–7.50 (m, 4H, Ar–H), 7.53 (d, J = 15.63 Hz, 1H, CHPh) ppm. δ_C (50 MHz; CDCl₃, Me₄Si) = 45.5 (CH₃), 49.1 (CH₂), 50.2 (CH₂), 53.6 (CH₂), 61.1 (CH), 63.4 (CH₂), 67.5 (CH₂), 108.4 (CH), 124.0 (CH), 128.5 (CH), 129.3 (CH), 129.6 (C), 123.7 (C), 131.1 (CH), 132.7 (C), 142.6(CH). m/z 364 (M⁺). Found: C, 59.2; N, 7.0; N, 11.3 calcd. for C₁₈H₂₅N₃O₃S C, 59.5; H, 6.9; N,11.6.

2-Nitro-N-(1-methyl-5-morpholino-1,2,3,6-tetrahydro-pyridin-4-yl)-benzensolfonamide (5d)

Yield 87%; pale yellow solid; mp 95–97 °C (from Et₂O). ν_max/cm⁻¹ 3396 and 3215 (NH). δ_H (200 MHz; CDCl₃, Me₄Si) = 2.47 (s, 3H, CH₃N_D+6), 2.33–2.65 (m, 6H, 3CH₂N₅₊₆), 2.72–3.10 (m, 3H, CH₂-2-₅ + CH₂-2_D + CH₆), 3.65–3.80 (m, 4H, 2CH₂O), 5.89–5.96 (m, 1H, CH-5_D), 7.63–8.25 (m, 4H, ArH) ppm. δ_C (50 MHz; CDCl₃) = 26.3 (CH_2-5), 45.6 (CH_3-D), 45.5 (CH_3-5), 49.1 (CH_2-5), 50.2 (CH_2-5), 50.3 (CH_2-D), 51.7 (CH_2-5), 56.0 (CH_2-D), 57.6 (CH_2-D), 61.3 (CH-_D), 67.0 (CH₂-₅), 67.3 (CH_2-D), 112.2 (CH-_D), 125.2 (CH-_5+D), 129.4 (C-₅), 129.9, 131.1, 131.9, 132.7, 133.4, 134.4 (CH-_5+D), 133.0 (C-_D), 129.9 (C-₅), 136.4 (C-_5+D), 148.3 (C-_5+D). m/z 383 (M⁺). Found: C, 50.1; H, 6.0; N 14.4 calcd. for C₁₆H₂₂N₄O₅S C, 50.2; H,5.8; N, 14.6

4-Methyl-N-(8-methyl-2-morpholino-8-aza-bicyclo[3,2,1]oct-2-en-3-yl)benzensulfonamide (7a)

Yield 88%; white solid; mp 85–86 °C (from Et₂O). ν_max/cm⁻¹ 3435 (NH). δ_H (200 MHz; CDCl₃, Me₄Si) = 1.75–2.79 (m, 10H, 5CH₂), 2.27 (s, 3H, CH₃N), 2.47 (s, 3H, CH₃Ph), 3.24–3.55 (m, 2H, 2CHN), 3.61–3.71 (m, 4H, 2CH₂O), 7.28–732 (m, 2H, ArH), 7.69–7.87 (m, 2H, ArH) ppm. ¹³C NMR of mixture of imino C and enamino 7 forms (see discussion) δ_C (50 MHz; CDCl₃, Me₄Si) = 21.6 (CH_3-i+e), 24.8 (CH_2i), 27.6 (CH_2i), 30.2 (CH_2e), 30.7 (CH_2e), 35.3 (CH₃N_-i+e), 35.2 (CH_2e), 38.0 (CH_i), 50.5 (CH₂N_i), 51.1 (CH₂N_e), 55.5 (CH_i), 57.0 (CH_e), 62.8 (CH_e), 64.3 (CH_i), 67.2 (CH₂O_i), 67.3 (CH₂O_e), 123.9 (C_e), 127.0 (CH_e), 127.2 (CH_i), 129.5 (CH_e), 129.7 (CH_i), 134.0 (C_e), 137.5 (C_-e+i), 143.5 (C_e), 143.9 (C_i), 187.2 (C=N_i). mz 378(M⁺). Found: C, 60.3; H, 7.5; N, 11.0 calcd. for C₁₉H₂₇N₃O₃S C,60.4; H, 7.2; N, 11.1.

N-(8-Methyl-2-morpholino-8-aza-bicyclo[3,2,1]oct-2-en-3-yl)-4-nitrobenzensulfonamide (7b)

Yield 85%; pale yellow solid; mp 130–131 °C (from Et₂O). ν_max/cm⁻¹ 3436.0 (NH). δ_H (200 MHz; CDCl₃, Me₄Si) = 1.75–2.82 (m, 10H, 5CH2), 2.23 (s, 3H, CH₃N), 3.22–3.79 (m, 6H, 2CH + 2CH2O), 8.02–8.43 (m, 4H, ArH) ppm. δ_C (75 MHz; CDCl₃, Me₄Si) = 30.0 (CH₂), 30.9 (CH₂), 35.0 (CH₂), 35.6 (CH3), 50.6 (CH₂), 55.8 (CH), 57.2 (CH), 67.2 (CH₂), 122,8 (C), 124.4 (CH), 128.4 (CH), 134.8 (C), 146.5 (C), 150.4 (C). m/z 409(M⁺). Found: C, 52.7; H, 6.1; N, 13.6 calcd. for C₁₈H₂₄N₄O₅S C, 52.9; H, 5.9; N, 13.7.

N-(8-Methyl-2-morpholino-8-aza-bicyclo[3,2,1]oct-2-en-3-yl)-phenylethenesulfonamide (7c)

Yield 78%; white solid; mp 98–99 °C (from Et₂O). ν_max/cm⁻¹ 3435.4 (NH). δ_H (200 MHz; CDCl₃, Me₄Si) = 2.16–2.25 (m, 2H, CH₂), 2.44 (s, 3H, CH₃N), 2.61–2.65 (m, 4H, 2CH₂N), 3.01–3.10 (m, 2H, CH₂), 3.45–3.68 (m, 2H, 2CH), 3.68–3.73 (m, 4H, 2CH₂O), 3.80–3.84 (m, 2H, CH₂), 6.96 (d, J = 15.1 Hz, 1H, CHPh), 7.38–7.54 (m, 6H, CH + ArH) ppm. δ_C (50 MHz; CDCl₃, Me₄Si) = 29.6 (CH₂), 31.1 (CH₂), 34.6 (CH₂), 35.8 (CH₃), 44.9 (CH₂), 56.4 (CH), 57.9 (CH), 67.2 (CH), 123.6 (C), 126.6 (CH), 128 (CH), 129.4 (CH), 131.2 (CH), 132.6 (C), 141.7 (CH). m/z 390(M⁺). Found: C, 61.5; H, 7.1; N, 10.6 calcd. for C₂₀H₂₇N₃O₃S C, 61.7; H, 67.0, N, 10.79.

N-(8-Methyl-2-morpholino-8-aza-bicyclo[3,2,1]oct-2-en-3-yl)-(phenyl)-methansulfonamide (7d)

Yield 80%; white solid; mp 95–97 °C (from Et₂O). ν_max/cm⁻¹ 3437.5 (NH). δ_H (500 MHz; CDCl₃, Me₄Si) = 1.48–1.57 (m, 1H, H-6), 1.79–1.87 (m, 1H, H-7), 1.96–2.04 (m, 1H, H-4), 2.13-2.25 (m, 2H, H-6 and H-7), 2.37 (s, 3H, CH₃N), 2.52–2.60 (m, 4H, 2CH₂N), 2.72–2.80 (m, 1H, H-4), 3.31–3.37 (m, 1H, H-5), 3.47–3.51 (m, 1H, H-8), 3.57–3.63 (m, 4H, 2CH₂O), 4.36 (dd, AB system J = 14.2 Hz, 2H, CH₂Ph), 7.34–7.43 (m, 5H, ArH) ppm. ¹³C NMR for the imino form C: δ_C (125 MHz; CDCl₃, Me₄Si) 24.8 (CH₂), 27.4 (CH₂), 37.8 (CH₃), 51.0 (CH₂), 61.0 (CH₂), 62.8 (CH), 64.1 (CH), 67.5 (CH₂), 70.3 (CH), 128.6 (CH), 131.2 (CH), 188.6 (C=N); ¹³C NMR for the enamino form 7: δ_C (125 MHz; CDCl₃, Me₄Si) 28.9 (CH₂), 29.5 (CH₂), 33.9 (CH₂), 34.8 (CH₃), 44.9 (CH₂), 49.2 (CH₂), 55.8 (CH), 57.3 (CH), 60.8 (CH₂), 67.2 (CH₂), 122.8 (C), 128.1 (CH), 128.3 (C), 130.0 (CH). mz 378(M⁺). Found: C, 60.2; H, 7.4; N, 11.1 calcd. for C₁₉H₂₇N₃O₃S C, 60.4; H, 7.2; N, 11.1.

Acknowledgements

The authors are grateful to MIUR for financial support through the “FIRB – Programma “Futuro in Ricerca”” grant no. RBFR087YAY and to the “Centro Interuniversitario Lombardo per l'Elaborazione Automatica” (CILEA, Segrate, MI) for computational facilities. We also thank Dr Luca Basolo for the useful discussion upon the Bader's Atom in Molecules theory.

References

1. (a) For general applications, see: S. R. S. S. Kotti, C. Timmons and G. Li, Chem. Biol. Drug Des., 2006, 67, 101–114; (b) C. A. de Parrodi and E. Juaristi, Synlett, 2006, 2699–2715; (c) D. Lucet, T. Le Gall and C. Mioskowski, Angew. Chem., Int. Ed., 1998, 37, 2580–2627.
2. (a) S. Hashiguchi, A. Fujii, J. Takehara, T. Ikariya and R. Noyori, J. Am. Chem. Soc., 1995, 117, 7562–7563; (b) K. Matsumura, S. Hashiguchi, T. Ikariya and R. Noyori, J. Am. Chem. Soc., 1997, 119, 8738–8739; (c) D. Šterk, M. S. Stephan and B. Mohar, Tetrahedron Lett., 2004, 45, 535–537; (d) D. M. Tellers, M. Bio, Z. J. Song, J. C. McWilliams and Y. Sun, Tetrahedron: Asymmetry, 2006, 17, 550–553.
3. N. Ferri, A. Corsini, P. Bottino, F. Clerici and A. Contini, J. Med. Chem., 2009, 52, 4087–4090.
4. (a) R. Fusco, G. Bianchetti and D. Pocar, Gazz. Chim. Ital., 1961, 91, 933–957; (b) R. Fusco, G. Bianchetti, D. Pocar and R. Ugo, Chem. Ber., 1963, 96, 802–812; (c) F. Cassani, G. Celentano, E. Erba and D. Pocar, Synthesis, 2004, 1041–1046; (d) E. Beccalli, A. Contini and P. Trimarco, Tetrahedron Lett., 2004, 45, 3447–3449; (e) E. M. Beccalli, A. Contini and P. Trimarco, Tetrahedron, 2005, 61, 4957–4964.
5. (a) E. Erba, G. Mai and D. Pocar, J. Chem. Soc., Perkin Trans. 1, 1992, 2709–2712; (b) M. Battistini, E. Erba and D. Pocar, Synthesis, 1992, 1206–1208; (c) E. Erba, D. Pocar and P. Trimarco, J. Chem. Soc., Perkin Trans. 1, 1998, 3535–3539; (d) M. Battistini, E. Erba and D. Pocar, J. Chem. Soc., Perkin Trans. 1, 1993, 339–342; (e) E. M. Beccalli, A. Contini and P. Trimarco, Eur. J. Org. Chem., 2003, 3976–3984.
6. D. Pocar, L. M. Rossi, R. Stradi and P. Trimarco, J. Chem. Soc., Perkin Trans. 1, 1977, 2337–2340 and personal communication.
7. B. D. Wladkowski, R. H. Smith Jr. and C. J. Michejda, J. Am. Chem. Soc., 1991, 113, 7893–7897.
8. D. S. Reddy, W. R. Judd and J. Aubé, Org. Lett., 2003, 5, 3899–3902.
9. (a) E. M. Beccalli, G. Broggini, A. Contini, I. De Marchi, G. Zecchi and C. Zoni, Tetrahedron: Asymmetry, 2004, 15, 3181–3187; (b) A. Contini, D. Nava and P. Trimarco, J. Org. Chem., 2006, 71, 159–166; (c) A. Contini, S. Leone, S. Menichetti, C. Viglianisi and P. Trimarco, J. Org. Chem., 2006, 71, 5507–5514; (d) E. Borsini, G. Broggini, A. Contini and G. Zecchi, Eur. J. Org. Chem., 2008, 2808–2816; (e) M. C. Aversa, A. Barattucci, P. Bonaccorsi and A. Contini, J. Phys. Org. Chem., 2009, 22, 1048–1057; (f) F. Gassa, A. Contini, G. Fontana, S. Pellegrino and M. L. Gelmi, J. Org. Chem., 2010, 75, 7099–7106; (g) A. Casoni, E. Borsini, A. Contini, A. Ruffoni, S. Pellegrino and F. Clerici, Curr. Org. Chem., 2011, 15, 3514–3522.
10. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 6908–6918.
11. (a) A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans., 1993, 2, 799–805; (b) J. Andzelm, C. Kölmel and A. Klamt, J. Chem. Phys., 1995, 103, 9312–9320; (c) V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001; (d) M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681.
12. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
13. Y. Lan, L. Zou, Y. Cao and K. N. Houk, J. Phys. Chem. A, 2011, 115, 13906–13920.
14. K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096.
15. (a) Natural bond orbitals: A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926; (b) A. E. Reed, L. A. Curtiss and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
16. R. F. W. Bader, Atoms in molecules: A quantum theory, Clarendon Press, Oxford, 1994.
17. (a) E. A. B. Kantchev, Chem. Commun., 2011, 47, 10969–10971; (b) Y. Shen, Q. Meng, S. Huang, S. Wang, J. Gong and X. Ma, RSC Adv., 2012, 2, 7109–7119.
18. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
19. MOE V. 2010.10, Chemical Computing Group Inc., Montreal, Canada, http://www.chemcomp.com..
20. Gaussian 09, Revision A.1, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009.
21. F. Biegler-König, J. Schönbohm and D. Bayles, J. Comput. Chem., 2001, 22, 545–559.
22. R. Fusco, G. Bianchetti and S. Rossi, Gazz. Chim. Ital., 1961, 91, 825–840.
23. E. Vilsmaier, T. Herweck, M. Schummel, C. Tetzlaff, M. Dotzauer and U. Bergsträßer, Tetrahedron, 1998, 54, 7401–7416.

---

Footnotes

† This work is dedicated to our mentor and friend, Prof. D. Pocar, for his 50 year long exploration of triazoline chemistry.

‡ Electronic supplementary information (ESI) available: Further computational details, Cartesian coordinates, energies and thermochemical corrections for all the stationary points, NMR spectra of compounds 5a–d and 7a–d. See DOI: 10.1039/c2ra21592f

---