DOI:
10.1039/C2RA21242K
(Paper)
RSC Adv., 2012,
2, 7860-7867
Computational design and selection of optimal building blocks and linking topologies for construction of high-performance host materials†
Received
21st June 2012
, Accepted 26th June 2012
First published on 1st August 2012
Abstract
Two typical hole transport groups, carbazole and diphenylamine, and two typical electron transport groups, diphenylphosphine oxide and triphenylsilane, were linked to biphenyl at its ortho/meta/para-positions to investigate the effects of building blocks and linking topologies on the structural and electronic properties of such constructed host materials via density function theory calculation. It is found that the frontier orbital levels, energy band gap, and triplet energy of host molecules can be effectively tuned by different building blocks and linking topologies. The electron-transporting nature of π-conjugated molecules can be enhanced by connecting electron-withdrawing building blocks at the ortho or meta position, but not at the para-position. Employing asymmetric building blocks with meta-type topology would be an effective strategy for the design of high-performance bipolar host materials.
1. Introduction
Phosphorescent organic light-emitting diodes (PhOLEDs) are receiving much attention for their applications in full-color flat-panel displays and large-area solid-state lighting,1,2 because of their theoretically maximum internal efficiency of 100%.3 However, in such PhOLEDs the phosphorescent emitter should be doped within a host material in order to prevent concentration quenching of the phosphorescence.
An ideal host material should fulfill the following basic requirements: (1) a triplet energy (3Eg) larger than that of the triplet emitter molecules to avoid the guest-to-host back energy transfer; (2) suitable energy levels appropriately aligned with those of the neighboring active layers for facile and balanced charge injection; (3) fast and balanced charge transport; (4) appropriate molecular size; and (5) good thermal stability and the capability of forming good morphological films.
Although highly efficient green4 and red5 PhOLED devices have been developed, the realization of high performance blue PhOLEDs still remains a challenge mainly due to the lack of appropriate host materials. Recently, a large number of host materials have been developed according to the above mentioned requirements and blue PhOLEDs using these newly prepared host materials have exhibited much improved performances.6–8 Using carbazole-based bipolar hosts, Kido and co-workers fabricated sky-blue PhOLEDs with external quantum efficiency (EQE) of 24% and power efficiency (PE) of 46 lm W−1.9 By combining carbazole and phosphine oxide, Cho and Cheng reported a “universal” bipolar host molecule for red, green and blue PhOLEDs; their sky blue devices exhibit EQE of 23.5% and PE of 40.6 lm W−1.10 Using phosphine oxide-based bipolar hosts, Lee and co-workers fabricated deep-blue PHOLEDs with EQE of 25.1% at a low doping concentration of 3%.11 By combining triphenylsilane and diphenylamine, Yang, Ma and co-workers also reported a “universal” bipolar host molecule for red, green blue and white PhOLEDs; their sky-blue devices exhibit EQE of 16.1% and low efficiency roll-off.12
Among all these bipolar host materials, carbazole (CZ),13–17 diphenylamine (DA),18,19 diphenylphosphine oxide (DPO),20–25 and triphenylsilane (TS)26–29 were found to be the most widely used and highly effective building blocks in the molecular design of host materials. Meanwhile, ortho-, meta- and para-type were three common-used linking topologies. Although there are already some experimental and theoretical studies concerning the effects of core, side groups, and the linking topology on the properties of host materials,30–35 a systematic and detailed understanding of how different building blocks and linking topologies affect the properties of host materials is still missing, especially for building blocks of DPO and TS.
In this paper, CZ, DA (as typical hole transport groups) and DPO, TS (as typical electron transport groups) were linked to the widely used host core of biphenyl (such as in p-CBP) at its ortho/meta/para-position to investigate the effects of building blocks and linking topologies on the structural and electronic properties via density function theory (DFT) calculation (see Fig. 1). The HOMO/LUMO level, HOMO–LUMO band gap and triplet energy of ArBPs can be effectively tuned by the different building blocks and linking topologies. Employing asymmetric building blocks (especially CZ and DPO) at the meta-position of the π-conjugated molecules seems to be an effective strategy for the design of high-performance bipolar host materials.
2. Theoretical and computational methodology
2.1 Optimized structures at the ground, the lowest triplet, and the cationic and anionic states
The ground-state, ion state, and triplet state geometries were carefully optimized using the B3LYP36,37 functional and the 6-31G(d) basis set without any symmetry constraint. Vibrational frequencies were further calculated at the above-mentioned level to confirm that the optimized stationary points represented true minima on the respective potential energy surfaces. The triplet energy was evaluated as the total energy difference between the singlet- and triplet-states with consideration of zero-point vibrational energy (ZPVE) corrections. The excitation energies in the singlet (ES1) and triplet (ET1) states were obtained using the time-dependent density functional theory (TDDFT) method. The structure of o-PBP in the lowest triplet state was optimized with HF/6-31G(d) while the energy was obtained by B3LYP/6-31G(d) (Fig. S1, ESI†). All the calculations were performed using the Gaussian03 program package.
2.2 Internal reorganization energy
The charge (hole and electron) mobility of ArBPs was assessed by using the incoherent hopping model,38,39 which assumes a charge transport process between two adjacent reactions M± + M → M + M± where M is the neutral molecule interacting with neighboring oxidized or reduced M±. The hopping rates of charge transfer can be approximately described by the Marcus–Hush equation:40–42| |  |
(1)
|
where Vh/e is the electronic coupling matrix element between neighboring molecules in the organic single crystal, T is the absolute temperature, and k and ħ refer to the Boltzmann and Planck constants, respectively; λh/e is the hole/electron reorganization energy and could be calculated by the following equations:43
where λ+ is the relaxation energy of a neutral molecule M that captured a hole going toward the M+ optimum geometry on the potential energy surface of M+, and λ1 is the relaxation energy from a cation M+ extracting a hole going toward the M optimum geometry on the potential energy surface of M. E+(M)/E+(M+) represents the total energy of the cation species using the optimum geometry of M/M+, while E(M+)/E(M) represents the total energy of the neutral molecule using the optimum geometry of M+/M. The sum of λ+ and λ1 is the hole reorganization energy λh. Similarly, in the electron-transport process, λe = λ− + λ2.
Experimentally, Vh/e shows a rather narrow range of values, and would be even more limited because of the direct contacts in the amorphous solid films.44,45 As a result, the hole/electron mobility of ArBPs in this study is considered to be dominated by λh/e without consideration of Vh/e. According to the Marcus–Hush equation, lower λh/e means higher charge mobility.
2.3 Triplet exciton generation fraction
The triplet exciton generation fraction (χT) is an important indicator of the potential performance of host molecules which is related to triplet exciton formation in the host molecule. In this study, the χT of ArBPs was calculated by the following equations:46| | 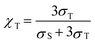 |
(2)
|
| |  |
(3)
|
where σS and σT represent the formation cross-sections of singlet and triplet excitons respectively, EbS and EbT are the binding energies of the singlet and triplet excitons, respectively, Eg is the HOMO–LUMO energy gap, and ES1 and ET1 are excitation energies from the ground state to the lowest excited singlet state and the lowest excited triplet state, respectively.
3. Results and discussion
3.1 Geometry in the ground and lowest excited triplet states
The o-/m-/p-ArBPs (CBP, NBP, PBP, SBP) have many conformations due to the rotation of the two central phenyl rings as well as the building blocks, for example, the syn- and anti-conformations of m-/p-CBP.31 The most stable conformations of all ArBPs were identified via B3LYP optimization after many trials with different initial structures (see Fig. 2).
 |
| | Fig. 2 Optimized geometries of o-PBP, m-PBP and p-PBP in the ground (S0) and the lowest triplet (T1) states. | |
To evaluate the different building blocks and their linking topologies in both the ground (S0) and the lowest triplet (T1) states, the bond length of C1–C1′ (d) and the dihedral angles C2–C1–C1′–C2′ (θ) of the common central biphenyl were investigated and listed in Table 1 as two key parameters. In S0 states, the d values of all o-/m-/p-ArBPs are close to that of BP (1.49 Å) ranging from 1.48 to 1.50 Å. The θ values of m-/p-ArBPs vary in a small range from 35.7° (p-NBP) to 40.4° (m-SBP) around that of BP (38.4°); while those of o-ArBPs are quite different with a large range from 85.7° (o-NBP) to 134.0° (o-CBP) according to the different building blocks: CZ > TS > DPO ≈ DA. In T1 states, the d values of m-/p-ArBPs are close to that of triplet state BP (1.39 Å) ranging from 1.40 to 1.41 Å; while the d values of o-ArBPs remain unchanged (1.50 Å) compared to the corresponding S0 state structures. The θ values of m-/p-ArBPs are close to that of BP in the T1 state (0°) varying from 0.1° (p-PBP) to 7.1° (m-NBP); while the θ values of o-ArBPs are nearly the same as those of S0 state structures. These results indicate that the different building blocks show significant influences to the structure of central biphenyl for the o-ArBPs but not for the m-/p-ArBPs. When ArBPs were excited from S0 to T1, the central biphenyls of m-/p-ArBPs tend to be planar with shorter C1–C1′, while those of o-ArBPs remain almost unchanged, suggesting much more significant interference of the linking topologies in the o-ArBPs. The particular geometries of o-ArBPs endow them with particular optoelectronic properties, which will be discussed later.
Table 1 C1–C1′ bond lengths (d/Å), C2–C1–C1′–C2′ dihedral angles (θ/°) and dipole moment (μ/D) of symmetric ArBPs in the ground (S0) and lowest triplet (T1) states
| Molecule |
S0 |
T1 |
|
d
|
θ
|
μ
|
d
|
θ
|
μ
|
|
o-CBP |
1.50 |
134.0 |
1.35 |
1.50 |
133.9 |
1.15 |
|
m-CBP |
1.49 |
37.6 |
2.53 |
1.40 |
0.1 |
1.38 |
|
p-CBP |
1.48 |
36.7 |
0.00 |
1.40 |
3.5 |
0.01 |
|
o-NBP |
1.50 |
85.7 |
0.88 |
1.50 |
82.4 |
2.07 |
|
m-NBP |
1.49 |
36.9 |
0.16 |
1.41 |
7.1 |
1.77 |
|
p-NBP |
1.48 |
35.7 |
0.00 |
1.41 |
3.1 |
0.00 |
|
o-PBP |
1.50 |
86.1 |
2.33 |
1.50 |
79.8 |
2.08 |
|
m-PBP |
1.49 |
39.0 |
4.34 |
1.40 |
2.3 |
5.63 |
|
p-PBP |
1.48 |
36.5 |
2.25 |
1.40 |
0.1 |
1.70 |
|
o-SBP |
1.50 |
112.9 |
0.46 |
1.50 |
113.1 |
0.44 |
|
m-SBP |
1.49 |
40.4 |
0.25 |
1.40 |
4.0 |
0.29 |
|
p-SBP |
1.48 |
36.3 |
0.01 |
1.40 |
1.7 |
0.05 |
| BP |
1.49 |
38.4 |
0.00 |
1.39 |
0.00 |
0.00 |
For an ideal host–guest system as proposed by Jeon et al.,47 the diameters of host molecules should be as large as possible to provide an ideal Dexter energy transfer condition. From Fig. 2, it seems that the diameters of ArBPs follow the order: p- > m- > o-type. This feature of different linking topology may influence the quantum efficiencies of the PhOLEDs at low triplet emitter concentration.
The dipole moment (μ) is another important parameter for both charge transport and charge injection. On the one hand, a higher dipole moment will lead to better electron push–pull abilities upon others and higher charge mobility, while on the other hand, it will also lead to a reduced charge mobility because of the dipolar disorder. Therefore, there exists a trade-off in the selection of the dipole moment of a host molecule. In S0 states (Table 1), the μ values of p-ArBPs are close to zero except for p-PBP, while those of o-/m-ArBPs are higher, ranging from 0.16 D (m-NBP) to 4.34 D (m-PBP). For the T1 states, the μ values of ArBPs show the exactly same trend as in the S0 states. Interestingly, the PBPs have the highest μ values among o-, m- and p-type, respectively. To gain further understanding of this result, the μ values of the functional segments of building blocks: phenyl-CZ, phenyl-DA, phenyl-DPO and phenyl-TS were calculated. Their μ values show the following order: phenyl-DPO (3.98 D) > phenyl-CZ (1.77 D) > phenyl-DA = phenyl-TS (0). This finding indicates that the high μ values of PBPs arise from the high intrinsic dipole moment of DPO, and as a result of the nonplanar molecular structure of DPO (unlike CZ), the μ value would not be zero even in p-type topology. A DPO with high intrinsic dipole moment is very attractive for the modulation of the dipole moment of a host molecule, and it has been experimentally found that the blue PhOLEDs with DPO-containing molecules as host have very high external quantum efficiency (25.1%). In addition, the o-/m-type linking topologies were predicted to be much more effective than the p-type in the modulation of dipole moment.
3.2 Frontier molecular orbitals
The HOMO and LUMO levels of host materials are two key factors for the design of PhOLEDs. A typical device structure of blue PhOLEDs is as follows:21 ITO/MoO3 as anode; N,N′-bis(naphthalen-1-yl)-N,N′-bis(phenyl)benzidine (NPB) and 4,4′,4′′-tri(N-carbazolyl)triphenylamine (TCTA) as hole transport layers; FIrpic as the emitter; 1,3,5-tris(N-phenylbenzimidazol-2-yl)benzene (TPBI) as electron transport layer, and LiF/Al as cathode (see Fig. 3). For an ideal host molecule, the HOMO level should be close to that of TCTA and higher than that of TPBI, while the LUMO level should be close to that of TPBI and lower that of TCTA, to lead to good charge transport and exciton blocking.
 |
| | Fig. 3 Calculated energy level diagram of HOMO and LUMO levels (in eV) for NPB, TCTA and TPBI. | |
From Table 2, the HOMO levels of CBPs are in a narrow range of −5.41 to −5.31 eV, which is moderately lower than those of NBPs (−4.98 to −4.73 eV), but rather higher than those of PBPs (−6.41 to −6.21 eV) and those of SBPs (−6.23 to −6.03 eV). This feature of HOMO levels of ArBPs can be mainly attributed to the effect of the different building blocks, since the same trend of HOMO levels is observed in the corresponding functional segments of building blocks: DA > CZ > TS > DPO. However, the variation of LUMO levels is relatively complex with changes in a large range, suggesting the LUMO levels are not merely determined by the building blocks (DA > TS > CZ ≈ DPO) but by the interaction of the building block and central biphenyl (the linking topology). Therefore, the obviously larger Eg values of PBPs and SBPs are attributed primarily to the much lower HOMO levels, when compared to those of CBPs and NBPs. Sample model compounds of the various host building blocks (phenyl-CZ, phenyl-DA, phenyl-DPO and phenyl-TS) also show these trends of frontier molecular orbitals.
Table 2 HOMO and LUMO energies, HOMO–LUMO energy gaps (Eg), adiabatic ionization potentials (IP(a)), and electron affinities (EA(a)) of symmetric ArBPs
| Molecule |
HOMO |
LUMO |
E
g
|
IP(a) |
EA(a) |
|
o-CBP |
−5.41 |
−1.05 |
4.36 |
6.51 |
−0.03 |
|
m-CBP |
−5.37 |
−1.18 |
4.20 |
6.43 |
0.11 |
|
p-CBP |
−5.31 |
−1.23 |
4.09 |
6.27 |
0.21 |
|
o-NBP |
−4.98 |
−0.43 |
4.55 |
6.07 |
−0.55 |
|
m-NBP |
−4.93 |
−0.76 |
4.17 |
5.97 |
−0.13 |
|
p-NBP |
−4.73 |
−0.81 |
3.92 |
5.64 |
−0.05 |
|
o-PBP |
−6.21 |
−0.78 |
5.43 |
7.11 |
−0.21 |
|
m-PBP |
−6.31 |
−1.13 |
5.18 |
7.37 |
0.15 |
|
p-PBP |
−6.41 |
−1.43 |
4.98 |
7.44 |
0.52 |
|
o-SBP |
−6.23 |
−0.71 |
5.53 |
7.17 |
−0.28 |
|
m-SBP |
−6.04 |
−0.78 |
5.26 |
7.07 |
−0.15 |
|
p-SBP |
−6.03 |
−1.05 |
4.99 |
7.04 |
0.18 |
| phenyl-CZ |
−5.33 |
−0.65 |
4.80 |
6.79 |
−0.72 |
| phenyl-DA |
−4.95 |
−0.30 |
4.65 |
6.35 |
−1.01 |
| phenyl-DPO |
−6.83 |
−0.76 |
6.07 |
8.15 |
−0.41 |
| phenyl-TS |
−6.58 |
−0.53 |
6.05 |
7.75 |
−0.66 |
| BP |
−6.05 |
−0.67 |
5.37 |
7.60 |
−0.72 |
For most symmetric ArBPs, the HOMO levels increase in the order: o- < m- < p-type (except PBP), while the LUMO levels decrease in the order: o- > m- > p-type, resulting in the trend of Eg values: o- > m- > p-type. This result indicates that the π-conjugation increases according to the different linking positions (o- < m- < p-type) on the central biphenyl (BP). The twisting angle between the two phenyl groups of BP (θ in Table 1) is the key for this trend, and some o-type ArBPs even have larger Eg than BP due to the large θ of these compounds. The adiabatic IP and EA values of ArBPs show exactly the same trend as the HOMO and LUMO levels, making the discussion above more reliable.
The typical device structure mentioned above may fit CBPs well, but it may not work so well with NBPs, PBSs and SBPs because of their inappropriate HOMO and LUMO levels. The LUMO levels of NBPs are higher than that of TCTA (−0.91 eV) and the HOMO levels of PBPs and SBPs are lower than that of TPBI (−5.66 eV), which suggests a difficult hole or electron injection when employing this device structure. Some new device structures are required when employing NBPs, PBPs and SBPs as hosts.
The frontier molecular orbital (HOMO and LUMO) electron density distributions are shown in Fig. 4. All the frontier molecular orbitals of ArBPs show π character. For CBPs, the HOMOs are mainly concentrated in the central biphenyl and the LUMOs are concentrated in the side carbazole. The obvious separation between HOMO and LUMO implies that the one-electron HOMO–LUMO transition would become a typical charge-transfer (CT) transition, which is preferable for efficient hole- and electron-transporting properties and the prevention of reverse energy transfer. For p-type NBP, PBP and SBP, both HOMOs and LUMOs are mostly localized in the central biphenyl; while for the corresponding m- and o-type ones, they spread partly to the corresponding host building blocks, suggesting that m- and o-type topologies are better than the p-type one as host materials.
 |
| | Fig. 4 The HOMO and LUMO levels (in eV) and their corresponding isosurface plots of symmetric ArBPs. | |
3.3 Triplet energy
The lowest triplet energy is the most important criterion for hosts, and it must be higher than that of the guests to suppress the back energy transfer from guests to hosts, which means, for (deep) blue PhOLEDs, it should be larger than 2.70 eV. In order to precisely predict the lowest triplet energy, two methods were adopted (see Fig. 5). One is the triplet excitation energy (ET1) obtained from the lowest excitation energy of absorption spectra and the other is the triplet energy (3Eg) obtained from the total molecular energy difference between the lowest triplet state and the ground state. The 3Eg values correlate qualitatively well with the ET1 values and the Eg values. In comparison with the experimental results (Table 3), 3Eg gives closer predictions, indicating its better reliability. Two obvious features can be observed for 3Eg and ET1: (1) the 3Eg values of PBPs and SBPs are higher than for the same types of CBPs and NBPs, which indicates that the building blocks of DPO and TS are better for host materials; (2) the 3Eg values of ArBPs decrease in the following order: o- > m- > p-type, which indicates that the linking topology of o/m-type is better in the molecular design of host materials. It should be noted that the differences between 3Eg and ET1 of o-ArBPs are smaller than those of m-/p-ArBPs, probably due to the nearly unchanged molecular structures when molecules were excited to the triplet state as discussed in section 3.1. These results indicate that the lowest triplet energy of ArBPs can be effectively tuned by the different building blocks and linking topologies.
 |
| | Fig. 5 Calculated triplet energies (3Eg), triplet excitation energies (ET1) and HOMO–LUMO energy gaps (Eg) of the symmetric ArBPs. | |
Table 3 Triplet energies (3Eg) and experimental triplet energies (3Egexp), excitation energies in the singlet (ES1) and triplet (ET1) states, and triplet exciton generation fractions (χT) (in eV) of symmetric ArBPs
| Molecule |
3
E
g
|
3
E
g
exp
|
E
S1
|
E
T1
|
ΔEST |
χ
T
|
|
From ref. 16.
From ref. 19.
|
|
o-CBP |
2.97 |
3.00a |
3.69 |
3.17 |
0.52 |
62.91 |
|
m-CBP |
2.83 |
2.84a |
3.65 |
3.17 |
0.48 |
61.38 |
|
p-CBP |
2.62 |
2.66a |
3.56 |
2.96 |
0.60 |
58.22 |
|
o-NBP |
3.07 |
|
3.91 |
3.25 |
0.66 |
59.85 |
|
m-NBP |
2.69 |
|
3.61 |
2.99 |
0.62 |
58.84 |
|
p-NBP |
2.39 |
|
3.42 |
2.69 |
0.73 |
55.01 |
|
o-PBP |
3.13 |
|
4.73 |
3.56 |
1.17 |
52.91 |
|
m-PBP |
2.86 |
|
4.71 |
3.25 |
1.46 |
42.33 |
|
p-PBP |
2.80 |
2.72b |
4.53 |
3.16 |
1.37 |
42.56 |
|
o-SBP |
3.49 |
|
4.81 |
3.56 |
1.25 |
52.12 |
|
m-SBP |
2.91 |
|
4.78 |
3.28 |
1.50 |
41.82 |
|
p-SBP |
2.79 |
|
4.54 |
3.16 |
1.38 |
42.49 |
The difference between the S1 and T1 excitation energy (ΔEST) and triplet exciton generation fraction (χT), are two additional indicators of the potential performance of host molecules, which are related to the triplet exciton formation in a host molecule.4,31,48 A smaller ΔEST and a larger χT are proposed to correlate to a better performance (Table 3). The ΔEST values of CBPs and NBPs (0.48–0.73 eV) are much smaller than those of PBPs and SBPs (1.17–1.50 eV); while the χT values of CBPs and NBPs (55.01–62.91) are much larger than those of PBPs and SBPs (41.82–52.91), suggesting that the triplet exciton formation in CBPs and NBPs are more effective when compared to PBPs and SBPs. It is also found that o-/m-type are better than the p-type for CBPs and NBPs while the o-/p-type are better than m-ype for PBPs and SBPs, which suggests that the different topologies also have great influence in triplet exciton formation.
3.4 Reorganization energy
The balance of charge (hole and electron) transport is crucial for high performance PHOLEDs. The charge mobility of ArBPs was investigated via the relaxation and reorganization energies (see Table 4), which can provide a qualitative indication of the charge-transporting rate (the lower the λ values, the higher the charge-transporting rate). As expected, the λh, λ+ and λ1 values of CBPs and NBPs are quite small, ranging from 0.03 to 0.27 eV, while the λe, λ− and λ2 values are much higher, ranging from 0.44 to 0.62 eV, which is consistent with the fact that CZ and DA are excellent hole transport building blocks. Except for the o-PBP and o-SBP, λ+, and λ− are very close to the corresponding λ1 and λ2, indicating balanced energy barriers between the injection and transfer of the hole/electron. The λh values of PBPs and SBPs (except o-PBP) are nearly the same (0.38–0.40 eV), while the λe value can be as low as 0.27 eV, which suggests that DPO and TS are good electron transport building blocks. As to the topology, the λh values of CBPs and NBPs increase in the order m- < o- < p-type, while the λe values of PBPs and SBPs increase in the order o- < m- < p-type, which suggests that the o-/m-types seem better than p-type in terms of charge transfer.
Table 4 Relaxation energies (λ+, λ1, λ− and λ2) and reorganization energies (λh and λe) of symmetric ArBPs (in eV)
| Molecule |
λ
+
|
λ
1
|
λ
−
|
λ
2
|
λ
h
|
λ
e
|
λ
h/λe |
|
o-CBP |
0.05 |
0.05 |
0.20 |
0.24 |
0.10 |
0.44 |
0.23 |
|
m-CBP |
0.02 |
0.01 |
0.26 |
0.29 |
0.03 |
0.55 |
0.05 |
|
p-CBP |
0.06 |
0.08 |
0.23 |
0.27 |
0.14 |
0.50 |
0.28 |
|
o-NBP |
0.07 |
0.05 |
0.18 |
0.29 |
0.12 |
0.47 |
0.26 |
|
m-NBP |
0.03 |
0.04 |
0.29 |
0.33 |
0.07 |
0.62 |
0.11 |
|
p-NBP |
0.13 |
0.14 |
0.30 |
0.27 |
0.27 |
0.57 |
0.48 |
|
o-PBP |
0.31 |
0.87 |
0.15 |
0.13 |
1.18 |
0.28 |
4.21 |
|
m-PBP |
0.21 |
0.19 |
0.20 |
0.24 |
0.40 |
0.44 |
0.92 |
|
p-PBP |
0.18 |
0.20 |
0.32 |
0.34 |
0.38 |
0.66 |
0.57 |
|
o-SBP |
0.15 |
0.25 |
0.07 |
0.20 |
0.40 |
0.27 |
1.46 |
|
m-SBP |
0.22 |
0.16 |
0.16 |
0.19 |
0.39 |
0.35 |
1.09 |
|
p-SBP |
0.19 |
0.21 |
0.27 |
0.30 |
0.40 |
0.57 |
0.71 |
| phenyl-CZ |
0.05 |
0.05 |
0.14 |
0.16 |
0.10 |
0.31 |
0.33 |
| phenyl-DA |
0.06 |
0.06 |
0.11 |
0.15 |
0.11 |
0.26 |
0.44 |
| phenyl-DPO |
0.11 |
0.10 |
0.24 |
0.18 |
0.21 |
0.42 |
0.49 |
| phenyl-TS |
0.08 |
0.09 |
0.07 |
0.07 |
0.17 |
0.14 |
1.30 |
| BP |
0.19 |
0.17 |
0.30 |
0.25 |
0.36 |
0.56 |
0.64 |
It should be noted that both the electron and hole transport units in PBPs and SBPs are the central biphenyls, since the HOMO and LUMO distributions of PBPs and SBPs are mainly concentrated in them (see Fig. 4). The λh values of PSPs and SBPs are very close to that of BP (0.36 eV), which is consistent with the fact that electron-withdrawing groups DPO and TS have little influence on the hole transport ability. Comparing the λe values of PSPs and SBPs with that of BP, it is found that by introducing electron-withdrawing groups DPO and TS at the para-position, the λe values become larger instead of smaller, while at the ortho- and meta-position, the λe values are significantly reduced. Though it is well known that the electron-transport nature of π-conjugated molecules can be modulated by introducing electron-withdrawing substituents, this result suggests that the linking topology also has a significant effect, that means, by introducing electron-withdrawing groups at ortho- or meta-position, the electron transport ability of host materials would be significantly enhanced, while at the para-position electron transport ability would not be improved.
3.5 Asymmetric ArBPs
As we discussed above, the too low HOMO levels, unseparated HOMO and LUMO distributions, and ineffective triplet exciton formation are three disadvantages which have limited the use of PBPs and SBPs as host materials although their electron transport abilities are much enhanced by employing DPO and TS building blocks. Experimentally, the PhOLED employing p-PBP as host material has shown relatively poor performance.20 One solution is to employ asymmetric topology (a hole transport building block and a electron transport building block).30,32 From Tables 5 and 2, the HOMO levels of CPBPs and CSBPs are close to that of phenyl-CZ (−5.33 eV) ranging from −5.38 to −5.15 eV, while those of NPBPs and NSBPs are close to that of phenyl-DA (−4.95 eV) ranging from −5.02 to −4.79 eV. This result suggests that the HOMO levels of molecules with asymmetric building blocks are determined by the building blocks with a higher HOMO level. As for the HOMO and LUMO distributions of asymmetric ArBPs (see Fig. 6), the HOMOs are mainly concentrated on the CZ and DA blocks while the LUMOs are mostly localized in the central biphenyl, resulting in obvious separations. Moreover, the ΔEST values are reduced while the χT values are increased in asymmetric ArBPs when compared to those of PBPs and SBPs, which should be recognized as another advantage of the asymmetric substitution. Thus, employing asymmetric building blocks is proved to be an effective way to avoid the disadvantages of PBPs and SBPs, and may also be effective in enhancing the electron transport abilities of host molecules.
 |
| | Fig. 6 The HOMO and LUMO levels (in eV) and their corresponding isosurface plots for asymmetric ArBPs. | |
Table 5 HOMO and LUMO energies, HOMO–LUMO energy gaps (Eg), triplet energies (3Eg), excitation energies in the singlet (ES1) and triplet (ET1) states, triplet exciton generation fractions (χT), and reorganization energies (λh and λe) (in eV) of asymmetric ArBPs
| Molecule |
HOMO |
LUMO |
E
g
|
3
E
g
|
E
S1
|
E
T1
|
ΔEST |
χ
T
|
λ
h
|
λ
e
|
λ
h/λe |
|
o-CPBP |
−5.15 |
−0.94 |
4.21 |
2.99 |
3.62 |
3.18 |
0.44 |
63.37 |
0.24 |
0.51 |
0.47 |
|
m-CPBP |
−5.28 |
−1.18 |
4.10 |
2.82 |
3.60 |
3.18 |
0.42 |
61.97 |
0.16 |
0.46 |
0.35 |
|
p-CPBP |
−5.38 |
−1.34 |
4.04 |
2.67 |
3.56 |
3.02 |
0.54 |
58.37 |
0.17 |
0.58 |
0.29 |
|
o-CSBP |
−5.24 |
−0.82 |
4.43 |
2.97 |
3.76 |
3.18 |
0.58 |
61.67 |
0.18 |
0.56 |
0.32 |
|
m-CSBP |
−5.33 |
−1.03 |
4.30 |
2.70 |
3.75 |
3.17 |
0.58 |
59.24 |
0.17 |
0.41 |
0.41 |
|
p-CSBP |
−5.30 |
−1.13 |
4.17 |
2.49 |
3.66 |
3.05 |
0.61 |
57.72 |
0.19 |
0.57 |
0.33 |
|
o-NPBP |
−4.79 |
−0.83 |
3.96 |
3.03 |
3.42 |
3.14 |
0.28 |
66.43 |
0.30 |
0.48 |
0.63 |
|
m-NPBP |
−4.91 |
−0.98 |
3.93 |
2.83 |
3.42 |
2.96 |
0.46 |
61.19 |
0.24 |
0.50 |
0.48 |
|
p-NPBP |
−5.02 |
−1.12 |
3.91 |
2.69 |
3.46 |
2.77 |
0.69 |
54.20 |
0.08 |
0.62 |
0.13 |
|
o-NSBP |
−4.93 |
−0.69 |
4.24 |
2.85 |
3.59 |
3.08 |
0.51 |
62.56 |
0.17 |
0.56 |
0.30 |
|
m-NSBP |
−4.94 |
−0.75 |
4.19 |
2.75 |
3.61 |
3.03 |
0.58 |
59.84 |
0.15 |
0.47 |
0.32 |
|
p-NSBP |
−4.93 |
−0.92 |
4.01 |
2.52 |
3.54 |
2.80 |
0.74 |
54.05 |
0.20 |
0.57 |
0.35 |
From Table 5, it is found that the λe values of asymmetric m-ArBPs and o-NPBP are significantly reduced when compared to that of BP, and the λh/λe values are increased when compared to those of CBPs and NBPs. It is also found that the triplet energies of m-ArBPs are the most appropriate since they are equal to or just slightly higher than 2.7 eV, which may help to reduce the open-voltage of blue PhOLED. Thus, asymmetric substitution at the meta-position would be an effective strategy for the design of high-performance bipolar host materials; because of the much enhanced electron transport ability and most appropriate triplet energy level. Moreover, m-CPBP may have the best performance among the m-ArBPs for two reasons: first, its LUMO level (−1.18 eV) is most close to that of TPBI (−1.24 eV), which suggests the most facile electron injection between m-CPBP and TPBI; second, except for o-NPBP (whose LUMO is too high), it has the smallest ΔEST (0.42 eV) and largest χT (61.97), which suggest the most effective triplet exciton formation in the host molecule.
4. Conclusion
Two typical hole transport groups, carbazole and diphenylamine, and two typical electron transport groups, diphenylphosphine oxide and triphenylsilane, were connected to biphenyl at its ortho/meta/para-positions to form various symmetric and asymmetric ArBPs. DFT calculations were carried out to reveal the effects of these widely used building blocks of host materials and their linking topologies on the structural and electronic properties of such ArBPs.
It is found that: (1) the structures of o-ArBPs differ significantly from those of m-/p-ArBPs whether in the ground state or in the lowest triplet state; (2) the high μ values of PBPs arise from the intrinsic dipole moment of triphenylphosphine oxide, and the μ value would not be zero even for a p-type topology due to the nonplanar molecular structure of triphenylphosphine oxide; (3) the HOMO/LUMO level, HOMO–LUMO energy gap, and triplet energy of ArBPs can be effectively tuned by the different building blocks and linking topologies. The HOMO levels of molecules containing diphenylphosphine oxide show an unusual trend which may result from the its intrinsic nature; (4) the modulation effect of electron-withdrawing substituents on the electron-transporting nature of π-conjugated molecules would be influenced by the linking topology significantly, that means, by introducing electron-withdrawing groups at ortho- or meta-position, the electron transport ability of host molecules would be significantly enhanced, while at the para-position electron transport ability would not be improved and could be even poorer; (5) employing asymmetric building blocks (especially carbazole and diphenylphosphine oxide) at the meta-position of π-conjugated molecules would be an effective strategy for the design of high-performance bipolar host materials, because of the much enhanced electron transport ability, appropriate triplet energy level, and compatible frontier orbital energy levels. Although this work has been restricted to host molecules with biphenyl as linking core, we believe that the findings of this study will be very informative in the design and development of new bipolar hosts for blue PhOLEDs.
Acknowledgements
We thank the National Basic Research Program of China (2009CB930601), National Natural Science Foundation of China (20804020, 60976019, 20905038 and 20974046), The Ministry of Education of China (No. IRT1148), National Natural Science Foundation of Jiangsu Province (BK2011751), Scientific Research Foundation of Nanjing University of Posts and Telecommunications (NY210017, NY210046), and Program for Postgraduates Research Innovations in University of Jiangsu Province (CXZZ11_0412).
References
- M. A. Baldo, D. F. O'Brien, Y. You, A. Shoustikov, S. Sibley, M. E. Thompson and S. R. Forrest, Nature, 1998, 395, 151–154 CrossRef CAS.
- M. A. Baldo, S. Lamansky, P. E. Burrows, M. E. Thompson and S. R. Forrest, Appl. Phys. Lett., 1999, 75, 4 CrossRef CAS.
- C. Adachi, M. A. Baldo, M. E. Thompson and S. R. Forrest, J. Appl. Phys., 2001, 90, 5048–5051 CrossRef CAS.
- S. Su, C. Cai and J. Kido, Chem. Mater., 2011, 23, 274–284 CrossRef CAS.
- Y. Tao, Q. Wang, L. Ao, C. Zhong, J. Qin, C. Yang and D. Ma, J. Mater. Chem., 2010, 20, 1759–1765 RSC.
- A. Chaskar, H. Chen and K. Wong, Adv. Mater., 2011, 23, 3876–3895 CrossRef CAS.
- S. O. Jeon and J. Y. Lee, J. Mater. Chem., 2012, 22, 4233–4243 RSC.
- Y. Tao, C. Yang and J. Qin, Chem. Soc. Rev., 2011, 40, 2943–2970 RSC.
- S. Su, H. Sasabe, T. Takeda and J. Kido, Chem. Mater., 2008, 20, 1691–1693 CrossRef CAS.
- H. Chou and C. Cheng, Adv. Mater., 2010, 22, 2468–2471 CrossRef CAS.
- S. O. Jeon, S. E. Jang, H. S. Son and J. Y. Lee, Adv. Mater., 2011, 23, 1436–1441 CrossRef CAS.
- S. Gong, Y. Chen, J. Luo, C. Yang, C. Zhong, J. Qin and D. Ma, Adv. Funct. Mater., 2011, 21, 1168–1178 CrossRef CAS.
- P. Schroegel, A. Tomkeviciene, P. Strohriegl, S. T. Hoffmann, A. Koehler and C. Lennartz, J. Mater. Chem., 2011, 21, 2266–2273 RSC.
- Y. Zheng, A. S. Batsanov, V. Jankus, F. B. Dias, M. R. Bryce and A. P. Monkman, J. Org. Chem., 2011, 76, 8300–8310 CrossRef CAS.
- S. Zhang, R. Chen, J. Yin, F. Liu, H. Jiang, N. Shi, Z. An, C. Ma, B. Liu and W. Huang, Org. Lett., 2010, 12, 3438–3441 CrossRef CAS.
- S. Gong, X. He, Y. Chen, Z. Jiang, C. Zhong, D. Ma, J. Qin and C. Yang, J. Mater. Chem., 2012, 22, 2894–2899 RSC.
- R. F. Chen, G. H. Xie, Y. Zhao, S. L. Zhang, J. Yin, S. Y. Liu and W. Huang, Org. Electron., 2011, 12, 1619–1624 CrossRef CAS.
- Z. An, R. Chen, J. Yin, G. Xie, H. Shi, T. Tsuboi and W. Huang, Chem.–Eur. J., 2011, 17, 10871–10878 CrossRef CAS.
- S. Takizawa, V. A. Montes and P. Anzenbacher Jr., Chem. Mater., 2009, 21, 2452–2458 CrossRef CAS.
- P. E. Burrows, A. B. Padmaperuma, L. S. Sapochak, P. Djurovich and M. E. Thompson, Appl. Phys. Lett., 2006, 88, 183503 CrossRef.
- D. Yu, F. Zhao, C. Han, H. Xu, J. Li, Z. Zhang, Z. Deng, D. Ma and P. Yan, Adv. Mater., 2012, 24, 509–514 CrossRef CAS.
- C. Han, G. Xie, H. Xu, Z. Zhang, L. Xie, Y. Zhao, S. Liu and W. Huang, Adv. Mater., 2011, 23, 2491 CrossRef CAS.
- J. Zhao, G. Xie, C. Yin, L. Xie, C. Han, R. Chen, H. Xu, M. Yi, Z. Deng, S. Chen, Y. Zhao, S. Liu and W. Huang, Chem. Mater., 2011, 23, 5331–5339 CrossRef CAS.
- W. Jiang, L. Duan, J. Qiao, G. Dong, L. Wang and Y. Qiu, Org. Lett., 2011, 13, 3146–3149 CrossRef CAS.
- S. O. Jeon, K. S. Yook, C. W. Joo and J. Y. Lee, Adv. Mater., 2010, 22, 1872 CrossRef CAS.
- X. F. Ren, J. Li, R. J. Holmes, P. I. Djurovich, S. R. Forrest and M. E. Thompson, Chem. Mater., 2004, 16, 4743–4747 CrossRef CAS.
- S. Gong, Q. Fu, Q. Wang, C. Yang, C. Zhong, J. Qin and D. Ma, Adv. Mater., 2011, 23, 4956–4959 CrossRef CAS.
- S. Gong, Y. Chen, X. Zhang, P. Cai, C. Zhong, D. Ma, J. Qin and C. Yang, J. Mater. Chem., 2011, 21, 11197–11204 RSC.
- Y. J. Cho and J. Y. Lee, J. Phys. Chem. C, 2011, 115, 10272–10276 CAS.
- L. S. Sapochak, A. B. Padmaperuma, X. Cai, J. L. Male and P. E. Burrows, J. Phys. Chem. C, 2008, 112, 7989–7996 CAS.
- J. Yin, S. L. Zhang, R. F. Chen, Q. D. Ling and W. Huang, Phys. Chem. Chem. Phys., 2010, 12, 15448–15458 RSC.
- X. Gu, H. Zhang, T. Fei, B. Yang, H. Xu, Y. Ma and X. Liu, J. Phys. Chem. A, 2010, 114, 965–972 CrossRef CAS.
- D. Kim, S. Salman, V. Coropceanu, E. Salomon, A. B. Padmaperuma, L. S. Sapochak, A. Kahn and J. Bredas, Chem. Mater., 2010, 22, 247–254 CrossRef CAS.
- D. Kim, V. Coropceanu and J. Bredas, J. Am. Chem. Soc., 2011, 133, 17895–17900 CrossRef CAS.
- S. Salman, D. Kim, V. Coropceanu and J. Brédas, Chem. Mater., 2011, 23, 5223–5230 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS.
- M. Malagoli and J. L. Bredas, Chem. Phys. Lett., 2000, 327, 13–17 CrossRef CAS.
- B. C. Lin, C. P. Cheng, Z. Q. You and C. P. Hsu, J. Am. Chem. Soc., 2005, 127, 66–67 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- J. Yin, R. Chen, S. Zhang, H. Li, G. Zhang, X. Feng, Q. Ling and W. Huang, J. Phys. Chem. C, 2011, 115, 14778–14785 CAS.
- J. Yin, R. Chen, S. Zhang, Q. Ling and W. Huang, J. Phys. Chem. A, 2010, 114, 3655–3667 CrossRef CAS.
- S. F. Nelsen, D. A. Trieber, R. F. Ismagilov and Y. Teki, J. Am. Chem. Soc., 2001, 123, 5684–5694 CrossRef CAS.
- S. F. Nelsen and F. Blomgren, J. Org. Chem., 2001, 66, 6551–6559 CrossRef CAS.
- S. W. Yin, L. P. Chen, P. F. Xuan, K. Q. Chen and Z. Shuai, J. Phys. Chem. B, 2004, 108, 9608–9613 CrossRef CAS.
- W. S. Jeon, T. J. Park, S. Y. Kim, R. Pode, J. Jang and J. H. Kwon, Org. Electron., 2009, 10, 240–246 CrossRef CAS.
- J. Wu, Y. Liao, S. Wu, H. Li and Z. Su, Phys. Chem. Chem. Phys., 2012, 14, 1685–1693 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Optimized geometries of o-PBP in the lowest triplet (T1) and cationic states using B3LYP/6-31G(d). See DOI: 10.1039/c2ra21242k/ |
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here.