Predicting the interactions of organometallic ruthenium ethylenediamine complexes with mononucleotides: insights from density functional theory

Abstract

The thermodynamics and kinetics for the binding of the potential anticancer complex [(η⁶-benz)Ru(en)(H₂O)]²⁺ (benz = benzene, en = ethylenediamine) (1) to nucleotides under neutral and acidic conditions were studied by density functional theory (DFT) calculations, employing 5′-guanosine monophosphate (5′-GMP) and 5′-adenosine monophosphate (5′-AMP) as model reactants. Based on the different binding modes, there were four pathways located for each nucleotide, two stepwise (a and b) and two concerted (c and d). In line with experiments, the reaction first proceeded with the binding of the 5′-phosphate group, and then underwent a slow intramolecular rearrangement to the N7 purine binding products. For 5′-GMP, concerted pathways are also possible based on our calculated results. The reaction of 5′-GMP is faster under acidic conditions than under neutral conditions. However, for the reaction of 5′-AMP, the first step of the phosphate binding is apparently more facile in a neutral environment than in an acidic one. Due to the thermodynamic sink of the phosphate bound intermediates, the second step of the intramolecular rearrangement from phosphate to A(N7)-binding exhibited a prohibitively high free energy of activation under neutral conditions. An approximately 9 kcal mol⁻¹ difference in the reaction between 5′-GMP and 5′-AMP shows a clear preference for the binding of 5′-GMP over 5′-AMP, in agreement with experimental observation. It was also revealed that the phosphate as a hydrogen bond acceptor played an important role in the interaction of the Ru–arene complexes with nucleotides.

---

1. Introduction

After the successful development of the inorganic complex cisplatin for applications as an anticancer drug,¹ ruthenium complexes have been studied with great interest for their potential use as therapeutic anticancer agents with lower toxicity than their platinum counterparts.^2–6 A new class of organometallic “piano-stool” Ru^II–arene anticancer complex of the type [(η⁶-arene)Ru(XY)Cl] has emerged as promising antitumor compounds.⁷ The XY sites can be taken up by two monodentate ligands or one bidentate ligand, and the arene ligand can take many forms, including tetrahydroanthracene, biphenyl, or p-cymene.^8–18 The π–π stacking interactions between these extended arene systems and a base can have a significant influence on both the kinetics and thermodynamics of DNA binding.^{10–12,14,15} These Ru-centered arene complexes are non-cross-resistant with cisplatin towards cancer cells, and this indicates that their mechanism of action differs from the anticancer drug cisplatin and its analogs.⁷ Selective binding of the metal complexes to nucleobases is influenced by metal coordination, hydrogen bonding, and hydrophobic and electronic interactions. Ru^II–arene complexes, [(η⁶-arene)Ru(XY)Cl]ⁿ⁺, containing a neutral N,N-chelate (e.g. en) bind selectively to guanine (G),^{10–12,14,15,19} and those containing an anionic O,O-chelate (e.g. acetylacetonate) have similar affinities for both G and adenine (A).²⁰ Both hydrogen-bonding and nonbonding repulsive interactions between the exocyclic groups on the bases and the chelate ligands in Ru–arene complexes lead to their selective properties.²⁰

Recently, efforts have been devoted to a theoretical description of the effects of Ru anticancer complexes. Sadler and coworkers investigated the aquation process using the non-relativistic Perdew–Wang gradient-corrected functional (PW91), which is crucial in the process of the drug's activation.²¹ Deubel and Lau had first calculated the transition structure for the reaction of [(η⁶-benz)Ru(en)(H₂O)]²⁺ with G at the B3LYP level, and their preliminary results indicated a concerted pathway.²² Rothlisberger and coworkers also investigated the reactions of [(η⁶-arene)Ru(en)L]²⁺ compounds with nucleobases and DNA using the BP86, CPMD and QM/MM methods.^23–25 At the same time, Burda and coworkers also studied the aquation of [(η⁶-arene)Ru(en)Cl]²⁺ and its reactions with some model nucleobases using B3LYP, where a smaller rate constant for G exchange was unexpectedly found in comparison with A.²⁶ A two-step reaction mechanism of G exchange was suggested where the Ru-O6(G) coordination is formed first. However, it was only plausible for single stranded DNA or RNA rather than for undistorted double stranded DNA. This is because in dsDNA, the O6(G) atom is involved in Watson–Crick hydrogen bonding with a cytosine C4–NH₂ of the complementary strand.²⁵ Platts and coworkers explained the selectivity of diamine ruthenium arene complexes from a thermodynamic perspective employing the BH and H method.²⁷ Then Platts also investigated the interactions of Ru–arene complexes with base pair steps using the B97-D method.²⁸ Although the reaction mechanisms of ruthenium arene-based complexes with nucleic acids were extensively investigated, specific interactions between highly charged moieties, such as negatively charged phosphate groups, have apparently not yet been studied using high level computational methods. This would induce some error in exploring the interactions of the complexes with a nucleobase, because of neglecting the additional possibilities for more potential H-bonds and electrostatic interactions, etc. Some experimental and theoretical reports in the literature pointed out that the phosphate backbone played an important role in DNA binding, such as stereo-specific hydrogen-bonding.^29–33 Sadler and coworkers inferred from NMR data that intramolecular hydrogen bonding between the NH of cis-PtA2 and the phosphate backbone of DNA is believed to influence the structure of the Pt-DNA adduct and hence the activity of the platinum complex.³⁰ Afterwards, they also reported a potential binding mechanism of [(η⁶-arene)Ru(en)Cl)]⁺ complexes with some nucleotides,¹¹ but the specific H-bond interactions between them remain unclear. The reaction pathways for reaction with 5′-GMP bases were proposed from the NMR data: first, the reactive aqua complex [(η⁶-benz)Ru(en)(H₂O)]²⁺ rapidly reacted with the 5′-phosphate of 5′-GMP, followed by a slow displacement of the bound phosphate by N7.¹¹ However, these observations could not exclude the possibility that the coordinated water would be directly exchanged with N7 to produce the N7GMP adduct. Therefore, our work here will address these mechanistic questions.

2. Computational details

As shown in Scheme 1, we concentrate on the reaction of [(η⁶-benz)Ru(en)(H₂O)]²⁺ (1) with nucleic acid derivatives as models, 5′-guanosine monophosphate (5′-GMP) and 5′-adenosine monophosphate (5′-AMP) under both neutral and acidic conditions, in order to determine the energy profiles of the reactions and the potential modes of interaction with DNA. In order to compare the results with previous work,²⁶ we adopted the B3LYP functional, which has been demonstrated to be effective in the calculation of metal–arene complexes.^22,26,34,35 In order to confirm the proper convergence to equilibrium and transition state geometries, a vibrational frequency analysis was done at this level of theory as well. The intrinsic reaction coordinate (IRC) method^36,37 was performed to confirm that the transition states found connected the relevant reactants and products. For computation of the reaction pathways, various energetic terms were computed with the incorporation of thermal effects at a temperature of 298.15 K. To obtain accurate energies for the reaction surfaces, single-point energies were further calculated using the COSMO model^38–40 in water and a larger basis set [6-311++G(d,p) for non-metal atoms and LanL2DZ(f) for the Ru atom where ξ_f = 1.235].⁴¹ This approach has been successfully applied to study the structures and reaction mechanisms for Ru–arene complexes and other metallic complexes.^25,26,42,43 All of the calculations were carried out using the Gaussian 03 program suite.⁴⁴

Scheme 1 Structures and atom numbering for 1 and the mononucleotides.

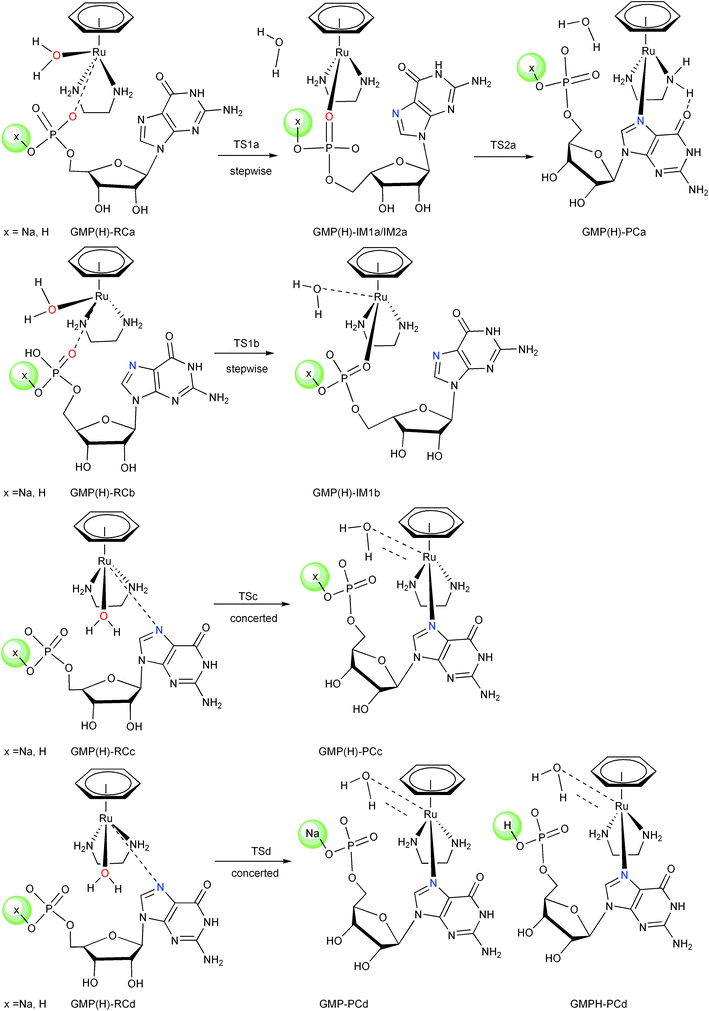
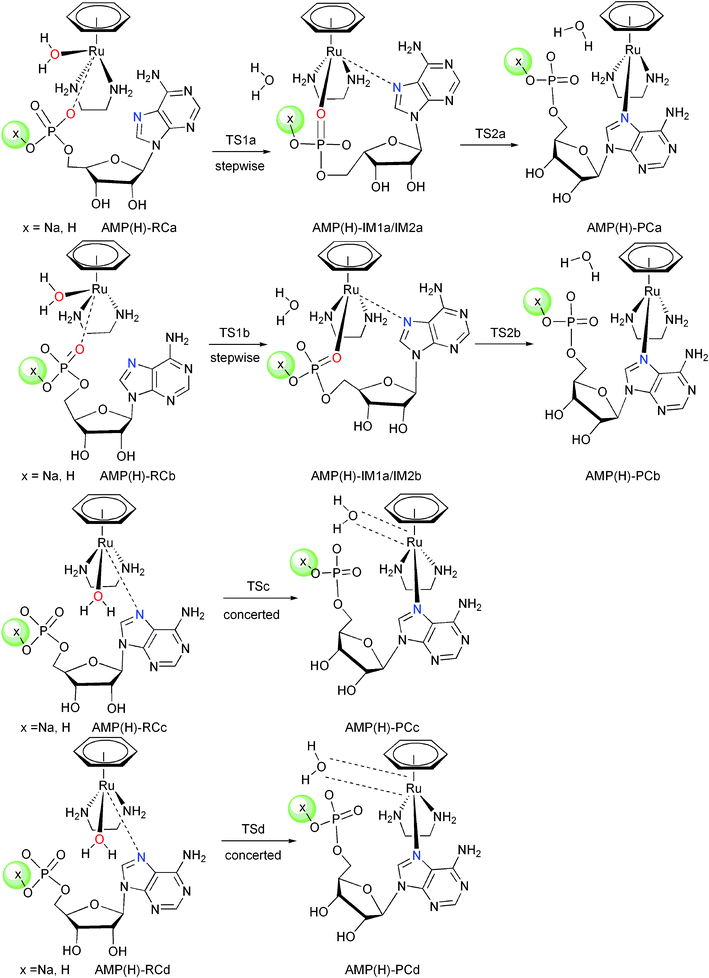
The experimental pK_a values for 5′-GMP and 5′-AMP (–OPO₃²⁻/–OPO₂(OH)⁻ are 6.20 and 6.23, respectively, and their pK_a values will further decrease upon binding with Ru–arene complexes.^11,30 In light of this, the Na ion was added to our computational model as a counterion for the phosphate group so as to avoid artificial electrostatic effects, which may interfere with the Ru binding under neutral conditions.^32,33 To simulate acidic conditions, we have also computed a model where the Na ion is replaced with a proton. Thus, both of these models carry a molecular charge of +1 in the singlet electronic state. The nucleotides are oriented cis to the coordinated water, as the trans conformation was demonstrated to be unfavorable in the ligand substitution of Ru–arene complexes.^25,34 According to the proposed mechanism of Sadler and coworkers,¹¹ the reactions of 1 with nucleotides were stepwise processes, in which the first step is water and phosphate substitution, and the second step is the intramolecular exchange. There are two pathways in stepwise reactions considering the different conformations of the en as shown in Schemes 2 and 3. One pathway has the N1 (en) pointing away from the coordinated water molecule (path a), and the other has N1 (en) pointing towards the coordinated water molecule (path b). Besides the two stepwise pathways described above, two other possible concerted pathways c and d were also considered (see Schemes 2 and 3), in which N7 of the purine directly exchanges with the coordinated water molecule.

Scheme 2 Investigated reaction pathways for 5′-GMP under neutral and acidic conditions.

Scheme 3 Investigated reaction pathways for 5′-AMP under neutral and acidic conditions.

3. Results and discussion

3.1. Reactions of 1 with 5′-GMP

The investigated reaction pathways for the 5′-GMP molecule under neutral and acidic conditions are depicted in Scheme 2. 5′-GMP was bound to complexes firmly via strong H-bonds with coordinated water and amine hydrogen by phosphate and N7(G). As shown in Scheme 2, there are four binding modes in which a/b and c/d differ in the conformation of en.

As shown in Fig. 1 of the optimized structures, proton transfer from the coordinated water to O2 of the phosphate is observed in all of the optimized reactant structures (the average R_O2–H5 is 1.02 Å) under neutral conditions. This is due to the strong electrostatic interaction between the Ru atom and the phosphate group. We examined the thermodynamic stability of these species compared to that of the starting materials (SM), that is 1 and 5′-GMP (H). The relative free energies along the reaction pathways shown in Scheme 2 are shown in Fig. 2. As depicted in Fig. 2a, the trend of stability is GMP-RCa > GMP-RCc > GMP-RCb > GMP-RCd. Inspecting the structures shown in Fig. 1, the origin of these energetic differences becomes evident. In GMP-RCa, the strong hydrogen bonding network was formed as N2–H3^⋯N7, O1–H5^⋯O2 and N2–H4^⋯O4, but N2–H3^⋯N7 was absent in GMP-RCb. In GMP-RCc and GMP-RCd, the N7 atom only forms weak H-bonds with H6 of water.

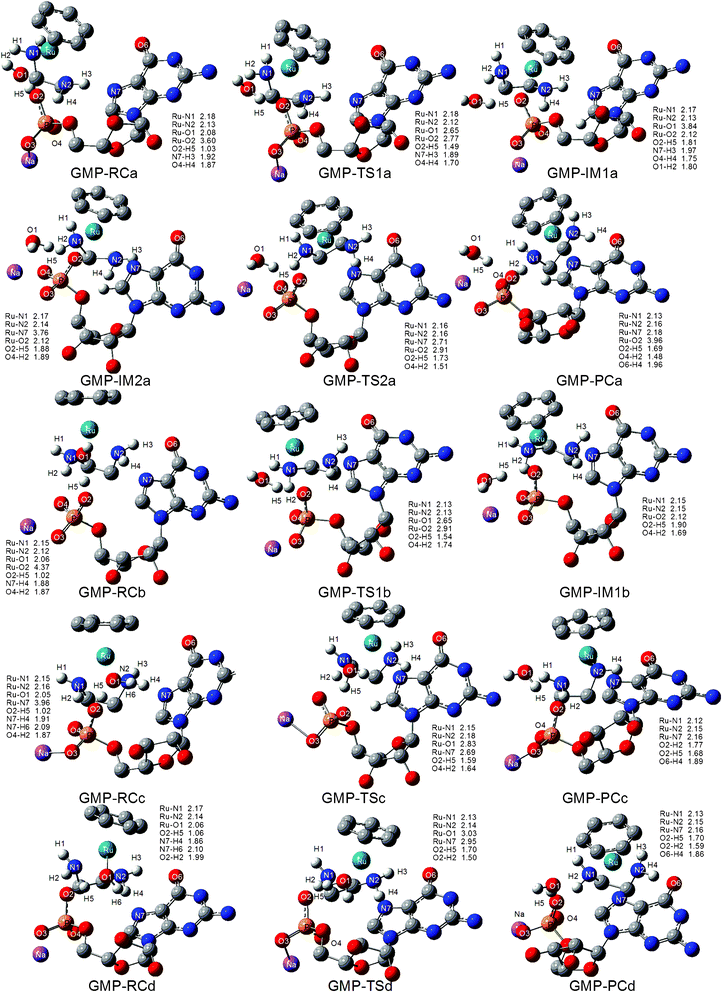Fig. 1 Optimized structures for the species and selected structural parameters of the reaction of 1 with 5′-GMP under neutral conditions. Some hydrogen atoms are omitted for clarity. The distances reported are in Angstroms.

Fig. 2 Free energy profiles of the reactions with 5′-GMP in neutral (a) and in acidic (b) conditions. SM is the starting materials, that is 1 and 5′-GMP.

As shown in Scheme 2, there are four possible pathways, two stepwise (a and b) and two concerted (c and d). Pathway a starting from GMP-RCa is discussed first. With the movement of the coordinating water molecule away from the Ru center, the nucleophilic oxygen O2 of the phosphate attacks the Ru atom to form a 7-coordinated transition state, GMP-TS1a, in which the Ru–O1 (water) and Ru–O2 (phosphate) distances are 2.65 and 2.77 Å, respectively. The imaginary frequency observed in the transition state is 171i cm⁻¹, and the vibrational mode indicates that there is a rupture of the Ru–O1 (water) bond and the formation of Ru–O2 (phosphate) bond. The intermediate of this step is GMP-IM1a, in which the phosphate is bound to Ru and the coordinated water molecule becomes a solvent molecule and forms H-bonds with the amine hydrogen and the O2 of the phosphate. R_O1–H2 and R_O2–H5 are 1.80 and 1.81 Å, respectively. GMP-IM1a lies 7.1 kcal mol⁻¹ lower in free energy relative to the SM, suggesting that it could persist long enough for characterization. Indeed, this intermediate has been observed experimentally via¹H and ³¹P NMR spectroscopy, and had a 54.3% distribution after 55 min of reaction of [(η⁶-bip)Ru^II(en)(H₂O)]²⁺ (bip = biphenyl) with 5′-GMP.¹¹ The next step is the intramolecular rearrangement from O2 of the phosphate to N7(G). Before the initiation of this step, GMP-IM1a will rearrange to GMP-IM2a, in which the hydrogen bond between O4 and H4 in GMP-IM1a is broken to form another one between O4 and H2. The GMP-IM2a intermediate is less stable than GMP-IM1a by 3.1 kcal mol⁻¹, and this can be attributed to weaker H-bonds in GMP-IM2a (R_O4–H2 = 1.89 Å and R_N7–H3 = 2.69 Å) than those of GMP-IM1a (R_O4–H4 = 1.75 Å and R_N7–H3 = 1.97 Å). The GMP-TS2a, with an imaginary frequency of 107i cm⁻¹, corresponds to the transition state for the leaving of the phosphate O2 and the N7(G) attack of the Ru atom to form the final N7(G) adduct. The Ru–O2 distances in GMP-IM2a, GMP-TS2a and GMP-PCa increase from 2.12 to 2.91 to 3.96 Å, respectively, while the Ru–N7 distances shorten from 3.76 to 2.71 to 2.18 Å, respectively. In the product GMP-PCa, the N7(G) binds to Ru and a strong hydrogen bond forms between O6 and H4 (R_O6–H4 = 1.72 Å), which was also present in the crystal structures of [(η⁶-bip)Ru(en)(9EtG)]²⁺ and [(η⁶-bip)-Ru(en)(Guo)]²⁺.^{10–12,14,15} This step is the rate-determining step, with an activation free energy of 25.8 kcal mol⁻¹ relative to GMP-IM1a. The reaction is exothermic by 6.6 kcal mol⁻¹. This is in agreement with the experimentally proposed mechanism: the displacement of bound phosphate by N7(G) is much slower compared to the phosphate binding reaction.

As displayed in Fig. 2a, pathway b starts from GMP-RCb. The transition state structure of the first step of the water and phosphate exchange reaction is GMP-TS1b. It is characterized by an imaginary frequency of 127i cm⁻¹, in which the Ru–O1 (water) bond is breaking and the Ru–O2 (phosphate) bond is forming. Compared to GMP-TS1a, the distances of Ru–O1 and Ru–O2 in GMP-TS1b become longer, being 2.65 and 2.91 Å, respectively. The intermediate is GMP-IM1b, in which the phosphate is bound to Ru and the coordinated water molecule becomes a solvent molecule and forms H-bonds with O2 of the phosphate, with R_O2–H5 being 1.90 Å. The relative free energy of GMP-TS1b is 21.3 kcal mol⁻¹, much higher than those of GMP-TS1a and GMP-TS2a (11.4 and 18.7 kcal mol⁻¹ respectively), thus making this mechanism kinetically inhibited. This is possibly due to the larger steric effect for pathway b. The subsequent step of pathway b was therefore not considered.

Two possible concerted pathways that start from GMP-RCc and GMP-RCd were also investigated, and these pathways are denoted as pathways c and d, respectively, in which the coordinated water directly exchanges with the N7(G) in 5′-GMP. The imaginary frequencies observed in the transition states are 108i cm⁻¹ for GMP-TSc and 106i cm⁻¹ for GMP-TSd, and analysis of these vibrational modes indicates that there is a rupture of the bond between Ru and the coordinated water (Ru–O1), accompanied by the simultaneous formation of the Ru–N7(G) bond. GMP-TS1c is more compact, with the distances of Ru–O1 and Ru–N7 being 2.83 and 2.69 Å, respectively, compared to GMP-TS1d in which the Ru–O1 and Ru–N7 bond distances are 3.03 and 2.95 Å, respectively. The relative free energies of pathways c and d are almost equal, being 17.4 and 18.0 kcal mol⁻¹, respectively. The overall reactions of GMP-PCc and GMP-PCd are both exothermic by 8.1 and 6.8 kcal mol⁻¹, respectively. Interestingly, during the geometry optimization of GMP-PCd, the orientation of the dihedral angle of en flipped to become similar to that of en in GMP-PCc.

Inspecting the above four reaction pathways, it could be noted that the relative free energies of GMP-TS2a, concerted GMP-TSc and GMP-TSd are similar, being 18.7, 17.4 and 18.0 kcal mol⁻¹, respectively. Experimentally, the phosphate intermediates formed during the reaction mixing time slowly rearranged into Ru-N7GMP, and then eventually disappeared after 22 h.¹¹ Plausibly, these three computed pathways compete to yield the N7GMP product, in partial agreement with the proposed mechanism by Sadler, which was a stepwise pathway for the 5′-GMP reaction.

As shown in Scheme 2, the reaction mechanisms of 1 with 5′-GMP under acidic conditions are very similar to the pathways found under neutral conditions described above. The optimized structures, given in the ESI (Fig. S1†), will not be discussed further. Overall, the H-bonds in the acidic species are a little longer than in the neutral species, suggesting that the interactions between 1 and 5′-GMP become weaker under acidic conditions. There are also four pathways, two stepwise (a and b) and two concerted (c and d) pathways under acidic conditions for the reaction of 1 with 5′-GMP. As shown in Fig. 2b, the relative free energy of the transition state of water and phosphate exchange reaction (GMPH-TS1a) is 15.5 kcal mol⁻¹, much lower than that of pathway b, which is 25.8 kcal mol⁻¹. Obviously, pathway a is much more favorable for the water and phosphate exchange reaction compared to pathway b. GMPH-IM1a lies at 0.5 kcal mol⁻¹ in free energy relative to the SM, and is essentially thermoneutral. The next step is the intramolecular rearrangement from O2 of the phosphate to the N7GMPH adduct through the GMPH-TS2a transition state. In the concerted pathways c and d, the relative free energies of GMPH-TSc and GMPH-TSd are 21.5 and 20.0 kcal mol⁻¹, respectively, comparable to that of GMPH-TS2a, which is 21.7 kcal mol⁻¹ relative to the SM. The free energies of the final products GMPH-PCa, GMPH-PCc and GMPH-PCd are −3.4, −3.1 and −4.2 kcal mol⁻¹, respectively, suggesting that they are stable at ambient temperature. Analogous to the reaction under neutral conditions, the reaction pathways under acidic conditions can be described as follows: first, the reactive aqua complex 1 rapidly reacts with the 5′-phosphate of 5′-GMP. Then, the phosphate intermediates can partly go through a slow displacement of the bound phosphate by G. The remaining phosphate intermediates may possibly return to the reactants through concerted pathways c and d to yield the thermodynamically more stable N7GMPH product.

Compared to the activation free energies of the 5′-GMP reaction under neutral conditions (24.5 kcal mol⁻¹), the overall activation free energy for Ru-N7GMP formation is 20.0 kcal mol⁻¹ under acidic conditions. This suggests that the reaction is faster under acidic than under neutral conditions. This is in agreement with experimental results, where the reactions of 5′-GMP were observed to be much slower at high pH; t_1/2 for formation of Ru-N7GMP increased from 1.1 to 5.0 h when the pH was raised from 5.37 to 9.40.¹¹

3.2. Reactions of 1 with 5′-AMP

The reactions of 1 with 5′-AMP have been studied under neutral and acidic conditions as well. The proposed mechanisms are presented in Scheme 3. The optimized structures for the stationary points along the proposed process under neutral conditions are displayed in Fig. 3 and the corresponding free energy profiles for the reactions in Scheme 3 are compiled in Fig. 4.

Fig. 3 Optimized structures for the species and selected structural parameters of the reaction of 1 with 5′-AMP under neutral conditions. Some hydrogen atoms are omitted for clarity. The distances reported are in Angstroms.

Fig. 4 Free energy profiles of the reactions with 5′-AMP under neutral (a) and under acidic (b) conditions. SM is the starting materials, that is 1 and 5′-AMP.

Under neutral conditions, the 5′-AMP was bound to complexes via strong H-bonds with the coordinated water molecule and the amine hydrogen by phosphate and N7(A) with four binding modes. In these structures (Fig. 3), the en and water act as hydrogen-bond donors, whereas the phosphate groups and the adenine rings, respectively, are hydrogen-bond acceptors. As reflected in Fig. 4, the trend of stability of the reactants is AMP-RCd > AMP-RCa > AMP-RCb > AMP-RCc, and this can be ascribed to the differences in the H-bonding network. Proton transfer between the O atom of the phosphate and the H atom of water is also found in the optimized reactants, due to the strong electrostatic interaction between the Ru atom and the phosphate group.

Pathways a and b are stepwise reactions (Scheme 3). Pathway a starts with AMP-RCa, yielding the phosphate bound AMP-IM1a via the transition state AMP-TS1a, in which the Ru–O1 bond distance is 2.77 Å and the Ru–O2 bond distance is 2.85 Å. The relative free energy of AMP-TS1a is 13.8 kcal mol⁻¹, in which a strong H-bond network is formed (R_O2–H5 = 1.59 Å, R_O4–H4 = 1.80 Å, R_N7–H3 = 2.09 Å). Before the second step, AMP-IM1a transforms to the more stable intermediate AMP-IM2a, in which O4 of the phosphate previously bound to H4 now becomes connected to H2 of the amine. The reaction yields the final N7AMP adduct from AMP-IM2a to AMP-PCa via AMP-TS2a, in which the breaking Ru–O2 bond is 3.12 Å and the forming Ru–N7 bond is 2.91 Å. The relative free energy of AMP-IM2a is −11.0 kcal mol⁻¹ and this indicates that this intermediate is a thermodynamic sink. This result implies that the formation of AMP-PCa would have to pass an effective barrier of 33.8 kcal mol⁻¹, which suggests that N7AMP binding is kinetically prohibitive. These data are in good agreement with experimental results, which showed the presence of only a 5′-phosphate adduct when 5′-AMP reacted with [(η⁶-bip)Ru(en)Cl]⁺ at pH 7.2.¹¹

Pathway b starts with AMP-RCb, and yields the phosphate bound AMP-IM1b via the transition state AMP-TS1b, with R_Ru–O1 = 2.81 Å and R_Ru–O2 = 2.70 Å. The relative free energy of AMP-TS1b is 19.5 kcal mol⁻¹. Compared to AMP-TS1a, AMP-TS1b lacks an H-bond from the N7 of A. In the subsequent step, the phosphate bound intermediate AMP-IM2b transformed to the N7AMP adduct AMP-PCb, via the transition state AMP-TS2b (106.1i cm⁻¹). The relative energy of AMP-TS2b is 25.6 kcal mol⁻¹, higher than that of AMP-TS1b. Therefore, the second step is the rate-determining step in pathway b.

Concerted pathways c and d were investigated where the coordinated water molecule directly exchanged with the adenine to form the N7AMP adducts. The imaginary frequencies for the transition states AMP-TSc and AMP-TSd are 73i cm⁻¹ and 95i cm⁻¹, respectively, corresponding to the Ru–O1 and Ru–N7 bonds being broken and formed, respectively. The relative free energies of pathways c and d are 31.0 and 26.9 kcal mol⁻¹, respectively, much higher than those of AMP-TS2a and AMP-TS2b, which are 22.8 and 25.6 kcal mol⁻¹, respectively. Consequently, under neutral conditions, stepwise pathway a is the most favorable among the four investigated pathways.

As shown in Scheme 3, a very similar reaction pathway was found for the reaction of 1 with 5′-AMP under acidic conditions in comparison with neutral conditions. There are also four pathways, two stepwise (a and b) and two concerted (c and d). Therefore, the structural characteristics described in Fig. S2† are not discussed in detail. As shown in Fig. 4b, the relative free energy of the first step of the water and phosphate exchange reaction pathway a (AMPH-TS1a) is 21.5 kcal mol⁻¹, and that of the second step of the intramolecular exchange reaction (AMPH-TS2a) is 29.5 kcal mol⁻¹. Surprisingly, the relative free energy of AMPH-TS1b is 24.8 kcal mol⁻¹, and that of AMPH-TS2b is 23.1 kcal mol⁻¹. Inspection of the structure of AMPH-TS2b showed that a strong H-bond network is formed between the solvent water, 5′-AMP and the en ligand (R_O1–H1 = 1.83 Å, R_O2–H2 = 1.78 Å, R_O4–H5 = 1.64 Å, R_N7–H4 = 2.22 Å). Therefore pathway b is more favorable than pathway a, and the first step is the rate-determining step in pathway b. The relative free energy of concerted AMPH-TSc and AMPH-TSd are 31.1 and 36.1 kcal mol⁻¹, respectively. The reactions are all endothermic by 7.0–13.0 kcal mol⁻¹, higher values than those found under neutral conditions. Consequently, the formation of the N7AMP adducts under acidic conditions are not favored kinetically or thermodynamically. In the phosphate binding step, the activation barrier is 24.8 kcal mol⁻¹ under acidic conditions, which is greater by 11.0 kcal mol⁻¹ than under neutral conditions. The results are again in accordance with results from experimental studies, which observed that the phosphate binding intermediate of 5′-AMP reached its maximum intensity at pH ca. 7.2 and then decreased in intensity at either lower or higher pH.¹¹

From the results obtained, we can see that the relative conformation of en has an important influence on the energetics of the system. As to the water–phosphate exchange process in stepwise pathways, pathway a (N1 (en) pointing away from the coordinated water molecule) leads to a much faster reaction as compared to pathway b (N1 (en) pointing towards the coordinated water molecule) for 5′-GMP in both neutral and acidic conditions. Comparing the results for both nucleotides reveals marked differences in their binding preferences of 5′-GMP over 5′-AMP under neutral conditions. First, the ∼9 kcal mol⁻¹ difference between the activation free energies for the 5′-GMP and 5′-AMP binding reactions translates to a ratio of reaction rates of about 7 orders of magnitude, which sufficiently demonstrates the prominent selectivity of 1 toward 5′-GMP kinetically. This is quite different from a previous study, which reported an activation free energy difference of 3.9 kcal mol⁻¹ between the G and A substitution for 1, without considering the phosphate group.²⁶ This difference originated to a large extent from the hydrogen bond network between the Ru–arene complexes and the nucleotides. Secondly, the 5′-GMP reactions are calculated to be significantly exothermic, while the 5′-AMP reactions are endothermic, suggesting that binding to 5′-GMP is thermodynamically more favorable compared to 5′-AMP under both neutral and acidic conditions.

4. Conclusions

Our calculations revealed reasonable pathways for the binding of the potential anticancer complex 1 to nucleotides 5′-GMP and 5′-AMP under neutral and acidic conditions. There were four pathways designed for the reactions of 1 with 5′-GMP and 5′-AMP under both neutral and acidic conditions. In line with the results from experimental observations,¹¹ the reactants first yielded a stable phosphate bound intermediate and then underwent a rate-determining intramolecular exchange to produce the final N7(G) binding product. But concerted pathways for 5′-GMP, in which the N7(G) directly exchanged with the coordinated water molecule, potentially complement the previously anticipated stepwise mechanism. By inspection of the corresponding free energy profiles, the reaction with 5′-GMP has a free energy of activation of 24.5 kcal mol⁻¹ under neutral conditions and 20.0 kcal mol⁻¹ under acidic conditions. Meanwhile, for the reaction with 5′-AMP, the stepwise pathway a was the preferred pathway, and the intramolecular exchange of N7(A) with the phosphate group is the rate-determining step, with a prohibitive activation free energy of 33.8 kcal mol⁻¹ under neutral conditions. Moreover, the phosphate binding under acidic conditions exhibited a much higher barrier than under neutral conditions, which validates the experimental findings that the phosphate binding of 5′-AMP decreased in intensity at lower pH values.

The significant differences between the activation energies (about 9 kcal mol⁻¹) for the 5′-GMP and 5′-AMP binding reactions sufficiently accounts for the prominent selectivity for 5′-GMP and 5′-AMP observed in experiments. Moreover, the 5′-GMP reactions are calculated to be significantly more exothermic than the 5′-AMP exchange reactions. As reflected in the structural analysis of the reactants, intermediates and transition states, the phosphate as a hydrogen bond acceptor played an indispensable role in the interaction of the Ru–arene complexes with the nucleotides.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Nos. 20725103, 20831006, 20821001, 20973204,21172274, 21173273), the Guangdong Provincial Natural Science Foundation (No. 9351027501000003), the National Basic Research Program of China (973 Program No. 2007CB815306) as well as the Fundamental Research Funds for the Central Universities and by a grant from the Research Grants Council of Hong Kong (HKU 7039/07P). This work was partially sponsored by the high performance grid computing platform of Sun Yat-sen University.

References

1. J. Reedijk, Eur. J. Inorg. Chem., 2009, 1303–1312.
2. H. K. Liu and P. J. Sadler, Acc. Chem. Res., 2011, 44, 349–359.
3. S. H. van Rijt and P. J. Sadler, Drug Discovery Today, 2009, 14, 1089–1097.
4. A. M. Pizarro and P. J. Sadler, Biochimie, 2009, 91, 1198–1211.
5. A. Levina, A. Mitra and P. A. Lay, Metallomics, 2009, 1, 458–470.
6. G. Gasser, I. Ott and N. Metzler-Nolte, J. Med. Chem., 2011, 54, 3–25.
7. G. Suss-Fink, Dalton Trans., 2010, 39, 1673–1688.
8. R. E. Morris, R. E. Aird, P. D. Murdoch, H. M. Chen, J. Cummings, N. D. Hughes, S. Parsons, A. Parkin, G. Boyd, D. I. Jodrell and P. J. Sadler, J. Med. Chem., 2001, 44, 3616–3621.
9. R. E. Aird, J. Cummings, A. A. Ritchie, M. Muir, R. E. Morris, H. Chen, P. J. Sadler and D. I. Jodrell, Br. J. Cancer, 2002, 86, 1652–1657.
10. H. M. Chen, J. A. Parkinson, S. Parsons, R. A. Coxall, R. O. Gould and P. J. Sadler, J. Am. Chem. Soc., 2002, 124, 3064–3082.
11. H. M. Chen, J. A. Parkinson, R. E. Morris and P. J. Sadler, J. Am. Chem. Soc., 2003, 125, 173–186.
12. H. M. Chen, J. A. Parkinson, O. Novakova, J. Bella, F. Y. Wang, A. Dawson, R. Gould, S. Parsons, V. Brabec and P. J. Sadler, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 14623–14628.
13. O. Novakova, J. Kasparkova, V. Bursova, C. Hofr, M. Vojtiskova, H. M. Chen, P. J. Sadler and V. Brabec, Chem. Biol., 2005, 12, 121–129.
14. H. K. Liu, S. J. Berners-Price, F. Y. Wang, J. A. Parkinson, J. J. Xu, J. Bella and P. J. Sadler, Angew. Chem., Int. Ed., 2006, 45, 8153–8156.
15. H. K. Liu, F. Y. Wang, J. A. Parkinson, J. Bella and P. J. Sadler, Chem.–Eur. J., 2006, 12, 6151–6165.
16. C. Scolaro, T. J. Geldbach, S. Rochat, A. Dorcier, C. Gossens, A. Bergamo, M. Cocchietto, I. Tavernelli, G. Sava, U. Rothlisberger and P. J. Dyson, Organometallics, 2006, 25, 756–765.
17. A. Dorcier, P. J. Dyson, C. Gossens, U. Rothlisberger, R. Scopelliti and I. Tavernelli, Organometallics, 2005, 24, 2114–2123.
18. P. J. Dyson and W. H. Ang, Eur. J. Inorg. Chem., 2006, 4003–4018.
19. H.-K. Liu, J. A. Parkinson, J. Bella, F. Wang and P. J. Sadler, Chem. Sci., 2010, 1, 258–270.
20. A. Habtemariam, M. Melchart, R. Fernandez, S. Parsons, I. D. Oswald, A. Parkin, F. P. Fabbiani, J. E. Davidson, A. Dawson, R. E. Aird, D. I. Jodrell and P. J. Sadler, J. Med. Chem., 2006, 49, 6858–6868.
21. F. Y. Wang, A. Habtemariam, E. P. L. van der Geer, R. Fernandez, M. Melchart, R. J. Deeth, R. Aird, S. Guichard, F. P. A. Fabbiani, P. Lozano-Casal, I. D. H. Oswald, D. I. Jodrell, S. Parsons and P. J. Sadler, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 18269–18274.
22. D. V. Deubel and J. K. C. Lau, Chem. Commun., 2006, 2451–2453.
23. C. Gossens, I. Tavernelli and U. Rothlisberger, J. Chem. Theory Comput., 2007, 3, 1212–1222.
24. C. Gossens, I. Tavernelli and U. Rothlisberger, J. Am. Chem. Soc., 2008, 130, 10921–10928.
25. C. Gossens, I. Tavernelli and U. Rothlisberger, J. Phys. Chem. A, 2009, 113, 11888–11897.
26. Z. Futera, J. Klenko, J. E. Sponer, J. Sponer and J. V. Burda, J. Comput. Chem., 2009, 30, 1758–1770.
27. K. Gkionis, J. A. Platts and J. G. Hill, Inorg. Chem., 2008, 47, 3893–3902.
28. S. T. Mutter and J. A. Platts, J. Phys. Chem. A, 2011, 115, 11293–11302.
29. P. Yang and M. L. Guo, Coord. Chem. Rev., 1999, 185–6, 189–211.
30. S. J. Berners-Price, U. Frey, J. D. Ranford and P. J. Sadler, J. Am. Chem. Soc., 1993, 115, 8649–8659.
31. P. J. Sadler, A. Habtemariam, J. A. Parkinson, N. Margiotta, T. W. Hambley and S. Parsons, J. Chem. Soc., Dalton Trans., 2001, 362–372.
32. J. V. Burda, M. Zeizinger and J. Leszczynski, Phys. Chem. Chem. Phys., 2004, 6, 3585–3590.
33. S. J. Lippard, Y. Mantri and M. H. Baik, J. Am. Chem. Soc., 2007, 129, 5023–5030.
34. H. L. Wang, N. J. DeYonker, H. Gao, C. P. Tan, X. T. Zhang, L. N. Ji, C. Y. Zhao and Z. W. Mao, RSC Adv., 2012, 2, 436–446.
35. H. Wang, N. J. DeYonker, H. Gao, L. Ji, C. Zhao and Z.-W. Mao, J. Organomet. Chem., 2012, 704, 17–28.
36. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
37. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
38. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans., 1993, 2, 799–805.
39. J. Andzelm, C. Kölmel and A. Klamt, J. Chem. Phys., 1995, 103, 9312–9320.
40. A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235.
41. W. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. F. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111–114.
42. M. E. Alberto, M. F. A. Lucas, M. Pavelka and N. Russo, J. Phys. Chem. B, 2009, 113, 14473–14479.
43. M. F. A. Lucas, M. Pavelka, M. E. Alberto and N. Russo, J. Phys. Chem. B, 2009, 113, 831–838.
44. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven Jr, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople,Gaussian 03, Revision D.01, Gaussian, Inc., Wallingford CT, 2004.

---

Footnote

† Electronic supplementary information (ESI) available: The relative energies for all the reactions, optimized structures of reactions under acid conditions and IRC along the reaction coordinate for the GMP-TSc and Cartesian coordinates. See DOI: 10.1039/c2ra20984e

---