Light-harvesting and electronic contacting capabilities of Ru(II) Ipa rod and star complexes–first principles predictions

Abstract

Homoleptic ([Ru(L)₃]²⁺) and heteroleptic (Ru(NCS)₂(bpy)(L)) complexes carrying rigid anchor-cum-spacer ligands (L), comprised of ethynylene–phenylene spacer groups and a designated anchor group, including the isophthalic group (Ipa), have been studied computationally using density functional theory (DFT) and time-dependent density functional theory (TD-DFT) calculations. The results of the calculations are related to recently measured photophysical properties of selected complexes, and provide theoretical insight into the capabilities of the complexes to mediate interfacial electronic interactions. Opportunities to use the rigid spacer motifs to differentiate structural control and interfacial electronic interactions in heterogeneous systems are discussed, including predictions of promising strategies to enhance long-range interfacial electronic contacting capabilities using star complexes with new anchor group motifs.

---

Introduction

Molecular functionalization of metal oxide semiconductor surfaces such as TiO₂ is important for a broad range of emerging applications that includes dye-sensitized solar cells (DSSCs), heterogeneous catalysts, and sensors.^1–6 Studies under controlled experimental conditions point to significant opportunities to achieve both structural and functional control over molecule-semiconductor interfaces. Such control can be used to optimize important electronic interactions such as ultrafast surface electron transfer through chemical modifications of designated anchor and spacer groups linking the molecules to the surface.^7–11 It does, however, remain particularly challenging to control the binding of molecular species to widely used nanostructured materials because of the wealth of possible adsorption sites and binding modes. From a functional perspective, mixed binding modes and structural heterogeneity easily translate into difficulties to control the interfacial electronic properties, and it is therefore a significant challenge to achieve improved functional control in materials that display inherent structural disorder.^12,13

One strategy to provide enhanced interfacial control is to develop new molecular sensitizers and tailor-made anchor units capable of providing enhanced control of the surface binding and interfacial electronic properties for nanostructured materials. Controlling long-range photoinduced surface electron transfer processes in dye-sensitized solar cells is, in this respect, a problem of particular technological importance that provides a prototype illustration of the formidable challenge. Several innovative anchor and spacer group motifs, e.g. push–pull linkers, rigid rods, and tripodal anchors, have been developed in recent years that provide enhanced photophysical properties (i.e. HOMO–LUMO tuning) and capabilities to bind functional molecular components, such as chromophores, to nanostructured metal oxide semiconductor materials, such as TiO₂.¹¹ More recent approaches involve encapsulating dyes in a host molecule.^14–18 Also, the development of homoleptic complexes of ruthenium, so called “star” complexes,^19,20 aim at shielding the chromophoric unit from the heterogeneity of the semiconductor surface, resulting in reduced aggregation and degradation,^15,17 and control over the charge transfer processes (slower recombination).^15,16

Ru(II) polypyridyl complexes are widely used for light-harvesting in a broad range of photochemical applications, including e.g. dye-sensitized solar cells, artificial photosynthesis, and photobiology, because of their favorable ground and excited state photophysical properties, high tunability, and excellent chemical stability.^21–27 Recently, homoleptic Ru(II) polypyridyl chromophores were combined with rigid linker groups in so-called RuStar complexes as a promising strategy to achieve enhanced control of interfacial properties relevant for long-range electron transfer, including, in particular, evidence that the linkers of the RuStar complexes successfully enforce the physical separation of the Ru-chromophore part of the sensitizer from the semiconductor surface.^19,20 It is, in this context, of fundamental interest to provide a better understanding of how the physical separation of the chromophores from the nanostructured surfaces relate to electronic interactions across the bridging anchor groups, and to investigate how such electronic interactions may be affected by chemical modifications of the bridging unit.

Many theoretical studies of ruthenium complexes have been published in recent years. In particular, Density Functional Theory (DFT) and Time-Dependent DFT (TD-DFT) currently offer good possibilities for theoretical studies of ground and excited state properties of relevance for photoelectrochemical applications.^28,29 This includes several studies by us, and others, to investigate properties of Ru-dyes for solar energy conversion applications using hybrid DFT and TD-DFT methods.^{30–32,36–39} First principles molecular design of new light-harvesting complexes provides significant opportunities to tailor structural and electronic properties to the specific needs of particular photoelectrochemical and optoelectronic applications, e.g. in terms of the light-harvesting capabilities and excited state properties. For example, the [Ru(dqp)₂]²⁺ complex (dqp is 2,6-di(quinolin-8-yl)pyridine) provides one recent demonstration of the emerging possibilities to design new Ru(II) complexes that combine favorable structural and electronic properties for solar energy conversion applications from first principles predictions.^30–32 Theoretical modeling has also been employed in recent years to provide explicit insight into the surface binding and electronic contacting capabilities of several sensitizers to TiO₂ substrates,^8,33 with examples ranging from organic molecules³⁴ to Ru-dyes,³⁵ as well as including examples of sensitizers with spacer groups¹² and advanced anchor motifs such as Ipa rods^36,40 and tripods.¹³

In this work, we focus on calculations of Ru(II) polypyridyl complexes with rigid anchor-cum-spacer groups. This study is conducted with the aim to elucidate how variations in the complex composition affect the electronic properties of these complexes. The investigated complexes include both homoleptic and heteroleptic complexes comprising a set of ligands, L1–L9, shown in Fig. 1. The heteroleptic complexes have the general form [Ru(NCS)₂(bpy)(L)], i.e. the Ru^II chromophore part includes two thiocyanate (NCS⁻) groups that constitutes a well-known motif from the efficient DSSC sensitizer RuN3.¹ These complexes are referred to as RuN3 complexes. The homoleptic complexes having the general form [Ru(L)₃]²⁺ represent the new star strategy to control the chromophore-nanostructure distance.¹⁹ These complexes are referred to as RuStar complexes. In order to specify a particular RuN3 or RuStar complex that carries one of the ligands, L# (L1–L9), we refer to complexes as RuN3–L# and RuStar–L#, respectively.

Fig. 1 Chemical structures of the investigated RuN3 and RuStar complexes, as well as the associated substituted bipyridyl ligands L1–L9 carrying rigid rod anchor-cum-spacer groups (R) at one or both of the 4,4′-positions.

This allows extensive comparisons yielding theoretical insight into the electronic properties of these complexes to promote rational design of new sensitizers that simultaneously combine structural and electronic control at interfaces. Furthermore, the computational results are compared to recent experimental findings in order to assess how the complex structures and electronic properties combine to affect the functionality, in particular long-range electronic contacting capabilities via surface electron transfer, of these complexes for use in nanostructured photoelectrochemical devices such as dye-sensitized solar cells. Photoelectrochemical properties of some Ru complexes with alternative anchor groups that have not yet been investigated experimentally are finally predicted from quantum chemical calculations.

Methods

All quantum chemical calculations have been performed using the Gaussian09 program.⁴¹ All geometries of the investigated complexes were first optimized using the PBE0 functional^42–44 together with a standard Stuttgart/Dresden (SDD) double-zeta quality basis set and accompanying 28 electron effective core potential (ECP) for ruthenium.⁴⁵ Simulated absorption spectra have been obtained from calculated TD-DFT excitations using an arbitrary Gaussian energy broadening of 0.3 eV. Electronic properties and molecular excitations were subsequently calculated using the same PBE0 functional and SDD basis set combination employing time-dependent DFT calculations in a polarisable continuum model⁴⁶ of acetonitrile for all investigated complexes presented in the results section. Excitation calculations were performed for 10 excited states for the ligands, and 40–60 excited states for the Ru complexes, as necessary, to include spectral features with wavelengths down to ca. 350 nm, with further details given in the ESI.†

The performance of the excitation calculations has also been investigated using alternative DFT functionals, basis sets, and treatment of the solvent environment for RuN3–L1 and RuStar–L5 as prototype complexes as described in the remainder of this methods section.

Including a solvent is found to have a significant influence on the RuN3–L1 complex (shown in Fig. S1, ESI†), with spurious low-energy excitations appearing in the vacuum calculation. This is similar to what has previously been discussed in-depth for related Ru-rod complexes.³⁶ On the other hand, for the symmetric RuStar–L5 complex, the solvent treatment is found to have only a small influence on the calculated spectrum (shown in Fig. S2, ESI†).

The basis set dependence of the results was also investigated for PBE0 calculations with different basis sets in acetonitrile. Calculations were carried out for the RuN3–L1 and RuStar–L5 complexes, using the standard LANL2DZ⁴⁷ and SDD ECP-basis sets, as well as all electron basis sets up to triple zeta, with diffuse and polarization functions for H, C, N, and S atoms, together with the SDD ECP-basis set for Ru. The calculated absorption spectra (shown in Fig. S3 and S4, ESI†) show moderate spectral shifts (within a range of ca. 25 nm for the MLCT peak maximum, around 500 nm) but with very similar spectral shapes for all basis sets.

Finally, the ability of several DFT functionals to reproduce essential features of the optical spectra has been evaluated for the RuN3–L1 and RuStar–L5 complexes using time-dependent DFT calculations. The tested functionals include the standard hybrid B3LYP⁴⁸ and PBE0 functionals, as well as the range-separated CAM-B3LYP,⁴⁹ ωB97x,⁵⁰ and LC-ωPBE⁵¹ functionals. Results for the RuN3–L1 and RuStar–L5 complexes are shown in panels a and b of Fig. 2, respectively. The results for RuN3–L1 can be compared to the experimental absorption spectrum.¹⁹ This displays a broad MLCT absorption peak with a maximum around 530 nm. The absorption extends ca. 700 nm, although the relatively poor and featureless experimental absorption makes it difficult to assess precisely how far to the red there are actual low-intensity excitations. A low-energy excitation limit is, however, provided by the observation of photoluminescence at 760 nm. Towards higher energies, there is a weak minimum at ca. 440 nm, followed by a peak with increased absorption below 400 nm. There is a noticeable trend for the different functionals where both the absorption onset and MLCT maximum is gradually blue-shifted in the order B3LYP–PBE0–CAM-B3LYP–ωB97x–LC-ωPBE. While it is hard to specify the absorption onset experimentally, the MLCT absorption maximum around 530 nm is reasonably well captured by the traditional hybrid functionals B3LYP and PBE0. The range-separated functionals appear to give MLCT maxima that are shifted somewhat to shorter wavelengths, with CAM-B3LYP coming closest to the experimental spectral maximum of the range-separated functionals.

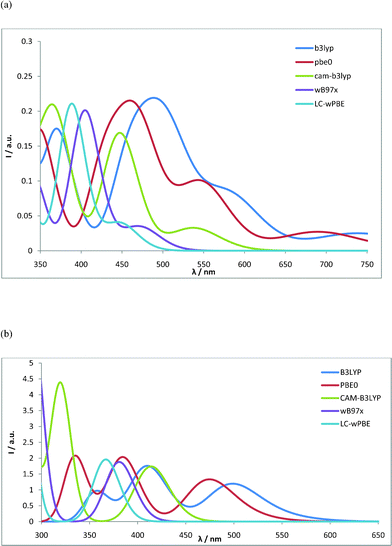Fig. 2 TD-DFT calculated optical absorption spectrum using different DFT functionals. (a) RuN3–L1 spectra calculated in acetonitrile with 6–31G(d) basis set on H, C, N, O, and S and SDD ECP-basis set on Ru. (b) RuStar–L5 spectra calculated in acetonitrile with the SDD ECP-basis set on all atoms.

The experimental absorption spectrum has been measured for the so-called short star Ru-complex, which is here referred to as RuStar–L5.²⁰ It consists of a broad MLCT absorption peak around 490 nm, followed by a second absorption peak below 400 nm. The different functionals give significantly different values for the first absorption maximum, with rather good spectral matching for the hybrid B3LYP and PBE0 functionals, and the range-separated functionals tending to have their peaks at shorter wavelengths compared to the experiment.

In light of the method tests presented here, work to further improve the spectral calculations, e.g. by mimicking experimental conditions (such as thermal fluctuations or the presence of counter ions, etc.), and considering higher level electronic structure calculations, could be interesting for a more detailed method-oriented investigation beyond the scope of the present investigation. For the purposes of the present investigation in which the main focus is to explain spectral trends and provide strategies to modify the electronic properties for large dyes, we judge that the accuracy of the standard hybrid functional PBE0, together with the SDD ECP plus valence double-zeta basis sets, offer reasonable accuracy to systematically study the full series of complexes.

Results

The results are arranged below so that first the ligands are presented, secondly the heteroleptic RuN3 complexes of the form [Ru(NCS)₂(bpy)(L)], and finally the homoleptic RuStar complexes of the form [Ru(L)₃]²⁺ where L are the bpy ligands substituted with various linker groups. This allows comparisons to be made primarily for species of similar type in terms of charge, metal coordination environment, and absorption threshold.

Ligands

The various rod and star ligands (L1–L9) have first been studied by themselves, including DFT geometry optimizations and TD-DFT excitation calculations. HOMO and LUMO energies, as well as TD-DFT absorption thresholds, are presented in Table 1, and simulated absorption spectra are compared in Fig. 3 and 4. The ligand results are discussed rather briefly here, as these calculations are used mainly for reference purposes in investigations of Ru complexes constructed using these ligands presented below.

Fig. 3 Simulated absorption spectra for ligands L1 (black), L2 (red), L3 (green), and L4 (blue).

Fig. 4 Simulated absorption spectra for ligands L5 (black), L6 (red), L7 (green), L8 (blue), and L9 (orange).

Table 1 Calculated frontier molecular orbital energies (in eV), absorption thresholds (in eV and nm for energy and wavelength respectively), and oscillator strengths for the lowest excitation for L1–L9

Ligand	HOMO (eV)	LUMO (eV)	E 1 (eV)	λ 1 (nm)	f 1
L1	−7.46	−2.50	3.89	318	0.0042
L2	−7.11	−2.36	4.01	309	0.0279
L3	−6.51	−2.46	3.48	356	2.1783
L4	−6.43	−2.49	3.35	370	1.5602
L5	−7.11	−2.40	4.03	308	0.0000
L6	−6.50	−2.49	3.42	363	4.5184
L7	−6.32	−2.52	3.26	381	2.3407
L8	−7.01	−2.56	3.83	324	2.9356
L9	−6.92	−3.16	3.22	385	3.3217

---

The HOMO and LUMO energies essentially reflect the expected behavior, with decreased HOMO–LUMO gaps for ligands with extended conjugation due to the presence of elongated anchor-cum-spacer groups. The LUMO energies are expected to be of particular importance for photophysical properties of the Ru-polypyridyl complexes, as these levels are typically involved in low-energy Metal-to-Ligand Charge-Transfer (MLCT) excitations. The calculated LUMO energies fall in a narrow range from −2.36 to −2.56 eV for all investigated ligands, except for L9 that constitutes an important exception with a significantly shifted LUMO energy at −3.16 eV. This suggests that complexes incorporating this anchor moiety are likely to suffer from reduced excited state energies. This may in turn also influence the capability for electron transfer of excited electrons to wide bandgap semiconductors, such as TiO₂, negatively, as this depends on the interfacial energy level alignment between the excited state of the donor and the conduction band edge of the semiconductor substrate.

The calculated excitation spectra for the ligands are divided into two groups. Firstly, spectra are shown in Fig. 3 for L1–L4, i.e. for the group of ligands consisting of the single-rod L2–L4 as well as the ligand L1. Secondly, the spectra for the remaining L5–L9 carrying two rods each are shown in Fig. 4.

The excitation spectra for L1–L4 shown in Fig. 3 show a gradual shift to longer absorption thresholds with a concomitant increase in oscillator strength for the first absorption peak as the conjugation of the ligands increase with expanded anchor groups. There is, in particular, a noticeable divide between L1 and L2 with weaker first absorption peaks around 300 nm, on the one hand, and L3 and L4 with stronger first absorption peaks located at ca. 360 nm.

As expected, the spectra for ligands L5–L9 shown in Fig. 4 show stronger absorption (larger calculated oscillator strengths) in the 300–400 nm range compared to the corresponding single-rod ligands discussed above. This effect is particularly noticeable in the stronger oscillator strengths for the first excited state, where L3 was the only ligand with a strong calculated oscillator strength for the first transition, as detailed in Table 1. The strongest single absorption feature is a peak at ca. 360 nm for L6, while L7 and L9 show significant absorption extending further towards longer wavelengths with absorption thresholds beyond 380 nm. It is also interesting to note that the para-substituted L8 is calculated to have its first absorption peak shifted to longer wavelengths by ca. 20 nm compared to L5, which has an identical bpy-rod part but a different carboxylic acid anchor group motif.

RuN3 type complexes

Calculated results for the HOMO and LUMO energies, as well as the absorption thresholds and oscillator strengths for the lowest excitations, are given in Table 2 for the investigated RuN3 type complexes. The HOMO energies all fall in a small energy range from −5.57 to −5.38 eV, consistent with the notion that the HOMO levels are dominated by metal centered (Ru 4d) contributions (see also the discussion below). All LUMO levels also fall within a rather narrow range of −2.8 ± 0.2 eV, except the complex with L9. This ligand was special in this respect by itself, as discussed for the free ligands above, illustrating that free ligand properties also often carry over the properties of complete metal complexes.

Table 2 Calculated frontier molecular orbital energies and absorption thresholds for the RuN3 type complexes with L1–L9

Complex	HOMO (eV)	LUMO (eV)	E 1 (eV)	λ 1 (nm)	f 1
RuN3–L1	−5.57	−2.99	1.64	755	0.0264
RuN3–L2	−5.40	−2.67	1.90	653	0.0936
RuN3–L3	−5.38	−2.70	1.90	652	0.1421
RuN3–L4	−5.40	−2.69	1.86	665	0.0078
RuN3–L5	−5.44	−2.79	1.77	699	0.0520
RuN3–L6	−5.41	−2.80	1.78	695	0.0762
RuN3–L7	−5.42	−2.82	1.78	697	0.0787
RuN3–L8	−5.44	−2.87	1.74	712	0.0604
RuN3–L9	−5.45	−3.26	1.61	772	0.0834

---

Calculated optical absorption spectra for the investigated complexes are shown in Fig. 5 for the complexes with ligands L1–L4, and in Fig. 6 for the complexes with L5–L9. All complexes show evidence for the presence of MLCT excitations at wavelengths beyond 450 nm in addition to the strong [small pi, Greek, tilde]π* excitations with wavelengths shorter than 400 nm. The largest oscillator strengths in the MLCT region are calculated for star complexes with ligands L6, L7, and L9 as shown in Fig. 6. Of these the MLCT maximum of the complex carrying L9 is shifted significantly towards longer absorption wavelengths (>600 nm).

Fig. 5 Simulated absorption spectra for the RuN3 type complexes with L1 (black), L2 (red), L3 (green), L4 (blue).

Fig. 6 Simulated absorption spectra for the RuN3 type complexes with L5 (black), L6 (red), L7 (green), L8 (purple), and L9 (blue).

RuStar complexes

Homoleptic RuStar complexes measuring up to 4 nm in diameter, have recently been presented as a viable alternative to enforce physical separation of the Ru core from a mesoscopically structured semiconducting substrate, such as nano-TiO₂.^19,20 The rigid and symmetric linkers of the Stars effectively shield the Ru core, and thus provide excellent possibilities to control the chromophore-semiconductor distance, with concomitant opportunities to achieve improved interfacial control over surface electron transfer processes, including photoinduced electron injection from the Ru dye to the substrate, as well as subsequent recombination.

Calculated electronic properties (frontier orbital energies and TD-DFT first excitation data) are given in Table 3 for the computationally investigated RuStar complexes. As for the RuN3 complexes described above, the HOMO energies are again similar for all complexes due to their metal character. However, it can be noted that the HOMO energies of the star complexes are shifted to lower energies compared to the corresponding energies for the Ru-rod complexes, an effect that is mainly ascribed to the effect of the electron rich thiocyanate ligands in the RuN3 complexes and the net positive charge (+2) of the star complexes. This also shifts the calculated absorption thresholds for the star complexes to higher energies, with a calculated range of 500–550 nm.

Table 3 Calculated frontier molecular orbital energies and absorption thresholds for the RuStar complexes with L2, and L5–L9

Complex	HOMO (eV)	LUMO (eV)	E 1 (eV)	λ 1 (nm)	f 1
RuStar–L2	−6.43	−3.05	2.44	509	0.0179
RuStar–L5	−6.49	−3.22	2.37	524	0.0615
RuStar–L6	−6.33	−3.20	2.32	534	0.1621
RuStar–L7	−6.52	−3.09	2.31	537	0.1333
RuStar–L8	−6.48	−3.28	2.34	530	0.0796
RuStar–L9	−6.51	−3.50	2.28	545	0.1323

---

Calculated absorption spectra for selected star complexes are shown in Fig. 7. The spectra show MLCT absorption bands in the 450–450 nm region of the visible spectrum. The complexes based on L6 and L9 stand out as having comparatively strong and red-shifted MLCT bands with maxima around 500 nm, and extending to ca. 550 nm. Such extensions of the light-harvesting capabilities to cover a broader part of the solar spectrum in the visible region are important for solar energy conversion applications.

Fig. 7 Simulated absorption spectra for the RuStar complexes with L2 (black), L5 (red), L6 (green), L8 (blue), and L9 (orange).

Discussion

The calculated electronic properties of the investigated complexes are relevant firstly for the tuning of the optical absorption and the electrochemical properties of the complexes by themselves. However, these complexes have been designed primarily to offer a possibility to control the interaction with electron acceptor moieties such as nanostructured TiO₂ electrodes. Although the calculations presented here have been performed on the dye molecules themselves, it is interesting to consider to what extent the molecular electronic properties can be expected to influence surface interactions such as photoinduced surface electron transfer. For this purpose it is pertinent to consider the delocalization of the frontier orbitals towards the anchoring groups.

Fig. 8 first illustrates the localized nature of the metal centered (Ru 4d) HOMO level for complexes with short and long anchor-cum-spacer groups, respectively. The calculations show that the physical separation of the metal centre from any surface enforced by the ligands in the star complexes effectively isolates the hole on oxidized metal complexes in a way that is compatible with significantly reduced electronic coupling to the substrate. This is consistent with significantly reduced ground state recovery through back-transfer across the legs of the star ligands.¹⁹

Fig. 8 HOMO levels for the RuStar–L5 and RuStar–L6 complexes showing similar localization of metal centered (Ru 4d) HOMO levels in star type complexes with different rigid anchor-cum-spacer side group lengths.

Fig. 9 shows the delocalization of the LUMO on several of the investigated ligands in selected RuN3 complexes. The calculations show differences in the degree of delocalization across the entire anchor-cum-spacer group for different ligands. In particular, the complexes with L6 and L7 show a marked decrease of LUMO delocalization towards the anchoring part of the molecules, compatible with significantly reduced interfacial electronic coupling. In contrast, the complexes carrying the para-substituted L8 and L9 both show much more pronounced delocalization extending onto the anchor groups. The increased delocalization of the LUMO level towards the anchor group in the para-substituted L8 and L9 ligands is in line with similar findings in previously investigated types of sensitizers.¹ In view of the evidence for poor injection of the first Ru^II-star complexes,^19,20 L8 and L9 thus provide promising strategies for promoting long-range interfacial electron transfer in new Ru^II-star complexes.

Fig. 9 LUMO levels of selected RuN3 complexes with ligands (a) L2, (b) L5, (c) L6, (d) L7, (e) L8, and (f) L9.

Conclusions

Structural and electronic properties have been investigated for a number of Ru^II complexes carrying rigid rod anchor-cum-spacer groups using first principles DFT and TD-DFT calculations. The calculations provide significant insight into how the rigid rods can be utilized to tailor the electronic properties. The calculated confinement of the frontier molecular orbitals around the metal centre with little extension onto the anchor groups provide an explanation for recent observations of slow interfacial electron transfer using these ligands.¹⁹ Furthermore, the calculations predict significant opportunities for combining the electronic properties with structural influence on surface binding capabilities in order to tailor light-harvesting and surface electron transfer capabilities of these types of rod and star complexes. In particular, the calculations provide predictions for the development of new anchor group motifs that can be used to control long-range interfacial electron transfer processes in RuStar complexes through use of alternative anchor motifs, such as in the new ligands L8 and L9 that have the potential to couple chromophores more strongly to the surface electronically, compared to the Ipa group present in ligands L2–L7. This work provides a guide for continued efforts to synthesize new ligands for Ru complexes with strategically modified interfacial contacting capabilities.

Acknowledgements

The Swedish Research Council (VR) as well as the Knut and Alice Wallenberg Foundation are acknowledged for financial support. The calculations have been performed using resources provided by the Swedish National Supercomputing Center (NSC) and the Lund University Supercomputing facility (LUNARC). EG is grateful for funding from the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences of the U.S. Department of Energy (DE-FG02-01ER15256).

References

1. A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Dye-Sensitized Solar Cells., Chem. Rev., 2010, 110, 6595–6663.
2. S. Ardo and G. J. Meyer, Chem. Soc. Rev., 2009, 38, 115.
3. L. M. Peter, The Gratzel Cell: Where Next?, J. Phys. Chem. Lett., 2011, 2, 1861–1867.
4. D. M. Adams, et al., J. Phys. Chem. B, 2003, 107, 6668.
5. U. Diebold, Surf. Sci. Rep., 2003, 48, 53.
6. Y. Sun, S. N. Collins, L. E. Joyce and C. Turro, Inorg. Chem., 2010, 49, 4257.
7. J. Schnadt, P. A. Bruhwiler, L. Patthey, J. N. O'Shea, S. Södergren, M. Odelius, R. Ahuja, O. Karis, M. Bässler, P. Persson, H. Siegbahn, S. Lunell and N. Mårtensson, Nature, 2002, 418, 620.
8. P. Persson, R. Bergström, L. Ojamäe and S. Lunell, Adv. Quantum Chem., 2002, 41, 203.
9. E. Galoppini, W. Z. Guo, W. Zhang, P. G. Hoertz, P. Qu and G. J. Meyer, J. Am. Chem. Soc., 2002, 124, 7801.
10. E. Galoppini, Coord. Chem. Rev., 2004, 248, 1283.
11. L. Gundlach, R. Erstorfer and F. Willig, J. Phys. Chem. C, 2007, 111, 13586.
12. P. Persson, M. J. Lundqvist, R. Ernstorfer, W. A. Goddard III and F. Willig, J. Chem. Theory Comput., 2006, 2, 441.
13. S. Thyagarajan, E. Galoppini, P. Persson, J. M. Giaimuccio and G. J. Meyer, Langmuir, 2009, 25, 9219.
14. M. Freitag and E. Galoppini, Energy Environ. Sci., 2011, 4, 2482–2494.
15. C. Pagba, G. Zordan, E. Galoppini, L. Piatnitski Eugene, S. Hore, K. Deshayes and P. Piotrowiak, J. Am. Chem. Soc., 2004, 126, 9888–9889.
16. S. A. Haque, J. S. Park, M. Srinivasarao and J. R. Durrant, Adv. Mater., 2004, 16, 1177–1181.
17. H. Choi, S. O. Kang, J. Ko, G. Gao, H. S. Kang, M.-S. Kang, M. K. Nazeeruddin and M. Grätzel, Angew. Chem., Int. Ed., 2009, 48, 5938–5941.
18. M. Freitag and E. Galoppini, Langmuir, 2010, 26, 8262–8269.
19. P. G. Johansson, Y. Zhang, M. Abrahamsson, G. J. Meyer and E. Galoppini, Chem. Commun., 2011, 47, 6410.
20. Y. Zhang, E. Galoppini, P. G. Johansson and G. J. Meyer, Pure Appl. Chem., 2011, 83, 861–868.
21. J.-P. Sauvage, J.-P. Collin, J.-C. Chambron, S. Guillerez and C. Coudret, Chem. Rev., 1994, 94, 993.
22. H. B. Gray and J. R. Winkler, Annu. Rev. Biochem., 1996, 65, 537.
23. V. Balzani, A. Juris, M. Venturi, S. Campagna and S. Serroni, Chem. Rev., 1996, 96, 759.
24. E. A. Medlycott and G. S. Hanan, Coord. Chem. Rev., 2006, 250, 1763.
25. P. S. Wagenknecht and P. C. Ford, Coord. Chem. Rev., 2006, 255, 591.
26. S. Campagna, F. Puntoriero, F. Nastasi, G. Bergamini and V. Balzani, Top. Curr. Chem., 2007, 280, 117.
27. A. Magnuson, M. Anderlund, O. Johansson, P. Lindblad, R. Lomoth, T. Polivka, S. Ott, K. Stensjö, S. Styring, V. Sundström and L. Hammarström, Acc. Chem. Res., 2009, 42, 1899.
28. A. Vlcek and S. Zalis, Coord. Chem. Rev., 2007, 251, 258.
29. C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816.
30. M. Abrahamsson, M. Jäger, T. Österman, L. Eriksson, P. Persson, O. Johansson, H.-C. Becker and L. Hammarström, J. Am. Chem. Soc., 2006, 128, 12616–12617.
31. M. Abrahamsson, M. Jäger, J. Kumar, T. Österman, P. Persson, H.-C. Becker, O. Johansson and L. Hammarström, J. Am. Chem. Soc., 2008, 130, 15533–15542.
32. T. Österman, M. Abrahamsson, H.-C. Becker, L. Hammarström and P. Persson, J. Phys. Chem. A, 2012, 116, 1041.
33. W. R. Duncan and O. V. Prezhdo, Annu. Rev. Phys. Chem., 2007, 58, 143.
34. P. Persson, R. Bergström and S. Lunell, J. Phys. Chem. B, 2000, 104, 10348.
35. P. Persson and M. J. Lundqvist, J. Phys. Chem. B, 2005, 109, 11918.
36. M. J. Lundqvist, E. Galoppini, G. J. Meyer and P. Persson, J. Phys. Chem. A, 2007, 111, 1487.
37. M. Abrahamsson, M. J. Lundqvist, H. Wolpher, O. Johansson, L. Eriksson, J. Bergquist, T. Rasmussen, H.-C. Becker, L. Hammarström, P.-O. Norrby, B. Åkermark and P. Persson, Inorg. Chem., 2008, 47, 3540–3548.
38. O. A. Borg, S. S. M. C. Godinho, M. J. Lundqvist, S. Lunell and P. Persson, J. Phys. Chem. A, 2008, 112, 4470.
39. S. Fantacci and F. De Angelis, Coord. Chem. Rev., 2011, 255, 2704.
40. S. K. Pal, V. Sundström, E. Galoppini and P. Persson, Dalton Trans., 2009, 10, 021.
41. M. J. Frisch et al., GAUSSIAN 09 (revision A.02), Gaussian, Inc., Wallingford, CT, 2009.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
44. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
45. M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866.
46. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.
47. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270.
48. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
49. T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51.
50. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
51. Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425.

---

Footnote

† Electronic supplementary information (ESI) available: Calculated TD-DFT excitation information for the investigated molecules, as well as method tests for selected complexes, is given. See DOI: 10.1039/c2ra21240d

---