Effect of stress state on the domain configuration and switching behavior in ferroelectric thin films

Abstract

The effect of ferroelastic coupling in ferroelectric thin films under in-plane compressive and tensile stress states was investigated under the framework of the Landau–Ginzburg–Devonshire theory coupled with microscopic examinations and characterization measurements. Piezoresponse force microscopy imaging and synchrotron studies suggested the presence of increased c-domain population in PLZT films (Pb_0.92La_0.08Zr_0.52Ti_0.48O₃) under compressive stress than tensile stress. Stress-induced ferroelectric order (SFO) persisted in PLZT films at temperatures greater than the Curie temperature. The SFO was dependent on the magnitude of the stress, not the stress state, and PLZT films on nickel and silicon substrates exhibited stress-induced remanent polarization values of 8 μC cm⁻² and 4 μC cm⁻², respectively. Pre-stressing thin films using thermal expansion mismatch shows promise as a method to develop high-temperature piezoelectric devices and has advantages over inducing misfit strains.

---

1. Introduction

Lead lanthanum zirconate titanate (PLZT) bulk ceramics are being extensively studied because they exhibit exceptional dielectric, ferroelectric, piezoelectric, pyroelectric, and electro-optic properties that can be used in different applications.^1–3 This material is formed by moderate to heavy doping of lanthanum in lead zirconate titanate (PZT) solid solution. PLZT compositions in both rhombohedral and tetragonal phases exhibit diffuse phase transition (DPT) and frequency dispersion (relaxor behavior) in the temperature dependent dielectric properties.^1–5 Increasing the lanthanum (≥8%) doping in PZT solid solution decreases the tetragonality (c/a ratio) to near unity, approaching a pseudocubic structure resulting in an increasing degree of relaxor behavior.^1–3 Due to the high dielectric permittivity and very large electromechanical and electro-optic coefficients, relaxor thin films have applications in microelectromechanical systems (MEMS), nonvolatile memories, capacitors, sensors, and electro-optic modulators.

Historically, piezoelectric lead-based thin films have been deposited on silicon substrates for various MEMS applications.^6,7 As researchers strive to reduce the cost of such devices, more efforts are being dedicated to fabricating these films on inexpensive metallic substrates. Many techniques have already been used to coat PZT and PLZT films on copper,^8–10 nickel,¹¹ titanium,⁶ and stainless steel.⁶ The fundamental stress–strain–electric field relationship or coupling changes in devices made on metallic substrates compared to conventional silicon substrates due to the ferroelastic nature of PZT/PLZT films and the different stress states present in the films. In metallic and silicon substrates, the piezoelectric films are in biaxial in-plane compressive and tensile stress, respectively, induced by the thermal expansion mismatch of the substrate during cooling from the crystallization temperature. The stress state dictates the domain distribution, domain switching dynamics, and the dielectric, piezoelectric, and ferroelectric properties of the films.^12–14 To enable the choice of substrate and induced stress states that are suitable for various applications, a systematic understanding of the underlying device physics is necessary. In this investigation, we studied the domain distribution and switching dynamics of polycrystalline Pb_0.92La_0.08Zr_0.52Ti_0.48O₃ (PLZT 8/52/48) thin films under opposite stress states within the Landau–Ginzburg–Devonshire (LGD) framework and correlated these findings with the visual evidence from the microscopic localized polarization response and measured average polarization response of the films on silicon and nickel substrates.

2. Results and discussion

The LGD phenomenological theory expresses the elastic Gibbs free energy, ΔG, in terms of polarization (P_i), stress (X_i), electric field (E_i), and temperature (T).^15–18 In the ferroelectric state (T < T_c), the Gibbs free energy profile has a characteristic double minima (double-well shape), defining the equilibrium spontaneous polarization states of the B-site ion. An applied field opposite to the direction of the polarization decreases the minima in the direction of the field and enables the B-site ion to overcome the energy barrier to switch the polarization state. For tetragonal phases, P₁ = P₂ = 0 and P₃ ≠ 0; for two-dimensional stresses induced in thin films deposited on silicon or metallic substrates, X₁ = X₂ ≠ 0 and X₃ = X₄ = X₅ = X₆ = 0.¹⁹ Therefore, the elastic Gibbs free energy reduces to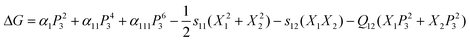 (1)

The calculated ΔG values from eqn (1) for PLZT films on silicon and nickel substrates at room temperature are shown in Fig. 1. Detailed calculations of free energy, stress levels, and material constants are given in the ESI†. Note that an in-plane biaxial compressive stress (which prevails in films on nickel substrates) extends the depth of the well in the free energy profile, increasing the energy barrier for polarization switching, while an in-plane tensile stress (which prevails in films on silicon substrates) induces the opposite effect. Since the unit cell behaves elastically under stress, one can expect the tetragonality of the unit cell to increase with in-plane (lateral) compressive stress while it decreases with in-plane tensile stress. The manifestation of such behavior can also be seen in Fig. 1, where the minima in the free energy profile, which defines spontaneous polarization, appearing at ±0.66 C m⁻² and ±0.48 C m⁻² for films on nickel and silicon, respectively. Therefore, the films under in-plane compression would exhibit a more well defined and prominent out-of-plane ferroelectric character than films under tension.

Fig. 1 Gibbs free energy profiles of PLZT under stress-free (X₁, X₂ = 0), tensile (180 MPa), and compressive (−525 MPa) stress states. Tensile and compressive stress states correspond to films deposited on silicon and nickel substrates, respectively.

Due to the ferroelastic nature of the material, one can expect a completely different domain configuration and switching dynamics in films under different stress states. Therefore, we used vector piezoresponse force microscopy (PFM) to study the local polarization and domain configuration dependence on stress state. Kholkin et al.²⁰ reported that in as-grown PLZT ceramics, the ferroelectric domain structure changes very slightly across the thickness of the sample. Since the AC voltage applied to the probe tip is insufficient to polarize the ferroelectric domains, it is assumed that the ferroelectric domains in PFM images for PLZT/Pt/Si and PLZT/LNO (LaNiO₃)/Ni (Fig. 2) are representative across at least hundreds of nanometers. In PLZT/Pt/Si, the boundaries of ferroelectric domains in Fig. 2(b) are vague, similar to the relaxation behavior of bulk PLZT after polarizing was retracted for several hours.²⁰ Only certain grains exhibit an out-of-plane piezoresponse. In Fig. 2(e) the PLZT/LNO/Ni shows a uniform and stronger out-of-plane piezoresponse (c-domains) compared with the PLZT/Pt/Si. Note that the full color scale in each image is different, and the PLZT/LNO/Ni always exhibits larger piezoresponse than that of the PLZT/Pt/Si. The clean boundaries and uniform contrast of ferroelectric domains in Fig. 2(e) suggest that, in the as-deposited state, almost every grain exhibits out-of-plane polarizations in the PLZT/LNO/Ni. Comparison of Fig. 2(b) and 2(e) shows that the piezoresponse cannot be sustained in PLZT/Pt/Si as easily as in PLZT/LNO/Ni, suggesting that the PLZT on silicon bears more resemblance to relaxor ferroelectric than normal ferroelectric. The lateral PFM shown in Fig. 2(c,f) gives an insight to the potential a-domain distribution along one of the axes of biaxial strain. In the PLZT/Pt/Si, the areas full of y-components of polarization in Fig. 2(c) extend over a couple of grains and seldom overlap with those grains with z-components of polarization in Fig. 2(b). Fig. 2(f) shows that the y-components of polarization in PLZT/LNO/Ni scatter mostly at the grain boundaries. The ratio of lateral-to-vertical piezoresponse is higher in the PLZT/Pt/Si (160 μV/200 μV) than in the PLZT/LNO/Ni (400 μV/600 μV), suggesting that in the as-deposited state more a-domains can be probed in PLZT/Pt/Si. The ratios of areas with z-components over areas with y-components (c-domains/a-domains) in PLZT/Pt/Si are also smaller than in the PLZT/LNO/Ni.

Fig. 2 Piezo force microscopy images of the (a, d) surface topography, as well as (b, e) vertical and (c, f) lateral (along y-direction) piezoresponse of PLZT/Pt/Si (top) and PLZT/LNO/Ni (bottom) sample. The color scale corresponds to the direction of polarization component along z- and y-directions.

X-ray diffraction (XRD) patterns can also confirm the orientation of the films under different stress states. Although regular XRD for bulk ceramics can clearly distinguish 002/200 peaks, corresponding to c- and a-domain populations, it cannot do so for films with nanometer grain sizes.^21–24 Studying peak splits becomes even more difficult and complicated for several reasons. First, PZT and PLZT thin films have much smaller lattice parameters compared to their bulk counterparts.²⁵ Second, higher La content reduces the tetragonality and approaches pseudocubic structure.^25,26 Third, films in this work are polycrystalline and not oriented or textured. Lastly, morphotropic PZT (52/48) compositions are less tetragonal compared to titanium-rich PZT (20/80, 40/60) or PbTiO₃.^1,27,28 For example, clear 002/200 reflections were reported for PZT (53/47) and PLZT (8/53/47) bulk ceramics,²⁹ whereas this reflection was not observed in polycrystalline PZT 53/47 on Pt-Si,³⁰ PZT (52/48) on copper,⁸ or PLZT (8/52/48)³¹ on nickel alloy substrates. Therefore, we used highly brilliant undulator radiation from a synchrotron light source with a slit collimated small incident beam size to study the orientation of the domains in the nano-grain films on silicon and nickel at grazing angles. As shown in Fig. 3, the resulting patterns show no clear distinction in the 002/200 peak for the film on silicon, but the 002 and 200 peaks are clearly visible for films on nickel substrates as observed for PZT (25/75).²¹ It should be noted here that the amount of c-axis texture formed in PLZT on nickel substrates is much lower than reported by Tuttle et al.³² for PZT (20/80) on MgO (100) substrates, although the stress levels are much higher in PLZT films on nickel. This difference is believed to be mainly due to the Ti-rich composition studied and the preferential orientation caused by the MgO substrate. This result also supports our observation of the increase of the presence of c-oriented domains in films made on nickel compared to silicon substrates. The stress across the thickness of the film can be assumed to be uniform, and the domain configuration observed with PFM and XRD should be representative across the thickness of the film because the ratio of the thicknesses of the substrate and film is greater than 400, and the lattice parameters reported previously³³ with regular XRD are similar to those derived from Fig. 3. To correlate the observed microscopic domain configuration and the macroscopic behavior, we measured the dielectric properties of the films.

Fig. 3 Synchrotron XRD of PLZT films on silicon and nickel substrates at 17 keV.

The polarization vs. voltage (P–E) response of PLZT films on Pt/Si and LNO/Ni at 1 kHz is shown in Fig. 4 (left). Although films on both substrates exhibit a well-defined hysteresis loop, the shapes of the polarization curves differ substantially. The films on silicon exhibit coercive field, remanent polarization (P_r), and saturation polarization (P_sat) values of ∼21 kV cm⁻¹, ∼8 μC cm⁻², and ∼40 μC cm⁻², respectively, whereas the corresponding values are ∼39 kV cm⁻¹, ∼30 μC cm⁻², and ∼52 μC cm⁻² for films on nickel. Similar differences were reported by Tuttle et al.³² for PZT (60/40) on sapphire and Pt-Si substrates, although no in situ evidence with electric field was provided. These macroscopic properties are a direct manifestation of the Gibbs free energy profile and the observed domain configuration in these films. The measured coercive field for films under compressive stress is higher than that under tensile stress because the energy barrier for polarization switching, as seen in Fig. 1, is higher for films under compressive stress. Note that the remanent polarization of PLZT on nickel is more than three times that on silicon. As evident from the PFM and XRD results, in-plane biaxial compressive stress provides a mechanical driving force that favors the growth of c-domains, which are aligned parallel to the applied field, resulting in higher remanent polarization in films on nickel. In films on silicon, the in-plane biaxial tensile stress favors the growth of a-domains that are perpendicular to the applied field, lowering the remanent polarization. Since the effect of in-plane compressive stress and applied electric field on the domain act in the same direction in films on nickel, some of the metastable domains that have switched in the direction of the field to a stable state remain in that configuration even after the removal of the electric field (to minimize elastic and electrostatic energy), while in films on silicon the tensile stress would act in a direction opposite to the electric field; and upon removal of the field, the tensile stress would bring some of the domains back to the original configuration. This effect would contribute to the lower P_r in silicon than in nickel. The increase in P_r with increase in the volume fraction of c-domains is consistent with the results of Funakubo et al.³⁴ for PZT. Furthermore, the difference in the measured P_r of films under opposite stress states also has an intrinsic contribution from the difference in the spontaneous polarizations (free energy minima) in the unit cell, as discussed above. Similar differences in the hysteresis curves for the piezoelectric coefficient (d₃₃) vs. voltage plot obtained by PFM are evident in Fig. 4 (right).

Fig. 4 Polarization hysteresis loops (left) and d₃₃ hysteresis loops (right) of PLZT films under tensile (silicon) and compressive (nickel) stress states.

As seen in the PFM images (Fig. 2), in films under in-plane compression and zero applied field, more domains are aligned closer to parallel or parallel to the direction of the applied field. Therefore, when an electric field is applied, domains that are not exactly parallel to the field are readily aligned, resulting in higher saturation polarization. For films under tension, the stress acts in the opposite direction to the applied electric field, thus requiring more energy to align domains in the direction of the field. This condition lowers the saturation polarization. This effect is due to the preferential orientation of the domains perpendicular to the surface of the nickel substrate caused by lateral (in-plane) compressive stress, while the domains are arranged parallel to the surface of the silicon substrate due to the in-plane tensile stress.

To correlate the effect of stress on domain configuration at the microscopic level and the observed macroscopic dielectric behavior, we measured the dielectric constant and polarization at different temperatures. Fig. 5 shows the dielectric constant of PLZT/Pt/Si and PLZT/LNO/Ni films from room temperature to 350 °C. In general, both films exhibit a diffuse phase transition. The dielectric behavior indicates that the ferroelectric–paraelectric phase transition temperature (Curie temperature, T_c) is lower for PLZT/Pt/Si (∼175 °C) than for PLZT/LNO/Ni (∼300 °C). These T_c values are significantly different from the ∼220 °C for bulk PLZT (8/52/48) reported in the literature.^1,35 It is well known that the T_c (determined by relative permittivity maxima) shifts to higher or lower temperatures if the film is placed under a substantial compressive or tensile stress, respectively.^36,37 For example, Rossetti et al.³⁸ reported a 50 °C increase in the Curie temperature for c-axis-oriented PbTiO₃ thin films under a 400 MPa compressive stress. Although the relative permittivity behavior showed a maxima within the temperature range tested for PLZT on LNO/Ni and Pt-Si, the dielectric loss measured was relatively flat for films on both substrates in the temperature range, as reported earlier.³⁹ The dielectric loss was 5–8% and 3–4% for PLZT/LNO/Ni and PLZT/Pt/Si, respectively. The reason for the lack of maxima in the dielectric loss behavior, similar to that reported by Kim et al.²⁶ for PLZT films on copper substrates, is still unclear and remains to be investigated. The insets to Fig. 5 show the P–E loops of the PLZT/Pt/Si and PLZT/LNO/Ni films at various temperatures. Ferroelectric hysteresis behavior can be clearly observed in films under tension and compression at temperatures above their respective Curie temperature, suggesting the existence of stress-induced ferroelectric order irrespective of the stress state. This is comparable to the stress-induced ferroelectric behavior observed in relaxor PLZT (10/65/35) on copper substrates.²⁶

Fig. 5 Dielectric constant as a function of temperature for PLZT films made on silicon and nickel substrates. Inset shows the P–E loops at selected temperatures. The dielectric loss in the temperature range was 5–8% and 3–4% for PLZT/LNO/Ni and PLZT/Pt/Si, respectively In the P–E loop insets, x-axis units are in volts, and y-axis units are in μC cm⁻².

Fig. 6 shows the change in P_r in PLZT/Pt/Si and PLZT/LNO/Ni samples as a function of temperature. In second-order phase transition ferroelectrics, the spontaneous polarization decays as temperature increases and vanishes at the Curie temperature.^40,41 By contrast, as observed in Fig. 6, P_r decreases gradually with temperature and attains residual polarization values of ∼4 μC cm⁻² and ∼8 μC cm⁻² past the Curie temperature in films on silicon and nickel, respectively. We believe that the measured polarization contains intrinsic contributions (spontaneous polarization from ferroelectric material) superimposed on extrinsic contributions (stress-induced polarization). To isolate these two effects, we modeled the decrease in polarization with temperature by using a second-order phase transition equation. We found that the best fit (R > 0.99) was for a T_c of ∼205 °C and ∼210 °C for films on silicon and nickel, respectively. These values agree well with the T_c of ∼220 °C reported in the literature for bulk PLZT 8/52/48.^1,35

Fig. 6 Remanent polarization of PLZT films on silicon (tensile) and nickel (compressive) substrates at different temperatures. Dotted lines show the second-order phase transition fit. The shaded areas represent the residual-stress-induced polarization. Inset illustrates the summation of two different contributions to the observed polarization response.

Much literature exists detailing the non-linear decrease of polarization under increasing stress in PZT-based materials. Zhou et al.⁴² have reported a ∼90% decrease in P_r for poled PZT under a uniaxial compressive stress of ∼150 MPa, and upon further application of stress up to 400 MPa, the P_r decreased <5%. Since the calculated stress levels induced by thermal expansion mismatch are much higher than 150 MPa, it is reasonable to assume that the polarization contribution due to the biaxial stress is constant in the temperature range tested. This assumption is supported by the finding that the measured P_r does not vary much above T_c (250–350 °C) in Fig. 6. The addition of the intrinsic and extrinsic contributions (as illustrated in the inset) would explain the observed temperature-dependent polarization behavior in these two films. Two observations are worth noting here: (1) the existence of residual polarization and its magnitude are independent of the stress state (compressive or tensile); however, the magnitude of P_r is positively correlated to the magnitude of the stress, as also suggested by LGD theory; (2) the rate at which the remanent polarization decreases is dependent on the stress state.

3. Experimental

A 0.5 molar Pb_0.92La_0.08Zr_0.52Ti_0.48O₃ (PLZT 8/52/48) solution was prepared by dissolving appropriate amounts of lead acetate trihydrate, titanium isopropoxide, zirconium propoxide, and lanthanum nitrate hexahydrate in 2-methoxyethanol. We used 20 mol% excess lead in the starting solution to compensate for the lead loss during the high-temperature crystallization. The details of the solution synthesis are reported elsewhere.¹¹ Stock solutions (0.3 M) of LaNiO₃ (LNO) were prepared by dissolving lanthanum nitrate and nickel acetate in 2-methoxyethanol and refluxing for 2 h inside a glove box.

Polished nickel substrates were ultrasonically cleaned in acetone and methanol prior to the deposition. LNO solution was spin coated onto the substrate at 3000 rpm for 30 s, pyrolyzed at 450 °C for 5–10 min, and crystallized at 650 °C for 2–5 min in air. This process was repeated five times to build the desired thickness with a final annealing at 650 °C for 20 min in air. PLZT stock solution was spin coated onto platinized silicon and LNO-buffered nickel substrates at 3000 rpm for 30 s. Films were then pyrolyzed at 450 °C for 10 min and crystallized at 650 °C for 5 min, with a final annealing of 650 °C for 20 min in air after 10 layers. The final thicknesses of the LNO and PLZT films were ∼0.4 μm and ∼1 μm, respectively. Platinum top electrodes (diameter of 250 μm and thickness of 100 nm) were then deposited by electron beam evaporation using a shadow mask.

Dielectric measurements were made as a function of temperature with an Agilent E4980A LCR meter using an oscillator level of 0.1 V, 10 kHz in conjunction with a Signatone QuieTemp® probe station with hot stage (Lucas Signatone Corp., Gilroy, CA). Radiant Technologies Precision Premier II Tester was used to measure the polarization-field hysteresis loops.

Piezoresponse force microscopy (PFM) was used to probe the ferroelectric domain configuration in PLZT. No top electrode was deposited at the areas of interest in order to correlate the surface morphology with the ferroelectric domain structures. The samples were not polarized at the areas of interest. The edge of the scan area was aligned parallel to the edge of the sample, so that the bi-axial strain can be viewed as well as along the edges. A Pt-coated tip (PPP-EFM, Nanosensors) served as the top electrode as well as sensors to monitor volume change due to piezoelectric effects under AC voltage modulation. The AC modulation voltage was 2V_rms (root mean square) at 17 kHz. A lock-in amplifier (SR850, Stanford Research Systems) was used to extract the direction and magnitude of polarization. The vertical PFM detects the components of polarization normal to the surface, and the lateral PFM detects the polarization components perpendicular to the cantilever axis, defined as the y-direction in the text.⁴³ Note that the magnitude of the piezoresponse is uncalibrated and is thus only indicative rather than a real piezoresponse.

The X-ray diffraction (XRD) measurements were performed at beamline 12-ID-D of the Advanced Photon Source in Argonne National Laboratory. The energy of synchrotron X-ray used was 17 keV with a Si (111) monochromator. To obtain a diffraction profile from only the region of PLZT film, an incident angle of 0.5° was used, and the 200 peaks of PLZT films were measured by the θ–2θ scan method with a step size of 0.02°. The measurement time was 50 s for each point to obtain enough diffracted X-ray intensity.

4. Conclusion

To summarize, we studied the domain configuration and switching behavior in polycrystalline ferroelectric thin films under opposite stress states. The combination of PFM imaging and high-energy synchrotron XRD studies suggested the presence of more c-domains in films under biaxial in-plane compressive stress (nickel) compared to tensile stress (silicon). Our results also indicate that the switchable domains/polarization is greater than the non-switchable domains in films under compressive stress and vice versa in films under tensile stress. Stress-induced ferroelectric order in PLZT thin films under compressive as well as tensile stresses was observed at temperatures greater than T_c. We also correlated the unit cell level LGD theory calculations and microscopic domain configuration with the macroscopic electrical measurements to understand the underlying physics in ferroelectric systems under different stress states. This understanding enables the choice of diverse substrates to engineer the induced stress state/magnitude of ferroelectric films and tailor the ferroelectric properties to different applications. For example, pre-stressing films can be used as a method to develop high temperature ferroelectrics, where ferroelectric order can be induced in thin films by controlling the residual stress and stress state via the choice of substrate with different thermal expansion coefficients than the ferroelectric thin film. This method opens the gate to the development of regular low-temperature ferroelectric materials for use in a wide variety of high temperature applications. Thermal expansion strain can be easily induced and is advantageous over misfit strains because it does not require the use of single-crystal substrates, proper growth conditions for orientation, or expensive high vacuum deposition techniques, nor does it pose thickness limitations.^44,45

Acknowledgements

This work was supported by the U. S. Department of Energy, Vehicle Technologies Program, under Contract DE-AC02-06CH11357. The work benefited from the use of PFM supported by Office of Science, Office of Basic Energy Sciences under Contract DE-AC02-06CH11357. Authors thank Dr Hua Zhou at the Advanced Photon Source for help with the XRD measurements. All model calculations, sample preparation, and experiments were planned, conducted, and analyzed by M.N. The PFM experiments and analysis were conducted by M.P. and S. H.; S.T., and S.L. contributed equally to the manuscript.

References

1. G. H. Haertling, J. Am. Ceram. Soc., 1999, 82(4), 797–818.
2. G. H. Haertling and C. E. Land, J. Am. Ceram. Soc., 1971, 54, 1–11.
3. G. H. Haertling, Ferroelectrics, 1987, 75, 25–55.
4. X. Dai, Z. Xu and D. Viehland, Philos. Mag. B, 1994, 70, 33–48.
5. J. F. Li, X. Dai, A. Chow and D. Viehland, J. Mater. Res., 1995, 10, 926–38.
6. G. L. Brennecka, J. F. Ihlefeld, J. P. Maria, B. A. Tuttle and P. G. Clem, J. Am. Ceram. Soc., 2010, 93(12), 3935.
7. G. L. Brennecka, C. M. Parish, B. A. Tuttle, L. N. Brewer and M. A. Rodrigues, Adv. Mater., 2008, 20, 1407.
8. A. I. Kingon and S. Srinivasan, Nat. Mater., 2005, 4, 233.
9. M. D. Losego, L. H. Jimison, J. F. Ihlefeld and J.-P. Maria, Appl. Phys. Lett., 2005, 86, 172906.
10. M. Narayanan, D.-K. Kwon, B. Ma and U. Balachandran, Appl. Phys. Lett., 2008, 92, 252905.
11. B. Ma, M. Narayanan and U. Balachandran, Mater. Lett., 2009, 63, 1353–1356.
12. Q. M. Zhang and J. Zhao, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 1999, 46, 1518–26.
13. R. J. Ong, D. A. Payne and N. R. Sottos, J. Am. Ceram. Soc., 2005, 88, 2839–47.
14. A. Gruverman, B. J. Rodriguez, A. I. Kingon, R. J. Nemanich and A. K. Tagantsev, App. Phys. Lett., 2003, 83, 728–730.
15. A. F. Devonshire, Adv. Phys., 1954, 3(10), 85–130.
16. A. Amin, R. E. Newnham and L. E. Cross, Phys. Rev. B, 1986, 34(3), 1595.
17. M. Budimir, D. Damjanovic and N. Setter, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 174106.
18. D. Damjanovic, J. Am. Ceram. Soc., 2005, 88(10), 2663.
19. M. A. Hassan, I. Kanno and H. Kotera, Vacuum, 2006, 461–467.
20. A. Kholkin, A. Morozovska, D. Kiselev, I. Bdikin and B. Rodriguez, et al. , Adv. Funct. Mater., 2011, 21, 1977–87.
21. R. J. Zednik, A. Varatharajan, M. Oliver, N. Valanoor and P. C. McIntyre, Adv. Funct. Mater., 2011, 21, 3104–3110.
22. V. Anbusathaiah, D. Kan, F. C. Kartawidjaja, R. Mahjoub and M. A. Arredondo, et al. , Adv. Mater., 2009, 21, 3497.
23. Y. K. Kim, H. Morioka, R. Ueno, S. Yokoyama, H. Funakubo, K. Lee and S. Baik, Appl. Phys. Lett., 2006, 88, 252904.
24. C. A. Randall, N. Kim, J. P. Kucera, W. Cao and T. R. Shrout, J. Am. Ceram. Soc., 1998, 81, 677–88.
25. M. Tyunina, J. Levoska, A. Sternberg and S. Leppavuori, J. Appl. Phys., 1998, 84, 6800–10.
26. T. Kim, J. N. Hanson, A. Gruverman and A. I. Kingon, Appl. Phys. Lett., 2006, 88, 262907.
27. Y. Ehara, S. Utsugi, M. Nakajima, T. Yamada, T. Iijima, H. Taniguchi, M. Itoh and H. Funakubo, Appl. Phys. Lett., 2011, 98, 141914.
28. S. Yokoyama, Y. Honda, H. Morioka, S. Okamoto and H. Funakubo, et al. , J. Appl. Phys., 2005, 98, 094106.
29. S. M. Gupta, J. F. Li and D. Viehland, J. Am. Ceram. Soc., 1998, 81, 557–64.
30. Y. L. Tu and S. J. Milne, J. Mater. Res., 1995, 10, 3222–31.
31. B. Ma, M. Narayanan, S. Tong and U. Balachandran, J. Mater. Sci., 2010, 45, 151–157.
32. B. A. Tuttle, J. A. Voigt, T. J. Garino, D. C. Goodnow, R. W. Schwartz and D. L. Lamppa, et al., IEEE 8th International Symposium on Applied Ferroelectrics, Edited by M. Liu, A. Safari, A. Kingon, and G. Haertling, (IEEE, New York), 1992, 344–348.
33. S. Tong, M. Narayanan, B. Ma, R. E. Koritala, S. Liu, U. Balachandran and D. Shi, Acta Mater., 2011, 59, 1309–1316.
34. H. Funakubo, Ferroelectric Thin Films: Basic properties and Device Physics for Memory Applications, ed. M. Okuyama and Y. Ishibashi, 2005, pp 84.
35. K. Wojcik, J. Blaszczak and J. Handerek, Ferroelectrics, 1986, 70, 39–46.
36. J. M. Wesselinowa and Al.B. Dimitrov, Phys. Status Solidi B, 2007, 244, 2242–2253.
37. N. A. Pertsev, A. G. Zembilgotov, S. Hoffmann, R. Waser and A. K. Tagantsev, J. Appl. Phys., 1999, 85, 1698–1701.
38. G. A. Rossetti, L. E. Cross and K. Kushida, Appl. Phys. Lett., 1991, 59, 2524–26.
39. B. Ma, D. K. Kwon, M. Narayanan and U. Balachandran, Mater. Lett., 2008, 62, 3573–75.
40. S. R. Shannigrahi, F. E. H. Tay, K. Yao and R. N. P. Choudhary, J. Eur. Ceram. Soc., 2004, 24, 163–170.
41. H. Zhu and D. P. Chu, J. Phys.: Condens. Matter, 2011, 23, 495901.
42. D. Zhou, M. Kamlah and D. Munz, J. Eur. Ceram. Soc., 2005, 25, 425–432.
43. S. Hong, J. A. Klug, M. Park, A. Imre, M. J. Bedzyk, K. No, A. Perford-Long and O. Auciello, J. Appl. Phys., 2009, 105, 061619.
44. K. J. Choi, M. Biegalski, Y. L. Li, A. Sharan and J. Schubert, et al. , Science, 2004, 306, 1005.
45. J. H. Haeni, P. Irvin, W. Chnag, R. Uecker and P. Reiche, et al. , Nature, 2004, 430, 758.

---

Footnotes

† Electronic Supplementary Information (ESI) available. See DOI: 10.1039/c2ra20678a

‡ Please contact only for queries relating to PFM.

---