Effect of chelate ring and rigidity on Se⋯N interactions: a computational study

Abstract

The intramolecular Se⋯N interactions between the selenium and the nitrogen atom in three series of o-substituted organoselenium compounds has been studied using density functional theory (DFT). The nature and the strength of these interactions and their dependence on substituents, the chelate ring size as well as the rigidity are predicted using a B3LYP/6-31G(d)/LanL2DZ method. The strength of the Se⋯N interactions is found to be dependent on the nature of Se–X (X = Cl, Br, I, SPh, CH₂Ph; Ph: Phenyl) acceptor orbitals and follow the order I > Br > Cl > SPh > CH₂Ph. The natural bond orbital (NBO) analysis using DFT methods points to n_N→σ^*_Se–X electron delocalization as the key contributing factor towards Se⋯N nonbonding interactions. Both NBO and atoms in molecules (AIM) methods suggest that the intramolecular interaction in the organoselenium compounds is dominantly covalent in nature. Studies on the effect of solvent on the Se⋯N interaction show that a polar solvent stabilizes the Se⋯N interactions by shortening the Se⋯N distances.

---

Introduction

The importance of nonbonding interactions has been widely recognized in chemistry, biochemistry, crystallography and material sciences. Nonbonding interactions involving a divalent selenium atom have an important influence on the structures, properties, and reactivities of organoselenium compounds and have received immense attention in recent times.¹ Organochalcogen compounds having intramolecular E⋯Y interactions (where E = Se or Te; Y = O, N, S etc.) play a very important role in the areas of (1) enzyme mimetics;^2–4 (2) asymmetric synthesis/catalysis;^5,6 (3) isolation of monomeric metal chalcogenolates, which are useful precursors for the metal organic chemical vapour deposition (MOCVD) of semiconducting materials,⁷ where these complexes are generally polymeric with bridging chalcogenolate ligands; (4) ‘template-free’ synthesis of novel Schiff base macrocycles containing selenium and tellurium.⁸

The main evidence for such intramolecular nonbonding E⋯Y interactions is the distance between the two heteroatoms determined by X-ray crystallography¹ and ⁷⁷Se/¹²⁵Te NMR.⁹ Computational methods based on electronic structure calculations have also been proved to be very useful in understanding the nature and magnitude of such intramolecular interactions.¹⁰ The detailed studies on such systems suggest that the interaction between a heteroatom Y (Y = N, O, S, halogens etc.) lone pair orbital and a σ*_E–X orbital (E = Se/Te) leads to a weak unsymmetrical hypervalent bond. The collinear geometry between the donor atom (Y) and the E–X σ* acceptor orbital helps in maximizing the orbital interaction between the donor lone pair and the E–X anti bonding orbital and the geometry around the divalent selenium/tellurium is distorted T-shaped. The Y⋯E–X angle ranges from 165 to 180° depending on the strength of the Y⋯E interaction. The stronger the interaction, the more linear the Y⋯E–X angle. The bonding scheme of this interaction is described as three-centre four-electron [3c–4e] bonding. A pair of electrons occupies the nonbonding orbital and another pair of electrons occupies the bonding orbital of the molecular orbital. As a result, the E–X bonds get elongated and Y⋯E length shortens. Thus, one of the reasons of the origin of the Y⋯E interaction is due to the hypervalent nature of E. Although the hypervalency in divalent chalcogens increases in the order O < S < Se < Te, the basic factors responsible for the origin and the strength of such interactions are not completely understood.

In view of this, we will present results for intramolecular Se⋯N nonbonding interactions in a series of ortho substituted arylchalcogenides as studied using DFT, NBO and the quantum theory of AIM analysis. The effect of factors like substituent, chelate ring and rigidity on these interactions will also be discussed.

Computational methods

Gaussian09¹¹ was used as the source program for geometry optimization, for NBO¹² calculations, for NBO deletion analysis and for wavefunction calculation for AIM¹³ analysis. All the geometries were fully optimized using the hybrid B3LYP exchange correlation functional¹⁴ with a 6-31G(d) basis set, except for iodine, where we used the LanL2DZ basis set. Frequency calculations were performed for all the compounds to check (no imaginary frequencies) the stationary points as minima on the potential energy surface. Solvent effects were studied using the polarized continuum model (PCM).¹⁵ The topological analysis of electron density with Badar's theory of AIM was analyzed using AIM2000¹⁶ software. Since bond path cannot be traced to the nuclei of atoms described by effective core potential,^13d for calculation of wavefunctions for all iodine compounds, we ran single point calculations at the optimized geometries (at B3LYP/LanL2DZ level) using a B3LYP/6-311G* method.

System studied

We studied the Se⋯N nonbonding interactions in the three series of organoselenium compounds containing an sp² hybridized nitrogen in the oxazoline and oxazine groups as the donor and the Se–X bond as the acceptor [X = Cl, Br, I, SPh and CH₂Ph; Ph: Phenyl] (Fig. 1). In the first series (1a–e), the donor N atom is part of a six membered oxazine ring, while in the second (2a–e) and the third (3a–e) series it is part of a five membered oxazoline ring. In the third series, we have a rigid aromatic ring compared to the rest. Our aim is to study (a) the effect of different substituents, X, for a given series, (b) the effect of rigidity (series 2 and 3) and chelate ring (series 1 and 2) on Se⋯N nonbonding interactions in the gas phase as well as in the presence of solvent (CHCl₃).

Fig. 1 The organoselenium compounds 1a–e, 2a–e and 3a–e investigated in this study.

Results and discussion

In this work, we have employed the B3LYP/6-31G(d)/LanL2DZ level of theory to study the Se⋯N nonbonding interactions. This level of DFT has been successfully employed in a number of previous theoretical studies of organoselenium compounds.^10d–f To check the accuracy of our results, we compare (in Table 1) the molecular structures of selected compounds with those determined by X-ray crystallography. All the angles considered are well reproduced (maximum deviation is 3.5°). For the cases of bond lengths, most of them are well reproduced (deviation below 0.08 Å). Relatively larger deviations for the bond lengths are obtained for 2c, 3c and 3e, which may be due to intermolecular interactions in the solid state.^10g Overall, the important atomic distances and angles of all the compounds in the solid state are reasonably reproduced by our calculations and are in agreement with earlier DFT work.^10d Selected structural parameters of the optimized geometries of the compounds are summarized in Table 2. From the dihedral angles for the Se–X and C–N bonds, with respect to the aromatic ring (ω_{X–Se–C–C(c)} and ω_{N–C–C–C(Se)}, respectively), it is clear that compounds 1a–e, 2a–e and 3a–c possessed planar structures (between 175°–180° and 0°–6°), while non-planar structures were obtained for 3d (165° and 26°) and 3e (134° and 70°). The N⋯Se–X angle (Table 2) is almost linear (174°–178°) for all the compounds studied except 3e (152°). In addition, the relatively shorter atomic distances between Se and N atoms (r_Se⋯N) compared to sum of their van der Waals radii [r_vdw(Se) +r_vdw(N) = 1.90 + 1.55 = 3.45 Å]¹⁷ indicates the presence of a hypervalent Se⋯N interaction for all the studied compounds.

Table 1 Comparison of structural parameters of selected compounds to those determined by X-ray crystallographic analysis

Compounds	r Se–C (Å)	r Se⋯N (Å)	r Se–X (Å)	θ N⋯Se–X (°)	θ C–Se–X (°)	Remark
1c	1.965	2.204	2.907	178.2	99.1	This work
	(1.896)	(1.971)	(2.983)	(179.7)	(97.2)	(Ref. 20)
	0.069	0.033	−0.076	−1.5	1.9	Difference
1d	1.946	2.476	2.277	177.2	100.7	This work
	(1.937)	(2.458)	(2.25)	(176.4)	(100.4)	(Ref. 20)
	0.009	0.018	0.027	0.8	0.3	Difference
1e	1.924	2.653	2.014	176.4	99.7	This work
	(1.909)	(2.686)	(1.975)	(174)	(100.2)	(Ref. 20)
	0.015	−0.033	0.039	2.4	−0.5	Difference
2c	1.977	2.259	2.881	178.3	99.4	This work
	(1.945)	(2.133)	(2.777)	(177.7)	(97.4)	(Ref. 21)
	0.032	0.126	0.104	0.6	3.0	Difference
2e	1.923	2.756	2.005	175.3	99.9	This work
	(1.916)	(2.798)	(1.966)	(175.4)	(100.2)	(Ref. 21)
	0.007	−0.042	−0.039	−0.1	0.3	Difference
3c	1.983	2.2	2.908	178.2	99.5	This work
	(—)	(2.059)	(2.83)	(175.3)	(97.5)	(Ref. 19)
	—	0.141	0.078	2.9	2.0	Difference
3e	1.926	3.26	1.987	151.9	99.8	This work
	(1.916)	(3.384)	(1.979)	(—)	(98)	(Ref. 19)
	0.01	0.124	0.008	—	1.8	Difference

---

Table 2 Selected structural parameters of the compounds calculated using the B3LYP/6-31G(d)/LanL2DZ method

Compounds	r Se–X (Å)	r Se⋯N (Å)	θ N⋯Se–X (°)	ω X–Se–C–C(C) (°)	ω N–C–C–C(Se) (°)
1a	2.362	2.204	176.4	178.7	1
1b	2.487	2.229	177.3	178.7	1.1
1c	2.907	2.204	178.2	179	0.5
1d	2.277	2.476	177.2	178.4	3.5
1e	2.014	2.653	174	174.5	5.5
2a	2.339	2.259	176.2	−179.4	−0.8
2b	2.462	2.294	177.2	−179.4	−0.8
2c	2.881	2.259	178.3	−180	0
2d	2.25	2.608	177.5	−179.8	1.9
2e	2.005	2.756	175.3	−178.3	−1.3
3a	2.358	2.211	175.9	178.5	2.1
3b	2.481	2.236	176.9	178.6	2.6
3c	2.908	2.2	178.2	179.9	−0.1
3d	2.254	2.585	174.7	165.3	26.2
3e	1.987	3.26	151.9	133.6	70.1

---

It has been suggested that the Se⋯Y (Y = O, N, F) interactions consist of an electrostatic and a covalent contribution.^10d,f Thus, to estimate (approximately) the extent of electrostatic contributions to Se⋯N interactions, we calculated the electrostatic interaction energy between Se and N atoms from their charges obtained by natural population analysis (NPA). In this calculation, we assumed a point charge model so that the charge is located at the respective nuclei.^10d The calculated electrostatic contribution to the Se⋯N interaction (E_el) and the NPA charges on Se and N atoms (q_Se and q_N, respectively) are given in Table 3.The values of E_el follow the order SPh < CH₂Ph < Br < I < Cl for series 1 and 2 and CH₂Ph < SPh < Br < I < Cl for 3. For a given X, the order is 2 < 3 < 1 (for X = Cl, Br, I) and for X = SPh, CH₂Ph the trend is 3 < 2 < 1. This trend is nearly according to the electronegativity of X attached to the Se atom. The NPA charge on the Se atom also increases with the E_el. We observe quite good correlation (R = 0.904) of E_el with q_Se (Fig. 2). However, q_N does not correlate so well with E_el. These observations are very similar to those of other intramolecular chalcogen interactions.^10d,e

Table 3 Summary of NPA, NBO and NBO deletion analysis for the compounds under study using the B3LYP/6-31G(d)/LanL2DZ method

Compounds	q N (e)	q Se (e)	E el (kcal mol^−1)	E Se…N (kcal mol^−1)	E del (kcal mol^−1)	△q(σ*) (e)	△q(N) (e)	Covalency factor (χ)
1a	−0.557	0.555	46.58	63.63	77.26	−0.199	0.203	0.814
1b	−0.552	0.486	39.97	59.08	73.73	−0.189	0.194	0.798
1c	−0.596	0.457	41.04	72.95	97.57	−0.177	0.224	0.814
1d	−0.545	0.358	26.17	22.85	27.92	−0.105	0.1	0.637
1e	−0.536	0.449	30.13	11.58	13.32	−0.051	0.05	0.521
2a	−0.555	0.544	44.39	50.96	64.62	−0.185	0.189	0.778
2b	−0.552	0.472	37.72	45.28	59.22	−0.173	0.177	0.756
2c	−0.603	0.437	38.74	58.97	82.74	−0.18	0.214	0.778
2d	−0.541	0.352	24.25	13.44	17.05	−0.074	0.072	0.55
2e	−0.53	0.452	28.87	7.5	9.12	−0.036	0.037	0.454
3a	−0.555	0.534	44.52	59.41	74.28	−0.194	0.202	0.81
3b	−0.551	0.465	38.05	54.83	70.67	−0.183	0.192	0.793
3c	−0.608	0.444	40.75	71.42	98.04	−0.177	0.227	0.817
3d	−0.539	0.327	22.64	11.89	14.75	−0.064	0.064	0.565
3e	−0.511	0.358	18.64	—	—	—	—	0.124

---

Fig. 2 Plot of the magnitude of the ionic contribution, E_el (calculated by considering point charges for Se and N atoms), with the charge on the selenium atom, (q_Se).

To estimate the covalent contribution to the Se⋯N interactions, we used NBO second order perturbation and NBO deletion analysis. The NBO method, based on local block eigenvectors of a one-particle density matrix, predicts bonds and lone pairs of an optimized Lewis structure of a molecule from ab initio wavefunctions.¹² Delocalization of electron density between occupied (bond or lone pair) NBOs and formally unoccupied (antibonding or Rydberg) NBOs corresponds to a stabilizing interaction. In the NBO deletion technique, a selected set of NBOs from a donor–acceptor pair is deleted and the energy change (loss of delocalization energy) associated with this process provides information on the interaction between the respective orbitals.

We studied the orbital interactions between the lone pairs of the nitrogen atom (n_N) and the antibonding orbital of the Se–X bond (σ*_Se⋯X). Our NBO study indicated the absence of n_N→σ*_Se⋯X orbital interaction for the compound 3e. The NBO second order perturbation energies for n_N→σ*_Se⋯X orbital interactions (E_Se⋯N) are presented in Table 3. The values of E_Se⋯N range from 11.58 to 72.95 kcal mol⁻¹ for 1a–e, 7.5 to 58.97 kcal mol⁻¹ for 2a–e and 11.89 to 71.42 kcal mol⁻¹ for 3a–d. Also, these interaction energies increase in the order CH₂Ph < SPh < Br < Cl < I for all series and for a given X, the order is 2 < 3 < 1 (except for X = SPh where it is 3 < 2 < 1). This trend is more or less according to the electrophilicity of the Se–X bond and the nucleophilicity of the N atom for the Se⋯N interactions. The NBO deletion energies (E_del), which provide information on the orbital interaction energies associated with the Se atom and the chelating N atom, follow the same trend as those of the E_Se⋯N. These factors clearly suggest that the n_N→σ*_Se⋯X orbital interactions contribute significantly to the stability of Se⋯N interactions in these compounds.

It is known that a strong Se⋯N interatomic distance causes shortening of the Se⋯N interatomic distance and an increase in the linearity of the N⋯Se–X alignment.¹⁸ This indeed is observed from the present calculations. However, the X-ray study of selenenyl halides shows that the bond angles N⋯Se–X (X = Cl, Br or I) deviate from 180° as the Se⋯N interaction increases (e.g.1b: Se⋯N = 2.052 Å and N⋯Se–Br = 175.15°; 1c: Se⋯N = 2.059 Å, N⋯Se–I = 175.26°).^19–21 This is probably due to the presence of intermolecular interactions between Se and X (X = Cl, Br or I). The intermolecular interaction increases when the electronegativity of the halogen atom decreases and hence is greatest for X = I. The weakest Se⋯N interaction is observed in all the aryl benzyl selenides compared to the selenenyl halides and selenenyl sulphides, maybe due to the presence of the benzyl group, which cannot accept electron density from the selenium. This is in agreement with the experimental observations (Se⋯N; 1e: 3.3842 Å; 3e: 2.798 Å).^19,21

The value of E_Se⋯N depends on at least two factors: (a) the distance between the Se and N atom (r_Se⋯N) and (b) the donor ability of the N atom. To find out the contribution of each of these factors, we reoptimized the geometries of the compounds at the fixed Se⋯N distances and then calculated the E_Se⋯N of all the compounds (see Table 4). It is clear from Table 4 that the values of E_Se⋯N are highly dependent on r_Se⋯N and almost comparable E_Se⋯N values were obtained for a fixed Se⋯N distance for series 1, 2 and 3 (for a given X). The relatively higher E_Se⋯N values of compound 1, compared to those of 3 and 2, may be due to the difference in the size of chelate rings containing a donor nitrogen atom.

Table 4 Comparison of the NBO second-order perturbation energies among series 1, 2 and 3 for a given X at a fixed Se⋯N distance

X	r Se⋯N (Å)	E Se⋯N (kcal mol^−1)
		1	2	3
Cl	2.211	62.4	59.04	59.41
Br	2.236	57.93	54.43	54.83
I	2.2	73.7	70.35	71.42
SPh	2.585	16.43	14.48	11.89
CH2Ph	3.26	0.81	0.85	—

---

The values for E_Se⋯N (and E_del) decrease with an increase in Se⋯N distance (r_Se⋯N) for all the compounds. The single correlation curve between E_Se⋯Nversus r_Se⋯N (Fig. 3) and E_delversus r_Se⋯N (Fig. 4) clearly show that the nature of the interactions in all the studied compounds are the same. The changes in orbital occupancies of the lone pair of nitrogen (n_N) and σ*_Se⋯X orbitals (△q = q_del−q) during NBO deletion analysis are displayed in Table 3. The significant decrease of charge of the σ*_Se⋯X orbitals and a similar increase of charge for the n_N orbitals upon NBO deletion suggest that the nature of orbital interaction is electron delocalization from the lone pair of the N atom to the anti-bonding orbital of Se–X (i.e. n_N→σ*_Se⋯X). This dominant contribution of n_N→σ*_Se⋯X charge transfer in the intramolecular Se⋯N bonding is supported by relatively high values (up to 81%) of covalency factor χ for the intramolecular coordination Se⋯N bond (Table 3). The values of χ follow the same trend as E_Se⋯N and E_del (CH₂Ph < SPh < Br < Cl < I for all series and for a given X, the order is 2 < 3 < 1) and show a single correlation curve (Fig. 5) for all the compounds.

Fig. 3 Variation of NBO second order perturbation energies (E_Se⋯N) with the Se⋯N distances (r_Se⋯N).

Fig. 4 Variation of NBO deletion energies (E_del) with the Se⋯N distances (r_Se⋯N).

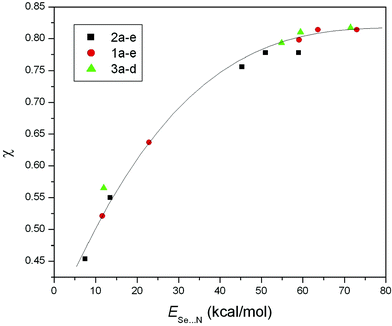Fig. 5 Plot of covalency factor (χ) with the NBO second order perturbation energies (E_Se⋯N).

The strength of the Se⋯N interactions has been observed in the order CH₂Ph < SPh < Br < Cl ≈ I. The ionic contribution (E_el) decreases in the order Cl > I > Br > SPh > CH₂Ph and the covalent contribution (E_Se⋯N) decreases in the order I > Cl > Br > SPh > CH₂Ph (Table 3). However, the total strength (ionic + covalent) decreases in the order I ≈ Cl > Br > SPh > CH₂Ph. The observed trend for halides may be due to the negligence of intermolecular interaction during our theoretical calculations. These interactions, which are often present in the organoselenenyl halides in the solid state, have a significant affect on the Se⋯N interactions. However, the Se⋯N bond distances of organoselenenyl halides 1a [1.9695 Å(av.)],²⁰1b (1.975 Å)²⁰ and 1c (1.971 Å)²⁰ from the X-ray studies follow the trend Br > Cl ∼ I. These halides either have very weak or no intermolecular interactions. Also for organoselenenyl halides 3b (2.052 Å)¹⁹ and 3c (2.059 Å)¹⁹ (absence of intermolecular interactions due to the presence of a sterically more demanding group), Se⋯N bond distances are very close. Furthermore, for organoselenenyl halides of 2 (where the intermolecular interaction is greatest among the three series studied here), the trend of Se⋯N distances is Cl (2a, 2.052 Å) < Br (2b, 2.063 Å) < I (2c, 2.133 Å).

In summary, introduction of rigidity (for 3) onto the backbone of 2, or replacing the five membered oxazoline ring in 2 by a six membered oxazine ring in 1, enhances the strength of Se⋯N nonbonding interactions; the latter effect seems to be more dominant. This is in accordance with the experimental findings. For example, the Se–N distances in 1a, 1b and 1c are 1.9695 (average), 1.975 (average) and 1.971 Å, respectively, whereas for 2a, 2b and 2c they are 2.052(2), 2.063(3) and 2.133 Å, respectively. Similar trends have also been observed for similar organotellurium compounds.²²

Atoms in molecules (AIM) analysis

As an alternative method to study the nonbonding Se⋯N interaction, we used Bader's theory of AIM,¹³ which involves topological analysis of electron density between two interacting atoms. According to this theory, atoms that are chemically bonded have their nuclei linked by a (single) bond path (a single line of locally maximum electron density) and they share a bond critical point (a point on the bond path with the lowest value of the electron density). The presence of a (3, −1) bond critical point (BCP) along the bond path (BP) is a universal indicator of chemical bonding. Chemical bonding interactions are characterized and classified according to the properties of the electron densities (ρ_b), Laplacian of electron density (∇²ρ_b) and the total energy densities (H_b) at the BCP. In general, ρ_b is greater than 0.20 au in a shared (covalent) bond and less than 0.10 au in a closed-shell interaction (ionic, van der Waals, hydrogen bonding, etc.). The Laplacian of electron density also provides valuable information. A positive value of ∇²ρ_b indicates a closed-shell bonding while a negative value indicates covalent bonding. In strongly polar bonding (e.g. C–X, where X = O, N, F) there is a significant accumulation of electron density between the nuclei, as in all shared interactions, but the Laplacian in this type of bonding can be of either sign.^13c The total electronic energy density at the BCP (H_b) is negative for interactions with significant sharing of electrons, its magnitude reflecting the ‘‘covalence’’ of the interaction.

The presence of BCP between Se and N atoms and the ring critical point (RCP) for the five membered ring formed with the phenyl ring due to Se⋯N interaction was observed for all the studied compounds, except 3e. The electron density at RCP (ρ_rcp), along with the other AIM parameters (ρ_Se⋯N, ∇²ρ_Se⋯N and H_Se⋯N) for the Se⋯N interaction, are given in Table 5. The values of ρ_Se⋯N for the studied compounds range from 0.0237 to 0.0736 e Å⁻³, which are in between a typical covalent bond (e.g. ρ_C–C ≈ 0.24 e Å⁻³) and that of hydrogen bond (ρ_H–Bond ≈ 0.002–0.04 e Å⁻³). Similar values were reported for Se⋯N interactions by Sharma et al.^10d The values of ρ_Se⋯N follow the trend CH₂Ph < SPh < Br < Cl < I for all series, and 2 < 3 < 1 for a given X. This trend is similar to that for E_Se⋯N and E_del. This is not surprising because a covalent interaction in AIM theory is related to orbital interactions in NBO analysis. The values of E_Se⋯N and E_del correlate nicely with ρ_Se⋯N (Fig. 6 and 7, respectively), indicating a dominant covalent contribution in the Se⋯N interactions. The values of ρ_rcp lie in the range 0.014 to 0.0248 e Å⁻³ and increase in the order CH₂Ph < SPh < I < Br < Cl for all three series, and for a given X: 2 < 3 < 1. The values of ∇²ρ_Se⋯N obtained (Table 5) are all positive (range: 0.07 to 0.138 e Å⁻⁵) and follow the overall trend CH₂Ph < SPh < I < Br < Cl for series 2, 3 and CH₂Ph < SPh < Br < Cl ≈ I for series 1; and for a given X: 1 < 2 < 3. All positive values indicate a dominant electrostatic character, which is in contrast to “dominant covalent contribution” as predicted by NBO analysis. Thus, we analyze the total energy density at the critical point (H_Se⋯N), which is known to be more reliable in identifying the type of interactions (electrostatic or covalent).^23,10d The calculated values of H_Se⋯N (Table 5) are mostly negative (except 1d, 1e, 2d and 2e) indicating dominant covalent interaction, as predicted by NBO analysis. The values of H_Se⋯N become more negative for stronger Se⋯N interactions (shorter r_Se⋯N) and are positive with weaker Se⋯N interactions. This correlation is quite evident from Fig. 8.

Table 5 The AIM analysis data of the electron density (ρ_Se⋯N), its Laplacian (∇²ρ_Se⋯N) and the total energy density (H_Se⋯N) at the bond critical point along with the electron density at the ring critical point (ρ_rcp) due to Se⋯N interactions

Compounds	ρ Se⋯N (e Å^−3)	ρ rcp (e Å^−3)	∇^2ρSe⋯N (e Å^−5)	H Se⋯N (e Å^−4)
1a	0.0736	0.0248	0.123	−0.0076
1b	0.0706	0.0242	0.115	−0.0059
1c	0.0752	0.0237	0.124	−0.0121
1d	0.043	0.0193	0.076	0.0006
1e	0.0302	0.0163	0.07	0.0012
2a	0.0641	0.023	0.133	−0.0112
2b	0.0602	0.022	0.127	−0.0092
2c	0.0659	0.0223	0.127	−0.0179
2d	0.0319	0.016	0.087	0.0002
2e	0.0237	0.0139	0.085	0.0004
3a	0.0706	0.0242	0.141	−0.015
3b	0.0677	0.0236	0.137	−0.0132
3c	0.0738	0.0234	0.132	−0.0171
3d	0.0338	0.0178	0.089	−0.0001

---

Fig. 6 Correlation plot of the NBO second order perturbation energies (E_Se⋯N) with the electron density (ρ_Se⋯N) at the bond critical point of the Se⋯N interaction. ρ_Se⋯N is in units of e Å⁻³.

Fig. 7 Correlation plot of the NBO deletion energies (E_del) with the electron density (ρ_Se⋯N) at the bond critical point of the Se⋯N interaction. ρ_Se⋯N is in units of e Å⁻³.

Fig. 8 Variation of AIM total energy density (H_Se⋯N) at the bond critical point with the Se⋯N distances (r_Se⋯N). H_Se⋯N are given in units of e Å⁻⁴.

The AIM dual-parameter analysis (plot of H_Se⋯Nversus ∇²ρ_Se⋯N) for weak to strong interaction is shown in Fig. 9. Most of the points fall in the fourth quadrant (H_Se⋯N < 0, ∇²ρ_Se⋯N > 0; more shared-shell character) indicating strong Se⋯N interaction. A few points lie on first quadrant (H_Se⋯N > 0, ∇²ρ_Se⋯N > 0), indicating that the electron density at BCP is neither stabilized nor concentrated, i.e. weak Se⋯N interactions.

Fig. 9 Variation of AIM total energy density (H_Se⋯N in units of e Å⁻⁴) with the Laplacian of the electron density (in units of e Å⁻⁵) at the bond critical point.

Detailed inspection of the AIM analysis reveals some interesting facts. Several intramolecular interactions have been observed for all the systems discussed in the present study (Fig. 1) from the AIM analysis through BCP and RCP.²⁴ These interactions have not been reported for the solid state structures of these compounds^19–21 and are discussed below.

(A) The common features that have been observed for all cases i.e. for 1–3 (except 3e) are; (1) the presence of Se⋯N interactions and (2) the presence of interaction between the substituents X and the aryl hydrogen ortho to the Se–X group. Similar observations have been made by Sunoj et al. earlier.^10e A representative diagram of 1a showing both Se⋯N and Se⋯H interactions is given in Fig. 10.²⁴

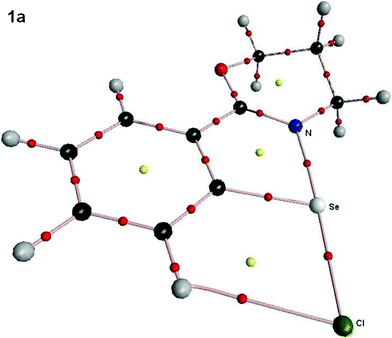Fig. 10 Molecular plot of 1a (X = Cl) showing Se⋯N and Se⋯H bond critical points (small red spheres) and the corresponding ring critical points (yellow spheres) arising due to intramolecular interactions.

(B) Besides these above interactions, the existence of an additional interaction between the Se atom and the aryl hydrogen ortho to the S atom from the SPh group could be identified through Se⋯H BCPs and the corresponding RCPs for compounds 1d, 2d and 3d. One of the representative cases is shown in Fig. 11.

Fig. 11 Molecular plot of 2d (X = SPh) showing the Se⋯N, S⋯H and Se⋯H bond critical points (small red spheres) and the corresponding ring critical points (yellow spheres) arising due to intramolecular interactions.

(C) Furthermore, another interaction in addition to (A) between oxygen and aryl hydrogen ortho to the oxazoline ring is predicted for the compound 1e.²⁴

(D) Interestingly, along with the interactions described in (A), interactions between the oxygen and carbon atom (of the phenyl ring attached to the naphthyl ring) have been observed for the sterically hindered compounds 3a–d.²⁴

(E) More interestingly, although compound 3e (Fig. 12) does not have a Se⋯N interaction, existence of several other intramolecular interactions have been predicted by our AIM studies. (1) The interaction between the hydrogen atom of the methyl group of the oxazoline ring and the hydrogen atom of the methyl group of the phenyl ring perpendicular to the naphthyl ring results in the formation of a 12 membered chelate ring. (2) The hydrogen atom of the other methyl group of the oxazoline ring interacts with the selenium atom forming a eight membered chelate ring. (3) A 6-membered chelate ring arises from the interaction of the aryl hydrogen ortho to the –CH₂– group and the oxygen atom of the oxazoline ring. (4) Additionally, another 5-membered chelate ring results from the interaction of the same aryl hydrogen ortho to the –CH₂– group and the selenium atom.

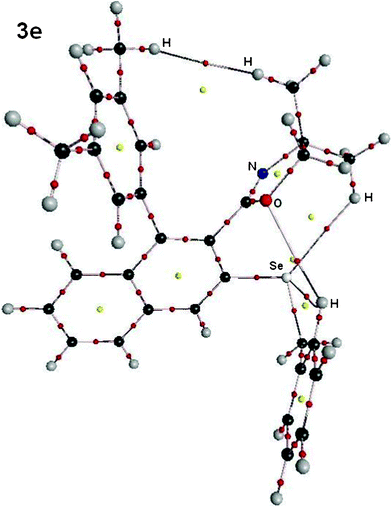Fig. 12 Molecular plot of 3e (X = CH₂Ph) showing the H⋯H, O⋯H, Se⋯H bond critical point (small red spheres) and the corresponding ring critical points (yellow spheres) arising due to intramolecular interactions.

To sum up, the AIM analysis reveals that the electron density at the Se⋯N BCP shows a very good correlation with the computed intramolecular interaction energies (from NBO analysis) and hence suggests a dominant covalent nature of the intamolecular interactions. Also, several types of intramolecular interactions other than Se…N are predicted.

Solvent effect

In order to study the effect of a polar solvent on Se…N interactions, we use the Tomasi's PCM at the B3LYP/6-31G(d)/LanL2DZ level in CHCl₃ solvent. The values reported in Table 6 show that the Se…N distances are much shorter and the values of E_Se…N are larger than those of the gas phase values. This indicates that the Se⋯N interactions in polar solvent become stronger than those of the gas phase. This is in contrast to the usual belief that a compound having an intramolecular Se⋯N interaction (having less exposed polar surface in solution) would destabilize the structure by weakening the Se⋯N interaction. A similar observation was also obtained recently by Sharma et al.^10d

Table 6 A comparison of Se⋯N distances and the NBO energies of the compounds studied in the gas phase and in CHCl₃

Compounds	r Se⋯N (Å)	r Se⋯N (CHCl3) (Å)	E Se⋯N (kcal mol^−1)	E Se⋯N (CHCl3) (kcal mol^−1)
1a	2.204	2.092	63.63	93.36
1b	2.229	2.13	59.08	82.02
1c	2.204	2.088	72.95	105.48
1d	2.476	2.409	22.85	28.31
1e	2.653	2.665	11.58	11.16
2a	2.259	2.123	50.96	81.62
2b	2.294	2.171	45.28	68.85
2c	2.259	2.103	58.97	97.63
2d	2.608	2.574	13.44	15.06
2e	2.756	2.776	7.5	7.05
3a	2.211	2.092	59.41	90.52
3b	2.236	2.132	54.83	78.25
3c	2.2	2.074	71.42	108.15
3d	2.585	2.536	11.89	14.32
3e	3.26	3.151	—	0.68

---

Conclusions

A comparison of the Se⋯N interaction in the organoselenium compounds derived from 2-phenyl-5,6-dihydro-4H-1,3-oxazine and 4,4-dimethyl-2-phenyl-oxazoline and 2-[1-(3,5-dimethylphenyl)-2-naphthyl]-4,5-dihydro-4,4-dimethyl-1,3-oxazole have been made to study the effect of rigidity and ring size on Se⋯N interaction. In line with earlier studies, the origin of Se⋯N interaction was identified to be due to orbital interaction involving the delocalization of nitrogen lone pair electrons into the suitably aligned Se–X antibonding orbital (n_N→σ^*_Se–X) and both electrostatic and covalent contributions are important for this interaction. Computed interaction energies (NBO second order perturbation and NBO deletion energies) revealed that the extent of interaction depends strongly on the nature of substituent attached to selenium (i.e. on the nature of the Se–X acceptor orbital) and roughly follows the order CH₂Ph < SPh < Br < Cl < I. For a given X, the strength of Se⋯N interaction follows the order 2 < 3 < 1. Thus, introduction of a naphthyl ring in place of phenyl (3versus2) as well as introduction of an oxazine ring in place of an oxazoline ring (1versus2) favors (strengthens) the Se⋯N interaction. However, the latter (ring size) effect is stronger than the former (steric effect) one. The strength of this interaction is highly dependent on the distance between the Se and N atoms (almost similar values of interaction energies are obtained for same Se⋯N distances), which is the outcome of the specific structure of a compound. The quantified interactions were found to correlate well with the structural parameters as well as topological properties of electron density at the Se⋯N BCP obtained using AIM analysis. The AIM analysis suggests that the nature of Se⋯N interaction is predominantly covalent. Larger Se⋯N interaction energies and shorter Se⋯N distances in polar solvent (CHCl₃) compared to those of gas phase values indicate that the Se⋯N interaction is favorable in polar solvent.

Acknowledgements

AP thanks DST, New Delhi for financial support under the WOS-A scheme (SR/WOS-A/CS-23/2010). The support from BITS, Pilani-K. K. Birla Goa Campus is gratefully acknowledged. We thank Dr A. Chattopadhyay for providing part of the computing resources.

References

1. A. J. Mukherjee, S. S. Zade, H. B. Singh and R. B. Sunoj, Chem. Rev., 2011, 110, 4357–4416 and references therein.
2. (a) T. G. Chasteen and R. Bentley, Chem. Rev., 2003, 103, 1; (b) G. Mugesh, W. W. du Mont and H. Sies, Chem. Rev., 2001, 101, 2125.
3. (a) G. Mugesh and H. B. Singh, Chem. Soc. Rev., 2000, 29, 347; (b) G. Mugesh, A. Panda, N. S. Punekar, H. B. Singh and R. J. Butcher, Chem. Commun., 1998, 2227; (c) G. Mugesh, A. Panda, N. S. Punekar, H. B. Singh and R. J. Butcher, J. Am. Chem. Soc., 2001, 123, 839; (d) M. Iwaoka and S. Tomoda, J. Chem. Soc., Chem. Commun., 1992, 1165–1167; (e) M. Iwaoka and S. Tomoda, J. Am. Chem. Soc., 1994, 116, 2557–2561; (f) T. Wirth, S. Häuptli and M. Leuenberger, Tetrahedron: Asymmetry, 1998, 9, 547–550; (g) T. G. Back and Z. Moussa, J. Am. Chem. Soc., 2002, 124, 12104–12105; (h) C. A. Bayse, R. A. Baker and K. N. Ortwine, Inorg. Chim. Acta, 2005, 358, 3849–3854; (i) B. K. Sarma and G. Mugesh, Inorg. Chem., 2006, 45, 5307–5314; (j) K. P. Bhabak and G. Mugesh, Chem.–Eur. J., 2007, 13, 4594–4601; (k) B. K. Sarma and G. Mugesh, Org. Biomol. Chem., 2008, 6, 965–974; (l) B. K. Sarma and G. Mugesh, Chem.–Eur. J., 2008, 14, 10603–10614; (m) G. Mugesh and W.-W. du Mont, Chem.–Eur. J., 2001, 7, 1365; (n) L. Engman, D. Stern, I. A. Cotgreave and C. M. Andersson, J. Am. Chem. Soc., 1992, 114, 9737; (o) Y. You, K. Ahsan and M. R. Detty, J. Am. Chem. Soc., 2003, 125, 4918; (p) L. Engman, D. Stern, M. Pelcman and C. M. Andersson, J. Org. Chem., 1994, 59, 1973; (q) K. Vessman, M. Ekstorm, M. Verglund, C. M. Andersson and L. Engman, J. Org. Chem., 1995, 60, 4461.
4. G. Mugesh, A. Panda, S. Kumar, S. D. Apte, H. B. Singh and R. Butcher, Organometallics, 2002, 21, 884.
5. (a) K. Fujita, M. Iwaoka and S. Tomoda, Chem. Lett., 1994, 923–926; (b) K. Fujita, K. Murata, M. Iwaoka and S. Tomoda, Tetrahedron, 1997, 53, 2029–2048; (c) M. Iwaoka and S. M. Tomoda, J. Chem. Soc., Chem. Commun., 1992, 1165; (d) T. Wirth, Tetrahedron Lett., 1995, 36, 7849; (e) R. Kaur, H. B. Singh and R. P. Patel, J. Chem. Soc., Dalton Trans., 1996, 2719; (f) S. Fukuzawa, K. Takahashi, H. Kato and H. Yamazaki, J. Org. Chem., 1997, 62, 7711; (g) S. Uemura, Phosphorus, Sulfur Silicon Relat. Elem., 1998, 219, 136–138; (h) K. Hiroi, Y. Suzuki and I. Abe, Tetrahedron: Asymmetry, 1999, 10, 1173; (i) H. Ehara, M. Noguchi, S. Sayama and T. Onami, J. Chem. Soc., Perkin Trans. 1, 2002, 1429; (j) C. Bolm, M. Kesselgraber, A. Grehz, N. Hermanns and J. P. Hilderbrand, New J. Chem., 2001, 25, 13; (k) A. L. Braga, M. W. Paixao, D. S. Ludtke, C. C. Silveira and O. E. D. Rodrigues, Org. Lett., 2003, 5, 2635.
6. (a) Organoselenium Chemistry: A Practical Approach, T. G. Back., Ed.; Oxford University Press, New York, 1999; (b) T. Wirth, Tetrahedron, 1999, 55, 1; (c) T. Wirth, Angew. Chem., Int. Ed., 2000, 39, 3740; (d) Organoselenium Chemistry: Modern Development in Organic Synthesis, T. Wirth, Ed; Springer-Verlag: Berlin, Germany, 2000; (e) Y. Nishibayashi and S. Uemura, Top. Curr. Chem., 2000, 208, 201 Also see.; (f) L. Uehlin and T. Wirth, Org. Lett., 2001, 3, 2931; (g) M. Uchiyama, M. Oka, S. Harai and A. Ohta, Tetrahedron Lett., 2001, 42, 1931; (h) T. G. Back, Z. Moussa and M. Parvez, J. Org. Chem., 2002, 67, 499; (i) M. Tiecco, L. Testaferri, C. Santi, C. Tomassini, F. Marini, L. Bagnoli and A. Temperini, Tetrahedron: Asymmetry, 2002, 11, 4645; (j) M. Tiecco, L. Testaferri, C. Santi, C. Tomassini, F. Marini, L. Bagnoli and A. Temperini, Chem.–Eur. J., 2002, 8, 1118; (k) L. Uehlin, G. Fragale and T. Wirth, Chem.–Eur. J., 2002, 8, 1125; (l) S. S. Khokhar and T. Wirth, Angew. Chem., Int. Ed., 2004, 43, 631; (m) G. Fragale and T. Wirth, Eur. J. Org. Chem., 1998, 1361–1369; (n) G. Fragale, M. Neuburger and T. Wirth, Chem. Commun., 1998, 1867–1868; (o) M. Tiecco, L. Testaferri, C. Santi, C. Tomassini, F. Marini, L. Bagnoli and A. Temperini, Angew. Chem., Int. Ed., 2003, 42, 3131.
7. (a) A. N. Gleizes, Chem. Vap. Deposition, 2000, 6, 155; (b) M. Lazell, P. O'Brien, D. J. Otway and J.-H. Park, J. Chem. Soc., Dalton Trans., 2000, 4479; (c) J. D. Sandman, L. Li, S. Tripathy, J. C. Stark, L. A. Acampora, B. M. Foxman and L. A. Foxman, Organometallics, 1994, 13, 348; (d) P. J. Bonasia and J. Arnold, J. Organomet. Chem., 1993, 449, 147; (e) Y. Cheng, T. J. Emge and G. Brennan, Inorg. Chem., 1994, 33, 3711; (f) Y. Cheng, T. J. Emge and G. Brennan, J. Inorg. Chem., 1996, 35, 3342; (g) Y. Cheng, T. J. Emge and G. Brennan, Inorg. Chem., 1996, 35, 7339; (h) G. Mugesh, H. B. Singh and R. J. Butcher, Inorg. Chem., 1998, 37, 2663; (i) G. Mugesh, H. B. Singh and R. J. Butcher, J. Organomet. Chem., 1999, 577, 243; (j) K. Kandasamy, H. B. Singh and G. Wolmershäuser, Inorg. Chim. Acta, 2005, 358, 207.
8. (a) A. Panda, Coord. Chem. Rev., 2009, 253, 1056–1098; (b) A. Panda, Coord. Chem. Rev., 2009, 253, 1947–1965; (c) A. Panda, S. Panda, K. Srivastava and H. B. Singh, Inorg. Chim. Acta, 2011, 372, 17–31.
9. A. Panda and H. B Singh, NMR of Organoselenium and Organotellurium Compounds, Ed. Z. Rappoport, Chichester, Wiley, 2012 (under revision).
10. (a) M. Iwaoka and S. Tomoda, J. Am. Chem. Soc., 1996, 118, 8077; (b) H. Komatsu, M. Iwaoka and S. Tomoda, Chem. Commun., 1999, 205–206; (c) M. Iwaoka, H. Komatsu and S. Tomoda, Chem. Lett., 1998, 969; (d) B. K. Sharma and G. Mugesh, ChemPhysChem, 2009, 10, 3013; (e) D. Roy and R. B. Sunoj, J. Phys. Chem. A, 2006, 110, 5942; (f) M. Iwaoka, H. Komatsu, T. Katsuda and S. Tomoda, J. Am. Chem. Soc., 2004, 126, 5309; (g) M. Iwaoka, H. Komatsu, T. Katsuda and S. Tomoda, J. Am. Chem. Soc., 2002, 124, 1902; (h) S. K. Tripathi, U. Patel, D. Roy, R. B. Sunoj, H. B. Singh, G. Wolmershäuser and R. J. Butcher, J. Org. Chem., 2005, 70, 9237.
11. Gaussian 09, Revision B.01, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2010.
12. (a) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926; (b) A. E. Reed, L. A. Curtiss, J. E. Carpenter and F. Weinhold, NBO version 3.1.
13. (a) R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, New York, 1990; (b) P. Popelier, Atoms in Molecules: An Introduction, Pearson, Harlow, 2000; (c) R. J. Gillespie, P. L. A. Popelier, Chemical Bonding and Molecular Geometry, Oxford University Press, New York, 2001; (d) C. F. Matta, R. J. Boyd, The Quantum Theory of Atoms in Molecules, Wiley-VCH, 2007.
14. (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789; (b) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
15. S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129.
16. F. Biegler-Konig, J. Schonbohm and D. Bayles, J. Comput. Chem., 2001, 22, 545–559.
17. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
18. M. Iwaoka and S. Tomoda, J. Org. Chem., 1995, 60, 5299.
19. K. Kandasamy, S. Kumar, H. B. Singh, R. J. Butcher and K. T. Holman, Eur. J. Inorg. Chem., 2004, 1014.
20. S. Kumar, K. Kandasamy, H. B. Singh, G. Wolmershäuser and R. J. Butcher, Organometallics, 2004, 23, 4199.
21. G. Mugesh, A. Panda, H. B. Singh and R. J. Butcher, Chem.–Eur. J., 1999, 5, 1411.
22. (a) S. D. Apte, S. S. Zade, H. B. Singh and R. J. Butcher, Organometallics, 2003, 22, 5473; (b) T. A. Hamor, H. Chen, W. R. McWhinnie, S. L. W. McWhinnie and Z. Majeed, J. Organomet. Chem., 1996, 523, 53; (c) S. Kumar, H. B. Singh and G. Wolmershäuser, J. Organomet. Chem., 2005, 690, 3149.
23. D. Cremer and E. Kraka, Angew. Chem., 1984, 96, 612–614.
24. See Supporting Information for further details†.

---

Footnote

† Electronic supplementary information (ESI) available: B3LYP/6-31G(d)/LanL2DZ optimized geometries and AIM molecular plots of all the studied compounds. See DOI: 10.1039/c2ra20591b

---