DOI:
10.1039/C2RA00751G
(Paper)
RSC Adv., 2012,
2, 2836-2841
Effect of functionalization on the interfacial binding energy of carbon nanotube/nylon 6 nanocomposites: a molecular dynamics study
Received
16th September 2011
, Accepted 14th January 2012
First published on 9th February 2012
Abstract
The critical challenge for preparing carbon nanotube (CNT)/polymer nanocomposites is how to create a strong interfacial binding energy (IBE) between the polymer matrix and the CNT. Molecular dynamics simulations of nylon 6 melts and its composite with pristine CNT or functionalized CNT embedded have been performed. The properties of the nanocomposites are investigated with the IBE between CNT and nylon 6. The non-bond energies from both vdW and electrostatic interactions, are calculated for nylon 6 and CNT functionalized by different groups. Our calculational results show that the vdW interaction energies of all the functionalized CNT/nylon 6 composites are close to that of the pristine CNT/nylon 6 composite, implicating the electrostatic interactions are responsible for the strong IBE of the functionalized CNT/nylon 6 composites. Therefore, the functionalized CNT can expand the application of polymer in actual production.
I. Introduction
Polymer/nanoparticle interfaces play an important role in new applications involving hybrid materials, where nanoparticles are added to a polymer to alter its structural and mechanical properties without affecting the main chemical features of the supporting matrix.1 Of the carbon-based nanofillers, carbon nanotubes (CNTs) have attracted considerable attention due to their intrinsic mechanical and electrical properties, and thermal stability. The properties of polymer/CNTs composites have been intensively investigated by experiments.2–4 The most relevant issues are to disperse CNTs well in polymer matrix and to create a strong interfacial binding between the polymer matrix and the CNTs.5,6 Therefore, it is necessary to pay attention to the suitable chemical or physical treatments that may lead to different surface morphologies of carbon nanotubes, which may improve their dispersion and adhesion in the polymer matrix. Thostenson et al.7 reported that the characteristics of polymer/CNTs composites are mostly dependent on the polymers and the processing used to make the composites. Guadagno et al.8 investigated the mechanical properties of epoxy composites altered by multi-wall carbon nanotubes (MWCNTs) modified with oxatyl. Their results show that the storage modulus can increase with the addition of unfuntionalized MWCNTs, whereas a constant value or even a weak reduction was observed for functionalized nanotubes. Rong et al.9 reported that the mechanical properties and crystallization behavior of poly(ether ether ketone) (PEEK) are influenced by the modification of MWCNTs, and improved mechanical properties appear in the functionalized CNT/PEEK composites. Therefore, the study on the influences of modified CNTs is important for the new applications of polymer/CNT composites.
Nylon is a well known engineering thermoplastic used in electric installation, transportation equipment, spinning and other aplications, because of its outstanding combination of good mechanical properties and easy process-ability.10 Recently, the nylon 6 nanocomposites with carbon have been demonstrated to show excellent properties.11–13 Mahfuz et al.11 reported that the Young's modulus and strength of the nanophased nylon 6 filaments increased by 220% and 164%, respectively with the addition of only 1 wt% MWCNTs. Gao et al.12 have synthesized SWNT–nylon 6 composites, which exhibit excellent properties. Their results show that SWNTs with a higher concentration of carboxylic acid (–COOH) groups can form a stronger SWNT–nylon interfacial interaction, which consequently improves the mechanical properties. As we know, the interfacial properties of CNT and nylon 6 are difficult to observe directly by experiments at the molecular level. If we want to design favorable microscopic and macroscopic structures of polymers, we need to know much more about the interfacial properties of nanocomposites at the molecular level.
For these reasons, we consider that molecular dynamics (MD) simulations can serve as a powerful tool for investigating the interfacial characteristics of CNT and polymers. Wei et al.14 conducted MD simulations to investigate the thermal expansion and diffusion characteristics of CNT/polymer composites. Yang et al.15 used MD simulations to study the interaction between CNT and polymers. They found that the specific monomer structure plays a very important role in determining the strength of interaction between CNTs and polymers. Recently, the simulations by Zheng et al.16 and Frankland et al.17 show that the CNTs modified with functional groups or polymer chains can greatly influence the properties of the nanocomposites.
In this paper, we performed the MD simulations to study the detail of interfacial interaction between a CNT and nylon 6 matrix. Since the functional group modifications on CNT are very important for the interfacial interaction and the dispersion of CNTs in the polymers, the present work emphasizes the examination of the effects of the different functional groups on the surface of the CNT. We also discuss the mechanism of interaction of the different atoms, which are expected to enhance the understanding for the interfacial interaction between CNTs and polymers.
II. Experimental Section
II.I. Method
The MD simulations are carried out with the Discover module in Materials studio18 and the Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies (COMPASS) are used as the atomic force field.19 The COMPASS force field has been successfully used in the investigation of organic and inorganic materials.20,21 We have used the COMPASS force field to simulate the interactions between PE/PP/PS/PPA/PPV and the SWCNT.22 The force field potential can be represented as follows:23| | | Etotal = Evalence + Ecross-term+ Enonbond | (1) |
where the first term Evalence is the valence energy. The second term Ecross-term is the cross-term interaction energy. The third term Enonbond is the nonbond interaction energy. In detail, every term is expressed as follows:| |  | (2) |
| |  | (3) |
| |  | (4) |
Where b and b′ are the bond lengths, θ is the two-bond angle, ϕ is the dihedral torsion angle, χ is the out of plane angle, q is the atomic charge, ε is the dielectric constant, rij is the i − j atomic separation distance. b0, Ki (i = 2–4), θ0, Hi (i = 2–4), ϕi0(i = 2–4), Vi (i = 1–3), Fbb′, b0′,Fθθ′, θ0′,Fbθ, Fbϕ, Fb′θ, Fi (i = 1–3), Fθϕ, Fϕθθ′, Aij, and Bij are system dependent parameters implemented in the Discover module of Materials Studio.
II.II. Model
For nanocomposites systems, we use nylon 6 as the matrix, which is a well known engineering thermoplastic used in a variety of engineering areas. Considering its excellent mechanical and physical properties,24,25 single wall CNTs are used as the embedded fiber in this study. The matrix of nylon 6 consists of 80 short chains, with 4 repeating units in each chain (Fig. 1a). The present CNT has a length of 24.6 Å (total of 200 atoms) with the volume fraction of about 2% (Fig. 2). The periodic boundary condition is used in our simulations. For the nylon 6 composite systems, the initial cell size is 42.04 × 42.04 × 34.82 (total 6396 atoms in the unit cell). Recent experiments confirm that the presence of –COOH functional groups on CNTs can improve the dispersion into the matrix, and carbon nanotubes functionalized with –COOH have strong interfacial interactions with many polymer matrices.12,13 In the present work, the samples are reinforced by either pristine CNTs or modified CNTs (see in Fig. 3). The various groups, including different functional groups (–COOH, –OH, –NH2, and –CH3) and different oxygen containing functional groups (–OH, –COOH, –COCOOH, and –CH(COOH)2), are investigated in the present work.
 |
| | Fig. 1 (a) Molecular model of nylon 6 and (b) carboxyl group functionalized CNT. | |
 |
| | Fig. 2 The initial CNT–nylon 6 system (a) side view and (b) top view (to observe the spatial arrangement of the polymer chains clearly, hydrogen atoms are eliminated in the image). | |
 |
| | Fig. 3 (a) Pristine CNT/nylon 6 system and (b) functionalized CNT/nylon 6 system. | |
Firstly, the MD with NPT ensemble (p = 1 bar, T = 500 K) is run for 300 ps to make the composite systems reach their equilibrium. Then, the system is gradually cooled to 250 K at a rate of 50 K/200 ps, and a further simulation of 200 ps is run to ensure the system to reach equilibrium at the chosen temperatures. Fig. 4 shows that the time evolution of total potential energy of the functionalized CNT/nylon 6 system at different temperatures. The total potential energies decrease little after 10 ps, which implies that the simulation time of 200 ps is long enough for the systems to reach equilibrium. The method is the same as that used in our previous work.26 The time step is 1 fs and the cutoff distance is 9.5 Å are used in the present work. The Anderson method is applied to control the temperature of the system.27,28
 |
| | Fig. 4 The time evolution of total potential energy of functionalized CNT/nylon 6 system at the different temperatures (the CNT functionalized by 10% carboxyl (–COOH)). | |
III. Results and discussion
III.I. Influence of temperature on the different concentrations of chemical functionalization
The composites reinforced by CNTs on which 0, 2, 6, or 10% of the carbon atoms with a bonded carboxyl (–COOH) are used to examine the effect of temperature on the chemical functionalization.
In order to investigate the binding strength of the interfacial interaction, we calculate the interfacial binding energy (IBE) between nylon 6 and a CNT. Generally, the IBE is estimated from the difference between the potential energy of the composite system and the potential energy for the polymer matrix and the corresponding CNT as follows:16,29
| | | ΔE = Etotal − (ECNT + Epolymer) | (5) |
where
Etotal is the total potential energy of the composite,
ECNT is the total potential energy of the CNT without the
polymer, and the
Epolymer is the total potential energy of the
polymer without the CNT.
Fig. 5 shows the IBE between nylon 6 and the CNT as a function of the temperature. The IBE of the nylon 6 composite with CNTs functionalized by 10% carboxyl groups is strongly enhanced in comparison with the composite with the pristine CNTs. From Fig. 5, it can also be observed that the energy difference between the lower temperature and the higher temperature is very little for the composite system using pristine CNTs, indicating that the temperature has little effect on the IBE of this system. On the contrary, for the composite system containing the CNTs with higher functionalization (10%), the energy difference between the lower temperature and the higher temperature is obvious. It implies that the IBE depends on both the concentration of the chemical functionalization and the temperature of the system. Some more discussion for the interfacial interaction between nylon 6 and CNT will be presented in next section.
 |
| | Fig. 5 IBE as a function of temperature for the nylon 6 composite systems. | |
Fig. 6 shows the densities of the neat nylon 6 and its composite with CNTs embedded change along with the temperature. The present computations give a density of 1.03 g cm−3 for bulk nylon 6 at 300 K is close to the 1.09 g cm−3 of the experimental value at room temperature,30 which implies the present computational policy for the density is acceptable. Fig. 6 also shows that the density of the CNT/nylon 6 composite system is strongly enhanced with the increase of the density of the functionalization in the whole temperature range. Comparing Fig. 6 with Fig. 5, we find that the increase in the density corresponds to the enforcement of the interactions between the nylon 6 and the functionalized CNTs, which implies that the interaction plays an important role on the densities of the composite systems.
 |
| | Fig. 6 Density as a function of temperature for the nylon 6 and its composite with embedded CNT. | |
The glass transition temperature Tg is very important for the application of the materials. The Tg is related to the density of the system. Generally, the location of the discontinuity at the curve of density vs. temperature is the position of Tg.14 We have compared our Tg value for neat nylon 6 with the experimental value to validate our cooling rate because the Tg value depends strongly on the cooling rate. Our computational 352 K for the Tg of neat nylon 6 (see Fig. 7) is close the upper limit of the experimental report,11,30–31 which implies the present cooling rate is valid to determine the Tg of the nylon 6 systems. Our computed Tg is 392 K for the nylon 6/CNT composite. The present increase 40 K of Tg after adding CNTs is the same as the result of previous MD simulations conducted on a similar system.14 This increase of Tg is evidently due to the presence of CNTs which may have imposed a limit on the mobility of the molecules of nylon 6. For the free volume in the liquid state, recent experiments pointed out that the molecular mutation is relatively easy because the unoccupied volume is large. As the melt temperature is lowered, the free volume would be reduced until there would not be enough free space to allow molecular translational or rotational motion. With the infusion of CNTs, this space is evidently further reduced.2 Our simulations show that the molecules of nylon 6 are strongly adsorbed on the surface of the CNTs, so that the mobility of the molecules is reduced.
 |
| | Fig. 7 Glass transition temperature Tg for neat nylon 6 and its composite system. | |
III.II. Effect of the functionalization with different functional groups
Now we throw light on the case for nylon 6 composites with the CNTs functionalized with different functional groups. For the CNTs, 6% of the carbon atoms have randomly bonded with different types of functional groups (including –COOH, –OH, –NH2, and –CH3). Fig. 8 shows the IBE as a function of temperature for nylon 6 and the functionalized CNTs. The figure shows that the different groups attached to the CNT will result in different IBEs between the CNT and nylon 6. It is found that the effects of the groups on the IBEs between the CNT and nylon 6 are as follows: –COOH > –OH > –NH2 > –CH3, and the IBE with the CNT modified with –COOH groups is the strongest one of these composite systems. Apart from the –CH3 groups, the other functional groups increase the IBE between a functionalized CNT and nylon 6. This clearly implies that the functional groups play an important role in the interfacial properties of polymer–CNT nanocomposites. The results also show that the strength of the IBE between CNTs and the polymers can be controlled by choosing different functional groups.
 |
| | Fig. 8 IBE as a function of temperature for nylon 6 composite with different chemical functionalized CNT (different groups randomly chemisorbed to 6% of carbon atoms). | |
The binding strength between the functionalized CNT and nylon 6 is related to the nonbond potential energy between the molecules of nylon 6 and the CNT as well as the functional groups. The total nonbond potential energy of nylon 6 and a CNT is the sum of energy between pair sof atom i and j by eqn (4). Since there is no chemical bonding between the CNT and the polymer matrix, the origins of the CNT–polymer interactions mainly include the electrostatic and the van der Waals (vdW) forces. Since a pristine CNT exhibits no net charge, there are hardly any electrostatic interactions between the pristine CNTs and polymers although the centers of the positive and the negative electric charges of nylon 6 do not overlap. Therefore, the interaction between a pristine CNT and nylon 6 is solely via vdW forces. While we add functional groups to the CNT wall, which will result the electrostatic interactions in the functionalized CNT–nylon 6 composite because the centers of the positive and the negative electric charges of the functional groups do not overlap. To quantify the effect of a CNT modified with the different types of functional groups, we compute both the vdW and the electrostatic energies for the nylon 6/CNT systems. Fig. 9 and 10 show the vdW and the electrostatic energies of the nylon 6/CNT systems. From the figures we easily find that the electrostatic interactions are much stronger than vdW interactions for all the nylon 6/CNT systems. We also find that the functional groups exert a significant effect on the electrostatic interactions, although they hardly change the corresponding vdW interactions. The effects of functional groups on the electrostatic interactions are as follow: –COOH > –OH > –NH2 > –CH3. This is consistent with the effects of the different groups on the IBEs between the functionalized CNT and nylon 6. This indicates that the electrostatic interactions play the dominant role in the interfacial interaction between the functionalized CNTs and nylon 6.
 |
| | Fig. 9 The van der Waals energies between the atoms of nylon 6 and the atoms of different functional groups on the CNT surface. | |
 |
| | Fig. 10 The electrostatic energies between the atoms of nylon 6 and the atoms of different functional groups on the CNT surface. | |
III.III. The role of the oxygen atoms in the functional groups
From the interaction potential energies between nylon 6 and CNTs functionalized with different functional groups in the above section, one can find that the interactions for the groups containing O atoms are obviously stronger than those of the groups containing no O atoms. To determine the influence of different oxygen containing functional groups, we consider the composites of nylon 6 with CNTs modified with the functional groups containing different types of oxygen atoms (including –OH, –COOH, –COCOOH, and –CH(COOH)2). Fig. 11 shows the interaction energy between nylon 6 and CNTs as a function of temperature. It is found from the figure that the interaction energies increase along with the increase in the number of oxygen atoms in the functional groups. This implies that the O atoms in the functional groups really play an important role on the IBE and the diffusive properties of the polymer chains in the composites.
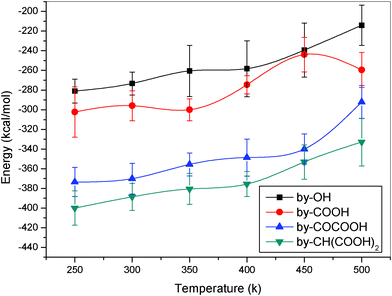 |
| | Fig. 11 IBE as a function of temperature for the nylon 6 composite with different oxygen containing functional groups (different oxygen containing groups randomly chemisorbed to 6% of the carbon atoms). | |
As discussed above, the strong interfacial interaction between the functionalized CNTs and the polymer main chains results from the contribution of the different functional groups. The nonbond energies come from the vdW and the electrostatic interactions. Moreover, our calculational results show that the vdW interaction energies of all the functionalized CNT/nylon 6 composites are close to that of the pristine CNT/nylon 6 composite, therefore, the strong interfacial interactions should be attributed to the electrostatic interactions contributed by the different functional groups.
Conclusions
The IBEs of the functionalized CNT/nylon 6 composites were investigated with MD simulation. We found that the IBE between CNT and nylon 6 can be enhanced by different functional groups. After analyzing their effects, we find all the considered groups but –CH3 can increase the IBE of the composite of nylon 6 and functionalized CNTs. Moreover, more O atoms in the functional group will result a larger IBE. It is found that the vdW interaction energies of all the functionalized CNT/nylon 6 composites are close to that of the pristine CNT/nylon 6 composite and the strong interfacial interactions should be attributed to the electrostatic interactions. Our simulations also show that the nylon 6/CNT composite has a higher Tg than that of neat nylon 6. Our simulations provide valuable understanding for the mechanism, physical characteristics of the interfacial interactions of CNT–polymer composites.
Acknowledgements
This work was supported by the National Science Foundation of China under grant no. NSFC-10974078 and NSFC-11174117.
References
- G. Tsagaropoulos and A. Eisenberg, Macromolecules, 1995, 28, 396–398 CrossRef CAS.
- B. Fiedler, F. H. Gojny, M. H. G. Wichmann, M. C. M. Nolte and K. Schulte, Compos. Sci. Technol., 2006, 66, 3115–3125 CrossRef CAS.
- M. Moniruzzaman and K. I. Winey, Macromolecules, 2006, 39, 5194–5205 CrossRef CAS.
- J. N. Coleman, U. Khan, W. J. Blau and Y. K. Gun'ko, Carbon, 2006, 44, 1624–1652 CrossRef CAS.
- P. Ajayan and J. Tour, Nature, 2007, 447, 1066–1068 CrossRef CAS.
- X. L. Xie, Y. W. Mai and X. P. Zhou, Mater. Sci. Eng., R, 2005, 49, 89–112 CrossRef.
- E. T. Thostenson, Z. F. Ren and T. W. Chou, Compos. Sci. Technol., 2001, 61, 1899–1912 CrossRef CAS.
- L. Guadagno, B. D. Vivo, A. D. Bartolomeo, P. Lamberti, A. Sorrentino, V. Tucci, L. Vertuccio and V. Vittoria, Carbon, 2011, 49, 1919–1930 CrossRef CAS.
- C. R. Rong, G. Ma, S. L. Zhang, L. Song, Z. Chen, G. B. Wang and P. M. Ajayan, Compos. Sci. Technol., 2010, 70, 380–386 CrossRef CAS.
-
M. Kohan, Nylon plastics handbook, Hanser, New York, 1995 Search PubMed.
- H. Mahfuz, A. Adnan, V. K. Rangari, M. M. Hasan, S. Jeelani, W. J. Wright and S. J. DeTeresa, Appl. Phys. Lett., 2006, 88, 083119–083121 CrossRef.
- J. B. Gao, M. E. Itkis, A. P. Yu, E. Bekyarova, B. Zhao and R. C. Haddon, J. Am. Chem. Soc., 2005, 127, 3847–3854 CrossRef CAS.
- J. B. Gao, B. Zhao, M. E. Itkis, E. Bekyarova, H. Hu, V. Kranak, A. P. Yu and R. C. Haddon, J. Am. Chem. Soc., 2006, 128, 7492–7496 CrossRef CAS.
- C. Y. Wei, D. Srivastava and K. Cho, Nano Lett., 2002, 2, 647–650 CrossRef CAS.
- M. J. Yang, V. Koutsos and M. Zaiser, J. Phys. Chem. B, 2005, 109, 10009–10014 CrossRef CAS.
- Q. B. Zheng, Q. Z. Xue, K. Y. Yan, X. L. Gao, Q. Li and L. Z. Hao, Polymer, 2008, 49, 800–808 CrossRef CAS.
- S. J. V. Frankland, A. Caglar, D. W. Brenner and M. Griebel, J. Phys. Chem. B, 2002, 106, 3046–3048 CrossRef CAS.
-
Accelrys Materials Studio 3.2, Accelrys Software, Inc.,San Diego, 2005.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- Q. B. Zheng, Q. Z. Xue, K. Y. Yan, L. Z. Hao, Q. Li and X. L. Gao, J. Phys. Chem. C, 2007, 111, 4628–4635 CAS.
- K. Y. Yan, Q. Z. Xue, D. Xia, H. J. Chen, J. Xie and M. D. Dong, ACS Nano, 2009, 3, 2235–2240 CrossRef CAS.
- W. Liu, C. L. Yang, Y. T. Zhu and M. S. Wang, J. Phys. Chem. C, 2008, 112, 1803–1811 CAS.
- M. Grujicic, G. Cao and W. N. Roy, Appl. Surf. Sci., 2004, 227, 349–363 CrossRef CAS.
- P. M. Ajayan, O. Stephan, C. Colliex and D. Trauth, Science, 1994, 265, 1212–1214 CAS.
- J. S. Yang, C. L. Yang, M. S. Wang, B. D. Chen and X. G. Ma, Phys. Chem. Chem. Phys., 2011, 13, 15476–15482 RSC.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393 CrossRef CAS.
- H. C. Andersen, J. Comput. Phys., 1983, 52, 24–34 CrossRef CAS.
- J. N. Coleman, U. Khan, W. J. Blau and Y. K. Gun'ko, Carbon, 2006, 44, 1624–1652 CrossRef CAS.
- C. Lv, Q. Z. Xue, D. Xia, M. Ma, J. Xie and H. J. Chen, J. Phys. Chem. C, 2010, 114, 6588–6594 CAS.
- T. D. Fornes and D. R. Paul, Polymer, 2003, 44, 3945–3961 CrossRef CAS.
- R. Greco and L. Nicolais, Polymer, 1976, 17, 1049–1053 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. 













