DOI:
10.1039/C1RA00677K
(Paper)
RSC Adv., 2012,
2, 1598-1604
Order–disorder transition in the (1−x)Li2TiO3–xMgO system (0 ≤ x ≤ 0.5)†
Received
5th September 2011
, Accepted 15th November 2011
First published on 22nd December 2011
Abstract
The order–disorder phase transition of magnesium lithium titanate solid–solution (1−x)Li2TiO3–xMgO (0 ≤ x ≤ 0.5) ceramics prepared by conventional solid-state processing has been examined. The phase and structural analysis was carried out using electron diffraction, neutron diffraction and high-resolution transmission electron microscopy. Both electron and neutron diffraction results revealed the onset of an order-to-disorder transition at 0.3 < x < 0.4. Superlattice reflections found in certain regions of x = 0.2 samples and most areas of x = 0.3 samples were caused by a twin structure stabilized by Mg incorporation. Rietveld refinements of neutron diffraction data suggested a random distribution of Mg on the Li 4e sites and equal distribution of Mg on the two Ti 4e sites for x ≤ 0.3. As the Mg content continues to increase, the crystal symmetry transforms from monoclinic to cubic rocksalt. Consequently, the cation ordering on the 8f and 4d sites of the C2/c structure became corrupted and turned into short-range ordering on the 4a sites of a cubic structure with  symmetry, resulting in diffuse scattering in electron diffraction patterns.
symmetry, resulting in diffuse scattering in electron diffraction patterns.
1. Introduction
Lithium titanate (Li2TiO3) is an important oxide ceramic for various applications. It has recently been investigated as a microwave dielectric material1 and the properties were greatly improved by integrating Mg into the structure.2 Owing to its good chemical stability in air, acceptable mechanical strength, low activation and excellent tritium release characteristics at low temperatures, lithium titanate is also a promising tritium breeding material for fusion reactors.3–9 It can also be used as an electrode material in lithium-ion batteries10–12 and as a double-layer cathode material in molten-carbonate fuel cells.13 Layered lithium transition-metal-oxide electrodes, LiMO2 (M = Fe, Co, Ni, or Mn), become unstable at low lithium content when lithium cells are charged above 4.3 V. To stabilize the structure, Li2TiO3 can be structurally integrated into the LiMO2 component to yield “composite” structures with short-range order domains rather than true solid solutions.14–21
The rocksalt-structured Li2TiO3 compound has been reported22 with a monoclinic structure in the space group C2/c. In this model, the Li+ resides on the 8f, 4d, and 4e sites and Ti4+ occupies two different 4e sites. The resultant structure consists of cation layers perpendicular to [001], the composition of which alternates from either pure Li+ to (Li+ + Ti4+). In this rocksalt superstructure phase, both the anion and cation coordination octahedra are edge-shared through three-dimensional networks.23 The compound undergoes an order–disorder phase transition on heating above 1215 °C.24 The disordered cubic polymorph forms an extensive range of solid solutions with both excess lithia and titania at high temperature. By forming solid solutions with MgO, the order–disorder transition temperature decreases rapidly.25 A previous study by Bian and Dong2 on the XRD patterns of (1−x)Li2TiO3-xMgO ceramics (0 ≤ x ≤ 0.5) revealed a complete phase transition from monoclinic to cubic rocksalt at room temperature for x ≥ 0.4 by the presence of only cubic (111) and (200) peaks at 37° and 43°, respectively. The small hump they reported around 2θ = 20° can be interpreted as evidence of short-range order. In order to understand the influence of Mg on the order–disorder transition in terms of charge ordering, electron diffraction and microscopy were carried out for various compositions. Evidence of the crystallographic evolution and the ordering mechanism are provided and discussed in this study.
2. Experimental
Ceramic samples in the (1−x)Li2TiO3–xMgO (0 ≤ x ≤ 0.5) system were prepared by a conventional solid-state reaction process. High-purity MgO (99.0%, Guo-Yao Co. Ltd., Shanghai, China), Li2CO3 (99.9%, Guo-Yao Co. Ltd., Shanghai, China) and TiO2 (99.7%, Zhongxing Electronic materials Co. Ltd, Hubei, China) were weighed according to the above formula and mixed by ball milling for 24 h in ethanol using zirconia milling media. The slurries were dried and calcined at a temperature of 700–1100 °C for 2 h in an alumina crucible. The calcining temperature increased with increasing MgO content. The calcined powders were milled for 24 h, mixed with 7 wt% PVA (molecular weight 1700, hydrolysis level 88%) as a binder, dried and granulated. The granulated powders were pressed uniaxially under 100 MPa pressure into pellets of 10 mm diameter and 4–5 mm thickness followed by sintering between 1200 and 1350 °C for 2 h. In order to prevent lithium volatilization, the compacts were muffled with powders of the same composition. Samples to be examined via the transmission electron microscope (JEM 2100-HR, JEOL, Japan) were prepared by thinning pellets to electron transparency using conventional ceramographic techniques followed by precision ion polishing (model 691, Gatan, USA). Neutron powder data have been collected at room temperature on the high-resolution powder diffractometer HB-2A at the High Flux Isotope Reactor at Oak Ridge National Laboratory using 12′-31′-6′ collimation and with a neutron wavelength of 1.50 Å {Ge (115)}. More details about the HB-2A instrument can be found in the work of Garlea et al.26 Non-isotopically-enriched Li was used throughout this study. The crystallographic structures were refined using JANA2006 software using the cubic NaCl (x = 0.3 and x = 0.4) and Li2TiO3 (x = 0.1 and x = 0.2) structure types, known from the literature,27–29 as starting models.
3. Result and discussion
Electron diffraction was conducted on magnesium lithium titanate solid solution samples, (1−x)Li2TiO3–xMgO (0 ≤ x ≤ 0.5). Fig. 1 shows the selected area electron diffraction patterns (SADPs) taken along the pseudocubic <100> ([100]pc || [301]m). The electron diffraction patterns from the three compositions with the lowest Mg contents (0 ≤ x ≤ 0.2) can be unambiguously indexed according to the monoclinic model in the space group C2/c (No. 15) whereas similar patterns taken along [100]c for x = 0.4 and 0.5 can be indexed according to the fcc rocksalt model. In agreement with the XRD patterns reported by Bian et al.,2 a clear phase transition from monoclinic to cubic can be seen from x = 0.3 to x = 0.4. In addition, the diffuse scattering seen for x ≥ 0.4 indicates a disordered structure which might correspond to the disordered γ-Li2TiO3 phase. Electron diffraction patterns taken at other low-index zones also show such a transition (Fig. 2). Extra superlattice reflections observed for x = 0.3 in Fig. 1(d) and 2(d) are the result of twinning. Reflections from the two unique twin variants are outlined with either ovals (horizontal or vertical) or diamonds. Reflections left unmarked are common to all variants. Both patterns from the two variants in Fig. 1(d) can be indexed as <301>, making the twin plane { }. The superlattice reflections which appear in the [
}. The superlattice reflections which appear in the [ ]m patterns of Fig. 2 can be described by a modulation wave vector, q, as shown in Fig. 2(d). In real space, 1/q = Q which has a length of 2d(131)m = 4.783 Å, which is close to d(002)m = 4.789 Å. The extra {odd, even, odd} and {even, odd, even} reflections like those circled in Fig. 2(d) are caused by double diffraction; however, it should be noted that the {020} and {040} type reflections are fainter than those observed in typical Li2TiO3 structures (Fig. 2(a)–(c)). Reflections shown within the horizontal ovals arise from an [010] oriented domain, which is related through a
]m patterns of Fig. 2 can be described by a modulation wave vector, q, as shown in Fig. 2(d). In real space, 1/q = Q which has a length of 2d(131)m = 4.783 Å, which is close to d(002)m = 4.789 Å. The extra {odd, even, odd} and {even, odd, even} reflections like those circled in Fig. 2(d) are caused by double diffraction; however, it should be noted that the {020} and {040} type reflections are fainter than those observed in typical Li2TiO3 structures (Fig. 2(a)–(c)). Reflections shown within the horizontal ovals arise from an [010] oriented domain, which is related through a  twin plane to a
twin plane to a  variant, unique reflections from which are shown outlined with diamonds. The indexing shown in the overall pattern has been calculated according to this variant, which is, in turn, related through a
variant, unique reflections from which are shown outlined with diamonds. The indexing shown in the overall pattern has been calculated according to this variant, which is, in turn, related through a  twin plane to a
twin plane to a  variant, unique reflections from which are shown outlined with vertical ovals. The mirror symmetry in the pattern shows that the effect is indistinguishable from a twin plane on {101} or
variant, unique reflections from which are shown outlined with vertical ovals. The mirror symmetry in the pattern shows that the effect is indistinguishable from a twin plane on {101} or  relating [010] and
relating [010] and  variants. Reflections common to all variants are left un-annotated.
variants. Reflections common to all variants are left un-annotated.
![SADPs of (1−x)Li2TiO3–xMgO for (a) x = 0, (b) x = 0.1, (c) x = 0.2, and (d) x = 0.3 parallel to [301]m and (e) x = 0.4 and (f) x = 0.5 parallel to [100]c.](/image/article/2012/RA/c1ra00677k/c1ra00677k-f1.gif) |
| | Fig. 1 SADPs of (1−x)Li2TiO3–xMgO for (a) x = 0, (b) x = 0.1, (c) x = 0.2, and (d) x = 0.3 parallel to [301]m and (e) x = 0.4 and (f) x = 0.5 parallel to [100]c. | |
![SADPs of (1−x)Li2TiO3–xMgO for (a) x = 0, (b) x = 0.1, (c) x = 0.2, and (d) x = 0.3 parallel to []m, and (e) x = 0.4 and (f) x = 0.5 parallel to [110]c.](/image/article/2012/RA/c1ra00677k/c1ra00677k-f2.gif) |
| | Fig. 2 SADPs of (1−x)Li2TiO3–xMgO for (a) x = 0, (b) x = 0.1, (c) x = 0.2, and (d) x = 0.3 parallel to [ ]m, and (e) x = 0.4 and (f) x = 0.5 parallel to [110]c. ]m, and (e) x = 0.4 and (f) x = 0.5 parallel to [110]c. | |
To further examine the origin of the superstructure reflections, high-resolution transmission electron microscopy (HRTEM) was performed. Fig. 3(a) shows a HRTEM image of the x = 0.3 sample projected along [ ]m with the corresponding SADP showing superlattice reflections, inset. Four different regions marked with capital letters in Fig. 3(a) refer to three types of superstructures, as indicated by three different fast Fourier transform (FFT) images. Regions A and B yield type I diffraction (Fig. 3(b)), that is,
]m with the corresponding SADP showing superlattice reflections, inset. Four different regions marked with capital letters in Fig. 3(a) refer to three types of superstructures, as indicated by three different fast Fourier transform (FFT) images. Regions A and B yield type I diffraction (Fig. 3(b)), that is, 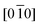 . Region C yields type II (Fig. 3(c)), or [010]. When these two FFT images are combined, the resultant image is type III diffraction, shown in Fig. 3(d). This pattern can be interpreted as above, that is two <010> variants related through {101} or
. Region C yields type II (Fig. 3(c)), or [010]. When these two FFT images are combined, the resultant image is type III diffraction, shown in Fig. 3(d). This pattern can be interpreted as above, that is two <010> variants related through {101} or  twinning. The superposition of type III diffraction upon the expected Li2TiO3 [
twinning. The superposition of type III diffraction upon the expected Li2TiO3 [ ]m patterns (Fig. 2(a)), caused by further twinning on
]m patterns (Fig. 2(a)), caused by further twinning on , yields diffraction patterns like the experimental one shown in the inset. To visualize the superstructures on a larger scale, a small objective aperture was used to include a small number of superstructural diffracted electron beams. Fig. 4 shows the bright-field and dark-field images for these superstructures, which appear as submicron coherent precipitates.
, yields diffraction patterns like the experimental one shown in the inset. To visualize the superstructures on a larger scale, a small objective aperture was used to include a small number of superstructural diffracted electron beams. Fig. 4 shows the bright-field and dark-field images for these superstructures, which appear as submicron coherent precipitates.
![(a) HRTEM image taken parallel to the []m zone axis with corresponding SADPs inset for the x = 0.3 sample. (b) FFT of region A and B, (c) FFT of region C and (d) FFT of region D.](/image/article/2012/RA/c1ra00677k/c1ra00677k-f3.gif) |
| | Fig. 3 (a) HRTEM image taken parallel to the [ ]m zone axis with corresponding SADPs inset for the x = 0.3 sample. (b) FFT of region A and B, (c) FFT of region C and (d) FFT of region D. ]m zone axis with corresponding SADPs inset for the x = 0.3 sample. (b) FFT of region A and B, (c) FFT of region C and (d) FFT of region D. | |
![TEM images parallel to the []m zone axis of the x = 0.3 sample. Both (a) bright-field and (b) dark-field images show precipitates.](/image/article/2012/RA/c1ra00677k/c1ra00677k-f4.gif) |
| | Fig. 4 TEM images parallel to the [ ]m zone axis of the x = 0.3 sample. Both (a) bright-field and (b) dark-field images show precipitates. ]m zone axis of the x = 0.3 sample. Both (a) bright-field and (b) dark-field images show precipitates. | |
To examine the diffraction patterns caused by the twin domains shown in the FFT images (Fig. 3), an attempt was made to search for such superstructures in x = 0.2 samples since conventional selected area diffraction (SAD) apertures are too large for the submicron superstructures in x = 0.3 samples. Fig. 5 shows the bright-field TEM image taken along [ ]m with associated SADPs taken within the marked areas. The micron-scale substructures in x = 0.2 are larger than those in x = 0.3. As such, SAD apertures could be used to select the areas of interest for electron diffraction. Five different types of SADP appeared in different regions within a single grain. Electron diffraction taken at the small region I shows it to be in the [
]m with associated SADPs taken within the marked areas. The micron-scale substructures in x = 0.2 are larger than those in x = 0.3. As such, SAD apertures could be used to select the areas of interest for electron diffraction. Five different types of SADP appeared in different regions within a single grain. Electron diffraction taken at the small region I shows it to be in the [ ]m orientation (Fig. 5(b)). SADPs taken in regions II and III (Fig. 5(c) and (d)), corresponding to the FFT images shown in Fig. 3(c) and (b), can be interpreted as variants parallel to <010>. The combination of SADPs from regions II and III yields the pattern from region IV (Fig. 5e). The combination of the patterns from regions I, II and III yields the complicated diffraction pattern shown in Fig. 5(f). What looks like a ½(131)m superlattice reflection (q) in the [
]m orientation (Fig. 5(b)). SADPs taken in regions II and III (Fig. 5(c) and (d)), corresponding to the FFT images shown in Fig. 3(c) and (b), can be interpreted as variants parallel to <010>. The combination of SADPs from regions II and III yields the pattern from region IV (Fig. 5e). The combination of the patterns from regions I, II and III yields the complicated diffraction pattern shown in Fig. 5(f). What looks like a ½(131)m superlattice reflection (q) in the [ ]m zone (Fig. 2(d)) is actually attributable to the (002)m reflection in the [010]m zone (Fig. 5(c)). Regardless of the large difference in size of the substructures in the x = 0.2 and x = 0.3, samples of both compositions retain the structure of ordered monoclinic Li2TiO3. Fig. 6 shows the bright-field TEM image obtained parallel to <301>m with associated electron diffraction patterns taken within the marked regions. Again, the complicated pattern of superlattice reflections (Fig. 6(d)), which is identical to that in Fig. 1(d), can be explained by the overlap of
]m zone (Fig. 2(d)) is actually attributable to the (002)m reflection in the [010]m zone (Fig. 5(c)). Regardless of the large difference in size of the substructures in the x = 0.2 and x = 0.3, samples of both compositions retain the structure of ordered monoclinic Li2TiO3. Fig. 6 shows the bright-field TEM image obtained parallel to <301>m with associated electron diffraction patterns taken within the marked regions. Again, the complicated pattern of superlattice reflections (Fig. 6(d)), which is identical to that in Fig. 1(d), can be explained by the overlap of 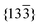 twin variants (parallel to <301>) with each other in region III (Fig. 6(a) and (d)).
twin variants (parallel to <301>) with each other in region III (Fig. 6(a) and (d)).
![(a) TEM image of sample x = 0.2 projected along []m with the corresponding SADPs corresponding to (b) region I, (c) region II, (d) region III, (e) region IV, and (f) region V.](/image/article/2012/RA/c1ra00677k/c1ra00677k-f5.gif) |
| | Fig. 5 (a) TEM image of sample x = 0.2 projected along [ ]m with the corresponding SADPs corresponding to (b) region I, (c) region II, (d) region III, (e) region IV, and (f) region V. ]m with the corresponding SADPs corresponding to (b) region I, (c) region II, (d) region III, (e) region IV, and (f) region V. | |
![(a) TEM image of sample x = 0.2 projected along [301]m with the corresponding SADPs taken in (b) region I, (c) region II, and (d) region III.](/image/article/2012/RA/c1ra00677k/c1ra00677k-f6.gif) |
| | Fig. 6 (a) TEM image of sample x = 0.2 projected along [301]m with the corresponding SADPs taken in (b) region I, (c) region II, and (d) region III. | |
The ionic radii for Ti4+, Li1+ and Mg2+ in sixfold coordination are 0.62, 0.76 and 0.72 Å, respectively.30 Accordingly in the magnesium lithium titanate solid solution, Mg might reside on either Li or Ti sites (4e). In order to maintain charge balance, if two Mg2+ cations replace Li+, there should be one other Mg residing on a Ti site:
| |  | (1) |
When the Mg content is low in the solid solution, it is likely that it mainly resides on the Li/Ti (4
e) site and the monoclinic structure is retained. With increasing Mg content (
x ≥ 0.3), due to the large size difference between Mg
2+ (0.72 Å) and Ti
4+ (0.62 Å), there is a slight increase in the lattice parameters as evidenced by a slight shift of diffraction peaks toward lower angles in the XRD patterns
2 and the neutron diffraction patterns (
Fig. 7) as well. To reduce the lattice strain energy, the grains become slightly disordered with a small ordered substructure which appears as a coherent precipitate (
Fig. 4). With further increase of the Mg content (
x > 0.3), the phase transforms into a more disordered cubic
γ-Li
2TiO
3 phase.
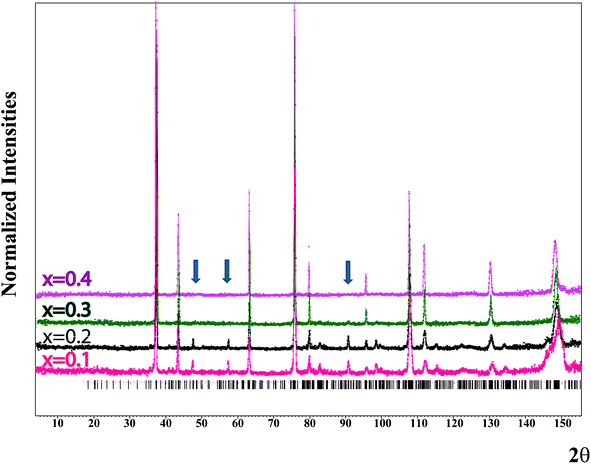 |
| | Fig. 7 (1−x)Li2TiO3–xMgO neutron powder diffraction pattern obtained on HB-2A at room temperature for x = 0.1, 0.2, 0.3 and 0.4. Dots indicate the normalized profile. The solid line is the calculated profile. The additional arrows show the characteristic superstructural peaks observed for x = 0.1, 0.2 and 0.3. | |
Neutron powder diffraction has been attempted to elucidate the atomic arrangement in the (1−x)Li2TiO3–xMgO (for x = 0.1, 0.2, 0.3 or 0.4) series. Fig. 7 shows clearly that for the compositions x = 0.1 and x = 0.2, additional peaks are observed to be consistent with the monoclinic Li2TiO3 structure type, whereas for the x = 0.4 composition the peak positions are in agreement with the cubic NaCl structure type. For x = 0.3, the situation is intermediate. Indeed, most of the diffraction pattern is consistent with the NaCl structure type; however, some weak peaks (especially at ∼90°) are associated with the Li2TiO3 superstructure type. For this special composition both structure models have been attempted for refinement. In order to charge-balance and be consistent with the (1−x)Li2TiO3–xMgO doping mechanism, several choices for occupational constraints can be introduced depending on whether or not full occupancy on the various sites is maintained. Several models have been tested in order to consider various scenarios: (1) an independent distribution of Mg on all three 4e sites, (2) an equal distribution of Mg on the three 4e sites, (3) constraining only the Mg content of the two Ti 4e sites to be equal, or(4) an equal distribution of Mg on all five cation sites. Based on the refinements for x = 0.1, 0.2 and 0.3, the third scenario (Mg distributed on all three 4e sites but equally on the two Ti ones) yields the best results, with physically meaningful values for the atomic displacement parameters (ADPs). The refined cell parameters as well as the observed reliability factors for x = 0.1, 0.2 and 0.3 are summarized in Table 1. Tables 2–4 list all the atomic positions, ADPs and occupation parameters for these compositions. A summary of the calculated bond lengths and bond valencies is given in Table 5. There is a slight increase in the Li3/Mg3 bond valence and a corresponding decrease in the Ti1/Mg1 and Ti2/Mg2 bond valencies as a result of Mg residing on the Li3 and Ti1/Ti2 sites. Accounting for the partial site occupancies in the monoclinic model, the refined compositional x parameters are 0.05, 0.14, and 0.25 for the nominal compositions x = 0.1, 0.2, and 0.3, respectively. In the cubic model, equivalent x parameters were refined as 0.28 and 0.42 for nominal compositions x = 0.3 and 0.4, respectively.
Table 1 Refinement results for (1−x)Li2TiO3–xMgO for x = 0.1,0.2 and 0.3 according to the C2/c model
| Compound (1-x)Li2TiO3–xMgO |
x = 0.1 |
x = 0.2 |
x = 0.3 |
|
a/Å |
5.0798 (4) |
5.0856 (3) |
5.0903 (2) |
|
b/Å |
8.8076 (5) |
8.8096 (5) |
8.8164 (2) |
|
c/Å |
9.7729 (5) |
9.7696 (5) |
9.7579 (4) |
|
β (°) |
100.158 (6) |
100.123 (4) |
100.121 (2) |
| Cell mass (g mol−1) |
104.83 |
107.97 |
110.34 |
| Cell volume/Å3 |
430.4 |
430.9 |
431.1 |
| Crystallite Density (g cm−3) |
3.2347 |
3.3094 |
3.3994 |
|
R
obs (%) |
4.12 |
4.05 |
3.94 |
Table 2 Atomic parameters, occupancies and equivalent displacement parameters (Å2) for (1−x)Li2TiO3–xMgO for x = 0.1 according to the C2/c model
| Atom |
Site |
Occupancy |
x
|
y
|
z
|
U
eq
|
| Li1 |
8f |
1 |
0.231 (5) |
0.080 (3) |
0.011 (2) |
0.016 (2) |
| Li2 |
4d |
1 |
0.750 |
0.250 |
0 |
0.016 (2) |
| Li3 |
4e |
0.934 (14) |
0 |
0.924 (11) |
0.750 |
0.0102 (18) |
| Mg3 |
4e |
0.066 (14) |
0 |
0.924 (11) |
0.750 |
0.0102 (18) |
| Ti1 |
4e |
0.983 (4) |
0 |
0.583 (5) |
0.750 |
0.0102 (18) |
| Mg1 |
4e |
0.017 (4) |
0 |
0.583 (5) |
0.750 |
0.0102 (18) |
| Ti2 |
4e |
0.983 (4) |
0.500 |
0.750 (5) |
0.750 |
0.0102 (18) |
| Mg2 |
4e |
0.017 (4) |
0.500 |
0.750 (5) |
0.750 |
0.0102 (18) |
| O1 |
8f |
1 |
0.1407 (13) |
0.7410 (13) |
0.6359 (10) |
0.0121 (4) |
| O2 |
8f |
1 |
0.6089 (14) |
0.9148 (12) |
0.6385 (8) |
0.0121 (4) |
| O3 |
8f |
1 |
0.3645 (13) |
0.5947 (11) |
0.8639 (8) |
0.0121 (4) |
Table 3 Atomic parameters, occupancies and equivalent displacement parameters (Å2) for (1−x)Li2TiO3–xMgO for x = 0.2 according to the C2/c model
| Atom |
Site |
Occupancy |
x
|
y
|
z
|
U
eq
|
| Li1 |
8f |
1 |
0.2306 (6) |
0.0710 (4) |
0.9920 (3) |
0.023 (3) |
| Li2 |
4d |
1 |
0.75 |
0.25 |
0 |
0.023 (3) |
| Li3 |
4e |
0.792 (18) |
0 |
0.946 (18) |
0.75 |
0.0167 (11) |
| Mg3 |
4e |
0.208 (18) |
0 |
0.946 (18) |
0.75 |
0.0167 (11) |
| Ti1 |
4e |
0.948 (5) |
0 |
0.584 (3) |
0.75 |
0.0167 (11) |
| Mg1 |
4e |
0.052 (5) |
0 |
0.584 (3) |
0.75 |
0.0167 (11) |
| Ti2 |
4e |
0.948 (5) |
0.5 |
0.749 (3) |
0.75 |
0.0167 (11) |
| Mg2 |
4e |
0.052 (5) |
0.5 |
0.749 (3) |
0.75 |
0.0167 (11) |
| O1 |
8f |
1 |
0.1363 (14) |
0.7538 (5) |
0.6360 (10) |
0.0271 (4) |
| O2 |
8f |
1 |
0.6178 (15) |
0.9146 (16) |
0.6352 (8) |
0.0271 (4) |
| O3 |
8f |
1 |
0.3706 (14) |
0.5889 (17) |
0.8661 (8) |
0.0271 (4) |
Table 4 Atomic parameters, occupancies and equivalent displacement parameters (Å2) for (1−x)Li2TiO3–xMgO for x = 0.3 according to the C2/c model
| Atom |
Site |
Occupancy |
x
|
y
|
z
|
U
eq
|
| Li1 |
8f |
1 |
0.248 (13) |
0.087 (8) |
0.004 (6) |
0.036 (5) |
| Li2 |
4d |
1 |
0.750 |
0.250 |
0 |
0.036 (5) |
| Li3 |
4e |
0.604 (17) |
0 |
0.885 (15) |
0.750 |
0.014 (3) |
| Mg3 |
4e |
0.396 (17) |
0 |
0.885 (15) |
0.750 |
0.014 (3) |
| Ti1 |
4e |
0.901 (4) |
0 |
0.905 (8) |
0.750 |
0.014 (3) |
| Mg1 |
4e |
0.099 (4) |
0 |
0.905 (8) |
0.750 |
0.014 (8) |
| Ti2 |
4e |
0.901 (4) |
0.500 |
0.753 (4) |
0.750 |
0.014 (3) |
| Mg2 |
4e |
0.099 (4) |
0.500 |
0.753 (4) |
0.750 |
0.014 (3) |
| O1 |
8f |
1 |
0.1306 (18) |
0.754 (4) |
0.6282 (10) |
0.0282 (3) |
| O2 |
8f |
1 |
0.6261 (20) |
0.914 (4) |
0.6285 (9) |
0.0282 (3) |
| O3 |
8f |
1 |
0.380 (2) |
0.583 (4) |
0.8707 (10) |
0.0282 (3) |
Table 5 Selected bond lengths and bond valencies (1−x)Li2TiO3–xMgO for x = 0.1, 0.2 and 0.3 according to the C2/c model
| Compound (1−x)Li2TiO3–xMgO |
x = 0.1 |
x = 0.2 |
x = 0.3 |
| Bond length (Å) of Li1 (8f) - O |
|
|
|
| Li1–O1 |
2.1970 |
2.2165 |
2.1199 |
| Li1–O1′ |
2.0937 |
2.1974 |
2.0113 |
| Li1–O2 |
2.3092 |
2.0914 |
2.1679 |
| Li1–O2′ |
2.0967 |
2.2096 |
2.0868 |
| Li1–O3 |
2.1460 |
2.0244 |
2.0840 |
| Li1–O3′ |
2.0753 |
2.1028 |
2.1084 |
| Bond length (Å) of Li2 (4d) - O |
|
|
|
| Li2–O1 x 2 |
2.1862 |
2.1699 |
2.1129 |
| Li2–O2 x 2 |
2.1897 |
2.1474 |
2.0829 |
| Li2–O3 x 2 |
2.0619 |
2.0937 |
2.1192 |
| Bond length (Å) of Li3/Mg3 (4e) - O |
|
|
|
| Li3/Mg3–O1 x 2 |
2.1525 |
2.2044 |
1.8619 |
| Li3/Mg3–O2 x 2 |
2.0922 |
2.0847 |
2.0728 |
| Li3/Mg3–O3 x 2 |
2.0600 |
1.8886 |
2.2491 |
| Bond length (Å) of Ti1/Mg1 (4e) - O |
|
|
|
| Ti1/Mg1–O1 x 2 |
1.9930 |
2.0567 |
1.9760 |
| Ti1/Mg1–O2 x 2 |
1.9750 |
2.0199 |
2.0585 |
| Ti1/Mg1–O3 x 2 |
1.9877 |
2.0222 |
2.1154 |
| Bond length (Å) of Ti2/Mg2 (4e) - O |
|
|
|
| Ti2/Mg2–O1 x 2 |
1.9655 |
1.9847 |
2.0395 |
| Ti2/Mg2–O2 x 2 |
1.9527 |
1.9953 |
2.0247 |
| Ti2/Mg2–O3 x 2 |
1.9632 |
1.9928 |
2.0637 |
| Bond valence of |
|
|
|
| Li1–O (8f) |
0.96 |
0.99 |
1.10 |
| Li2–O (4d) |
0.97 |
0.98 |
1.07 |
| Li3/Mg3–O (4e) |
1.14 |
1.51 |
1.76 |
| Ti1/Mg1–O (4e) |
3.77 |
3.28 |
3.13 |
| Ti2/Mg2–O (4e) |
4.03 |
3.68 |
3.16 |
| O1 |
1.91 |
1.71 |
2.19 |
| O2 |
1.95 |
1.87 |
1.84 |
| O3 |
2.05 |
2.13 |
1.62 |
The use of natural lithium, with a coherent scattering length of bc = −1.90 fm, did not cause any significant problems in the refinement. In any event, natural lithium is >94% 7Li (bc = −2.22 fm). Its use with Mg (bc = 5.375 fm) means that on average there is very little scattering on the shared Li3 site (0.1 ≤ x ≤ 0.3), especially for compositions near x = 0.2. In fact, the scattering theoretically vanishes if x = 0.1733. The use of pure 7Li would bring the zero-scatter composition up to 0.1913, further complicating the refinement for x = 0.2. Even so, this effect is likely to introduce some uncertainty in the shared Li3/Mg3 site occupancies and may be partly responsible for the differences in the refined and calculated x values.
As previously described, the (1−x)Li2TiO3–xMgO crystal structure for x = 0.4 can be well described using the  cubic space group. Using that space group, all the cations randomly share the 4a position at (0,0,0) whereas the oxygen ions fully occupy the 4b at (0,½,0). In order to maintain both full occupancy and charge neutrality, some constraints on the 4a positional occupancy must be applied. The constraints on occupancy (occ.) are as follows: occ.(Mg) = y; occ.(Ti) = 2/3(1−y) and occ.(Li) = 1/3(1−y) where
cubic space group. Using that space group, all the cations randomly share the 4a position at (0,0,0) whereas the oxygen ions fully occupy the 4b at (0,½,0). In order to maintain both full occupancy and charge neutrality, some constraints on the 4a positional occupancy must be applied. The constraints on occupancy (occ.) are as follows: occ.(Mg) = y; occ.(Ti) = 2/3(1−y) and occ.(Li) = 1/3(1−y) where  With these constraints in place, the refinements quickly converge to the values listed in Table 6. Background coefficients, scale factors, isotropic strain terms in the profile function and absorption were also refined for a total of 15 parameters in each pattern. For the x = 0.3 composition, despite the existence of weak superstructure peaks, the cubic model was also used to obtain an average structure; however, it should be noted that the monoclinic model (Robs = 3.94) yields a slightly better result as compared to the cubic one (Robs = 3.98).
With these constraints in place, the refinements quickly converge to the values listed in Table 6. Background coefficients, scale factors, isotropic strain terms in the profile function and absorption were also refined for a total of 15 parameters in each pattern. For the x = 0.3 composition, despite the existence of weak superstructure peaks, the cubic model was also used to obtain an average structure; however, it should be noted that the monoclinic model (Robs = 3.94) yields a slightly better result as compared to the cubic one (Robs = 3.98).
Table 6 Refined Mg, Ti and Li occupancies in (1−x)Li2TiO3–xMgO for x = 0.3 and x = 0.4 according to the model in 
| Composition (x) |
lattice constant a (Å) |
Occ.(Mg) in %, Refined x value |
Occ.(Ti) in (%) |
Occ.(Li) in (%) |
R
obs (%) |
| 0.3 |
4.15673 (13) |
11.3 (x∼0.113) |
29.6(2) |
59.1(2) |
3.98 |
| 0.4 |
4.16133 (8) |
19.2 (x∼0.192) |
24.7(2) |
56.1(2) |
3.81 |
Patterns from x=0.4 (Fig. 1(e) and Fig. 2(e)) and 0.5 (Fig. 1(f) and Fig. 2(f)) samples contained distinctive arrangements of diffuse scattering in addition to the strong Bragg reflections expected from the NaCl–type lattice. The shape of the diffuse scattering caused by short-range order is similar to that observed in transition-metal carbides and nitrides31–32 as well as in LiFeO233–34 with a NaCl-related structure and has been analyzed theoretically by Sauvage and Parth.35–36 While the diffuse scattering in transition-metal carbides and nitrides was related to a short-range order of vacancies, in the case of disordered α–LiFeO2, the diffuse scattering was a result of disordered Li and Fe cation sites in the NaCl–type lattice.33–34 Similarly, the diffuse scattering observed in the x ≥ 0.4 samples can be interpreted as a result of a random distribution of Li, Ti and Mg on the 4a sites with some short-range order in the cubic rocksalt lattice. When the structure transforms from ordered monoclinic to disordered cubic, the occupancy of Mg on the 8f and 4d Li sites in the C2/c symmetry, which become the 4a sites in the 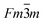 structure break the ordering which results in some degree of short-range order on the cation sites.
structure break the ordering which results in some degree of short-range order on the cation sites.
4. Conclusion
The order–disorder transition in magnesium lithium titanate solid-solution samples, (1−x)Li2TiO3–xMgO (0 ≤ x ≤ 0.5) was investigated by electron diffraction, neutron diffraction and HRTEM. The superlattice reflections in electron diffraction patterns for x = 0.2 and x = 0.3 samples were caused by twin variants. The addition of Mg into the ordered monoclinic rocksalt Li2TiO3 structure ultimately yields and stabilizes the disordered cubic γ–Li2TiO3 phase. When the Mg content is low (x = 0.1 and x = 0.2), the monoclinic phase is retained with Mg residing on either Li or Ti sites (4e). For x = 0.3, the situation is intermediate. When the Mg content increases still further (x = 0.4 and x = 0.5), the phase transforms into disordered cubic γ–Li2TiO3 phase with Mg randomly distributed in the structure with some degree of short-range ordering, which causes diffuse scattering in electron diffraction patterns.
Acknowledgements
This work has been supported by the US Agency for International Development and the National Academy of Sciences under the Pakistan-US Science, and Technology Cooperative Program, Award No. PGA-P280420 and the National Science Foundation of China (NSFC), Award No. 50872081. Additional support from the National Science Foundation Major Research Instrumentation Program, Award No. 0521315, is also gratefully acknowledged.
References
- L. L. Yuan and J. J. Bian, Ferroelectrics, 2009, 387, 123 CrossRef CAS.
- J. J. Bian and Y. F. Dong, J. Eur. Ceram. Soc., 2010, 30, 325 CrossRef CAS.
- J. P. Kopasz, J. M. Miller and C. E. Johnson, J. Nucl. Mater., 1994, 212–215, 927 CrossRef CAS.
- N. Roux, J. Avon, A. Floreancing, J. Mougin, B. Rasneur and S. Ravel, J. Nucl. Mater., 1996, 233–237, 1431 CrossRef CAS.
- K. Tsuchiya and H. Kawamura, J. Nucl. Mater., 2000, 283–287, 1380 CrossRef CAS.
- C. Alvani, S. Casadio, V. Contini, A. Di Bartolomeo, J. D. Lulewicz and N. Roux, J. Nucl. Mater., 2002, 307–311, 837 CrossRef CAS.
- J. D. Lulewicz and N. Roux, J. Nucl. Mater., 2002, 307–311, 803 CrossRef CAS.
- K. Tsuchiya, M. Nakamichi, A. Kikukawa, Y. Nagao, M. Enoeda, T. Osaki, K. Ioki and H. Kawamura, J. Nucl. Mater., 2002, 307–311, 817 CrossRef CAS.
- K. Tsuchiya, H. Kawamura, T. Takayama and S. Kato, J. Nucl. Mater., 2005, 345, 239 CrossRef CAS.
- L. Zhang, X. Wang, H. Noguchi, M. Yoshio, K. Takada and T. Sasaki, Electrochim. Acta, 2004, 49, 3305 CrossRef CAS.
- C. S. Johnson, J. -S. Kim, A. J. Kropf, J. Kahaian, J. T. Vaughey and M. M. Thackeray, J. Power Sources, 2003, 139, 119 Search PubMed.
- M. Vijayakumar, S. Kerisit, Z. Yang, G. L. Graff, J. Liu, J. A. Sears, S. D. Burton, K. M. Rosso and J. Hu, J. Phys. Chem. C, 2009, 113, 20108 CAS.
- V. Chauvaut and M. J. Cassir, Electroanal. Chem., 1999, 9, 474 Search PubMed.
- L. Zhang, T. Muta, H. Noguchi, X. Wang, M. Zhou and M. Yoshio, J. Power Sources, 2003, 117, 137 CrossRef CAS.
- M. Tabuchi, A. Nakashima, H. Shigemura, K. Ado, H. Kobayashi, H. Sakaebe, K. Tatsumi, H. Kageyama, T. Nakamura and R. Kanno, J. Mater. Chem., 2003, 13, 1747 RSC.
- H. Shigemura, M. Tabuchi, H. Sakaebe, H. Kobayashi and H. Kageyama, J. Electrochem. Soc., 2003, 150, A638 CrossRef CAS.
- L. Zhang and H. Noguchi, Electrochem. Commun., 2002, 4, 560 CrossRef CAS.
- L. Zhang and H. Noguchi, J. Electrochem. Soc., 2003, 150, A607 CrossRef.
- J. S. Kim, C. S. Johnson and M. M. Thackeray, Electrochem. Commun., 2002, 4, 205 CrossRef CAS.
- C. S. Johnson, J. S. Kim, A. J. Kropf, A. J. Kahaian, J. T. Vaughey and M. M. Thackeray, Electrochem. Commun., 2002, 4, 492 CrossRef CAS.
- J. S. Kim, C. S. Johnson, J. T. Vaughey, M. M. Thackeray, S. A. Hackney, W. Yoon and C. P. Grey, Chem. Mater., 2004, 16, 1996 CrossRef CAS.
- J. F. Dorrian and R. E. Newnham, Mater. Res. Bull., 1969, 4, 179 CrossRef CAS.
- G. C. Mather, C. Dussarrat, J. Etourneau and A. R. West, J. Mater. Chem., 2000, 10, 2219 RSC.
- G. Izquierdo and A. R. West, Mater. Res. Bull., 1980, 15, 1655 CrossRef CAS.
- M. Castellanos and A. R. West, J. Mater. Sci., 1979, 14, 450 CrossRef CAS.
- V. O. Garlea, B. C. Chakoumakos, S. A. Moore, G. B. Taylor, T. Chae, R. G. Maples, R. A. Riedel, G. W. Lynn and D. L. Selby, Appl. Phys. A: Mater. Sci. Process., 2010, 99, 531 CrossRef CAS.
- W. H. Bragg and W. L. Bragg, Proc. R. Soc. London, Ser. A, 1913, 88, 428 CrossRef CAS.
- J. F. Dorian and R. E. Newnham, Mater. Res. Bull., 1969, 4, 179 CrossRef.
- K. K. Kataoka, Y. Takahashi, N. Kijima, H. Nagai, J. Akimoto, Y. Idemoto and K. Ohshima, Mater. Res. Bull., 2009, 44, 168 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, A32, 751 CrossRef CAS.
- J. Billingham, P. S. Bell and M. H. Lewis, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1972, A28, 602 CrossRef.
- P. Li and J. M. Howe, Acta Mater., 2003, 51, 1261 CrossRef CAS.
- J. G. Alpress, J. Mater. Sci., 1971, 6, 313 CrossRef.
- J. M. Cowley, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1973, A29, 537 CrossRef.
- M. Sauvage and E. Parthé, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1972, A28, 607 CrossRef.
- M. Sauvage and E. Parthé, Acta Cryst., 1974, A30, 239 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here.  symmetry, resulting in diffuse scattering in electron diffraction patterns.
symmetry, resulting in diffuse scattering in electron diffraction patterns. }. The superlattice reflections which appear in the [
}. The superlattice reflections which appear in the [ ]m patterns of Fig. 2 can be described by a modulation wave vector, q, as shown in Fig. 2(d). In real space, 1/q = Q which has a length of 2d(131)m = 4.783 Å, which is close to d(002)m = 4.789 Å. The extra {odd, even, odd} and {even, odd, even} reflections like those circled in Fig. 2(d) are caused by double diffraction; however, it should be noted that the {020} and {040} type reflections are fainter than those observed in typical Li2TiO3 structures (Fig. 2(a)–(c)). Reflections shown within the horizontal ovals arise from an [010] oriented domain, which is related through a
]m patterns of Fig. 2 can be described by a modulation wave vector, q, as shown in Fig. 2(d). In real space, 1/q = Q which has a length of 2d(131)m = 4.783 Å, which is close to d(002)m = 4.789 Å. The extra {odd, even, odd} and {even, odd, even} reflections like those circled in Fig. 2(d) are caused by double diffraction; however, it should be noted that the {020} and {040} type reflections are fainter than those observed in typical Li2TiO3 structures (Fig. 2(a)–(c)). Reflections shown within the horizontal ovals arise from an [010] oriented domain, which is related through a  twin plane to a
twin plane to a  variant, unique reflections from which are shown outlined with diamonds. The indexing shown in the overall pattern has been calculated according to this variant, which is, in turn, related through a
variant, unique reflections from which are shown outlined with diamonds. The indexing shown in the overall pattern has been calculated according to this variant, which is, in turn, related through a  twin plane to a
twin plane to a  variant, unique reflections from which are shown outlined with vertical ovals. The mirror symmetry in the pattern shows that the effect is indistinguishable from a twin plane on {101} or
variant, unique reflections from which are shown outlined with vertical ovals. The mirror symmetry in the pattern shows that the effect is indistinguishable from a twin plane on {101} or  relating [010] and
relating [010] and  variants. Reflections common to all variants are left un-annotated.
variants. Reflections common to all variants are left un-annotated.
![SADPs of (1−x)Li2TiO3–xMgO for (a) x = 0, (b) x = 0.1, (c) x = 0.2, and (d) x = 0.3 parallel to [301]m and (e) x = 0.4 and (f) x = 0.5 parallel to [100]c.](/image/article/2012/RA/c1ra00677k/c1ra00677k-f1.gif)
![SADPs of (1−x)Li2TiO3–xMgO for (a) x = 0, (b) x = 0.1, (c) x = 0.2, and (d) x = 0.3 parallel to []m, and (e) x = 0.4 and (f) x = 0.5 parallel to [110]c.](/image/article/2012/RA/c1ra00677k/c1ra00677k-f2.gif)
 ]m, and (e) x = 0.4 and (f) x = 0.5 parallel to [110]c.
]m, and (e) x = 0.4 and (f) x = 0.5 parallel to [110]c. ]m with the corresponding SADP showing superlattice reflections, inset. Four different regions marked with capital letters in Fig. 3(a) refer to three types of superstructures, as indicated by three different fast Fourier transform (FFT) images. Regions A and B yield type I diffraction (Fig. 3(b)), that is,
]m with the corresponding SADP showing superlattice reflections, inset. Four different regions marked with capital letters in Fig. 3(a) refer to three types of superstructures, as indicated by three different fast Fourier transform (FFT) images. Regions A and B yield type I diffraction (Fig. 3(b)), that is, 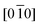 . Region C yields type II (Fig. 3(c)), or [010]. When these two FFT images are combined, the resultant image is type III diffraction, shown in Fig. 3(d). This pattern can be interpreted as above, that is two <010> variants related through {101} or
. Region C yields type II (Fig. 3(c)), or [010]. When these two FFT images are combined, the resultant image is type III diffraction, shown in Fig. 3(d). This pattern can be interpreted as above, that is two <010> variants related through {101} or  twinning. The superposition of type III diffraction upon the expected Li2TiO3 [
twinning. The superposition of type III diffraction upon the expected Li2TiO3 [ ]m patterns (Fig. 2(a)), caused by further twinning on
]m patterns (Fig. 2(a)), caused by further twinning on , yields diffraction patterns like the experimental one shown in the inset. To visualize the superstructures on a larger scale, a small objective aperture was used to include a small number of superstructural diffracted electron beams. Fig. 4 shows the bright-field and dark-field images for these superstructures, which appear as submicron coherent precipitates.
, yields diffraction patterns like the experimental one shown in the inset. To visualize the superstructures on a larger scale, a small objective aperture was used to include a small number of superstructural diffracted electron beams. Fig. 4 shows the bright-field and dark-field images for these superstructures, which appear as submicron coherent precipitates.![(a) HRTEM image taken parallel to the []m zone axis with corresponding SADPs inset for the x = 0.3 sample. (b) FFT of region A and B, (c) FFT of region C and (d) FFT of region D.](/image/article/2012/RA/c1ra00677k/c1ra00677k-f3.gif)
 ]m zone axis with corresponding SADPs inset for the x = 0.3 sample. (b) FFT of region A and B, (c) FFT of region C and (d) FFT of region D.
]m zone axis with corresponding SADPs inset for the x = 0.3 sample. (b) FFT of region A and B, (c) FFT of region C and (d) FFT of region D.![TEM images parallel to the []m zone axis of the x = 0.3 sample. Both (a) bright-field and (b) dark-field images show precipitates.](/image/article/2012/RA/c1ra00677k/c1ra00677k-f4.gif)
 ]m zone axis of the x = 0.3 sample. Both (a) bright-field and (b) dark-field images show precipitates.
]m zone axis of the x = 0.3 sample. Both (a) bright-field and (b) dark-field images show precipitates. ]m with associated SADPs taken within the marked areas. The micron-scale substructures in x = 0.2 are larger than those in x = 0.3. As such, SAD apertures could be used to select the areas of interest for electron diffraction. Five different types of SADP appeared in different regions within a single grain. Electron diffraction taken at the small region I shows it to be in the [
]m with associated SADPs taken within the marked areas. The micron-scale substructures in x = 0.2 are larger than those in x = 0.3. As such, SAD apertures could be used to select the areas of interest for electron diffraction. Five different types of SADP appeared in different regions within a single grain. Electron diffraction taken at the small region I shows it to be in the [ ]m orientation (Fig. 5(b)). SADPs taken in regions II and III (Fig. 5(c) and (d)), corresponding to the FFT images shown in Fig. 3(c) and (b), can be interpreted as variants parallel to <010>. The combination of SADPs from regions II and III yields the pattern from region IV (Fig. 5e). The combination of the patterns from regions I, II and III yields the complicated diffraction pattern shown in Fig. 5(f). What looks like a ½(131)m superlattice reflection (q) in the [
]m orientation (Fig. 5(b)). SADPs taken in regions II and III (Fig. 5(c) and (d)), corresponding to the FFT images shown in Fig. 3(c) and (b), can be interpreted as variants parallel to <010>. The combination of SADPs from regions II and III yields the pattern from region IV (Fig. 5e). The combination of the patterns from regions I, II and III yields the complicated diffraction pattern shown in Fig. 5(f). What looks like a ½(131)m superlattice reflection (q) in the [ ]m zone (Fig. 2(d)) is actually attributable to the (002)m reflection in the [010]m zone (Fig. 5(c)). Regardless of the large difference in size of the substructures in the x = 0.2 and x = 0.3, samples of both compositions retain the structure of ordered monoclinic Li2TiO3. Fig. 6 shows the bright-field TEM image obtained parallel to <301>m with associated electron diffraction patterns taken within the marked regions. Again, the complicated pattern of superlattice reflections (Fig. 6(d)), which is identical to that in Fig. 1(d), can be explained by the overlap of
]m zone (Fig. 2(d)) is actually attributable to the (002)m reflection in the [010]m zone (Fig. 5(c)). Regardless of the large difference in size of the substructures in the x = 0.2 and x = 0.3, samples of both compositions retain the structure of ordered monoclinic Li2TiO3. Fig. 6 shows the bright-field TEM image obtained parallel to <301>m with associated electron diffraction patterns taken within the marked regions. Again, the complicated pattern of superlattice reflections (Fig. 6(d)), which is identical to that in Fig. 1(d), can be explained by the overlap of 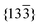 twin variants (parallel to <301>) with each other in region III (Fig. 6(a) and (d)).
twin variants (parallel to <301>) with each other in region III (Fig. 6(a) and (d)).![(a) TEM image of sample x = 0.2 projected along []m with the corresponding SADPs corresponding to (b) region I, (c) region II, (d) region III, (e) region IV, and (f) region V.](/image/article/2012/RA/c1ra00677k/c1ra00677k-f5.gif)
 ]m with the corresponding SADPs corresponding to (b) region I, (c) region II, (d) region III, (e) region IV, and (f) region V.
]m with the corresponding SADPs corresponding to (b) region I, (c) region II, (d) region III, (e) region IV, and (f) region V.![(a) TEM image of sample x = 0.2 projected along [301]m with the corresponding SADPs taken in (b) region I, (c) region II, and (d) region III.](/image/article/2012/RA/c1ra00677k/c1ra00677k-f6.gif)


 cubic space group. Using that space group, all the cations randomly share the 4a position at (0,0,0) whereas the oxygen ions fully occupy the 4b at (0,½,0). In order to maintain both full occupancy and charge neutrality, some constraints on the 4a positional occupancy must be applied. The constraints on occupancy (occ.) are as follows: occ.(Mg) = y; occ.(Ti) = 2/3(1−y) and occ.(Li) = 1/3(1−y) where
cubic space group. Using that space group, all the cations randomly share the 4a position at (0,0,0) whereas the oxygen ions fully occupy the 4b at (0,½,0). In order to maintain both full occupancy and charge neutrality, some constraints on the 4a positional occupancy must be applied. The constraints on occupancy (occ.) are as follows: occ.(Mg) = y; occ.(Ti) = 2/3(1−y) and occ.(Li) = 1/3(1−y) where  With these constraints in place, the refinements quickly converge to the values listed in Table 6. Background coefficients, scale factors, isotropic strain terms in the profile function and absorption were also refined for a total of 15 parameters in each pattern. For the x = 0.3 composition, despite the existence of weak superstructure peaks, the cubic model was also used to obtain an average structure; however, it should be noted that the monoclinic model (Robs = 3.94) yields a slightly better result as compared to the cubic one (Robs = 3.98).
With these constraints in place, the refinements quickly converge to the values listed in Table 6. Background coefficients, scale factors, isotropic strain terms in the profile function and absorption were also refined for a total of 15 parameters in each pattern. For the x = 0.3 composition, despite the existence of weak superstructure peaks, the cubic model was also used to obtain an average structure; however, it should be noted that the monoclinic model (Robs = 3.94) yields a slightly better result as compared to the cubic one (Robs = 3.98).
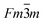 structure break the ordering which results in some degree of short-range order on the cation sites.
structure break the ordering which results in some degree of short-range order on the cation sites.