Pair distribution function analysis and Mössbauer study of defects in microwave-hydrothermal LiFePO₄

Abstract

Olivine-type LiFePO₄ is nowadays one of the most important cathode materials of choice for high-energy lithium ion batteries. Its intrinsic defectivity, and chiefly the so-called lithium ironanti-site, is one of the most critical issues when envisaging electrochemical applications. This paper reports a combined diffractometric (Synchrotron Radiation XRD with Rietveld and PDF analyses) and spectroscopic (Mössbauer) approach able to give a thorough characterization of the material defectivity. Such analytical procedure has been applied to a sample prepared following an innovative microwave-assisted hydrothermal synthesis route that, in a few minutes, allowed us to obtain a well crystallized material. PDF analysis, which is applied for the first time to this type of battery material, reveals the presence of disorder possibly due to Li/Fe exchange or to a local symmetry lowering. A 5% amount of iron on the lithium site has been detected both by PDF as well as by Mössbauer spectroscopy, which revealed a small percentage of Fe³⁺ on the regular sites.

---

1 Introduction

LiFePO₄ is the likely cathode material of choice for lithium ion batteries.^1–4 Several studies have been recently devoted to the optimization of this material through the development of new synthesis routes that favoured the formation of particles with specific morphologies (nanoparticles, hollow sphere, oriented platelet-like shaped geometries and so on), which are considered promising for electrochemical applications.^5,6 Among the synthetic routes available nowadays, the hydrothermal method is often used for its low operating temperature, but it requires long reaction times and can produce olivine-type material with non-homogeneous particles dimension and shape. Recently, an innovative procedure based on the simultaneous application of microwaves and hydrothermal processes has been proposed in order to overcome these limitations.^7–10 Irradiation of pressurized vessels made of materials, such as Teflon®, which do not absorb microwave energy, can lead to fast and volumetric heating of the reaction solution.¹¹ Under these conditions a uniform temperature is rapidly reached, and nucleation and growth can occur in a very restricted temperature range when solid compounds are precipitated.¹² Within this approach, unique morphologies and/or metastable crystalline phases can be generated.¹³

Olivine-type material prepared by hydrothermal or precipitation methods has been recognised as intrinsically defective due to the low temperature and short times of synthesis;^14–16 for this reason, further thermal treatments are necessary in order to remove the structural defects making the material suitable for electrochemical applications. The most cited defect is the lithium ironanti-site, which has been addressed both by experimental work^17–19 and by theoretical energy computation.²⁰ Very often during the preparation of the material small percentages of Fe³⁺ are formed and lithium vacancies should be invoked for charge balancing; these intrinsic defects have been recently discussed and observed through the use of Mössbauer and XAS spectroscopies as well as with magnetisation measurements.^15,21,22

In addition to these established spectroscopic techniques used for the investigation of the local order, atomic Pair Distribution Function (PDF) analysis is now emerging as a powerful tool for the study of defects. This approach was initially proposed for amorphous materials and for liquids but, owing to recent technological developments, it is now currently applied also to crystalline oxides.^23,24 Recently, this technique has been applied in combination with Li MAS-NMR to the study of battery materials such as LiNi_0.5Mn_0.5O₂ and nano-FeF₃.^25,26

In this work we propose a combined use of Synchrotron Radiation X-ray Powder Diffraction (SR-XRPD) with Rietveld analysis, PDF analysis and of Mössbauer spectroscopy for the defect characterization of crystalline LiFePO₄, prepared by means of an innovative microwave-assisted hydrothermal synthesis performed at low temperature for a few minutes. Besides the intrinsic interest to develop a fast and efficient method for LiFePO₄ synthesis, our specific aim was to obtain a defective material as a benchmark to test our characterization approach. The investigation of the structural disorder has been carried out, for the first time to the best of our knowledge, by combining the Rietveld method and the PDF analysis on synchrotron radiation data. The defect models have been supported by Mössbauer spectroscopy, which allowed characterization of the iron environment and oxidation state.

2 Experimental details

2.1 Synthesis

The LiFePO₄ sample was prepared by microwave assisted hydrothermal synthesis by the reactive system FeSO₄·7H₂O (Aldrich ≥ 99.0%), NH₄H₂PO₄ (Aldrich ≥ 99.9%) and CH₃COOLi·2H₂O (Fluka ≥ 99.0%) in the molar ratio 1 : 1 : 3 (Fe:P:Li). These reagents were dissolved in a polyvinylpyrrolidone (PVP, Aldrich) aqueous solution. In order to obtain a carbon coated sample, suitable for further electrochemical tests, glucose was added to the reaction mixture. The synthesis was performed in Teflon® lined digestion vessels after the addition of N₂ to prevent iron oxidation. The initial and final solution pH values were in the range 4.5–5. After the preparation of the reaction mixture, the sealed vessel was hydrothermally treated using a microwave digestion system Ethos TC (Milestone) operating at 2.45 GHz at 170 °C for 15 min with precise control of time, temperature, pressure and microwave power. After the reaction the precipitated powder was filtered, washed and dried in an oven at 80 °C overnight.

An ICP-OES Perkin Elmer Optima 3300 DV was used for the elemental analysis measurements to verify the sample stoichiometry.

2.2 Characterization

2.2.1 Synchrotron X-ray powder diffraction . Synchrotron Radiation X-Ray powder diffraction pattern measurements were performed at the Swiss Light Source Materials Science (SLS-PD) beamline Powder Diffraction (PD) station. The sample was mounted in 0.3 mm Lindemann capillaries spinning at 10 Hz and measured in Debye Scherrer (transmission) geometry at nominal 0.49 Å using the 1-dimensional MYTHEN silicon solid-state high resolution detector.²⁷ Whole powder diffraction pattern was collected over 140 degrees in 2θ. The working photon wavelength and the 2θ zero offset were carefully calibrated by recording the diffraction pattern from a silicon standard (NIST 640C) and performing a LeBail refinement with an in-house refinement program optimized for the MS-PD beamline optics and detectors. The result of the silicon refinement has given for λ the value of 0.49052 ± 0.000131 Å. The scattering from the sample holder (empty capillary), the scattering from air (no sample/no capillary) as well as the experimental μR factor (μ = linear absorption coefficient, R = sample thickness, i.e. capillary diameter) were recorded under the same identical experimental conditions according to the data collection strategy described elsewhere.²⁸

2.2.2 Rietveld refinement. The pattern was refined on the basis of the Rietveld method by means of the TOPAS3.0 software.²⁹ The olivine-type material structure (JCPDS 40-1499) belongs to the Pnma space group (s.g.). In this structure Li is in the 4a site (0, 0, 0), Fe, P, O1 and O2 are in the 4c site (x, ¼, z) and O3 is in the general 8d site (x, y, z). Three models were tested:

Model A: Non-defective structure.

Model B: Fe Frenkel defect in the (0.38,0.45,0.42) interstitial site.²⁰

Model C: Li-Feanti-site pair defect in which iron and lithium are partially exchanged on the respective sites.²⁰

The refined parameters were scale factor, zero-error, 9 background coefficients, lattice parameters, atomic position of Fe, P and O ions, anisotropic thermal factors and occupancies.

2.2.3 Pair Distribution Function analysis. PDF analysis was performed on SR-XRPD data. Data were processed to obtain the PDF using PDFgetX2³⁰ and the structural modeling was carried out using the PDFfit2 software.³¹ The three models presented above were tested on the g(r) function up to 10 Å.

In addition, a different model based on a space group with a lower symmetry with respect to the orthorhombic Pnma was also tested. Some attempts to fit the g(r) with symmetry related subgroups of Pnma led to satisfactory results only with the s.g. P2₁. The maximum multiplicity of this s.g. is two, so the crystal structure is now described by two crystallographic sites for Li, Fe, P and O1, O2 ions and four sites are needed for the O3 ion. During the modelling, the β angle of the unit cell was maintained to 90° and the lithium site was kept with (0,0,0) coordinates, due to the low X-ray scattering factor of Li ion.

In general, the occupancies were refined using suitable constraints and the total amount of the cations was fixed to the stoichiometric quantity. The fitted parameters were the scale factor, the lattice constants, the anisotropic thermal factors, the occupancies and the dynamic correlation factor (δ) which takes into account the correlated motion between atom pairs.

2.2.4 Mössbauer spectroscopy. Mössbauer spectra, in the velocity range ± 5 mm s⁻¹, were collected at three different temperatures (75.2, 150 and 293 K) by means of a WissEl™ mod. MVT 1000 spectrometer, calibrated by using a standard metal iron foil, and an Oxford™ flux cryogenic system with a base-temperature of 1.8 K. The source is an Rh-matrix ⁵⁷Co with a recoilless fraction f_s = 0.76, as indicated by the manufacturer. The absorber (14 mm diameter) was prepared by using 57 mg of the LiFePO₄ sample and contains 13.11 mg cm⁻² of natural iron: the value derives from a compromise between a good signal to noise ratio and a not so large distortion of the line shape due to saturation effect.³² The expected value of the effective Mössbauer thickness of the absorber (t_a) is about 7.7 times the corresponding recoilless fraction.

A survey at the published literature on the subject reveals that spectra similar to the ones reported below were fitted by introducing broad Lorentzian lines, site distributions and/or by considering dynamical effects^15,33–43 which cause the Mössbauer line shape to deviate from the standard Lorentzian trend. Anyway, we note that in ref. 15,33–43 the authors use the linear approximation disregarding the line shape distortions due to the sample thickness, which become significant even at 8% absorption peaks.

Since the saturation effect determines a larger reduction of the absorption at resonance than off resonance, data analysis performed in linear approximation introduces spurious distributions of sites density.⁴⁴ These distributions are mainly localized near the highest peaks and they are likely to be the sources of errors in the physical interpretation of the results. Moreover, in the presence of dynamical effects (electronic relaxation, atomic diffusion, etc.) the spectrum shape and, consequently, the saturation effects change with the temperature. Therefore, the use of the linear approximation may lead to wrong evaluations of the relaxation times and of related physical parameters (i.e.activation energy, diffusion coefficient and so on).

Furthermore, the aim of the present analysis is to reveal small site contributions of about 5–10% of the total iron amount. However, since the standard fitting procedure based on Lorentzian profiles and linear approximation generally leads to erroneous evaluation of weak and/or poorly resolved contributions,⁴⁵ we chose to use the transmission integral³² in order to take into account simultaneously all the broadening/distortion effects:⁴⁴

where indicates the source line shape given by a Voigt profile whose Lorentzian component has a natural linewidth and the Gaussian one is suitable to reproduce the total line width of the source provided by the manufacturer, Γ_s = 1.03 mm s⁻¹. Moreover, f_s^r is the reduced source recoilless fraction given by , the effective thickness t_a determines the spectrum saturation and the Mössbauer cross section σ(ω) contains the hyperfine fields distributions and/or the relaxation characteristic times.

We focus on the crucial role of f_s^r , whose fitted value is strongly correlated to t_a one and to the physical parameters values that appear in σ(ω) . Therefore, eqn (1) cannot be properly used unless you verify the correctness of the f_s value provided by the manufacturer, by means of alternative methods,^46,47 where coincidence and anticoincidence Pulse Height Analysis (PHA) measurements are scheduled, too.

Since the quadrupolar splitting distributions reported in literature are approximately Gaussian^35,37 and their effects on the line shape are not always easily distinguishable from the ones connected with dynamical processes, we chose to express σ(ω) throughout Voigt doublets⁴⁸ having Lorentzian component of natural linewidth while the Gaussian one, describing all the above broadening/distortion effects, was treated as free parameter. Therefore, we stress that the Γ_g values reported on Table 6 indicate only the Gaussian broadenings and not the total linewidths, in fact Γ_tot = Γ_s + Γ_n + Γ_g + ΔΓ_ta ≅ 0.21 + Γ_g + 0.027t_a

2.2.5 Scanning Electron Microscopy . The scanning electron microscopy (SEM) determinations were obtained with a Zeiss EVO®-MA10-HR microscope on Au sputtered sample.

3- Results

3.1- SEM

Fig. 1 shows the SEM micrographs of the sample. Two different ranges of particle size are visible, large particles (Fig. 1a) with a length of 8 to 10 μm and thickness of 4.5 μm are covered with aggregates of fused crystallites with a similar elongated parallelepiped shape in the range 0.5–1.0 μm (Fig. 1b). Within each group of primary particles a certain homogeneity has been observed in morphology and dimensions.

Fig. 1 SEM images of the LiFePO₄ sample at low (a) and high (b) magnification.

3.2 Average structure: Rietveld refinement

The structural refinement was carried out on the basis of Models A, B and C. Table 1 reports the main structural refined parameters, the discrepancy factors and the bond lengths of LiO₆ and FeO₆ octahedra for Model A. Comparable lattice parameters and atomic fractional coordinates are obtained within the three models. Regarding the defective models, a quantity of about 1.4% of interstitial iron (Model B) and of about 1.7% of Li/Fe substitution (Model C) is present.

Table 1 Lattice parameters, atomic fractional coordinates, occupancy factors, bond lengths and discrepancy factors from Rietveld refinement on the basis of Model A

		Model A
a/Å		10.3268(1)
b/Å		5.9975(1)
c/Å		4.6945(1)
Atomic fractional coordinates	Fe	0.2818(4)
		0.9747(9)
	P	0.0946(7)
		0.4167(1)
	O1	0.0986(2)
		0.7432(4)
	O2	0.4540(2)
		0.2063(4)
	O3	0.1663(1)
		0.0425(2)
		0.2804(2)
Li–O/Å		2*2.091(2)
		2*2.177(2)
		2*2.179(2)
Fe–O/Å		2*2.048(2)
		2.084(2)
		2.183(2)
		2*2.243(2)
Rwp		3.39
Gof		5.80
RB		2.10

---

Satisfactory discrepancy factors were found for all the models, even if the Fe Frenkel one seems less favored, as revealed by the values of the anisotropic thermal factors, which are unusually high and characterized by significant standard deviations. As an example, the comparison between the calculated and observed patterns for Model C is reported in Fig. 2.

Fig. 2 Comparison between observed (blue line) and calculated (red line) patterns from the Rietveld refinement of the Model C. In the bottom the difference plot (gray line) and the bars indicating the angular positions of the reflections of olivine-type material are also reported.

3.3 Local structure: PDF analysis

The synchrotron diffraction pattern was processed to extract the reduced structure function: the Fourier transform of the normalized scattering intensity gives the PDF G(r). The maximum Q value used to extract the PDF was 17 Å⁻¹.

As already stated, the best-fit of the PDF was carried out by considering the three models. Fig. 3a shows the comparison between experimental and calculated PDF for the non-defective structure (Model A). The structural refinement doesn't lead to a satisfactory fit, as demonstrated by the difference curve at the bottom of Fig. 3a. Both the models B and C allow us to improve the fit in comparison to Model A (see Fig. 3b and c), and similar discrepancy factors are obtained. In Table 2 the main structural parameters are reported together with the discrepancy factors. The occupancies obtained for each model did reveal the presence of about 4% of interstitial iron and, in the case of Li/Fe exchange, of about 3.5% of substitutional iron. Comparing the three models, A and B present similar lattice parameters. In contrast, Model C gives different values which are close to those obtained by the Rietveld refinement. The u_ij parameters are of the order of 10⁻³ Ų and are not reported for the sake of simplicity. Table 3 reports the bond lengths of the different polyhedra.

Fig. 3 Graphical comparison between calculated (red line) and observed (black line) PDF for (a) Model A (b) Model B and (c) Model C.

Table 2 Lattice parameters, atomic fractional coordinates, cation distribution and discrepancy factors from PDF refinement on the basis of the different model

	Model A	Model B	Model C
a/Å	10.3568(1)	10.3606(1)	10.3397(1)
b/Å	6.0232(1)	6.0209(1)	6.0160(1)
c/Å	4.6539(1)	4.6668(1)	4.6743(1)
Fe	0.2818(1)	0.2821(2)	0.2809(3)
	0.9821(1)	0.9773(2)	0.9775(3)
Fe(Frenkel)		0.3570(4)
		0.4373(4)
		0.3823(4)
P	0.0992(2)	0.1021(2)	0.1015(1)
	0.4221(2)	0.4103(2)	0.4129(1)
O1	0.0927(1)	0.0869(1)	0.0903(1)
	0.7407(1)	0.7559(1)	0.7511(1)
O2	0.4498(2)	0.4527(2)	0.4582(2)
	0.1978(2)	0.1987(2)	0.1967(2)
O3	0.1726(1)	0.1739(1)	0.1737(1)
	0.0517(1)	0.0537(1)	0.0475(1)
	0.2837(1)	0.2832(1)	0.2805(1)
Calculated cationic distribution		[Li1]Li[Fe0.961(1)]Fe[Fe0.039(2)]i	[Li0.965(1)Fe0.035(1)]Li[Fe0.965(1)Li0.035(1)]Fe
Rwp	0.2072	0.1485	0.1545

---

Table 3 Bond lengths (Å) obtained from PDF refinement of the different models

	Model A	Model B	Model C
Li–O	2*2.125(1)	2*2.092(1)	2*2.112(1)
	2*2.156(1)	2*2.117(2)	2*2.118(2)
	2*2.244(1)	2*2.258(3)	2*2.242(3)
Fe–O	2.009(1)	2.046(3)	2*2.067(1)
	2*2.092(1)	2*2.091(2)	2.099(1)
	2*2.162(2)	2*2.166(1)	2*2.172(2)
	2.257(3)	2.271(1)	2.238(2)
Fe(i) –O		1.729(3)
		1.953(2)
		2.023(1)
		2.057(2)

---

The same best-fit procedure was also performed by considering the P2₁ space group. The relative structural parameters are presented in Table 4 and the bond lengths in Table 5. The comparison between experimental and calculated PDF is shown in Fig. 4. The graphical observation and the value of R_wp indicate the good quality of the structural model. The defective models were also tested with this structure, obtaining slightly improved R_wp, and a defect amount of about 7% for Fe Frenkel, and 5.2% for anti-site.

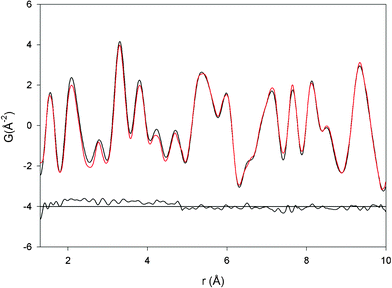Fig. 4 Graphical comparison between calculated (red line) and observed (black line) PDF for P2₁ model.

Table 4 Main structural parameters and discrepancy factors from PDF analysis by using P2₁s.g.

a, b, c/Å		10.3306(1), 6.0093(1), 4.6838(1)
Atomic fractional coordinates	Fe1	0.7218(2) 0.7393(2) 0.0296(2)
	Fe2	0.7848(2) 0.2463(1) 0.5245(2)
	P1	0.8986(3) 0.7501(2) 0.5738(2)
	P2	0.4005(1) 0.7472(1) 0.8978(1)
	O1	0.9045(2) 0.7341(2) 0.2460(2)
	O2	0.5922(3) 0.2740(2) 0.7580(2)
	O3	0.5414(1) 0.7527(1) 0.8014(2)
	O4	0.9569(3) 0.2624(2) 0.2987(1)
	O5	0.8291(1) 0.5457(1) 0.6688(1)
	O6	0.3210(2) 0.5467(3) 0.7500(2)
	O7	0.8324(2) 0.9503(3) 0.7178(1)
	O8	0.6815(1) 0.4321(2) 0.2615(1)
Calculated cationic distribution		[Li0.948(1)Fe0.052(1)]Li[Fe0.948(1)Li0.052(1)]Fe
Rwp		0.112

---

Table 5 Bond lengths (Å) obtained from the G (r) refinement with P2₁s.g.

Li1–O	Li2–O	Fe1–O	Fe2–O	P1–O	P2–O
2.048(2)	2.052(1)	2.143(2)	1.975(1)	1.490(3)	1.524(4)
2.069(3)	2.094(1)	2.149(2)	1.976(2)	1.539(5)	1.584(5)
2.155(1)	2.117(2)	2.161(1)	2.056(2)	1.540(2)	1.614(3)
2.198(4)	2.206(3)	2.182(1)	2.070(3)	1.610(5)	1.621(2)
2.203(1)	2.220(1)	2.246(2)	2.071(1)
2.366(2)	2.254(2)	2.332(3)	2.277(3)

---

3.4- Mössbauer spectroscopy

All the Mössbauer spectra show two broadened lines and a diffuse background between them (Fig. 5). As reported above, the fitting procedure was performed by applying the integral transmission method and using for f_s^r the value of 0.66 coming from the above described calibration procedure. Four subspectra (doublets) are suitable to reproduce the experimental line shape (Fig. 6). The values of the parameters suggest that the (1), (2) and (3) subspectra are due to Fe²⁺ while the (4) can be ascribed to Fe³⁺. The fitting parameters, consisting of isomer shift (δ), quadrupolar splitting (Δ), effective thickness (t_a) and Gaussian broadening (Γ_g), are reported in Table 6 for the three experimental temperatures. The (1) and (2) subspectra show very similar values of δ and Δ, while the (3) one is characterized by different values. Therefore, the (2) subspectrum can be connected with the same site of (1) but in a less regular geometry. Furthermore, the isomer shift increases weakly when T is lowered, as a result of the second-order Doppler shift.³³ As far as the quadrupolar splitting is concerned, the values related to the first three sites, i.e.Fe²⁺, increases weakly when T is lowered while for the last site it does not change, as expected; therefore, the chemical-physical environment does not vary significantly in the explored temperature range. The main contribution (1) is characterized by a Γ_nat-order Gaussian broadening, that could arise from the presence of two not equivalent iron sites if the space group were P2₁. Higher broadenings are observed for the (2) and (3) doublets. Γ_g variations with T for all the Fe²⁺ sites are of the same order of magnitude of the standard deviations; on the contrary, the Γ_g value for the Fe³⁺ site appears to grow appreciably when T is lowered. Finally, t_a for the Fe²⁺ sites as a whole increases when T is lowered as expected from the Mössbauer factor thermal trend. As far as Fe³⁺ site is concerned, the effective thickness grows more remarkably since it goes from a value just above the detection limit at room temperature to a well detectable one at 75.2 K.

Table 6 Isomer shift (referred to Rh matrix), quadrupolar splitting, Gaussian broadening and effective thickness for the four sites obtained from the fits of Mössbauer spectra, whose respective χ² values are reported, too

T/K	Site	δ (mm s^−1)	Δ (mm s^−1)	Γg (mm s^−1)	t a	χ ^2
293	1	1.108(1)	2.943(3)	0.065(3)	3.0(1)	1046
	2	1.137(7)	2.84(2)	0.17(1)	1.4(1)
	3	1.33(4)	1.7(2)	0.38(6)	0.27(5)
	4	0.72(2)	∼0.	∼0.	0.03(1)
150	1	1.199(1)	3.027(3)	0.077(4)	3.5(3)	1054
	2	1.222(6)	2.94(2)	0.17(1)	1.5(2)
	3	1.40(6)	2.0(2)	0.49(5)	0.27(5)
	4	0.86(2)	∼0.	0.08(3)	0.06(1)
75.2	1	1.231(1)	3.05(3)	0.078(5)	3.2(4)	1057
	2	1.249(6)	3.01(1)	0.18(2)	2.0(3)
	3	1.38(6)	2.1(3)	0.41(7)	0.24(8)
	4	0.89(2)	∼0.	0.10(2)	0.09(1)

---

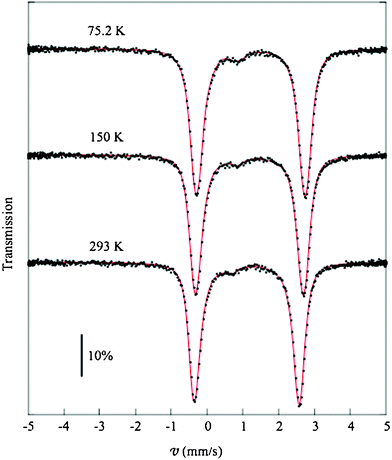Fig. 5 Mössbauer spectra collected at 75.2 ,150.0 and 293.0 K and the respective fitted line shapes.

Fig. 6 Mössbauer cross section line shapes for the four sites at 293.0 K.

Since t_a values of (3) and (4) subspectra are low, further fits were carried out—not reported here for the sake of simplicity—by using only three contributions rather than four, as performed in ref. 43. The main result of these further fits is that the fitting parameters of the lowest subspectrum converge upon values similar to the ones of (3) and (4) sites reported on Table 6. For this reason it seems to be reasonable to fit the data by means of four subspectra.

We also tried to fit the spectra by forcing the quadrupolar splitting for the Fe³⁺ site to values in the range of those ones reported in literature^15,33–43 (from 0.4 to 1.2 mm s⁻¹). These attempts lead to remarkable increases of χ² up to 2200. Moreover, the results were not numerically stable and they approach the ones reported in Table 6 by removing the constraint on the quadrupolar splitting.

As far as the subspectrum (4) is concerned, the broadening of the corresponding line could be connected with a superparamagnetic behaviour in a range just above the blocking temperature. At the same time, we note that the respective thickness values grow. These two facts analyzed as a whole could be better interpreted in the framework of dynamical processes, as the ones connected with charge hopping.^35–37 This interpretation could agree with the large value of the isomer shift, which is close to the upper limit expected for a six coordinate Fe³⁺.¹⁵ Anyway, we are confident that He-liquid temperature range measurements are required to clarify the features and the processes involving the Fe³⁺ site.

On the basis of the present data, from t_a values reported in Table 6, by taking into account the correlation coefficients coming out from the fits and averaging the three results, we estimate the iron percentage associated to (3) and (4) subspectra: ∼5% and ∼1%, respectively, in the assumption that the absorption recoilless fractions of all the sites share the same thermal trend.

4 Discussion

The results of the Rietveld refinement and of the PDF analysis are somewhat different, but this is expected due to the different length scales probed by the two techniques. In fact, it is well known that while the Rietveld method is a powerful tool for the investigation of the average structure, the PDF technique gives reliable information on the local structure of the investigated compounds. From PDF analysis, a clear indication of the need to introduce defects in the olivine-type structure comes out. It is well known in the literature that LiFePO₄, especially if prepared by hydrothermal synthesis, can show defects that affect the electrochemical functionality. Because of the intrinsic interest of the synthesis method we used, it is worthwhile to investigate if the combination of hydrothermal synthesis and microwave radiation could give origin to a higher amount of defects. The question whether microwave radiation could increase the point defects when heating crystalline lattices has already been answered by Booske et al.⁴⁹ From the thermodynamic point of view, the microwave photon energy at 2.5 GHz is in the order of magnitude of 1 × 10⁻⁴ eV, while the activation enthalpy for cation or anion vacancy formation in oxides falls in the range 1–5 eV. The activation enthalpy for the motion of these vacancies is somewhat 40–60% less, but still 3 orders of magnitude higher than microwave photon energy. So it is most likely that microwave absorption proceeds in classical (continuum) fashion, leading to thermal heating of the solution at an energy level not sufficient to activate ion/vacancy mobility in the solid particles. Although the fast synthetic process combining hydrothermal and microwave techniques is responsible for LiFePO₄ lattice defects in the particles, these defects can not be recovered by the well known microwave ionic mobility enhancement due to low temperature and short reaction time.⁴⁹

Among the possible crystal defects, the anti-site one has been observed frequently with an iron amount on the lithium site ranging between 3 and 7%.^17–19 Theoretical studies were also devoted to investigate the main possible defects of the olivine-type structure, and energy calculations suggest the anti-site defect is favoured with respect to interstitial lithium and iron.²⁰ In our case, the defective models chosen on the basis of these indications allowed us to obtain a better agreement between the observed and calculated PDF (see Fig. 3 and Table 2). The graphical observation reveals an overall improvement of the best-fit, likely due to a general better assessment of the atomic positions, that leads to significant variations of the bond lengths as shown in Table 3. The defective models seem to introduce the shrinking of LiO₆ octahedra from an average value of 2.175 Å to about 2.157 Å for model C and this difference is well beyond the bond lengths standard deviations. On the other hand, the FeO₆ octahedra slightly expand when introducing the defect. The Li Frenkel defect has also been taken into account because of its relatively low energy of formation,²⁰ but both the Rietveld refinement and the PDF analysis did reveal its amount is approximately zero. Anyway, it should be considered that the low X-ray scattering power of Li ions does not allow a sure response on this type of defect. The amount of anti-site defects found for our sample both from Rietveld (1.7%) and PDF analysis (3.5%), this last corresponding to the formula [Li_0.965(1)Fe_0.035(1)]_Li[Fe_0.965(1)Li_0.035(1)]_Fe, is in the range usually reported in the literature. The lattice parameters are often used as fingerprints of defect type and amount.^16–17,19 In our case values close to the ones of ordered LiFePO₄, but slightly contracted and not expanded as expected in the case of Li/Fe exchange, are found. Our lattice parameter behaviour seems instead comparable to that observed in presence of complex defects due to the co-existence of Li vacancies, Fe³⁺ and Li/Fe mixing.¹⁶ The Model C is completely comparable to the Model B at least at this level of investigation; in fact the R_wp values and the graphical comparisons are similar at all. About 4% of interstitial iron in tetrahedral coordination is found from the Model B. Considering the cationic radii for Fe²⁺ and Fe³⁺ in an octahedral or tetrahedral environment,⁵⁰ it is reasonable to expect that the interstitial iron is Fe³⁺. The presence of low amounts of Fe³⁺ in this olivine-type material is not surprising considering that iron easily undergoes oxidation,^{51 and references therein} despite of the precautions taken during the synthesis. Moreover, some authors refer to the presence of Fe³⁺ in the regular octahedral sites as an inherent or native defect of LiFePO₄, linked to the lithium vacancy or to iron on Li site.^16,22 The chemical analysis revealed a Li/Fe ratio of about 1, thus confirming that the Li vacancies are present in low amount. This agrees with the low percentage of Fe³⁺ revealed by Mössbauer analysis (about 1%: subspectrum 4). The Model B should not be considered reliable also taking into account the energy computation, which highlighted energy values too high for the formation of this defect.²⁰ Therefore, Fe³⁺ could be placed on the regular iron sites or on the lithium ones, but Mössbauer spectroscopy, at least within the investigated temperature range, cannot give precise information on its location: we confirm the opportunity of recolling spectra at He-liquid temperature range. The (1), (2) and (3) contributions were attributed to Fe²⁺ with different local environments: (1) is due to iron on its regular sites, (2) is related to iron in regular sites but in a less regular geometry and, finally, (3) might represent iron located on Li sites, since both δ and Δ parameters (see Table 6) are different from those of (1) and (2), and in particular the higher value of Γ_g indicates a more distorted local environment in agreement with a substitutional site model: this result is in agreement with the literature.⁴³ The amount of this Fe/Li substitution can be quantified in about 5%, in agreement with the PDF analysis.

A detailed observation of the graphical comparison (Fig. 3) of the PDF fit put into evidence that some discrepancies are still present in the graphical comparison and for this reason the model with a lower symmetry s.g. than the orthorhombic Pnma has been considered. This is a common procedure used for the study of local order.^52,53 The lowering of the symmetry can be considered an alternative approach to explain the intrinsic disorder of LiFePO₄. An advantage of this approach is related to the removal of the symmetry constraints of the crystallographic sites in the orthorhombic s.g. that, on the contrary, in P2₁ are no more in special positions thus allowing shifts of the atomic coordinates with a significant improvement of the best-fit (Table 4 and Fig. 4). However, lithium ions are retained in the (0, 0, 0) position because of their low X-ray scattering factor, that makes it difficult to locate their exact position during the refinement. Observing the bond lengths (Table 5), the polyhedra LiO₆ and FeO₆ appear to be, as expected, more distorted in comparison to those obtained with the orthorhombic s.g. In particular, the Li1O₆ octahedron is stretched with an average Li–O bond of 2.173 Å, while the Li2O₆ one shows shorter bonds with an average value of 2.157 Å. The iron octahedra are more distorted, with mean bond lengths of 2.202 Å and 2.071 Å for Fe1 and Fe2, respectively. The implementation of the anti-site defect in the P2₁s.g. leads to a slight improvement of the discrepancy factor with respect to the non-defective model. It is reasonable to expect the defect models do not significantly improve the refinement result, since the possibility of octahedra distortion is already taken into account by the lowering of the symmetry. From the PDF fit the 5% of anti-site defect has been found, in good agreement with the Mössbauer results. Considering the amount of Fe³⁺ found by the Mössbauer technique, an equivalent amount of lithium vacancies should be considered for charge balancing, thus obtaining the formula [□_0.007Li_0.941(1)Fe_0.052(1)]_Li[Fe_0.948(1)Li_0.052(1)]_Fe. We have to remark that, from the values of mean bond lengths for Fe1 and Fe2 sites in P2₁s.g., the respective lattice contributions to Δ deviate each other of ∼10%. Consequently, Mössbauer spectroscopy is not able to distinguish between them since the lattice contribution for Fe²⁺ is only the 10% of the whole quadrupolar splitting. Therefore, it is difficult to choose between the P2₁ and Pnma space groups only on the basis of Mössbauer spectroscopy, but the better agreement with the anti-site amount determined for the P2₁ one, seems to argue in favour of this hypothesis. Moreover, the synthesis procedure, performed at low temperature for so short times, which locally could not favour a complete crystallization of the material, could justify the presence of less regular Fe²⁺ sites, suggested by Mössbauer spectroscopy.

Conclusion

In this work the joint contributions of Mössbauer spectroscopy, Rietveld refinement and PDF analysis allowed a detailed study of the local order of LiFePO₄, prepared at low temperature by means of rapid microwave-assisted hydrothermal synthesis. The PDF analysis was applied for the first time to the LiFePO₄ structure, and allowed us to obtain an original insight onto the defects distribution. The anti-site defect and the symmetry lowering resulted more probable from the point of view of the PDF approach, and Mössbauer spectroscopy confirmed these findings. In particular, 5% of anti-site defects has been determined and also the presence of a small amount (about 1%) of Fe³⁺, whose actual symmetry could be better investigated in the He-liquid temperature range, has been revealed.

Here, we demonstrated that a proper combination of spectroscopic and diffractometric investigations, corroborated by modern distribution function analysis on an educated models guess, can be an invaluable tool in the material scientist's arsenal. Future work will be devoted to the evaluation of the LiFePO₄ defect content as a function of the synthesis time and temperature, and of its relationship with the cathode electrochemical response.

Acknowledgements

The XRD experiment was performed at the Materials Science beamline PD station at the Swiss Light Source (SLS), Paul Scherrer Institut, Villigen, Switzerland. The authors kindly thank Dr Fabia Gozzo (SLS) for assistance during the SR-XRPD experiments performed as part of the hands-on activities at the International School “Diffraction at the Nanoscale Nanocrystals, Defective & Amorphous Materials”, which was held at the Paul Scherrer Institut in May 24-30 2010 (http://user.web.psi.ch/powder2010/). Dr M. Sturini (University of Pavia) is acknowledged for the ICP measurements. Ente Cassa di Risparmio di Firenze is thanked for its financial support (Contract No. 2010.0419).

References

1. W.-J. Zhang, J. Power Sources, 2011, 196, 2962–2970.
2. B. L. Ellis, K. T. Lee and L. F. Nazar, Chem. Mater., 2010, 22, 691–714.
3. J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603.
4. B. Scrosati and J. Garche, J. Power Sources, 2010, 195, 2419–2430.
5. M.-H. Lee, J.-Y. Kim and H.-K. Song, Chem. Commun., 2010, 46, 6795–6797.
6. S. Ferrari, R. L. Lavall, D. Capsoni, E. Quartarone, A. Magistris, P. Mustarelli and P. Canton, J. Phys. Chem. C, 2010, 114, 12598–12603.
7. A. Vadivel Murugan, T. Muraliganth and A. Manthiram, J. Phys. Chem. C, 2008, 112, 14665–14671.
8. A. Manthiram, A. Vadivel Murugan, A. Sarkar and T. Muraliganth, Energy Environ. Sci., 2008, 1, 621–638.
9. G. Yang, H. M. Ji, H. D. Liu, K. F. Huo, J. Fu and P. K. Chu, J. Nanosci. Nanotechnol., 2010, 10, 980–986.
10. A. Vadivel Murugan, T. Muraliganth and A. Manthiram, J. Electrochem. Soc., 2009, 156, A79–A83.
11. K.-M. Huang, Z. Lin and X. -Q. Yang, Prog. Electromagn. Res., 2004, 49, 273–289.
12. C. Leonelli, Contribution at the 44th Annual Microwave Power Symposium of International Microwave Power Institute (IMPI), Denver, 2010.
13. A. Rizzuti and C. Leonelli, Powder Technol., 2008, 186, 255–262.
14. T. Zhao, W. Chu, H. Zao, X. Liang, W. Xu, M. Yu, D. Xia and Z. Wu, Nucl. Instrum. Methods Phys. Res., Sect. A, 2010, 619, 122–127.
15. S. Hamelet, P. Gibot, M. Casas-Cabanas, D. Bonnin, C. P. Grey, J. Cabana, J. B. Leriche, J. Rodriguez-Carvajal, M. Courty, S. Levasseur, P. Carlach, M. Van Thournout, J. M. Tarascon and C. Masquelier, J. Mater. Chem., 2009, 19, 3979–3991.
16. P. Gibot, M. Casas Cabanas, L. Laffont, S. Levasseur, P. Carlach, S. Hamelet, J. M. Tarascon and C. Masquelier, Nat. Mater., 2008, 7, 741–747.
17. M. S. Whittingham, Chem. Rev., 2004, 104, 4271–4301.
18. S. Yang, Y. Song, P. Y. Zavalij and M. S. Whittingham, Electrochem. Commun., 2002, 4, 239–244.
19. J. Chen and M. S. Whittingham, Electrochem. Commun., 2006, 8, 855–858.
20. M. S. Islam, D. J. Driscoll, C. A. J. Fisher and P. R. Slater, Chem. Mater., 2005, 17, 5085–5092.
21. M. Giorgetti, M. Berrettoni, S. Scaccia and S. Passerini, Inorg. Chem., 2006, 45, 2750–2757.
22. K. Zaghib, A. Mauger, J. B. Goodenough, F. Gendron and C. M. Julien, Chem. Mater., 2007, 19, 3740–3747.
23. S. J. L. Billinge and I. Levin, Science, 2007, 316, 561–565.
24. T. Egami and S. J. L. Billinge, Underneath the Bragg Peaks: Structural Analysis of Complex Materials, Elsevier, Oxford, 2003.
25. J. Breger, N. Dupre, P. J. Chupas, P. L. Lee, T. Proffen, J. B. Parise and C. P. Grey, J. Am. Chem. Soc., 2005, 127, 7529–7537.
26. N. Yamakawa, M. Jiang, B. Key and C. P. Grey, J. Am. Chem. Soc., 2009, 131, 10525–10536.
27. A. Bergamaschi, A. Cervellino, R. Dinapoli, F. Gozzo, B. Henrich, I. Johnson, P. Kraft, A. Mozzanica, B. Schmitt and X. Shi, J. Synchrotron Radiat., 2010, 17, 653–668.
28. Diffraction at the nanoscale. Nanocrystals, defective and amorphous materials. Edited by Guagliardi, A.; Masciocchi, N. Insubria University press, 2010.
29. AXS Bruker, TOPAS V3.0; General profile and structural analysis software for powder diffraction data; User Manual Bruker AXS: Karlsruhe, Germany, 2000.
30. P. F. Peterson, M. Gutmann, T. Proffen and S. J. L. Billinge, J. Appl. Crystallogr., 2000, 33, 1192–1192.
31. C. L. Farrow, P. Juas, J. W. Liu, D. Brynden, E. S. Bozin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219.
32. C. Yi-Long and Y. De-Ping, Mössbauer Effect in Lattice Dynamics; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, 2007.
33. L. Aldon, A. Perea, M. Womes, C. M. Ionica-Bousquet and J.-C. Jumas, J. Solid State Chem., 2010, 183, 218–222.
34. J.-F. Martin, M. Cuisinier, N. Dupré, A. Yamada, R. Kanno and D. Guyomard, J. Power Sources, 2011, 196, 2155–2163.
35. H. Tan and B. Fultz, J. Phys. Chem. C, 2011, 115, 7787–7792.
36. J. L. Dodd, I. Halevy and B. Fultz, J. Phys. Chem. C, 2007, 111, 1563–1566.
37. H. J. Tan, J. L. Dodd and B. Fultz, J. Phys. Chem. C, 2009, 113, 2526–2531.
38. Z. Liu, D. Dong, M. Liu, Y. Sui, W. Su, Z. Qian and Z. Li, Hyperfine Interact., 2005, 163, 13–27.
39. K. Hirose, T. Honma, Y. Doi, Y. Hinatsu and T. Komatsu, Solid State Commun., 2008, 146, 273–277.
40. B. Hannoyer, A. A. M. Prince, M. Jean, R. S. Liu and G. X. Wang, Hyperfine Interact., 2006, 167, 767–772.
41. M. Maccario, L. Croguennec, A. Wattiaux, E. Suard, F. Le Cras and C. Delmas, Solid State Ionics, 2008, 179, 2020–2026.
42. K. T. Fehr, R. Hochleitner, E. Schmidbauer and J. Schneider, Phys. Chem. Miner., 2007, 34, 485–494.
43. Z. Li and I. Shinno, Mineral. J., 1997, 19, 99–107.
44. D. G. Rancourt, Nucl. Instrum. Methods Phys. Res., Sect. B, 1989, 44, 199–210.
45. G. M. Bancroft, Mössbauer spectroscopy: an introduction for Inorganic Chemists and Geochemists, McGraw Hill, Maidenhead, 1973.
46. G. Spina, E. Pugliese, L. Cianchi, F. Del Giallo, M. Lantieri and P. Moretti, J. Phys.: Conf. Ser., 2010, 217, 012015.
47. M. Capaccioli, L. Cianchi, F. Del Giallo, P. Moretti, F. Pieralli and G. Spina, Nucl. Instrum. Methods Phys. Res., Sect. B, 1995, 101, 280–286.
48. J. Puerta and P. Martin, Appl. Opt., 1981, 20, 3923–3928.
49. J. H. Booske, R. F. Cooper and I. Dobson, J. Mater. Res., 1992, 7, 495–501.
50. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, A32, 751.
51. M. Bini, M. C. Mozzati, P. Galinetto, D. Capsoni, S. Ferrari, M. S. Grandi and V. Massarotti, J. Solid State Chem., 2009, 182, 1972–1981.
52. R. Cerny, Y. Filinchuk and S. Bruhne, Intermetallics, 2009, 17, 818–825.
53. L. Malavasi, H. -J. Kim and T. Proffen, J. Appl. Phys., 2009, 105, 123519.

---