Hydrolysis of glucose-6-phosphate in aged, acid-forced hydrolysed nanomolar inorganic iron solutions—an inorganic biocatalyst?†
Xiao-Lan
Huang‡§
*a and
Jia-Zhong
Zhang§
b
aCIMAS, Rosenstiel School of Marine and Atmospheric Science, University of Miami, Miami, Florida, 33149, USA. E-mail: xiaolan.huang@ymail.com.; Fax: 1-513-252-2332; Tel: 1-513-569-7409
bOcean Chemistry Division, Atlantic Oceanographic and Meteorological Laboratory, National Oceanic and Atmospheric Administration (NOAA), Miami, Florida, 33149, USA
First published on 1st November 2011
Abstract
Phosphate ester hydrolysis is one of the most important chemical processes in biological systems. Although catalysis by the natural phosphoesterases, e.g., purple acid phosphatase (PAP) and its biomimetics, are well known in biochemistry, it has been reported that some metals and mineral phases can significantly facilitate the hydrolysis of phosphate ester. Here we report for the first time that aged, acid-forced hydrolysed nanomolar inorganic iron solutions significantly promoted the hydrolysis of glucose-6-phosphate (G6P), and that the reaction kinetics followed the Michaelis–Menten equation. The catalysis was inhibited by tetrahedral oxyanions in an order of WO4 > MoO4 > PO4. The newly formed oxo-bridge or hydroxo-bridge during the iron-aging process might contribute to this biocatalytic effect, though the detailed mechanism is still unclear. Further studies are needed in order to understand the (hydr)oxo-bridged Fe–Fe structure in water and its role in organic phosphorus transformation. This catalyst might be one of many ubiquitous sets of inorganic enzymes yet to be discovered in nature that act as a bridge between the inorganic and organic worlds, and would have played a critical role in the origin of life.
1. Introduction
Glucose-6-phosphate (G6P), an example of a phosphate ester, is glucose sugar phosphorylated on carbon 6, and widely distributed in nature, including water and soil.1–3 As an essential process of life,4–8G6P hydrolysis is catalyzed by various enzymes, including phosphoesterases9–15 such as purple acid phosphatase (PAP). It is also known that their biomimetics, i.e., metals, especially iron, chelated to special organic ligands, can significantly promote the hydrolysis of phosphate ester.16–28 Moreover, it has been reported that some metals29–32 and mineral phases33–37 can significantly facilitate the hydrolysis of ester phosphate, including nucleoside phosphates. Therefore, understanding the behavior of phosphate ester hydrolysis is important for biology and biogeochemistry as it is relevant to phosphate availability in the environment.2,38–43 | ||
| Fig. 1 Hydrolysis of G6P in a 16.5 nM Fe(NO3)3 solution aged for 14 months at room temperature (22 ± 2 °C). (a) Concentration of IP and G6P during 20 μM G6P hydrolysis. (b) Pseudo first-order reaction kinetics of G6P. (c) Double reciprocal (initial velocity and initial concentration of G6P) plot (Lineweaver–Burk plot) of G6P from 5 to 250 μM. (d) Initial velocity of G6P hydrolysis (v) as a function of the initial concentration of G6P. | ||
| Fe source | Manufacturer | Aging time (month) | Total Fe conc. (nM) | Rate constant (10−6 s−1) | Half-life (h) |
|---|---|---|---|---|---|
| a The hydrolysis rate constant of initial 20 μM G6P in DIW is 1.53 × 10−7 s−1, and the half-life is 1255 h. | |||||
| Fe(NO3)3 | J.T.Baker | 14 | 16.5 | 30.17 | 6.4 |
| Riedel-de Haën | 4 | 16.5 | 5.08 | 37.8 | |
| 100 | 2.96 | 65.6 | |||
| 6 | 1000 | 18.77 | 10.3 | ||
| Iron standard solution (metal Fe in 0.3 M HNO3) | J.T.Baker | 4 | 1 | 2.38 | 81.0 |
| 2.5 | 4.85 | 39.7 | |||
| 7.5 | 7.22 | 26.7 | |||
| 50 | 6.38 | 30.2 | |||
| 100 | 6.55 | 29.4 | |||
| 200 | 6.58 | 29.2 | |||
| 500 | 8.14 | 23.6 | |||
| 1000 | 5.86 | 32.8 | |||
| FeCl3 | J.T.Baker | 16 | 2 | 6.59 | 29.2 |
| 10 | 4.95 | 38.9 | |||
| Riedel-de Haën | 4 | 10 | 3.28 | 58.6 | |
| 100 | 0.83 | 231.9 | |||
| Fe(ClO4)3 | Aldrich | 4 | 10 | 2.46 | 78.4 |
| 100 | 0.61 | 318.3 | |||
| Fe(NH4)2(SO4)2 | EM Science | 16 | 16.5 | 9.49 | 20.3 |
| Fe-EDTA | Self-made | 16 | 16.5 | 4.24 | 45.4 |
Recently, we discovered that hydrolysis of G6P is significantly promoted by aged, acid-forced hydrolysed nanomolar iron solutions, and the presence of some tetrahedral oxyanions in solution act as inhibitors in an order of WO4 > MoO4 > PO4. The kinetics of G6P hydrolysis in these nanomolar inorganic iron solutions can be described by the Michaelis–Menten equation. Here, we report these interesting phenomena and hypothesize that the (hydr)oxo-bridged Fe–Fe structure in the aged iron solution contributes to the observed catalytic effect.
2. Experimental
Deionized water (DIW), used for preparing standards, reagents, and aged iron solutions, was purified first with a distilling unit and then by a Millipore Super-Q Plus water system that produced water with a resistivity of 18 MΩ cm. All reagents and aged iron solutions were stored in polypropylene bottles (or containers) that were immersed in a 10% HCl solution overnight, followed by rinsing three times with DIW and then drying at 60 °C in an oven for 5–10 h prior to their use.All chemicals used were of analytical grade (AR or GR), and used as received. Glucose-6-phosphate (D(+)-glucopyranose 6-phosphate sodium salt, G-6-P Na, C6H12NaO9P, F. W. 282.12), glycerol 2-phosphate (β-glycerophosphate disodium salt hydrate, G2P, C3H7Na2O6P, F. W. 216.04), ribose-5-phosphate (D-ribofuranose 5-phosphate disodium salt, R5P, C5H9Na2O8P·xH2O, F. W. 274.07), and fructose 1-phosphate (D-fructose 1-phosphate sodium salt, F1P, C6H11O9PNa2, F. W. 304.10), were purchased from Sigma and stored in a freezer (−20 °C). A 50 mM stock solution for each organic phosphorus compound was made individually, stored in a refrigerator at 4 °C, and diluted to suitable concentrations for daily hydrolysis experiments.
Inorganic phosphate (IP) derived from the hydrolysis of G6P was determined by a modified method of Murphy and Riley in which the final total pHT of the test solution (sample mixed with reagents) was 1.0 (H/Mo = 70).44 An ammonium molybdate reagent was prepared by mixing 2.4 g of ammonium molybdate ((NH4)6MO7O24·4H2O, Merck, GR), 25 mL of concentrated sulfuric acid (H2SO4, 96–98%, J.T. Baker), and 50 mL of 0.3% antimony potassium tartrate (K(SbO)C4H4O6)2·H2O, Fisher) solution and diluting the mixture to 1 L with DIW. An ascorbic acid solution was prepared daily by dissolving 1 g of ascorbic acid (C6H8O6, Aldrich, AR) in 100 mL of DIW. Prior to sample analysis, a colour reagent was prepared by mixing equal volumes of the molybdate reagent with the ascorbic acid solution. One ml of the colour reagent was then added to 4 ml of the sample and mixed. After 10 min, absorbance of phosphoantimonyl-molybdenum blue was measured at 890 nm with background corrections at 780 to 1020 nm by a Hewlett-Packard 8453 UV-visible spectrophotometer.
2.1. Preparation of aged iron salt solutions
Since acidic environments significantly reduce the rate of iron(III) hydrolysis,45–48 six series of inorganic iron(III) salt solutions were made by rapid dilution under acidic conditions to nanomolar concentrations. Five different iron salts and a commercial iron standard solution for atomic absorption spectrophotometry (J.T.Baker, prepared by dissolving metal Fe in 0.3 M HNO3 to yield a concentration of 1000 mg ml−1) were used. The total iron concentration in the solutions used for G6P hydrolysis experiments ranged from 1 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 nM, and the maximum aging time was 16 months.
000 nM, and the maximum aging time was 16 months.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 (Fe
4 (Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EDTA) to make a 1 mM Fe-EDTA solution and subsequent step-wise dilutions (10 times dilution at each step). After 3 months, a 50 nM Fe solution was made from the aged 500 nM Fe solution by dilution with DIW. After another 2 months of aging, 2 mM of NaHCO3 was added to the 50 nM aged iron solution, to yield a final concentration of 16.5 nM iron in 0.67 mM NaHCO3. The pH of the aged iron solution was adjusted to 6.3 ± 0.1 by adding either 0.1 M HCl or 0.1 M NaOH or 20 mM NaHCO3 five times during the aging process. A noticeable catalytic reactivity was detected after 6 months of aging. The final measurement was made at either 14 or 16 months.
EDTA) to make a 1 mM Fe-EDTA solution and subsequent step-wise dilutions (10 times dilution at each step). After 3 months, a 50 nM Fe solution was made from the aged 500 nM Fe solution by dilution with DIW. After another 2 months of aging, 2 mM of NaHCO3 was added to the 50 nM aged iron solution, to yield a final concentration of 16.5 nM iron in 0.67 mM NaHCO3. The pH of the aged iron solution was adjusted to 6.3 ± 0.1 by adding either 0.1 M HCl or 0.1 M NaOH or 20 mM NaHCO3 five times during the aging process. A noticeable catalytic reactivity was detected after 6 months of aging. The final measurement was made at either 14 or 16 months.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 000 nM Fe(NO3)3 solutions.
A 100 mM Fe solution was prepared by dissolving 2.02 g of Fe(NO3)3·9H2O (Riedel-de Haën, AR, F. W. 404.00) in a dilute HNO3 solution (pH 3.0). This solution was then diluted with DIW (pH 6.2) step-by-step (10 times dilution at each step) to produce 1000 and 10
000 nM Fe(NO3)3 solutions.
A 100 mM Fe solution was prepared by dissolving 2.02 g of Fe(NO3)3·9H2O (Riedel-de Haën, AR, F. W. 404.00) in a dilute HNO3 solution (pH 3.0). This solution was then diluted with DIW (pH 6.2) step-by-step (10 times dilution at each step) to produce 1000 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 nM Fe solutions. The dilution process was completed within 10 min. The pH of these iron solutions was adjusted to 6.3 ± 0.1 after aging for 140 to 300 days. The hydrolysis rate of G6P was measured at 6 and 10 months. All inhibition experiments and buffer effects were made with this aged 1000 nM Fe solution.
000 nM Fe solutions. The dilution process was completed within 10 min. The pH of these iron solutions was adjusted to 6.3 ± 0.1 after aging for 140 to 300 days. The hydrolysis rate of G6P was measured at 6 and 10 months. All inhibition experiments and buffer effects were made with this aged 1000 nM Fe solution.
2.2. Measurement of hydrolysis rate of G6P
The increase in concentration of IP due to hydrolysis of G6P was measured at suitable time intervals with a modified colorimetric method after G6P was added to the aged iron solution. The concentration of G6P at a given time, t, was calculated using [G6P]t = [G6P]0 − [IP]t, where [G6P]0 is an initial concentration of G6P and [G6P]t and [IP]t are the concentrations of G6P and IP at time t, respectively. A small amount of IP was initially present in the G6P as an impurity, and was subtracted as a blank. The first-order hydrolysis rate constant, k (s−1), was determined from the slope of the linear portion of a log[G6P]tvs. time (s) plot. The typical correlation coefficient of the linear fitting was 0.99*; the duration of the hydrolysis experiments ranged from 24 to 48 h (with the exception of the control). The time courses of formation of phosphorantimonylmolybdenum blue complex from phosphate released from hydrolysis of 20 μM G6P in an aged (4 months) 1000 nM iron solution at room temperature (22 ± 2 °C) at different hydrolysis time (0, 1, 3, and 6 h) is presented in the ESI Fig. 1.†In the early stages of these experiments, either azide or CHCl3 was added to the aged iron solution to test for potential microbial contamination. No significant difference was observed between inhibitor-added and no-inhibitor-added experiments. In the subsequent experiments reported here, none of the microbial inhibitors were used.
2.3. Inhibition experiments with different tetrahedral oxyanions
All inhibition experiments were conducted with the 10 month aged 1000 nM Fe(NO3)3 solution. The tetrahedral oxyanions included orthophosphate (PO4), molybdate (MoO4) and tungstate (WO4), and were added as a stock solution into the aged iron solution before the G6P solutions were introduced. IP concentration was measured at different times and the hydrolysis rate constant was calculated as described in the previous section.3. Results and discussion
3.1. Promotion effect of sugar phosphate hydrolysis in aged iron solutions
G6P hydrolysis without enzymes is a slow process in DIW and fresh nanomolar inorganic iron solutions. The concentration of IP in the solution containing 20 μM G6P in pure water (DIW, pH 6.2) was 0.42 ± 0.02 μM initially (t = 0), and increased slowly with time. The IP concentration was 0.59 ± 0.08 μM at 24 h, and reached up to 2.4 μM after 9 days at room temperature (22 ± 2 °C). The IP concentrations in the fresh nanomole inorganic iron solutions (0.5 to 50 nM Fe(NO3)3) was 0.82 ± 0.11 μM after 24 h. However, after G6P was added into the aged nanomolar inorganic iron salt solutions, made by acid-forced hydrolysis, the IP was rapidly released. For example, after an initial 20 μM of G6P was added into a 14 month aged 16.5 nM Fe(NO3)3 solution (pH=6.3) at room temperature, IP was rapidly increased due to the hydrolysis of G6P. The concentration of IP at 1, 3 and 6.7 h was 2.8, 6.4 and 10.6 μM, respectively. Therefore, the hydrolysis of G6P was significantly promoted in the aged inorganic iron solution (Fig. 1a). Like metal ions as well as natural and biomimetic enzymes, the kinetics of G6P hydrolysis in the aged iron solution can be described as the pseudo-first-order reaction (Fig. 1b).22,23,29,30,32,49–51 In this experiment, the decrease in G6P concentration, [G6P]t, due to its hydrolysis can be expressed as a function of hydrolysis time, t, as| log[G6P]t = −0.0000131t − 4.718 (r2 = 0.999) | (1) |
The corresponding reaction rate constant (k) was 3.02 × 10−5 s−1, and the half-life (t1/2) was 6.38 h. In contrast, the average reaction rate constant in DIW and these fresh unaged nanomolar inorganic iron solutions was 1.53 × 10−7 and 1.98 × 10−7 s−1, respectively, and the half-life was 1255 and 1100 h, respectively. It is noted that the hydrolysis rate constant in the aged iron solution was much higher than previously reported rates in the presence of the millimole metals.29–32
The first-order reaction kinetics predicts a constant half-life of reaction regardless of the initial reactant concentrations. Consequently, the initial hydrolysis velocity of G6P (vo) is the product of the hydrolysis rate constant (k) multiplying the initial concentration of G6P ([G6P]0). However, the half-lifes and the hydrolysis rate constants at different initial G6P concentrations were not constant. For G6P hydrolysis at an initial concentration of 100 μM, the reaction rate constant was 8.83 × 10−6 s−1, and the half-life was 21.8 h. This suggests that there was some intermediate product formation related to the initial concentration of G6P and a constant equilibrium of intermediate products might be established during the hydrolysis process, after the initial G6P was introduced into the aged iron solution. Similar to the general chemical process of catalysis, inorganic phosphate was released and the activated iron species were regenerated. It was observed that the initial velocity of G6P hydrolysis in the aged iron solution can be described by the Michaelis–Menten equation, a typical behavior of biocatalysis, in a range from 5 to 250 μM (Fig. 1c, and 1d).
 | (2) |
The maximum initial velocity of G6P hydrolysis was about 1 nM s−1, or 3.6 μM h−1, and the Michaelis–Menten constant (Km) was 13.7 μM. This is in strong contrast to previously reported promotion effects by metals29–32 and minerals.33–37
The promotion effect of G6P hydrolysis can be extended to 2500 μM in this aged iron solution with a k of 6.53 × 10−7 s−1, and t1/2 of 295 h. It should be pointed out that the concentration of phosphorus in the solution was 103–105 higher than that of iron (e.g., 16.5 nM Fe and 2500 μM G6P).
The measured hydrolysis rate constants of the initial 20 μM G6P with different sources of iron, made by acid-forced hydrolysis, are listed in Table 1. There were some differences in the hydrolysis rate constants among the different salts. The half-life for 4 month aged Fe(NO3)3 (16.5 nM), FeCl3 (10 nM) and Fe(ClO4)3 (10 nM) was 37.8, 58.6 and 78.4 h, respectively, though they were in the same order of magnitude. The nitrate ion, which is found in ferric nitrate, is also an oxidising agent though it has been suggested that nitrate exerts little, if any, effect on the hydrolytic polymerization of ferric ion.52,53 Both ferric and ferrous salts have a promoting effect, although the ferrous ions would have been partially oxidized to ferric ion during the aging process.54
These aged iron solutions also catalyzed the hydrolysis of other sugar phosphates, including glycerol 2-phosphate (3-carbon, G2P), ribose-5-phosphate (5-carbon, R5P), and fructose 1-phosphate (6-carbon, F1P) (Table 2). Preliminary results show that the hydrolysis rate constants at a given sugar phosphate concentration are the same order of magnitude among these different sugar phosphates. It is also noted that the rates of 5-carbon and 3-carbon sugar phosphates (R5P and G2P) are higher than those of 6-carbon sugar phosphate (G6P and F1P). As expected, the promotion effect was also found for the other phosphorus ester compounds, including the energy metabolism compounds (AMP, ADP and ATP, and even polyphosphate and pyrophosphate) as well as the RNA model compound (4-nitrophenyl phosphate ester). However, no promotion effects were observed for the hydrolysis of phosphonates (C–P bonded compounds, e.g., 2-aminoethylphosphonic acid, phosphono-formic acid) and inositol hexakisphosphate (IP6) (data not shown).
| Sugar phosphate | Aged Fe solution | Initial OP (μM) | Rate constant (10−6 s−1) | Half-life (h) |
|---|---|---|---|---|
| Glycerol-2-phosphate (G2P) | Fe standard solution, 7.5 nM, 4 mo. | 10 | 12.69 | 15.2 |
| 20 | 6.40 | 30.1 | ||
| 50 | 3.45 | 55.8 | ||
| 500 | 0.51 | 374.3 | ||
| Fe(NO3)3, 1000 nM, 6 mo. | 20 | 30.12 | 6.4 | |
| FeCl3, 2 nM, 16 mo. | 20 | 5.29 | 36.4 | |
| Fe(NH4)2(SO4)2, 16.5 nM, 16 mo. | 20 | 11.44 | 16.8 | |
| Ribose-5-phosphate (R5P) | Fe standard solution, 7.5 nM, 4 mo. | 10 | 13.92 | 13.8 |
| 20 | 8.15 | 23.6 | ||
| Fe(NO3)3, 1000 nM, 6 mo. | 20 | 25.19 | 7.6 | |
| FeCl3, 2 nM, 16 mo. | 20 | 7.24 | 26.6 | |
| Fe(NH4)2(SO4)2, 16.5 nM, 16 mo. | 20 | 16.16 | 11.9 | |
| Fuctose-1-phosphate (F1P) | Fe standard solution, 7.5 nM, 4 mo. | 10 | 8.66 | 22.2 |
| 20 | 5.25 | 36.4 | ||
| Fe(NO3)3, 1000 nM, 6 mo. | 20 | 17.08 | 11.3 | |
| FeCl3, 2 nM, 16 mo. | 20 | 5.29 | 36.4 | |
| Fe(NH4)2(SO4)2, 16.5 nM, 16 mo. | 20 | 8.50 | 22.6 |
Further experiments with a range of 1 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 nM ferric standard solution (pH ≈ 6.3) were carried out to investigate the contribution of iron concentration to the aging process. The hydrolysis rate constants of initial 20 μM G6P in all these nanomolar (1 to 1000 nM) aged iron solution increased with aging time at room temperature (22 ± 2 °C) (Fig. 2). After 4 months of aging, the hydrolysis reaction rate constant of initial 20 μM G6P in aged iron solutions increased from 0.15 to 10 (× 10−6 s−1), and the half-life of G6P hydrolysis decreased from 2 months to ∼1 day (Fig. 2). It is noted that the time of aging needed to achieve an appreciable G6P hydrolysis rate constant was closely related to the total iron concentration. For iron concentrations less than 100 nM, it took less than a month; whereas for higher iron concentrations (200 to 1000 nM), it took more than two months. However, no direct correlations between the hydrolysis rate constants at the same initial concentration of G6P and the total iron concentrations were observed, which might imply that the catalytic characteristics of aged iron solution is very complex. No significant promotion effect was observed if the iron concentration was more than 1000 nM, even if the aging time was extended up to 14 months (data not shown).
000 nM ferric standard solution (pH ≈ 6.3) were carried out to investigate the contribution of iron concentration to the aging process. The hydrolysis rate constants of initial 20 μM G6P in all these nanomolar (1 to 1000 nM) aged iron solution increased with aging time at room temperature (22 ± 2 °C) (Fig. 2). After 4 months of aging, the hydrolysis reaction rate constant of initial 20 μM G6P in aged iron solutions increased from 0.15 to 10 (× 10−6 s−1), and the half-life of G6P hydrolysis decreased from 2 months to ∼1 day (Fig. 2). It is noted that the time of aging needed to achieve an appreciable G6P hydrolysis rate constant was closely related to the total iron concentration. For iron concentrations less than 100 nM, it took less than a month; whereas for higher iron concentrations (200 to 1000 nM), it took more than two months. However, no direct correlations between the hydrolysis rate constants at the same initial concentration of G6P and the total iron concentrations were observed, which might imply that the catalytic characteristics of aged iron solution is very complex. No significant promotion effect was observed if the iron concentration was more than 1000 nM, even if the aging time was extended up to 14 months (data not shown).
 | ||
| Fig. 2 Hydrolysis rate constant (k) of 20 μM G6P as a function of aging time in solutions of different iron concentrations. | ||
3.2. Inhibition effect of tetrahedral oxyanions on the hydrolysis of G6P
When the tetrahedral oxyanions were introduced into this aged iron solution, the hydrolysis of G6P was significantly inhibited (Fig. 3a). In the experiments with initial 20 μM G6P in the 10 month aged 1000 nM iron solution, addition of 10 μM PO4 reduced the hydrolysis reaction rate constant to 60% of the control (without PO4), and the half-life was 5.51 h. When the PO4 concentration was increased to 40 μM, the rate constant was reduced to 40%, and the half-life was 10.34 h. In the presence of 1 μM MoO4, the hydrolysis rate constant was reduced to 78%, and the corresponding half-life was 4.01 h. In the presence of 10 μM MoO4, the hydrolysis rate constant was further reduced to 12%, and the corresponding half-life was 26.3 h. When the molybdate was increased to millimolar concentrations, no hydrolysis of G6P was observed even at a higher concentration of G6P (100 μM). The strongest inhibition effect was observed in the presence of WO4. The rate constant was approximately 43% when 1 μM WO4 was added into the aged iron solution; the corresponding half-life of G6P was 7.42 h. When the concentration of WO4 was increased to 10 μM WO4, the rate constant was further reduced to 3%, and the corresponding half-life was extended to 109.3 h. It was found that the percentage reduction in hydrolysis reaction rate constant (y) is a rational function of the tetrahedral oxyanion concentration (x in μM), which can be expressed as the following equation | (3) |
 | ||
| Fig. 3 Glucose-6-phosphate hydrolysis in a 10 month aged , 1000 nM Fe(NO3)3 solution at room temperature (22 ± 2 °C). (a) Kinetics of hydrolysis of G6P (20 μM initial) in the aged iron solution with no addition, and with addition of 1 μM MoO4, 1 μM WO4 and 10μM PO4. (b) Percentage reduction of the hydrolysis rate constant (k) of initial 20 μM G6P as a function of the concentration of different tetrahedral oxyanions. | ||
The inhibition effect was also closely related to the initial concentration of the G6P (Fig. 4), and the modes of tetrahedral oxyanions and G6P were competitive. The aged iron solutions might be bound to either the tetrahedral oxyanions (PO4, MoO4, and WO4) or G6P to form two different intermediates, but cannot bind to both at any given moment (Fig. 5). The intermediates with G6P release IP, and the process of G6P hydrolysis is completed with the regeneration of the active binding sites on the aged iron species. The intermediates with the tetrahedral oxyanions prevent the binding of G6P, and also have a dissociation reaction to regenerate the active binding sites on the aged iron species.
 | ||
| Fig. 4 Inhibiting behavior of different tetrahedral oxyanions on the hydrolysis of glucose-6-phosphate in a 10 month aged, 1000 nM Fe(NO3)3 solution at room temperature (22 ± 2 °C). (a) Effect of initial concentration of G6P on the initial hydrolysis velocity of G6P. (b) Lineweaver–Burk plot of aged iron solutions in the absence and presence of tetrahedral oxyanions. | ||
 | ||
| Fig. 5 Schematic diagram of the catalysis process of G6P hydrolysis in the presence of the tetrahedral anions in the aged inorganic iron solutions. E is the aged inorganic iron species; A is the active binding sites on the aged iron species. S is G6P and I is tetrahedral anions. ES and EI are the two intermediates. | ||
Results indicate that the apparent affinity of G6P to the Fe–Fe bond in the aged iron solution (binding sites) might decrease due to the competition of the inhibitor (PO4, MoO4 and WO4), while the maximum velocity of G6P hydrolysis (vmax) was still unchanged. The catalytic and inhibition behaviors of this aged iron solution in the presence of 5 to 125 μM G6P can be described by the Michaelis–Menten equation. From the linear relationship observed in the Lineweaver–Burk plot, the apparent Michaelis–Menten constant (Kmapp) can be calculated using the following:
 | (4) |
 | (5) |
where the [G6P]o is the initial concentration of G6P (M), [I] is the concentration of inhibitor (M), Km is Michaelis–Menten constant, and Ki is the inhibitor’s dissociation constant.
The Michaelis–Menten equations for G6P hydrolysis in the 10 month aged iron solution were as follows:
without any addition:
 | (6) |
with 1μM MoO4:
 | (7) |
with 1 μM WO4:
 | (8) |
with 5 μM PO4:
 | (9) |
with 10 μM PO4:
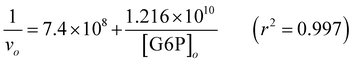 | (10) |
The Km, the G6P concentration at which the hydrolysis velocity reached one-half of maximum velocity (vmax/2), was 2.7 μM G6P in this aged iron solution with no inhibitors added, and the Kmapp with the addition of 1 μM WO4, MoO4, and 5 μM PO4 and 10 μM PO4 was 46.2, 14.1, 11.1 and 17.1μM G6P, respectively. Therefore, the Ki of WO4, MoO4, and PO4 was determined to be 0.06, 0.24 and 1.6–1.9 μM, respectively.
The Km of the aged iron solution was also related to the total Fe concentration. The higher the concentration of iron in solution, the lower the concentration of G6P was at one-half maximum velocity. This probably accounts for the fact that we could not observe the catalytic effect in the iron solution with high concentrations (Fig. 2), and the maximum velocities of G6P hydrolysis in both 16.5 nM and 1000 nM aged Fe solutions were very similar at around 1 to 1.35 nM s−1.
It is interesting to compare the catalytic behavior of aged iron solution to natural phosphoesterase and their biomimetic, though the velocities of hydrolysis G6P in aged iron solutions are much lower than that of phosphoesterase. For natural phosphoesterase, Km and Ki of PO4 is usually in the millimolar range;55–60 only Ki of WO4 and MoO4 is in the micromolar range.57,58,61–63 The value of Km of G6P is 920 μM for phosphoesterase extracted from sweet potato50 and 300–310 μM for those from soybean seed.64 Besides, the modes of molybdate and tungstate inhibition are noncompetitive.57,58,61–65 Only orthophosphate is competitive57,58 in most cases.
A more significant difference between the aged iron solutions and the natural phosphoesterase is revealed in their response to the fluoride ion. While the activity of all known natural phosphoesterases is very sensitive to fluoride even at micromolar levels,59,63–69 no change in the catalytic activity of these aged iron solutions were found even when the final concentration of fluoride in solutions reached 0.5 M. Another significant difference is their response to the buffer solutions. Usually, the natural phosphoesterase still has great activity within the pH range of the buffer. However, no significant promotion effect on sugar phosphate hydrolysis was observed when the buffer solution (e.g., tris, citrate) was introduced into these aged iron solutions at a similar pH (5.0–7.5) range (ESI Table 1†). The activity of these aged iron solutions decreased rapidly within 10 min, with the exception of the acetic acid-acetate buffer (the highest acetate concentration tested was 0.25 M). This is in agreement with previous observations that many buffers can significantly decrease the promotion of the metal ion on the hydrolysis of nucleoside phosphate.29–31 All of these behaviors of the aged iron solution suggest that they are different from the natural enzyme.
It is well known that iron speciation changes due to hydrolysis during the aging process, though controversy still exists over the identity and stability of the species formed in solution, and of the interaction of iron with other species.46,70–75 It has been suggested recently that diiron or polyiron oxide with the oxo-bridge or hydroxo-bridge (bond) might be formed in the iron solution during the aging process.74 Based on quantum-chemical calculations using density-functional theory, dihydroxobridging binuclear compounds can be present in aqueous solutions, as binuclear dihydroxobridging [Fe(H2O)4(μ-OH)2Fe(H2O)4]n+ and oxobridging [Fe(H2O)5(μ-O)Fe·(H2O)5]n+ (n = 2, 4) cations in the hydrolysis products of the cations [Fe(H2O)6]m+ (m = 2, 3).76 The hydroxo-bridged Fe–(OH)2–Fe dimers are the structure units in the polymetric hydroxo complex, which are dependent on pH and aging time.77,78 Direct experimental evidence has demonstrated the existence of dinuclear and polynuclear complexes in a 0.1 mM FeCl3 solution. The electrospray ionization time-of-flight mass spectrometry has detected a variety of mononuclear and polynuclear iron–oxohydroxo–chloride complexes in Fe solution at a pH range of 2–6.6.79 The (hydr)oxo-bridged Fe–Fe structure has been confirmed at the interface of iron oxide (solid) to water.80–83 It was suggested that water reacts dissociatively on the iron oxide surface, leading to a structure with both terminal and bridge (hydr)oxy groups. The μ-(hydr)oxo ligand bridge between Fe–Fe also occurs in nanocrystalline ferrihydrite.84 It is reasonable to assume that the aged, acid-forced hydrolysed nanomolar iron solutions comprise species with a μ-(hydr)oxo ligand bridge.
The μ-(hydr)oxo ligand bridge is a universal feature in dinuclear phosphoesterase.10,11,15 It has been hypothesized that a “phosphoesterase motif” provides the scaffold for an active site dinuclear metal centre in the members of the phosphoesterase family.12,85–88 They involve the cleavage of phosphoester bonds, including acid and alkaline phosphatases, bacterial exonucleases, diadenosine tetraphosphatase, 5′-nucleotidase, phosphodiesterase, sphingomyelin phosphodiesterase, which is an enzyme involved in RNA debranching, a phosphatase in the bacteriophage genome, as well as the family of ser/thr protein phosphatase (PP1, PP2A, and calcineurin).12,15,86 Furthermore, it has also been reported that the tetrahedral oxyanions inhibit the hydrolysis of phosphate ester by these phosphoesterases.59,63,65–69 Moreover, the μ-(hydr)oxo ligand bridge was recognized in artificial phosphatase studies,17–19 which yielded the principles of binucleating ligand design.24–27 As a result, many biomimetics with capability to catalyze phosphate ester hydrolysis have been synthesized based on this special structure.18,21–23,25,28 It is believed that the catalytic effect of phosphatases and their biomimetics on the hydrolysis of phosphate monoesters, including sugar phosphate, is due to the net transfer of the phosphoryl group directly to water through a binuclear metal center that produces inorganic phosphate and that the nucleophile is a metal-coordinated hydroxide or the bridging hydroxo/oxo group.10,12,15,51,86,89 Therefore, the common feature between these aged iron solutions and the phosphoesterases (natural and synthesized biomimetics complexes) is a kind of acceleration of electron transfer rate in the structure of the μ-(hydr)oxo ligand between the metals, particularly iron.
Different nanostrutures of iron oxide have been synthesised by different laboratories,90–95 and it has been shown that they have different functions.96–99 One example is ferromagnetic nanoparticles with its intrinsic peroxidase activity,96–98 with which it was demonstrated that their hydrolysis kinetics follow the Michaelis–Menten equation.96,97 Essentially, similar to phosphoesterase, an iron center with oxo bonds is also the basic structure of many peroxidases and their mimetics.100–106 Some PAPs were reported to have the activity of peroxidases.107,108 Meanwhile, nanoparticles of iron oxide have been observed in the natural environment,109–112 though some reports mentioned that the nanostructure of iron oxide can also be mediated by bacteria.113–115 However, as recognized recently, the structure and reactivity of iron nanoparticles, even in the aqueous solution, changes with time or the aging process.116 Thus, it is clear that the behavior of iron oxide nanostructures in nature is very complex. It is believed that nanometre size iron oxides and (oxyhydr)oxides are ubiquitous in the earth and range from ultra-fine aerosols to precipitates or coatings in soil and sediments.110,117–123 Nanomolar levels of ferric ion might have existed on the ocean surface of the early earth due to photo-oxidation, even in the absence of oxygen in the atmosphere,124 though ferrous ion (II) is presumed to be the dominant form of iron in the sea at that time.125 The elevated CO2 levels that are likely to have prevailed in the atmosphere at that time could have resulted in a neutral or mildly acidic ocean.125 Moreover, it has been reported that ferric ion is present in the hydrothermal ecosystem, which is also believed to have been the realm where life first emerged.126–130 It was also documented that magnetite (Fe3O4) must have been present in the Earth at that time through the process of serpentinization, i.e., the reaction of olivine- and pyroxene-rich rocks with water.131–133
The relevance of this observation is not only to phosphorus metabolism in biology and the phosphorus cycle in geochemistry, but also to the essence of biocatalysts. It demonstrates that these aged nanomolar inorganic iron(III) solutions perform the same function as enzymes (natural and biomimetics) that have metal complexes ligated to either polypeptides or organic ligands. Natural and biomimetic phosphoesterases and aged inorganic iron solutions might have the same unique μ-(hydr)oxo bridge and metal center to perform enzymatic functions. This is supported by the concept of the metal's role as “constrained” for the selective uptake and catalytic activity in metallo-enzyme catalysis.134–136 Pauling stated “the specificity of the physiological activity of substances is determined by the size and shape of molecules, rather than primarily by their chemical properties, and that the size and shape find expression by determining the extent to [which] these regions of the two molecules are complementary in structure... The enzyme is closely complementary in structure to the “activated complex” for the reaction catalyzed by the enzyme”.137 Therefore, these aged nanomolar inorganic iron solutions might serve as a “primitive enzyme”138 or as an “inorganic biocatalyst”. In other words, all of life's catalysts are enzymes, although only protein and RNA (ribozyme) are identified as enzymes in modern biochemistry.139–144
Conclusions
Aged, acid-forced hydrolysed nanomolar inorganic iron solutions were found to have phosphoesterase activity, which significantly promoted the hydrolysis of phosphate ester following Michaelis–Menten kinetics. Moreover, the catalysis was inhibited by tetrahedral oxyanions with inhibition strength in an order of WO4 > MoO4 > PO4. The activity was related to the aging process and total iron concentrations, but the detailed mechanism is still unknown. Further work is needed to understand the nature of the (hydr)oxo-bridged Fe–Fe structure in water and its potential role in organic phosphorus transformation in geochemistry. However, this observation and reported intrinsic peroxidase-like activity of ferromagnetic nanoparticles96 demonstrates that “the chain of life is of necessity a continuous one, from the mineral at one end to the most complicated organism at the other”, as proposed by Leduc.145 The hydrolysed iron solutions might be just one of ubiquitous sets of undiscovered inorganic biocatalysts (enzymes) in nature. Such inorganic enzymes might act as a bridge between the inorganic and organic worlds and would have played important roles in the origin of life. Discovery of further inorganic enzymes might provide clues on the emergence of life and a potential solution to the puzzle of “chicken and egg” in life's evolution.138,146–153Acknowledgements
X.L.H. greatly appreciates the precious comments of Drs. R.J.P. Williams, Michael J. Russell, Gerhard Schenk and Jianping Xu and personal encouragements from Drs. Tsung-Hung Peng, Peter B. Ortner, Robert Atlas and Mr. Yu-Dong Sun for this study. X. L. H also thanks Ms. Gail Derr and Dr Raghuraman Venkatapathy for English editing. Financial support for the experimental parts of the study was provided by NOAA's Center for Sponsored Coastal Ocean Research to J. Z. Z. All statements, findings, conclusions and recommendations are of the authors and do not necessarily reflect the views of Pegasus Technical Services Inc., University of Miami or NOAA or the U. S. Department of Commerce.References
- P. J. Worsfold, L. J. Gimbert, U. Mankasingh, O. N. Omaka, G. Hanrahan, P. Gardolinski, P. M. Haygarth, B. L. Turner, M. J. Keith-Roach and I. D. McKelvie, Talanta, 2005, 66, 273–293 CrossRef CAS.
- D. M. Karl, K. M. Björkman, in Biogeochemistry of Marine Dissolved Organic Matter, D. A. Hansell and C. A. Carlson, Academic Press, San Diego, 2002, pp. 249–366 Search PubMed.
- M. Espinosa, B. L. Turner and P. M. Haygarth, J. Environ. Qual., 1999, 28, 1497–1504 CrossRef CAS.
- F. H. Westheimer, Science, 1987, 235, 1173–1178 CAS.
- J. R. Knowles, Annu. Rev. Biochem., 1980, 49, 877–919 CrossRef CAS.
- A. C. Hengge, in Adv. Phys. Org. Chem., ed. J. P. RichardAcademic Press, 2005, pp. 49–108 Search PubMed.
- T. A. S. Brandao and A. C. Hengge, in Comprehensive Natural Products II, ed. M. Lew and L. Hung-WenElsevier, Oxford, 2010, pp. 315–348 Search PubMed.
- J. K. Lassila, J. G. Zalatan and D. Herschlag, Annu. Rev. Biochem., 2011, 80, 669–702 CrossRef CAS.
- J. E. Coleman, Annu. Rev. Biophys. Biomol. Struct., 1992, 21, 441–483 CrossRef CAS.
- D. E. Wilcox, Chem. Rev., 1996, 96, 2435–2458 CrossRef CAS.
- G. W. Oddie, G. Schenk, N. Z. Angel, N. Walsh, L. W. Guddat, J. D. Jersey, A. I. Cassady and D. A. Hume, Bone, 2000, 27, 575–584 CrossRef CAS.
- F. Rusnak and P. Mertz, Physiol. Rev., 2000, 80, 1483–1521 CAS.
- M. D. Jackson and J. M. Denu, Chem. Rev., 2001, 101, 2313–2340 CrossRef CAS.
- S. Hamdan, P. D. Carr, S. E. Brown, D. L. Ollis and N. E. Dixon, Structure, 2002, 10, 535–546 CrossRef CAS.
- N. Mitic, S. J. Smith, A. Neves, L. W. Guddat, L. R. Gahan and G. Schenk, Chem. Rev., 2006, 106, 3338–3363 CrossRef CAS.
- D. R. Jones, L. F. Lindoy and A. M. Sargeson, J. Am. Chem. Soc., 1983, 105, 7327–7336 CrossRef CAS.
- D. M. Kurtz Jr, Chem. Rev., 1990, 90, 585–606 CrossRef.
- C. Duboc-Toia, S. Menage, J.-M. Vincent, M. T. Averbuch-Pouchot and M. Fontecave, Inorg. Chem., 1997, 36, 6148–6149 CrossRef CAS.
- J. Chin, Curr. Opin. Chem. Biol., 1997, 1, 514–521 CrossRef CAS.
- R. Than, A. A. Feldmann and B. Krebs, Coord. Chem. Rev., 1999, 182, 211–241 CrossRef.
- S. Albedyhl, M. T. Averbuch-Pouchot, C. Belle, B. Krebs, J. L. Pierre, E. Saint-Aman and S. Torelli, Eur. J. Inorg. Chem., 2001, 1457–1464 CrossRef CAS.
- C. Liu, S. Yu, D. Li, Z. Liao, X. Sun and H. Xu, Inorg. Chem., 2002, 41, 913–922 CrossRef CAS.
- P. Karsten, A. Neves, A. J. Bortoluzzi, M. Lanznaster and V. Drago, Inorg. Chem., 2002, 41, 4624–4626 CrossRef CAS.
- C. Belle and J.-L. Pierre, Eur. J. Inorg. Chem., 2003,(23), 4137–4146 CrossRef CAS.
- F. Verge, C. Lebrun, M. Fontecave and S. Menage, Inorg. Chem., 2003, 42, 499–507 CrossRef CAS.
- D. E. C. Ferreira, W. B. De Almeida, A. Neves and W. R. Rocha, Phys. Chem. Chem. Phys., 2008, 10, 7039–7046 RSC.
- L. R. Gahan, S. J. Smith, A. Neves and G. Schenk, Eur. J. Inorg. Chem., 2009,(19), 2745–2758 CrossRef CAS.
- M. Jarenmark, M. Haukka, S. Demeshko, F. Tuczek, L. Zuppiroli, F. Meyer and E. Nordlander, Inorg. Chem., 2011, 50, 3866–3887 CrossRef CAS.
- R. M. Milburn, M. Gautem-Basek, R. Tribolet and H. Sigel, J. Am. Chem. Soc., 1985, 107, 3315–3321 CrossRef CAS.
- H. Sigel, Coord. Chem. Rev., 1990, 100, 453–539 CrossRef CAS.
- H. Sigel, Inorg. Chim. Acta, 1992, 198–200, 1–11 CrossRef CAS.
- H. Sigel and P. E. Amsler, J. Am. Chem. Soc., 1976, 98, 7390–7400 CrossRef CAS.
- A. Torrents and A. T. Stone, Environ. Sci. Technol., 1991, 25, 143–149 CrossRef CAS.
- D. S. Baldwin, J. K. Beattie, L. M. Coleman and D. R. Jones, Environ. Sci. Technol., 1995, 29, 1706–1709 CrossRef CAS.
- D. S. Baldwin, J. K. Beattie and D. R. Jones, Water Res., 1996, 30, 1123–1126 CrossRef CAS.
- D. S. Baldwin, J. K. Beattie, L. M. Coleman and D. R. Jones, Environ. Sci. Technol., 2001, 35, 713–716 CrossRef CAS.
- R. Olsson, R. Giesler, J. S. Loring and P. Persson, Langmuir, 2010, 26, 18760–18770 CrossRef CAS.
- J. Z. Zhang and X. L. Huang, Environ. Sci. Technol, 2007, 41, 2789–2795 CrossRef CAS.
- K. B. Follmi, Earth-Sci. Rev., 1996, 40, 55–124 CrossRef CAS.
- K. G. Raghothama, Annu. Rev. Plant Physiol. Plant Mol. Biol., 1999, 50, 665–693 CrossRef CAS.
- K. R. Reddy, G. A. O'ConnorC. L. Schelske, Phosphorus Biogeochemistry in Subtropical Ecosystems, Lewis, Boca Raton, Florida, 1999 Search PubMed.
- X. L. Huang, Y. Chen and M. Shenker, Plant Soil, 2005, 271, 365–376 CrossRef CAS.
- X.-L. Huang and J.-Z. Zhang, Environ. Sci. Technol., 2010, 44, 7790–7795 CrossRef CAS.
- J. Z. Zhang, C. J. Fischer and P. B. Ortner, Talanta, 1999, 49, 293–304 CrossRef CAS.
- E. Matijevic and P. Scheiner, J. Colloid Interface Sci., 1978, 63, 509–524 CrossRef CAS.
- C. M. J. Flynn, Chem. Rev., 1984, 84, 31–41 CrossRef CAS.
- K. Kandori, T. Shigetomi and T. Ishikawa, Colloids Surf., A, 2004, 232, 19–28 CrossRef CAS.
- S. Music, S. Krehula and S. Popovic, Mater. Lett., 2004, 58, 2640–2645 CrossRef CAS.
- C. A. Bunton and H. Chaimovich, Inorg. Chem., 1965, 4, 1763–1766 CrossRef CAS.
- G. Schenk, Y. Ge, L. E. Carrington, C. J. Wynne, I. R. Searle, B. J. Carroll, S. Hamilton and J. De Jersey, Arch. Biochem. Biophys., 1999, 370, 183–189 CrossRef CAS.
- A. Blasko and T. C. Bruice, Acc. Chem. Res., 1999, 32, 475–484 CrossRef CAS.
- D. Y. Davydov, Russ. J. Inorg. Chem., 2005, 50, 962–965 Search PubMed.
- K. Kandori, S. Ohnishi, M. Fukusumi and Y. Morisada, Colloids Surf., A, 2008, 331, 232–238 CrossRef CAS.
- L. Guimarães, H. A. de Abreu and H. A. Duarte, Chem. Phys., 2007, 333, 10–17 CrossRef.
- S. Burman, J. C. Davis, M. J. Weber and B. A. Averill, Biochem. Biophys. Res. Commun., 1986, 136, 490–497 CrossRef CAS.
- J. W. Pyrz, J. T. Sage, P. G. Debrunner and L. Que Jr, J. Biol. Chem., 1986, 261, 11015–11020 CAS.
- S. S. David and L. Que Jr, J. Am. Chem. Soc., 1990, 112, 6455–6463 CrossRef CAS.
- J. B. Vincent, M. W. Crowder and B. A. Averill, Biochemistry, 1991, 30, 3025–3034 CrossRef CAS.
- D. C. Crans, C. M. Simone, R. C. Holz and L. Que Jr, Biochemistry, 1992, 31, 11731–11739 CrossRef CAS.
- G. Schenk, L. E. Carrington, S. E. Hamilton, J. D. Jersey and L. W. Guddat, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1999, 55, 2051–2052 CrossRef CAS.
- Z. Wang, L. J. Ming, L. Que Jr, J. B. Vincent, M. W. Crowder and B. A. Averill, Biochemistry, 1992, 31, 5263–5268 CrossRef CAS.
- J. S. Lim, M. A. S. Aquino and A. G. Sykes, Inorg. Chem., 1996, 35, 614–618 CrossRef CAS.
- T. W. Elliott, N. MitiÄ, L. R. Gahan, L. W. Guddat and G. Schenk, J. Braz. Chem. Soc., 2006, 17, 1558–1565 CrossRef CAS.
- C. V. Ferreira, E. M. Taga and H. Aoyama, Plant Sci., 1999, 147, 49–54 CrossRef CAS.
- X. Wang and L. Que Jr, Biochemistry, 1998, 37, 7813–7821 CrossRef CAS.
- M. Dietrich, D. Munstermann, H. Suerbaum and H. Witzel, Eur. J. Biochem., 1991, 199, 105–113 CrossRef CAS.
- M. W. Crowder, J. B. Vincent and B. A. Averill, Biochemistry, 1992, 31, 9603–9608 CrossRef CAS.
- N. J. Reiter, D. J. White and F. Rusnak, Biochemistry, 2002, 41, 1051–1059 CrossRef CAS.
- E. Balogh, A. M. Todea, A. Muller and W. H. Casey, Inorg. Chem., 2007, 46, 7087–7092 CrossRef CAS.
- R. M. Milburn and W. C. Vosburgh, J. Am. Chem. Soc., 1955, 77, 1352 CrossRef CAS.
- R. H. Byrne, Y.-R. Luo and R. W. Young, Mar. Chem., 2000, 70, 23–35 CrossRef CAS.
- J.-P. Jolivet, Metal Oxide Chemistry and Synthesis: From Solution to Solid State, Wiley, Chichester, 2000 Search PubMed.
- R. Crichton, Inorganic Biochemistry of Iron Metabolism: From Molecular Mechanisms to Clinical Consequences, Wiley, Chichester, 2001 Search PubMed.
- J.-P. Jolivet, E. Tronc and C. Chaneac, C. R. Geosci., 2006, 338, 488–497 CrossRef CAS.
- A. Navrotsky, L. Mazeina and J. Majzlan, Science, 2008, 319, 1635–1638 CrossRef CAS.
- N. Panina, A. Belyaev, A. Eremin and P. Davidovich, Russ. J. Gen. Chem., 2010, 80, 889–894 CrossRef CAS.
- O. Y. Pykhteev and A. A. Efimov, Russ. J. Inorg. Chem., 1999, 44, 494–499 Search PubMed.
- A. Baev and E. Evsei, Russ. J. Inorg. Chem., 2010, 55, 508–522 CrossRef CAS.
- H. Hellman, R. S. Laitinen, L. Kaila, J. Jalonen, V. Hietapelto, J. Jokela, A. Sarpola and J. Rämö, J. Mass Spectrom., 2006, 41, 1421–1429 CrossRef CAS.
- V. Barron and J. Torrent, J. Colloid Interface Sci., 1996, 177, 407–410 CrossRef CAS.
- C. M. Eggleston, A. G. Stack, K. M. Rosso, S. R. Higgins, A. M. Bice, S. W. Boese, R. D. Pribyl and J. J. Nichols, Geochim. Cosmochim. Acta, 2003, 67, 985–1000 CrossRef CAS.
- K. S. Tanwar, C. S. Lo, P. J. Eng, J. G. Catalano, D. A. Walko, G. E. Brown Jr, G. A. Waychunas, A. M. Chaka and T. P. Trainor, Surf. Sci., 2007, 601, 460–474 CrossRef CAS.
- T. P. Trainor, A. M. Chaka, P. J. Eng, M. Newville, G. A. Waychunas, J. G. Catalano and G. E. Brown, Surf. Sci., 2004, 573, 204–224 CrossRef CAS.
- F. M. Michel, L. Ehm, S. M. Antao, P. L. Lee, P. J. Chupas, G. Liu, D. R. Strongin, M. A. A. Schoonen, B. L. Phillips and J. B. Parise, Science, 2007, 316, 1726–1729 CrossRef CAS.
- J. B. Vincent and B. A. Averill, FEBS Lett., 1990, 263, 265–268 CrossRef CAS.
- D. L. Lohse, J. M. Denu and J. E. Dixon, Structure, 1995, 3, 987–990 CrossRef CAS.
- F. Rusnak, L. Yu and P. Mertz, JBIC, J. Biol. Inorg. Chem., 1996, 1, 388–396 CrossRef CAS.
- S. Zhuo, J. C. Clemens, D. J. Hakes, D. Barford and J. E. Dixon, J. Biol. Chem., 1993, 268, 17754–17761 CAS.
- W. W. Cleland and A. C. Hengge, Chem. Rev., 2006, 106, 3252–3278 CrossRef CAS.
- Y. Hou, J. Yu and S. Gao, J. Mater. Chem., 2003, 13, 1983–1987 RSC.
- F. Jiao, J. C. Jumas, M. Womes, A. V. Chadwick, A. Harrison and P. G. Bruce, J. Am. Chem. Soc., 2006, 128, 12905–12909 CrossRef CAS.
- D. Kim, N. Lee, M. Park, B. H. Kim, K. An and T. Hyeon, J. Am. Chem. Soc., 2009, 131, 454–455 CrossRef CAS.
- Y. Zeng, R. Hao, B. Xing, Y. Hou and Z. Xu, Chem. Commun., 2010, 46, 3920–3922 RSC.
- S. Liu, F. Lu, R. Xing and J. J. Zhu, Chem.–Eur. J., 2011, 17, 620–625 CrossRef CAS.
- S. Laurent, D. Forge, M. Port, A. Roch, C. Robic, L. Vander Elst and R. N. Muller, Chem. Rev., 2008, 108, 2064–2110 CrossRef CAS.
- L. Gao, J. Zhuang, L. Nie, J. Zhang, Y. Zhang, N. Gu, T. Wang, J. Feng, D. Yang, S. Perrett and X. Yan, Nat. Nanotechnol., 2007, 2, 577–583 CrossRef CAS.
- H. Wei and E. Wang, Anal. Chem., 2008, 80, 2250–2254 CrossRef CAS.
- C. Yang, J. Wu and Y. Hou, Chem. Commun., 2011, 47, 5130–5141 RSC.
- Y. Ce, W. Jiajia and H. Yanglong, Chem. Commun., 2011, 47, 5130–5141 RSC.
- J. H. Dawson, Science, 1988, 240, 433–439 CAS.
- K. D. Karlin, Science, 1993, 261, 701–708 CAS.
- B. Eulering, M. Schmidt, U. Pinkernell, U. Karst and B. Krebs, Angew. Chem., Int. Ed. Engl., 1996, 35, 1973–1974 CrossRef CAS.
- J. Bernadou and B. Meunier, Chem. Commun., 1998, 2167–2173 RSC.
- S. de Lauzon, B. Desfosses, D. Mansuy and J.-P. Mahy, FEBS Lett., 1999, 443, 229–234 CrossRef CAS.
- B. Meunier, J. Bernadou, in Metal-Oxo and Metal-Peroxo Species in Catalytic Oxidations, ed. B. Meunier, Springer Berlin/Heidelberg, 2000, pp. 1–35 Search PubMed.
- L. Westerheide, F. K. Müller, R. Than, B. Krebs, J. Dietrich and S. Schindler, Inorg. Chem., 2001, 40, 1951–1961 CrossRef CAS.
- A. R. Hayman and T. M. Cox, J. Biol. Chem., 1994, 269, 1294–1300 CAS.
- V. Veljanovski, B. Vanderbeld, V. L. Knowles, W. A. Snedden and W. C. Plaxton, Plant Physiol., 2006, 142, 1282–1293 CrossRef CAS.
- J. F. Banfield, S. A. Welch, H. Zhang, T. T. Ebert and R. L. Penn, Science, 2000, 289, 751–754 CrossRef CAS.
- C. Anastasio S. T. Martin in Nanoparticles and the Environment, ed. J. F. Banfield and A. Navrotsky, The Mineralogical Society of America, 2001, pp. 293–349 Search PubMed.
- Y. Guyodo, A. Mostrom, R. L. Penn and S. K. Banerjee, Geophys. Res. Lett., 2003, 30, 1512 CrossRef.
- J. R. Rustad and A. R. Felmy, Geochim. Cosmochim. Acta, 2005, 69, 1405–1411 CrossRef CAS.
- M. Farina, D. M. S. Esquivel and H. G. P. Lins De Barros, Nature, 1990, 343, 256–258 CrossRef CAS.
- A. Arakaki, H. Nakazawa, M. Nemoto, T. Mori and T. Matsunaga, J. R. Soc. Interface, 2008, 5, 977–999 CrossRef CAS.
- A. A. Bharde, R. Y. Parikh, M. Baidakova, S. Jouen, B. Hannoyer, T. Enoki, B. L. V. Prasad, Y. S. Shouche, S. Ogale and M. Sastry, Langmuir, 2008, 24, 5787–5794 CrossRef CAS.
- D. R. Baer, J. E. Amonette, M. H. Engelhard, D. J. Gaspar, A. S. Karakoti, S. Kuchibhatla, P. Nachimuthu, J. T. Nurmi, Y. Qiang, V. Sarathy, S. Seal, A. Sharma, P. G. Tratnyek and C. M. Wang, Surf. Interface Anal., 2008, 40, 529–537 CrossRef CAS.
- C. H. Swartz, A. L. Ulery and P. M. Gschwend, Geochim. Cosmochim. Acta, 1997, 61, 707–718 CrossRef CAS.
- J. F. Banfield, H. Zhang, in Nanoparticles in the environment, ed. J. F. Banfield and A. Navrotsky, The Mineralogical Society of America, 2001, pp. 1–58 Search PubMed.
- J. M. Bigham, R. W. Fitzpatrick, D. G. Schulze, in Iron Oxides, ed. J. B. Dixon and D. G. Schulze, Soil Science Society of America, 2002 Search PubMed.
- R. M. Cornell and U. Schwertmann, The Iron Oxides: Structure, Properties, Reactions, Occurrences and Uses, Wiley-VCH, NY, 2003 Search PubMed.
- R. L. Penn, C. Zhu, H. Xu and D. R. Veblen, Geology, 2001, 29, 843–846 CrossRef CAS.
- C. van der Zee, D. R. Roberts, D. G. Rancourt and C. P. Slomp, Geology, 2003, 31, 993–996 CrossRef CAS.
- G. A. Waychunas, C. S. Kim and J. F. Banfield, J. Nanopart. Res., 2005, 7, 409–433 CrossRef CAS.
- P. S. Braterman, A. G. Cairns-Smith and R. W. Sloper, Nature, 1983, 303, 163–164 CrossRef CAS.
- R. J. P. Williams, J. J. R. Frausto Da Silva, The chemistry of evolution: The development of our ecosystem, Elsevier, Amsterdam, The Netherlands, 2006 Search PubMed.
- J. B. Corliss, Origins Life Evol. Biosphere, 1986, 16, 192–193 CrossRef.
- G. Macleod, C. McKeown, A. J. Hall and M. J. Russell, Origins Life Evol. Biosphere, 1994, 24, 19–41 CrossRef CAS.
- M. J. Russell and A. J. Hall, J. Geol. Soc., 1997, 154, 377–402 CrossRef CAS.
- W. Nitschke and M. J. Russell, J. Mol. Evol., 2009, 69, 481–496 CrossRef CAS.
- W. Martin, J. Baross, D. Kelley and M. J. Russell, Nat. Rev. Microbiol., 2008, 6, 805–814 CAS.
- D. S. Kelley, J. A. Karson, G. L. Früh-Green, D. R. Yoerger, T. M. Shank, D. A. Butterfield, J. M. Hayes, M. O. Schrenk, E. J. Olson, G. Proskurowski, M. Jakuba, A. Bradley, B. Larson, K. Ludwig, D. Glickson, K. Buckman, A. S. Bradley, W. J. Brazelton, K. Roe, M. J. Elend, A. Delacour, S. M. Bernasconi, M. D. Lilley, J. A. Baross, R. E. Summons and S. P. Sylva, Science, 2005, 307, 1428–1434 CrossRef CAS.
- M. Schulte, D. Blake, T. Hoehler and T. McCollom, Astrobiology, 2006, 6, 364–376 CrossRef CAS.
- M. J. Russell, A. J. Hall and W. Martin, Geobiology, 2010, 8, 355–371 CrossRef CAS.
- H. B. Gray, B. G. Malmström and R. J. P. Williams, JBIC, J. Biol. Inorg. Chem., 2000, 5, 551–559 CrossRef CAS.
- R. J. P. Williams, Chem. Commun., 2003, 1109–1113 RSC.
- J. M. Thomas and R. J. P. Williams, Philos. Trans. R. Soc. London, Ser. A, 2005, 363, 765–791 CrossRef CAS.
- L. Pauling, Nature, 1948, 161, 707–709 CrossRef CAS.
- I. Fry, The Emergence of Life on Earth, Rutger University Press, New Brunswick, 2000 Search PubMed.
- J. R. E. Kohler, Isis, 1973, 64, 181–196 Search PubMed.
- A. J. Zaug and T. R. Cech, Science, 1986, 231, 470–475 CAS.
- G. J. Narlikar and D. Herschlag, Annu. Rev. Biochem., 1997, 66, 19–59 CrossRef CAS.
- A. L. Smith, ed., Oxford dictionary of biochemistry and molecular biology, Oxford University Press., Oxford 2000 Search PubMed.
- T. Cech, Science, 2000, 289, 878–879 CrossRef CAS.
- D. A. Kraut, K. S. Carroll and D. Herschlag, Annu. Rev. Biochem., 2003, 72, 517–571 CrossRef CAS.
- S. Leduc, The Mechanism Of Life William Heinemann, Londan, 1911 Search PubMed.
- A. I. Oparin, The Origin of Life, The Macmillan Company, New York 1938 Search PubMed.
- G. Cairns-Smith, Genetic Takeover and the Mineral Origins of Life, Cambridge University Press, Cambridge, UK, 1982 Search PubMed.
- W. Gilbert, Nature, 1986, 319, 618 CrossRef.
- G. Wachtershauser, Microbiol. Mol. Biol. Rev., 1988, 52, 452–484 CAS.
- A. Lazcano, G. E. Fox and J. F. Oroin The Evolution of Metabolic Function, ed. R. P. Mortlock, CRC Press, Boca Raton, 1992, pp. 237–295 Search PubMed.
- C. de Duve, Vital Dust: The Origin And Evolution Of Life On Earth, Basic BooksNew York, 1995 Search PubMed.
- F. J. Dyson, Origins of Life, Cambridge University, Cambridge, 1999 Search PubMed.
- P. Herdewijn, M. V. Kisakürek ed. Origin of Life: Chemical Approach, Wiley-VCH Verlag GmbH, 2008 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Fig. 1: time course of formation of phosphoantimonylmolybdenum blue complex from phosphate released during hydrolysis of 20 μM G6P in an aged-4 month, 1 μM iron solution at room temperature (22 ± 2 °C) at different hydrolysis times. Table 1: effect of tris-buffer solution on the G6P hydrolysis in an aged-14 month, 1 μM iron solution. See DOI: 10.1039/c1ra00353d |
| ‡ Present address: Pegasus Technical Services Inc., 46 E Hollister St., Cincinnati, OH 45219, USA |
| § X.-L. H. instigated this study and performed the experiments, and wrote the draft of the manuscript. X.-L. H. and J.-Z. Z. designed the experiments, and prepared the final manuscript. |
| This journal is © The Royal Society of Chemistry 2012 |
