Analysis of phase transitions in molecular solids: quantitative assessment of phonon-mode vs intra-molecular spectral data

Abstract

The efficacy of phonon-mode spectral data (20–400 cm⁻¹) in identifying and characterising phase transitions is for the first time compared directly with traditional “fingerprint” intra-molecular spectral data (400–3800 cm⁻¹) for a model molecular system, using a range of statistical approaches and algorithms. Both data sets were collected in the same experiment, allowing a direct comparison. We find that phonon-mode data offer a reliable method of identifying phase transitions, whereas the intra-molecular are inherently unsuitable. Our results are likely to apply widely to solid-solid transformations.

---

Introduction

The vibrational spectroscopies, which comprise infra-red (IR), Raman and inelastic neutron scattering (INS), are widely employed in the characterisation of materials, in areas as diverse as pigments, explosives, agrochemicals, minerals, ceramics, and pharmaceuticals.^1–11 These techniques are used either as single-point measurements, in which a single sample is characterised, or as parametric methods in which spectra are recorded as a function of a particular parameter (for example, variable temperature for in situ studies,¹² position for chemical mapping, magnetic field for magneto-electrical properties, hydrostatic pressure, etc). In order to maximise the information that can be gathered in a single experiment, a suitable choice of overall method, and a data collection strategy, must be made. Employing infra-red spectroscopy as an example: near-IR (4000–12500 cm⁻¹) methods are well suited to process analytical technologies due to the penetrating nature of near-IR radiation, which allows reliable bulk sampling and is compatible with various experimental geometries; mid-IR (400–4000 cm⁻¹) methods are well suited to chemical characterisation via measurement of the energies of the intra-molecular bonds; and terahertz (THz) (10–400 cm⁻¹) spectroscopy is well suited to the analysis of molecular solids, including materials which contain the same molecule but in different local environments such as polymorphs, salts, etc, as the THz spectra measure the energies of the inter-molecular interactions which are expected to be very different between various solid forms of the same molecule (this is not necessarily the case for mid-IR).

Of the three main vibrational spectroscopies, INS is unsuitable for general applications due to limited access to neutron sources, and also the often prohibitively long data acquisition times. Infra-red methods have the benefit of short acquisition times but collection of data across a wide spectral range requires the use of several dedicated instruments (due to the requirement in IR spectroscopy for a radiation source to have the same energy as the vibration being probed). For example, to collect THz-frequency data a THz spectrometer is required, whereas mid-IR data require an entirely separate mechanism of generating the incident radiation and therefore an entirely separate data acquisition instrument. In order to directly compare the efficacy of different data collection strategies for characterisation of materials, specifically the use of different spectral windows (the aim of this work), it is clearly a pre-requisite to collect comparable data. We therefore employ Raman spectroscopy, in which a very wide spectral window data set can be collected under identical conditions on the same instrument, in order to compare quantitatively the use of THz-frequency (phonon-mode, i.e. intermolecular bands) data with mid-IR frequency (intramolecular bands) for characterisation of phase transitions in a model molecular system.

There is a relatively limited amount of published work to date dealing with phonon-mode Raman spectroscopy, in large part due to the fact that the improvement in standard Rayleigh rejection filters is very recent. This can be contrasted with the body of work on THz infra-red spectroscopy.¹³ It has been stated by several researchers (including one of the current authors) that the phonon-mode data—whether in Raman or THz infra-red—from 10–400 cm⁻¹ are more sensitive to inter-molecular interactions and crystalline forms (polymorph, solvate, etc) than the data from 400–3800 cm⁻¹. In crystalline materials the phonon-mode bands are quantised and thus yield relatively sharp peaks; in amorphous materials they are not quantised and instead a broad feature is observed over this region (known as the boson peak^14–18). Examples from the field of Raman spectroscopy include the use of phonon-mode data to distinguish between polymorphs.^19–21 Although the enhanced sensitivity of the phonon-mode (THz frequency) data to solid-state information when compared with “molecular fingerprint” (mid-IR) data is intuitive,^22,23 to the best of our knowledge there exist no studies which address this through a direct comparison of the two spectral windows in a thorough and statistically rigorous manner. For a direct comparison the phonon-mode and intra-molecular data should ideally be collected on the same instrument, and thus Raman spectroscopy is the obvious (and indeed the only) viable technique. This direct comparison of phonon-mode and intra-molecular spectra using Raman spectroscopy therefore forms the basis of the present study. For this comparison we employ a model compound, paracetamol (acetaminophen), which is known to exhibit phase transitions between various solid forms. We investigate and compare the efficacy of mid-IR frequency data (predominantly probing intra-molecular bands) with THz-frequency data (predominantly probing inter-molecular bands) for the spectral classification of the different solid forms.

Paracetamol is a very common analgesic, and is a very well characterised model system, for which both intra-molecular and phonon-mode have been reported. In the solid state it can adopt three polymorphs and an amorphous form, and has been well characterised by several researchers including ourselves. Crystal structures of the three polymorphs are available and indicate that the molecular conformation is relatively invariant.^24–26 The melting temperature of form I is 169–170 °C, form II melts at 154–157 °C and the melting point of form III is 143 °C.^27–30 The glass transition occurs in the region of 25 °C. On heating the glass, it is possible to isolate all three polymorphs for certain experimental configurations. It therefore forms an excellent well-characterised model system which undergoes several successive phase transformations on heating. Full Raman spectral data, including phonon-mode data, have been presented for all solid forms.²⁰ A previous paper by Kauffman et al. reported the results of simultaneous differential scanning calorimetry and Raman spectroscopy to this system, including principal component analysis of the Raman data.³¹ The Raman data of Kauffman, and their analysis by PCA, are relevant to the work reported below. The study of Kauffman covered the spectral range 350–4000 cm⁻¹, which is the range traditionally accessible using a standard Raman spectrometer. We are fortunate in that our Raman spectrometer can collect meaningful data over the spectral range 20–4000 cm⁻¹, which includes the phonon-mode spectral window, and we are thereby able to directly compare the use of phonon-mode and intra-molecular Raman spectroscopy in characterising the transformations between different forms in this model system. The different forms are generated as per several literature reports, namely through melt-quenching of liquid paracetamol to generate the amorphous form, followed by slow heating (−100 to 180 °C) to drive the system from a high-energy amorphous state to the lowest energy crystalline state, following Ostwald's rule of stages.^20,27–30 A spectrum is collected every 1 °C (total 281 spectra), and these spectra are analysed as outlined below.

Our study is aimed at investigating the utility of low-wavenumber (less than 400 cm⁻¹) Raman data in characterisation of phase transitions in organic solids, and in particular comparing these low-wavenumber data with data from the more traditional mid-IR frequency range (400–4000 cm⁻¹). Our work represents the first direct comparison of these two spectral regions and is intended as a general guide to experimental design for future researchers who may consider employing vibrational spectroscopy for characterisation of molecular solids. A model and well-characterised polymorphic pharmaceutical system is employed.

Experimental

The Raman spectra were collected in back-scattering geometry using a HORIBA Jobin Yvon Ltd LabRAM HR system, interfaced with an Olympus BX51 optical microscope. This system has an 800 mm beam path and offers the highest spectral resolution available in a commercial Raman spectrometer. A laser wavelength of 532.7 nm was employed, and an objective lens of ×50 magnification. The laser power was 300 mW and the laser spot diameter was approximately 1 micron. In order to reduce as far as possible any issues with sub-sampling, or laser-induced sample heating, the laser spot was scanned over a 20 × 20 micron² area during data collection using the “Duoscan” module supplied with the instrument. The spectrometer was calibrated using the Rayleigh scattering, the peak position of silicon (520.7 cm⁻¹), and the spline files provided by the manufacturer. All spectra were collected in the same day under the same conditions in order to minimise where possible any calibrations issues due to instrumental thermal drift, etc.³² Each spectrum covered the spectral range 20–3800 cm⁻¹, the lower limit corresponds approximately with the cut-off of our Rayleigh rejection filter (estimated ca. 30 cm⁻¹, data are collected from slightly lower to ensure that all important spectral information is available), and the upper with the limit of useful spectral data from the sample.‡ Each spectrum contained 2580 data points, and a total of 281 spectra were collected, making an overall total of 724,980 data points in the experiment. Spectra were collected under confocal conditions, using a confocal aperture of 300 microns. The Raman light was dispersed by a 600 lines per mm grating, along a total beam path of 800 mm, with Raman spectra recorded using a Synapse CCD which was thermoelectrically cooled. Spectral resolution (i.e. typical peak width) is estimated to be mainly determined by the sample, and of the order of 4 cm⁻¹. Measurement parameters were 2 s per window, repeated twice to allow automated cosmic ray removal, unless otherwise stated. The spectra (20–3800 cm⁻¹) were collected in several windows and merged into a single spectrum using the LabSpec software supplied with the instrument.

The as-received crystalline powder sample was placed onto a glass microscope slide, a cover slip was placed on top of the sample, and the sample was loaded into a Linkam hot-stage (model LTS350, with TMS94 temperature controlling programmer and LNP94 cooling system and a 2 litre dewar for liquid Nitrogen). Temperature control and data collection were computer-controlled, and the sample stage was adjusted for optimal height automatically prior to each measurement. The hot-stage was flushed with nitrogen gas throughout the experiment. There is perhaps some evidence for a small discrepancy between the recorded and actual temperatures within the hot-stage§, but this effect is quite small and does not impact on our analysis.

The sample was heated to 180 °C (above the melting point of 169 °C), held at this temperature for 5 min, and cooled at a rate of 30 °C min⁻¹ to −100 °C to isolate a purely amorphous sample. Raman data were then collected on heating from −100 to 180 °C at 1 °C increments. A heating rate of 1 °C min⁻¹ was employed between individual temperatures. Temperature was allowed to stabilise prior to each data collection so the overall (underlying) heating rate is significantly lower than 1 °C min⁻¹.

The signal : noise ratio of the spectra improves gradually from −100 to −10 °C, this may be intrinsic but is thought to be due to the formation of ice on the hot-stage windows at these low temperatures, which subsequently melts on heating. The signal : noise ratio also drops above the melting point (169 °C), this is likely due to flow of the liquid out of the sampling volume of the spectrometer and is largely unavoidable in the current experimental configuration. With the exception of these two temperature windows, the quality of the spectra (signal : noise ratio) is excellent across the vast majority of the temperature range. Example spectra are given the supplementary information, Fig. S1.†

Data were analysed visually (necessarily subjectively) and using a variety of statistical approaches. Prior to statistical analyses, the data (entire spectra) were subject to background subtraction which was performed using the LabSpec software with a second-order polynomial. For analysis the spectral range was divided into phonon-mode (20–400 cm⁻¹) and intra-molecular (400–3800 cm⁻¹) spectral regions, the former containing a total of 73060 data points and the latter a total of 651920 data points for all experiments.

Statistical analyses were performed within the R software package,³³ which is open-source, freely available and fully documented. For principal component analysis the separate pcaMethods library³⁴ was employed (routine “pca”); the default of singular variable decomposition was used to generate the components. The first two principal components are reported for the PCA (the first twenty were calculated). Data were either employed raw or scaled. Where scaling was performed, all spectra were scaled for intensity prior to the analysis by dividing the mean-centred data by their root-mean-square using the standard “scale” function within R, otherwise all parameters employed were the default for the particular software/statistics routine.

The hierarchical agglomerative clustering is implemented within the default installation of R (routine “hclust”). For the hierarchical agglomerative clustering four and five clusters were defined, with a distance matrix being calculated using the Euclidean distance measure. A total of seven separate clustering algorithms were employed in the hierarchical agglomerative clustering, in order to examine whether the choice of clustering algorithm affected the clusters formed.

All raw data and details of the statistical analyses performed (R scripts) are available in the supplementary material for information and reference, and it should be possible to reproduce all of the results in this paper from the information given therein.

Results

Initial visual inspection

The scaled Raman data collected as a function of temperature (total 281 spectra) for the heating of amorphous paracetamol and its subsequent transformations are presented in Fig. 1, for all data (Fig. 1a), phonon-mode data (Fig. 1b) and selected intra-molecular bands (Figs. 1c and 1d). Example spectra are also given for reference in the supplementary information, Fig. S1,† and a subset of spectra (covering the transformations) is presented in the supplementary information, Fig. S2.†

Fig. 1 Scaled experimental Raman spectra as a function of temperature for spectral windows: a) 20–3800 cm⁻¹; b) 20–400 cm⁻¹; c) 1200–1350 cm⁻¹; d) 1450–1700 cm⁻¹.

From simple inspection of Fig. 1, it can be seen that spectra can be quickly classified into five main regions, separated sequentially by temperature. Comparison with previous work^27–30,35 indicates that these correspond to: amorphous (−100 to 69 °C); to form III (70 to 110 °C); via a slow transition in the range 112–120 °C to form II (121 to 140 °C); to form I (141 to 165–168 °C); to the final melt (169 to 180 °C). The transformations are more visually apparent in the phonon-mode spectra range (20–400 cm⁻¹) than in the intra-molecular spectra range (400–3800 cm⁻¹); this has been previously noted and commented on in detail.²⁰ There is also some evidence for the presence of a glass transition (amorphous solid → supercooled liquid) around 35 °C. Overall the data presented in Fig. 1 agree very well with previous literature and therefore form a suitable model data set with which to investigate and directly compare the utility of phonon-mode Raman data, and intra-molecular Raman data for characterising the phase transitions and spectrally classifying the various forms of paracetamol. Note that the transformation II → I was not observed and in fact did not occur in a very similar study by Kaufmann et al.³¹ The transformation is clear and unambiguous from our data, and it is equally clear from the data of Kaufmann et al. that this transformation did not occur in their experiment (their Fig. 3 can be directly compared with our Fig. S3 to further illustrate this). The reason for the slight difference in crystallisation pathways is almost certainly the effect of nucleation, which is known to be a highly stochastic phenomenon.³⁶ In the work of Kaufmann et al. form I did not nucleate following the melt of form II (despite form I being the thermodynamically stable from the temperature range 156–169 °C), whereas in our experiment form II underwent a solid–solid polymorphic transformation to form I at 140 °C.

In the context of the statistical analyses which will be reported below, it is important to note at this point that any meaningful and reliable statistical analysis must at the very least be able to reproduce the majority of the observations discussed above, and that any analysis which is not in agreement with the visual observations is almost certainly unreliable. Statistical analysis of the data may of course reveal new details about the experiments which have not been noted in the (subjective) discussion above, but an agreement with the visual observations is a minimum criterion for physically meaningful results.

PCA analysis

Principal component analysis (henceforth PCA) is an extremely well established mathematical operation,³⁷ in which a larger number of observations are transformed by rotation into a smaller number of orthogonal variables, known as principal components, each of which is characterised by a score (single vector variable) and a loading (as many variables as were in a single original data set). PCA has a wide variety of applications, including as a clustering algorithm. It is useful for analysis of phase transformations,¹ because the new orthogonal co-ordinate set is defined in terms of the variance of the data, with the first axis having the most variance, etc. Any physical transformation must be defined by a variance in some property, and hence PCA is useful for the study of phase transitions such as those discussed in this work. PCA does not require a definition of the number of clusters, but rather a definition of the number of orthogonal components (principal components, henceforth PCs) into which the data should be resolved. All analyses detailed below report results from the first two principal components which remain unchanged if more components are chosen and which capture the majority of variance in the data (90% of the variance for the phonon-mode data and 54% for the intramolecular data). For further details the reader is referred to standard textbooks and online manuals^38,39 in addition to the computational code contained in the supplementary information to this paper.†

The PCA results are presented as scores plots (PC1 against PC2) in Fig. 2, and the variation in the score as a function of temperature in Fig. 3. The four panels in Fig. 2 present data for the intra-molecular spectral range 400–3800 cm⁻¹ and the phonon-mode spectral range 20–400 cm⁻¹ ranges, and illustrate the effects of pre-scaling data against using raw, uncorrected data. In PCA it is generally important to pre-scale data before analysis (see standard textbooks, for example “Multivariate data analysis: in practice”³⁸), especially for cases in which the variance of the data sets is not constant across data sets.

Fig. 2 Scores plots for molecular-mode and phonon-mode data, scaled and unscaled as labelled. Colour codes: black = −100 to 69 °C; blue = 70 to 111 °C; indigo = 112–120 °C; green = 121–140 °C; orange = 141–161 °C; red = 162–180 °C.

Focussing therefore on the pre-scaled data in Fig. 2, the key observation, which may be made from visual inspection of the plots, is that from the intra-molecular data no clear clustering of spectra is observed (and therefore the phase transformations are not obvious), whereas from the analysis of the phonon-mode data, four clear and obvious clusters are formed. Correlation of the data points with temperature (and the visual inspection of the spectra outlined earlier) indicates that the four clusters correspond to: 1) amorphous solid and melt (black data points); 2) crystalline form III (blue data points); 3) crystalline form II (green data points); and 4) crystalline form I (orange data points).

The variation in PC1 and PC2 as a function of temperature in Fig. 3 presents the same information (pre-scaled data) as in Fig. 2, but this time as a function of temperature. It is immediately clear that analysis of the intra-molecular spectral window (Fig. 3a) allows the glass transition, the crystallisation of the supercooled liquid, and the melting point to be identified. The various solid–solid polymorphic transformations however are not clear from these data. In marked contrast, for the phonon-mode spectral window (Fig. 3b), the PCA results clearly and unambiguously identify all transitions expected (glass, crystallisation of form III, the various solid → solid transformations, and the melt). These results are in complete agreement with the scores plots presented in Fig. 2 and discussed briefly above.

Fig. 3 Variation in scores as a function of temperature for spectral ranges: a) intra-molecular 400–3800 cm⁻¹; b) phonon-mode 20–400 cm⁻¹. PC 1 in black, PC 2 in red. The transformation temperatures noted by eye are indicated by dashed vertical lines. SCL = super-cooled liquid.

From an initial inspection of Fig. 2 and 3, we can therefore immediately conclude that the phonon-mode data are far more suitable for the study and characterisation of phase transformations than the intra-molecular data.

Considering Figs. 2 and 3 in more detail, the temperatures at which transitions occur between the clusters derived from the phonon-mode data correspond extremely well with the various phase transformations expected (and which were noted earlier from the visual inspection of the data). The transformation from amorphous (black data points) to form III (blue data points) corresponds to crystallisation from the supercooled liquid (it occurs at 69–70 °C which is well above the glass transition temperature of 25 °C, but below the melting point of form I at 169 °C). This transformation is instantaneous on our experimental time-scale—there are no experimental points which link the amorphous cluster with the form III cluster. The form III cluster exists until 110 °C, after which a slow transition (mainly on PC2) occurs (indigo data points), until by 120 °C a new cluster is formed. This cluster (green data points) corresponds to crystalline form II, which is stable until 139 °C, at which point another abrupt transition occurs. At 140 °C a new cluster (orange data points), corresponding to form I, is evident. Form I is stable until melting occurs. The melting point of form I has been repeatedly determined to be at 169 °C—in the current experiment the transformation from form I to the melt seems to occur gradually, with several points (in red) linking the form I cluster and the amorphous/liquid cluster. This is curious—one might expect the melting to occur sharply. From inspection of the raw data (Fig. S2 in supplementary information†) it seems that the melting of form I is a rather gradual process, in which the intensity of the Raman signal decreases steadily in the temperature range 161–169 °C. One possible explanation would be a temperature gradient across the sample, however given the abruptness of (for example) the SCL → III and the II → I transformations, it seems that this is unlikely. At the present moment it is not clear why the melting transformation should appear gradual in our data, but it seems likely that this is an experimental artefact which results from sample movement in the stage as the melting point is approached, rather than anything which is intrinsic to the melting of paracetamol.

The relatively diffuse nature of the amorphous/liquid cluster, compared to the tight definition of the crystalline clusters, is in full accord with glassy materials exhibiting a range of relaxation states, whereas crystalline materials possess a single thermodynamic ground state. The amorphous and liquid states are separated only by the glass transition, in which symmetry-breaking does not occur (unlike, for example, glass to crystal, crystal to liquid etc). Thus it is reasonable that the glass and the liquid define the same cluster, and that this cluster should be more diffuse than any of the clusters formed from the crystalline phases.

Our key conclusion from the PCA results (via consideration of Fig. 2 and 3) is that phonon-mode data are suitable for clear and unambiguous differentiation between solid forms of materials (specifically paracetamol), whereas intra-molecular data are not. This stands in some contrast to the conclusions of Kauffman et al.,³¹ who undertook an essentially identical experiment (albeit with access to data in the 350–4000 cm⁻¹ range only, and data collected every 3 °C rather than every 1 °C as in the present work) and concluded that data in the intra-molecular spectral window are suitable for differentiating between various forms of paracetamol. Direct comparison of our work and that of Kauffman is difficult for two reasons: i) the raw data of Kauffman et al., and their numerical routines, are not publicly available; ii) in our experiment a transformation II → I occurred at 140 °C, whereas in the experiments of Kauffman et al. this did not occur and their sample melted at the melting point of form II (156 °C) as discussed earlier. Their assignment of three rather than four clusters was therefore reasonable for their data, as their experiments isolated the amorphous form, plus crystalline forms III and II. In contrast, a full description of our data requires four clusters, with form I being required in addition to those observed by Kauffman et al.

Returning to whether or not the intra-molecular data are suitable for classifying spectra according to the phase present, it is important to note that in the work of Kauffman et al., data pre-scaling was not applied (see their experimental section p1312). As outlined earlier pre-scaling of data is typically essential for a robust and reliable statistical analysis. To allow a direct assessment of whether spectral classification is possible using unscaled data (the Kauffman procedure) we present in Fig. 2 the results of PCA of our data with no pre-scaling applied. For the intra-molecular data it is immediately apparent that the separation of the various physical forms is not very distinct at all for this analysis. The majority of the variation in both PC1 and PC2 occurs for the amorphous/liquid spectra. Forms III and II are very poorly separated. Form I is hardly distinct from the liquid melt. For the unscaled phonon-mode data the separation of the different forms is again very indistinct.

Overall therefore we can state that regardless of the exact nature of the statistical routine applied to the data, the intra-molecular spectra in the range 400–3800 cm⁻¹ are not sufficiently different for the various forms of paracetamol to allow reliable spectral classification. The phonon-mode data in contrast offer a clear and reliable differentiation of the forms, if the usual and recommended practice of pre-scaling^38,39 is applied to the data prior to analysis.

Although the enhanced sensitivity to these polymorphic transformations of the phonon-mode data over the intra-molecular data is intuitive, it is at first sight rather puzzling that the limited range intra-molecular data presented in Fig. 1c (1200-1350 cm⁻¹) and Fig. 1d (1450–1700 cm⁻¹) clearly show the transformations even from simple visual inspection, whereas the PCA of the entire intra-molecular data (pre-scaled) in Fig. 2 (400–3800 cm⁻¹) does not. To clarify this apparent disparity, PCA was performed on the data shown in Fig. 1d, i.e. the limited spectral range 1450–1700 cm⁻¹. These results are presented in Fig. S4a (supporting information†). Obvious and physically meaningful clustering is observed, which corresponds directly with both the visual inspection of the data (Fig. 1) and the phonon-mode PCA (Fig. 2b and 3b). Overall, there are (visually) more similarities than differences in the entire intra-molecular data (400–3800 cm⁻¹) between the different solid forms, and is therefore reasonable that PCA is unable to reliably assign the spectra to the various polymorphs of paracetamol. However careful selection of a limited spectral region in which clear visual differences are present (1450–1700 cm⁻¹), and subsequent analysis of that spectral region by PCA allows the spectra to be assigned correctly.

We can therefore conclude that for the current model system, a limited sub-set of the intra-molecular data can in certain cases discriminate between polymorphs, whereas use of the entire intra-molecular data range does not. We note that it is not apparent from the outset which limited spectral range to use: for example, employing data in the range 2800–3200 cm⁻¹ does not lead to any clustering (Fig. S4b, supporting information†). These results again support our observation that the phonon-mode data are reliable for discriminating between polymorphs, whereas the intra-molecular data are not reliable.

The extreme difference between the PCA results for the intra-molecular mode (Fig. 2, 3b) and phonon-mode (Fig. 2, 3a) spectral data is noteworthy, and illustrates the strongly enhanced sensitivity of the phonon-mode data to solid state forms. If only intra-molecular data are available (as is often the case with older generation Raman spectrometers for example, and with all mid-IR systems), great care must be taken both in data selection and data processing when employing only intra-molecular spectra data to investigate physical transformations between solids.

We now turn to an entirely separate statistical technique to assess the relative reliability of phonon-mode and intra-molecular Raman data for the study of phase transitions, in order to further validate the results outlined above.

Hierarchical agglomerative clustering analysis

Hierarchical agglomerative clustering (henceforth HA clustering) is a description of a set of statistical techniques which are extremely well established and widely applicable methods of clustering numerical data, including Raman spectra.^40–42 The methods involve various operations on a distance matrix generated from the original data sets. The results from the HA clustering can be grouped using various criteria. In the current work, each of the 281 spectra was assigned to one of four clusters. For further details of the HA clustering the reader is referred to review articles and online manuals,⁴³ as well as the computational routines used in this work (available in the supplementary information†).

The basic premise employed in the current work is as follows: for data which allow reliable clustering, the choice of HA clustering algorithm should not materially affect the results of the clustering; whereas for data which do not allow reliable clustering, the choice of algorithm may change the clustering observed. As with the PCA, any reliable clustering should lead to physically meaningful clusters. In the context of the current work two useful rules of thumb are: 1) clusters should be separated at the known transition temperatures between the various forms of paracetamol; 2) clustered spectra should be spread sequentially in temperature.

Results of seven different hierarchical clustering analyses are presented in Fig. 4a, for the phonon-mode data, and in 4b for the intra-molecular data. Four clusters were requested as output from the analysis. The known transition temperature between the various forms of paracetamol are also shown in the Fig. 4.

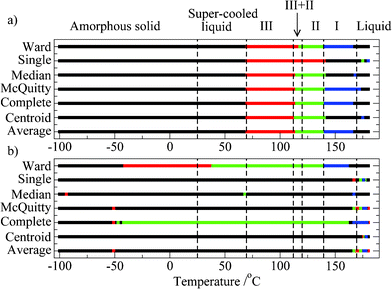Fig. 4 Results of HA clustering analyses for spectral ranges a) 20–400 cm⁻¹; b) 400–3800 cm⁻¹. The algorithm used is given at the left, and clusters are indicated by colours. Note that in this case the colours are arbitrary and do not relate directly to the various physical forms.

The first point to note from analysis of the phonon-mode data (Fig. 4a) is that all seven clustering algorithms produce similar (albeit not identical) clustering results. The four clusters in general correspond well with: 1) amorphous/liquid; 2) form III; 3) form II; 4) form I. The only exception is for the “single” algorithm, which places forms III and II in the same cluster. The glass transition is not detected by any of the algorithms (even when five clusters are requested, data not shown). However all of the other transitions (crystallisation; form III; form II; form I; melt) are clearly defined, and occur at physically meaningful temperatures which correspond well with those deduced in the earlier analyses.

Overall the clustering of the spectra, using the phonon-mode data as input; appears to be reliable and robust, with all of the physical transformations of paracetamol assigned, with the exception of the glass transition. The inability of HA clustering to detect the glass transition is most likely due to the very similar spectra from the amorphous solid, and the supercooled liquid. However it is of note that PCA unambiguously identified the glass transition temperature whereas HAC did not.

The results of the HA clustering analyses for the spectral window 400–3800 cm⁻¹ are given in Fig. 4b, where it is clear that the seven different algorithms do not yield similar clusters. Five of the seven algorithms appear totally insensitive to the different solid physical forms of paracetamol, with the “single”, “median”, “McQuitty”, “centroid” and “average” algorithms clustering all data from −100 to 168 °C. Not a single algorithm (applied to this data range) is capable of providing useful information on the various transformations, despite the presence of several signature peaks in the molecular region (Fig. 1, and as discussed earlier). It appears that despite the minor differences in peak positions in this spectral region between the different forms, the patterns are overall sufficiently similar that the clustering algorithms are unable to distinguish the different solid forms present in this experiment.

The results from the HA clustering analyses clearly and unambiguously indicate that the phonon-mode data are highly suitable for differentiating the various forms of paracetamol encountered in our experiment. In contrast, the intra-molecular data (including the traditional “fingerprint” region) are not. The use of seven different clustering algorithms for each analysis provides confidence that this difference between the two data ranges is not an artefact of our methodology. In the context of assigning the different physical forms of paracetamol, the results mirror those obtained from PCA, in which the phonon-mode data were demonstrably superior to the intra-molecular data for the characterisation of phase transformations.

The work outlined above has a number of potential applications. Firstly, it points the way to development of more appropriate spectroscopic instrumentation for materials analysis, in that any attempts to extend the wavenumber range available should focus primarily on the low-wavenumber capabilities. Second, it suggests that online Raman monitoring of processes in which solid–solid phase changes are of importance should, where possible, employ low-wavenumber data if possible. Third, the statistical approaches outlined above can readily be applied to situations in which automated classification of materials is important, for example in manufacturing plant, further in situ monitoring, etc. Finally, it demonstrates that automated screening for polymorphism in pharmaceutical materials can be readily achieved by online monitoring of recrystallisation from the glass state as a material is heated; sample requirements are of the order of mg or less.

Conclusion

For the first time we have used statistical methods to directly compare the use of phonon-mode (20–400 cm⁻¹) and traditional intra-molecular (400–3800 cm⁻¹) Raman spectra for identification and characterisation of phase transformations in solids. Both data sets were collected under exactly the same experimental conditions and are therefore directly comparable. We find that the use of phonon-mode data allows a very strongly enhanced sensitivity to these phase transformations, in agreement with previous qualitative discussions. While visual inspection allows ready identification of major spectral differences, a thorough statistical analysis allows relatively minor spectroscopic differences such as the glass transition to be identified. Our statistical results are derived from two totally different and well-established clustering methods: principal component analysis; and hierarchical agglomerative clustering. For the former, the importance of pre-scaling data was demonstrated. For the latter, seven different algorithms were employed to ensure (as far as possible) the validity of our results. Overall we find that phonon-mode data (20–400 cm⁻¹) are far more suitable for the spectroscopic identification of phase transitions than traditional mid-IR data (400–3800 cm⁻¹).

References

1. A. Heinz, C. J. Strachan, K.C. Gordon and T. Rades, Analysis of solid-state transformations of pharmaceutical compounds using vibrational spectroscopy, J. Pharm. Pharmacol., 2009, 61, 971–988.
2. L. Burgio and R. J. H. Clark, Library of FT-Raman spectra of pigments, minerals, pigment media and varnishes, and supplement to existing library of Raman spectra of pigments with visible excitation, Spectrochim. Acta, Part A, 2001, 57, 1491–1521.
3. J. Oxley, et al., Raman and infrared fingerprint spectroscopy of peroxide-based explosives, Appl. Spectrosc., 2008, 62, 906–915.
4. S. Armenta, S. Garrigues and M. Guardia, Determination of iprodione in agrochemicals by infrared and Raman spectrometry, Anal. Bioanal. Chem., 2007, 387, 2887–2894.
5. R. L. Frost, L. Duong and W. Martens, Molecular assembly in secondary minerals – Raman spectroscopy of the arthurite group species arthurite and whitmoreite, Neues Jahrb. Mineral., Monatsh., 2003, 2003, 223–240.
6. V. Hopfe, E. H. Korte, P. Klobes and W. Grählert, Optical Data of Rough-Surfaced Ceramics: Infrared Specular and Diffuse Reflectance versus Spectra Simulation, Appl. Spectrosc., 1993, 47, 423–429.
7. J. Bernstein, Polymorphism in Molecular Crystals, 2002, Oxford University Press, USA.
8. R. Hilfiker, Polymorphism: in the Pharmaceutical Industry, 2006, Wiley-VCH.
9. J. Aaltonen, et al. Solid form screening–a review, Eur. J. Pharm. Biopharm., 2009, 71, 23–37.
10. J. Lu and S. Rohani, Polymorphism and crystallization of active pharmaceutical ingredients (APIs), Curr. Med. Chem., 2009, 16, 884–905.
11. A. W. Newman and S. R. Byrn, Solid-state analysis of the active pharmaceutical ingredient in drug products, Drug Discovery Today, 2003, 8, 898–905.
12. M. M. Tlili, et al. Characterization of CaCO3 hydrates by micro-Raman spectroscopy, J. Raman Spectrosc., 2002, 33, 10–16.
13. J. A. Zeitler, et al. Terahertz pulsed spectroscopy and imaging in the pharmaceutical setting--a review, J. Pharm. Pharmacol., 2007, 59, 209–223.
14. A. I. Chumakov, et al. Collective nature of the boson peak and universal transboson dynamics of glasses, Phys. Rev. Lett., 2004, 92, 245508.
15. T. S. Grigera, V. Martín-Mayor, G. Parisi and P. Verrocchio, Phonon interpretation of the “boson peak” in supercooled liquids, Nature, 2003, 422, 289–292.
16. B. Guillot and Y. Guissani, Boson Peak and High Frequency Modes in Amorphous Silica, Phys. Rev. Lett., 1997, 78, 2401.
17. Hehlen, et al. Hyper-raman scattering observation of the boson peak in vitreous silica, Phys. Rev. Lett., 2000, 84, 5355–5358.
18. V. K. Malinovsky and A. P. Sokolov, The nature of boson peak in Raman scattering in glasses, Solid State Commun., 1986, 57, 757–761.
19. A. Brillante, I. Bilotti, R. G. D. Valle, E. Venuti and A. Girlando, Probing polymorphs of organic semiconductors by lattice phonon Raman microscopy, CrystEngComm, 2008, 10, 937–946.
20. S. Al-Dulaimi, A. Aina and J. Burley, Rapid polymorph screening on milligram quantities of pharmaceutical material using phonon-mode Raman spectroscopy, CrystEngComm, 2010, 12, 1038–1040.
21. J. A. Zeitler, et al. Characterization of temperature-induced phase transitions in five polymorphic forms of sulfathiazole by terahertz pulsed spectroscopy and differential scanning calorimetry, J. Pharm. Sci., 2006, 95, 2486–2498.
22. J. C. Decius and R. M. Hexter, Molecular Vibrations in Crystals, 1978, McGraw-Hill Education.
23. A. S. Davydov, Theory of Molecular Excitons , 1962 , McGraw Hill Books, New York.
24. M. Haisa, S. Kashino, R. Kawai and H. Maeda, The Monoclinic Form of p-Hydroxyacetanilide, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 1283–1285.
25. M. Haisa, S. Kashino and H. Maeda, The orthorhombic form of p-hydroxyacetanilide, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 2510–2512.
26. M.-A. Perrin, M. A. Neumann, H. Elmaleh and L. Zaske, Crystal structure determination of the elusive paracetamol Form III, Chem. Commun., 2009, 3181–3183.
27. J. C. Burley, M. J. Duer, R. S. Stein and R. M. Vrcelj, Enforcing Ostwald’s rule of stages: isolation of paracetamol forms III and II, Eur. J. Pharm. Sci., 2007, 31, 271–276.
28. P. Martino, P. Conflant, M. Drache, J.-P. Huvenne and A.-M. Guyot-Hermann, Preparation and physical characterization of forms II and III of paracetamol, J. Therm. Anal., 1997, 48, 447–458.
29. S. Gaisford, A. B. M. Buanz and N. Jethwa, Characterisation of paracetamol form III with rapid-heating DSC, J. Pharm. Biomed. Anal., 2010, 53, 366–370.
30. S. Qi, P. Avalle, R. Saklatvala and D. Q. M. Craig, An investigation into the effects of thermal history on the crystallisation behaviour of amorphous paracetamol, Eur. J. Pharm. Biopharm., 2008, 69, 364–371.
31. J. F. Kauffman, L. M. Batykefer and D. D. Tuschel, Raman detected differential scanning calorimetry of polymorphic transformations in acetaminophen, J. Pharm. Biomed. Anal., 2008, 48, 1310–1315.
32. S. Šašić, Pharmaceutical Applications of Raman Spectroscopy , 2007 , Wiley-Interscience.
33. R. D. C. Team, R: A Language and Environment for Statistical Computing. (Vienna, Austria, 2008).at <http://www.R-project.org>.
34. W. Stacklies, H. Redestig, M. Scholz, D. Walther and J. Selbig, pcaMethods a bioconductor package providing PCA methods for incomplete data, Bioinformatics, 2007, 23, 1164–1167.
35. G. L. Perlovich, T. V. Volkova and A. Bauer-Brandl, Polymorphism of paracetamol, J. Therm. Anal. Calorim., 2007, 89, 767–774.
36. J. P. Leonard and J. S. Im, Stochastic modeling of solid nucleation in supercooled liquids, Appl. Phys. Lett., 2001, 78, 3454.
37. K. Pearson, On lines and planes of closest fit to systems of points in space, Philosophical Magazine, 1901, 2, 559–572.
38. K. H. Esbensen, D. Guyot, F. Westad and L. P. Houmøller,Multivariate data analysis: in practice: an introduction to multivariate data analysis and experimental design , 2002, Multivariate Data Analysis.
39. I. T. Jolliffe, Principal component analysis , 2002 , Springer.
40. J. Grognux and J.-L. Reymond, Classifying enzymes from selectivity fingerprints, ChemBioChem, 2004, 5, 826–831.
41. G. Barr, G. Cunningham, W. Dong, C. J. Gilmore and T. Kojima, High-throughput powder diffraction V: the use of Raman spectroscopy with and without X-ray powder diffraction data, J. Appl. Crystallogr., 2009, 42, 706–714.
42. C. Romesburg, Cluster Analysis for Researchers , 2004, Lulu.com.
43. F. Murtagh, A Survey of Recent Advances in Hierarchical Clustering Algorithms, The Computer Journal, 1983, 26, 354–359.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c1ra00422k

‡ For the sake of simplicity we include all data collected in our statistical analysis. It is trivial to demonstrate using the raw data and numerical routines provided that changing the lowest wavenumber cut-off for our data makes no real difference to our results. A demonstration of this is provided in the supplementary information.†

§ For example, the glass transition seems to occur at 35 °C in our data set, whereas it is very well established through DSC that 25 °C is a more appropriate value. However the melting point observed in our work seems reasonable, as do the temperatures of the other phase transitions. As the various transitions of paracetamol are very well documented (and are in any case subject to the stochastic nature of nucleation), and as the main thrust of this work is to classify the different forms, this is not an issue of any real consequence.

---