Ab initio investigations on the crystal structure, formation enthalpy, electronic structure, chemical bonding, and optical properties of experimentally synthesized isoreticular metal–organic framework-10 and its analogues: M-IRMOF-10 (M = Zn, Cd, Be, Mg, Ca, Sr and Ba)

Abstract

The equilibrium solid-state structure, electronic structure, formation enthalpy, chemical bonding, and optical properties of IRMOF-10 and its alkaline earth metal analogues M-IRMOF-10 (M = Cd, Be, Mg, Ca, Sr, Ba) have been investigated with density functional calculations. The unit cell volume and atomic positions were fully optimized with the GGA functional. This supplements the incomplete experimental structural parameters available for Zn-IRMOF-10. The calculated bulk moduli decrease monotonically from Zn to Cd, and from Be to Ba, and indicate that Zn-IRMOF-10 and its analogues are relatively soft materials. The estimated bandgap values are in the range 2.9 to 3.0 eV, indicating nonmetallic character. Importantly, the bandgaps within the M-IRMOF-10 series (containing a rather long 4,4′-biphenyldicarboxylate linker) are smaller than those within the M-IRMOF-1 series (shorter benzene dicarboxylate linker). The optical properties (dielectric function ε(ω), refractive index n(ω), absorption coefficient α(ω), optical conductivity σ(ω), reflectivity R(ω), and electron energy-loss spectrum L(ω)) of the M-IRMOF-10 series were computed. The observation of very small reflectivities over a wide energy range suggests possible uses in hybrid solar cell applications. The main characteristics of the optical properties are similar for the whole series although differences are seen in the details. An analysis of chemical bonding in the M-IRMOF-10 series reveals as might be anticipated that M–O bonds are largely ionic whereas C–O, C–H and C–C exhibit mainly covalent interactions. The BOP values of M–O decrease through the series when going from Zn to Cd, and from Be to Ba, i.e. the ionicity increases and the covalency decreases for the M–O bonds.

---

I. Introduction

MOFs constitute a rather new class of porous materials that are considered for many applications, including catalysis, petrochemistry, gas adsorption and storage (e.g., H₂, CH₄, CO₂, etc.), selective separation, sensing, molecular recognition, and much more.¹ Within the huge MOF family of structures, the series of isoreticular metal–organic frameworks (IRMOF-1–16), prepared by Yaghi and coworkers,^2–4 may have attracted most attention. Systematic changes in linker size and linker functionalization affects the adsorptive and diffusive properties of the material. Interestingly, MOFs have been recently considered as suitable preconcentrators for detection of explosive compounds,⁵i.e. detection at parts per trillion levels.⁶ In this respect, several MOFs have shown effective selective preconcentration properties, i.e., IRMOF-1,^7–10IRMOF-3,⁸IRMOF-8,¹¹ and IRMOF-10.^8,12 A predictive understanding of the relationship between MOF structure and its corresponding physicochemical properties will help match MOFs to a particular application. Optical and electronic properties may be of relevance concerning the suitability of MOFs to act as sensors when exposed to adsorbing species. Currently, limited experimental or computational techniques are used to establish structure/property relationships, mostly on a case-by-case basis.

Compared to the “prototypical” IRMOF-1 (also known as MOF-5) in which tetranuclear Zn clusters are linked by a benzene-1,4-dicarboxylate unit, IRMOF-10¹³ with its longer 4,4′-biphenyldicarboxylate linker has received much less attention concerning its physicochemical properties. IRMOF-10 was first synthesized by Yaghi and coworkers.^2–4,13 The higher surface area and pore sizes of IRMOF-10¹⁴ is a key feature for its use for gas absorption and separation and hydrogen storage.^15–23 Interestingly, exceptional negative thermal expansion has been reported for Zn-IRMOF-10.²⁴ Other than adsorption and separation properties, scarce attention has been paid to other properties of IRMOF-10, e.g., structural stability, mechanical properties, chemical bonding, optical properties, etc. Interestingly, even its solid-state structure remains to be well characterized: The crystals of Zn-IRMOF-10 were too small for collection of quality X-ray intensity data and instead, the structure was assigned by a simple simulation (see ref. 13, supplementary info p.70): The unit cell constants and space group information of a related IRMOF-12 was used to build the IRMOF-10 structure. The simulated powder diffraction pattern of the predicted structure was in reasonable, but far from perfect, agreement with the measured PXRD patterns of IRMOF-10 and IRMOF-12. Under such circumstances, structural optimization based on computational calculations should be an indispensable tool to determine and/or confirm the solid-state structure since many experimentally determined MOF structures are relatively coarse. In this respect, the contributions from Mellot-Draznieks and coworkers to predict structures by computational tools are particularly noteworthy.^25–32

Recent reports on MOFs as semiconductors^33,34 have triggered intense research in this area and is a motivation for studying their electronic and optical properties. The quantum confinement of inorganic semiconductor entities (such as dots or wires) in close contact with organic molecules makes the optical properties of MOFs particularly interesting. To our knowledge, there are until now no detailed theoretical reports on these aspects of M-IRMOF-10 available.

Herein, we present a comprehensive computational study on the solid-state structure, stability, electronic structure, formation energy, chemical bonding, and mechanical properties of the experimentally known Zn-IRMOF-10 using DFT calculations with the GGA-PBE functional as implemented in the VASP code.^35,36 Moreover, analogues of Zn-IRMOF-10, i.e., M-IRMOF-10 with M = Cd, Be, Mg, Ca, Sr, and Ba are studied systematically. The optical properties of this whole M-IRMOF-10 series were calculated using the CASTEP module³⁷ of the Material Studio 5.0 program.³⁸ The acquired insight should be valuable for future uses of the M-IRMOF-10 series of materials as photocatalysts, photoactive materials for photovoltaic cells, and components for electroluminescence devices.

Computational details are provided in the following section. The details of the results and discussions are then described, including structural details, formation energies, electronic structures, chemical bonding, calculated band structures, and finally optical properties. In order to conveniently present the comprehensive results in this work, we use the experimentally synthesized, Zn-based IRMOF-10 as the main line for the discussion and analysis for the whole series. Moreover, we compare and discuss the analogues (i.e., M-IRMOF-10, with M ≠ Zn) with IRMOF-10 (M = Zn)³⁹ and try to elucidate systematic trends in the properties for the whole series. The findings for M-IRMOF-10 will also be compared with data for the M-IRMOF-1 analogues, recently published by us.^40,41

II. Computational details

The Vienna ab initio simulation package (VASP)^35,36 has been used for the total-energy calculations to study the structural stability and to establish equilibrium structural parameters. The generalized gradient approximation (GGA)^42–44 includes the effects of local gradients in the charge density for each point in the materials and generally gives better equilibrium structural parameters than the local density approximation (LDA). Hence, the GGA functional was used for all calculations. The projector-augmented-wave (PAW)^36,45 Perdew, Burke, and Ernzerhof (PBE)⁴⁴ pseudo-potentials based on GGA were used to describe the ion-electron interactions. A criterion of 0.01 meV atom⁻¹ was placed on the self-consistent convergence of the total energy and all calculations were made with plane-wave cutoff of 500 eV, which guarantees that absolute energies are converged to within a few meV/f.u. This has been tested to be accurate and reliable for M-IRMOF-10 systems considered in the present study. Brillouin-zone integration was performed with a Gaussian broadening of 0.2 eV during all relaxations. The conjugated-gradient algorithm based on Hellmann-Feynman forces was used to relax the ions into their instantaneous equilibrium positions. The forces and the stress tensors were used to determine the search directions to identify the ground state (i.e., the total energy is not taken into account). This algorithm is very fast and efficient when the initial structures are far away from the ground state. Forces on the ions were calculated using the Hellmann-Feynman theorem as the partial derivatives of the free electronic energy with respect to the atomic positions and adjusted using the Harris-Foulkes correction to the forces. The atoms were relaxed toward equilibrium until the Hellmann-Feynman forces were less than 10⁻³ eV Å⁻¹.

Because we deal with a rather large system (166 atoms per primitive cell), the Γ-point alone is sufficient for sampling the Brillouin zone during geometry optimization. However, in order to arrive to an accurate band structure we have used a sufficient number of k-points for the band structure calculations. The DOS calculations were performed on the fully optimized structure with only Γ-point alone. However, the DOS was calculated in a fine energy grid (1801 points) due to the narrow band features so as to visualize DOS correctly.

To gauge the bond strength and character of bonding, we have analyzed bond overlap population (BOP) values with on the fly pseudopotential estimated on the basis of the Mulliken population as implemented in the CASTEP code.³⁷ In order to understand the chemical bonding and interactions between constituents in the M-IRMOF-10 series, charge density, charge transfer, and electron localization function (ELF)^46–49 analyses were performed based on the results obtained from the VASP calculations. We have also calculated the optical properties including dielectric function, absorption coefficient, reflectivity, refractive index, optical conductivity, and energy loss function for the M-IRMOF-10 series with ultrasoft pseudopotential by using the CASTEP code. In parallel with optical properties calculations, we also calculated the band structure with ultrasoft pseudopotential for the whole series with CASTEP, which will provide some hints and useful information to understand the electronic structures and optical properties of these materials. The method used for the calculation of optical properties and band structures has been proven to be reasonable and compared favorably with corresponding experimental spectra in previous contributions from our and other groups.^{40,41,50–60}

III. Results and discussions

A. Structural details

Zn-IRMOF-10 is a member of a series of IRMOFs with oxide-centered Zn₄O tetrahedra as nodes linked by organic molecules and can be synthesized based on the reticular synthesis strategy proposed by Yaghi and coworkers.^4,13,61 In Zn-IRMOF-10 the organic linker is 4,4′-biphenyldicarboxylate (4,4′-BPDC).

Zn-IRMOF-10 can be obtained in highly crystalline form with high specific surface areas of ca. 5000 m² g⁻¹.^14,62 Its crystal structure has 664 atoms (eight formula units of Zn₄O(BPDC)₃) in the conventional unit cell with cubic Fm3̄m symmetry (no. 225) and the reported lattice parameter is a = 34.281 Å.¹³ Its primitive cell has 166 atoms, including two nodes and six linker molecules, corresponding to two Zn₄O(BPDC)₃ formula units. The computed solid-state structure of Zn-IRMOF-10 is illustrated in Fig. 1. The different crystallographic sites in Zn-IRMOF-10 include one type of Zn, two types of O, five types of C, and two types of H occupying 32f, 8c, 96k, 96k, 48g, 96k, 48g, 48g, 96k, and 96k Wyckoff positions, respectively. The M-substituted analogues of Zn-IRMOF-10 are readily visualized by the replacement of Zn⁺² ions with M⁺² metal ions (i.e., M = Cd, Be, Mg, Ca, Sr, and Ba). It is assumed that they will have the same space group and Wyckoff positions as Zn-IRMOF-10, and the equilibrium structural parameters were estimated from structural optimization accordingly.

Fig. 1 The crystal structure of the M-IRMOF-10 (M = Zn, Cd, Be, Mg, Ca, Sr, Ba) series in the cubic Fm3̄m symmetry (no. 225). The atoms with labels M, O1, O2, C1, C2, C3, C4, C5, H1, and H2 are chemically distinct sites and will be addressed in the discussion of the chemical bonding and interpretation of the partial density of states (PDOS).

B. Structural optimization of the M-IRMOF-10 series from total-energy calculations

As commented in the Introduction, the crystals of Zn-IRMOF-10 were too small for collection of quality X-ray intensity data and hence Yaghi and coworkers obtained the structural data from a simulated structure.¹³ When the simulated structure data based on Yaghi's reported atomic coordinates for Zn-IRMOF-10 (p. 70 of Supplementary Information to ref. 13) were imported in Materials Studio according to the given space group, additional H and C atoms were generated and it was necessary to “merge” the extra and the original atoms, thus slightly adjusting the positions, to produce a reasonable input structure with the visualization tool in Materials Studio.³⁸ The computed ground-state structure was then obtained from this input structure by full geometry optimization, i.e. the atom positions and cell parameters were fully relaxed. This computationally fully optimized structure of Zn-IRMOF-10 then served as the starting structure for the other M-IRMOF-10 structures by replacement of the Zn atoms by Cd and the alkaline earth metal atoms Be, Mg, Ca, Sr, and Ba before new structural optimization are made.

The structural optimization was achieved by first relaxing the atomic positions globally using the force-minimization technique, by keeping the lattice constant (a) and cell volume (V) fixed to the crystallographically determined values. Then the theoretical ground-state volume was determined with optimized atomic positions by varying the cell volume within ±10% of the experimentally determined volume. The calculated total energy as a function of volume was fitted to the so-called equation of state (EOS) to calculate the bulk modulus (B₀) and its pressure derivative (B₀'). In order to cross-check the calculated B₀ and B₀' values, the E–V data were fitted into three different EOS, i.e. Murnaghan,⁶³ Birch,⁶⁴ and Universal equation of states (UEOS).⁶⁵ The bulk modulus and its pressure derivative (in parentheses) obtained from the E–V curve using the UEOS are 9.09 GPa (3.12) for M = Zn, 8.30 GPa (2.36) for Cd, 11.49 GPa (1.28) for Be, 8.74 GPa (7.00) for Mg, 7.32 GPa (3.64) for Ca, 6.57 GPa (9.31) for Sr, and 6.10 GPa (4.23) for Ba in the M-IRMOF-10 series. The corresponding results derived from the two other EOSs can be found in Table 1.

Table 1 Optimized equilibrium lattice constant (a/Å), bulk modulus (B₀ (GPa)), and its pressure derivative (B₀') for M-IRMOF-10 (M = Zn, Cd, Be, Mg, Ca, Sr, Ba)

Material M-IRMOF-10	a/Å^a	B 0 (GPa)^b	B 0 ' ^b
a Data in < > from ref. 66, experimental data in ≪ ≫ from ref. 13. b Data without brackets from Universal EOS; data in ( ) from Murnaghan EOS; data in [ ] from Birch-Murnaghan 3rd-order EOS; data in < > from theoretical DFTB calculations in ref. 66.
Zn	34.831 <35.348> ≪34.280≫	9.09 (9.08) [9.09] <6.00>	3.12 (3.09) [3.11]
Cd	36.085	8.30 (8.30) [8.30]	2.36 (2.38) [2.44]
Be	33.095	11.49 (11.49) [11.50]	1.28 (1.26) [1.20]
Mg	34.877	8.74 (8.74) [8.74]	7.00 (6.96) [6.99]
Ca	36.474	7.32 (7.32) [7.32]	3.64 (3.64) [3.65]
Sr	37.358	6.57 (6.56) [6.57]	9.31 (9.27) [9.29]
Ba	38.288	6.10 (6.10) [6.10]	4.23 (4.20) [4.22]

---

It is seen that the B₀ and B₀' values estimated from three different EOS derived from the E–V data are nearly identical, indicative of the reliability of our results. Moreover, the bulk moduli decrease monotonically when one moves from Zn to Cd, and from Be to Ba. On the other hand, there is no clear trend in their pressure derivatives within these two series, i.e. their pressure derivatives change randomly. Interestingly, it is consistently seen that for any given metal M, the values for the bulk moduli for the M-IRMOF-10 series are 35–41% smaller than for the recently studied^40,41M-IRMOF-1 series. These smaller value of the bulk moduli are associated with the linker lengths. As the compressibility of MOFs at low pressure is mainly decided by these organic linkers, the longer size of the linker in IRMOF-10 diminishes the repulsive interaction between nodes during compression and hence its bulk modulus is reduced. It may also be noted that the presently calculated B₀ values of Zn-IRMOF-10 are larger than the value of 6.00 GPa⁶⁶ previously obtained by DFTB calculations. The previous data were calculated from the elastic constants which are obtained from total energy change after application of a suitable strain. There are no experimentally measured bulk modulus values available yet for any of these compounds with which our results may be compared, and we hope that the present study will motivate experimentalists to study the mechanical properties of the M-IRMOF-10 and M-IRMOF-1 series.

The optimized equilibrium atomic positions and lattice parameters, along with the corresponding experimental values for IRMOF-10, are listed in Table 2. The lattice parameter of IRMOF-10 in the present work (34.8312 Å) is in good agreement with the experimental data (34.2807 Å)¹³ and also with the available theoretical value obtained from DFTB calculations (35.348 Å).⁶⁶ Note that the magnitudes of previously reported DFTB data are generally somewhat greater than the present results, which will also be demonstrated in the following discussion (see Table 3) of bond lengths and angles. The present results are closer to the experimental data (which were not high resolution ones, as already commented) than the previously reported DFTB results.⁶⁶ The lattice parameters for the whole series are listed in Table 1. It can be seen that from Zn to Cd, and from Be to Ba, the optimized equilibrium lattice constants increase with the atomic number (i.e., a_Zn < a_Cd; a_Be < a_Mg < a_Ca < a_Sr <a_Ba) largely as a consequence of the increase in atomic radii of the central metal atoms. The optimized bond lengths and angles for the whole series, together with the experimentally reported values for M = Zn, are listed in Table 3.

Table 2 Optimized equilibrium structural parameters for IRMOF-10

Details	PBE-GGA	Expt^a
a Experimental data from p.70 in Supplementary Information to ref. 13.
Crystal system	Cubic	Cubic
Space group	Fm3̄m (225)	Fm3̄m (225)
Atoms/cell (fcc)	166	166
a/Å	34.8312	34.2807
V/Å^3	42257.64	40285.53
Atom type	Atomic positions (x, y, z)
Zn1 (32f)	(0.2827, 0.2174, 0.2174)	(0.2828, 0.2172, 0.2172)
O1 (8c)	(1/4, 1/4, 1/4)	(1/4, 1/4, 1/4)
O2 (96k)	(0.2731, 0.2269, 0.1624)	(0.2735, 0.2265, 0.1618)
C1 (96k)	(0.2745, 0.2255, 0.0824)	(0.2747, 0.2253, 0.0822)
C2 (48g)	(1/4, 1/4, 0.1029)	(1/4, 1/4, 0.1028)
C3 (96k)	(0.2744, 0.2256, 0.0425)	(0.2747, 0.2248, 0.0413)
C4 (48g)	(1/4, 1/4, 0.1458)	(1/4, 1/4, 0.1448)
C5 (48g)	(1/4, 1/4, 0.0213)	(1/4, 1/4, 0.0206)
H1 (96k)	(0.2936, 0.2064, 0.0982)	(0.2921, 0.2083, 0.0962)
H2 (96k)	(0.2936, 0.2064, 0.9018)	(0.2916, 0.2073, 0.0275)

---

Table 3 Optimized bond lengths (Å) and bond angles (°) for M-IRMOF-1 (M = Zn, Cd, Be, Mg, Ca, Sr, and Ba) at their equilibrium volumes

M	C1–C2	C1–C3	C2–C4	C3–C5	C5–C5	C4–O2	C1–H1	C3–H2	M–O1	M–O2	O1–M–O2	O2–M–O2
a The experimental data in ( ) are from the structure made from the coordinates from the Supplementary Information in ref. 13. b The data in < > are from ref. 66.
Zn	1.402	1.390	1.493	1.411	1.485	1.279	1.090	1.089	1.970	1.970	111.509	107.359
	(1.391)^a	(1.402)	(1.442)	(1.403)	(1.413)	(1.280)	(0.960)	(0.960)	(1.946)	(1.953)	(111.988)	(106.842)
			<1.460>^b			<1.319>			<2.074>	<2.088>	<107.000>
Cd	1.402	1.390	1.499	1.411	1.485	1.278	1.090	1.089	2.178	2.201	108.469	110.455
Be	1.402	1.390	1.486	1.411	1.486	1.275	1.090	1.089	1.717	1.635	115.441	102.896
Mg	1.402	1.390	1.491	1.411	1.486	1.278	1.090	1.089	1.988	1.959	110.607	108.312
Ca	1.402	1.390	1.495	1.411	1.486	1.277	1.090	1.089	2.269	2.241	106.315	112.434
Sr	1.402	1.390	1.497	1.411	1.485	1.277	1.090	1.089	2.432	2.405	104.325	114.090
Ba	1.402	1.391	1.500	1.411	1.486	1.277	1.090	1.089	2.606	2.578	102.402	115.519

---

From Table 2, it may be noted that there are some discrepancies in the structural parameters (which can be readily understood given the fact that the experimental data were obtained from a simulated structure, as briefly commented already), but by and large the atomic coordinates of experimental and computational results agree quite well. The bond lengths and bond angles between the constituents in M-IRMOF-10 at the optimized equilibrium volume are given in Table 3. A comparison of the optimized equilibrium bond lengths (Å) and bond angles (°) for Zn-IRMOF-10 with the experimental data reveals that the agreement between experiment and theory is quite good for IRMOF-10 (Zn entries in Table 3). The optimization nicely demonstrates how computations can be an indispensable tool to resolve the details of solid-state structures of complex systems when there are ambiguities or uncertainties in experimentally available structure data. Computational simulations have made dramatic advances in the past two decades, and today, accurate prediction of structural properties of novel molecules and exotic extended structures is possible. It is therefore reasonable to suggest that poor-resolution experimental data on MOFs should be supplemented with computational simulations and structure optimizations as a standard tool to establish more reliably the detailed structures of new MOFs.

C. Energy of formation considerations

Information about formation enthalpies constitute an excellent means to establish whether theoretically predicted phases are likely to be stable and such data may serve as a guide to evaluate possible synthesis routes. Several interesting reports have appeared in the literature concerning computation of reaction enthalpies by consideration of electric total energies, zero-point energy vibrational correction, and thermal contribution (within the harmonic approximation).⁶⁷ Of course, kinetic factors can also play a notable role during synthesis.⁶⁸ Here, we are primarily interested to know whether a particular hypothetical compound is likely to be synthesizable or not on energetic grounds. We believe that our approach, to be described below, will give qualitatively sound trends in stabilities, although a quantitatively accurate prediction of reaction enthalpies cannot be expected. Further, for the estimation of the vibrational entropy contribution to the total energy, phonon calculations within the harmonic approximation should be performed. As the number of atoms involved in the present calculations is very large, such computationally intensive phonon calculations are outside the scope of the present study. It should also be mentioned that relative stability orders from reaction enthalpies calculations usually refer to one material having different structures (phases). Importantly, the IRMOF-10 material synthesized by Yaghi and coworkers exists (at least so far) as only one phase.¹³ This experimentally reported high symmetric phase attracted much attention from both experiment and theory. Here, we focused on the viability of synthesizing this highly symmetric framework phase using alkaline-earth elements instead of Zn in IRMOF-10. There are several ways to evaluate the reaction energies; our approach of starting from the elements is but one. An alternative approach might be to mimic the experimental synthesis conditions involving the reaction between Zn₄O(OH)₆ and the dicarboxylic acid linker.⁶⁶

In our case, we explore the thermodynamic feasibility of assembling these M-IRMOF-10 materials from the elements (eq 1). Thus, as part of this approach we have computed the total energies for C (R-3m), O₂ (P4/mmm), H₂ (P4/mmm), Zn (P6₃/mmc), Cd (P6₃/mmc), Be (P6₃/mmc), Mg (P6₃/mmc), Ca (Fm3̄m), Sr (Fm3̄m), and Ba (Im-3m) in their ground state structures with full geometry optimization. The reaction enthalpies for MOF formation were calculated from the difference in the total energy between the products and reactants involved in the reactions concerned. We focus on the formation enthalpies of the analogues (M-IRMOF-10, M = Cd, Be, Mg, Ca, Sr, Ba) relative to the experimentally synthesized Zn-IRMOF-10. Through this comparison, a general insight can be gained into the relative stabilities for the whole series when different metals are substituted into the nodes. The results establish unambiguously that eqn 1 depicts exothermic reactions for the experimentally synthesized Zn-IRMOF-10 as well as the analogous, yet hypothetical, M-IRMOF-10 series.

8M + 13O₂ + 84C + 24H₂ → M₈O₂₆C₈₄H₄₈ (M-IRMOF-10, M = Zn, Cd, Be, Mg, Ca, Sr, Ba) (1)

The magnitudes of the calculated formation enthalpies given in Table 4 (where data for the M-IRMOF-1 series are included for comparison) show that (1) the stability of Cd-IRMOF-10 is nearly the same as that of Zn-IRMOF-10, (2) the M-IRMOF-10 (M = Be, Mg, Ca, Sr and Ba) series is more stable than Zn-IRMOF-10, and (3) the stabilities (ca. −50 kJ mol⁻¹) of the M-IRMOF-10 (M = Be, Mg, Ca, Sr and Ba) compounds are very similar since they have comparable formation enthalpies. The magnitude of the calculated formation enthalpy for Zn-IRMOF-10 (−35.12 kJ mol⁻¹) is somewhat smaller than that for Zn-IRMOF-1 (−46.02 kJ mol⁻¹). Nevertheless, the value is sufficiently large to render Zn-IRMOF-10 stable, which is of course consistent with the fact that it is readily synthesized.¹³ For the alkaline earth metal members of the M-IRMOF-10 series, the formation enthalpies are consistently ca. 14–16 kJ mol⁻¹ less negative than for the analogous M-IRMOF-1 member. Nevertheless, the still rather large negative values for the enthalpies of formation for the M-IRMOF-10 series suggest that it might be possible to synthesize all these compounds as stable phases. We eagerly await the experimental synthesis and investigation of the properties of the predicted M-IRMOF-10 series of compounds.

Table 4 Calculated enthalpies of formation (ΔH; kJ mol⁻¹) for the M-IRMOF-10 and M-IRMOF-1 (M = Cd, Be, Mg, Ca, Sr, Ba) compounds

M-IRMOF-10 ^a
M	Zn	Cd	Be	Mg	Ca	Sr	Ba
ΔH (kJ mol^−1)	−35.12	−31.25	−47.01	−47.63	−50.67	−49.71	−48.76

---

M-IRMOF-1 ^b
a This work, according to eqn 1. b From ref. 41, based on the analogous reaction to eqn 1.
M	Zn	Cd	Be	Mg	Ca	Sr	Ba
ΔH (kJ mol^−1)	−46.02	−40.96	−61.69	−62.53	−66.56	−65.34	−64.12

---

D. Electronic structure

The data for Zn-IRMOF-10 will serve as a typical example of electronic structure evaluation for the whole series. The total electronic density of states (TDOS) and partial density of states (PDOS) are displayed in separate figures for convenient visualization and analysis. The TDOS and PDOS at the equilibrium volume for Zn-IRMOF-10 are displayed in Fig. 2 and 3, respectively. The calculated band gap E_g for Zn-IRMOF-10 is 2.925 eV, which is comparable to a recent DFTB calculation that resulted in 3.07 eV,⁶⁶ indicating nonmetallic character. The calculated band gap of IRMOF-10 is substantially smaller than that of IRMOF-1 (MOF-5) at 3.5 eV.¹⁵ It appears that it is the linker rather than the node that primarily determines the band gap in IRMOF-1vs.IRMOF-10: The 4,4′-biphenyldicarboxylate linker in IRMOF-10 is longer than the 1,4-benzenedicarboxylate linker in IRMOF-1. TDOS for the remaining parts of the series will be discussed later.

Fig. 2 The calculated total density of states (TDOS) for Zn-IRMOF-10 in the cubic Fm3̄m symmetry (no. 225).

Fig. 3 The calculated total density of states (TDOS) and partial density of states (PDOS) for Zn-IRMOF-10 in the cubic Fm3̄m symmetry (no. 225).

Unfortunately, there are yet no experimental data on the band gap value of Zn-IRMOF-10 reported in the literature with which the calculations can be compared. It should be noted that DFT calculated band gap values tend to be generally lower than experimentally determined ones; such an underestimation of the calculated band gaps is an intrinsic feature of the ab initio method and is related to a DFT limitation in not taking into account the discontinuity in the exchange–correlation potential.⁶⁹ To overcome this discrepancy, the so-called scissor operator,⁷⁰ Δ, can be introduced, which effectively eliminates the difference between the theoretical and experimental gap values by means of a simple rigid shift of the unoccupied conduction band with respect to the valence band. In line with this, for E_g of bulk ZnO, the calculated band gaps are significantly smaller than the experimental values. (LDA = 0.744/0.573 eV; GGA = 0.804/0.641 eV, LDA + U = 1.988/1.486 eV , GW = 2.255/2.100 eV, experimental 3.455/3.300 eV for ZnO–w/ZnO–z, respectively).⁷¹ In a recent contribution,⁴⁰ we found that the DFT calculations of MOF-5 unexpectedly gave a band gap value in very good agreement with that obtained from experimental studies.^72,73 It may be of interest to extend this study to other MOFs that are constructed from various organic dicarboxylic acid linkers and the Zn₄O nodes to understand more about the role of linkers on the electronic structure and optical properties of the materials. Metric parameters within the Zn clusters of IRMOF-10 and MOF-5 closely match those of bulk ZnO (Zn–O distances are 1.970 Å, 1.936 to 1.948 Å, and 1.974 to 1.983 Å, O–Zn–O angles are 107.366° to 111.502°, 107.7° to 111.2° and 108.3° to 110.7° in IRMOF-10, MOF-5 and bulk ZnO, respectively). Though the bond distances and angles are comparable between Zn-IRMOF-10 and ZnO, significant differences in material properties may arise from the isolated nature of the oxide nodes which are expected to act like quantum dots, and also from the perturbation arising from the organic linker BPDC.

Since the partial density of states (PDOS) is closely relevant to the chemical bonding, the PDOS of IRMOF-10 (Fig. 3) will be discussed in more detail in the following subsection dealing with the characteristics of chemical bonding. The PDOS for the remaining members (M = Cd, Be, Mg, Ca, Sr and Ba) in the M-IRMOF-10 series can be found in Figures S7–S12 in the ESI.† In general, the PDOS for each type of atoms (i.e., C, H and O; all three types constitute the linker BPDC), except for the metal atoms, are similar in each material within the series, with essentially the same characteristic peaks and positions for each type of atoms. Thus, we conclude that there are no discernible differences between the linker properties in the different materials within this series.

Figures S7–S12 in the ESI† show that there are significant differences in the PDOS when the transition metals (Zn and Cd) are compared to main-group metals (Be to Ba). Within the main-group metals, there are also differences, since some (e.g., Ca to Ba) have d-electrons in the pseudopotential for the calculations, whereas others (Be and Mg) only have s- and p-electrons. Differently phrased, the d-states of Zn and Cd atoms are dominantly contributed in the valence band, whereas both s- and p-states of Be and Mg atoms are dominantly contributed in both valence and conduction bands. For Ca, Sr, and Ba atoms, the p-states are dominantly contributed in the valence bands, while the d-states are dominantly contributed in the conduction bands.

In order to visualize the effect of changes in the metal ion on the electronic structure, the total electronic density of states (TDOS) at the equilibrium volume for the whole M-IRMOF-10 series of compounds is displayed in Fig. 4. The band gap (E_g) values obtained from the TDOS curves in Fig. 4 are in the range 2.9 to 3.0 eV for all members of the M-IRMOF-10 series, invariant of the metal. This indicates that all these materials are nonmetals. The characteristic peaks of TDOS for all these compounds are quite similar, which implies that the calculated band gaps within the M-IRMOF-10 series have a common structural origin that is similar to Zn-IRMOF-10. From the PDOS of IRMOF-10 in Fig. 3 and the PDOS of the remaining parts of this series in Figures S7–S12 in the ESI† we can infer the origin of E_g for the whole series. It is essentially the p-states of the C2, C3 and C5 atoms of the linker that determine the band gap for the whole series. This is in agreement with the conclusions concerning the PDOS above. Thus, it is the linker, rather than the node, that determines the E_g in the M-IRMOF-10 series. On this basis, it can also be appreciated that the greater band gap values in the M-IRMOF-1 series, ca. 3.5 eV, is also invariant to changes in the metal,⁴¹ and consistent with the idea that it is the linker that determines the value of band gap in isoreticular MOF series. In order to substantiate this finding we are currently investigating the role of various linkers on band gap changes in a series of MOF systems.

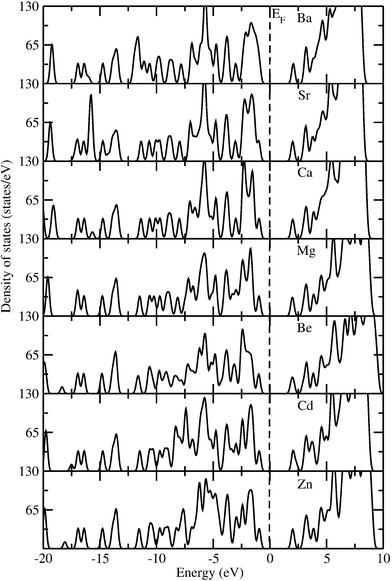Fig. 4 Calculated total density of states (TDOS) for M-IRMOF-10 series (M = Zn, Cd, Be, Mg, Ca, Sr, Ba) in the equilibrium cubic structure with Fm3̄m symmetry (no. 225).

It is a quite interesting observation that the band gap is unaffected by the metal replacement in the M-IRMOF-10 series. This implies that the degree of localization or delocalization of valence electrons of M(II) ions, or the changes in the bonding interaction between M and O, will not significantly affect the band gap value of the M-IRMOF-10 materials. However, a different case was reported in a recent theoretical study where Choi et al. reported⁷⁴ that it is possible to tune electronic band gaps from semiconducting to metallic states by substitution of Zn(II) ions in MOF-5 with Co(II) ions. Such differences in the electronic properties by cation replacement can be understood as follows. All the compounds in the M-IRMOF-10 series have the same linkers and similar nodes. Although the alkaline earth metals in this series have different atomic numbers and atomic or ionic radii, they have the same valence shell electron configurations. The replacement of divalent Zn ions in IRMOF-10 with divalent alkaline-earth metal ions gives similar electronic structure and bonding behavior. The isoelectronic nature of the compounds within this series and their isostructural characteristics contribute to the similar TDOS patterns and the very similar band gap values. In contrast, the transition metal ion Co(II) is very different from the main group alkaline earth metals, as this ion may have different bonding interactions with the linker oxygen atoms than Zn(II) or the alkaline-earth ions; this can contribute to the tuning process of the band gap of MOF-5 and its Co congener. Moreover, Co(II) ions often exhibit spontaneous magnetic ordering which will also contribute to metallic behavior. As Co has a highly different valence electron configuration compared with alkaline-earth metals, the 3d electrons of Co should play an important role in the band gap tuning process. Thus, the use of metal atoms with different electron configurations allows the tuning of the electronic structure of MOF-5 type materials.

As discussed above, the DFT calculated band gap E_g is generally smaller than the experimental one, which can be corrected by a scissor operator. In the following we will briefly discuss and compare theoretical and experimental band gap values for Zn-IRMOF-10, and make comparisons with the calculated data for the hypothetical systems M-IRMOF-10 and their corresponding bulk binary oxides (Table 5). As mentioned, calculated band gap values for the M-IRMOF-10 systems are almost constant, independent of the different cations. In contrast, the experimental band gap values for the binary oxides of the corresponding cations are quite different: In particular, the binary oxides have much higher band gap values than the corresponding M-IRMOF-10 series. Whereas the band gap values of ZnO and MOF-5 are almost the same, there is not a one-to-one correspondence between the band gap values of the other IRMOFs and their respective binary oxidesMO. This suggests that the origin of band gap formation in MOFs is different from that in binary oxides, which agrees with the above conclusion that band gaps in the isoelectronic systems under investigation originate from the linkers rather than from the metals. Importantly, if detailed information about the origin of band gap in MOFs is desired, one should aim at understanding the electronic structure and chemical bonding in MOFs in some detail and it is therefore advisable to perform ab initio calculations.

Table 5 Estimated band gap values (Theo. E_g) for the M-IRMOF-10 from CASTEP calculations. Experimental band gap values (Exp. E_g) for IRMOF-1, ZnO, CdO, and alkaline earth metals oxides (MO)

M-IRMOF-10	Theo. Eg (eV)	MO	Exp. Eg (eV)
Zn-IRMOF-10	2.925	ZnO-w/-z ^71	3.455/3.300 ^71
Cd-IRMOF-10	2.942	CdO	2.16 ± 0.02 ^75
Be-IRMOF-10	2.834	BeO	10.7 ^76
Mg-IRMOF-10	2.905	MgO	7.2 ^77
Ca-IRMOF-10	2.912	CaO	6.2 ^77
Sr-IRMOF-10	2.953	SrO	5.3 ^77
Ba-IRMOF-10	2.977	BaO	4.0 ^77
IRMOF-1 (MOF-5)	3.4–3.5 ^40		3.4–3.5 ^72,73

---

E. Characteristics of chemical bonding

i. From partial density of states. The distribution of various electronic states in the valence band and the conduction band can be characterized from the PDOS of Zn-IRMOF-10. The d- and s-states of Zn and H atoms, respectively, contribute dominantly in the valence band. Both s- and p-states of C and O atoms also contribute to the VB. The p-states of neighbors (i.e. C1 and C2, C2 and C4, C1 and C3, C3 and C5) are distributed energetically in the same range and spatially distributed such as to effectively overlap to form very strong covalent bonds. The s-states of H1 and H2 can overlap with the p-states of C1 and C3, respectively, to form covalent bonds. The p-state of C4 overlaps with that of O2 to form a directional bond between them. The d-states of Zn are well localized, and the Zn s electrons are transferred to the neighboring atoms, leading to ionic Zn–O bonding. Thus, the picture emerges—as might be anticipated—that the linker acts as an entity that is covalently bonded internally and linked to the Zn nodes by a largely ionic interaction. This is consistent with the following analysis of charge density and ELF.

An analysis of the PDOS in Figures S7–S12 in the ESI† leads to the same conclusion regarding the whole M-IRMOF-10 series. The main difference in chemical bonding in the series arises from the relative importance of ionic vs. covalent contributions to M–O bonding: At the extremes, there is more covalent and less ionic character in the Be–O bond compared with the Ba–O bond, even though both bonds are dominated by the ionic components.

ii. From charge density/transfer, ELF and BOP analyses. Charge density/transfer, ELF,^46–49 and bond overlap population (BOP)/Mulliken population analyses can shed further light on the bonding situation. The charge density plots in Fig. 5a and Figures S1a–S6a in the ESI† show that the organic linker is a molecule-like subunit with normal covalent C–C, C–H, and C–O bonds. Charges are spherically distributed at the M and O sites, characteristic for systems having ionic interactions; this is further corroborated by the fact that there is no noticeable charge density distributed between the M and O atoms.

Fig. 5 Calculated charge density (a), charge transfer (b), and electron localization function (c) plots for IRMOF-10 in the (110) plane.

The charge-transfer contour Δρ is the self-consistent electron density in a particular plane, ρ_comp, from which is subtracted the electron density of the overlapping free atoms in the same lattice, ρ_atom, i.e., Δρ(r) = ρ_comp − ρ_atom, which allows the visualization of how electrons are redistributed in a particular plane compared to free atoms due to the bonding in the compound. Fig. 5b and Figures S1b–S6b in the ESI† show charge-transfer plots for all M-IRMOF-10 species investigated. It is evident that electrons are transferred from M to O sites, but not entirely in an isotropic fashion. The anisotropic charge transfer from M to the O sites indicates iono-covalent bonding between M and O with a predominant ionic contribution. The nonspherical electron distributions between neighboring C, H, and O atoms clearly indicate strong covalent bonding. From Fig. 5c and Figures S1c–S6c in the ESI,† it can be inferred that the large value of ELF at the O site indicates strongly paired electrons with local bosonic character. The negligibly small ELF between M and O, and the small value of ELF at the M sites (partially due to the presence of d electrons for the transition metals Zn and Cd) with spherically symmetric distribution again indicate predominant ionic bonding between M and O. The ELF distribution at the O site is polarized towards the M atoms, indicating directional bonding between M and O. A certain polarized character is found in the ELF distribution at the H sites in the M-IRMOF-10 series, indicating polar covalent bonding. There is as expected a maximum in the ELF between the covalently bonded C atoms and between C and O atoms.

Bond overlap population (BOP) values were calculated on the basis of a Mulliken population analysis.⁷⁸ A high BOP value indicates a strong covalent bond, while a low BOP value indicates an ionic or nonbonding interaction. The calculated BOP values for the M–O, C–O, C–C, and C–H bonds are displayed in Table 6. BOP values for the M–O bonds in the MOFs are in the range 0.26–0.29 for M = Zn, 0.22–0.23 for Cd, 0.36–0.37 for Be, 0.23 for Mg, 0.14–0.18 for Ca, 0.14–0.17 for Sr, and 0.11–0.16 for Ba, respectively. The data suggest a predominant ionic character to the M–O bonding, and the extent of covalent character decreases down in a group (Zn–O > Cd–O; Be–O > Mg–O > Ca–O > Sr–O > Ba–O. The high BOP values for the C–H, C–C, and C–O bonds are consistent with strong covalent bonds.

Table 6 Mulliken effective charge (MEC) and bond overlap populations (BOP) and Bader charges (BC) for M-IRMOF-10^a

Material	Atom site	MEC (e)	BOP	BC (e)
a The atomic numbering scheme is according to Fig. 1.
IRMOF-10	Zn	+1.29	0.26–0.29 (Zn–O)	+1.3874
	O1	−1.05	0.26 (O1–Zn)	−1.3197
	O2	−0.65	0.29 (O2–Zn)	−1.7593
	C1	−0.25	1.08 (C1–C2)	+0.0285
			1.12 (C1–C3)
	C2	−0.06	0.85 (C2–C4)	−0.0773
	C3	−0.26	1.09 (C3–C5)	+0.0033
	C4	+0.61	0.90 (C4–O2)	+2.6528
	C5	−0.01	0.91 (C5–C5)	+0.0478
	H1	+0.28	0.89 (H1–C1)	+0.0574
	H2	+0.27	0.91 (H2–C3)	+0.0059
Cd–IRMOF–10	Cd	+1.27	0.22–0.23 (Cd–O)	+1.3186
	O1	−1.02	0.22 (O1–Cd)	−1.2036
	O2	−0.66	0.23 (O2–Cd)	−1.7435
	C1	−0.25	1.08 (C1–C2)	+0.0411
			1.12 (C1–C3)
	C2	−0.06	0.84 (C2–C4)	−0.0661
	C3	−0.26	1.09 (C3–C5)	+0.0284
	C4	+0.63	0.90 (C4–O2)	+2.6782
	C5	−0.01	0.91 (C5–C5)	+0.0210
	H1	+0.28	0.89 (H1–C1)	+0.0282
	H2	+0.27	0.91 (H2–C3)	−0.0100
Be–IRMOF–10	Be	+1.14	0.36–0.37 (Be–O)	+2.0000
	O1	−0.96	0.37 (O1–Be)	−2.0057
	O2	−0.63	0.36 (O2–Be)	−1.9083
	C1	−0.26	1.07 (C1–C2)	−0.0348
			1.12 (C1–C3)
	C2	−0.05	0.85 (C2–C4)	+0.0426
	C3	−0.26	1.09 (C3–C5)	+0.0421
	C4	+0.60	0.91 (C4–O2)	+2.6488
	C5	−0.01	0.91 (C5–C5)	−0.0817
	H1	+0.31	0.87 (H1–C1)	+0.0803
	H2	+0.27	0.91 (H2–C3)	+0.0164
Mg–IRMOF–10	Mg	+1.57	0.23 (Mg–O)	+2.0000
	O1	−1.28	0.23 (O1–Mg)	−2.0009
	O2	−0.71	0.23 (O2–Mg)	−1.9081
	C1	−0.25	1.08 (C1–C2)	+0.0358
			1.13 (C1–C3)
	C2	−0.07	0.85 (C2–C4)	−0.0738
	C3	−0.26	1.09 (C3–C5)	+0.0095
	C4	+0.60	0.91 (C4–O2)	+2.6625
	C5	−0.01	0.91 (C5–C5)	+0.0396
	H1	+0.28	0.89 (H1–C1)	+0.0426
	H2	+0.27	0.90 (H2–C3)	+0.0062
Ca–IRMOF–10	Ca	+1.35	0.14–0.18 (Ca–O)	+1.6187
	O1	−1.15	0.18 (O1–Ca)	−1.4976
	O2	−0.70	0.14 (O2–Ca)	−1.8235
	C1	−0.26	1.07 (C1–C2)	+0.0242
			1.12 (C1–C3)
	C2	−0.06	0.83 (C2–C4)	−0.0336
	C3	−0.26	1.09 (C3–C5)	+0.0308
	C4	+0.65	0.88 (C4–O2)	+2.6887
	C5	−0.01	0.91 (C5–C5)	−0.0035
	H1	+0.31	0.86 (H1–C1)	+0.0511
	H2	+0.27	0.90 (H2–C3)	−0.0232
Sr–IRMOF–10	Sr	+1.38	0.14–0.17 (Sr–O)	+1.6184
	O1	−1.14	0.17 (O1–Sr)	−1.4708
	O2	−0.70	0.14 (O2–Sr)	−1.8229
	C1	−0.26	1.07 (C1–C2)	+0.0267
			1.12 (C1–C3)
	C2	−0.06	0.82 (C2–C4)	−0.0096
	C3	−0.26	1.09 (C3–C5)	−0.0154
	C4	+0.64	0.89 (C4–O2)	+2.7104
	C5	−0.01	0.91 (C5–C5)	−0.0139
	H1	+0.30	0.86 (H1–C1)	+0.0446
	H2	+0.27	0.90 (H2–C3)	+0.0066
Ba–IRMOF–10	Ba	+1.37	0.11–0.16 (Ba–O)	+1.6197
	O1	−1.08	0.16 (O1–Ba)	−1.4326
	O2	−0.70	0.11 (O2–Ba)	−1.8284
	C1	−0.26	1.07 (C1–C2)	+0.0168
			1.12 (C1–C3)
	C2	−0.06	0.82 (C2–C4)	−0.0548
	C3	−0.26	1.09 (C3–C5)	+0.0342
	C4	+0.64	0.89 (C4–O2)	+2.7269
	C5	−0.01	0.91 (C5–C5)	−0.0146
	H1	+0.30	0.86 (H1–C1)	+0.0536
	H2	+0.27	0.90 (H2–C3)	−0.0256

---

We have also calculated the Mulliken effective charges and bond overlap populations of the corresponding oxides (MO) with the same GGA-PBE functional as was used to calculate the M-IRMOF-10 series. The M–O BOP values within MO are 1.13 (Zn), 1.02 (Cd), 1.44 (Be), 1.33 (Mg), 0.84 (Ca), 0.88 (Sr), and 0.75 (Ba). The MEC values for M in the MO oxides are 0.84 (Zn), 0.82 (Cd), 0.79 (Be), 0.97 (Mg), 1.04 (Ca), 0.97 (Sr), and 0.96 (Ba) |e|. Thus, the general trend of M–O BOP values and MEC values of M within the MO oxides are similar for the whole series. We conclude that our computational methods predict quite well the general trend for the whole series.

In summary, the M–O bonds in the nodes of M-IRMOF-10 series have predominant ionic character similar to that present in MO, whereas the C–H, C–O and C–C bonds in the linkers have covalent interactions. The analyses based on charge density/transfer, ELF, and bond overlap population (BOP)/Mulliken population analyses give a consistent view of the bonding in the M-IRMOF-10 series, and agrees with the situation in MOF-5⁴⁰ and the M-IRMOF-1 series,⁴¹ as recently described by us.

The calculated Mulliken charges (MEC) are reported in Table 6. The MEC values are +0.27 to +0.31|e| for H, +1.29|e| for M = Zn, +1.27|e| for Cd, +1.14|e| for Be, +1.57|e| for Mg, +1.35|e| for Ca, +1.38|e| for Sr and +1.37|e| for Ba, respectively. The C1 and C3 atoms connected to H1 and H2 bear negative charges (−0.28 to −0.31|e| and −0.27|e|, respectively). However, the C2 (which bears the carboxylate group) and C5 (which connects the phenyl rings in the linker) atoms bear nearly zero charge (−0.05 to −0.07|e| and −0.01|e|, respectively). The carboxylate C atoms bear positive charges (+0.60 to +0.65|e|). Finally, the oxygen atom in the M₄O node has nearly a single unit of negative charge (−1.05|e| for M = Zn, −1.02|e| for Cd, −0.96 for Be, −1.28 for Mg, −1.15 for Ca, −1.14 for Sr, and −1.08 for Ba), which indicates that the four M atoms together have transferred a charge corresponding to one electron to the central O1. The O2 oxygen atoms in the BDC linker bear negative charges (−0.63 to −0.71|e|) indicating that there is partial electron transfer from M to O2.

iii. Bader topological analysis. Although there is no unique definition to identify how many electrons are associated with an atom in a molecule or an atomic group in a solid, it has nevertheless proved useful in many cases to perform Bader topological analyses.^79–81 In the Bader charge (BC) analysis, each atom of a compound is surrounded by a surface (called a Bader region) that runs through minima of the charge density, and the total charge of an atom is determined by integration of electrons within the Bader region. The calculated Bader charges for the M-IRMOF-10 series are given in Table 6. The BC for M and O (includes O1 and O2) in the M-IRMOF-10 series compounds indicate that the interaction between M and O is almost ionic, as nearly two electrons (+1.39|e| for M = Zn, +1.32|e| for Cd, +2.00|e| for Be, +2.00|e| for Mg, +1.62|e| for Ca, +1.62|e| for Sr, and +1.62|e| for Ba) are transferred from M to O. This finding is consistent with the DOS and charge density analyses. Within the M₄O units, M donates 1.32 to 2.00 electrons, which is slightly smaller than that in a pure ionic picture. The trend is associated with the noticeable covalency present between M and O as demonstrated by the ELF and BOP analyses, discussed above. The results from the BC analysis are fully consistent with the charge density, charge transfer, ELF, MEC, and PDOS analyses.

F. Band structure and optical properties

The recent report on the semiconducting behavior of MOFs³⁴ has triggered intense research in this area including the synthesis and characterization of various semiconducting MOFs with the aim to develop new materials for optoelectronic applications. The optical properties for M-IRMOF-10 are here of interest, for example in view of potential uses of this material in hybrid solar cell applications as an active material or in the buffer layer between the electrodes and inorganic active materials. Studies of optical properties of MOFs will also be of fundamental importance, since these properties not only depend on the occupied and unoccupied parts of the electronic structure, but also carry information about the character of the bands. Insight into the excited-state electronic properties of M-IRMOF-10 may also be important for certain applications. It may be noted that the moisture sensitivity of Zn-IRMOF-10 presents obstacles to many practical uses of this material.

The central quantity of the optical properties is the dielectric function ε(ω), which describes the features of linear response of the system to electromagnetic radiation, which again governs the propagation behavior of radiation in the medium. Here ε(ω) is connected to the interaction of photons with electrons. Its imaginary part ε₂(ω) can be derived from interband optical transitions between the occupied and unoccupied bands including appropriate momentum matrix elements to take care of the selection rules, and its real part ε₁(ω) can be derived from ε₂(ω) by the Kramer-Kronig relationship.⁵⁰ The real part of ε(ω) in the limit of zero energy (or infinite wavelength) is equal to the square of the refractive index n(ω). All the frequency dependent linear optical properties, such as refractive index n(ω), absorption coefficient α(ω), optical conductivity σ(ω), reflectivity R(ω), and electron energy-loss spectrum L(ω) can be deduced from ε₁(ω) and ε₂(ω).

We have conducted CASTEP calculations to estimate the optical properties of the whole M-IRMOF-10 series (M = Zn, Cd, Be, Mg, Ca, Sr and Ba), and the results from the optical calculations for Zn-IRMOF-10 are shown in Fig. 6. The calculated optical properties of the remaining members of the series can be found in Figures S13–S18 in the ESI.† For the convenience of our discussion, we focus on the properties of Zn-IRMOF-10 as a representative case before a comparison is made within this series.

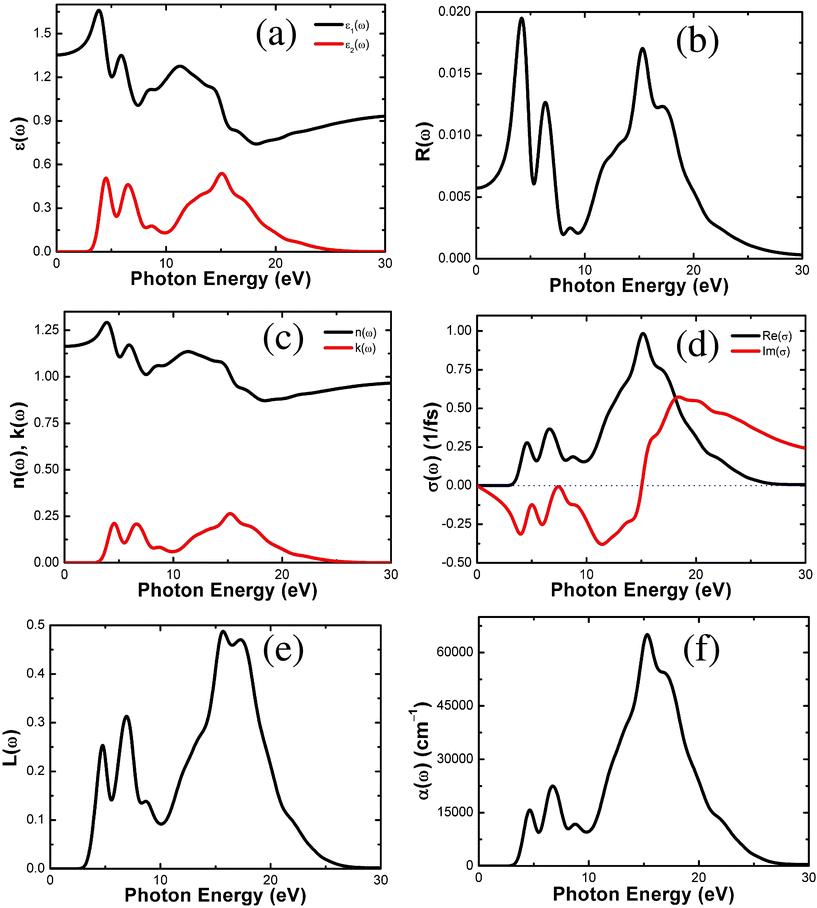Fig. 6 Calculated optical properties for Zn-IRMOF-10: (a) dielectric function ε(ω), (b) reflectivity R(ω), (c) refractive index n(ω); extinction coefficient k(ω), (d) optical conductivity σ(ω), (e) energy loss function L(ω), and (f) absorption α(ω).

There are three main peaks in the ε₂(ω) plot (Fig. 6a) of Zn-IRMOF-10, located at ca. 4.51, 6.52, and 15.13 eV, the latter accompanied by broad shoulders. Figures S13a–S18a in the ESI† show that characteristic peaks and positions are similar for each material in the series. The real part of dielectric function, ε₁(ω) (Fig. 6a and Figures S13a–S18a in ESI†) allows the estimation the value of the refractive index n(ω) at infinite wavelength or zero energy (i.e., n(0)) at about 1.1651 (Zn), 1.1537 (Cd), 1.1827 (Be), 1.1580 (Mg), 1.1442 (Ca), 1.1373 (Sr), and 1.1318 (Ba). Thus, n(0) is rather constant in the range 1.13 to 1.18 for the whole series. At low frequency (0—2.95 eV), the imaginary part ε₂(ω) is zero below the band gap, which is consistent with the order of band gaps for the M-IRMOF-10 series.

The reflectivity spectrum (Fig. 6b) of Zn-IRMOF-10 shows sharp peaks at 4.17, 6.37, and 15.29 eV, the latter accompanied by shoulders. The two low-frequency peaks mainly arise from Zn(3d) → C/O(2p) as well as H(1s) → C/O(2p) interband transitions. A similar situation pertains to the reflectivity curves for M-IRMOF-10 (M = Cd, Be, Mg, Ca, Sr and Ba), Fig. S13b–S18b in the ESI.† Here, the two sharp low-frequency peaks mainly arise from the transitions Cd(3d) → C/O(2p) and H(1s) → C/O(2p) for M = Cd; Be(2s,2p) → C/O(2p) and H(1s) → C/O(2p) for Be; Mg(3s,3p) → C/O(2p) and H(1s) → C/O(2p) for Mg; Ca(4p,4d) → C/O(2p) and H(1s) → C/O(2p) for Ca; Sr(5p,5d) → C/O(2p) and H(1s) → C/O(2p) for Sr; and Ba(6p,6d) → C/O(2p) and H(1s) → C/O(2p) for Ba. The reflectivity approaches zero when the energy exceeds 30 eV for the whole series. The values of reflectivity at infinite wavelength are 0.005730 (Zn), 0.005015 (Cd), 0.007016 (Be), 0.005332 (Mg), 0.004523 (Ca), 0.004098 (Sr), and 0.003751 (Ba). Thus, passing from Zn to Cd, and from Be to Ba, the reflectivity consistently decreases. One general finding here is that the calculated reflectivity in the whole frequency range is much smaller than that in typical inorganic solids. This was also seen for M-IRMOF-1,^40,41 and this may prove to be an important advantage if MOFs are to be used in optoelectronic devices (such as solar cells and LEDs) where low reflectivity is desired.

Zn-IRMOF-10 has a finite value of the refractive index n(ω) (Fig. 6c) in the range 2.95 to 30 eV. The extinction coefficient k(ω) (the imaginary part of the complex refractive index) shows three peaks at 4.57, 6.63, and 15.24 eV, the latter with broad shoulders. The refractive indexes n(ω) for M-IRMOF-10 (M = Cd, Be, Mg, Ca, Sr and Ba) are depicted in Figures S13c–S18c in the ESI.† Similar characteristics are seen for the whole series. The refractive index n(ω) at infinite wavelength (i.e., n(0)) has already been commented in the dielectric function ε(ω) paragraph.

The optical conductivity σ(ω) plot of Zn-IRMOF-10 is shown in Fig. 6d. The real part of the complex conductivity has its three main three sharp peaks at 4.57, 6.63, and 15.17 eV. The optical conductivity σ(ω) plots of M-IRMOF-10 (M = Cd, Be, Mg, Ca, Sr and Ba) are depicted in Figures S13d–S18d in the ESI;† the characteristics of the main peaks are similar throughout the whole series.

The electron energy-loss function L(ω) (Fig. 6e) is an important optical parameter describing the energy loss of a fast electron traversing in a certain material. The peaks in the L(ω) spectra represent the characteristics associated with the plasma resonance and the corresponding frequency is the so-called plasma frequency above which the material is a dielectric [ε₁(ω) > 0] and below which the material behaves like a metallic compound in some sense [ε₁(ω) < 0]. In addition, the peaks of the L(ω) spectra overlap the trailing edges in the reflection spectra. The peak of L(ω) of Zn-IRMOF-10 at 6.93 eV corresponds to the reduction of R(ω). There are five plasma frequencies at ca. 4.74, 6.93, 8.68, 15.70, and 17.29 eV. In Figures S13e–S18e in the ESI,† it is seen that the characteristic main peaks of M-IRMOF-10 (M = Cd, Be, Mg, Ca, Sr and Ba) are quite similar except that the two broad peaks with the strongest intensities for Zn, Cd, Be, Mg (at ca. 15.70 and 17.29 eV for M = Zn) have the appearance of a single sharp peak for Ca, Sr, and Ba.

Zn-IRMOF-10 has an absorption band (Fig. 6f) ranging from 2.95 to 30 eV, which exhibits three sharp peaks at around 4.63, 6.74, and 15.29 eV. The characteristics of the main peaks are similar for M-IRMOF-10 (M = Cd, Be, Mg, Ca, Sr and Ba; Figures S13f–S18f in the ESI)†. The main differences arise from the appearance of an additional peak at ca. 25.0–28.0 eV for M = Ca, Sr and Ba, which is absent for M = Zn, Cd, Be, and Mg.

The calculated optical properties of M-IRMOF-10 series in this work are similar to that of M-IRMOF-1 in our recent contributions,^40,41 which is consistent with the fact that the M-IRMOF-10 and M-IRMOF-1 series have similar topological structures, with common nodes and closely related linkers.

In conjunction with the optical properties calculations we have also computed the band structures of the whole M-IRMOF-10 (M = Zn, Cd, Be, Mg, Ca, Sr and Ba) series. The calculated band structure for Zn-IRMOF-10 is shown in Fig. 7. The band structures of the remaining members of the series are displayed in Figures S19–S24 in the ESI.† For the high symmetry directions in the Brillouin zone sampling, CASTEP automatically chose the W–L–Γ–X–W–K path for the face-centered cubic (fcc) symmetry Brillouin zone of M-IRMOF-10 series. From Fig. 7 and Fig. S19–S24 it is apparent that the band gap for the whole series is essentially constant at ca. 2.9–3.0 eV, independent of the central metal atoms in the framework nodes. The bands in the valence band as well as in the conduction band are almost parallel and dispersionless. The bands at the VB maximum and CB minimum for Zn-IRMOF-10 are very flat, which is also the case for the other members of the series. This appears to be a common feature for MOF materials.^11,82 This flat band behavior makes it impossible to unequivocally identify whether the band gap is direct or indirect. However, we still can gain some qualitative information from the band structures that helps to understand the electronic structures of MOF materials and provides further insight into their optical properties. We look forward to future experimental determination of band structures of the M-IRMOF-10 series, so that experiment and theory can be reconciled.

Fig. 7 The electronic band structure of Zn-IRMOF-10. The Fermi level is set to zero and placed in the valence band maximum.

IV. Conclusions

We have presented a detailed investigation on the electronic structure, chemical bonding behavior, ground-state properties, and optical properties of the whole M-IRMOF-10 (M = Zn, Cd, Be, Mg, Ca, Sr and Ba) series using first-principles methods. The following important conclusions are obtained:

(1) The calculations show that each material in the M-IRMOF-10 series is soft and “formed” in the high symmetric face-centered cubic (Fm3̄m, 225) crystal structure; it is demonstrated that computational simulations nicely complement experiments to accurately determine the equilibrium structural parameters for complicated MOFs systems.

(2) The large negative formation enthalpy of IRMOF-10 is consistent with the fact that it has already been synthesized by experiments. The prediction of a series of hypothetical materials M-IRMOF-10 (M = Cd, Be, Mg, Ca, Sr and Ba) with large negative formation enthalpy hopefully will inspire and guide synthetic efforts in this direction.

(3) Electronic charge density, charge transfer, ELF, MEC and BOP analyses shed light on the nature of the M–O, C–O, C–H, and C–C bonding. The analyses consistently support the notion that the bonding interaction between M–O is mainly an ionic interaction, whereas those between C–O, C–H, and C–C are normal covalent interactions. The ionicity of the M–O bonds decreases and the covalency increases when passing from Zn to Cd, and from Be to Ba.

(4) Electronic density of states and band structures study show that the band gap for the whole M-IRMOF-10 series is ca. 2.9–3.0 eV, resulting in a nonmetallic character. Until now, there are no experimental studies available to verify our results, but we hope to motivate experimentalists to measure the band gap of this series. Importantly, the band gap of the M-IRMOF-10 series at 2.9–3.0 eV is independent of the identity of the metal in this isoelectronic series of structures. Furthermore, the band gap is substantially lower than the 3.5 eV value found for the analogous M-IRMOF-1 series. Thus, a systematic variation of the linker may allow the fine-tuning of band gap values in a given MOF family. This should influence research in this area and facilitate the synthesis of semiconducting MOFs with appropriate band gap values for materials applications in for optoelectronic devices.

(5) The calculated optical properties of M-IRMOF-10 series provide useful information for future experimental exploration. Overall, the peak intensities of the calculated optical spectra for the M-IRMOF-10 systems are around 30% higher (especially the reflectivity and absorption coefficient) than for M-IRMOF-1. This is associated with the introduction of an additional benzene structural sub-unit in the M-IRMOF-10 system. However, the peak positions and distributions are almost the same for both classes. The observation of very low reflectivity over a wide energy range show that these materials may have potential uses in hybrid solar cell applications as an active material or in the buffer layer between the electrodes and inorganic active materials. Moreover, potential applications may be found in organic semiconducting devices such as field-effect transistors, solar cells, and organic light-emitting devices (OLEDs).

Acknowledgements

We gratefully acknowledge the Research Council of Norway for financial support and for the computer time at the Norwegian supercomputer facilities.

References

1. Chem. Soc. Rev., 2009, 38. Issue 5: Special issue on MOFs.
2. H. Li, M. Eddaoudi, T. L. Groy and O. M. Yaghi, J. Am. Chem. Soc., 1998, 120, 8571–8572.
3. M. Eddaoudi, D. B. Moler, H. Li, B. Chen, T. M. Reineke, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2001, 34, 319–330.
4. N. W. Ockwig, O. Delgado-Friedrichs, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2005, 38, 176–182.
5. Z. Ni, J. P. Jerrell, K. R. Cadwallader and R. I. Masel, Anal. Chem., 2007, 79, 1290–1293.
6. B. C. Dionne, D. P. Rounbehler, E. K. Achter, J. R. Hobbs and D. H. Fine, J. Energ. Mater., 1986, 4, 447–72.
7. R. Xiong, J. T. Fern, D. J. Keffer, M. Fuentes-Cabrera and D. M. Nicholson, Mol. Simul., 2009, 35, 910–919.
8. R. Xiong, K. Odbadrakh, A. Michalkova, J. P. Luna, T. Petrova, D. J. Keffer, D. M. Nicholson, M. A. Fuentes-Cabrera, J. P. Lewis and J. Leszczynski, Sens. Actuators, B, 2010, B148, 459–468.
9. K. Odbadrakh, J. P. Lewis, D. M. Nicholson, T. Petrova, A. Michalkova and J. Leszczynski, J. Phys. Chem. C, 2010, 114, 3732–3736.
10. T. Petrova, A. Michalkova and J. Leszczynski, Struct. Chem., 2010, 21, 391–404.
11. K. Odbadrakh, J. P. Lewis and D. M. Nicholson, J. Phys. Chem. C, 2010, 114, 7535–7540.
12. R. Xiong, D. J. Keffer, M. Fuentes-Cabrera, D. M. Nicholson, A. Michalkova, T. Petrova, J. Leszczynski, K. Odbadrakh, B. L. Doss and J. P. Lewis, Langmuir, 2010, 26, 5942–5950.
13. M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472.
14. T. Düren, F. Millange, G. Férey, K. S. Walton and R. Q. Snurr, J. Phys. Chem. C, 2007, 111, 15350–15356.
15. J. Fu and H. Sun, J. Phys. Chem. C, 2009, 113, 21815–21824.
16. V. I. Isaeva and L. M. Kustov, Russ. J. Gen. Chem., 2007, 77, 721–739.
17. H. Frost, T. Düren and R. Q. Snurr, J. Phys. Chem. B, 2006, 110, 9565–9570.
18. M. Suri, M. Dornfeld and E. Ganz, J. Chem. Phys., 2009, 131, 174703.
19. T. Stergiannakos, E. Tylianakis, E. Klontzas and G. E. Froudakis, J. Phys. Chem. C, 2010, 114, 16855–16858.
20. R. Babarao and J. Jiang, Langmuir, 2008, 24, 6270–6278.
21. S. Keskin and D. S. Sholl, Energy Environ. Sci., 2010, 3, 343–351.
22. K. S. Walton, A. R. Millward, D. Dubbeldam, H. Frost, J. J. Low, O. M. Yaghi and R. Q. Snurr, J. Am. Chem. Soc., 2008, 130, 406–407.
23. T. Düren and R. Q. Snurr, J. Phys. Chem. B, 2004, 108, 15703–15708.
24. D. Dubbeldam, K. S. Walton, D. E. Ellis and R. Q. Snurr, Angew. Chem., Int. Ed., 2007, 46, 4496–4499.
25. F.-X. Coudert, C. Mellot-Draznieks, A. H. Fuchs and A. Boutin, J. Am. Chem. Soc., 2009, 131, 11329–11331.
26. F. Salles, A. Ghoufi, G. Maurin, R. G. Bell, C. Mellot-Draznieks and G. Férey, Angew. Chem., Int. Ed., 2008, 47, 8487–8491.
27. C. Mellot-Draznieks, J. Mater. Chem., 2007, 17, 4348–4358.
28. C. Mellot-Draznieks, J. Dutour and G. Férey, Angew. Chem., Int. Ed., 2004, 43, 6290–6296.
29. C. Mellot-Draznieks, J. Dutour and G. Férey, Z. Anorg. Allg. Chem., 2004, 630, 2599–2604.
30. C. Mellot-Draznieks and G. Férey, Curr. Opin. Solid State Mater. Sci., 2003, 7, 13–19.
31. G. Férey, C. Mellot-Draznieks and T. Loiseau, Solid State Sci., 2003, 5, 79–94.
32. C. Mellot-Draznieks, S. Girard, G. Férey, J. C. Schön, Z. Cancarevic and M. Jansen, Chem.–Eur. J., 2002, 8, 4102–4113.
33. F. X. Llabres i Xamena, A. Corma and H. Garcia, J. Phys. Chem. C, 2007, 111, 80–85.
34. C. G. Silva, A. Corma and H. Garcia, J. Mater. Chem., 2010, 20, 3141–3156.
35. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
36. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
37. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744.
38. Materials Studio, ver. 4.2, Accelrys, San Diego, CA, 2007.
39. Note that the designation IRMOF-10 will describe the experimentally synthesized IRMOF-10 with Zn as the specific metal center in the framework, whereas M-IRMOF-10 (M = Zr, Cd, Be, Mg, Ca, Sr and Ba) will designate the parent IRMOF-10 as well as its M-substituted analogues.
40. L.-M. Yang, P. Vajeeston, P. Ravindran, H. Fjellvåg and M. Tilset, Inorg. Chem., 2010, 49, 10283–10290.
41. L.-M. Yang, P. Vajeeston, P. Ravindran, H. Fjellvåg and M. Tilset, Phys. Chem. Chem. Phys., 2011, 13, 10191–10203.
42. J. P. Perdew, in Electronic Structure of Solids 1991, ed. P. Ziesche and H. Eschrig, Akademie Verlag, Berlin, Editon edn 1991, 11–20.
43. J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter, 1996, 54, 16533–16539.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953–17979.
46. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
47. A. Savin, A. D. Becke, J. Flad, R. Nesper, H. Preuss and H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1991, 30, 409–412.
48. A. Savin, O. Jepsen, J. Flad, O. K. Andersen, H. Preuss and H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1992, 31, 187–188.
49. B. Silvi and A. Savin, Nature, 1994, 371, 683–686.
50. P. Ravindran, A. Delin, R. Ahuja, B. Johansson, S. Auluck, J. M. Wills and O. Eriksson, Phys. Rev. B: Condens. Matter, 1997, 56, 6851–6861.
51. A. Delin, P. Ravindran, O. Eriksson and J. M. Wills, Int. J. Quantum Chem., 1998, 69, 349–358.
52. P. Ravindran, A. Delin, B. Johansson, J. M. Wills and O. Eriksson, Phys. Rev. B: Condens. Matter, 1999, 59, 15680–15693.
53. P. Ravindran, A. Delin, B. Johansson, O. Eriksson and J. M. Wills, Phys. Rev. B: Condens. Matter, 1999, 59, 1776–1785.
54. P. Ravindran, H. Fjellvåg, A. Kjekshus, A. Delin and O. Eriksson, Phys. Rev. B: Condens. Matter, 2002, 65, 064445.
55. S. Z. Karazhanov, P. Ravindran, U. Grossner, A. Kjekshus, H. Fjellvåg and B. G. Svensson, Solid State Commun., 2006, 139, 391–396.
56. S. Z. Karazhanov, P. Ravindran, P. Vajeeston, A. Ulyashyn, T. Finstad and H. Fjellvåg, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 76, 075129.
57. M. G. Brik, J. Phys.: Condens. Matter, 2009, 21, 485502.
58. J. Chen, G. Zhao, Y. Sun and T. Liu, Solid State Commun., 2010, 150, 897–900.
59. Q. Xia, J. Yi, Y. Li, Y. Peng, H. Wang and C. Zhou, Solid State Commun., 2010, 150, 605–608.
60. Y. C. Cheng, X. L. Wu, J. Zhu, L. L. Xu, S. H. Li and P. K. Chu, J. Appl. Phys., 2008, 103, 073707.
61. O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714.
62. J. K. Schnobrich, K. Koh, K. N. Sura and A. J. Matzger, Langmuir, 2010, 26, 5808–5814.
63. F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247.
64. F. Birch, Phys. Rev., 1947, 71, 809–824.
65. P. Vinet, J. H. Rose, J. Ferrante and J. R. Smith, J. Phys.: Condens. Matter, 1989, 1, 1941–1963.
66. A. Kuc, A. Enyashin and G. Seifert, J. Phys. Chem. B, 2007, 111, 8179–8186.
67. H. H.-M. Yeung, M. Kosa, M. Parrinello, P. M. Forster and A. K. Cheetham, Cryst. Growth Des., 2011, 11, 221–230.
68. L. N. Appelhans, M. Kosa, A. V. Radha, P. Simoncic, A. Navrotsky, M. Parrinello and A. K. Cheetham, J. Am. Chem. Soc., 2009, 131, 15375–15386.
69. J. P. Perdew and M. Levy, Phys. Rev. Lett., 1983, 51, 1884–1887.
70. Z. H. Levine and D. C. Allan, Phys. Rev. B: Condens. Matter, 1991, 43, 4187–4207.
71. S. Z. Karazhanov, P. Ravindran, A. Kjekshus, H. Fjellvåg, U. Grossner and B. G. Svensson, J. Appl. Phys., 2006, 100, 043709.
72. S. Bordiga, C. Lamberti, G. Ricchiardi, L. Regli, F. Bonino, A. Damin, K.-P. Lillerud, M. Bjørgen and A. Zecchina, Chem. Commun., 2004, 2300–2301.
73. M. Alvaro, E. Carbonell, B. Ferrer, F. X. Llabrés i Xamena and H. Garcia, Chem.–Eur. J., 2007, 13, 5106–5112.
74. J. H. Choi, Y. J. Choi, J. W. Lee, W. H. Shin and J. K. Kang, Phys. Chem. Chem. Phys., 2009, 11, 628–631.
75. P. H. Jefferson, S. A. Hatfield, T. D. Veal, P. D. C. King, C. F. McConville, J. Zuniga-Perez and V. Munoz-Sanjose, Appl. Phys. Lett., 2008, 92, 022101.
76. A. L. Ivanovskii, I. R. Shein, Y. N. Makurin, V. S. Kiiko and M. A. Gorbunova, Inorg. Mater., 2009, 45, 223–234.
77. A. M. Stoneham and J. Dhote, A compilation of crystal data for halides and oxides, University College London, London, 2002.
78. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840.
79. R. F. W. Bader, Atoms in molecules: A quantum theory, Clarendon Press, Oxford, 1990.
80. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
81. C. F. Guerra, J.-W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189–210.
82. M. Fuentes-Cabrera, D. M. Nicholson, B. G. Sumpter and M. Widom, J. Chem. Phys., 2005, 123, 124713.

---

Footnote

† Electronic supplementary information (ESI) available: The calculated charge density, charge transfer, and electron localization function (ELF) plots, the total density of states (TDOS) and partial density of states (PDOS), the optical properties and band structures for M-IRMOF-10 (M = Cd, Be, Mg, Ca, Sr and Ba). See DOI: 10.1039/c1ra00187f

---