Modelling complex biological systems using an agent-based approach†
Mike
Holcombe
a,
Salem
Adra
a,
Mesude
Bicak
a,
Shawn
Chin
e,
Simon
Coakley
a,
Alison I.
Graham
c,
Jeffrey
Green
c,
Chris
Greenough
e,
Duncan
Jackson
g,
Mariam
Kiran
a,
Sheila
MacNeil
f,
Afsaneh
Maleki-Dizaji
a,
Phil
McMinn
a,
Mark
Pogson
a,
Robert
Poole
c,
Eva
Qwarnstrom
b,
Francis
Ratnieks
d,
Matthew D.
Rolfe
c,
Rod
Smallwood
a,
Tao
Sun
f and
David
Worth
e
aDepartment of Computer Science, University of Sheffield, UK
bDepartment of Cell Biology, School of Medicine, University of Sheffield, UK
cDepartment of Molecular Biology and Biotechnology, University of Sheffield, UK
dDepartment of Biology and Environmental Science, University of Sussex, UK
eSoftware Engineering Group, Rutherford Appleton Laboratory, STFC, UK
fDepartment of Engineering Materials, University of Sheffield, UK
gDepartment of Computing and Engineering, University of Ulster, UK
First published on 3rd November 2011
Abstract
Many of the complex systems found in biology are comprised of numerous components, where interactions between individual agents result in the emergence of structures and function, typically in a highly dynamic manner. Often these entities have limited lifetimes but their interactions both with each other and their environment can have profound biological consequences. We will demonstrate how modelling these entities, and their interactions, can lead to a new approach to experimental biology bringing new insights and a deeper understanding of biological systems.
Insight, innovation, integrationThis paper explores a number of different biological systems from a molecular level, cellular and tissue and also the level of communities. In each case the research identifies new discoveries—the role of actin filaments and Iκ-B sequestration in cells; how correct levels of ArcA in aerobic–anaerobic transitions in bacteria; the mechanics of wound healing in tissue and the principles underlying ant foraging. Using highly detailed agent-based models derived in close partnership with experimental work provides significant benefits. Experimentalists find this approach very intuitive and enlightening. The paper describes projects where biologists and modellers have worked together very closely. The process is an iterative one and the models and data gathering are closely aligned and benefit each other. |
Introduction
Traditional mathematical and computational approaches to understanding biological systems concentrate on modelling homogeneous populations of molecules, cells, or organisms and calculating change over time, but without an appreciation of what is happening at the individual level. A complementary approach is to focus on individuals—in all their variation—and to explore what emerges from their interactions. Agent-based or individual-based modelling provides a way of doing this, but has been limited in the past by: difficulties of scaling the models up to a realistic size; the typically ad hoc manner in which models are developed and programmed; and the arbitrary adoption of rules that seem to generate plausible emergent behaviour. It is essential that the agents are both biologically plausible as entities and that their behaviour is based on experimental measurements.The necessity for determining accurate parameters in agent-based models is in contrast with traditional modelling techniques which only require a small set of parameters to test specific hypotheses. Testing of narrow hypotheses can clearly minimise assumptions, but a major drawback is that the system effects of variables outside the model's parameters cannot be explored. Agent-based models allow the identification of unexpected emergent effects of previously unconsidered, or underestimated, variables. By definition the emergent behaviour of complex biological systems is highly unpredictable and unlikely to be captured by a traditional modelling approach where hypothesis testing assumes that the modeller has a clear idea of how the system functions. Thus agent-based modelling represents a shift back to traditional scientific inquiry allowing us to focus on asking specific questions about a system's emergent behaviour, but without blindly assuming we fully understand the system being studied. We contend that traditional modelling approaches require a full understanding of system properties so as to make predictions about future behaviour, whereas agent-based modelling facilitates the development of that understanding.
We discuss here how a powerful software framework, FLAME1 has been used successfully in a number of cases to deliver new insights in biology. FLAME is the Flexible Large-scale Agent-based Modelling Environment and it has been developed to run very efficiently on both desktop computers and massively parallel supercomputers. Biological systems are highly complex and modelling them demands great computational power. They also need to be defined very carefully and the basis of any model should be both transparent and formalised as far as possible, and in a language that biologists can understand. There is a growing requirement in systems biology, and in experimental biology, that models and data be made publicly available, so that critical review and independent validation are possible. The FLAME specification approach meets these requirements and is one of the key factors in the success of this framework.
Modelling rationale
Multi-scale modelling is an essential approach to dealing with complex biological models where certain aspects of the model need to be represented at higher levels of detail and inter-related with other parts of the model that involve components or aspects which can be modelled at a lower level of detail. Our approach has been to use a high-level representation of functions (rules) for speed and simplicity, and introduce the details of the mechanisms that are involved only when this is necessary in order to examine the effect of changes in, for instance, a particular signalling pathway. In principle, an agent-based approach can be used at any level from the whole organism down to the molecule, thus generating emergent behaviour at all levels. The representation of the agents as X-machines is very general, so any function within the X-machine could be substituted by another X-machine which calculated the function, thus generating a hierarchy of X-machines at all levels. Whilst this is conceptually feasible (and even attractive!), it is neither practicable nor desirable to build a complete model of an organism in molecular detail. Some method of abstracting away detail between levels is essential for computability, and there are also cogent arguments for making use of models developed by other research groups.We therefore developed the means for incorporating models described in CellML, SBML, or as sets of differential equations. Our aim was to devise a generic modelling technique which enabled sub-cellular signalling pathways to be easily imported and plugged into an agent-based representation of a cell. To enable wide applicability, we have adopted a modular and flexible approach to link our agent-based modelling environment FLAME with existing tools such as COPASI2 and JSim.3 As the functions of an agent modelled using FLAME can be of any desired complexity, linking FLAME (http://www.flame.ac.uk) to such existing tools (COPASI and JSIM) was realised by providing wrappers that can be used by an agent's function to call COPASI or JSIM and request them to simulate a certain sub-cellular model specified in any of the modelling languages they support (e.g. CellML (www.cellml.org), SBML (sbml.org) and MML (nsr.bioeng.washington.edu/jsim/)). The main advantages that are provided to us by interfacing FLAME with COPASI and JSIM include:
• the ability to reuse curated and widely available models
• the ability to import sub-cellular models specified in widely used modeling languages such as SBML or CellML
• the ability to connect agent-based models of cellular behaviour (micro level) to mathematical (continuum) models of whole tissues or organs (macro level) and sub-cellular signalling pathways and biochemical networks (sub-cellular level)
• the facility to connect agent-based models to widely used ODE and PDE solvers and
• the promotion of multiparadigm and multiscale computational modelling.
COPASI (Complex Pathway SImulator) is a software application for the simulation and analysis of biochemical networks. COPASI provides the following main features: stochastic and deterministic time course simulation (ODE solver); metabolic control analysis/sensitivity analysis; optimization of arbitrary objective functions; parameter estimation; import and export of SBML; ODE Solving Capability; and a command line version for batch processing. The individual agent is defined using a markup language (XMML {X-MachineMarkup Language). In the environment tag, a data structure called ‘copasi data’ is defined to encapsulate the data that will be used by COPASI (for instance, the name and concentration of a metabolite). The user-defined data structure `copasi data' is then used in the agent's memory. The initial values are provided in the initialization file (an xml file). More technical details about FLAME, and FLAME/COPASI can be found on http://www.flame.ac.uk and http://www.imagwiki.org.
FLAME/COPASI allowed us to develop a 3D, multiscale, agent-based model of the human epidermis and to model the re-epithelialisation process.
The same approach has been used to link FLAME and JSim. JSim is a software application for the simulation and analysis of biochemical networks. JSim provides features similar to the ones provided by COPASI, but in addition has the following valuable features: the ability to import CellML models as well as SBML models; the ability to solve PDEs as well as ODEs, and automatic balancing and checking of units.
We will look at a number of specific cases of the application of the FLAME approach: starting with models at the molecular level where the agents are key molecules in a specific cell; then we look at an example of tissue modelling where agents are cells in a section of tissue; and finish with an example where agents are individual organisms in a colony of social insects.
![The whole inflammatory network, including NF-kB to the left, GTP-ases and the MAP kinase cascade in the centre and structural components involved in mechano-transduction to the right. [Qwarnstrom private communication].](/image/article/2012/IB/c1ib00042j/c1ib00042j-f1.gif) | ||
| Fig. 1 The whole inflammatory network, including NF-kB to the left, GTP-ases and the MAP kinase cascade in the centre and structural components involved in mechano-transduction to the right. [Qwarnstrom private communication]. | ||
Fig. 2(a) illustrates the different agent types—the toll-like and IL-1 receptors of the TIR-family are special molecules located on the cell membrane. They are stimulated into action through the influence of specific ligands constituting bacterial components or a cytokine called interleukin-1, released when the body detects infection or inflammation, and are specified in XMML. There are also receptor molecules, which recognise and dock the NF-kB transcription factor at the nuclear pore for transport into the nucleus where it is able to ‘turn on’ a number of special genes that lead to the production of proteins that are the response of the cell to the infection. The other agents are the key molecules such as IKK and IκB in various forms. The model then implements the various chemical reactions that take place between these agents. There are several thousands of each these agents and the simulations try to faithfully represent what is known about this complex series of reactions.
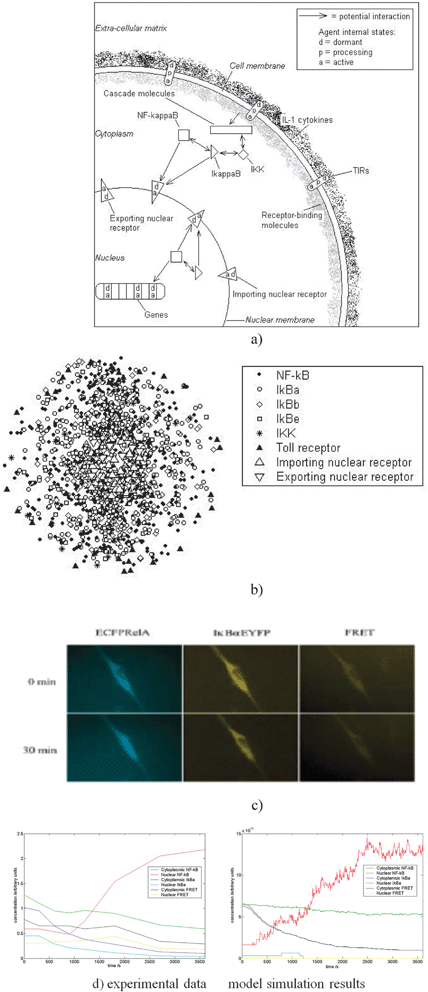 | ||
| Fig. 2 Formulation and validation of the agent-based model. (a) Simplified diagram of the principal pathway agents in the model. Each agent can exist in a number of states. (b) Three-dimensional visualisation of the positions of agents in the model at a moment in time. The cell is scaled down to reduce computation, containing in the order of 1000 agents. Concentrations of molecules are based on biological data. The genes that NF-κB can activate are placed randomly along a line at the centre of the nucleus. (c) Images of single cells transfected with ECFPrelA and IκBαEYFP. Prior to stimulation, both components are located in the cytoplasm (top row). Following pathway activation, NF-κB translocates to the nucleus whilst IκBα and NF-κB-IκBα complex levels fall. (d) Quantitation of single cell data as in (c) (left graph) and model results (right graph) following TIR activation over the same time period. Results are for a single cell, and demonstrate fundamental similarities with experiment.5 | ||
Using single cell data, the model demonstrated remarkable agreement with the experimental data. It also allowed us to investigate local activity. In particular, we could represent elements of the cytoskeleton such as actin filaments in the model (Fig. 3).
 | ||
| Fig. 3 The actin filaments are represented here, for the sake of clarity, as straight lines. | ||
Experimental data indicated that there is a mismatch between the amount of IκB in the cell and the amount needed for the NF-κB pathway. Using the model, we tested a hypothesis the surplus was sequestered in the actin filaments under normal conditions, and this was experimentally validated.5
Experimental work with E. coli involves the use of Chemostats: bioreactors that control and measure all key operating conditions, including growth rate under strictly defined conditions. Chemostats allow the measurements of transient properties (metabolite levels, fluxes, H+/O ratios, QO2, etc.) to be performed in standardized ways that can be replicated in different laboratories.
This is the focus of the Systems Understanding of Microbial Oxygen (SUMO) project, a multi-national project in the Systems Biology of MicroOrganisms (SysMO) initiative.
Oxygen availability profoundly affects E. coli bioenergetics, and through the synthesis of alternative electron transport chainsE. coli exploits any available O2 to support aerobic respiration—the most energetically efficient mode of growth.7,8 Thus, E. coli has two well-characterized alternative terminal oxidases; Cyd has a very high affinity for O2 and is used under micro-aerobic conditions, whereas Cyo has a relatively lower affinity for O2 and is used under normoxic conditions (Fig. 4). The synthesis of these alternative oxidases is regulated by two main transcription factors: the fumarate and nitrate reduction regulator (FNR) and the two-component aerobic respiratory control (ArcBA) system (reviewed by ref. 9). These regulators can sense changes in O2 availability—FNR is a direct O2 sensor, whereas ArcBA senses O2 indirectly10,11—to re-programme gene expression such that the most appropriate electron transport chain is synthesized in any particular niche. Hence, in the absence of O2, expression of cyo is repressed by FNR and phosphorylated ArcA (ArcA∼P), whereas expression of cyd is also repressed by FNR but activated by ArcA∼P (Fig. 4). Furthermore, the primary signal for switching ArcBA and FNR off (O2) is consumed by the terminal oxidases, forming a negative feedback loop (Fig. 4). Thus, the activities of FNR and Arc are the primary determinants of the extent to which each oxidase is synthesized, but measuring these activities experimentally is technically demanding. Therefore, it was argued that multi-scale and multi-level modelling could reveal new insight into the operation of this important regulatory circuit. The flexible agent-based supercomputing framework FLAME provided the basis for the integration of three complementary modelling approaches: kinetic, reduced-order kinetic, and agent/hybrid modelling (Fig. 5). Each of the modelling approaches contributes by addressing questions that are difficult to incorporate within a single modelling framework.
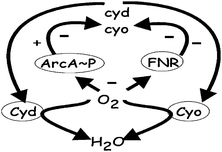 | ||
| Fig. 4 The basic relationships, both excitatory (+) and inhibitory (−), between the transcriptional regulators (FNR and ArcA∼P), the genes encoding the alternative oxidases (cyd and cyo) and the oxidase proteins (Cyd and Cyo). The transcription factors are switched off when oxygen (O2) is abundant, allowing maximum expression of cyo (FNR and ArcA∼P no longer repress expression) and basal level expression of cyd (FNR no longer represses but ArcA∼P does not activate). When intermediate amounts of O2 are available ArcA∼P is able to activate expression of cyd, leading to maximal cyd expression under micro-aerobic conditions. In the absence of O2 both FNR and ArcA∼P are active and expression of cyd and cyo is repressed. Reduction of O2 to H2O by the terminal oxidases affects the level of signal perceived by the regulators. | ||
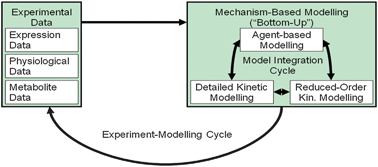 | ||
| Fig. 5 Experiment-modelling cycle. | ||
Thus, the activities of FNR and Arc are the primary determinants of the extent to which each oxidase is synthesized, but measuring these activities experimentally is technically demanding and thus accurate models play an important role understanding what is going on. Each of the modelling approaches contributes by addressing questions that are difficult to incorporate within a single modelling framework, Fig. 5.
In the model, Fig. 6, each individual molecule is represented as an autonomous agent that exists within the cellular environment and interacts with other molecules according to the biochemical situation. The specification of each of these agents is defined in the XMML language. The numbers of such molecules in a typical cell are known—between 5000 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for all of the proteins of interest. Molecules each have a location within the cell. Some, such as the oxidases, are located at the cell membrane, whereas others, like the regulators, are more uniformly distributed. Each agent communicates with the others via message passing that includes information about where each molecule is and what state it is in. Molecules can move through 3D space in the cell and interact with each other when close enough and in a suitable state. Molecules move differently in different regions of the cytoplasm and this was modelled by controlling the movement of agents in the different areas and changing their location by Brownian motion (random movement of particles suspended in a fluid) where appropriate. The agent-based model must of course agree with the corresponding reaction kinetics model in the circumstance where reaction kinetics can reasonably be applied (i.e. with large numbers of molecules of well-mixed chemicals). Since information about reacting chemicals is invariably given for such a situation, and because little information exists about individual molecular interactions, it is important that the necessary data for the agent-based model can be inferred from reaction kinetics. The interactions with O2 molecules have been modelled by interpreting the k rate in terms of interaction radius. The rate constant can now therefore be used to deduce information on local interactions. Disassociation was dealt with by applying a probabilistic k rate. Dissociation can easily be accounted for by making bound products separate randomly at a rate specified by the dissociation rate constant (using a uniform random distribution initially, though this could be modified as appropriate). Although this is straightforward, it may be an unnecessary consideration since the rate of dissociation is often negligible. Both k rates have been collected from literature and experimental biologists.
000 for all of the proteins of interest. Molecules each have a location within the cell. Some, such as the oxidases, are located at the cell membrane, whereas others, like the regulators, are more uniformly distributed. Each agent communicates with the others via message passing that includes information about where each molecule is and what state it is in. Molecules can move through 3D space in the cell and interact with each other when close enough and in a suitable state. Molecules move differently in different regions of the cytoplasm and this was modelled by controlling the movement of agents in the different areas and changing their location by Brownian motion (random movement of particles suspended in a fluid) where appropriate. The agent-based model must of course agree with the corresponding reaction kinetics model in the circumstance where reaction kinetics can reasonably be applied (i.e. with large numbers of molecules of well-mixed chemicals). Since information about reacting chemicals is invariably given for such a situation, and because little information exists about individual molecular interactions, it is important that the necessary data for the agent-based model can be inferred from reaction kinetics. The interactions with O2 molecules have been modelled by interpreting the k rate in terms of interaction radius. The rate constant can now therefore be used to deduce information on local interactions. Disassociation was dealt with by applying a probabilistic k rate. Dissociation can easily be accounted for by making bound products separate randomly at a rate specified by the dissociation rate constant (using a uniform random distribution initially, though this could be modified as appropriate). Although this is straightforward, it may be an unnecessary consideration since the rate of dissociation is often negligible. Both k rates have been collected from literature and experimental biologists.
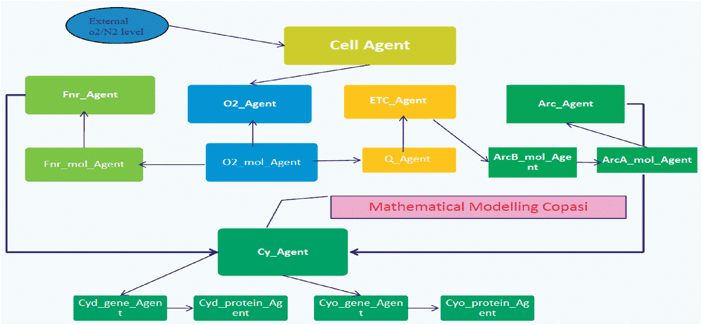 | ||
| Fig. 6 The hybrid model architecture for the E. coli model. | ||
Multiple binding of agents are added to reaction to deal with several chemical reactions, each molecule agent can seek interaction with several relevant types of molecule, with the appropriately sized interaction radius for each type.
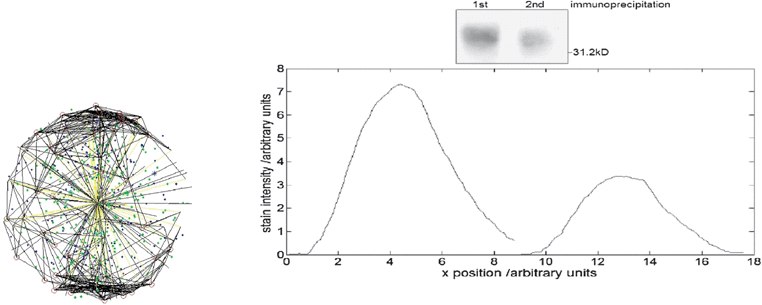
Three experimental measurements formed the basis of the model viz. the abundances of the oxidases Cyd and Cyo, the relative activity of the FNR protein in E. coli cultures grown under conditions of different O2 availability. Using these inputs the model was able to closely match the experimental measurements and predict the activity of ArcA in the system (Fig. 7). However, the predicted ArcA activity did not match ArcA activity predicted from measurement of transcription from an ArcA-regulated promoter.12 One possibility was that a third O2-responsive transcription factor might operate alongside FNR and ArcA to regulate both oxidases. Alternatively, the indirect nature of measuring ArcA activity using a reporter fusion could lead to inaccuracies. Therefore, new experimental data directly measuring ArcA phosphorylation was obtained and was found to match the model predictions very closely—see Fig. 7. Thus the simulations contributed to clarifying and correcting the current knowledge about the role of this important regulatory circuit. E. coli has to be able to change its metabolism to survive. The presence/absence of O2 is a key signal during E. coli infection. E. coli is used as a “cell factory” for making many drugs & chemicals and oxygen concentration is an important factor that affects yield.
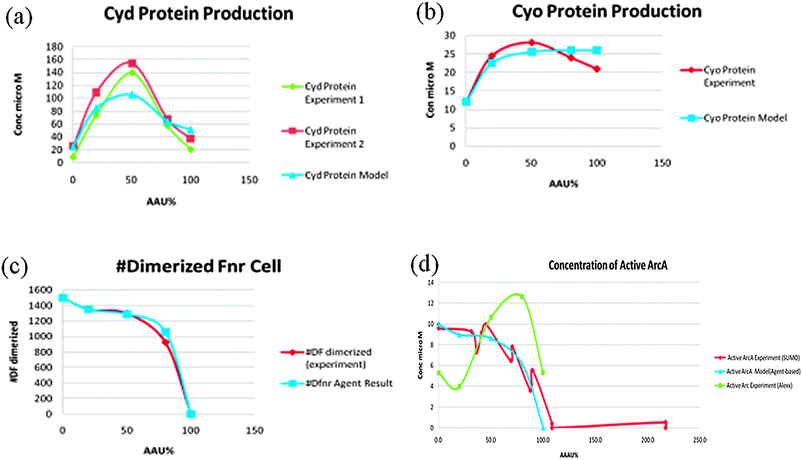 | ||
| Fig. 7 A comparison between experimental results and the model predictions. 6(d) shows the disparity between the model predictions and the original experimental data.13 | ||
The enzymes in the two pathways are regulated by two main transcription factors:
The fumarate & nitrate reduction protein (FNR) and the two-component anoxic redox control (Arc) system. These regulators can sense oxygen levels (Arc does this indirectly) and enzymes are activated/repressed in the respective pathways to utilise the most energy as possible from glucose.
Understanding the synthesis of alternative oxidases in E. coli can only be efficiently understood using multi-scale and multi-level modelling. We have integrated three different, complementary modelling approaches: kinetic, reduced-order kinetic, and agent/hybrid modelling. Each of the modelling approaches contributes by addressing questions that are difficult to incorporate within a single modelling framework. The flexible agent-based supercomputing framework FLAME provides the basis for this integration.
We emphasise the importance of both modularity and the integration of the system. Biological complexity requires us to break our systems into manageable components, but it also requires us to reassemble them because behaviours can emerge that we cannot understand from the components alone. The resulting models can provide predictions, be used as a scaffold for our emerging understanding of the data and identify gaps in our biological knowledge. Each component has used different modelling techniques that depend on the availability of biological data. The model has been extensively validated under controlled experimental conditions.
Some of the key ways in which the FLAME-SUMO model has been used is in the estimation of important kinetic parameters in these reactions. For example rate constants and concentrations cannot always be measured directly and the agent-based model provides a vehicle for experimenting with these values and then comparing the results with the experimental data derived from the chemostat experiments.
The agent-based models have also been used to estimate the level of resources needed by the colonies in order to reach a steady state in a way that may not be possible with other types of modelling.
Some of the key issues that needed to be addressed related to the division and migration of cells within a population, since these are fundamental concepts in the growth and repair of epithelial tissues. Each cell has a fundamental cell cycle that underpins cell growth and division, or provides alternative routes for specialisation (differentiation) and death (apoptosis). Progression around the cell cycle is affected by interactions with other cells, either through direct cell–cell contact or indirectly through the release and detection of soluble signalling factors, which may have a profound effect on behaviour. All of these factors have to be modelled.
When a cell grows during the cell cycle (Fig. 8) it needs more space in which to sit—where multiple cells in a tissue are also changing their size the agent model needs to deal with the conflicts whereby two cells might be overlapping—a situation that cannot happen in biology. Thus at the end of each iteration there has to be a stage where the calculation of the physical forces exerted by the cells on each other is calculated and the cells moved so that none overlap. When a cell has reached the point where division is the next step the model has to check whether there is physical space for the two daughter cells to occupy. Contact inhibition is checked in G1, and disables the cell from progressing to division (instead, a counter “contact_inhibited_ticks” is incremented, and after a while in such state, the cell might commit). Without dealing with these fundamental issues of space and physics the model would have no credibility with biologists.
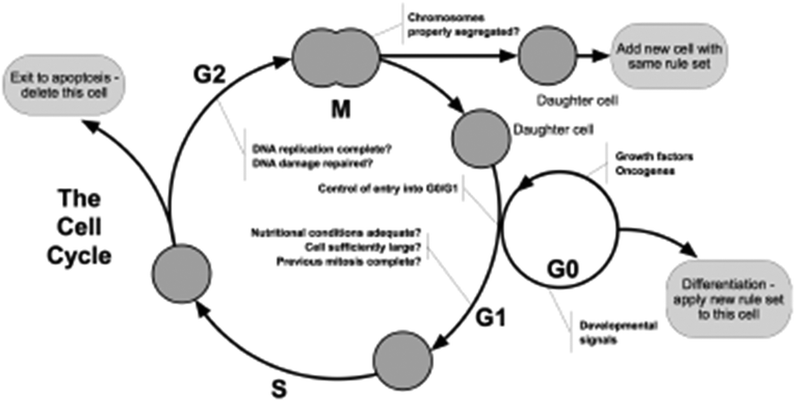 | ||
| Fig. 8 The basic cell cycle. | ||
The novel modelling technique encourages different types of questions to be asked of the biology and thus encourage fresh perspectives and new results. Already new light has been thrown on tissue repair by demonstrating that for skin cells to repair stem cells need to be distributed throughout the wound area, see Fig. 9.15,16
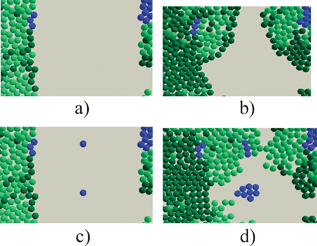 | ||
| Fig. 9 The role of stem cells (blue) in healing wounds—(a) represents a situation with few stem cells in the wound area and (b) is the outcome; (c) and (d) show the effect of a more uniform distribution of stem cells. | ||
The model was then used to investigate the relationship between cell migration and proliferation during epidermal wound healing at the cellular level and the actions of TGF-β1 on different keratinocyte populations at the sub-cellular level, see Fig. 10.17,18
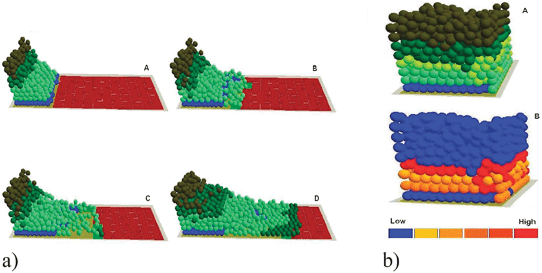 | ||
| Fig. 10 (a) In virtuo investigation of the influence of TGF-β1 on epidermal wound healing at the subcellular level. The virtual wound with normal proliferation and migration rates were simulated for (A) 0, (B) 200, (C) 400 and (D) 800 iterations. (b) The cells with high TGF-β1 expression levels in the Healed virtual epidermis—the stratified cells with relatively high expression level of TGF-β1 were labelled with yellow (A), In the integrated model different colours were used to represent keratinocyte stem cells (blue), transit amplifying (TA) cells (light green), committed cells (dark green), corneocytes (brown), provisional matrix (dark red), secondary matrix (green), basement membrane (BM) tile agent (light purple). Some of the cells with a relatively low expression level of TGF-β1 were also illustrated using a simple thermal image (B). | ||
In virtuo investigations indicated that both cell proliferation and migration are crucial for re-epithelialisation, suggesting delicate mechanisms to coordinate the behaviour of different keratinocyte populations. Further model analysis found that TGF-β1 played a positive role in epidermal wound healing by coordinating the behaviour of these keratinocyte populations.
Forager ants collect food and bring it back to the nest to feed the larvae, queens and other ants. This is the critical activity upon which the survival of the colony depends. Since food is often an ephemeral resource foraging communication has to be flexible to adapt to changing local circumstances. Ant pheromone trails provide an effective and efficient solution to the problem of locating and exploiting available food resources. After finding food ants lay chemicals in a trail from the food source to the nest providing positive feedback which recruits other ants to exploit the food source. The pheromone also acts as a chemical orientation signal to guide other ants.19 Thus recruitment and orientation are coupled in a single signal. The pheromone will decay or evaporate over time if it is not reinforced providing a negative feedback signal. Thus when a food source is exhausted ants will cease to be recruited to the decaying pheromone trail.
This seemingly simple feedback system has been the inspiration for a number of algorithms for solving complex computational problems. These algorithms are based on a superficial understanding of the biology. It is interesting to note that ant algorithms are generally applied to classical NP complete problems, which are very different to the classes of problems the ants are solving. Bio-inspired algorithms are tested on problems like the Travelling Salesman Problem but this is essentially a static problem, where the towns to be visited do not move, appear or disappear. However ant trails typically solve dynamic problem where it is imperative that foraging activity can rapidly be switched from one resource to a better one, and that exhausted or poor resources be abandoned.
Ant colonies contain diverse individuals where different castes of workers perform specific roles. I the Pharaoh's ants these heterogeneous agent communities contain general foragers but also a behavioural caste responsible for scouting known as ‘pathfinders.20 Pathfinder ants explore the environment and discover food sources but have special access to long-lived trail pheromones which allows them to inspect trails which have proved rewarding on previous days. All foragers can access short-lived pheromone trails which only last for minutes. In the Pharaoh's ant approximately 17% of the colony are pathfinder specialists. The use of multiple trail pheromones allows Pharaoh's ants to switch rapidly to high quality food sources when they are discovered.21
A notable discovery facilitated by agent-based modelling is that Pharaoh's ants produce trail networks with a treelike structure.19 The branches of this network have a mean bifurcation angle of 54 degrees, and this branching structure conveys important information to the ants. Simulations of foraging ant colonies prompted a new hypothesis of ant orientation in trail networks which was confirmed by extensive experimental observations.20 The information provided by trail bifurcations allows ants to determine the direction they are heading in a trail network. Thus if an ant is fed it should be walking towards the nest and only experiencing walking into a bifurcation, whereas an unfed ant should only experience the choice provided by encountering bifurcations. When an ant becomes disorientated and rejoins a trail network it can correct its course after passing through bifurcations. Experimental evidence showed that unfed ants can still detect bifurcations when they are returning to the nest which shows that they can smell the difference in conformation provided by the changing chemical topology of a bifurcation. It is not simply the case that unfed ants expect choices and respond accordingly when they are absent. Experimental evidence showed that unfed ants walking into a bifurcation towards the nest corrected their course shortly afterwards. Likewise fed ants meeting the fork of a bifurcation indicating they are heading away from the nest also corrected their course. Course corrections were observed in over 50% of experimental trials and corrections were optimised when the bifurcation angle approached the natural angle of 50–60 degrees. Fig. 11 illustrates one of the laboratory set-ups.
 | ||
| Fig. 11 Laboratory set-up showing Pharaoh's ants forming a trail bifurcation. | ||
Simulations using FLAME have provided considerable insight into the way ant foraging trail networks work. The importance of U-turning behaviour by specialists on ant trails was tested in simulations and shown to greatly enhance the speed with which new food discoveries were integrated into the trail network (Fig. 12).21 Comparison with simulated ant colonies lacking U-turning specialists demonstrated superior foraging efficiencies in the U-turners. X-machine modelling facilitated the development of sophisticated state-based models of individual ant agents, allowing the expression of the level of heterogeneity found in real ant societies. Models of ant behaviour have previously treated ant societies as composed of homogeneous individuals and our research shows that such an assumption is an impediment to the emergence of many colony-level adaptive phenomena which confer huge advantage to ant societies. Further research is addressing the micro-level of behaviour, by treating the individual deposition of the ‘drops’ of pheromone as agents with a limited dimension and lifetime allowing highly detailed modelling of trail behaviour. This level of detail, however, is computationally challenging and requires the use of parallel supercomputers.
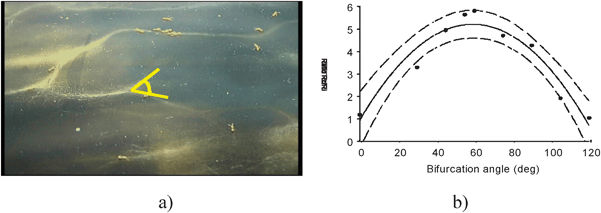 | ||
| Fig. 12 (a) Trail geometry from a typical foraging network (b) experimental data testing variation of bifurcation angles and the ratio of correct to incorrect orientations. | ||
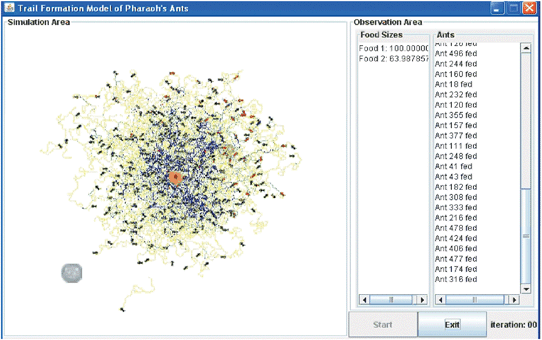 | ||
| Fig. 13 Screenshot of a simulation of a realistically sized colony of M. pharaonis using a supercomputer. | ||
FLAME is the only agent-based modelling framework capable of producing parallelisable models. Any model written in FLAME can be run in serial or parallel without any changes done to the model. e-Science, i.e. running models in parallel, is highly significant for progress in scientific research. If simulation of models takes more than 1 h to run on a single machine, this is very time consuming and costly. Therefore it is necessary to attain results quickly. Further, in agent-based modelling models can scale up exponentially depending on the number of agents and the functions to be performed. FLAME handles all these problems by accommodating large number of agents running in time defined by only an order of minutes. This is done automatically by FLAME which eliminates any manual effort for the modeller.
Fig. 14–16 show the processing times of our simulations on a laptop (Sony) and a supercomputer (Iceberg) with different number of cores. Processing times were reduced by six times when we ran our model in parallel compared to serial on the grid, which is extremely desirable for processing complex biological models.
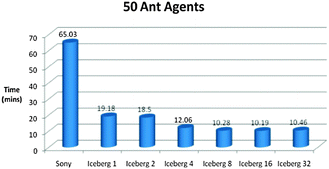 | ||
| Fig. 14 Time vs. Platform Chart for the Foraging Model initialised with 50 Ant Agents. The model was ran for 5000 iterations. (Specifications for Sony laptop: 2.4 GHz processor, 4 GB RAM; Specifications for Iceberg: 568 processor cores (results from 1, 2, 4, 8, 16 and 32 cores shown above), 435 GFLOPs). | ||
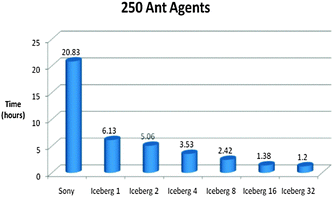 | ||
| Fig. 15 Time vs. Platform Chart for the Foraging Model initialised with 250 Ant Agents. The model was ran for 5000 iterations. (Specifications for Sony laptop: 2.4 GHz processor, 4 GB RAM; Specifications for Iceberg: 568 processor cores (results from 1, 2, 4, 8, 16 and 32 cores shown above), 435 GFLOPs). | ||
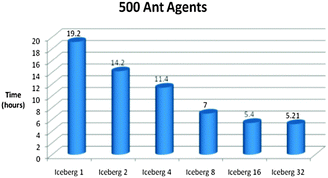 | ||
| Fig. 16 Time vs. Platform Chart for the Foraging Model initialised with 500 Ant Agents. The model was ran for 5000 iterations. (Specifications for Sony laptop: 2.4 GHz processor, 4 GB RAM; Specifications for Iceberg: 568 processor cores (results from 1, 2, 4, 8, 16 and 32 cores shown above), 435 GFLOPs). | ||
Conclusions
In all of these examples a software framework is used which enables very quick and detailed models to be constructed and simulations to be run, visualised and investigated. The framework, based on a dialect of the XML language, generates high quality software codes in C which are optimised for running on highly parallel computers capable of handling simulations of millions of agents in 3 dimensional virtual worlds. The approach enables the third perspective of in virtuo, alongside in vivo and in vitro, to be part of the biologist's toolkit and provides a powerful approach for exploring biological systems.Agent-based modelling also promotes greater collaboration and feedback between biologists and modellers. They are able to develop the idea of biological systems as sets of natural agents, such as molecules or cells, and conceptualise these system components as machines with state, internal properties and functions. A key step in this interaction is the production of a visual model as early in the modelling as is feasible. This greatly assists communication between biologists and modellers. The model of communication between agents is readily understood. The ease with which physical processes and other key factors can be integrated into the FLAME framework is another benefit.
There are a number of key principles that need to be observed if realistic models of biological systems are to be achieved. Biological systems exist in a physical three-dimensional world governed by the laws of physics. There is a strong temptation by computer scientists to abstract away some of these factors in order to make modelling and analysis more tractable. This may impede useful insights into biology since ignoring geometry and the real forces that dictate system behaviour can be very misleading. The advantage of agent-based modelling over traditional mathematical modelling, such as differential equations, is that many of the key determinants underpinning the emergence of complex system behaviour are found in behaviour of individual molecules, cells of organisms. Agent-based modelling enables us to understand the emergent development of structure and function and provides a deep understanding of biology. As the wise old maxim states, we must appreciate that ‘the devil is in the details’.
Acknowledgements
EPSRC, BBSRC, BTExact.References
- FLAME, http://www.flame.ac.uk/.
- S. Hoops, S. Sahle, R. Gauges, C. Lee, J. Pahle, N. Simus, M. Singhal, L. Xu, P. Mendes and U. Kummer, Copasi—a complex pathway simulator, Bioinformatics, 2006, 22(24), 3067–3074 CrossRef CAS.
- Gary M. Raymond, Erik A. Butterworth and James B. Bassingthwaighte, Jsim: Mathematical modeling for organ systems, tissues, and cells, Faseb J, 2007, 21(6) Search PubMed.
- Simon Coakley, Rod Smallwood and Mike Holcombe, From molecules to insect communities—how formal agent-based computational modelling is uncovering new biological facts, Scientiae Mathematicae Japonicae Online, 2006, e–2006, 765–778 Search PubMed.
- Mark Pogson, Rod Smallwood, Eva Qwarnstrom and Mike Holcombe, Formal agent-based modelling of intracellular chemical interactions, BioSystems, 2006, 85, 37–45 CrossRef CAS.
- M. Pogson, M. Holcombe, R. Smallwood and E. Qwarnstrom, Introducing Spatial Information into Predictive NF-κB Modelling—An Agent-Based Approach, PLoS One, 2008, 3(6), e2367, DOI:10.1371/journal.pone.0002367.
- J. R. Guest, J. Green, A. S. Irvine and S. Spiro, The FNR modulon and FNR-regulated gene expression, in Regulation of Gene Expression in Escherichia coli, ed. E. C. C. Lin and A. S. Lynch, R. G. Landes & Co, Austin, Texas, 1996, pp. 317–342 Search PubMed.
- R. B. Gennis and V. Stewart, Respiration, in Escherichia coli and Salmonella Cellular and Molecular Biology, F. C. Neidhardt (ed. in chief), 2nd edn, 1996, ASM Press, Washington DC, pp. 217–261 Search PubMed.
- J. Green and M. S. Paget, Bacterial redox sensors, Nat. Rev. Microbiol., 2004, 2, 954–966 CrossRef CAS.
- D. Georgellis, O. Kwon and E. C. Lin, Quinones as the redox signal for the Arc two-component signal transduction system of bacteria, Science, 2001, 292, 2314–2316 CrossRef CAS.
- A. J. Jervis, J. C. Crack, G. White, P. J. Artymiuk, M. R. Cheesman, A. J. Thomson, N. Le Bruin and J. Green, The O2 sensitivity of the transcription factor FNR is controlled by Ser24 modulating the kinetics of the [4Fe-4S] to [2Fe-2S] cluster conversion, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 4659–4664 CrossRef CAS.
- M. Bekker, S. Alexeeva, W. Lann, G. Sawers, J. Teixeira de Mattos and K. Hellingwerf, The ArcBA two-component system of Escherichia coli is regulated by the redox state of both the ubiquinone and menoquinone pool, J. Bacteriol., 2010, 192, 746–754 CrossRef CAS.
- S. Maleki-Dizaji, M. Rolfe, P. Fisher and M. Holcombe, A Systematic Approach to Understanding Bacterial Responses to Oxygen Using Taverna and Webservices, Proc. 13th International Conference on Biomedical Engineering, 2009, 23, 77–80 CrossRef.
- Tao Sun, Phil McMinn, Mike Holcombe, Rod Smallwood and Sheila MacNeil, Agent Based Modelling Helps in Understanding the Rules by Which Fibroblasts Support Keratinocyte Colony Formation, PLoS One, 2008, 3(5), e2129, DOI:10.1371/journal.pone.0002129.
- Tao Sun, Phil McMinn, Simon Coakley, Mike Holcombe, Rod Smallwood and Sheila MacNeil, An integrated systems biology approach to understanding the rules of keratinocyte colony formation, J. R. Soc. Interface, 2006, 4, 1077–1092 CrossRef.
- Dawn Walker, Steven Wood, Jennifer Southgate, Mike Holcombe and Rodney Smallwood, An integrated agent-mathematical model of the effect of intercellular signalling via the epidermal growth factor receptor on cell proliferation, J. Theor. Biol., 2006, 242, 774–789 CrossRef CAS.
- Tao Sun, Salem Adra, Sheila MacNeil, Mike Holcombe and Rod Smallwood, Exploring Hypotheses of the Actions of TGF-β1 in Epidermal Wound Healing Using a 3D Computational Multiscale Model of the Human Epidermis, PLoS One, 2009, 4(12), e8515, DOI:10.1371/journal.pone.0008515.
- Salem Adra, Tao Sun, Sheila MacNeil, Mike Holcombe and Rod Smallwood, Development of a Three Dimensional Multiscale Computational Model of the Human Epidermis, PLoS One, 2010, 5(1), e8511, DOI:10.1371/journal.pone.0008511.
- Duncan E. Jackson, Mike Holcombe and Francis L. W. Ratnieks, Trail geometry gives polarity to ant foraging networks, Nature, 2004, 432, 907–909 CrossRef CAS.
- D. E. Jackson, S. J. Martin, F. L. W. Ratnieks and M. Holcombe, Spatial and temporal variation in pheromone composition of ant foraging trails, Behav. Ecol., 2007, 18, 444–450 CrossRef; Elva J. H. Robinson, Duncan E. Jackson, Mike Holcombe and Francis L. W. Ratnieks, No entry' signal in ant foraging, Nature, 2006, 438, 442 CrossRef.
- D. Jackson, M. Bicak and M. Holcombe, Decentralized communication, trail connectivity and emergent benefits of ant trail networks, Journal of Memetic Computing (Online). M, 2010 Search PubMed.
Footnote |
| † In collaboration with the SysMO-SUMO consortium whose members are: K. Bettenbrock, M. Ederer, E. D. Gilles, S. Henkel, T. Sauter, O. Sawodny, S. Stagge, S. Steinsiek, J. Teixeira de Mattos and A. Ter Beek. |
| This journal is © The Royal Society of Chemistry 2012 |
