A statistical feature of Hurst exponents of essential genes in bacterial genomes

Abstract

At present, methods for determining essential genes depend on biochemical experiments. There is therefore a demand for the development of analysis methods and software for identifying essential genes, based on the common features of these genes. In this study, we employed the Hurst exponent as a characteristic parameter and analyzed its distribution among nine bacterial species. We found that most of the significance levels of the Hurst exponents of essential genes were higher than those of the corresponding full-gene-set. Conversely, most of the significance levels of the Hurst exponents of nonessential genes remained unchanged or only increased slightly. Therefore, we propose that this feature represents a restraint for pre- or post-design checking of bacterial essential genes in computer-aided design.

---

Insight, innovation, integration

Our study aimed to determine the common features of bacterial essential genes, to aid in the design of analysis methods and software for their identification. Because self-similarity exists in DNA sequences, we employed the Hurst exponent to characterize this property for genes in nine bacterial genomes, including essential and non-essential genes, and analyzed the distribution of their Hurst exponents, based on a normal distribution model, to study whether and how the self-similarity features change in reduced DNA sequences. We found that most of the significance levels of the Hurst exponents of the essential genes were higher than those of the corresponding full-gene-set. Conversely, most of the significance levels of the Hurst exponents of the nonessential genes remained unchanged or only increased slightly. Therefore, we propose that this feature represents a restraint for pre- or post-design checking of bacterial essential genes in computer-aided design.

1. Introduction

A minimal genome is generally defined as the smallest set of genes that allows for replication of an organism in a particular environment. To determine how many genes are required to make a cell is one of the basic purposes of minimal genome research.¹ This type of research is important for understanding primitive organisms in both a functional and evolutionary context, and may lead to findings of significance for the pharmacological and chemical industries, and the development of eco-friendly fuels. The genes that constitute a minimal genome are essential genes, and many studies have been performed to determine the minimal set of genes that is required to support a cellular life form.²

Two different approaches have been employed to construct a minimal genome: bottom-up and top-down. The bottom-up approach constructs an artificial genome by chemical synthesis, whereas the top-down approach uses an existing organism with the aim of simplifying its genome into a reduced form.³ Software and algorithms of computer-based design and simulation have been proposed to aid the synthetic approach. However, methods for determining essential genes still depend on biochemical experiments,^4,5 highlighting the need for identification of characteristic features of these genes to aid investigations into genome reduction.

Long-range correlation (or self-similarity) is a phenomenon that may arise in the analysis of very large spatial or time series data sets. This phenomenon has also been observed in DNA sequence, in both coding and non-coding regions.^6–8 The Hurst exponent is a characteristic parameter of self-similarity that has been used in many studies. Yu and Anh⁹ proposed a time series model based on the global structure of the complete genome, and used this model to study the classification and evolutionary relationship of bacteria. Liu et al.¹⁰ studied the distribution curves of the Hurst exponents of exon, intron and promoter sequences based on the Z-curve. Boekhorst et al.¹¹ studied the efficiency of rescaled range analysis and detrended fluctuation analysis in distinguishing between coding DNA, regulatory DNA and non-coding non-regulatory DNA of Drosophila melanogaster. The long-range correlation between hydrophilicity and flexibility, a common feature of proteins, along some 80-calcium binding protein sequences was examined by Craciun et al.¹² However, it remains unclear if and how these self-similarity features change in reduced DNA sequences.

In this study, we employed the Hurst exponent to characterize the self-similarity of genes in nine bacterial genomes, including essential and non-essential genes, and analyzed the distribution of their Hurst exponents based on a normal distribution model.

2. Materials and methods

2.1 Hurst exponent and the modified periodogram method

The Hurst exponent represents the degree of self-similarity of a data set. For a self-similar series with long-range dependence, the Hurst exponent is between 0.5 and 1. An increased Hurst exponent indicates an increase in the degree of self-similarity and long-range dependence.¹³ Many methods for determining the Hurst exponent have been developed. We selected the modified periodogram (MP) method,¹⁴ based on our previous experiments. The MP method compensates for the fact that most of the data in a log–log plot are at high frequencies in the periodogram method, which exerts a very strong influence on the least squares line fitted to the periodogram. In this modified method, the frequency axis is divided into logarithmically equally spaced boxes, and the periodogram values corresponding to the frequencies inside each box are averaged. The points at very low frequencies are left unchanged because there are relatively few. To facilitate the analysis, we implemented MP analysis using the hurstSpec function of the fractal package in the R software environment (R Development Core Team, 2010).

2.2 Materials

The essential gene lists of nine bacteria were downloaded from the database of essential genes (DEG; http://tubic.tju.edu.cn/deg/),¹⁵ and their genome files and sequence data were downloaded from the NCBI ftp site (ftp://ftp.ncbi.nih.gov/genomes/Bacteria/); this information is listed in Table 1. The EcoGene database (http://www.ecogene.org/) was also used to proofread the gene data from Escherichia coli.

Table 1 Information on the analysis objects

Analysis objects	NCBI RefSeq access number	Gene number (Full-gene-set)	Gene number (Essential)	Gene number (Actual)^a
a Some of the essential gene names listed in the DEG were not found in the corresponding genome file from NCBI.
Escherichia coli K-12 MG1655	NC_000913	4145	712	700
Acinetobacter ADP1	NC_005966	3307	499	493
Mycoplasma genitalium G37	NC_000908	475	381	364
Staphylococcus aureus NCTC 8325	NC_007795	2891	351	351
Bacillus subtilis 168	NC_000964	4176	271	244
Francisella novicida U112	NC_008601	1719	392	386
Mycobacterium tuberculosis H37Rv	NC_000962	3988	614	604
Salmonella typhimurium LT2	NC_003197	4423	230	228
Staphylococcus aureus N315	NC_002745	2583	302	297

---

2.3 Analytical procedures

The data were analyzed as follows:

(i) Nucleotide sequences were transformed into digital sequences by expressing each nucleotide as a digital number. The four nucleotides, A, G, C and T, were assigned the digital numbers 0, 1, 2 and 3, respectively.¹⁶ For example, a DNA fraction ATTCAC was transformed to 033202.

(ii) The subsequences corresponding to each gene were selected and their Hurst exponents were calculated based on the MP method in the R software.

(iii) The distribution properties of the Hurst exponents of the full-gene-set, the essential genes and the nonessential genes of each organism were analyzed using SPSS software (IBM, Armonk, NY) as follows.

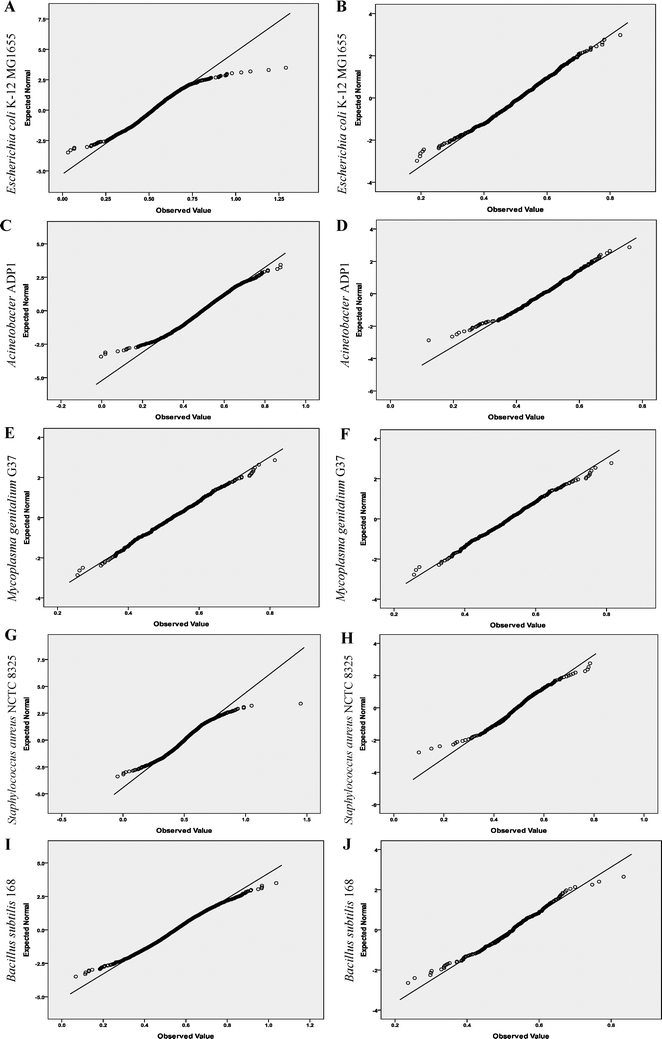
First, the distributions of the Hurst exponents of the full-gene-set, the essential genes and the nonessential genes of each organism were analyzed based on the quantile–quantile (Q–Q) plot. This is a graphical method for comparing two probability distributions, usually the sample distribution function and a theoretical distribution function. If the data follow the assumed theoretical distribution, the points on the Q–Q plot will fall approximately on a straight line; otherwise the points will depart from a straight line.

In our study, the straight line in a Q–Q plot represents the expected normal statistics. If the investigated data follow a normal frequency distribution, a plot of the data against the expected statistics should produce a straight line. All the plots were produced by the SPSS Analyze > Descriptive Statistics > Q–Q procedure.

Next, the significance levels of the Hurst exponents of the full-gene-set, the essential genes and the nonessential genes of each organism, based on a normal distribution, were calculated based on the Kolmogorov–Smirnov (K–S) test. This procedure provides a significance level, which is then used for quantitative evaluation of whether the datasets were significantly different from an assumed theoretical distribution.

In our study, the assumed distribution is normal distribution. A normal distribution hypothesis is refused when the significance level is less than 0.05, and is accepted when the significance level is greater than or equal to 0.05. All K–S tests were produced by the SPSS Analyze > Nonparametric Tests > 1-Sample K–S procedure.

3. Results

Q–Q plots of Hurst exponents are shown in Fig. 1. We observed that the essential gene data departed from linearity less than the corresponding full-gene-set, indicating the essential gene data followed a normal distribution more closely. K–S test results clearly show the degree of departure from linearity visible in the Q–Q plot (Table 2).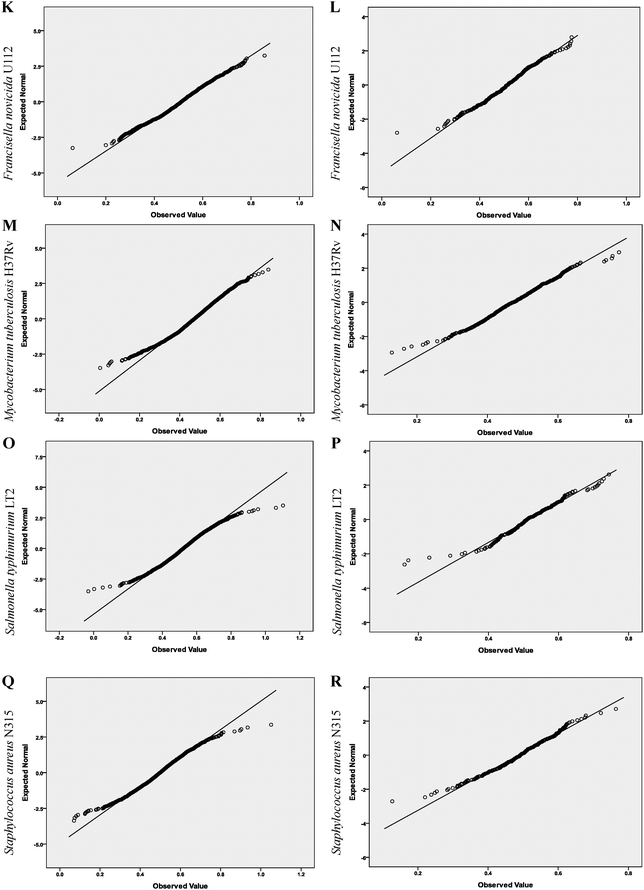

Fig. 1 Q–Q plots of the Hurst exponents of the full-gene-set and the essential genes of the nine objects. A, C, E, G, I, K, M, O and Q show Q–Q plots of the Hurst exponents of the full-gene-set of the nine objects, respectively. B, D, F, H, J, L, N, P and R show Q–Q plots of the Hurst exponents of the essential genes of the nine objects, respectively. The quantiles of the observed organism's distribution and normal distribution are plotted on the horizontal and vertical axis in each plot, respectively.

Table 2 Significance level of the nine objects

Analysis objects	NCBI RefSeq access number	Full-gene-set	Essential genes	Nonessential genes
Escherichia coli K-12 MG1655	NC_000913	0.000	0.575	0.000
Acinetobacter ADP1	NC_005966	0.052	0.492	0.083
Mycoplasma genitalium G37	NC_000908	0.996	0.957	0.576
Staphylococcus aureus NCTC 8325	NC_007795	0.000	0.099	0.002
Bacillus subtilis 168	NC_000964	0.004	0.425	0.005
Francisella novicida U112	NC_008601	0.048	0.320	0.074
Mycobacterium tuberculosis H37Rv	NC_000962	0.000	0.709	0.000
Salmonella typhimurium LT2	NC_003197	0.003	0.509	0.005
Staphylococcus aureus N315	NC_002745	0.005	0.287	0.017

---

The significance levels of the Hurst exponents for essential genes were greater than those of the corresponding full-gene-set for eight of the nine organisms studied. For example, the significance levels of E. coli strain K-12 MG1655 were <0.001 and 0.575, respectively. Similarly, the significance levels of Bacillus subtilis strain 168 were 0.004 and 0.425, respectively. These results indicate that a normal distribution exists for the Hurst exponent of the essential genes in these organisms. By contrast, in Mycoplasma genitalium strain G37 the significance levels for the essential genes were lower than for the full-gene-set, which we propose is because of the smaller genome of this organism (see Table 1).

We also observed that most of the significance levels of the Hurst exponents of the nonessential genes remained unchanged or increased slightly compared with those of the corresponding full-gene-set. For example, the significance levels of E. coli strain K-12 MG1655 remained unchanged (<0.001). Similarly, the significance levels of B. subtilis strain 168 showed a slight change from 0.004 to 0.005, indicating that a normal distribution hypothesis is refused for the Hurst exponent of the nonessential genes, contrary to the change in its essential genes. The significance levels of Acinetobacter strain ADP1 changed slightly, from 0.052 to 0.083. Although a normal distribution hypothesis is accepted in both states in this organism, the degree of significance is far lower. The results obtained with M. genitalium strain G37 did not follow the same trend, with a lower significance level being observed for its nonessential genes. Again, we propose that this is caused by the smaller size of the genome in this organism.

4. Discussion

Developments in the fields of biology and bioengineering have enabled researchers to create organisms with desired characteristics for a range of applications.¹⁷ There is now a demand for efficient software programs to accelerate this synthetic process. The basic aim of our study was to determine the common features of bacterial essential genes, to aid in the design of analysis methods and software for their identification.

We found that in most analyzed organisms the significance levels of the Hurst exponents of the essential genes were significantly higher than the corresponding full-gene-set, along with an increase in the degree of significance of the normal distribution. Correspondingly, in most analyzed organisms, the significance levels of the Hurst exponents of the nonessential genes remained unchanged or increased only slightly. In these cases, the degree of significance of the normal distribution also remained unchanged or increased only slightly. One organism that did not follow this trend was M. genitalium strain G37. We propose that the different features observed in this organism are derived from its small genome. Since the majority of free-living organisms contain much larger genomes, we suggest that the features of this organism could be used to determine the restraints of bacterial essential genes for use in pre- or post-design checking, especially in computer-aided design.

Our study represents the first stage of an investigation into the common features of essential genes and many issues remain to be resolved. For instance, the necessity of many genes remains to be determined,^18,19 and these findings may affect the results of statistical analyses. In this study, we used only nine prokaryotes from the DEG for our analysis. Further studies using a larger number of organisms, with more detailed essential gene information, are now needed to verify and improve the proposed method. In this regard, improvements in the essential gene database will aid this research further.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 61001157) and the Fundamental Research Funds for the Central Universities (Project No. CDJRC10160011).

References

1. M. K. Cho, D. Magnus and A. L. Caplan, et al., Genetics: Ethical considerations in synthesizing a minimal genome, Science, 1999, 286, 2087–2090.
2. S. A. Benner and A. M. Sismour, Synthetic biology, Nat. Rev. Genet., 2005, 6, 533–543.
3. L. Zhang, S. Chang and W. Jing, How to make a minimal genome for synthetic minimal cell, Protein Cell, 2010, 1, 427–434.
4. G. Alterovitz, T. Muso and M. F. Ramoni, The challenges of informatics in synthetic biology: from biomolecular networks to artificial organisms, Briefings Bioinf., 2010, 11, 80–95.
5. M. A. Marchisio and J. Stelling, Computational design tools for synthetic biology, Curr. Opin. Biotechnol., 2009, 20, 479–485.
6. C. A. Chatzidimitriou-Dreismann and D. Larhammar, Long-range correlations in DNA, Nature, 1993, 361, 212–213.
7. L. Q. Zhou, Z. G. Yu and J. Q. Deng, et al., A fractal method to distinguish coding and non-coding sequences in a complete genome based on a number sequence representation, J. Theor. Biol., 2005, 232, 559–567.
8. O. Clay, Standard deviations and correlations of GC levels in DNA sequences, Gene, 2001, 276, 33–38.
9. Z. G. Yu and V. Anh, Time series model based on global structure of complete genome, Chaos, Solitons Fractals, 2001, 12, 1827–1834.
10. H. Liu, Z. Liu and X. Sun, Studies of Hurst Index for Different Regions of Genes, in Bioinformatics and Biomedical Engineering, ICBBE 2007. The 1st International Conference on 2007, 2007, 238–240.
11. R. T. Boekhorst, I. Abnizova and C. Nehaniv, Discriminating coding, non-coding and regulatory regions using rescaled range and detrended fluctuation analysis, BioSystems, 2008, 91, 183–194.
12. D. Craciun, A. Isvoran and N. M. Avram, Long range correlation of hydrophilicity and flexibility along the calcium binding protein chains, Phys. A, 2009, 388, 4609–4618.
13. X. Lu, Z. R. Sun and H. M. Chen, et al., Characterizing self-similarity in bacteria DNA sequences, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 3578–3584.
14. A. Montanari, M. S. Taqqu and V. Teverovsky, Estimating long-range dependence in the presence of periodicity: An empirical study, Math. Comput. Modell., 1999, 29, 217–228.
15. R. Zhang and Y. Lin, DEG 5.0, a database of essential genes in both prokaryotes and eukaryotes, Nucleic Acids Res., 2009, 37, D455–D458.
16. G. L. Rosen, Examining Coding Structure and Redundancy in DNA, IEEE Eng. Med. Biol. Mag., 2006, 25, 62–68.
17. D. K. Ro, E. M. Paradise and M. Ouellet, et al., Production of the antimalarial drug precursor artemisinic acid in engineered yeast, Nature, 2006, 440, 940–943.
18. G. Posfai, G. Plunkett and T. Feher, et al., Emergent properties of reduced-genome Escherichia coli, Science, 2006, 312, 1044–1046.
19. J. H. Lee, B. H. Sung and M. S. Kim, et al., Metabolic engineering of a reduced-genome strain of Escherichia coli for L-threonine production, Microb. Cell Fact., 2009, 8(2).

---