Comparison of averaging techniques for the calculation of the ‘European average exposure indicator’ for particulate matter
Richard J. C.
Brown
* and
Peter T.
Woods
Analytical Science Division, National Physical Laboratory, Teddington, Middlesex TW11 0LW, UK. E-mail: richard.brown@npl.co.uk; Fax: +44 20 8614 0423; Tel: +44 20 8943 6409
First published on 18th November 2011
Abstract
A comparison of various averaging techniques to calculate the Average Exposure Indicator (AEI) specified in European Directive 2008/50/EC for particulate matter in ambient air has been performed. This was done for data from seventeen sites around the UK for which PM10 mass concentration data is available for the years 1998–2000 and 2008–2010 inclusive. The results have shown that use of the geometric mean produces significantly lower AEI values within the required three year averaging periods and slightly lower changes in the AEI value between the three year averaging periods than the use of the arithmetic mean. The use of weighted means in the calculation, using the data capture at each site as the weighting parameter, has also been tested and this is proposed as a useful way of taking account of the confidence of each data set.
Environmental impactThe Average Exposure Indicator (AEI) is an important new summary statistic in European legislation that attempts to calculate a single metric to assess the mass concentration of PM2.5 in each Member State. The legislation is not explicit as to exactly how these calculations should be performed. Therefore, the impact of this work lies in illustrating how different values for the AEI, and the change in the AEI, may be obtained depending on the averaging strategies used during calculation. This work will have major implications for Member States in Europe attempting to calculate their AEI and for the European Commission in providing guidance on this piece of legislation. The conclusions presented will help work towards comparability across Europe. |
Introduction
Pollutants in ambient air remain of concern because of their potential negative effect on human health and environmental sustainability. One of the most damaging pollutants in terms of human health is respirable particulate matter (PM) – especially particles with an aerodynamic diameter of 10 μm or less (PM10).1 Furthermore, as the understanding of how particles insult body tissues increases, attention is turning to the smaller PM size fractions (such as PM2.5), which are able to penetrate deeper into the lungs.2 As a result of these concerns there is significant national and European legislation in place to limit the exposure of citizens to this harmful PM by placing restrictions on the allowable mass concentration in ambient air of not only PM10 but also PM2.5.3 Rather than setting simple limit values which must be obtained, for example as in the case of the allowable mass concentration of lead in PM10 of 0.5 μg/m3, the requirements for PM have been made somewhat more complicated. In particular, the recent Directive 2008/50/EC on ambient air quality and clean air for Europe3 (the ‘Directive’) published by the European Commission established a ‘National Exposure Reduction Target’ for PM2.5 based on requirements to reduce PM2.5 concentrations in ambient air by 2020, according to a percentage that is dependant on their average concentration value in 2010. The quantity that is required to be reduced is the ‘Average Exposure Indicator’, and is defined in the legislation as:3“The Average Exposure Indicator expressed in μg/m3 (AEI) shall be based upon measurements in urban background locations in zones and agglomerations throughout the territory of a Member State. It should be assessed as a three-calendar year running annual mean concentration averaged over all sampling points established pursuant to Section B of Annex V [which establishes where and how many sampling sites each EU Member State should have]. The AEI for the reference year 2010 shall be the mean concentration of the years 2008, 2009 and 2010.”
The merit of the AEI is that it directs attention to overall population exposure rather than just focussing on high concentration ‘hotspots’. Indeed, action to reduce the AEI may be much more cost effective than action to eliminate high concentration hotspots where few people may be exposed. Therefore, the AEI relates to the concentration across a specified ensemble of monitoring locations (51 in the case of the UK4) over a period of three years, whilst target and limits values for particulate matter generally relate to the concentration at one site during one year. The AEI for year x is therefore the mean concentration measured during years x, (x − 1) and (x − 2). Table 1 is reproduced from the Directive3 and summarizes the requirements for exposure reduction. In addition, it is noteworthy that the ‘Exposure Concentration Obligation’ requires Member States to achieve AEIs of 20 μg/m3 by 2015. (Furthermore a limit value at each site, averaged over a calendar year, of 25 μg/m3 by 2015 and 20 μg/m3 by 2020 is also in place). These requirements are summarized graphically in Fig. 1.
| AEI in 2010/μg/m3 | Reduction target to be met by 2020 |
|---|---|
| ≤8.5 | 0% |
| >8.5 to <13 | 10% |
| ≥13 to <18 | 15% |
| ≥18 to <22 | 20% |
| ≥22 | 18 μg/m3 |
 | ||
| Fig. 1 A graphical representation of the requirements of the National Exposure Reduction Target in terms of the AEI measured in 2010 and the AEI to be achieved by 2020 (solid line). The diagonal dotted line represents the case of equal AEIs in 2010 and 2020 and thus, as indicated, the gap between this line and the solid line where positive represents the reduction in AEI required over the ten year period, and where negative represents the region where no reduction is required. The limit values (LV – relating to individual sites) and exposure concentration obligation (ECO – relating to the ensemble of AEI sites) are also indicated together with the years they must be achieved by. | ||
The subtlety in the consideration of these metrics is in exactly how they should be calculated. One issue is which sites should be chosen to perform this calculation. However, the ensemble of 51 monitoring locations that is relevant to the calculation of the AEI in the UK has already been decided,4 as per the instructions of the Directive, which required that selection of sites used to perform the AEI calculation be performed by September 2008.
This notwithstanding, there remain a number of possibilities for the calculation of the AEI itself, and these may have a significant influence on the values produced. This paper investigates these possibilities and the effect they have on the values obtained. Whilst there have been a number of studies looking at trends in PM and other pollutant concentrations in ambient air,5,6 and investigating population exposure,7 we believe this is the first specifically to address how the AEI might be calculated.
Experimental
Measurement data was obtained from Defra's UK-AIR website.8 All data was labelled as ratified and therefore it was assumed that all necessary data treatment had already occurred and any outliers had already been removed - although some negative data is still present in the data sets, the treatment of which is discussed below. To mirror the 2010 to 2020 assessment period the analogous 2000 to 2010 period was considered. There is no continuous data set available for a substantial number of sites for PM2.5 over this period, so PM10 was considered instead.Monitoring of PM10 levels in the UK has to date been largely based upon the use of tapered element oscillating microbalances (TEOM) analyzers, which can provide data with hourly resolution. A principal concern with the TEOM instrument has been that the filter is held at an elevated temperature in order to minimise errors associated with the evaporation and condensation of water vapour. However this can lead to the loss of the more volatile PM constituents and has led to the identification of differences between TEOM and manual filter-based gravimetric measurements at co-located sites. In the past, a factor of about 1.3 was applied to all TEOM-measured concentrations to estimate the gravimetric equivalent. Further studies commissioned by the UK Government to investigate these effects, and to provide a more robust relationship between the TEOM and the European manual gravimetric reference method, have led to the development of the Volatile Correction Method (VCM).9 The VCM uses measurements of volatile particulate matter made by nearby filter dynamics measurement system (FDMS) instruments to correct TEOM measurements for the loss of such volatile material. These corrected measurements have been demonstrated to be equivalent to the gravimetric reference method, and were rolled out across the UK network from 2007 onwards, and during the second AEI period considered in this paper.
There are hourly PM10 data available from 1998 to 2010 at 17 urban background sites which are also sites declared by the UK for the calculation of the AEI between 2010 and 2020. The 17 sites that have been used in this study are listed in Table 2 with the data capture achieved for the AEI calculation periods. It is acknowledged that measurement methods have changed during the 1998 to 2010 period (as discussed above); and indeed the accuracy of this PM mass concentration data is a hotly contested scientific field in its own right.10 However, we should not let this issue concern us unduly, since the aim of this work is to compare the effect of different averaging strategies on AEI values using the same data set each time, not to pronounce on the absolute magnitude of the AEIs calculated. In this respect the accuracy or otherwise of the data inputted does not affect the conclusions produced.
| Site Number | Site Name | Data capture 1998–2000 | Data capture 2008–2010 |
|---|---|---|---|
| 1 | Belfast Centre | 90.5% | 71.2% |
| 2 | Cardiff Centre | 98.0% | 71.0% |
| 3 | London Bloomsbury | 95.9% | 93.5% |
| 4 | Londonderry | 95.2% | 74.2% |
| 5 | Salford Eccles | 94.1% | 94.9% |
| 6 | Glasgow Centre | 97.2% | 62.2% |
| 7 | London North Kensington | 97.5% | 84.7% |
| 8 | Leamington Spa | 97.8% | 86.0% |
| 9 | Leeds Centre | 96.5% | 96.2% |
| 10 | Leicester Centre | 95.5% | 88.0% |
| 11 | Middlesbrough | 95.6% | 76.0% |
| 12 | Newcastle Centre | 96.9% | 93.2% |
| 13 | Nottingham Centre | 97.8% | 65.2% |
| 14 | Plymouth Centre | 95.1% | 50.2% |
| 15 | Sheffield Centre | 93.2% | 88.9% |
| 16 | Southampton Centre | 95.0% | 90.8% |
| 17 | Stoke-on-Trent Centre | 97.1% | 94.9% |
A commercially available Microsoft Excel plug-in, XLSTAT (Addinsoft), was used to generate summary statistics on the data sets. This includes descriptors such as the arithmetic mean, A, the weighted arithmetic mean, Aw, the geometric mean, G, and Pearson's median skewness coefficient, γ, where:
 | (1) |
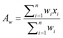 | (2) |
 | (3) |
 | (4) |
Because the calculation of the geometric mean necessitates using only positive values (as a result of the requirement to take the nth root of the product of the data), the data collected for each site has been pre-processed to remove zero or negative values. The scientific explanation for these hourly averages may be that some random noise on the signal produced by the instruments making these measurements (such as TEOMs) is expected and when this is combined with very low actual concentrations close to zero, some negative data is likely. However in some cases data up to −5 μg/m3 were observed and negative data often occurred for many hours in succession, which points to explanations other than short term noise, such as instrumental problems. Given that there is always a finite concentration of particulate matter present in ambient air, we propose that these values are best expressed in all cases as <1 μg/m3, especially when in the public domain. There is then an argument for using 1 μg/m3 to represent all these values when producing summary statistics; this would err on the side of caution and would ensure a more transparent calculation process. This notwithstanding, the removal of this data does not effect the conclusions of this paper as calculation methods are being compared and, more importantly, the proportion of zero or negative values is very low (less than 0.2% of the whole data set) and insignificant next to other forms of data loss. However, should some of the proposals in this paper get taken forward in AEI calculations a more robust method of treating and presenting negative data would have to be produced.
All data has been used, even those with data captures below those of the data quality objectives of the Directive.3 This is in part because the use of years with low data capture is an aspect of what is being tested in this paper, and partly because the Directive gives no explicit guidance as to whether years with unsatisfactory data capture are to be used in the AEI calculation, or whether data capture is to be considered over a one or a three year basis. Furthermore, we assume that data loss is random across the time periods in question, and also that because PM10 data shows less seasonal variability than other pollutants, such as PAHs,11 data losses over more lengthy periods will not affect the distribution of measured concentrations unduly.
Four different methods for calculation of the three year AEI in 2000 and 2010 at each site, j (AEI2000,jand AEI2010,j) have been considered:
I) Arithmetic mean of each individual year's data followed by an arithmetic mean of these three numbers
II) Geometric mean of each individual year's data followed by an arithmetic mean of these three numbers
III) Arithmetic mean of the entire three year data set
IV) Geometric mean of the entire three year data set
Three different methods of calculating the change in the AEI from 2000 to 2010 (ΔAEI) have then been considered:
A) Arithmetic mean over all sites to produce AEI 2000 (AEI2000) and AEI 2010 (AEI2010) and then calculation of the percentage change as: 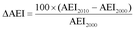
B) Calculation of the percentage change in the AEI at each site, j, as:  , followed by the arithmetic mean over all the individual site values
, followed by the arithmetic mean over all the individual site values
C) Weighted arithmetic mean over all sites, using as weights the data capture achieved by each site in each three year period, to produce AEI 2000 (AEI2000) and AEI 2010 (AEI2010) and then calculation of the percentage change as: 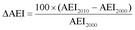
D) Calculation of the percentage change in the AEI at each site, j, as:  , followed by the weighted arithmetic mean over all the individual site values, using as weights the data capture achieved by each site across the 6 year period (as the average of the two three year periods).
, followed by the weighted arithmetic mean over all the individual site values, using as weights the data capture achieved by each site across the 6 year period (as the average of the two three year periods).
Assuming that the same combination of methods is used to calculate AEI2000 and AEI2010 this results in 16 different methods to calculate the change in the AEI from 2000 to 2010, ΔAEI.
Results and discussion
Whilst the guidance given on the AEI in the Directive apparently allows the possibility of several options for its calculation, there are certain methods that may be discounted. It is sensible that any method must utilise all the data produced, and therefore highly robust measures of the average, such as the median and the mode, which use only a very small proportion of the data produced are clearly unsatisfactory at any point in the calculation, whether within one site or across many sites. The mode has the additional problem that it will be to some extent dependent on the resolution of the data produced, and it is possible that a distribution may have more than one mode. For these additional reasons it has not been used in calculation of distribution skewness: Pearson's median skewness coefficient has been used instead.12This leaves the possibility of using weighted or un-weighted Pythagorean means. Weighted means based on weighting individual or daily data is a possibility, but in the absence of uncertainties for each data point it is difficult to produce credible weights for these data. Data capture is also an alternative weighting parameter, as shown above, but this is not possible for individual data points (whose data capture is either 0 or 100% by definition), and even for averaged daily values data capture is either 0 or 100% the vast majority of the time. Therefore we propose that if weighting of averaging methods is used it is applied using overall data capture percentages such as in methods C and D, where it may be used as a surrogate for statistical confidence in the data set.
Of the remaining available averaging techniques, we discount the quadratic mean (for evaluating changes in magnitude) and the harmonic mean (for evaluating changes in rates). This leaves the arithmetic mean and the geometric mean. The arithmetic mean is generally considered as the usual averaging technique in air quality studies, although it is likely to be disproportionately affected by outlying values. The reason for this is that most air quality data shows a log-normal distribution with a positive skew, i.e. a long tail at high concentrations.13 This is illustrated in Fig. 2. These log-normal distributions (often also referred to as skewed or skew-normal) are particularly common when mean values are low, variances large, and values cannot (theoretically) be negative14 – the characteristics exhibited by most ambient air quality data sets.
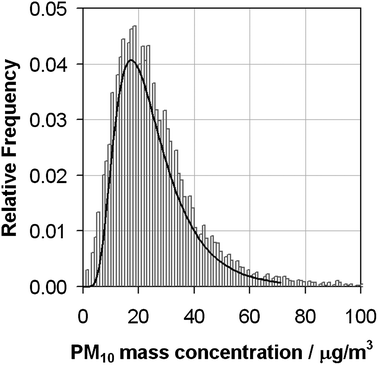 | ||
| Fig. 2 Relative frequency histogram of the measured PM10 mass concentration at the Belfast Centre monitoring site during 1999. The solid black line shows a fitted log-normal distribution. 70 of the 8434 values are in excess of 100 μg/m3. | ||
For log-normal distributions the location and scale properties of the distribution are more readily treated using the geometric mean and the geometric standard deviation.14,15 Furthermore the geometric mean is the proper mean to consider when examining proportional changes in data, which again applies to the percentage changes in AEI values being calculated here.16,17 The geometric mean is always less than or equal to the arithmetic mean. (These two means are only equal if every number in the list being averaged is the same).
The results of calculation of the three year AEI values using methods I, II, III and IV are shown in Table 3. It is clear that methods II and IV, the geometric mean methods, produce lower values of the AEI at all sites in all cases. In addition there is a significant drop in all 2010 AEI values as compared to all 2000 AEI values. This is clear from Fig. 3, which plots the data from Table 3. Indeed, method II produces results that are 17.1% lower on average than method I, and method IV produces results that are 17.4% lower on average than method III – in absolute PM10 concentration terms this relates to differences of 3.7 and 3.8 μg/m3, respectively. It is additionally clear that there is a very strong correlation between the values produced by the two geometric mean methods: the difference between methods II and IV averaged across all sites is only 0.5%. Equally there is strong correlation between the arithmetic mean methods: the difference between methods I and III averaged across all sites is only 0.2%.
| Site Number | AEI2000/μg/m3 | AEI2010/μg/m3 | ||||||
|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | I | II | III | IV | |
| 1 | 26.32 | 21.49 | 26.35 | 21.51 | 19.71 | 15.94 | 19.90 | 16.08 |
| 2 | 27.25 | 23.42 | 27.25 | 23.37 | 20.32 | 16.98 | 19.88 | 16.47 |
| 3 | 28.63 | 25.40 | 28.62 | 25.38 | 19.99 | 17.18 | 20.00 | 17.10 |
| 4 | 24.16 | 18.36 | 24.18 | 18.22 | 22.72 | 17.37 | 22.73 | 17.36 |
| 5 | 23.50 | 19.84 | 23.46 | 19.77 | 17.38 | 13.93 | 17.42 | 13.94 |
| 6 | 25.83 | 20.52 | 25.82 | 20.50 | 22.37 | 17.23 | 21.97 | 17.02 |
| 7 | 26.30 | 23.13 | 26.30 | 23.13 | 20.44 | 17.61 | 20.35 | 17.47 |
| 8 | 21.95 | 18.87 | 21.95 | 18.84 | 19.80 | 16.82 | 19.89 | 16.92 |
| 9 | 25.80 | 21.50 | 25.80 | 21.44 | 20.84 | 17.32 | 20.83 | 17.29 |
| 10 | 20.51 | 17.33 | 20.49 | 17.13 | 17.12 | 14.11 | 17.03 | 13.99 |
| 11 | 21.43 | 17.06 | 21.43 | 17.06 | 17.30 | 13.78 | 17.18 | 13.64 |
| 12 | 20.71 | 17.80 | 20.69 | 17.64 | 15.80 | 13.08 | 15.74 | 13.02 |
| 13 | 25.48 | 21.88 | 25.48 | 21.85 | 19.89 | 16.72 | 20.28 | 16.95 |
| 14 | 21.41 | 17.04 | 21.42 | 17.03 | 16.31 | 13.19 | 15.66 | 12.43 |
| 15 | 26.83 | 22.27 | 26.67 | 22.12 | 21.45 | 17.61 | 21.56 | 17.69 |
| 16 | 25.53 | 22.09 | 25.54 | 22.05 | 18.91 | 15.94 | 18.97 | 15.96 |
| 17 | 23.32 | 19.09 | 23.33 | 18.99 | 20.13 | 16.79 | 20.12 | 16.68 |
 | ||
| Fig. 3 The values of AEI2000 and AEI2010 calculated for each site using methods I, II, III and IV as indicated by the key, in decreasing order of the values of AEI2000 obtained using method I. Values obtained for methods III and IV have been offset by −0.25 μg/m3 for clarity. | ||
The difference between methods III and I and between methods IV and II is one of weighting. Methods I and II give each year equal weight in the AEI calculation regardless of their data capture, whereas methods III and IV give each data point equal weight and therefore this weights the AEI produced using the data capture in each year. If data capture is very similar across the three years under consideration there will be no significant difference between the results from methods III and I and from methods IV and II. Equally if there is no significant difference in the distribution of values across the years being considered then methods III and I and methods IV and II will produce similar results, regardless of data capture. However, if there are significant data capture differences between the years being considered and the distribution of values varies over these years then methods III and I and methods IV and II will produce noticeably different results: e.g.AEI 2010 for sites 2 and 14.
Fig. 4 displays the strong relationship between the arithmetic and geometric means calculated using methods I, II, II and IV. This shows a best-fit relationship of G = 0.83A. The average three year G/A ratio has shown a very slight decrease from 0.83 in 1998–2000 to 0.82 in 2008–2010. This may be as a result of a slight increase in the skewness of data over this period. Fig. 5 investigates this further by examining the relationship between the ratio of G/A and the skewness of the distribution of values in the data set. One might expect a priori that as the ratio of G/A increases the distribution skewness would decrease. This is because as skewness decreases we would expect the distribution of values to move from log-normal toward normal and as a result the arithmetic mean is less affected by the tail at high concentration and will move towards the geometric mean. However, the observed relationship is weak – this may be because the dynamic range of G/A values is rather narrow as a result of the relationship between the two quantities being so strong. There may also be additional variables imposing an influence, such as changes in the kurtosis of the distributions, which are beyond the scope of this paper. What is clearer from Fig. 5, in agreement with the conclusions of Fig. 4, is that the skewness of measured data appears to have increased over the assessment period. Considering the arithmetic mean and the standard error of the mean of the skewnesses values calculated for the three year data sets at each site the 1998–2000 value is 0.63 ± 0.02 whereas the 2008–2010 value is 0.74 ± 0.02. However, it may be that changes in measuring equipment, data processing and outlier removal have more to do with this observation than any changes in the UK pollution climate.
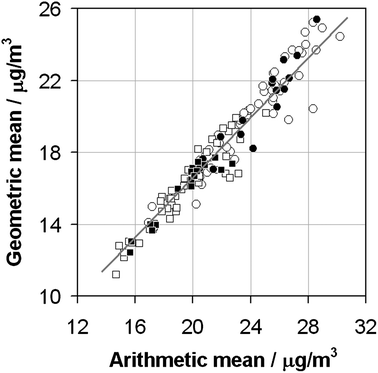 | ||
| Fig. 4 The relationship between arithmetic means and geometric means produced yearly using methods I and II (without the subsequent three year averaging) for 1998, 1999 and 2000 (open circles), and for 2008, 2009 and 2010 (open squares); and the three year means produced using methods III and IV for 1998–2000 (filled circles) and 2008–2010 (filled squares). The grey line represents the best linear fit to this data constrained through the origin and has a gradient of 0.83. | ||
 | ||
| Fig. 5 The relationship between the geometric mean to arithmetic mean ratio (G/A) and the Pearson median skewness (γ), produced yearly using methods I and II (without the subsequent three year averaging) for 1998, 1999 and 2000 (open circles), and for 2008, 2009 and 2010 (open squares); and the three year means produced using methods III and IV for 1998–2000 (filled circles) and 2008–2010 (filled squares). | ||
The overall UK AEI2000, AEI2010 and ΔAEI values produced using the various calculation methods are presented in Table 4. Because methods B and D produce ΔAEI for each site prior to producing a global average across all sites, these methods do not produce explicit AEI values for each three year period, hence the data missing from Table 4. In this case, in order to calculate AEI2000 to determine the ten year reduction target, it would first be necessary to refer back to methods A and C. This may be an issue in proposing the use of these techniques for reporting to the European Commission in support of legislation because of a lack of methodological consistency. To give an indication of the individual ΔAEI values at each site, produced using the methods B and D, these are displayed in Fig. 6. It is clear from Fig. 6 that there is a large range of ΔAEI values, from about −30% to −5%. However all results represent clear and significant reductions, especially since the average standard error of the mean (SEM) for the arithmetic mean calculations is less than 0.7% (relative) of the calculated values across the data set. In general, the largest reductions in AEI are observed for methods using the geometric mean, although sometimes this difference is small (for instance, site 9).
| Method | AEI2000/μg/m3 | AEI2010/μg/m3 | ΔAEI/% | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | I | II | III | IV | I | II | III | IV | |
| A | 24.41 | 20.42 | 24.40 | 20.35 | 19.44 | 15.98 | 19.38 | 15.88 | −20.4 | −21.8 | −20.6 | −22.0 |
| B | — | — | — | — | — | — | — | — | −20.1 | −21.3 | −20.4 | −21.6 |
| C | 24.41 | 20.42 | 24.40 | 20.36 | 19.42 | 16.00 | 19.38 | 15.93 | −20.4 | −21.6 | −20.5 | −21.8 |
| D | — | — | — | — | — | — | — | — | −20.2 | −21.4 | −20.4 | −21.5 |
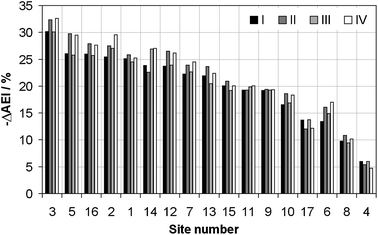 | ||
| Fig. 6 The percentage reduction in AEI from 2000 to 2010, calculated using methods I, II, II and IV as indicated in the key, for each of the sites considered in this study, ranked in decreasing order of the values obtaining using method I. | ||
The reductions in AEI observed in Table 4 decrease in the order IV > II > III > I, and in the order A > C > D > B. Hence the largest reductions are produced by the geometric mean techniques by an average of 1.2% points. The ΔAEI calculation techniques A and C, which produce UK wide AEIs, produce very slightly greater reductions (0.2% points) than methods B and D which calculate reductions at each site first. No difference at the one part in a thousand level is observed between techniques using weighting according to data capture (methods C and D) and those that do not use weighting (methods A and B). Whilst weighting according to data capture has not had a significant effect on the ΔAEI calculation presented here, presumably because of a relatively narrow spread in both AEIs and data captures and their random distributions with respect to each other, it remains a useful method to give more weight to data sets in which one has more confidence, i.e. those with high data capture.
The most significant output of Table 4 is the effect on meeting the requirements of the legislation as laid out in Table 1. Whilst recognizing that the legislation refers to PM2.5 and not PM10, and were the exercise to have been performed for PM2.5 the absolute values would be universally lower, if the situation set out in this paper was transposed into the 2010 to 2020 assessment:
• If the UK had used methods AI, AIII, CI or CIII to calculate the AEI, the 2010 AEI result would have fallen into the bracket of ≥22 μg/m3, in which case the target for reduction would have been 18 μg/m3 and the UK would have failed to meet its obligation.
• If, however, were the UK to have used methods AII, AIV, CII or CIV, the 2010 AEI result would have fallen into the ≥18 to <22 μg/m3 bracket and the requirement for AEI reduction would have been 20% which would have been met with an average of 1.8% points below the required level.
• Furthermore, if we increase the legislative limits in Table 1 by an empirically observed PM10/PM2.5 mass concentration ratio in the UK of approximately 1.6 18 to better match the data obtained by this study, this assessment may be repeated. In this case had the UK used methods AI, AIII, CI or CIII to calculate the AEI, the initial 2010 AEI result would have fallen into the recalculated ≥20.8 to <28.8 μg/m3 bracket in which case the target for reduction would have been 15%, which would have been met reasonably comfortably. Were to the UK to have used methods AII, AIV, CII or CIV, the initial 2010 AEI result would have fallen into the recalculated ≥13.6 to <20.8 μg/m3 bracket and the requirement for AEI reduction would have been 10%, which would have been met by an even greater margin.
Conclusions
It has been shown that calculation of the AEI and ΔAEI may be performed in several ways within the procedures given in the Directive, which are not explicit. The effect of these different calculation methods has been applied to PM10 mass concentration data at 17 UK urban background sites, which are also part of the UK's ensemble of sites for the 2010 to 2020 assessment. The potential effect of compliance with legislation has also been demonstrated.It is possible that methods that do not involve the direct calculation of a three year AEI – such as methods B and D – may be more difficult to implement in the context of the legislation, although they still calculate ΔAEI acceptably. Further, we propose that weighting according to data capture is a sensible and pragmatic mechanism as it, in effect, takes account of the confidence associated with a data set. Although it has not been seen to have much effect in this study, it may be relevant if sites with very low data capture are to be included in the AEI calculation (since this is not clear from the legislation).
This leaves the preferred calculation methods as CIII or CIV, with the remaining difference between these methods being the use of the arithmetic mean and geometric mean respectively. The geometric mean has the advantage of producing significantly lower AEI values and slightly lower ΔAEI values than the arithmetic mean. It is also the more mathematically correct function for calculating summary statistics from log-normal distributions and when considering proportional changes in data sets. The only disadvantage of the geometric mean is that it requires the removal of zero or negative data prior to use. However, as stated above, the value of such data in ratified data sets available to the public is questionable, and if such data were reported as <1 μg/m3 and assumed to be 1 μg/m3 for the purpose of calculation this problem is solved. However, use of the arithmetic mean is historically considerably more common in air quality studies and so it is likely that CIII would prove the most universally acceptable method.
The greatest barrier to the more widespread use of the geometric mean in air quality studies would seem to be the deeply ingrained usage of the arithmetic mean in formulating legislation and producing summary statistics in support of legislation. Given that the effect on human health is the most important feature of air quality monitoring, we should perhaps consider instead which averaging technique best represents human exposure to PM in the context of the epidemiological evidence suggesting how PM exposure affects health.19 That is to say, is relevant human exposure best represented by cumulative exposure over long periods, in which case the arithmetic mean is more suitable, or is exposure to high concentration events of more importance, in which case the geometric mean is the better metric. Moving further down this line of argument one may even wish to consider weighting AEIs determined at each site by the population of the city or conurbation that the site in question is representative of.20
Acknowledgements
The UK Government Department for Business Innovation and Skills' funding of the National Measurement System's Chemistry and Biology Knowledge Base Programme is gratefully acknowledged.References
- B. Brunekreef and S. T. Holgate, Lancet, 2002, 360, 1233–42 CrossRef CAS.
- A. D. Kappos, P. Bruckmann, T. Eikmann, N. Englert, U. Heinrich, P. Höppe, E. Koch, G. H. M. Krause, W. G. Kreyling, K. Rauchfuss, P. Rombouti, V. Schulz-Klemp, W. R. Thiel and H. Erich Wichmann, Int. J. Hyg. Environ. Health, 2004, 207, 399–407 CrossRef CAS.
- European Commission, Directive 2008/50/EC of the European Parliament and of the Council of 21 May 2008, Off. J. Eur. Union, 2008, L152, pp. 1–44 Search PubMed. On ambient air quality and cleaner air for Europe.
- Report AEAT/ENV/R/2837, QA/QC Procedures for the UK Automatic Urban and Rural Air Quality Monitoring Network (AURN), AEA, Harwell, 2009 Search PubMed.
- I. Barmpadimos, C. Hueglin, J. Kellel, S. Henne and A. S. H. Prévôt, Atmos. Chem. Phys., 2011, 11, 1813–1835 CrossRef CAS.
- R. J. C. Brown, J. Environ. Monit., 2010, 12, 665–671 RSC.
- B. Denby, M. Cassiani, P. de Smet, F. de Leeuw and J. Horalek, Atmos. Environ., 2011, 45, 4220–4229 CrossRef CAS.
- UK-AIR website, http://uk-air.defra.gov.uk/ (assessed September 2011).
- Volatile Correction Model, http://www.volatile-correction-model.info/ (assessed September 2011).
- D. C. Green, G. W. Fuller and T. Baker, Atmos. Environ., 2009, 43, 2132–2141 CrossRef CAS.
- A. S. Brown and R. J. C. Brown, Chemosphere, 2011 Search PubMed , submitted.
- J. F. Kenney, E. S. Keeping, Mathematics of Statistics Part 1, Princeton, USA, 3rd ed., 1962 Search PubMed.
- S. Bartoletti and N. Loperfido, Stochastic Environ. Res. Risk Assess., 2009, 24, 513–517 Search PubMed.
- E. Limpert, W. A. Stahel and M. Abbt, BioScience, 2001, 51, 341–352 CrossRef.
- F. Tomei, S. Ghittori, M. Imbriani, S. Pavanello, A. Carere, F. Marcon, A. Martini, T. P. Baccolo, E. Tomao, A. Zijno and R. Crebelli, Occup. Med., 2001, 51, 198–203 CrossRef CAS.
- D. W. Mitchell, Math. Gaz., 2004, 88, 42–144 Search PubMed.
- P. J. Fleming and J. J. Wallace, Commun. ACM, 1986, 29, 218–221 CrossRef.
- Y.-J. Liu and R. M. Harrison, Atmos. Environ., 2011, 45, 3267–3276 CrossRef CAS.
- R. I. Larsen, W. F. McDonnell, D. H. Horstman and L. J. Folinsbee, J. Air Waste Manage. Assoc., 1991, 41, 455–459 CAS.
- D. Ivy, J. A. Mulholland and A. G. Russell, J. Air Waste Manage. Assoc., 2008, 58, 711–720 CAS.
| This journal is © The Royal Society of Chemistry 2012 |
