A potassium-promoted Mo carbide catalyst system for hydrocarbon synthesis
Received
6th June 2012
, Accepted 7th August 2012
First published on 9th August 2012
Abstract
Potassium-promoted Mo carbide catalysts prepared by temperature-programmed carburization with H2–C3H8 have been evaluated for Fischer–Tropsch synthesis (FTS). Temperature-programmed carburization of MoO3–Al2O3 with a mixture of H2–C3H8 was a two-stage conversion involving the transformation of Mo oxide to the final carbide phase via an intermediate oxycarbide phase. Compensation effect and isokinetic relationship were observed for both oxycarbide and carbide phase formation suggesting that a similar topotactic mechanism was involved in the solid phase transformation. CO seemed to adsorb more strongly than H2 as implicated by its higher heat of desorption and site concentration. Both acid and basic centres were detected on the Mo carbide surface. The K-promoter increased site concentration for both weak and strong basic sites. The relationship between FT activity and K loading paralleled the trend in CO2 heat of desorption with K addition. FT activity attained a maximum at about 3%K loading. CO hydrogenation over the Mo carbide catalyst was most suitably described by an enolic intermediate mechanism. A generalized kinetic model was derived for predicting the reaction rate for individual hydrocarbons as a function of chain growth propagation and olefin-to-paraffin ratio.
Introduction
Following the original report by Levy and Boudart on the Pt-like characteristics of the Mo carbide catalyst,1 it has been considered a promising catalyst for the Fischer–Tropsch synthesis (FTS) of higher hydrocarbons.2,3 Other studies have shown that MoC1−x (0 ≤ x < 1) exhibited high olefin selectivity, carbon and sulphur resilience.4,5 This makes it an attractive catalyst for natural gas conversion to clean fuels since most gas fields contain sulphur compounds.
The common method for synthesizing Mo carbide with high surface area is temperature-programmed carburization between MoO3 and H2–CH4 at temperature greater than 1073 K. The physicochemical properties and catalytic performance of metal carbide are however influenced by the type of carburizing agent and conditions.6 The utilization of higher alkanes (C2+) as a carbon source has been shown to reduce the carburization temperature and improve the surface area7 albeit with a potential for high carbon deposition. H2–C3H8 was first used to synthesize an Al2O3-supported Mo carbide catalyst with a surface area of 92–204 m2 gcat−1 from a metal sulphide precursor with an optimum of H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3H8 = 5
C3H8 = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for negligible surface carbon resilience on the catalyst.8 Conventional FT catalysts are generally promoted by alkali addition. Thus, the possible substitution of expensive Pt noble metal with Mo carbide in FT catalysis may also benefit from similar promotion. Therefore, in this study, the effect of K loading (1–5 wt%) on supported Mo carbide prepared by temperature-programmed carburization using the H2–C3H8 mixture has been investigated. Specifically, the objective of this paper was to seek the correlation between K loading and the physicochemical properties as well as FT reaction metrics.
1 for negligible surface carbon resilience on the catalyst.8 Conventional FT catalysts are generally promoted by alkali addition. Thus, the possible substitution of expensive Pt noble metal with Mo carbide in FT catalysis may also benefit from similar promotion. Therefore, in this study, the effect of K loading (1–5 wt%) on supported Mo carbide prepared by temperature-programmed carburization using the H2–C3H8 mixture has been investigated. Specifically, the objective of this paper was to seek the correlation between K loading and the physicochemical properties as well as FT reaction metrics.
Experimental
10%MoC1−x/Al2O3 catalysts promoted with different levels of K (1–5 wt%) were prepared by a co-impregnation method. Calculated amounts of aqueous (NH4)6Mo7O24·4H2O and K2CO3 solution precursor were mixed with γ-Al2O3 (pre-treated at 973 K in air with 5 K min−1 for 6 h to ensure thermal stability) and stirred for 3 h. The resulting slurry was subsequently dried in an oven for 16 h at 403 K. Temperature-programmed carburization between the alumina-supported MoO3 and a mixture of H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3H8 = 5
C3H8 = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 50 mL min−1 was carried out in a computer-controlled fixed-bed microreactor at 973 K using a heating rate of 10 K min−1 for 2 h. FT evaluation was performed in situ in the same reactor by switching to a H2
1 at 50 mL min−1 was carried out in a computer-controlled fixed-bed microreactor at 973 K using a heating rate of 10 K min−1 for 2 h. FT evaluation was performed in situ in the same reactor by switching to a H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO feed mixture (7 different ratios) at 453–473 K and atmospheric pressure. A mean catalyst particle size of 100 μm and gas hourly space velocity (GHSV) of 10 L gcat−1 h−1 were used for all FT runs to ensure negligible internal and external transport resistances. Reproducibility check carried out for selected runs indicated an experimental error for rate measurement of between 2.4% and 5.1% depending on the carbon chain length.
CO feed mixture (7 different ratios) at 453–473 K and atmospheric pressure. A mean catalyst particle size of 100 μm and gas hourly space velocity (GHSV) of 10 L gcat−1 h−1 were used for all FT runs to ensure negligible internal and external transport resistances. Reproducibility check carried out for selected runs indicated an experimental error for rate measurement of between 2.4% and 5.1% depending on the carbon chain length.
The catalyst surface area, pore volume and pore diameter were measured on a Quantachrome Autosorb-1 unit with nitrogen physisorption at 77 K. A ThermoCahn TGA 2121 unit was used to carry out temperature-programmed carburization of Mo oxide with a gas containing 5H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1C3H8 from 303 to 973 K with 4 different heating rates (5–20 K min−1). Temperature programmed desorption runs were performed on a Micromeritics 2910 AutoChem to quantify heat of desorption, site concentration for acid (NH3-TPD), and basic sites (CO2-TPD) as well as reaction sites (CO-TPD, and H2-TPD). The catalyst sample was exposed to a flow of 10%NH3, 10%CO2, 10%CO, and 10%H2 diluted in an inert gas, respectively, for 1 h followed by controlled heating to 973 K with different ramping rates (5–30 K min−1). X-Ray diffraction measurement was carried out on a Philips X'pert Pro MPD system utilizing Ni-filtered Cu Kα with λ = 1.542 Å operating at 45 kV and 40 mA.
1C3H8 from 303 to 973 K with 4 different heating rates (5–20 K min−1). Temperature programmed desorption runs were performed on a Micromeritics 2910 AutoChem to quantify heat of desorption, site concentration for acid (NH3-TPD), and basic sites (CO2-TPD) as well as reaction sites (CO-TPD, and H2-TPD). The catalyst sample was exposed to a flow of 10%NH3, 10%CO2, 10%CO, and 10%H2 diluted in an inert gas, respectively, for 1 h followed by controlled heating to 973 K with different ramping rates (5–30 K min−1). X-Ray diffraction measurement was carried out on a Philips X'pert Pro MPD system utilizing Ni-filtered Cu Kα with λ = 1.542 Å operating at 45 kV and 40 mA.
Results and discussion
X-Ray diffraction measurement
Fig. 1 shows the XRD patterns of both undoped and K-promoted Mo carbide catalysts. The Joint Committee on Powder Diffraction Standards (JCPDS) database was used for analysing X-ray diffractograms.9 The high intensity peaks located at 45.7° and 66.7° may be attributed to the γ-Al2O3 support. It is evident that both face-centred cubic (FCC) α-MoC1−x (2θ = 36.6° and 61.3° for [111] and [220] respectively) and hexagonal closed packed (HCP) β-MoC1−x (34.0° and 39.5°) were formed in both K-free and K-modified Mo carbide catalysts. As seen in the 2%K–10%MoC1−x/Al2O3 pattern (b), the peak located at 19.5° was ascribed to the formation of KAl5O8 (or K2O·5Al2O3) while carbon deposition on the catalyst surface was observed at 2θ = 26.6°. Absence of peaks for MoO3 (2θ = 23.40°, 25.50° and 26.75°) in the carbide catalysts indicates that Mo oxide was completely converted to the carbide phase during carburization.
 |
| | Fig. 1 XRD patterns of (a) K-free and (b) K-promoted Mo carbide catalysts synthesized with H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3H8 = 5 C3H8 = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. 1. | |
Thermogravimetric studies
The profile for the temperature-programmed carburization of Mo oxide is illustrated in Fig. 2a. Two discernible peaks, P1 (at 650–700 K) and P2 (at a high temperature of 800–850 K), were ascribed to the formation of oxycarbide and carbide phases respectively.10,11 As seen in Fig. 2b, the peak temperature increased linearly with the heating rate. Thus, activation energy, Ea, and pre-exponential factor, A, for the production of oxycarbide and carbide may be computed from the Kissinger equation:12| |  | (1) |
where β, TP, and R are heating rate, peak temperature and universal gas constant respectively.
 |
| | Fig. 2 Temperature-programmed carburization of 1%K–10%MoC1−x/Al2O3 catalyst. | |
As seen in Table 1, activation energy values for transformation from MoO3 to oxycarbide were generally lower than those for the formation of carbide from the oxycarbide phase regardless of the K-promotion or the level of K-loading. Interestingly, activation energy and pre-exponential factor of both oxycarbide and carbide forms may be fitted to the expression given by eqn (2) (with R2 of 0.995) implicating the existence of a ‘compensation effect’ (cf.Fig. 3) where a and b are model parameters estimated as 1.76 × 10−4 and −1.32 (for oxycarbide), and 1.75 × 10−4 and −5.52 (for the carbide phase) respectively.
 |
| | Fig. 3 Evidence for the existence of a compensation effect. | |
The existence of a compensation effect and isokinetic relationship has been investigated in other studies to justify a common reaction mechanism for either a series of reactions over a specific catalyst or a particular reaction over a group of catalysts.13–15 Although the linear relationship between ln Aj and Eaj implicates a compensation effect, it does not necessarily guarantee the occurrence of an isokinetic phenomenon. The requirement for the existence of an isokinetic relationship may be derived from the criterion recommended by Liu and Guo15 as
| |  | (3) |
with
h and
kB being Planck and Boltzmann constant, respectively, while Δ
G≠j is the Gibbs free energy for the associated transition state complex during the carburization reaction. An isoequilibrium relationship exists if the plots of Δ
G≠jvs. T for all catalysts have a common point of intersection. As seen in
Fig. 4, there is a feasible isokinetic temperature,
Tiso, of about 685 K for both oxycarbide and carbide phases. The existence of compensation effect and isoequilibrium relationship with similar
Tiso suggests that the conversion from Mo oxide to oxycarbide and oxycarbide to carbide species was governed by a similar topotactic mechanism (substitutionary exchange of oxygen atoms in the MoO
3 lattice by carbon with negligible structural changes).
 |
| | Fig. 4 Evidence for the existence of an isokinetic relationship for both oxycarbide and carbide phases. | |
Table 1 Estimates of Ea and A for the formation of oxycarbide and carbide phases
| Catalysts |
Oxycarbide (P1) |
Carbide (P2) |
| Activation energy, Ea/kJ mol−1 |
Pre-exponential factor, A/s−1 |
Activation energy, Ea/kJ mol−1 |
Pre-exponential factor, A/s−1 |
| 10%MoC1−x/Al2O3 |
92.39 |
4.75 × 106 |
176.56 |
1.09 × 1011 |
| 1%K–10%MoC1−x/Al2O3 |
76.86 |
2.69 × 105 |
152.88 |
1.57 × 109 |
| 2%K–10%MoC1−x/Al2O3 |
111.98 |
7.63 × 107 |
128.55 |
2.49 × 107 |
| 3%K–10%MoC1−x/Al2O3 |
117.51 |
3.36 × 108 |
120.95 |
9.18 × 106 |
| 4%K–10%MoC1−x/Al2O3 |
91.61 |
2.19 × 106 |
108.16 |
4.83 × 105 |
| 5%K–10%MoC1−x/Al2O3 |
83.98 |
4.79 × 105 |
101.29 |
2.18 × 105 |
Fig. 5 shows that the activation energy for the carbide formation decreased rapidly with increased K loading in a hyperbolic approaching an asymptotic value at high K content probably due to the similarities between the solid properties of the high K content on Mo carbide and that of bulk K2O. The decrease in activation energy is indicative of the more facile Mo–carbon bond formation due to the higher electron density from the K dopant. Thus, the activation energy profile shown in Fig. 5 may be expressed by
| | 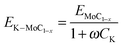 | (4) |
where
EK–MoC1−x and
EMoC1−x are activation energy for K-promoted and K-free Mo carbide catalysts respectively.
ω is the activation energy reduction coefficient estimated as 15.53 ± 0.07 while
CK is the potassium loading.
 |
| | Fig. 5 Influence of potassium loading on the carbide formation rate. | |
This observation is supported by the exponential rise in the carbide formation rate with K-loading seen in the same plot and appeared to hold at all heating rates used. However, the enhancement in the carbide rate cannot be indefinite since at a critical K loading, the catalyst properties would be nearly identical to the bulk of K2O and hence the carbide formation rate will level off. The carbide formation rate may be expressed by the empirical equation
where
rCarb,K and
rCarb,0 are the carbide formation rate of K-promoted and unpromoted MoC
1−x catalysts respectively.
λ is an enhancement factor for Mo carbide formation and is a function of the heating rate. There is a linear relationship between
λ and heating rate,
β, given by
eqn (6):
with
λ0 and
φ being associated model parameters estimated as 54.49 ± 0.38 and −1.14 ± 0.01, respectively. Hence,
eqn (5) may be rearranged as
| | | rCarb,K = rCarb,0eλ0CKeφβCK | (7) |
Physicochemical properties
As seen in Table 2, the BET area for the promoted Mo carbide catalysts ranges between 171 and 194 m2 gcat−1. Additionally, the unpromoted catalyst has a higher BET surface area, average pore volume, and average pore diameter than K-promoted Mo carbide catalysts. The surface area of Mo carbide decreased with increased K loading. However, the relatively small variation of BET area among the promoted catalysts suggests that the level of K addition is well below that for monolayer coverage and hence the K2O–MoC1−x crystallites are most likely well dispersed.
Table 2 Physical properties of Mo carbide catalysts
| Catalyst |
Average BET surface area/m2 g−1 |
Average pore volume/cm3 g−1 |
Average pore diameter/nm |
| Pure Al2O3 |
179.3 |
0.68 |
15.2 |
| 10%MoC1−x/Al2O3 |
194.0 |
0.73 |
15.0 |
| 1%K–10%MoC1−x/Al2O3 |
185.0 |
0.52 |
11.2 |
| 2%K–10%MoC1−x/Al2O3 |
184.3 |
0.64 |
13.8 |
| 3%K–10%MoC1−x/Al2O3 |
179.3 |
0.66 |
14.8 |
| 4%K–10%MoC1−x/Al2O3 |
175.22 |
0.61 |
14.8 |
| 5%K–10%MoC1−x/Al2O3 |
171.4 |
0.62 |
14.5 |
Temperature-programmed desorption runs for MoC1−x catalysts are shown in Fig. 6. The existence of both weak (P1 at 370–400 K) and strong (P2 at 580–600 K) basic centres on the surface of Mo carbide catalysts (cf.Fig. 6a) is evident. Indeed, as seen in Fig. 6b, the weak (510–540 K) and strong (690–720 K) acid sites were also detected from NH3-TPD profiles. However, the pure calcined Al2O3 support also possessed the weak acid centre suggesting that the strong acid site was formed during Mo carbide production, or in the Mo carbide phase.
 |
| | Fig. 6 Temperature-programmed desorption profiles for Mo carbide catalysts. (a) CO2-TPD, (b) NH3-TPD, (c) CO-TPD, (d) H2-TPD. | |
The nature of CO and H2 adsorption sites was also determined as shown in Fig. 6c and d. Interestingly, the CO desorption temperature window is almost identical to that for peak P2 during CO2 desorption (cf.Fig. 6a) suggesting that CO during the FT reaction was most likely adsorbed on a strong basic site. In particular, since the CO desorption temperature range (580–610 K) seen in Fig. 6c is higher than the FTS reaction window (453–523 K), this would suggest relatively high surface molecular CO coverage during the FT reaction. The H2-TPD spectrum shown in Fig. 6d, however, shows that relatively little H2 coverage (if any) would be present on the catalyst surface during CO hydrogenation.
Indeed, site characteristics are determined by these probe molecules using eqn (8):
| |  | (8) |
with
Edi and
Ai being heat of desorption (kJ mol
−1) and site concentration for species i, respectively (
cf.Tables 3 and 4), while
C is the instrument calibration constant.
Table 3 Basic and acid character of 3%K–10%MoC1−x/Al2O3 catalyst
| |
A
NH3 (mol NH3 gcat−1 × 105) |
E
NH3/kJ mol−1 |
A
CO2 (mol CO2 gcat−1 × 105) |
E
CO2/kJ mol−1 |
Temperature range/K |
| Weak acid site |
3.76 |
51.22 |
— |
— |
510–540 |
| Strong acid site |
6.21 |
60.88 |
— |
— |
690–720 |
| Weak basic site |
— |
— |
6.65 |
85.21 |
370–400 |
| Strong basic site |
— |
— |
9.56 |
143.87 |
580–610 |
Table 4 Physicochemical properties of active sites on 3%K–10%MoC1−x/Al2O3 catalyst for CO and H2 adsorption
| |
A
CO (mol CO gcat−1 × 105) |
E
CO/kJ mol−1 |
A
H2 (mol H2 gcat−1 × 105) |
E
H2/kJ mol−1 |
Temperature range/K |
| CO-TPD |
5.45 |
80.49 |
— |
— |
580–610 |
| H2-TPD |
— |
— |
1.52 |
26.22 |
500–610 |
Fig. 7a shows that basic site concentration, ACO2, increased with K loading while heat of desorption for basic sites (weak, EdW-Basic or strong, EdS-Basic) exhibited optimal values at between 2 and 3%K loading. The enhancement of CO2 adsorption with K loading may be ascribed to electron donation from K dopant to surface MoC1−x thus facilitating CO2 molecular chemisorption.16 In contrast, as seen in Fig. 7b, both acid site concentration (weak, AW-Acid and strong, AS-Acid acid sites) and heat of desorption for a strong acid centre, EdS-Acid, dropped exponentially with K content. The heat of desorption and site concentration for both acid and basic centres of the pure calcined Al2O3 support were also estimated as seen in Table 5. NH3 uptake on the weak acid site for the support seemed to be superior to that of doped and undoped catalysts while the difference in heat of desorption between support and catalysts was quite small. The formation of the Mo carbide phase enhanced the strength of the strong basic site (EdS-Basic > 57.42 kJ mol−1).
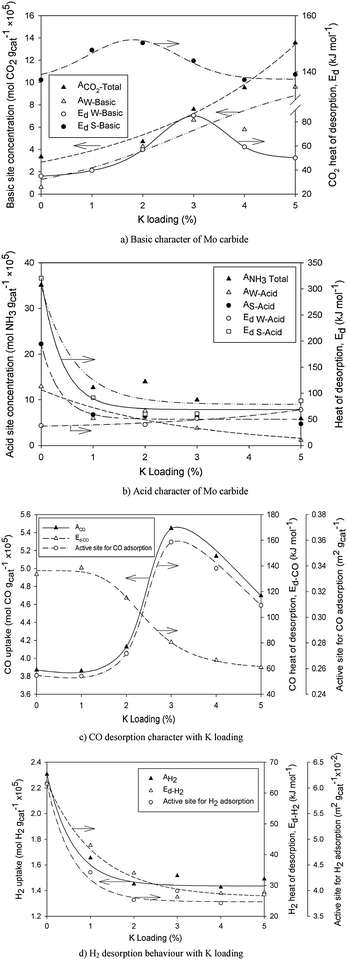 |
| | Fig. 7 Effect of K loading on basic, acid and reaction sites for Mo carbide catalysts. | |
Table 5 Physicochemical properties of pure calcined Al2O3 support
| |
Adsorbed NH3, ANH3 (mol NH3 gcat−1 × 105) |
Heat of desorption, Ed for NH3/kJ mol−1 |
Adsorbed CO2, ACO2 (mol CO2 gcat−1 × 105) |
Heat of desorption, Ed for CO2/kJ mol−1 |
| Pure calcined |
P1 |
P2 |
P1 |
P2 |
P1 |
P2 |
P1 |
P2 |
| Al2O3 support |
18.8 |
— |
50.00 |
— |
2.64 |
1.63 |
50.00 |
57.42 |
Fig. 7c shows that the CO uptake, ACO, increased with K loading consistent with the results for CO2-TPD. The higher electron density in the K-promoted catalyst means that the back donation of electrons from the CO molecule into the MoC1−x is reduced thus increasing molecular rather than dissociative CO adsorption. Therefore, the formation of oxygenated intermediate species during FTS will be more likely. In fact, the production of alcohols over K-promoted MoC1−x has been reported in the literature.17,18 Furthermore, CO heat of desorption appeared to decline with increased K loading and may be captured by the empirical relation;
| |  | (9) |
where
EdCO and
EdCO0 are CO heat of desorption for K-promoted and unpromoted catalysts, respectively, while
σ and
ψ are associated model parameters estimated as 2.02 ± 0.04 and 25.1 ± 0.51 in that order.
As seen in Fig. 7d, site concentration for H2 adsorption reduced with promoter modification and levelled off at about 3%K loading, almost parallel to the behaviour with respect to acid character (cf.Fig. 7b). It would appear that the rich electron environment provided by the K-promoter is detrimental to H2 chemisorption because it reduced the heat of desorption and adsorption site concentration. It may therefore be inferred that H2 probably adsorbed on an acidic site (both weak and strong).
Interestingly, a similar trend (hyperbolic decay) for both acid site and H2 active site characters with respect to potassium loading may be seen in Fig. 7b and d. The influence of K loading on the properties of acid site and H2-TPD attributes may be adequately captured by;
| | 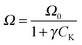 | (10) |
where
Ω is catalyst property (acid site, H
2 active site concentration or heat of desorption of these sites), while
Ω0 is catalytic attribute of the K-free Mo carbide catalyst and
γ is an electron density-related coefficient estimated in
Table 6.
Table 6 Estimated model parameters for eqn (10)
| |
H2 uptake, AH2 (mol H2 gcat−1) |
H2 heat of desorption, Ed-H2/kJ mol−1 |
Total NH3 uptake, ANH3 (mol NH3 gcat−1) |
Weak acid site concentration, AW-Acid (mol NH3 gcat−1) |
Strong acid site concentration, AS-Acid (mol NH3 gcat−1) |
Heat of desorption for strong acid site, ES-Acid/kJ mol−1 |
|
Ω
0
|
2.28 × 10−5 |
61.76 |
3.46 × 10−4 |
1.28 × 10−4 |
2.19 × 10−4 |
317.8 |
|
γ
|
0.14 |
0.36 |
1.06 |
0.76 |
0.14 |
1.82 |
Fischer–Tropsch performance evaluation
Influence of feed composition.
The performance of the Mo carbide catalysts for FTS was evaluated at 473 K with 7 different H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratios as seen in Fig. 8a. The CO consumption rate increased with the H2 mole fraction, yH2, and attained an optimum at 0.67 ≤ yH2 ≤ 0.75 which is somewhat lower than that for common FT catalysts (Co and Fe) where the maximum activity is often found in the region 0.8 < yH2 < 0.9.19 It would seem that the surface active site for hydrocarbon synthesis was the oxycarbide type centre, which is formed in situ by an initial molecular CO adsorption.20,21 In particular, since the reaction temperature window was within the H2 desorption temperature range, there was probably little or no surface H adatoms and formation of any surface hydrocarbon precursor species would most likely be due to H2 gas phase attack of the molecularly adsorbed CO.
CO ratios as seen in Fig. 8a. The CO consumption rate increased with the H2 mole fraction, yH2, and attained an optimum at 0.67 ≤ yH2 ≤ 0.75 which is somewhat lower than that for common FT catalysts (Co and Fe) where the maximum activity is often found in the region 0.8 < yH2 < 0.9.19 It would seem that the surface active site for hydrocarbon synthesis was the oxycarbide type centre, which is formed in situ by an initial molecular CO adsorption.20,21 In particular, since the reaction temperature window was within the H2 desorption temperature range, there was probably little or no surface H adatoms and formation of any surface hydrocarbon precursor species would most likely be due to H2 gas phase attack of the molecularly adsorbed CO.
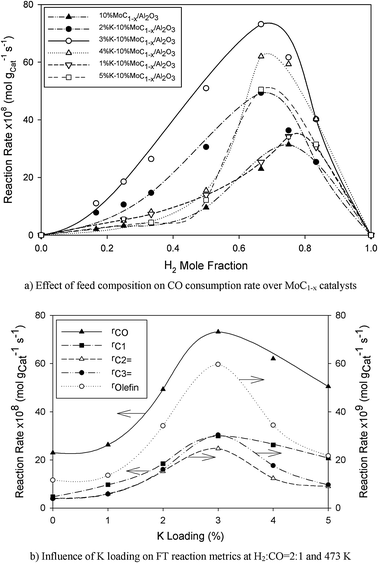 |
| | Fig. 8 FT activity of alumina-supported Mo carbide catalysts. | |
As seen in Fig. 8b, the reaction rate profile has a maximum at 3%K loading beyond which the FTS activity dropped. It is apparent that the FT reaction curve in Fig. 8b and the CO uptake-vs.-K loading behaviour (cf.Fig. 7c) as well as the profile describing the CO2 heat of desorption with respect to K loading (cf.Fig. 7a) are all parallel implicating a correlation between the catalyst activity and the physicochemical attributes (CO uptake and the basic site strength on the catalyst). Specially, the relation may be captured by;
| | 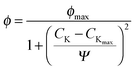 | (11) |
where
ϖ is the FT activity (or CO uptake or basic site strength) and
Ψ is the enhancement factor of the promoter on the catalyst attributes while
ϖmax is the maximum value of the particular attribute at the optimal K loading,
CKmax. Estimated model parameters are summarized in
Table 7.
Table 7 Computed model parameters for eqn (11)
| |
Methane formation rate, rC1/mol gcat−1 s−1 |
CO reaction rate, rCO/mol gcat−1 s−1 |
Olefin formation rate, rOlefin/mol gcat−1 s−1 |
Heat of desorption for weak basic site, EW-Basic/kJ mol−1 |
Heat of desorption for strong basic site, ES-Basic/kJ mol−1 |
CO uptake, ACO (mol CO gcat−1) |
|
ϕ
max
|
3.47 × 10−7 |
7.82 × 10−7 |
5.86 × 10−8 |
82.67 |
149.60 |
5.40 × 10−5 |
|
C
Kmax
|
3.64 |
3.54 |
3.05 |
3.27 |
1.93 |
3.06 |
|
Ψ
|
1.66 |
1.99 |
1.26 |
2.25 |
6.58 |
4.87 |
The 3%K–10%MoC1−x/Al2O3 catalyst seemed to be the optimal catalyst in terms of FT activity and olefin formation rate. However, the reaction rate decreased beyond 3%K loading probably due to weak CO adsorption and reduced surface concentration suggesting that a balance between excessive electron density and high electron-deficiency is required to obtain “best” FT activity. Fig. 9 shows the effect of CO uptake on FT activity over the Mo carbide catalyst. The hydrocarbon production rate increased with CO adsorption. However, the plot possesses a positive intercept suggesting that CO hydrogenation over Mo carbide catalysts requires an initial CO uptake, which is responsible for the formation of an active oxycarbide phase from the Mo carbide form. Generally, product distribution in FT synthesis is governed by a polymerization scheme. It is assessed from a fit of hydrocarbon formation rate data to the Anderson–Schulz–Flory model22 given as
| | | rn = kASF (1 − α)2αn−1 | (12) |
where
α is the chain growth probability whilst
rn is the hydrocarbon formation rate with carbon number,
n, and
kASF is the Anderson–Schulz–Flory constant.
Fig. 10 shows that the chain growth probability varied with the H
2 mole fraction and attained an optimal value at
yH2 between 0.25 and 0.5 depending on K loading. The optimum
α-values for the K-doped catalyst were greater than the pure MoC
1−x catalyst but occurred at a feed composition much lower
yH2. The decrease in
α at
yH2 higher than the optimum is indicative of a higher termination rate compared to the propagation rate. As seen in
Fig. 11, the chain growth factor increased with K loading and exhibited a maximum at around 3–4% depending on feed composition. The chain growth probability of K-promoted Mo carbide catalysts is lower than that of conventional FT catalysts (
i.e. Fe- and Co-based catalysts) with values of 0.8–0.9.
22 In fact, MoC
1−x catalysts were also reported to possess a low chain growth factor of less than about 0.41 in other studies.
23,24 In comparison with the literature, K addition improved the
α value of the Mo carbide catalyst by up to 52% even though FTS runs were carried out at atmospheric pressure in this study.
 |
| | Fig. 9 Effect of CO uptake on the FT reaction rate over Mo carbide catalysts. | |
 |
| | Fig. 10 Influence of H2 mole fraction on chain growth probability. | |
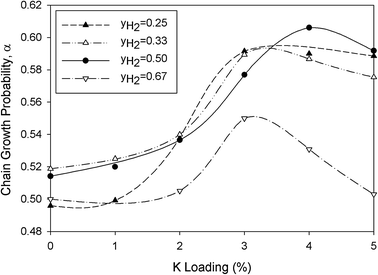 |
| | Fig. 11 Effect of promoter loading on chain growth probability at 473 K. | |
Table 8 shows the FT activity and selectivity for the K-promoted 10%MoC1−x/Al2O3 catalyst system at 473 K and H2–CO = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. CO conversion varied from 4.8% (unpromoted catalyst) to 12.7% (3%–10%MoC1−x/Al2O3 catalyst). High molecular weight hydrocarbon selectivity, C5+, improved with K loading and peaked at 3 wt% K whilst CH4 selectivity decreased with K addition (from 0–3 wt%) but increased up to 71% at high promoter loading. The C5+ and CH4 selectivity versus K-loading profiles are in agreement with the chain growth factor vs. promoter loading behaviour (cf.Fig. 11). Although the K promoter enhanced the olefin formation rate as seen in Fig. 8b, the unpromoted Mo carbide catalyst appeared to be the optimal catalyst in terms of olefin selectivity. As may be seen in Table 9, CO consumption rates over K-promoted Mo carbide catalysts seemed to be comparable with the performance using conventional FT catalysts suggesting that it could be a replacement for the expensive noble metal catalysts (Pt- and Ru-based systems).
1. CO conversion varied from 4.8% (unpromoted catalyst) to 12.7% (3%–10%MoC1−x/Al2O3 catalyst). High molecular weight hydrocarbon selectivity, C5+, improved with K loading and peaked at 3 wt% K whilst CH4 selectivity decreased with K addition (from 0–3 wt%) but increased up to 71% at high promoter loading. The C5+ and CH4 selectivity versus K-loading profiles are in agreement with the chain growth factor vs. promoter loading behaviour (cf.Fig. 11). Although the K promoter enhanced the olefin formation rate as seen in Fig. 8b, the unpromoted Mo carbide catalyst appeared to be the optimal catalyst in terms of olefin selectivity. As may be seen in Table 9, CO consumption rates over K-promoted Mo carbide catalysts seemed to be comparable with the performance using conventional FT catalysts suggesting that it could be a replacement for the expensive noble metal catalysts (Pt- and Ru-based systems).
Table 8 Fischer–Tropsch synthesis performance over K-promoted Mo carbide catalysts at 473 K and H2–CO = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1
| Catalyst |
CO conversion (%) |
FT product selectivity (%) |
| CH4 |
Olefin (C2+) |
Paraffin (C2+) |
C5+ |
| 10%MoC1−x/Al2O3 |
4.76 |
69.52 |
18.55 |
9.67 |
2.35 |
| 1%K–10%MoC1−x/Al2O3 |
5.44 |
69.33 |
9.21 |
16.21 |
2.97 |
| 2%K–10%MoC1−x/Al2O3 |
8.54 |
67.14 |
11.81 |
16.12 |
3.48 |
| 3%K–10%MoC1−x/Al2O3 |
12.66 |
66.73 |
13.27 |
15.91 |
3.61 |
| 4%K–10%MoC1−x/Al2O3 |
10.73 |
70.76 |
17.68 |
9.38 |
3.53 |
| 5%K–10%MoC1−x/Al2O3 |
8.74 |
71.22 |
7.50 |
16.53 |
3.43 |
Table 9 Summary of Fischer–Tropsch activity over conventional catalysts at H2–CO = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1
| Catalyst |
Reaction conditions |
CO consumption rate × 107 mol−1 gcat−1 s−1 |
Ref. |
| Temperature/K |
Pressure/atm |
| 0.2%Ru–33.5%Co/ZrO2–SiO2 |
463 K |
8.8 atm |
7.17 |
25
|
| 1.5%K–3.5%Cu–69%Fe/Al2O3 |
523 K |
31 atm |
6.67 |
26
|
| 20%Co/Al2O3 |
493 K |
20 atm |
9.30 |
27
|
| 10%Co–10%Mo/Al2O3 |
493 K |
20 atm |
0.96 |
27
|
| Ru-promoted 33.5%Co/ZrO2–Aerosil |
463 K |
6 atm |
3.72 |
28
|
| 4%K–6%Co–1%Mo/SiO2 |
523 K |
1 atm |
0.78 |
4
|
| 4%K–6%Co/SiO2 |
523 K |
1 atm |
2.39 |
4
|
| 1%K–Fe2O3 |
523 K |
8 atm |
3.00 |
29
|
| 2%K–10%MoC1−x/Al2O3 |
473 K |
1 atm |
4.93 |
This work |
| 3%K–10%MoC1−x/Al2O3 |
473 K |
1 atm |
7.32 |
This work |
| 4%K–10%MoC1−x/Al2O3 |
473 K |
1 atm |
6.20 |
This work |
Effect of reaction temperature.
Since 3%K–10%MoC1−x/Al2O3 exhibited highest CO and olefin reaction rate, it was utilized as a catalyst for additional FT runs over the range 453–473 K. Fig. 12 shows the rate profiles at three temperatures. It is evident that the optimal feed composition at yH2 = 0.67 was unchanged with reaction temperature and CO consumption rate improved with increasing reaction temperature. Interestingly, the chain growth probability also increased with temperature from 1.6% to 18.3% depending on feed composition. However, the α value may decrease at critical temperature due to an increase in the termination rate of surface olefinic species to paraffins and decreasing re-adsorptivity of α-olefins for chain propagation.30,31
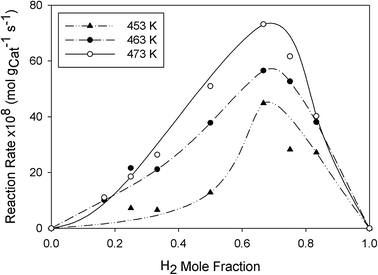 |
| | Fig. 12 Effect of reaction temperature on the CO reaction rate over 3%K–10%MoC1−x/Al2O3 catalyst. | |
From CO-TPD and H2-TPD experiments, it is apparent that CO has a higher heat of desorption than H2 and indeed, greater site concentration. Thus, CO will have a higher surface coverage than H2 during FTS and most likely molecularly adsorbed. Moreover, the desorption peak for H2 was located well within the temperature range for FTS (>453 K) suggesting that there would be little if any H2 on the catalyst surface during the reaction. This implies that gas phase H2 attack of the adsorbed CO molecule would be the preferred route for the formation of surface oxygenated species. In fact, St. Clair et al.32 have observed that H2 did not chemisorb on Mo carbide in the presence of CO. Furthermore, alcohols have been produced over the Mo carbide catalyst confirming the presence of precursor surface oxygenated species. Even so, Vo and Adesina21 have developed several models derived from both enolic and carbide mechanisms in which either associatively or dissociatively adsorbed CO reacts with (molecularly or dissociatively chemisorbed) H2 or in the gas phase for capturing the formation rate of individual hydrocarbons. They found that hydrocarbon synthesis over the Mo carbide system may be best represented as;
| |  | (13) |
| |  | (14) |
| | 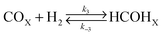 | (15) |
| |  | (16) |
or
| | | HCOHX + H2 → CH3OH + X (for alcohol formation) | (17) |
Chain growth propagation step;
| |  | (18) |
| |  | (19) |
| |  | (20) |
| |  | (21) |
where
R and
R′ are alkyl groups with
R possessing one carbon atom more than
R′. X is the active site formed
in situ by CO chemisorption on the surface of MoC
1−x catalyst. From
eqn (13), (14) and (15), we obtain
where
K1 =
k1/
k−1;
K2 =
k2/
k−2; and
K3 =
k3/
k−3.
θi is the fractional surface coverage for species i whilst
θ0 is the initial fractional vacancy on the MoC
1−x and
θ is the fractional active site formed
in situ by coordinative bonding of CO to a vacant Mo site.
For the methane production, eqn (16) may be assumed as an irreversible rate-controlling step, thus;
| | 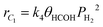 | (25) |
which after the formal procedure yields;
| |  | (26) |
with
Ka =
K1K2,
Kb =
K1K2K3, and
krxn =
k4Kb. The experimental data were then fitted to the methanation model. The estimated adsorption equilibrium constants,
Ki, and the methane reaction rate constant,
k4, are summarised in
Table 10. As seen in the parity plot (
cf.Fig. 13), there is a good correlation between experimental data at all temperatures and the proposed Eley–Rideal model.
Table 10 Computed model parameters for methanation reaction over 3%K–MoC1−x/Al2O3 catalyst
| Model parameters |
453 K |
463 K |
473 K |
BMV criteria |
|
K
1 (atm−1) |
0.83 |
0.62 |
0.50 |
|
K
2 (atm−1) |
10.52 |
5.14 |
4.01 |
|
K
3 (atm−1) |
1.27 |
1.90 |
2.18 |
|
k
4 (×107 mol gcat−1 s−1 atm−2) |
10.9 |
26.5 |
32.6 |
| ΔH1 (cal mol−1) |
−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814.90 814.90 |
Satisfied |
| ΔS1 (cal mol−1 K−1) |
−24.26 |
| ΔH2 (cal mol−1) |
−20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 579.50 579.50 |
Satisfied |
| ΔS2 (cal mol−1 K−1) |
−40.90 |
 |
| | Fig. 13 Parity plot for the methanation reaction model over 3%K–10%MoC1−x/Al2O3 catalyst. | |
The thermodynamic consistency of parameter estimates was also further checked against the Boudart–Mears–Vannice (BMV) criteria33 provided by eqn (27) and (28).
| | | 10 ≤ −ΔSi ≤ 12.2 − 0.0014 ΔHi | (28) |
where Δ
Sig is the entropy of CO in the gas phase, 47.3 (cal mol
−1 K
−1), whilst Δ
Hi and Δ
Si are experimental enthalpy (cal mol
−1) and entropy changes (cal mol
−1 K
−1), respectively, estimated from;
| | 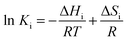 | (29) |
As seen in Table 10, the computed ΔHi and ΔSi values satisfied the BMV criteria. The activation energy (cf.Fig. 14) for production of CH4 and the HCOH building unit were also estimated as 97.81 and 48.26 (kJ mol−1), respectively, with the associated pre-exponential factor, A, of 2.31 × 105 and 4.86 × 105 (mol gcat−1 s−1).
 |
| | Fig. 14 Estimated activation energy for formation of CH4 and HCOH species. | |
From eqn (20) and (21), the production rate for olefin, rCnolefin, and paraffin, rCnparaffin, may be given as
| | | rCnolefin = ktoPH2θRCH2COH | (30) |
| |  | (31) |
where
kto and
ktp are termination rate constants to olefin and paraffin respectively. Thus, the termination rate,
rt, for a hydrocarbon with chain length,
n, may be obtained as;
| | | rt = rCn = rCnolefin + rCnparaffin = (kto + ktpPH2)PH2θRCH2COH | (32) |
Additionally, combining eqn (30) and (31), the olefin-to-paraffin ratio, ROP, may be derived as
| | 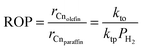 | (33) |
As seen in Fig. 15, the olefin-to-paraffin ratio for each carbon number increased linearly with decreasing H2 partial pressure in agreement with eqn (33).
 |
| | Fig. 15 Effect of H2 partial pressure on olefin-to-paraffin ratio for each hydrocarbon at 463 K. | |
Since HCOH species are the monomeric units for chain growth propagation, the relationship between θRCH2COH and θHCOH may be written as;
Substituting eqn (33) and (34) into eqn (32), the reaction rate for individual hydrocarbon, rCn, may be given as
| | 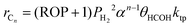 | (35) |
From eqn (25) and (35), the hydrocarbon synthesis rate for a given chain length, n, may be expressed as a function of olefin-to-paraffin ratio and chain growth probability;
| | | rCn = (ROP + 1)αn−1koxyrC1 | (36) |
where
koxy =
ktpk4−1.
Fig. 16 shows that the proposed reaction model gave a reasonable fit to the experimental data. Moreover, combining
eqn (25), (30) and (34), the olefin reaction rate,
rCnolefin, may be obtained as
| | 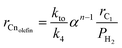 | (37) |
Experimental data were fitted to eqn (37) to estimate ktok4−1 at different reaction temperatures using Polymath 6.0 software for nonlinear regression. Since the activation energy for methane has been previously determined to be 97.8 (kJ mol−1), the intrinsic activation energy values for termination to olefins, Eto, and paraffins, Etp, may be computed individually as 141.4 and 166.2 (kJ mol−1), respectively, with the corresponding pre-exponential factor of 9.01 × 109 and 18.92 × 1010 (mol gcat−1 s−1). Given that the value of Eto is less than Etp, it is apparent that olefin is the primary hydrocarbon product for FTS over the Mo carbide catalyst. Furthermore, the lower value for CH4 activation energy compared to olefins and paraffins explains why the higher production rate of CH4 during FTS is due to kinetic control although thermodynamically higher hydrocarbons (olefins and paraffins) are more favourable.
 |
| | Fig. 16 Estimated koxy parameter for eqn (36) over 3%K–10%MoC1−x/Al2O3 catalyst. | |
Thus, by combining eqn (26) and (36), the FT reaction rate over the Mo carbide catalyst for individual hydrocarbon species with different feed compositions may be given as
| | 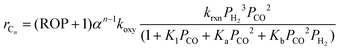 | (38) |
This equation may therefore be used for the kinetic evaluation of any hydrocarbons during FTS.
Conclusions
The promotional effect of K-addition to an alumina-supported MoC1−x catalyst during CO hydrogenation has been investigated. The Mo carbide catalyst was prepared via thermocarburization of MoO3 using a 5H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1C3H8 feed mixture with heating rates of 5–20 K min−1. Solid-state TGA indicated that the Mo oxide conversion proceeded via a 2-stage process involving the intermediate oxycarbide and a final carbide (MoC1−x) phase. K-addition influenced both the physicochemical properties (BET area, acid–base character, H2 and CO-TPD, and XRD measurements). FTS performance evaluation at various temperatures and feed composition (H2
1C3H8 feed mixture with heating rates of 5–20 K min−1. Solid-state TGA indicated that the Mo oxide conversion proceeded via a 2-stage process involving the intermediate oxycarbide and a final carbide (MoC1−x) phase. K-addition influenced both the physicochemical properties (BET area, acid–base character, H2 and CO-TPD, and XRD measurements). FTS performance evaluation at various temperatures and feed composition (H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratio) revealed that the optimum effect for nearly all reaction metrics (activity and olefin selectivity) occurred at about 3 wt% K loading. Reaction rate data supported the proposition of an Eley–Rideal type mechanism in which the hydrocarbon rate-controlling step was the reaction between surface CO and gas phase H2.
CO ratio) revealed that the optimum effect for nearly all reaction metrics (activity and olefin selectivity) occurred at about 3 wt% K loading. Reaction rate data supported the proposition of an Eley–Rideal type mechanism in which the hydrocarbon rate-controlling step was the reaction between surface CO and gas phase H2.
Acknowledgements
Thanks are due to Australian Research Council (ARC) for supporting the research programme in the Reactor Engineering & Technology Group, UNSW, through a Discovery Grant.
References
- R. L. Levy and M. Boudart, Science, 1973, 181, 547–549 CAS.
- G. S. Ranhotra, A. T. Bell and J. A. Reimer, J. Catal., 1987, 108, 40–49 CrossRef CAS.
- L. Zhao, F. Sotoodeh and K. J. Smith, Catal. Commun., 2010, 11, 391–395 CrossRef CAS.
- H. Chen and A. A. Adesina, Appl. Catal., A, 1994, 112, 87–103 CrossRef CAS.
- E. Furimsky, Appl. Catal., A, 2003, 240, 1–28 CrossRef CAS.
- T. Xiao, A. P. E. York, K. S. Coleman, J. B. Claridge, J. Sloan, J. Charnock and M. L. H. Green, J. Mater. Chem., 2001, 11, 3094–3098 RSC.
- T. Xiao, A. P. E. York, V. C. Williams, H. Al-Megren, A. Hanif, X. Zhou and M. L. H. Green, Chem. Mater., 2000, 12, 3896–3905 CrossRef CAS.
- T. H. Nguyen, T. V. Nguyen, Y. J. Lee, T. Safinski and A. A. Adesina, Mater. Res. Bull., 2005, 40, 149–157 CrossRef CAS.
- JCPDS Powder Diffraction File, International Centre for Diffraction Data, Swarthmore, PA, 2000.
- D.-V. N. Vo and A. A. Adesina, Fuel Process. Technol., 2011, 92, 1249–1260 CrossRef CAS.
-
D.-V. N. Vo and A. A. Adesina, in Synthetic liquids production and refining, ACS Symposium Series, ed. A. de Klerk and D. L. King, American Chemical Society, 2011, ch. 7, pp. 155–184 Search PubMed.
- H. E. Kissinger, Anal. Chem., 1957, 29, 1702–1706 CrossRef CAS.
- G. C. Bond, Catal. Today, 1999, 49, 41–48 CrossRef CAS.
- J. Zhang, H. Xu and W. Li, Appl. Catal., A, 2005, 296, 257–267 CrossRef CAS.
- L. Liu and Q.-X. Guo, Chem. Rev., 2001, 101, 673–696 CrossRef CAS.
- F. Solymosi and L. Bugyi, Catal. Lett., 2000, 66, 227–230 CrossRef CAS.
- J. S. Lee, S. Kim and Y. G. Kim, Top. Catal., 1995, 2, 127–140 CrossRef CAS.
- M. Xiang, D. Li, H. Qi, W. Li, B. Zhong and Y. Sun, Fuel, 2007, 86, 1298–1303 CrossRef CAS.
- A. A. Adesina, R. R. Hudgins and P. L. Silveston, Can. J. Chem. Eng., 1986, 64, 447–454 CrossRef CAS.
- C. Phamhuu, M. J. Ledoux and J. Guille, J. Catal., 1993, 143, 249–261 CrossRef CAS.
- D.-V. N. Vo and A. A. Adesina, Appl. Catal., A, 2011, 399, 221–232 CrossRef CAS.
-
R. B. Anderson, The Fischer–Tropsch Synthesis, Academic Press, New York, 1984 Search PubMed.
- H. Shou, D. Ferrari, D. G. Barton, C. W. Jones and R. J. Davis, ACS Catal., 2012, 2, 1408–1416 CrossRef CAS.
- A. Griboval-Constant, J.-M. Giraudon, G. Leclercq and L. Leclercq, Appl. Catal., A, 2004, 260, 35–45 CrossRef CAS.
- H. Schulz and M. Claeys, Appl. Catal., A, 1999, 186, 91–107 CrossRef CAS.
- E. V. Steen and H. Schulz, Appl. Catal., A, 1999, 186, 309–320 CrossRef.
- C. G. Cooper, T. H. Nguyen, Y. J. Lee, K. M. Hardiman, T. Safinski, F. P. Lucien and A. A. Adesina, Catal. Today, 2008, 131, 255–261 CrossRef CAS.
- H. Schulz and M. Claeys, Appl. Catal., A, 1999, 186, 71–90 CrossRef CAS.
- R. A. Dictor and A. T. Bell, J. Catal., 1986, 97, 121–136 CrossRef CAS.
- G. P. Van der Laan and A. A. C. M. Beenackers, Catal. Rev. Sci. Eng., 1999, 41, 255–318 CAS.
- D.-V. N. Vo, T.-H. Nguyen, E. M. Kennedy, B. Z. Dlugogorski and A. A. Adesina, Catal. Today, 2011, 175, 450–459 CrossRef CAS.
- T. P. St. Clair, S. T. Oyama and D. F. Cox, Surf. Sci., 2000, 468, 62–76 CrossRef CAS.
- M. Boudart, D. E. Mears and M. A. Vannice, Ind. Chim. Belge., 1967, 32, 281 CAS.
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3H8 = 5
C3H8 = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for negligible surface carbon resilience on the catalyst.8 Conventional FT catalysts are generally promoted by alkali addition. Thus, the possible substitution of expensive Pt noble metal with Mo carbide in FT catalysis may also benefit from similar promotion. Therefore, in this study, the effect of K loading (1–5 wt%) on supported Mo carbide prepared by temperature-programmed carburization using the H2–C3H8 mixture has been investigated. Specifically, the objective of this paper was to seek the correlation between K loading and the physicochemical properties as well as FT reaction metrics.
1 for negligible surface carbon resilience on the catalyst.8 Conventional FT catalysts are generally promoted by alkali addition. Thus, the possible substitution of expensive Pt noble metal with Mo carbide in FT catalysis may also benefit from similar promotion. Therefore, in this study, the effect of K loading (1–5 wt%) on supported Mo carbide prepared by temperature-programmed carburization using the H2–C3H8 mixture has been investigated. Specifically, the objective of this paper was to seek the correlation between K loading and the physicochemical properties as well as FT reaction metrics.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3H8 = 5
C3H8 = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 50 mL min−1 was carried out in a computer-controlled fixed-bed microreactor at 973 K using a heating rate of 10 K min−1 for 2 h. FT evaluation was performed in situ in the same reactor by switching to a H2
1 at 50 mL min−1 was carried out in a computer-controlled fixed-bed microreactor at 973 K using a heating rate of 10 K min−1 for 2 h. FT evaluation was performed in situ in the same reactor by switching to a H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO feed mixture (7 different ratios) at 453–473 K and atmospheric pressure. A mean catalyst particle size of 100 μm and gas hourly space velocity (GHSV) of 10 L gcat−1 h−1 were used for all FT runs to ensure negligible internal and external transport resistances. Reproducibility check carried out for selected runs indicated an experimental error for rate measurement of between 2.4% and 5.1% depending on the carbon chain length.
CO feed mixture (7 different ratios) at 453–473 K and atmospheric pressure. A mean catalyst particle size of 100 μm and gas hourly space velocity (GHSV) of 10 L gcat−1 h−1 were used for all FT runs to ensure negligible internal and external transport resistances. Reproducibility check carried out for selected runs indicated an experimental error for rate measurement of between 2.4% and 5.1% depending on the carbon chain length.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1C3H8 from 303 to 973 K with 4 different heating rates (5–20 K min−1). Temperature programmed desorption runs were performed on a Micromeritics 2910 AutoChem to quantify heat of desorption, site concentration for acid (NH3-TPD), and basic sites (CO2-TPD) as well as reaction sites (CO-TPD, and H2-TPD). The catalyst sample was exposed to a flow of 10%NH3, 10%CO2, 10%CO, and 10%H2 diluted in an inert gas, respectively, for 1 h followed by controlled heating to 973 K with different ramping rates (5–30 K min−1). X-Ray diffraction measurement was carried out on a Philips X'pert Pro MPD system utilizing Ni-filtered Cu Kα with λ = 1.542 Å operating at 45 kV and 40 mA.
1C3H8 from 303 to 973 K with 4 different heating rates (5–20 K min−1). Temperature programmed desorption runs were performed on a Micromeritics 2910 AutoChem to quantify heat of desorption, site concentration for acid (NH3-TPD), and basic sites (CO2-TPD) as well as reaction sites (CO-TPD, and H2-TPD). The catalyst sample was exposed to a flow of 10%NH3, 10%CO2, 10%CO, and 10%H2 diluted in an inert gas, respectively, for 1 h followed by controlled heating to 973 K with different ramping rates (5–30 K min−1). X-Ray diffraction measurement was carried out on a Philips X'pert Pro MPD system utilizing Ni-filtered Cu Kα with λ = 1.542 Å operating at 45 kV and 40 mA.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3H8 = 5
C3H8 = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.




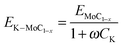





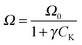
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratios as seen in Fig. 8a. The CO consumption rate increased with the H2 mole fraction, yH2, and attained an optimum at 0.67 ≤ yH2 ≤ 0.75 which is somewhat lower than that for common FT catalysts (Co and Fe) where the maximum activity is often found in the region 0.8 < yH2 < 0.9.19 It would seem that the surface active site for hydrocarbon synthesis was the oxycarbide type centre, which is formed in situ by an initial molecular CO adsorption.20,21 In particular, since the reaction temperature window was within the H2 desorption temperature range, there was probably little or no surface H adatoms and formation of any surface hydrocarbon precursor species would most likely be due to H2 gas phase attack of the molecularly adsorbed CO.
CO ratios as seen in Fig. 8a. The CO consumption rate increased with the H2 mole fraction, yH2, and attained an optimum at 0.67 ≤ yH2 ≤ 0.75 which is somewhat lower than that for common FT catalysts (Co and Fe) where the maximum activity is often found in the region 0.8 < yH2 < 0.9.19 It would seem that the surface active site for hydrocarbon synthesis was the oxycarbide type centre, which is formed in situ by an initial molecular CO adsorption.20,21 In particular, since the reaction temperature window was within the H2 desorption temperature range, there was probably little or no surface H adatoms and formation of any surface hydrocarbon precursor species would most likely be due to H2 gas phase attack of the molecularly adsorbed CO.

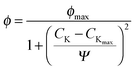



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. CO conversion varied from 4.8% (unpromoted catalyst) to 12.7% (3%–10%MoC1−x/Al2O3 catalyst). High molecular weight hydrocarbon selectivity, C5+, improved with K loading and peaked at 3 wt% K whilst CH4 selectivity decreased with K addition (from 0–3 wt%) but increased up to 71% at high promoter loading. The C5+ and CH4 selectivity versus K-loading profiles are in agreement with the chain growth factor vs. promoter loading behaviour (cf.Fig. 11). Although the K promoter enhanced the olefin formation rate as seen in Fig. 8b, the unpromoted Mo carbide catalyst appeared to be the optimal catalyst in terms of olefin selectivity. As may be seen in Table 9, CO consumption rates over K-promoted Mo carbide catalysts seemed to be comparable with the performance using conventional FT catalysts suggesting that it could be a replacement for the expensive noble metal catalysts (Pt- and Ru-based systems).
1. CO conversion varied from 4.8% (unpromoted catalyst) to 12.7% (3%–10%MoC1−x/Al2O3 catalyst). High molecular weight hydrocarbon selectivity, C5+, improved with K loading and peaked at 3 wt% K whilst CH4 selectivity decreased with K addition (from 0–3 wt%) but increased up to 71% at high promoter loading. The C5+ and CH4 selectivity versus K-loading profiles are in agreement with the chain growth factor vs. promoter loading behaviour (cf.Fig. 11). Although the K promoter enhanced the olefin formation rate as seen in Fig. 8b, the unpromoted Mo carbide catalyst appeared to be the optimal catalyst in terms of olefin selectivity. As may be seen in Table 9, CO consumption rates over K-promoted Mo carbide catalysts seemed to be comparable with the performance using conventional FT catalysts suggesting that it could be a replacement for the expensive noble metal catalysts (Pt- and Ru-based systems).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1









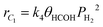

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814.90
814.90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 579.50
579.50
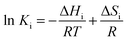




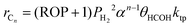
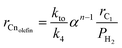

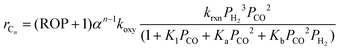
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1C3H8 feed mixture with heating rates of 5–20 K min−1. Solid-state TGA indicated that the Mo oxide conversion proceeded via a 2-stage process involving the intermediate oxycarbide and a final carbide (MoC1−x) phase. K-addition influenced both the physicochemical properties (BET area, acid–base character, H2 and CO-TPD, and XRD measurements). FTS performance evaluation at various temperatures and feed composition (H2
1C3H8 feed mixture with heating rates of 5–20 K min−1. Solid-state TGA indicated that the Mo oxide conversion proceeded via a 2-stage process involving the intermediate oxycarbide and a final carbide (MoC1−x) phase. K-addition influenced both the physicochemical properties (BET area, acid–base character, H2 and CO-TPD, and XRD measurements). FTS performance evaluation at various temperatures and feed composition (H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratio) revealed that the optimum effect for nearly all reaction metrics (activity and olefin selectivity) occurred at about 3 wt% K loading. Reaction rate data supported the proposition of an Eley–Rideal type mechanism in which the hydrocarbon rate-controlling step was the reaction between surface CO and gas phase H2.
CO ratio) revealed that the optimum effect for nearly all reaction metrics (activity and olefin selectivity) occurred at about 3 wt% K loading. Reaction rate data supported the proposition of an Eley–Rideal type mechanism in which the hydrocarbon rate-controlling step was the reaction between surface CO and gas phase H2.
