TAP studies on 2% Ag/γ–Al₂O₃ catalyst for selective reduction of oxygen in a H₂-rich ethylene feed

Abstract

Catalysts currently employed for the polymerization of ethylene have previously been found to deactivate in the presence of oxygen. It is, therefore, important that oxygen is removed from the ethylene feedstock prior to the polymerization. The Ag/γ–Al₂O₃ catalyst exhibits excellent activity and selectivity toward oxygen reduction with hydrogen in the presence of ethylene. TAP vacuum pulse experiments have been utilised to understand the catalytic behaviour of the Ag/γ–Al₂O₃ catalyst. TAP multi-pulse experiments have determined the types of active sites that are found on the Ag/γ–Al₂O₃ catalyst, and the intrinsic activity of these sites. The lifetime of the reactive adsorbed oxygen intermediate has also been determined through TAP consecutive pulse experiments. Multi-pulse and consecutive pulse data have been combined with ethylene adsorption/desorption rate constants to provide an overview of the Ag/γ–Al₂O₃ catalyst system.

---

Introduction

The use of molecular oxygen as an oxidising agent for the production of syngas, alkenes and other hydrocarbons from various feed stocks has become a topic of considerable interest in recent years.¹ One disadvantage is that it may not be possible to wholly exclude the presence of molecular oxygen in the product stream. While oxygen traps or distillation techniques can be used whenever the concentration of oxygen is small, and if there is a high concentration of hydrogen available, it may be more practical to reduce the oxygen to water, which is much easier to remove than oxygen.¹

One such instance where this might be applicable is the production of polyethylene from the ethylene monomer. High purity ethylene is required as the presence of oxygen (even in the parts per million range) can deactivate the polymerization catalyst. Therefore, the removal of oxygen via reduction without any oxidation or reduction of ethylene is a key process step. 2% Ag/γ–Al₂O₃ has been found to be a highly selective catalyst for this process.¹

Temporal Analysis of Products (TAP) has been recognized as a powerful method to investigate gas–solid reactions of a heterogeneous catalyst in order to obtain kinetic data on complex catalytic reaction mechanisms and other surface process studies such as diffusivities, heat of adsorption and reaction rate for an individual reaction.^2–5 Since catalytic processes consist of kinetic (chemical transformations) and transport phenomena, in order to obtain the kinetic information, the chemical phenomena need to be distinguished from the transport phenomena.⁶

In the TAP method, gas transport is not eliminated and the well-defined Knudsen diffusion regime is the only transport process.⁴ In order to maintain the Knudsen diffusion regime typical pulse intensities in TAP experiments are in the range of 10¹³–10¹⁵ molecules per pulse, with pulse widths of 250 μs and pulse rates between 0.1 and 50 pulses s⁻¹. In addition, performing the experiment in the limitation of Knudsen diffusion also minimizes the collisions between gas-phase molecules so that the transient response of the molecules in the TAP system is a measure of gas–solid interactions only. Furthermore, the use of the Thin Zone TAP reactor (TZTR) configuration ensures uniformity of the surface composition across the catalyst zone.⁷

TAP has been proven to provide useful characterisation of silver catalysts,^8–10 including Ag/Al₂O₃ catalysts^11,12 with the use of hydrogen and oxygen as probe molecules.^11,12 In a previous work, TAP studies were undertaken over four differently treated 2% Ag/γ–Al₂O₃ catalysts to obtain the equilibrium adsorption rate constants of ethylene using single pulse experiments.¹³

From these TAP single pulse experiments, the residence time (first moment, M₁) of the main probe molecules were determined. M₁ of a molecule is indicative of the average time an atom or molecule remains in the adsorbed state and it can be used to illustrate the strength of adsorption between the adsorbing molecule and catalyst surface. As was previously identified, ethylene undergoes a process of reversible adsorption over the Ag/γ–Al₂O₃ catalyst. This means that the methodology for the determination of the basic kinetic coefficients^6,14 can be applied.

The equilibrium adsorption rate constants r₁ (an apparent intermediate-gas constant)¹⁴ for ethylene over a range of temperatures were reported. The natural logarithms of the equilibrium adsorption rate constants were higher for the oxidized catalyst compared with the reduced catalyst. This may suggest that ethylene adsorbs more on the oxidized silver (Ag⁺) than on the reduced silver species (Ag⁰). The UV-vis results reported previously indicated that in the oxidized catalyst highly dispersed Ag⁺ species are present, all of which may adsorb the ethylene. In contrast, clusters of silver (Ag⁰) were present in the reduced samples, resulting in a lower dispersion. This is consistent with previous findings that even mildly reducing conditions can cause silver to aggregate.^15–17

The equilibrium adsorption rate constants for the heated catalyst are more similar to the reduced catalyst rather than the oxidised catalyst. This is to be expected given that the catalyst is heated under vacuum in TAP conditions, resulting in some reduction of the silver species. This comparison was also observed with the previously published UV-vis results where the thermally treated catalyst in helium clearly showed reduced Ag species.^15–17 This also explains the temperature dependence of the equilibrium adsorption rate constant of ethylene over the four treated catalysts. Clearly, the apparent equilibrium adsorption rate constant decreases as the temperature increases, which may be due to some aggregation of the silver, resulting in a decreased concentration of adsorption sites. For example, for the heated catalyst the natural logarithm of the equilibrium adsorption constant of ethylene decreased from 5.39 to 0.98 as the temperature was increased.

This preliminary study has been expanded, herein, to further understand the surface activity as a function of the oxidation state of the catalyst using multi-pulse and consecutive pulse methods.

Multi-pulse experiments can be used to produce a controlled change in the catalyst surface state and at the same time the responses of the reactant can be used to monitor changes in catalytic properties. Multi-pulse TAP experiments enable the quantification of the number and the intrinsic activities of surface active species, through derivation of basic kinetic coefficients.¹⁸

In consecutive pulse TAP experiments two different reactant mixtures from separate valves are used and a sequence of alternating pulses is employed. For example, one reactant is pulsed from one valve into the reactor at t = 0 s. The second reactant species is introduced from the other valve at t = x s (where x is varied over a number of time points). Consecutive pulse experiments have proved to be very effective in determining lifetime of intermediates while providing some mechanistic insights.^19,20

In the present work, oxygen and hydrogen multi-pulse experiments along with consecutive pulse experiments (which investigate the oxygen reduction reaction) are reported. The combination of the current work and the ethylene equilibrium adsorption rate constants provides an overview of the catalytic system, including a mechanistic insight and explanation for the high selectivity of the catalyst for oxygen reduction.

Experimental

TAP pulse-response experiments were performed in a TAP-1 reactor using a stainless steel micro-reactor (41 mm long, 5.5 mm i.d.). Further details on the TAP-1 system utilised can be found elsewhere.²⁰ 2% Ag/γ–Al₂O₃ catalyst (14 mg, particle size 150–250 μm) was packed in the middle of two beds of SiC. The temperature of the reactor was measured by a thermocouple positioned in the centre of the catalyst bed. All gases used were supplied by BOC and were of >99% purity. A Hiden HAL V quadrupole mass spectrometer was used to record the exit flow from the micro-reactor. The TZTR⁷ concept was used in all experiments and the TAP pulse responses were analysed and modelled using moment-based analysis.⁶

In the TAP experiments, an inert gas was pulsed along with the reactant to account for any change in pulse intensity during the experiments. The collection time of all pulse responses in each of the experiments was 2 s. Separate pulse experiments of each reactant mixture were conducted over an inert silicon carbide packing to obtain the diffusion only responses. This also allowed the quantification of a ratio of zeroth moment, M₀, of reactant to M₀ argon in the case of zero conversion, which was then utilised for analysis of the consecutive pulse experiments. The ratios between M₀ of the reactant and M₀ of argon also allowed for any change in pulse intensity during the pulse response experiments to be monitored.

Oxygen single pulse experiments

Single pulse experiments were designed to investigate the adsorption and the reaction properties of oxygen over 2% Ag/γ–Al₂O₃ at 100, 150 and 200 °C. Pulses consisted of a mixture of 50 : 50 O₂/Ar. The masses of interest recorded for this set of experiments were AMU 32 (O₂) and AMU 40 (Ar). For improved data collection, the responses reported in the results section are the average of 100 pulses.

Oxygen multi-pulse experiments

Oxygen multi-pulse experiments were conducted over the fresh 2% Ag/γ–Al₂O₃ sample at 200 °C. Pulses of 50 : 50 O₂/Ar were continued until the oxygen signal remained constant, i.e. the sample was fully oxidised. The masses of interest recorded for this set of experiments were AMU 32 (O₂) and AMU 40 (Ar).

Hydrogen multi-pulse experiments

Hydrogen multi-pulse experiments were conducted at 150 °C over fresh 2% Ag/γ–Al₂O₃ catalyst. Pulses of 50 : 50 H₂/Ar were continued until the hydrogen signal remained constant, i.e. the sample was fully reduced. The masses of interest recorded for this set of experiments were AMU 2 (H₂) and AMU 40 (Ar).

Consecutive pulse experiments

Consecutive pulse experiments were also conducted over the fresh 2% Ag/γ–Al₂O₃ catalyst. The reaction was performed at 100, 150 and 200 °C. H₂/Ar was pulsed simultaneously with O₂/Ar or with an increasing time delay between the pulses of reactants (at 0.1 s and 0.5 s). The masses of interest for this set of experiments were AMU 2 (H₂), AMU 32 (O₂) and AMU 40 (Ar). For each AMU recorded, 100 pulses were obtained and averaged in order to improve data collection accuracy.

Results

Oxygen single pulse experiments

The argon and oxygen responses from O₂/Ar single pulse experiments and the corresponding theoretical diffusion curves at 100, 150 and 200 °C are reported in Fig. 1 and 2 respectively. In all cases, the experimental curves are similar to the corresponding theoretical curves. From the argon responses it is clear that the Knudsen diffusion regime is maintained during experiments. Furthermore, there was no observable reversible adsorption of oxygen in the temperature range of study (100 to 200 °C), possibly because of the weak irreversible adsorption of oxygen, as is shown in the results from multi-pulse experiment at 200 °C in the next section.

Fig. 1 Argon pulse responses fitted with theory (solid lines) at 100 °C (), 150 °C () and 200 °C ().

Fig. 2 Oxygen pulse responses fitted with theory (solid lines) at 100 °C (), 150 °C () and 200 °C ().

Oxygen multi-pulse experiments

By calculation of M₀ the number of oxygen and argon molecules per pulse can be obtained. For these calculations, the M₀ values were obtained from a single pulse per AMU. The ratio between oxygen and argon response intensities (normalized zeroth moment, M_0n, of oxygen) was found to increase with pulse number (see ESI†, Fig. S1). Saturation of the catalyst surface was achieved when a constant M_0n of oxygen was observed, which occurred after ∼600 pulses of oxygen. During the 0–600 pulse interval the relative standard deviation (RSD) in M₀ of argon was 4.76%. Furthermore, the RSD of M_0n of oxygen in the 700–1300 pulse region (when oxygen is not consumed) has been calculated to be 1.46%. The combination of these RSD values indicates little variation (between 1 and 5%) of pulse intensity during the experiment, i.e. reproducible pulse profiles were obtained.

The characteristic Knudsen diffusion dependence of the residence time (first moment, M₁) on the molecular weight and temperature is defined in eqn (1):¹³

where τ_res is the residence time, D is the diffusivity, M_w is the molecular weight and T is the temperature. Measuring M₁ as a function of temperature for a range of inert gases provides an estimate for the theoretical diffusional residence time for oxygen in the system. A comparison between the experimental residence time and theoretical diffusional residence times is provided in the ESI† (Fig. S2). The experimental residence time is similar to the theoretical diffusional residence time after ∼200 pulses. Between 0 and 200 pulses a lower residence time is found compared with the diffusional contribution due to the reaction of oxygen with the catalyst.

Since pulse intensity can vary during the TAP multi-pulse experiment the pulse number is not suitable to directly represent the change in catalyst state. Therefore, the amount of O₂ consumed prior to each pulse was used, a method reported elsewhere.¹⁸ Single pulse O₂ conversion was determined as the ratio between the amount of O₂ consumed and the amount of O₂ pulsed. Once determined, single pulse O₂ conversion was plotted against the amount of oxygen atoms consumed (ESI†, Fig. S3).

The apparent rate constant of chemical transformation of O₂ (r₀) is reported in Fig. 3, where the number of active sites is proportional to the amount of oxygen consumed. The apparent rate constant r₀ initially decreased rapidly and then slowly decreased to zero. The point where the curve crosses the x-axis represents the total amount of oxygen consumed, which is ∼2.1 × 10⁻⁸ mole mg⁻¹ of catalyst, which is equivalent to a total of 2.94 × 10⁻⁷ moles of oxygen atoms consumed over the entire catalyst sample. Considering that there are a maximum total of 2.6 × 10⁻⁶ silver atoms in the catalyst sample, this means 1 oxygen atom is adsorbed per 8.8 silver atoms. Hence only 22% of the silver has been oxidised to Ag₂O.

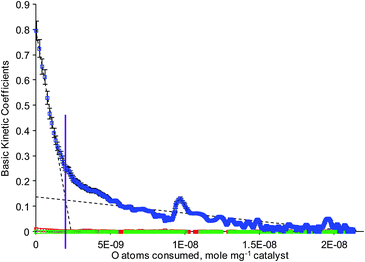Fig. 3 Basic kinetic coefficients derived from oxygen multi-pulse at 200 °C; r₀ () in s⁻¹, r₁ () dimensionless and r₂ () in s.

No fit of the data could be made using an r₀ dependency on the square of the oxidation degree utilising either a one or two active site model. The best fit is found using two separate linear regions which represent two independent r₀ rate kinetic constants as shown in Fig. 3. The two site model used is similar to that previously reported, where the amount of O consumed is proportional to the activity of the sites, i.e. k₁(1 − Θ₁) or k₂(1 − Θ₂), where Θ₁ and Θ₂ are the oxygen coverage over the more active and less active sites, respectively, while k₁ and k₂ represent the activity of the two sites.¹⁸ These two linear regions indicate two types of active sites and the gradient of these linear regions is directly related to the intrinsic activity of the oxygen species: the greater the gradient, the higher the activity.²⁰ The transition between the regions, as indicated by the intersection of the dashed lines (solid purple line), occurs at an oxygen consumption of ∼2.4 × 10⁻⁹ mole mg⁻¹ of catalyst. Clearly, the catalyst contains a greater number of the less active sites than the more active sites. It is also noticeable that ∼9 times more oxygen is consumed by the less active sites compared with the more active sites. These regions coincide with the slow and fast consumption of oxygen as observed in Fig. S3 (ESI†). Kinetic analysis of the oxygen responses indicates that the apparent intermediate-gas constant (r₁) and the apparent time delay by the solid material (r₂) were found to be nearly zero. The zero value of r₁ means that there was no significant relation between the adsorbed oxygen on the catalyst surface and gaseous oxygen, suggesting irreversible adsorption of the oxygen. The zero value of r₂ indicates that there was no time delay caused by the adsorption process, which suggests no significant oxygen desorption. The inference of the values of the three basic kinetic coefficients is that the process involved a one-step irreversible adsorption of oxygen.

Hydrogen multi-pulse experiments

In the case of a hydrogen multi-pulse experiment very low consumption of hydrogen per pulse was observed at the beginning of the experiment (see ESI†, Fig. S4). The M_0n of hydrogen increased only slightly before becoming stable after less than 200 pulses of hydrogen. In the 0–600 pulse interval the RSD of M₀ of argon was 0.89%, once again indicating reproducible pulse profiles during the experiment.

Since the change in M_0n of hydrogen is very small, it is difficult to quantify the amount of hydrogen consumed per pulse. Therefore, it is also difficult to quantify the total hydrogen atoms consumed, but it can be qualitatively defined as being in the region of 10⁻⁹ moles mg⁻¹ of catalyst (Fig. 4). This is the same order of magnitude as the quantity of the sites which are rapidly oxidised (Fig. S3, ESI†).

Fig. 4 Apparent rate constant of hydrogen, r₀, derived from hydrogen multi-pulse.

The measured and diffusional residence times of molecular hydrogen obtained from hydrogen multi-pulse are reported in Fig. 5. The results show that the measured residence time is higher than the calculated diffusional residence time, which was again determined from eqn (1). Furthermore, the measured residence time is reasonably constant throughout the experiment, which indicates that molecular hydrogen is delayed on the catalyst surface, possibly by reversible adsorption.

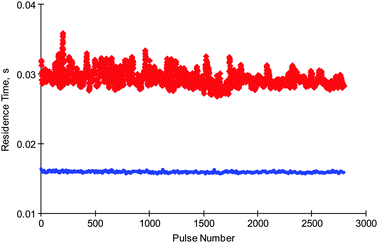Fig. 5 Comparison of experimental () and diffusional () residence times of hydrogen.

Consecutive pulse experiments

Unfortunately, the production of water from the reaction was very low and there was also a high water residual gas background in the mass spectrometer which resulted in a very low signal to noise ratio. Therefore, data interpretation from the water response was not possible and only the reactant responses were used for quantitative analysis.

Figs. 6 and 7 report the O₂ and H₂ pulse responses observed in the consecutive pulsing experiments respectively. The O₂/Ar was pulsed at 0 s followed by H₂/Ar pulsed at 0, 0.1 and 0.5 s.

Fig. 6 Area normalized O₂ responses observed in consecutive pulse experiments at 100 °C with different time delay of H₂ pulse (time = 0 (), 0.1 () and 0.5 s ()) compared with the O₂ single pulse experiment response ().

Fig. 7 Normalized H₂ responses observed in consecutive pulse experiments at 100 °C when H₂/Ar was pulsed at a time delay of 0 (), 0.1 () and 0.5 s ().

Fig. 6 reports the O₂ pulse responses from O₂/Ar single pulse experiments. In addition, consecutive pulse experiments are shown for O₂/Ar, followed by H₂/Ar with the latter pulsed with a time delay of 0 s, 0.1 s and 0.5 s. The results clearly show that when H₂ was pulsed at a time delay > 0 s (i.e. 0.1 and 0.5 s), similar O₂ responses were observed to the shape of the oxygen single pulse experiment response. A small difference was observed at ∼0.12 s for the 0.1 s time delay between pulses. This can be explained by either pressure perturbation or due to competitive adsorption of H₂ and O₂. The former is not consistent with the profiles observed when both pulse valves are pulsed simultaneously (see Fig. S5, ESI†). In this case, the resulting pulse response followed strictly the standard diffusion curve, indicating no convective contribution to the transport of the molecules. Therefore, the small change in pulse response shape is thought to be due to the competitive adsorption of H₂ and O₂ on the surface. This is also consistent with the small change observed in the response of the pulse tail which is below that found for the single pulse experiment. This is not observed for a time delay of 0.5 s as at this point H₂ and O₂ are not present simultaneously over the catalyst. When both O₂ and H₂ were pulsed simultaneously there is a difference in the shape of the oxygen response. This change in shape cannot be attributed to a pressure perturbation due to the simultaneous operation of both valves as the shapes of the argon response do not change when compared to the argon response from the oxygen single pulse experiment (see ESI†, Fig. S5). Therefore, this change in shape of oxygen response can be explained by the increased conversion of O₂ in these experiments (see Fig. 8 for comparison for the O₂ conversion).

Fig. 8 Conversion of oxygen at 100 °C (), 150 °C () and 200 °C (); conversion of hydrogen at 100 °C (), 150 °C () and 200 °C ().

Fig. 7 reports the difference in intensity of the H₂ responses when H₂/Ar was pulsed at different time delays (t = 0, 0.1 and 0.5 s) after the O₂/Ar pulse. The concentration of H₂ in the catalyst zone increased sharply and then returned to its baseline within 0.2 s of pulsing. The sharp hydrogen response observed is indicative of very fast Knudsen diffusion due to its low molecular weight (compared with O₂) and negligible hydrogen uptake according to results from the hydrogen multi-pulse (Fig. S4, ESI†). With increasing time delay between reactant pulses, the intensity of hydrogen response is increased, which indicates a decrease of hydrogen consumption. Again, this is due to a decrease in the amount of available active oxygen as time increases.

From the data reported in Figs. 6 and 7, conversions of oxygen and hydrogen have been calculated (Fig. 8). The oxygen and hydrogen conversions are temperature dependent, i.e. the conversion of both reactants increased due to the increased temperature. Therefore the reaction rate of the reduction of oxygen by hydrogen increases as the temperature increases. Given that the equilibrium adsorption rate constant for ethylene decreased as temperature increased, this explains why the 2% Ag/γ–Al₂O₃ catalyst is highly selective for the removal of oxygen from a hydrogen rich ethylene feed.

Furthermore, Fig. 8 also indicates that by increasing the time delay of hydrogen pulse (from t = 0 to 0.1 and 0.5 s), both oxygen and hydrogen consumption were found to decrease. This is due to the decreased amount of available active oxygen in the catalyst zone as the time at which hydrogen was pulsed was increased. These results show that both reactants need to be adsorbed from the gas phase and present on the surface together within the 0 to 0.5 s timescale; otherwise there will be no reaction. Some additional O₂ consumption was observed at 200 °C at the 0.5 s time delay. This is thought to be due to the re-oxidation of silver, which has been partially reduced as a result of being heated under vacuum.

Discussion

Previously reported analysis of ethylene single pulse experiments concluded that the rate of adsorption of ethylene decreased as temperature increased.¹³ In the same work, the rate of adsorption of oxygen was found to increase with temperature. The oxygen single pulse experiments reported, herein, can be fitted with theoretical Knudsen diffusional pulse responses. This indicates that any interaction between the catalyst and the oxygen is irreversible, i.e. if reversible adsorption had occurred responses much broader than the diffusional fit would have been observed.

The oxygen multi-pulse experiment provides a key insight into the interaction of oxygen with the catalyst. For instance, the trend in r₀ values has shown the presence of two active sites. There are a fewer number of the more active sites compared to the active sites with lower activity. Meanwhile, the values obtained for r₁ from the oxygen multi-pulse report no significant relation between the adsorbed oxygen on the catalyst surface and gaseous oxygen. Additionally, the r₂ values report no significant oxygen desorption. The observed r₁ and r₂ values, therefore, validated the statements made regarding the oxygen single pulse experiments, i.e. oxygen is adsorbing irreversibly.

As has been demonstrated previously, results from consecutive pulse experiments can be an indication of the type of mechanism that is involved in the reaction.²⁰ In the current work the hydrogen conversion is highest when both reactants are pulsed simultaneously. The hydrogen conversion decreases as the delay between oxygen and hydrogen pulses is increased. Hence, consecutive pulses have found that oxygen needs to be adsorbed on the surface for reaction to occur. Furthermore multi-pulse experiments found that hydrogen is delayed on the surface. Given that hydrogen adsorbs on the catalyst it is not possible to discount the Eley–Rideal mechanism; however the adsorption of hydrogen shows that the most likely mechanism is the Langmuir–Hinshelwood mechanism.

When this information is combined with the results of the single pulse and multi-pulse experiments, it is clear that the adsorbed oxygen is only available to react with the hydrogen for a brief time before diffusing into the catalyst bulk and forming silver oxide.

Conclusions

An examination of the uptake of oxygen as a function of the number of oxygen pulses during a multi-pulse experiment indicates irreversible adsorption of oxygen at 200 °C. In addition, the presence of high and low activity sites was observed with the number of less active sites higher than the more active sites.

Consecutive pulse experiments have identified the Langmuir–Hinshelwood mechanism as the most likely active process for the selective reduction of oxygen in a hydrogen rich ethylene feed over the 2% Ag/γ–Al₂O₃ catalyst. These consecutive pulse experiments determined that the reaction rate for the reduction of oxygen by hydrogen has been found to increase with temperature. Single pulse experiments reported previously¹³ found that the adsorption of ethylene on the catalyst becomes less favourable with increasing temperature. The combination of these final points explains the selectivity of the catalyst for the reduction of oxygen in a hydrogen rich ethylene feed.

Acknowledgements

Financial support from EPSRC under the CASTech project, and funding by the Thai government (BI) and DELNI (KM) are acknowledged.

Notes and references

1. B. Inceesungvorn, F. C. Meunier, C. Hardacre, R. Burch and K. Griffin, Chem. Commun., 2008, 6212.
2. J. T. Gleaves, J. R. Ebner and T. C. Kuechler, Catal. Rev. Sci. Eng., 1988, 30, 49.
3. J. T. Gleaves, G. S. Yablonskii, P. Phanawadee and Y. Schuurman, Appl. Catal., A, 1997, 160, 55.
4. J. Pérez-Ramírez and E. V. Kondratenko, Catal. Today, 2007, 121, 160.
5. J. T. Gleaves, G. S. Yablonskii, X. Zheng, R. Fushimi and P. L. Mills, J. Mol. Catal. A: Chem., 2010, 315, 108.
6. S. O. Shekhtman, G. S. Yablonsky, J. T. Gleaves and R. Fushimi, Chem. Eng. Sci., 2003, 58, 4843.
7. S. O. Shekhtman, G. S. Yablonsky, J. T. Gleaves and S. Chen, Chem. Eng. Sci., 1999, 54, 4371.
8. J. T. Gleaves, A. G. Sault, R. J. Madix and J. R. Ebner, J. Catal., 1990, 121, 202.
9. A. C. van Veen, O. Hinrichsen and M. Muhler, J. Catal., 2002, 210, 53.
10. J. Homeyer, E. V. Kondratenko, M. Bron, J. Kröhnert, F. C. Jentoft, R. Schögl and P. Claus, J. Catal., 2010, 269, 5.
11. E. V. Kondratenko, V. A. Kondratenko, M. Richter and R. Fricke, J. Catal., 2006, 239, 23.
12. V. A. Kondratenko, U. Bentrup, M. Richter, T. W. Hansen and E. V. Kondratenko, Appl. Catal., B, 2008, 84, 497.
13. A. Goguet, C. Hardacre, B. Inceesungvorn, K. Morgan and S. O. Shekhtman, Catal. Sci. Technol., 2011, 1, 760.
14. S. O. Shekhtman, N. Maguire, A. Goguet, R. Burch and C. Hardacre, Catal. Today, 2007, 121, 255.
15. B. Inceesungvorn, J. López-Castro, J. Calvino, S. Bernal, F. C. Meunier, C. Hardacre, K. Griffin and J. J. Delgado, Appl. Catal., A, 2011, 391, 187.
16. J. P. Breen, R. Burch, C. Hardacre and C. J. Hill, J. Phys. Chem. B, 2005, 109, 4805.
17. J. Shibata, K. I. Shimizu, S. Satokawa, A. Satsuma and T. Hattori, Phys. Chem. Chem. Phys., 2003, 5, 2154.
18. S. O. Shekhtman, A. Goguet, R. Burch, C. Hardacre and N. Maguire, J. Catal., 2008, 253, 303.
19. A. Goguet, S. O. Shekhtman, R. Burch, C. Hardacre, F. C. Meunier and G. S. Yablonsky, J. Catal., 2006, 237, 102.
20. K. Morgan, K. J. Cole, A. Goguet, C. Hardacre, G. J. Hutchings, N. Maguire, S. O. Shekhtman and S. H. Taylor, J. Catal., 2010, 276, 38.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2cy20295f

---