Non-photochemical laser-induced nucleation of supercooled glacial acetic acid†
Martin R.
Ward
,
Stephanie
McHugh
and
Andrew J.
Alexander
*
School of Chemistry, University of Edinburgh, Edinburgh, Scotland EH9 3JJ. E-mail: andrew.alexander@ed.ac.uk; Fax: +44 131 6504743; Tel: +44 131 6504741
First published on 17th November 2011
Abstract
Non-photochemical laser-induced nucleation (NPLIN) of glacial acetic acid (GAA) is demonstrated. The fraction of samples nucleated depends linearly on peak laser power density at low powers (<100 MW cm−2) with a threshold of (9.0 ± 4.2) MW cm−2; at higher laser powers the fraction reaches a plateau of 0.75 ± 0.24 (2σ uncertainties). A simple model based on polarizability of pre-nucleating clusters gives a value of the solid–liquid interfacial tension γSL = 15.5 mJ m−2. It is hoped that the results will stimulate new developments in experimental and theoretical studies of cluster structure and nucleation in liquids.
Introduction
Nucleation is a process of primary scientific importance because it is the starting point for solidification and crystallization.1 Nucleation is used to great effect for manufacture, e.g., for pharmaceuticals, electronic devices, agrochemicals, and optical materials. Likewise, nature exploits nucleation to build an astounding array of materials and structures,2 and there has been significant interest in harnessing new synthetic methods. Despite more than a century of investigation, our understanding of the dynamics leading up to the critical point of nucleation is still relatively vague, although a clearer picture involving a pre-nucleation phase is emerging.3The main difficulty with nucleation is its stochastic nature: knowing when and where to look would enable us to refine techniques for studying the dynamics. Moreover, we face the challenge of probing pre-nucleating clusters that may consist of only a few ions or molecules. Recently there has been a growing interest in the use of optical methods for inducing nucleation.4–9 Of the techniques that have been investigated, non-photochemical laser-induced nucleation (NPLIN) has shown particular promise.4 NPLIN can be initiated by exposing a metastable system, e.g., a supersaturated solution, to laser pulses of nanosecond duration.4,8,10–12 There is no damage to the material being studied: therefore, NPLIN offers a potential route to studying the dynamics of nucleation in a manner that resembles native, homogeneous nucleation.
The detailed microscopic mechanism for NPLIN has not yet been elucidated, and it is clear that not all substances are susceptible to the effect. It has been proposed that the mechanism involves interaction between the electric field of the laser light and the polarizability of pre-nucleating clusters, which become stabilized to act as nuclei.4,8,10,12,13 Karpov has suggested that metallic clusters, in particular those with high aspect ratios (needle shaped) would be particularly good candidates for NPLIN.14 Baron and co-workers demonstrated bubble nucleation from aqueous solutions supersaturated with CO2.15 Photoacoustic effects can also induce nucleation.5,6,16–18 Laser-induced nucleation of supercooled water has been demonstrated by Lindinger et al.; however, the focussed pulses caused optical breakdown and other photophysical effects.19 It is possible that reports of NPLIN could involve several different mechanisms; clearly, more work needs to be done to unravel these effects.
At the present time, experimental studies of NPLIN have been almost exclusively carried out in aqueous supersaturated solutions. By contrast, Sun et al. studied a single-component liquid crystalline phase transition in supercooled 4′-n-pentyl-4-cyanobiphenyl.13 The nematic director showed a clear tendency to align with the linear polarization vector of the laser light, and the authors concluded that order is transferred by enhancing fluctuations in the nematic phase in the direction of the electric field of the light. Ward et al. have recently investigated NPLIN in molten sodium chlorate and demonstrated a propensity towards nucleation of the same enantiomorph (levorotatory or dextrorotatory) of the cubic phase that was used prior to melting, most likely via a heterogeneous mechanism.12,20
The main advantage to studying a single-component system for NPLIN, is that the absence of solvent reduces the complexity of the phase transition, making it more attractive for experimental and theoretical study. Glacial acetic acid (GAA) is acetic acid (CH3COOH) almost completely void of water, and its melting point (Tm) is 16.6 °C.21 Molecular dynamics simulations of the homogeneous nucleation of acetic acid have been carried out previously, making it a prime target for experiments.
Experimental methods
Experiments were carried out with 2 cm3 samples of GAA (Fisher, ≥ 99.7%) filtered through 0.2 μm poly(tetrafluoroethene) (PTFE) syringe filters into rigorously cleaned pyrex tubes with PTFE-lined screwcap lids. Samples cooled by refrigeration to 3 °C could not be induced to nucleate either by laser pulses or by mechanical shock. Samples were cooled and maintained at −9 °C using a stirred bath consisting of dry ice in isopropyl alcohol. Fluctuations of more than 1 °C below this temperature often resulted in spontaneous nucleation, but samples were surprisingly still resistant to nucleation by shock. After maintaining samples at −9 °C for ten minutes, experiments were carried out quickly, with samples only removed from the dry-ice bath immediately prior to shooting with the laser. Samples were exposed to up to 10 s (100 pulses) of 7 ns, linearly polarized pulses of the 1064 nm light (Nd3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) YAG, Continuum, Surelite II-10 operating at 10 Hz). The diameter of the beam was 2.5 mm. The power was adjusted using a Glan–laser polarizer.22 A pulse energy of 1 mJ pulse−1 corresponded to a peak power density of 5.85 MW cm−2.
YAG, Continuum, Surelite II-10 operating at 10 Hz). The diameter of the beam was 2.5 mm. The power was adjusted using a Glan–laser polarizer.22 A pulse energy of 1 mJ pulse−1 corresponded to a peak power density of 5.85 MW cm−2.
Results
When nucleated, the sample was observed to completely solidify into a polycrystalline aggregate in less than 1 s. It was observed that at lower powers (<40 MW cm−2), samples required exposure to a greater number of pulses in order to nucleate. The mean exposure time required for nucleation was ∼3 s (30 pulses). In very few cases, samples were observed to nucleate after the ten second limit: these samples were not counted.In order to estimate the possible heating of samples resulting from absorption of the laser light, the near-infrared spectrum of GAA was measured (Fig. S1†). At 1064 nm, the absorption coefficient of acetic acid was found to be 0.0370 cm−1, smaller than that of water (0.144 cm−1).23 Following the procedure described by Ward et al.,22 we estimated the heating due to the laser pulses. For a single pulse at a peak power of 40 MW cm−2, the energy absorbed by acetic acid in the illuminated volume (0.046 cm3) corresponds to a temperature rise of 6 mK; at 900 MW cm−2, the rise is 0.14 K. The time between pulses (0.1 ms) allows conduction and convection to take place: for 100 pulses, we estimate corresponding temperature rises of 14 mK (40 MW cm−2) and 0.32 K (900 MW cm−2) in the whole sample (2 cm3). We conclude that the temperature rise at lower powers is negligible, but heating may become important at higher powers, particularly for longer exposure times.
Fig. 1 illustrates nucleation by the laser. The sample was completely solidified within 0.5 s. In general, nucleation was observed to occur at random points along the beam path, which agrees with our previous findings that the surface of the vessel is not a major locus for NPLIN.8
 | ||
| Fig. 1 A sequence of images illustrating NPLIN of GAA at −9 °C. The diameter of the tube was 13 mm, the laser pulse passed from right to left as viewed, and the time (in seconds) after firing of the pulse is shown for each frame. The linear laser polarization was horizontal, i.e., out of the plane of the images. Nucleation was observed in the center of the liquid, and the subsequent freezing process is complete within 0.5 s. | ||
A plot of the fraction of samples nucleated against peak laser power density is shown in Fig. 2. Approximately 40 samples were tested at each power, and 95% confidence intervals were calculated using the Wilson method.24 The fraction of samples nucleated was found to be linear at lower power densities, as shown in the inset. A weighted linear least-squares fit to the first ten points gives a threshold power density of (9.0 ± 4.2) MW cm−2, with a slope of (7.5 ± 1.5) × 10−3 cm2 MW−1 (2σ uncertainties).
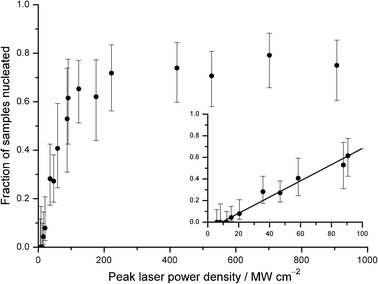 | ||
| Fig. 2 Plot of fraction of samples nucleated versus peak laser power density. Solid circles represent experimental data. Confidence intervals were obtained using the Wilson method for binomial distributions.24 The inset shows a linear dependence at lower laser power densities. The solid line represents a weighted fit (linear least-squares) to the first ten data points, giving a threshold power density of (9.0 ± 4.2) MW cm−2 and a slope of (7.5 ± 1.5) × 10−3 cm2MW−1. The data approach an upper threshold at high laser power densities of 0.75 ± 0.24. All uncertainties quoted are at the 95% confidence level. | ||
A threshold power has been seen in previous work on NPLIN of supersaturated urea,25KCl,8 and molten NaClO3.12 The laser power was monitored regularly, and fluctuations as high as ±5 MW cm−2 were observed. No NPLIN was observed at the three lowest powers; however, we do not rule out a nonzero probability of nucleation at powers <12 MW cm−2. At higher laser powers, the fraction of samples nucleated saturates at 0.75 ± 0.24. One reason for this may be heating of the sample by the laser, which could reduce supercooling, making samples more resistant to nucleation.
The period of the oscillating electric field of light at 1064 nm is 3.5 fs, which is much faster than the molecule can rotate (rotational period ∼30 ps in the gas phase).26 However, the molecule can interact with the electric field via the polarizability anisotropy, and this is the basis for the optical Kerr-effect (OKE) mechanism for NPLIN.4 The tendency would be for the most polarizable axis (x, the C–C bond)26 of the molecule to align along the electric field of the linearly polarized light, and for the least polarizable axis (z, perpendicular to the COO plane) to be distributed randomly around this direction.13 The energy gain for OKE alignment of a single molecule has been noted to be a small fraction (∼10−4kBT) of thermal energy, and it has been proposed that the mechanism relies on co-operative alignment of a number of molecules.13
The crystal structure of acetic acid is orthorhombic (Pna21) and is made up of chains of hydrogen-bonded acetic molecules.27,28 As shown in Fig. 3, the chain directions are orthogonal from layer to layer, which is incommensurate with the single axial alignment offered by the OKE. In the case of glycine, Garetz et al. showed that the final phase can be selected by the polarization of the light.10,13 Circularly polarized light favoured α-glycine (disk-like polarizability) and linearly polarized light favoured γ-glycine (rod-like polarizability).10 However, this remarkable polarization switching effect only operates within a small window of solution conditions. At lower supersaturations, both polarizations yield α-glycine; at higher supersaturations, both polarizations yield γ-glycine.13 Thus, it is evident that NPLIN can still operate, even with a mismatch between the symmetry of the polarizability and the polarization of the light.
 | ||
| Fig. 3 Crystal structure of acetic acid,28 looking along the a axis of the unit cell. The unit cell is shown as a box, with the b and c axes as labelled. The H atoms of the CH3 group are not displayed for clarity. Linear chains of molecules can be seen, aligned along the (b + c) and (c − b) directions (arrows). The most polarizable axis of the acetic acid molecule (parallel to the C–C bond) lies along the direction of the linear chains. The two directions for the chains are nearly orthogonal, which is incommensurate with the uniaxial alignment that would be promoted by the optical Kerr effect. | ||
Recent simulations suggest that although the OKE mechanism can lower the barrier to nucleation, the solute–solute interactions are simply too strong to allow significant alignment at the electric field strengths employed for NPLIN experiments.29 An alternative mechanism for NPLIN is based on the isotropic electronic polarizablity of pre-nucleating clusters, where the electric field lowers the free-energy of a dielectric particle surrounded by a medium with a lower relative permittivity.8 To explore the feasibility of this mechanism, we consider the refractive indices of solid (nS = 1.4357) and liquid (nL = 1.3614) acetic acid. The refractive indices of GAA at 1064 nm and −9 °C are not readily available, and so were estimated by extrapolation (see ESI for details†). The change in free energy due to the presence of the field is given by30
| ΔW(E) = −aVpE2 | (1) |
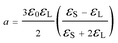 | (2) |
It may be possible that NPLIN occurs at impurity nanoparticles for which a > 0, where Vp represents the impurity. However, if impurity particles are the sole cause of NPLIN, then it is unclear why some systems appear to be resistant to the effect: e.g., we have observed NPLIN in aqueous solutions of potassium acetate but not sodium acetate. The observation of polarization switching would also be difficult to rationalize if impurities are the cause.10
As a starting point to examine the results, we adapt a simple classical NPLIN model based on the isotropic polarizabilty, as outlined previously.8,12 We find the linear slope of the experimental data is reproduced using a value for the solid–liquid interfacial tension of γSL = 15.5 mJ m−2. We were unable to find a previous estimate or measurement of this value in the literature. Using Digilov's semi-empirical approach for calculating interfacial tensions,31 we estimate γSL = 41.5 mJ m−2 at 16.6 °C. In the absence of data for GAA we use an estimate of dγSL/dT = 0.35 mJ m−2 K−1 (the value for water–ice32) to find γSL = 32.5 mJ m−2 at −9 °C, which is close to our experimental value.
The classical NPLIN model fails to reproduce the observed threshold. At the point of activation by the laser, the kinetics of growth becomes important, and the cluster must be fed to continue growing after the field is removed. We only count nucleation events that produce an observable solid after the laser pulse, and it may be that smaller nuclei are destroyed during early growth, perhaps due to subsequent laser pulses or gradients in temperature. Another failing of the classical NPLIN model is that—like the OKE model—the values of the energies involved appear to be too low (ΔW ∼ 10−3kBT) for the estimated critical cluster sizes. The model is crude because it draws only upon a handful of values of bulk properties for its parameters, such as the enthalpy of fusion and the melting point. These are failings of the model, however: the physical basis for the isotropic polarizability mechanism remains valid.
The molecular dynamics of nucleation (in CCl4 solvent) and melting of acetic acid have been studied by Gavezzotti.33,34 The nucleation study is complicated by additional solvent–solute non-polar interactions, nevertheless we expect similar structural motifs to dominate near the critical point. A large number of cyclic dimers and trimers were observed at early times, with larger clusters forming later; many of these larger clusters contained dimer and trimer sub-structures. Chains were observed among the larger clusters, but only on short timescales, and they were not the more rigid catemer chain structures as seen in the crystal structure. After some controversy, the most recent Raman spectroscopic measurements point unequivocally to the cyclic dimer as being the major species in the liquid.35
During melting simulations, localized hydrogen bonds are the first to be broken, with weaker dispersion forces acting co-operatively over longer range.33 Examining the analogy between nucleation and melting, Gavezotti noted that nucleation likely begins with formation of localized van der Waals clusters, followed by formation of hydrogen bonding to produce the finer structural detail as in the crystal. This picture of a loosely associated, disordered cluster clicking into order may be speculative, but has been suggested before for the case of NaCl.36 For NPLIN, we speculate that the energy gain provided by the electric field, which is present for the equivalent of thousands of intermolecular vibrational periods,35 assists the cluster in finding a pathway to a lower energy configuration. If this is the case, the polarizability interaction should favour certain molecular configurations within the cluster, i.e., specific directions on the multidimensional potential energy surface. It would be interesting to see if such changes to the potential energy surface resulting from a high strength electric field could be calculated ab initio, even for small clusters.
In summary, we have measured non-photochemical laser-induced nucleation (NPLIN) in the single-component system glacial acetic acid. The results can be reproduced reasonably well using a model based on activation of pre-nucleating clusters. However, exact details of the microscopic mechanism are still not clear, and it is hoped that these results will stimulate much needed experimental and theoretical activity towards understanding the NPLIN effect in particular, and nucleation in general.
Acknowledgements
The authors thank Dr Philip Camp for useful discussions about nucleation. We are grateful to the Science and Technology Facilities Council (STFC) and the Engineering and Physical Sciences Research Council (EPSRC) for supporting this work (EP/G067546/1).Notes and references
- J. W. Mullin, Crystallization, Butterworth-Heinemann, Oxford, 4th edn 2001 Search PubMed.
- A. W. Xu, Y. R. Ma and H. Colfen, J. Mater. Chem., 2007, 17, 415–449 RSC.
- P. G. Vekilov, Cryst. Growth Des., 2010, 10, 5007–5019 CAS.
- B. A. Garetz, J. E. Aber, N. L. Goddard, R. G. Young and A. S. Myerson, Phys. Rev. Lett., 1996, 77, 3475–3476 CrossRef CAS.
- H. Y. Yoshikawa, Y. Hosokawa and H. Masuhara, Jpn. J. Appl. Phys., 2006, 45, L23–L26 CrossRef CAS.
- K. Nakamura, Y. Hosokawa and H. Masuhara, Cryst. Growth Des., 2007, 7, 885–889 CAS.
- T. Sugiyama, T. Adachi and H. Masuhara, Chem. Lett., 2007, 36, 1480 CrossRef CAS.
- A. J. Alexander and P. J. Camp, Cryst. Growth Des., 2009, 9, 958–963 CAS.
- C. Duffus, P. J. Camp and A. J. Alexander, J. Am. Chem. Soc., 2009, 131, 11676–11677 CrossRef CAS.
- B. A. Garetz, J. Matic and A. S. Myerson, Phys. Rev. Lett., 2002, 89, 175501 CrossRef.
- I. S. Lee, J. M. B. Evans, D. Erdemir, A. Y. Lee, B. A. Garetz and A. S. Myerson, Cryst. Growth Des., 2008, 8, 4255–4261 CAS.
- M. R. Ward, G. W. Copeland and A. J. Alexander, J. Chem. Phys., 2011, 135, 114508 CrossRef.
- X. Y. Sun, B. A. Garetz and A. S. Myerson, Cryst. Growth Des., 2006, 6, 684–689 CAS.
- V. G. Karpov, Appl. Phys. Lett., 2010, 97, 033505 CrossRef.
- B. C. Knott, J. L. Larue, A. M. Wodtke, M. F. Doherty and B. Peters, J. Chem. Phys., 2011, 134 Search PubMed , 171102.
- A. Soare, R. Dijkink, M. R. Pascual, C. Sun, P. W. Cains, D. Lohse, A. I. Stankiewicz and H. J. M. Kramer, Cryst. Growth Des., 2011, 11, 2311–2316 CAS.
- M. D. L. de Castro and F. Priego-Capote, Ultrason. Sonochem., 2007, 14, 717–724 CrossRef.
- A. Fisher, R. M. Pagni, R. N. Compton and D. Kondepudi, in Nanoclusters: A Bridge across Disciplines, ed. P. Jena and A. W. Castleman, Elsevier, Amsterdam, The Netherlands, 2010 Search PubMed.
- B. Lindinger, R. Mettin, R. Chow and W. Lauterborn, Phys. Rev. Lett., 2007, 99, 045701 CrossRef CAS.
- M. R. Ward, G. W. Copeland and A. J. Alexander, Chem. Commun., 2010, 46, 7634–7636 RSC.
- CRC Handbook of Chemistry, Physics, ed. W. M. Haynes, CRC Press, Boca Raton, FL, 91st (Internet Version 2011) edn, 2011 Search PubMed.
- M. R. Ward, I. Ballingall, M. L. Costen, K. G. McKendrick and A. J. Alexander, Chem. Phys. Lett., 2009, 481, 25–28 CrossRef CAS.
- L. H. Kou, D. Labrie and P. Chylek, Appl. Opt., 1993, 32, 3531–3540 CrossRef CAS.
- L. D. Brown, T. T. Cai and A. DasGupta, Stat. Sci., 2001, 16, 101–133 Search PubMed.
- J. Matic, X. Y. Sun, B. A. Garetz and A. S. Myerson, Cryst. Growth Des., 2005, 5, 1565–1567 CAS.
- V. V. Ilyushin, E. A. Alekseev, S. F. Dyubko and I. Kleiner, J. Mol. Spectrosc., 2003, 220, 170–186 CrossRef CAS.
- R. E. Jones and D. H. Templeton, Acta Crystallogr., 1958, 11, 484–487 CrossRef CAS.
- I. Nahringbauer, Acta Chem. Scand., 1970, 24, 453–462 CrossRef CAS.
- B. C. Knott, M. F. Doherty and B. Peters, J. Chem. Phys., 2011, 134, 1–6 Search PubMed.
- J. O. Isard, Philos. Mag., 1977, 35, 817–819 CrossRef CAS.
- R. M. Digilov, Surf. Sci., 2004, 555, 68–74 CrossRef CAS.
- P. V. Hobbs, Ice Physics, Oxford University Press, New York, 1974 Search PubMed.
- A. Gavezzotti, J. Mol. Struct., 1999, 485–486, 485–499 CrossRef CAS.
- A. Gavezzotti, Chem.–Eur. J., 1999, 5, 567–576 CrossRef CAS.
- I. A. Heisler, K. Mazur, S. Yamaguchi, K. Tominaga and S. R. Meech, Phys. Chem. Chem. Phys., 2011, 13, 15573–15579 RSC.
- V. A. Garten and R. B. Head, Philos. Mag., 1963, 8, 1793–1803 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Near-infrared spectrum of acetic acid and calculations of refractive index. See DOI: 10.1039/c1cp22774b |
| This journal is © the Owner Societies 2012 |
