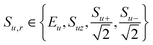A first-principles description of proton-driven spin diffusion

Abstract

Herein we design a reduced Liouville space for the simulation of proton-driven spin diffusion. Using this approach, the experimentally observed carbon-13 polarisation transfer in a powder sample undergoing magic-angle spinning is quantitatively described, directly from crystal geometry and without any adjustable parameters.

---

The concept of nuclear spin diffusion was introduced in 1949 by Bloembergen to account for unexpected values of relaxation times in solids containing paramagnetic impurities.¹ Spin diffusion, the transfer of nuclear spin polarisation driven by dipolar interactions, is a ubiquitous mechanism for the transport of polarisation in solids.² In a large range of systems the polarisation can be considered as a spatially dependent quantity that “diffuses” through the sample as a function of time.³ This spatial spin diffusion process has been the subject of extensive theoretical studies and has been observed directly in both real space⁴ and reciprocal space.⁵ When there exists a large difference in energy between the Zeeman energy levels that are involved in the transitions induced by the dipolar interaction, spin diffusion can be seen as occurring in frequency space and requires an external source of energy. This spectral spin diffusion⁶ process can be observed directly with 2D NMR techniques. The so-called proton-driven spin diffusion (PDSD) case, where the energy is provided by a bath of protons, has become a vital tool in NMR spectroscopy today, where it is the primary method used for structure determination in solids.^7–11 Simplified descriptions of PDSD based on spin thermodynamics have been developed.^6,12,13 However, spin diffusion, whether spatial or spectral, has been shown to be a fully coherent process involving large numbers of strongly coupled spins.¹⁴ In general, the so-called “exponential wall” of numerical simulations of large quantum-mechanical systems prevents the direct description of spin diffusion through the numerical integration of the equation of motion. Thus, more than sixty years after the discovery of spin diffusion, a full description of this phenomenon from first principles has yet to emerge.

The barrier to the exact description of PDSD using density-matrix simulations is in fact twofold. First, the transient dynamics of the transfer process depends on a potentially very large number of spin–spin interactions, as in a solid a given spin is coupled through space to many other spins. Second, the determination of the so-called quasi-equilibrium state of the system¹⁵ requires an even larger number of interactions, the detailed description of which is irrelevant. This second challenge can be thought of as a “thermodynamic wall”, since the prediction of the quasi-equilibrium state requires a large number of spins in an exact description. For example, polarisation transfer is drastically quenched in numerical simulations using small spin systems when large chemical-shift differences are taken into account,¹⁶ while experimentally diffusion is usually observed to equalise polarisation. In fact, it is precisely this absence of quenching that makes PDSD an attractive probe of structural information in biomolecules in the solid state.^8,16 In light of these two barriers, PDSD would appear to be an archetypal large-N problem.

Recently, several reduced-space simulation approaches have been proposed that benefit from polynomial rather than exponential scaling.^17–22 Of particular interest to solid-state NMR is the LCL method (named for its use of low-order correlations in Liouville space), which relies on an appropriate partition both of the spin system and of the multi-spin correlations in Liouville space. The LCL approach has been shown to accurately predict dipolar-driven polarisation transfer among a large system of strongly coupled proton spins.^17–19

In this communication we show that LCL calculations have an intrinsic property that gives rise to quasi-equilibrium states in which the total polarisation is uniformly distributed over all spins, even in the case of small spin systems. This property provides a way to accurately predict quasi-equilibrium states without the need to explicitly model large numbers of spins. We also find that surprisingly few protons are required to faithfully capture the transient dynamics. Thus, for the case of carbon-13 PDSD, only a few protons per carbon atom are required for an LCL simulation to converge to a quantitative reproduction of both the transient and long-term dynamics and so provide the most accurate prediction of experimentally observed PDSD data to date, capturing dynamic features related to structure that were previously inaccessible. This approach is applicable to powdered solids undergoing magic-angle spinning (MAS), that is, to the class of samples used in modern solid-state NMR spectroscopy. Under these conditions, LCL provides a small-N approach to solving what is otherwise an intrinsically large-N problem.

Consider a system of N_C carbons and N_Hprotons, for which we can define a set of product operators:

where
and
Here E is the identity operator, S_u+ and S_u− are raising and lowering operators, the products are over all carbons u and all protonsi, and q_r is the spin-order for the product operator B_r, i.e. the number of constituent single-spin operators that are not the identity. The basis set spans the full zero-quantum sub-space. (This restriction to the zero-quantum region of the full Liouville space is fully justified for the case of spontaneous polarisation transfer via the secular dipolar Hamiltonian. However, it is not a fundamental limitation of the simulation method.) Using such a basis set, a reduced Liouville space can be defined by excluding all correlations among more than q_C carbons or q_H protons. A schematic illustrating this spin–space reduction is shown in Fig. 1. Here we propose that truncation to q_C = 2 and q_H = 4 will provide sufficient accuracy. Previously reported results^17–19 have demonstrated that LCL simulations using a maximum proton spin order of 4 reliably and quantitatively reproduce proton spin diffusion (PSD) curves of powders undergoing magic-angle spinning. Therefore a maximum proton spin order of 4 is expected to accurately capture the dynamics of the proton bath. In the case of carbon-13 PDSD, there is typically a separation of time-scales between the slow transfer of polarisation between the carbon spin pairs and the fast decoherence of carbon–carbon correlations under the action of the surrounding proton bath.^6,12,13 This suggests that coherences involving more than 2 carbons can be excluded from the reduced Liouville space.

Fig. 1 A schematic of the reduced Liouville space used for the LCL simulations of proton-driven carbon-13 spin diffusion with q_C = 2 and q_H = 4. The indices u and v run over all of the available carbon spins, while the indices i, j, k and l run over the proton spins. The lines connecting the product operators represent the action of the various terms in the interaction Hamiltonian, where H_II, H_SS and H_IS are represented by the red, blue and green lines, respectively. The dashed lines indicate that the evolution to higher-order correlations has been blocked as a consequence of the Liouville space reduction.

The time-evolution of the density matrix under the influence of the interaction Hamiltonian can be calculated through numerical integration of the Liouville–von Neumann equation:

Here L_X is the reduced-space Liouvillian, i.e., the projection of the full Liouvillian L onto the reduced space.²³ In the case of carbon-13 PDSD, the interaction Hamiltonian H = H_S + H_IS + H_SS + H_II is the sum of the chemical-shift Hamiltonian H_S for the dilute S spins, the secular heteronuclear dipolar coupling Hamiltonian H_IS between the I and the S spins, and the secular homonuclear dipolar coupling Hamiltonians for the I and the S spins, respectively: H_II and H_SS. The chemical-shift term for the abundant I spins can also be included. However, in the case of strongly coupled proton spins, the inclusion of a chemical-shift term is not expected to significantly affect the observed polarisation transfer because the dipolar interactions of the proton bath are much stronger than the chemical-shift interactions.

The spin-diffusion curves presented herein were calculated using a numerical integration scheme based on the Suzuki–Trotter algorithm.²³ The details of this implementation, using the Tourbillon program, have been reported elsewhere.¹⁸ This numerical integration scheme is advantageous in that it does not require the explicit storage of the Liouvillian matrix. Only a single copy of the density matrix is stored and so the memory requirements of the simulation are minimised.

In the homonuclear case of proton spin diffusion, LCL simulations of polarisation transfer were shown to quantitatively reproduce full-space simulations of 10–12 spins for powdered samples undergoing magic-angle spinning.¹⁷ In contrast, comparisons of LCL and full-space simulations of polarisation transfer among weakly coupled spins in the presence of a bath of strongly coupled hetero-nuclei highlight some interesting differences between the spin dynamics of finite, isolated spin systems in full and reduced Liouville spaces.¹⁸ While the reduced-space and full-space simulations produce the same initial dynamics, the long-term quasi-equilibrium behaviour is markedly different.¹⁸

Systems for which the quasi-equilibrium single-spin polarisations eventually equalise, regardless of initial conditions, are characterised by only a single “relevant” constant of motion: the total polarisation.² In Liouville space, the constants of motion are the eigenoperators of the Liouvillian that correspond to eigenvalues of zero. A “relevant” constant of motion is, in this context, a constant of motion that contributes to the quasi-equilibrium value of the observables of interest. For an orthogonal set of constants of motion {A_m} chosen such that A₁ is the total polarisation, a uniform distribution of the total polarisation is observed if 〈A_m|S_uz〉 = 0 for any m > 1 and all u, where S_uz is the single-spin polarisation of spin u. Calculations of the constants of motion of medium sized spin systems (≤10 spins) in full space show that constants of motion other than the total polarisation contribute significantly to the quasi-equilibrium single-spin polarisations, in accordance with earlier numerical observations.^24,25 In contrast, in reduced-space LCL simulations, the total polarisation is always the only relevant constant of motion for spin systems of at least five homonuclear spins undergoing magic-angle spinning.²⁶ This equalisation of the polarisation for chemically-distinguishable groups of spins is expected to be observed experimentally in the limit of very large strongly-coupled spin systems.² Therefore, we postulate that this property introduced by the LCL spin–space reduction scheme, while preventing a direct validation with full-space simulations of medium-sized spin systems, will not be a source of inaccuracy for comparison with experiment, but rather an important feature that plays a key role in the success of this method, allowing us to bypass the thermodynamic wall and use a very much smaller number of spins in the LCL simulation than would be needed in a full-space description to obtain the same accuracy. Interestingly, the decrease in the number of relevant constants of motion is not observed in reduced-space simulations of static powders. A more detailed investigation into the underlying mechanisms of the spin dynamics and thermodynamics in reduced spaces is currently underway, the results of which will be the subject of a subsequent publication.

Fig. 2 presents a comparison between experimental proton-driven carbon-13 spin-diffusion build-up curves and LCL simulations performed directly from crystal geometry for a polycrystalline sample of L-histidine·H₂O·HCl undergoing 15 kHz MAS, in a static magnetic field of 16.4 T. These experimental data were previously published and all experimental details can be found in ref. 27. Fig. 2 demonstrates excellent agreement over the full time scale of the experiment. Significantly, the simulated build-up curves are obtained without any adjustable parameters. The comparison between simulation and experiment simply requires a renormalisation, which accounts for experimental factors such as the efficiency of the initial cross-polarisation step.²⁶ The LCL simulation shown here was performed with a system that consists of the 6 carbons and 10 protons of a single molecule of L-histidine in a reduced Liouville space that excludes coherences involving more than 2 carbons or more than 4 protons. This dramatically simple spin system seems to capture perfectly all the elements of the experimental behaviour.

Fig. 2 Comparison between experimental (circles) and simulated (solid line) proton-driven spin-diffusion build-up curves for a powder sample of L-histidine·H₂O·HCl undergoing 15 kHz MAS. The simulated curves were obtained from LCL simulations of a system of 6 carbons and 10 protons, consisting of a single molecule of L-histidine. Atomic coordinates are taken from a crystal structure (CSD entry: histcm12), determined by neutron diffraction on a single-crystal sample. The time step in the simulation is 0.5 μs, and a ZCW set of 50 orientations is used for the powder average.

Fig. 3 presents the result of increasing the number of protons included in the simulation for a representative sub-set of build-up curves.²⁶ Simulated build-up curves obtained with 13 protons do not show any significant improvements over the 10-proton case, suggesting that the latter are reasonably converged. However, the simulations performed with 7 protons show clear discrepancies with the experimental data. Comparisons between simulation and experiment, analogous to those presented in Fig. 2, were also made for MAS spinning rates of 10 kHz and 20 kHz. They demonstrate that LCL simulations accurately describe the effect of spinning.²⁶

Fig. 4 presents a comparison between a representative set of experimental build-up curves and full-space simulations performed with the software SPINEVOLUTION.²⁸ A system of 6 carbons and 7 protons, the largest accessible spin system in SPINEVOLUTION, is used. Other programs are similarly limited with regard to spin-system size.^28–30 The overall agreement between simulation and experiment is very poor, due in large part, it seems, to the quasi-equilibrium state of the full-space simulations. The departure from an equalisation of the quasi-equilibrium polarisations in small spin systems is especially significant when the carbon-chemical-shift terms are taken into account, as is necessary in a simulation of PDSD. Although a ¹H relaxation superoperator¹⁶ can be used to facilitate polarisation transfer among carbons, it has not as yet led to an accurate description of experimental measurements.

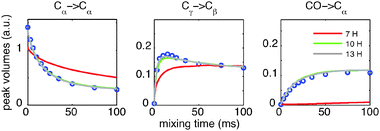Fig. 3 Comparison between experimental (circles) and simulated (solid line) proton-driven spin-diffusion build-up curves for a powder sample of L-histidine·H₂O·HCl undergoing 15 kHz MAS. A representative selection is shown. The simulated curves were obtained from LCL simulations of a system of 6 carbons and Nprotons, consisting of all the carbons in a molecule of L-histidine and the Nprotons that are the most strongly coupled to these carbons. The atomic coordinates, time step and orientations are the same as in Fig. 2.

Fig. 4 Comparison between experimental (circles) and simulated (solid line) proton-driven spin diffusion build-up curves for a powder sample of L-histidine·H₂O·HCl undergoing 15 kHz MAS. A representative selection is shown. The simulated curves were obtained from full-space simulations of a system of 6 carbons and 7 protons, consisting of all of the carbons in a molecule of L-histidine and the 7 protons that are the most strongly coupled to these carbons. The atomic coordinates, time-step and orientations are the same as in Fig. 2.

A comparison between the full-space and reduced-space simulations in Fig. 2 and 4 suggests that the remarkable agreement between the LCL simulations and experiment is the result of two factors. First, it is clear from Fig. 4 that the maximum number of protons achievable with the SPINEVOLUTION software (7 in this case) is insufficient to accurately capture the spin dynamics of the proton bath. The favourable polynomial scaling properties of the LCL simulation allow for additional protons to be included and so convergence is achieved with respect to the action of the proton bath. Second, in striking contrast to the behaviour obtained for full-space simulations, the experimental spin diffusion build-up curves display a full equilibration of the carbon polarisation, a feature accurately reproduced by the LCL simulations due to the unique spin-dynamic property introduced by the spin–space restriction scheme.

Taken together, the set of LCL simulations presented in this letter are, to the best of our knowledge, the first quantitative first-principles prediction of carbon-13 PDSD in a multi-spin system calculated directly from crystal geometry without any adjustable parameters.

Acknowledgements

This work was supported in part by the Agence Nationale de la Recherche (ANR-2010-BLAN-0806-01).

Notes and references

1. N. Bloembergen, Physica (Amsterdam), 1949, 15, 386–426.
2. B. H. Meier, Adv. Magn. Opt. Reson., 1994, 18, 1–116.
3. A. Abragam, Principles of Nuclear Magnetism, Oxford University Press, Oxford, 1983.
4. K. W. Eberhardt, S. Mouaziz, G. Boero, J. Brugger and B. H. Meier, Phys. Rev. Lett., 2007, 99, 227603.
5. W. R. Zhang and D. G. Cory, Phys. Rev. Lett., 1998, 80, 1324–1327.
6. D. Suter and R. R. Ernst, Phys. Rev. B: Condens. Matter, 1985, 32, 5608–5627.
7. F. Castellani, B. van Rossum, A. Diehl, M. Schubert, K. Rehbein and H. Oschkinat, Nature, 2002, 420, 98–102.
8. T. Manolikas, T. Herrmann and B. H. Meier, J. Am. Chem. Soc., 2008, 130, 3959–3966.
9. C. Wasmer, A. Lange, H. Van Melckebeke, A. B. Siemer, R. Riek and B. H. Meier, Science, 2008, 319, 1523–1526.
10. I. Bertini, A. Bhaumik, G. De Paepe, R. G. Griffin, M. Lelli, J. R. Lewandowski and C. Luchinat, J. Am. Chem. Soc., 2010, 132, 1032–1040.
11. X. H. Peng, D. Libich, R. Janik, G. Harauz and V. Ladizhansky, J. Am. Chem. Soc., 2008, 130, 359–369.
12. P. M. Henrichs, M. Linder and J. M. Hewitt, J. Chem. Phys., 1986, 85, 7077–7086.
13. A. Kubo and C. A. McDowell, J. Chem. Soc., Faraday Trans., 1988, 84, 3713–3730.
14. S. Zhang, B. H. Meier and R. R. Ernst, Phys. Rev. Lett., 1992, 69, 2149–2151.
15. M. Goldman, Spin Temperature and Nuclear Magnetic Resonance in Solids, Oxford University Press, Oxford, 1970.
16. A. Grommek, B. H. Meier and M. Ernst, Chem. Phys. Lett., 2006, 427, 404–409.
17. M. C. Butler, J.-N. Dumez and L. Emsley, Chem. Phys. Lett., 2009, 477, 377–381.
18. J.-N. Dumez, M. C. Butler and L. Emsley, J. Chem. Phys., 2010, 133, 224501.
19. J.-N. Dumez, M. C. Butler, E. Salager, B. Elena-Herrmann and L. Emsley, Phys. Chem. Chem. Phys., 2010, 12, 9172–9175.
20. H. J. Hogben, P. J. Hore and I. Kuprov, J. Chem. Phys., 2010, 132, 174101.
21. I. Kuprov, J. Magn. Reson., 2008, 195, 45–51.
22. I. Kuprov, N. Wagner-Rundell and P. J. Hore, J. Magn. Reson., 2007, 189, 241–250.
23. M. Suzuki, S. Miyashita and A. Kuroda, Prog. Theor. Phys., 1977, 58, 1377–1387.
24. R. Bruschweiler and R. R. Ernst, Chem. Phys. Lett., 1997, 264, 393–397.
25. J. S. Waugh, Mol. Phys., 1998, 95, 731–735.
26. See ESI†.
27. J.-N. Dumez and L. Emsley, Phys. Chem. Chem. Phys., 2011, 13, 7363–7370.
28. M. Veshtort and R. G. Griffin, J. Magn. Reson., 2006, 178, 248–282.
29. M. Bak, J. T. Rasmussen and N. C. Nielsen, J. Magn. Reson., 2000, 147, 296–330.
30. P. Hodgkinson and L. Emsley, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 201–239.

---

Footnotes

† Electronic supplementary information (ESI) available: (A) A description of the procedure used to determine the “relevant” constants of motion of a given simulation; (B) a detailed description of the comparison between simulated and experimental build-up curves; (C) additional sets of build-up curves. See DOI: 10.1039/c1cp22662b

‡ Present address: California Institute for Quantitative Biosciences, University of California, Berkeley, CA 94720, USA.

---