Improved chemical energy component analysis
Received
1st August 2011
, Accepted 14th October 2011
First published on 15th November 2011
Abstract
An improved SCF energy decomposition scheme is proposed in which a special treatment is introduced for those “ionic” one-center electron–electron repulsion energy contributions which arise from the use of doubly filled bonding orbitals. These terms characterize the bonding pattern rather than the state of the atoms, therefore they are attributed to the bonds and are redistributed between them in accord with the bond orders. This permits one to solve the dilemma which we had with the previous decomposition schemes, and obtain very “chemical” one- and two-center energy components, characterizing well the bonding situation in different molecules.
1. Introduction
Energy decomposition may be a valuable tool for interpreting the results of quantum chemical calculations and connecting them with the genuine chemical concepts. In the framework of the 3-dimensional analysis based on Bader's topological “atoms in molecules” theory,1 the SCF energy of a molecule breaks down spontaneously into a sum of contribution of the individual atoms and of the pairs of atoms.2,3 This is a very important result from the conceptual point of view, and one wishes to obtain a similar decomposition also when a “Hilbert space analysis” is applied, i.e., when the analysis is based on the fact that atom-centered basis orbitals are used in the calculations. That aim could easily be reached in the semiempirical theories where only one- and two-center integrals are used.4 Clementi had undertaken a straightforward analysis based on the centers of the integrals in the ab initio case,5 and his results showed that the existence of the three- and four-center integrals led to the appearance of significant three- and four-atomic energy components, which is hardly meaningful from a chemical point of view: we do not usually consider large primary three- and four-atomic chemical interactions. (Even such collective effects as aromaticity can be qualitatively understood without such terms, as the success of the simple Hückel method also indicated.)
In papers6–9 we have considered different possibilities permitting to circumvent that problem and to present the total molecular energy obtained in SCF calculations as a sum of atomic and diatomic contributions—either exactly or approximately, but to a good accuracy. In the scheme called “chemical energy component analysis” (CECA) the three- and four-center effects were compressed into one- and two-center ones by subjecting the three- and four-center integrals to a projective integral approximation.6 The individual energy component of the CECA scheme sums exactly to the total energy only for diatomic molecules, while in the general case they give only a good approximation. Two exact schemes have also been considered, they were denoted E1 and E2 in the paper.8 In their case the individual terms were assigned to the different atoms or pairs of atoms according to the basis orbitals (and nucleus) occurring in the “ket” of the respective integral. These schemes differ in treating the kinetic energy integrals. In scheme E1—similarly to CECA—the kinetic energy is considered as constituting a part of the intraatomic Hamiltonian and is treated accordingly. In scheme E2 (it has been first introduced in ref. 7) the kinetic energy gives direct contributions to both mono- and diatomic energy components, simply according to the centers involved in each integral.
One may introduce the same integral approximations as used in CECA also in schemes E1 and E2 and get their approximate counterparts A1 and A2, respectively.8 The sum of A1 or A2 energy components gives exactly the same approximation to the total SCF energy as does the CECA scheme. However, neither A1 nor A2 gives results coinciding to CECA: CECA differs from A1 by assigning some minor terms called “basis extension” ones10 to two-center terms instead of the atomic ones.
When considering these energy decomposition schemes, we have arrived at a dilemma:9 one either gets (in schemes E2, A2) two-center energy components which have values “on the chemical scale” at the equilibrium conformations of the molecules, but behave counter-intuitively when the bonds are stretched (they become more negative and not less negative with the increasing bond lengths) or the two-center components have a qualitative correct distance-dependence but are too large in absolute value (schemes CECA, E1, A1). In the first case the quick decay of the kinetic energy integrals gives rise to the counter-intuitive distance dependence mentioned. In the second case the too negative two-center components are compensated by large positive deviations in the one-energy components—they are much less negative than the free-atom energies.†
The energy decomposition with wrong distance dependence is hardly acceptable, so one had to prefer the second choice.9 That was quite adequate in many respects, e.g., permitted to predict the fragmentation patterns of mass-spectra, similarly or even better than bond order indices do,12 but the present author could completely understand those chemists who expressed the opinion that they “do not buy such non-chemical numbers” (e.g.,ref. 13).
We note also in this context that in the “natural” energy decomposition scheme of the AIM theory,2,3 there are only one-center kinetic energy contributions due to the integration over disjunct atomic domains, and that is carried over to the LCAO “mapping” of that scheme.2 This fact represents another argument in favour of treating kinetic energy as a part of the atomic Hamiltonians.
In this situation it seemed meaningful to clarify the origin of those “too large” numbers. We could recall the observation that in the semiempirical MNDO theory the total formation energies are very well on the “chemical scale” (due to the parametrization to reproduce experimental heat of formation) but the two-center energy components are about as large as in our ab initio schemes (e.g.,ref. 14). This provided us with an extremely simple model on which the problem could be analyzed—the H2 molecule treated at the MNDO level.
Using the classical MOPAC program15 and the MNDO Hamiltonian,16 one obtains for the binding energy of the H2 molecule at an experimental interatomic distance of 0.74 Å the quite reasonable value of 4.396 eV = 101.4 kcal mol−1. However, the diatomic energy component is as large as −10.82 eV = −249.5 kcal mol−1. This is compensated by the one-center energy components: each of them is higher than the MNDO energy of a free hydrogen atom by 3.212 eV = 74.07 kcal mol−1. Owing to the fact that MNDO uses a minimal basis, the one-center energy components of the H2 molecule do not depend on the interatomic distance. They consist of the expectation value of the one-electron atomic Hamiltonian‡ that is equal to the MNDO energy of the free hydrogen atom, and an electron–electron repulsion term which is equal to the value 3.212 eV, mentioned above. The source of this number is obviously the following. Each hydrogen atom of the H2 molecule contains one electron on average, so the one-electron energy component is equal to the MNDO atomic energy of the free hydrogen, but the use of doubly filled orbitals means that the wave function contains both covalent and ionic terms, and the latter gives rise to some intraatomic electron repulsion which is absent in a free H atom. These ionic terms are responsible for the bad dissociation behaviour of the RHF function at large distances but, of course, they are present at every distance, and we now identify them as the source of imbalance in the one- and two-center energy components. In fact, one may conclude that these ionic energy components arise as consequences of the bond formation, therefore they should be assigned to the bond(s), rather than to the individual atoms: at the MNDO level there is no room for any true promotion of the hydrogen atom, so the hydrogen atom in the H2 molecule differs from the free atom only by the fact of being bonded. That does not justify its one-center energy to differ from that of the free atom.
The aim of the present paper is to develop an ab initio scheme of partitioning the Hartree–Fock (HF) energy, utilizing the above conclusion, i.e., such one in which those one-center “ionic” two-electron energy components which originate from the bonding are regrouped from the atoms to the bonds. The scheme should be developed in such a manner as to exclude any elements of arbitrariness, as far as that is only possible.
Presenting the total energy, a single quantity, as a sum of different components is usually not unambiguous, and one has to look for some physical or chemical guidelines in order to get meaningful results. For the reasons discussed below, in the present work we shall start with an exact energy decomposition scheme that has not been considered previously; it may be called an “exact version of CECA”. It permits one to keep the CECA philosophy but also to get rid of the “white noise” caused by the use of integral approximations in the original CECA. This scheme has first been obtained by observing that the integral approximations do not involve the terms in which our different schemes deviate from each other, so every energy component of the exact scheme E1 differs from that of the approximate scheme A1 exactly by the same amount as does E2 from A2. Thus one may calculate these corrections for either scheme E1 vs. A1 or E2 vs. A2, and by adding them to the respective CECA energy component one obtains an exact energy decomposition, too. The same result can also be obtained by starting from the E1 scheme and regrouping the terms by which A1 and CECA differ. The explicit formulae of the new scheme will be given below. They will be then modified in order to account for the special feature of the atomic ionic energy terms, as discussed above.
2.1. The conditions introduced
In accord with the discussion given in the Introduction, we should develop such a decomposition of the molecular HF energy into the sum of atomic and diatomic contributions, which satisfies the following additional conditions:
(1) In a minimal basis calculation the atomic energy component of the H atoms in the H2 molecule should be equal to the energy of the free H-atom in the given basis. The fulfillment of this requirement requires regrouping a part of the formally one-center electron–electron energy components to the bonds. For a more complex system the determination of these energy components and their distribution between the bonds should be done automatically, based on reasonable chemical–physical considerations.
(2) The sum of the one- and two-center energy components should reproduce the total molecular HF energy. It may be meaningful to have also a possible version representing a good approximation to the exact decomposition, in which one has to use one- and two-center integrals only, but three- and four-center ones are not needed. (In the present paper we shall concentrate on the exact version.)
2.2. The H2 model
In the ab initio case, even if a minimal basis set is used, the analysis is somewhat more complicated than in the MNDO one, due to the presence of interatomic overlap. Considering explicitly the one-electron part of the energy for the minimal basis H2 problem, one can easily see that neither scheme “1” nor scheme “2” discussed in ref. 8 are able to reproduce the one-electron energy of the free hydrogen atom corresponding to the given minimal basis, while the “chemical energy component analysis” (CECA) scheme6 fulfills that requirement. To see this, let us consider the expectation value of the one-electron Hamiltonianfor the minimal basis H2 problem. In (1) A is the intraatomic Hamiltonian of atom A and ÛB is the potential energy caused by nucleusB. Operators
A is the intraatomic Hamiltonian of atom A and ÛB is the potential energy caused by nucleusB. Operators  B and ÛA are defined analogously. Assuming that the basis orbitals χ1 and χ2 are centered on atoms A and B, respectively, and introducing the usual “density matrix” D for the doubly occupied orbital, one can write an expression symmetric in the two atoms:
B and ÛA are defined analogously. Assuming that the basis orbitals χ1 and χ2 are centered on atoms A and B, respectively, and introducing the usual “density matrix” D for the doubly occupied orbital, one can write an expression symmetric in the two atoms:| | 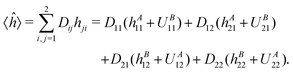 | (2) |
Thus the term containing  A is D11hA11 + D12hA21. In CECA6 the integral in the second term has been decomposed as
A is D11hA11 + D12hA21. In CECA6 the integral in the second term has been decomposed as| | hA21 = 〈χ2| A|χ1〉 = 〈χ2| A|χ1〉 = 〈χ2|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A A A|χ1〉 + 〈χ2|(1 − A|χ1〉 + 〈χ2|(1 − ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A) A) A|χ1〉 A|χ1〉 | (3) |
where ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A is the projector on the basis functions centered on atom A. In the given case
A is the projector on the basis functions centered on atom A. In the given case ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = |χ1〉〈χ1|, thus we get the term containing
A = |χ1〉〈χ1|, thus we get the term containing  A as
A as| | (D11 + D12S21)hA11 + 〈χ2|(1 − ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A) A) A|χ1〉 = hA11 + 〈χ2|(1 − A|χ1〉 = hA11 + 〈χ2|(1 − ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A) A) A|χ1〉 A|χ1〉 | (4) |
because D11 + D12S21 is Mulliken's gross atomic population on atom A and that is equal one for the H2 molecule. The term 〈χ2|(1 − ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A)
A) A|χ1〉 would vanish if χ1 were an exact eigenvector of
A|χ1〉 would vanish if χ1 were an exact eigenvector of  A or
A or ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A corresponded to a complete basis. In CECA that term was assigned to the diatomic energy component, so for the monoatomic one-electron energy component the energy of the free hydrogen atom is recovered, as it is required.
A corresponded to a complete basis. In CECA that term was assigned to the diatomic energy component, so for the monoatomic one-electron energy component the energy of the free hydrogen atom is recovered, as it is required.
Now, we shall consider the one-center two-electron energy components, which in the H2 case should completely be re-assigned to the bond, instead of the individual atoms. In the CECA scheme6 the two-electron part of the one-center energy is given for a closed-shell system as
| | 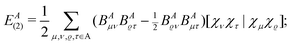 | (5) |
where
BA is the “projected density
matrix” introduced in
ref. 6, and we have been using here the [12|12] convention for the two-electron integrals. As there is only one basis orbital on each atom, a simple derivation shows that the same quantity can be expressed in the H
2 case simply as the integral
where
φA is the intraatomic part of the molecular orbital (MO)
φ of the H
2 problem and
ψA is defined as the atomic projection of
φ,
i.e.,
ψ =
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) Aφ.
Aφ.
One has to extract the quantity EA(2) from the CECA atomic energy component of each atom and add it to the diatomic energy component. Then the requirement of recovering the free-atom energy for each H atom in the H2 problem treated with a minimal basis will be fulfilled and the total energy—the sum of atomic and diatomic energy components—remains unchanged.
The meaning of the equality (6) may be clarified by considering the case when there is no interatomic overlap—as in the MNDO one discussed in the Introduction. Then the MO φ is simply 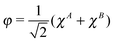 and
and 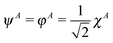 . Thus we get in that case EA(2) = ¼[χAχA|χAχA], i.e., the repulsion of two electrons on orbital χA, multiplied by the factor of ¼ following from the weight of the ionic term in the RHF wave function. In the general, overlapping case the appearance of the projected function ψA means that not only the net, but the full gross orbital population is accounted for in calculating the ionic terms. The form (6) of the ionic energy contribution will be utilized in our new scheme.
. Thus we get in that case EA(2) = ¼[χAχA|χAχA], i.e., the repulsion of two electrons on orbital χA, multiplied by the factor of ¼ following from the weight of the ionic term in the RHF wave function. In the general, overlapping case the appearance of the projected function ψA means that not only the net, but the full gross orbital population is accounted for in calculating the ionic terms. The form (6) of the ionic energy contribution will be utilized in our new scheme.
2.3. The “exact version of CECA”
According to the above considerations, for an approximate theory we shall start with the CECA energy decomposition,6 while for an exact one§ (that will be pursued here) we have to modify the formulae of the exact scheme “E1” discussed in ref. 8 by regrouping the terms containing the projectors like 1 − ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A, which were qualified as two-center “basis extension” ones,8,10 to the two-center energy components. Thus the relevant starting energy decomposition, which should then be modified by corrections for the ionic contributions, is given as
A, which were qualified as two-center “basis extension” ones,8,10 to the two-center energy components. Thus the relevant starting energy decomposition, which should then be modified by corrections for the ionic contributions, is given as| | 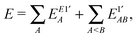 | (7) |
where| | 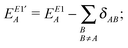 | (8) |
| | | EE1′AB = EE1AB + δAB + δBA; | (9) |
and the terms EE1A, EE1AB, δAB and δBA were defined in ref. 8. Here we consider the closed shell case only, so we can perform some simplifications and write| | 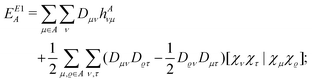 | (10) |
| | 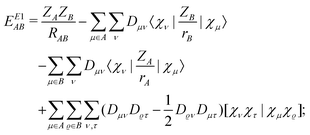 | (11) |
| | 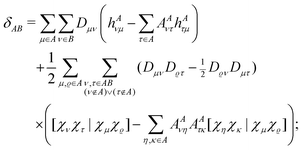 | (12) |
and δBA is obtained by interchanging A and B. In these equations the two-electron integrals are defined by using the convention [12|12], and the coefficients AAντ arising from the projections are defined as| | 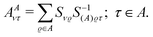 | (13) |
with S−1(A)ϱτ being an element of the inverse overlap matrix for atom A. In eqn (12) the restriction 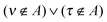 is introduced because for terms with both indices ν,τ ∈ A the difference in the parentheses vanishes trivially. (The intraatomic block of matrix AA is a unit matrix.)
is introduced because for terms with both indices ν,τ ∈ A the difference in the parentheses vanishes trivially. (The intraatomic block of matrix AA is a unit matrix.)
In the actual calculations—due to “historical” reasons—we did not use these formulae directly; instead at first the energy decomposition according to the approximate CECA scheme6 has been accomplished, and then the terms obtained have been corrected with the differences calculated for the exact and approximate schemes E1 and A1 (or E2 and A2) as discussed above—that did not require any new programming. We hope that in the near future we will be able to write—and make available through the Internet—a new program realizing the above equations directly.
2.4. The MOs to be used in the analysis
In the H2 case there is only one MO, so the identification of the ionic two-electron energy term which is to be re-assigned to the bond does not represent a problem. In many-atomic molecules there are several MOs. Some of them are doubly filled core or lone-pair orbitals; the ionic energy contributions corresponding them, of course, represent intrinsic atomic characteristics and are by no ways related to any bonding. There are also more or less localized bonding MOs for which corrections of the type considered for the H2 case above should be quite appropriate—and there may be orbitals representing cases intermediate between these extremes. In addition, there is unitary freedom in selecting the occupied orbitals. In such a situation one needs a scheme in which the different terms are not hand-picked arbitrarily but are determined in a possibly optimal manner.
For this reason, one has to consider for each atom a different set of occupied (localized) orbitals—that one which may be considered to be privileged from the point of view of the given atom. The MOs appropriate for that purpose are those, the intraatomic parts of which are the effective atomic orbitals17,18 (essentially McWeeny's “natural hybrid orbitals”19). These are the localized MOs which have maximal, or at least stationary, weights of their intraatomic parts, i.e., those for which Mulliken's net atomic population corresponding to the given MO—the so called Magnasco–Perico localization criterion20—is stationary. These localized orbitals φli(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) can be obtained by a unitary transformation of the canonic MOs φcj(
) can be obtained by a unitary transformation of the canonic MOs φcj(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ):
):
| | 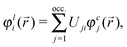 | (14) |
where the unitary matrix
U should diagonalize the matrix
Q with the elements
| | 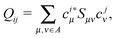 | (15) |
where
ciμ is the
μ-th LCAO coefficient of the
i-th canonic MO, and
Sμν is an element of the usual overlap
matrix. (The canonic orbitals are assumed orthonormalized,
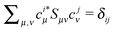
.). That means
The number of the orbitals to be considered for a given atom is given by min(
mA,
nocc), where
mA is the number of basis functions on atom
A and
nocc is the number of occupied orbitals in the molecule. (The “unnecessary” solutions, if any, correspond to zero eigenvalues
Mi.) There are other algorithms, too, which one can use for determining these localized orbitals.
17,18
The localized orbitals φli(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) can also be expanded in terms of the original basis orbitals χμ(
) can also be expanded in terms of the original basis orbitals χμ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ):
):
| | 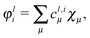 | (17) |
with the coefficients given by
| | 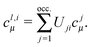 | (18) |
The privileged character of the orbitals φli is due to the fact that this is the only orthonormalized set of localized orbitals, for which the intraatomic parts of the orbitals also form an orthogonal atomic basis; the latter also diagonalize the intraatomic part of the density matrix.18 According to the experience, for non-hypervalent atoms the number of localized orbitals with eigenvalues Mi significantly differing from zero always coincides with the number of classical minimal basis orbitals of that atom. Therefore, by this set of orbitals one can clearly distinguish the doubly filled orbitals, the bonding orbitals and the practically empty basis orbitals of each atom.
2.5. The “ionic” corrections of the energy decomposition
Similarly to the case discussed for the H2 molecule, for every MO φli corresponding to atom A we may define its intraatomic part φAi| | 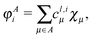 | (19) |
and its projection on the subspace of the basis orbitals centered on atom A| | 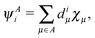 | (20) |
where the coefficients d can be expressed through the adjoint of matrix A defined above as| | 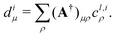 | (21) |
Every localized MO gives an “ionic” contribution to the one-center energy of atom A, which can be expressed, in terms of these notations, as
| | | EAi(2) = [ψAiψAi|φAiφAi], | (22) |
in full analogy with
eqn (6) we had in the H
2 case. However, for the core or lone-pair orbitals these ionic terms are inherently of atomic nature, while for the bonding orbitals they should be attributed to the bond(s). Instead of considering that question on a case-to-case basis, we introduce the following general treatment for solving that problem in a general fashion, permitting the intermediate cases to be also treated appropriately.
A doubly filled atomic orbital or an empty atomic orbital does not contribute to valence VA of the atom,21
| | 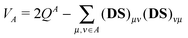 | (23) |
while an orbital forming a non-polarized bond contributes one to that valence. (In
eqn (23)QA = ∑
μ∈A(
DS)
μμ is Mulliken's gross atomic population on atom
A.) Therefore, we multiply the integral in
eqn (22) by the contribution
ViA of the corresponding effective atomic orbital
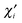
(normalized version of the intraatomic component
φAi) to the total valence, and extract product
VAi [
ψAiψAi|
φAiφAi] from the one-center energy—and add it to the two-center energy components, distributed according to the bond orders formed by the effective AO in question.
The contribution of the i-th effective atomic orbital to the valence of atom A (partial valence) can be obtained by rewriting eqn (23) in terms of the effective AOs 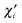 ; one gets
; one gets
| | 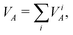 | (24) |
with
| | 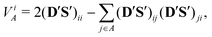 | (25) |
where
D′ and
S′ being the density and overlap matrices, respectively, transformed to the new basis orbitals
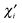
used on atom
A. (The basis orbitals on the other atoms may be considered unchanged.)
The known relationship between valences and sums of the bond orders21 holds for the partial valences and partial bond-orders, too:
| | 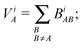 | (26) |
—it is based on the idempotency relationship (
DS)
2 = 2
DS valid for the closed-shell determinant wave functions. The partial bond order
BiAB corresponding to the effective AO
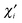
of atom A can be written as
| | 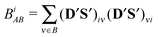 | (27) |
As shown in ref. 22, the matrix product D′S′ of the transformed matrices can be expressed in terms of the original ones as
where
matrix T is the matrix describing the transformation from the original basis functions
χμ to the new ones:
| | 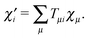 | (29) |
In the present case matrix T is a unit matrix, except its block connecting the new and old basis orbitals on atom A, and the same holds for its inverse. Because the “effective” AOs are orthonormalized, one has for the AA-block of matrix T the equality
from which
which permits the partial bond orders
BiAB to be calculated in an easy fashion as
| | 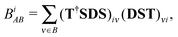 | (32) |
where it has been taken into account that
Tμν =
Tνμ =
δμν if
ν ∈
B;
B ≠
A. The partial valences
ViA need not be calculated explicitly by using
eqn (25), but may be simply obtained as sums according to
(26).
Thus the final one- and two-center energy components are given by
| | 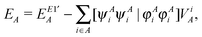 | (33) |
and
| | 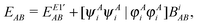 | (34) |
where
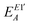
and
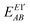
are given by
eqn (8) and (9), respectively.
3. Illustrative calculations
In order to test the viability of the idea of regrouping the intraatomic ionic electron–electron repulsion terms which are due to bonding, we have prepared an ad hoc stand alone suite of programs, representing versions of those (EFF-AO, APEX4) that are available from our website.23 The program reads the data in a “formatted check-point file” prepared in a previous “Gaussian” run and calculates everything else anew. All calculations were performed by using the standard 6-31G** basis, which is—according to our experience—very appropriate for studies of that type. (Of course, it was also checked that the requirement discussed above concerning the minimal basis H2 problem is met properly by the new program.) First of all we have repeated the calculations presented in ref. 6 for CECA and in the paper7 for the “exact” scheme (it was later called E2 in ref. 9), in order to see that the good properties of those methods have been conserved while their defects are corrected.
Tables 1–3 show the results in question. One may see that the new scheme apparently fulfills all the expectations, and the results may be called very “chemical”. The energy component corresponding to a C–C or C–H single bond is obtained to be about 150–170 kcal mol−1 (in absolute value), significantly less than the too large values (350–400 kcal mol−1) of the CECA and E1 schemes and greater than the somewhat underestimated values (100–120 kcal mol−1) of the E2 one¶ The non-bonded interactions are not much influenced with the corrections introduced here and we get results similar to those in ref. 6 and 7. In the cases where some significant difference occurs, there the present results seem much more reassuring: it was not easy to understand why one of the vicinal H⋯H interactions gave a small negative number in the ethane molecule6,7—here no such problem arises.
Table 1 Energy components of the methane ethane, ethylene and acetylene molecules calculated by using the 6-31G** basis set
| Atom(s) |
Energy component (6-31G**) ΔEA, EAB/kcal mol−1 |
|
Methane
|
Ethane
|
Ethylene
|
Acetylene
|
| C |
59.22 |
83.91 |
108.28 |
155.38 |
| H |
57.61 |
54.62 |
64.76 |
102.57 |
| C–C |
— |
−159.13 |
−296.59 |
−481.02 |
| C–H |
−168.13 |
−167.20 |
−167.22 |
−150.97 |
| H–H geminal |
8.21 |
8.58 |
10.05 |
— |
| H–H vicinal |
— |
2.30 (2x) |
2.97 |
5.03 |
| |
1.54 (1x) |
1.90 |
|
| C–H vicinal |
— |
5.92 |
6.51 |
−16.80 |
Table 2 Energy components of the benzene molecule calculated by using the 6-31G** basis set
| Atom(s) |
Energy component (6-31G**) ΔEA, EAB, kcal mol−1 |
| C |
162.62 |
| H |
73.69 |
| C1–C2 |
−291.46 |
| C1–C3 |
18.45 |
| C1–C4 |
21.52 |
| C1–H7 |
−157.23 |
| C1–H8 |
4.11 |
| C1–H9 |
−1.55 |
| C1–H10 |
−1.22 |
| H7–H8 |
2.92 |
| H7–H9 |
1.87 |
| H7–H10 |
1.37 |
Table 3 Energy components of the diborane molecule calculated by using the 6-31G** basis set
| Atom(s) |
Energy component (6-31G**) ΔEA, EAB/kcal mol−1 |
| B |
240.37 |
| H bridge |
−0.54 |
| H terminal |
−9.51 |
| B–H bridge |
−96.79 |
| B–H terminal |
−127.38 |
| B–B |
−112.62 |
| H bridge--H bridge |
27.73 |
| H bridge--H terminal |
2.44 |
| H terminal--H terminal |
3.71 |
| H terminal--H terminal′ |
0.97 |
| |
0.76 |
Fig. 1 displays how the C–C diatomic energy component changes when the bond is stretched; it shows that we have reached our goal of putting the diatomic energy components “to the chemical scale” conserving at the same time the adequate character of the distance dependence characteristic for those (CECA-type or E1) schemes, in which the kinetic energy is considered a part of the atomic Hamiltonian. Essentially we have got a nearly parallel shift of the “exact CECA” results to the chemically adequate range of values.
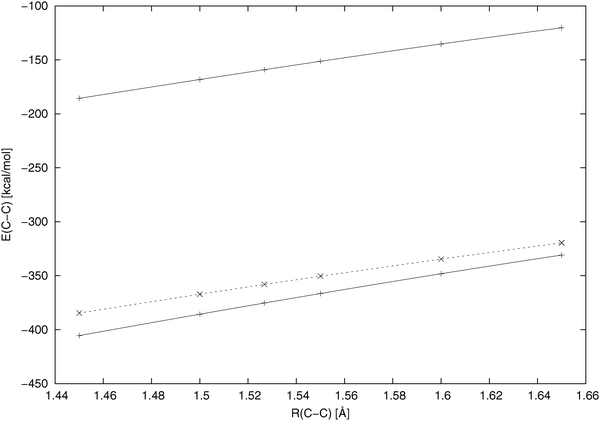 |
| | Fig. 1 The distance dependence of the C–C diatomic energy component of the ethane molecule when the bond is stretched (6-31G** calculation). Upper solid line: the present energy decomposition scheme; lower solid line: eqn (9), the “exact CECA” scheme; dashed line: eqn (11), the scheme denoted “E1” in ref. 9. | |
While the C–H energy components do not change too much from molecule to molecule, the one-center energy components—especially of the carbon atoms—vary significantly in the hydrocarbons studied. (The differences ΔEA with respect to the free ROHF atoms are always displayed.) In the previous studies practically no attention has been paid to the changes in the one-center energy components—they were either too far or too close to the free atomic energies, to be meaningfully compared. The new scheme gives a new possibility in this respect, too. Besides the atomic promotions,11 the main factor seems to be the following: an atom “collects” electrons during the molecule formation if that is favourable energetically. This energetic effect is expected to appear, in turn, in the one-center energy contributions: one may expect that the more negative atoms will exhibit lower energy components. Such a tendency may be seen in Fig. 2, in which the carbon one-center energy components of methane, ethane, butane, ethylene, and benzene are displayed against the gross Mulliken's atomic charges. Acetylene has, apparently, very strained carbon atoms; the respective point would be somewhat off to the curve drawn.
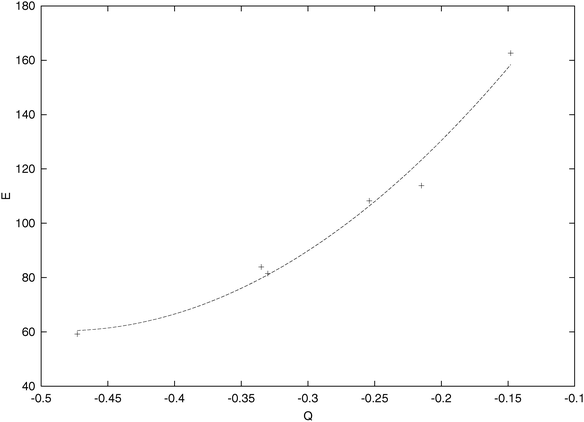 |
| | Fig. 2 The carbon one-center energy component (kcal mol−1) depending on Mulliken's gross atomic charge of the atom for several hydrocarbon molecules. | |
The connection between the one-center energies and the atomic charges appears even more prominent for systems containing heteroatoms, too. Table 4 displays some results for ethanol, glycine and N,N-dimethylformamide, (CH3)2N–CHO, molecules: the one-center energy components and the bonding two-center components are presented. (Where there are more than two atoms/bonds of a given type, then only the limiting values are displayed in parentheses.) One can see that the numbers obtained do completely agree with the chemical expectations: the different atoms exhibit one-center components characteristic to their nature and chemical environment: electronegative atoms (oxygen, nitrogen) have negative one-center components, carbon and hydrogen have positive ones; the more positive is the atom, the higher is its one-center energy. This leads to big differences between carbon and hydrogen atoms in the same molecule. Chemically similar atoms have, of course, similar one-center energies. Thus the two hydrogens in the CH2 group of the ethanol molecule have identical one-center energies of 45.7 kcal mol−1, while the CH3 group has two equivalent hydrogens (62.2 kcal mol−1) and one which differs somewhat (53.0 kcal mol−1). Similar tendencies hold for the C–H two-center energy components, too: −155.5 kcal mol−1 in the CH2 group and −170.1 (twice) and −166.0 kcal mol−1 in the CH3 one, respectively. Of course, the hydrogen atom in the OH group is positive, which leads to a rather high one-center energy component. The interaction between the positive hydrogen with the negative oxygen leads to an enhanced O–H two-center energy component, as compared with the C–H ones.
Table 4 One-center and bonding two-center energy components of the ethanol, glycine and N,N-dimethylformamide molecules calculated by using the 6-31G** basis set
| Atom(s) |
Energy component (6-31G**) ΔEA, EAB/kcal mol−1 |
|
Ethanol
|
Glycine
|
Dimethylformamide
|
| C (CH3) |
84.11 |
— |
— |
| C (CH2) |
228.72 |
155.58 |
— |
| C (COOH) |
— |
612.60 |
— |
| C (CHO) |
— |
— |
507.15 |
| O (COH) |
−163.59 |
−246.8 |
— |
O (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
— |
−212.39 |
−199.42 |
| N |
— |
−28.93 |
−140.54 |
| H (CH) |
(45.7; 62.2) |
61.5; 74.8 |
(50.7; 91.7) |
| H (OH) |
209.22 |
225.00 |
— |
| H (NH) |
— |
149.1; 160.9 |
— |
| C–C |
−183.69 |
−166.92 |
— |
| C–O (COH) |
−145.70 |
−223.98 |
— |
C–O (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
— |
−353.06 |
−339.54 |
| N–C (NH2CH2) |
— |
−170.21 |
— |
| N–C (CH3N) |
— |
— |
−176.8; −180.5 |
| N–C (NCO) |
— |
— |
−280.00 |
| C–H (CH3, CH2) |
(−155.5; −170.1) |
−165.0; −172.2 |
(−157.2; −163.2) |
| C–H (CHO) |
— |
— |
−118.79 |
| O–H |
−260.44 |
−250.20 |
— |
| N–H |
— |
−233.0; −235.1 |
— |
It seems not of too much meaning to discuss every atom and bond separately, not to speak about the large number of non-bonded interactions which also often represent significant interest. Instead, we mention that relative fine effects can be identified, too. For instance, in dimethylformamide molecules the N–C bonds connecting the nitrogen atom with the methyl group have significantly smaller (in absolute value) two-center energy components than the N–C bond connecting nitrogen with the CHO group: the N, C and O atoms form a small local π-system that leads to a larger N–C binding energy. Also, it may be worth mentioning that the two N–CH3 bonds are not identical; the somewhat shorter one has a little larger bond order and somewhat larger (in absolute value) diatomic energy contribution. This is what one expects. It may be mentioned in this connection that the previous E2 scheme gave these energy components in opposite order9 as a manifestation of its wrong distance dependence; that served as an argument against that scheme.
Another interesting feature of the dimethylformamide molecule is that it is one of the simplest systems in which the existence of the C–H⋯O intramolecular “hydrogen bond” has been postulated on the basis of its experimental geometry.24 That is well manifested in a non-negligible H⋯O bond order.9 The present energy decomposition method also gives the remarkable H⋯O two-center energy component of −13.9 kcal mol−1, significantly larger (in absolute value) than all the other H⋯O energy components (−4.7 to −6.2 kcal mol−1). However, the respective hydrogen one-center energy of 91.7 kcal mol−1 is also far off with respect to all the other ones, not exceeding 66 kcal mol−1. This indicates that the presence of a significant negative H⋯O energy component is symptomatic for such specific C–H⋯O interactions, but is not the single factor necessary for explaining them. (A deeper discussion of this problem is out of our present scope.)
These results—and a number of ones not shown here—indicate that we have succeeded with our aim of creating a decomposition scheme for partitioning the Hartree–Fock molecular energy into one- and two-center energy components reflecting well the chemical nature of the individual atoms and bonds. At the present the scheme is applicable for closed-shell (RHF) systems only; its extension to the open-shell systems (UHF level) represents the next challenge for us.
4. Conclusions
Here we have proposed an improved SCF energy decomposition scheme in which a special treatment is introduced for those “ionic” one-center electron–electron repulsion energy contributions which arise from the use of doubly filled bonding orbitals. These terms characterize the bonding pattern rather than the state of the atoms, therefore they are attributed to the bonds and are redistributed between them in accord with the bond orders. This permits one to solve the dilemma which we had with the previous decomposition schemes, and obtain very “chemical” one- and two-center energy components, characterizing well the bonding situation in different molecules.
Acknowledgements
The author acknowledges the partial financial support of the Hungarian Scientific Research Fund (grant OTKA 71816).
References
-
R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, U.K., 1990 Search PubMed.
- I. Mayer and A. Hamza, Theor. Chem. Acc., 2001, 105, 360 Search PubMed.
- P. Salvador, M. Duran and I. Mayer, J. Chem. Phys., 2001, 115, 1153 CrossRef CAS.
- H. Fischer and H. Kollman, Theor. Chim. Acta, 1970, 16, 163 CrossRef CAS.
- E. Clementi, J. Chem. Phys., 1967, 46, 3842 CrossRef CAS.
- I. Mayer, Chem. Phys. Lett., 2000, 332, 381 CrossRef CAS.
- I. Mayer, Chem. Phys. Lett., 2003, 382, 265 CrossRef CAS.
- I. Mayer, Phys. Chem. Chem. Phys., 2006, 8, 4630 RSC.
- I. Mayer, Faraday Discuss., 2007, 135, 439 RSC.
- A. Hamza and I. Mayer, Theor. Chem. Acc., 2003, 109, 91 Search PubMed.
- I. Mayer, Chem. Phys. Lett., 2010, 498, 366 Search PubMed.
- I. Mayer and Á. Gömöry, Chem. Phys. Lett., 2001, 344, 553 CrossRef CAS.
-
K. Vékey, private communication to the author (Budapest, ca. 2002).
- I. Mayer and Á. Gömöry, J. Mol. Struct. (THEOCHEM), 1994, 311, 331 CrossRef.
-
J. J. P. Stewart, Program MOPAC (Public domain), Version 7.00, 1993 Search PubMed.
- M. J. S. Dewar and W. Thiel, J. Am. Chem. Soc., 1977, 99, 4899 CrossRef CAS.
- I. Mayer, Chem. Phys. Lett., 1995, 242, 499 Search PubMed.
- I. Mayer, J. Phys. Chem., 1996, 100, 6249 Search PubMed.
- R. McWeeny, Rev. Mod. Phys., 1960, 32, 335 CrossRef.
- V. Magnasco and A. Perico, J. Chem. Phys., 1967, 47, 971 CAS.
- I. Mayer, Chem. Phys. Lett., 1983, 97, 270 CrossRef CAS.
-
I. Mayer, Eq. (7.38) in Simple Theorems, Proofs, and Derivations in Quantum Chemistry, Kluwer Academic/Plenum Publishers, New York, 2003 Search PubMed.
- See the web site http://occam.chemres.hu/programs.
- G. Schultz and I. Hargittai, J. Phys. Chem., 1993, 97, 4966 CrossRef CAS.
Footnotes |
| † In some of the previous publications it was not properly recognized that the differences between the one-center energy components and of the free atom energies cannot be simply identified with the promotion energies of the atoms in the molecule, because the one-center energy contributions also reflect delocalization and electron transfer effects etc. For a proper definition of the promotion energy we refer to ref. 11. |
| ‡ In the MOPAC program it is called “electron-nuclear attraction”, but obviously it should reflect also the one-center kinetic energy component. |
| § The individual energy component of the CECA scheme sum exactly to the total energy only for diatomic molecules.6 |
| ¶ In E2 the relatively small bonding energies occur along with one-center energy components that are too close to the free atom energies, as one can judge on the basis of comparison with the independent scheme of calculating atomic promotion energies.11 As discussed in the Introduction, the main problem with the E2 results was, however, in their counter-intuitive distance-dependence.9 |
|
| This journal is © the Owner Societies 2012 |
Click here to see how this site uses Cookies. View our privacy policy here.  ≡
≡  A + ÛB ≡
A + ÛB ≡  B + ÛA
B + ÛA A is the intraatomic Hamiltonian of atom A and ÛB is the potential energy caused by nucleusB. Operators
A is the intraatomic Hamiltonian of atom A and ÛB is the potential energy caused by nucleusB. Operators  B and ÛA are defined analogously. Assuming that the basis orbitals χ1 and χ2 are centered on atoms A and B, respectively, and introducing the usual “density matrix” D for the doubly occupied orbital, one can write an expression symmetric in the two atoms:
B and ÛA are defined analogously. Assuming that the basis orbitals χ1 and χ2 are centered on atoms A and B, respectively, and introducing the usual “density matrix” D for the doubly occupied orbital, one can write an expression symmetric in the two atoms: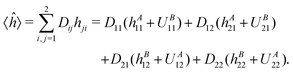
 A is D11hA11 + D12hA21. In CECA6 the integral in the second term has been decomposed as
A is D11hA11 + D12hA21. In CECA6 the integral in the second term has been decomposed as A|χ1〉 = 〈χ2|
A|χ1〉 = 〈χ2|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A
A A|χ1〉 + 〈χ2|(1 −
A|χ1〉 + 〈χ2|(1 − ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A)
A) A|χ1〉
A|χ1〉![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A is the projector on the basis functions centered on atom A. In the given case
A is the projector on the basis functions centered on atom A. In the given case ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = |χ1〉〈χ1|, thus we get the term containing
A = |χ1〉〈χ1|, thus we get the term containing  A as
A as![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A)
A) A|χ1〉 = hA11 + 〈χ2|(1 −
A|χ1〉 = hA11 + 〈χ2|(1 − ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A)
A) A|χ1〉
A|χ1〉![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A)
A) A|χ1〉 would vanish if χ1 were an exact eigenvector of
A|χ1〉 would vanish if χ1 were an exact eigenvector of  A or
A or ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A corresponded to a complete basis. In CECA that term was assigned to the diatomic energy component, so for the monoatomic one-electron energy component the energy of the free hydrogen atom is recovered, as it is required.
A corresponded to a complete basis. In CECA that term was assigned to the diatomic energy component, so for the monoatomic one-electron energy component the energy of the free hydrogen atom is recovered, as it is required.
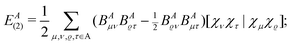
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) Aφ.
Aφ.
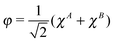 and
and 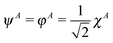 . Thus we get in that case EA(2) = ¼[χAχA|χAχA], i.e., the repulsion of two electrons on orbital χA, multiplied by the factor of ¼ following from the weight of the ionic term in the RHF wave function. In the general, overlapping case the appearance of the projected function ψA means that not only the net, but the full gross orbital population is accounted for in calculating the ionic terms. The form (6) of the ionic energy contribution will be utilized in our new scheme.
. Thus we get in that case EA(2) = ¼[χAχA|χAχA], i.e., the repulsion of two electrons on orbital χA, multiplied by the factor of ¼ following from the weight of the ionic term in the RHF wave function. In the general, overlapping case the appearance of the projected function ψA means that not only the net, but the full gross orbital population is accounted for in calculating the ionic terms. The form (6) of the ionic energy contribution will be utilized in our new scheme.![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A, which were qualified as two-center “basis extension” ones,8,10 to the two-center energy components. Thus the relevant starting energy decomposition, which should then be modified by corrections for the ionic contributions, is given as
A, which were qualified as two-center “basis extension” ones,8,10 to the two-center energy components. Thus the relevant starting energy decomposition, which should then be modified by corrections for the ionic contributions, is given as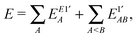
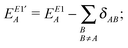
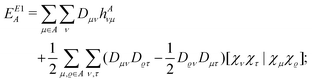
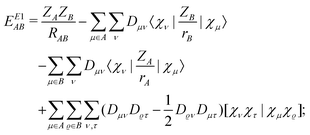
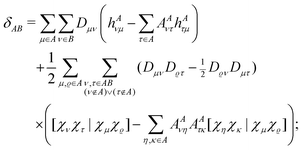
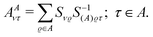
 is introduced because for terms with both indices ν,τ ∈ A the difference in the parentheses vanishes trivially. (The intraatomic block of matrix AA is a unit matrix.)
is introduced because for terms with both indices ν,τ ∈ A the difference in the parentheses vanishes trivially. (The intraatomic block of matrix AA is a unit matrix.)
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) can be obtained by a unitary transformation of the canonic MOs φcj(
) can be obtained by a unitary transformation of the canonic MOs φcj(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ):
):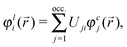
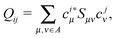
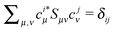 .). That means
.). That means![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) can also be expanded in terms of the original basis orbitals χμ(
) can also be expanded in terms of the original basis orbitals χμ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ):
):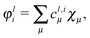
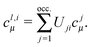
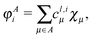
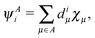
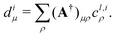
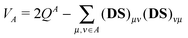
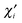 (normalized version of the intraatomic component φAi) to the total valence, and extract product VAi [ψAiψAi|φAiφAi] from the one-center energy—and add it to the two-center energy components, distributed according to the bond orders formed by the effective AO in question.
(normalized version of the intraatomic component φAi) to the total valence, and extract product VAi [ψAiψAi|φAiφAi] from the one-center energy—and add it to the two-center energy components, distributed according to the bond orders formed by the effective AO in question.
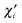 ; one gets
; one gets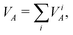
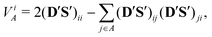
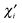 used on atom A. (The basis orbitals on the other atoms may be considered unchanged.)
used on atom A. (The basis orbitals on the other atoms may be considered unchanged.)
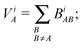
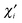 of atom A can be written as
of atom A can be written as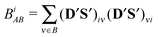
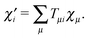
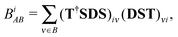
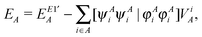
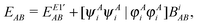
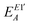 and
and 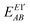 are given by eqn (8) and (9), respectively.
are given by eqn (8) and (9), respectively.


![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)
O)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)
O)