Experimental thermodynamics of free glycine conformations: the first Raman experiment after twenty years of calculations

Abstract

Low-frequency, gas-phase vibrational (Raman) spectroscopy was used in conjunction with a jet-cooled technique and ab initio calculations to study the intrinsic thermodynamic properties of the free (gas-phase) amino acid—glycine (Gly, H₂NCHRCOOH). The first experimental evaluation of the enthalpy differences between the Gly conformations in the vapor phase is presented. The enthalpy values were determined to be 0.33 ± 0.05 and 1.15 ± 0.07 kcal mol⁻¹ for the ccc and gtt rotamers, respectively; the corresponding relative entropy values were −2.86 ± 0.12 and −0.12 ± 0.16 cal mol⁻¹ K⁻¹, respectively. It was proven that the low-frequency Raman and infrared spectroscopy is capable of estimating intrinsic thermodynamic parameters of protein building blocks, such as intermolecular hydrogen bonds (ccc conformer) and rotation around one of the bonds (N–C, gtt conformer). The inaccuracy of the RRHO approximation to Gly conformers was experimentally confirmed. Benchmark data for quantum theory and molecular dynamics were provided.

---

1. Introduction

The intermolecular interactions of amino acids (AAs, H₂NCHRCOOH)—the building blocks of peptides and proteins—are responsible for the formation of the secondary structures of these biomolecules.¹ Unfortunately, liquid- or solid-state studies of these important interactions have been greatly influenced by solvent or environmental effects. The importance of intrinsic (gas-phase) studies has been widely accepted by the modern chemical community.² Only “biomolecules in the gas phase” can be regarded as systems in which the intrinsic interactions can be studied by modern physical, chemical, or physicochemical methods.²

Many of the current methods are based on mass spectrometry (MS) and are restricted to charged species.³ That has not been a major problem for AAs with positively or negatively charged R groups, but it is not useful for neutral amino acids with uncharged or hydrophobic side chains. In the latter case, the presence of a charge changes the properties of the amino acid and makes it difficult to match the experimentally observed values with the values obtained inside the protein or peptide.¹

Alternative approaches dealing with neutral (uncharged) amino acids are still relatively rare.⁴ The reason for the lack of methods for neutral AAs has been the extremely low abundance of AA in the gas phase in standard laboratory conditions. For example, the vapor pressure of glycine, H₂NCH₂COOH or R = H, only becomes measurable (∼0.1 Pa) at 100–150 °C.⁵ A further temperature increase would lead to decomposition of the substance (if a fast thermal heating technique was not applied).^5g The application of vibrational spectroscopy (infrared or Raman), which is well suited for studying intermolecular interactions,^2–5 is extremely limited at such substance concentrations. Another problem has been that the width of the vibrational lines rapidly grows with increasing temperature, making it difficult to interpret the observed vibrational spectra.^4,5 The problem with line resolution could be solved by the application of jet-cooled techniques.⁵ The drawback of jet-cooled methods has been the difficulties in studying the system under equilibrium conditions; it is impossible to accurately estimate the conformer content, hydrogen bond strength, or other thermodynamic parameters using this technique.⁵

That is why, even after 20 years of great theoretical interest,⁶ the experimental thermodynamics of free glycine (Gly) conformations are still unclear. The experimental energy difference between uncharged gas-phase Gly conformers has never been reported.⁶ The thermodynamics of the conformation equilibrium of the simplest amino acid is still unknown to this date.

In this report, the first experimental evaluation of the enthalpy differences between free amino acid conformations (Fig. 1) is presented. Glycine was chosen as the basic system.^5,6 The assignment of low-frequency vibrational bands was conducted by combining the theoretical (ab initio/DFT), the jet-cooled, and the gas-phase data.^5a,6i The thermochemical data were obtained by application of the van't Hoff equation (isochore) to the Raman spectrum of the gas-phase glycine.⁷ Overall, this study demonstrated the power of Raman spectroscopy for the recognition and analysis of intermolecular interactions in free and bound amino acids. The scheme of the Raman setup is shown in Fig. 2. See Experimental section and ref. 5a and 7 for a detailed discussion of the setup and experimental parameters.

Fig. 1 The first six lowest-energy conformers of the free (gas-phase) glycine (H₂NCH₂COOH, aminoethanoic acid). The nomenclature⁶ⁱ is based on the three torsion angles (e.g., gauche–cis–trans/gtc) and ref. 6e (e.g., Vn). The CCSD(T)/CBS relative electronic energies (in kcal mol⁻¹) are provided in square brackets.⁶ⁱ

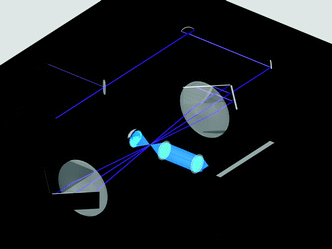Fig. 2 The principal scheme of the low-frequency Raman setup used.⁷ A 457 nm CW diode-pumped, solid-state laser beam was split into two unequal components using a partial reflectance plate beam splitter. The smaller part was sent to a laser power meter equipped with a high-sensitivity thermopile sensor. The larger part was sent to the gas-phase cell. A retroreflecting multipass cell (67 passes, three are shown) was made from two planoconvex lenses and four retroreflecting mirrors. The scattered light was collected using 90° geometry. To intensify the signal, the light scattered over a 270° angle (in the opposite direction) was reflected by a spherical mirror. The collected light was focused on the entrance slit of a Raman spectrometer.⁷

2. Experimental section

The low-frequency vibrational spectrum of the gas-phase glycine was recorded using a high-sensitivity Raman spectrometer.^5a,e,7 A spectral resolution of 4.2 and 2.1 cm⁻¹ was achieved. Spectral bands with signal-to-noise ratios (SNR) above 10 were used for the analysis. Biotechnology-grade glycine (>99.9%, Novosibirsk Institute of Organic Chemistry) was used throughout the study. The temperature range between 380 and 445 K (107 and 172 °C) was scanned with a constant step of 5 K (14 data points); Gly vapor pressure was used for spectrum registration.⁷ The minimal amino acid vapor pressure below 0.1 Pa^5a was reached. The duration for collecting one spectrum was set to 3 h. At each temperature, 2–12 spectra were used for averaging. It was controlled (Raman spectroscopy, mass spectrometry) that no (or negligible) sample decomposition occurs at the temperatures used. The correction for glycine adsorption on the cell walls and optical elements was performed according to ref. 7. Low-frequency background from the pure rotational transitions was predicted and subtracted before the spectrum analysis.⁷ Deconvolution of the vibrational bands⁷ was conducted for the precise evaluation of their integral intensities. Fitting parameters of glycine rotamers were adjusted by a robust least-squares procedure. Weighted (1/σ) least-squares regression was used for the thermodynamic (thermochemical) parameter evaluation. See also ref. 5e for extra discussion and acknowledgements.

3. Results and discussion

The experimental gas-phase vibrational Raman spectrum at 390 K (117 °C) is shown in Fig. 3. The spectrum was very complex due to the large width of each band, which was determined by its vibrational structure.^5f Spectral overlapping occurred in the 150–300 cm⁻¹ region. Fortunately, recent results of jet-cooled Raman spectroscopy, reported by Balabin,^5a enabled us to identify the bands and to assign them to the different Gly conformations. The trans–trans–trans (ttt) conformer had three characteristic bands in the frequency region studied, which were at 203.7 ± 1.1 (95%), 250.1 ± 1.1, and 458.1 ± 1.2 cm⁻¹; the cis–cis–cis (ccc) conformer had only one band at 302.9 ± 1.7 cm⁻¹; the gauche–trans–trans (gtt) structure had two bands at 171.1 ± 1.7 and 274.8 ± 1.9 cm⁻¹. Five out of the six (jet-cooled) bands can be clearly seen in Fig. 3. One gtt band (at 275 cm⁻¹) seemed to participate in a shoulder formation of the ttt 250 cm⁻¹ band.^5a Gas-phase peak positions were consistent with jet-cooled peaks, showing consistency within ∼2 cm⁻¹, as was expected for the resolution and vibrational temperature differences reported (114 vs. 390 K).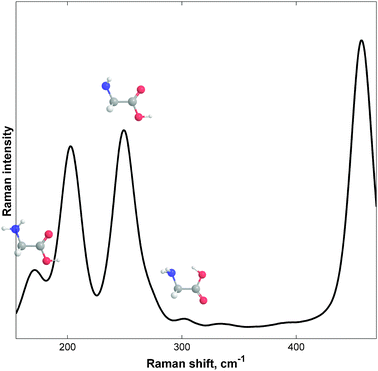

Fig. 3 The experimental gas-phase vibrational Raman spectrum (160–450 cm⁻¹) of free glycine (Gly) at 380 K (107 °C). Savitzky–Golay filtering (25-2) has been applied. See ref. 5a for the peak (band) assignments based on jet-cooled data.

Two minor peaks at ∼335 and ∼395 cm⁻¹ seemed to belong to overtones or combination modes of the ttt because of their temperature dependence. Note that no fundamental vibrations of any H₂NCH₂COOH conformer were expected in these regions.^5a,6 Because these bands did not appear in the jet-cooled (low-temperature) spectrum, they could be assigned to overtones/combination modes with confidence.⁸

In each band, there may, of course, be a contribution of hot bands, and the ratio of such a contribution also depends on the temperature. This factor may (slightly) affect the relative intensities of the bands, in addition to the relative population change among the isomers. Fortunately, the linearity of the van't Hoff plots (see below) proves that this contribution is negligible.

The right shoulder of the ttt 250 cm⁻¹ band could not be described by the gtt 275 cm⁻¹ band alone. From a previous study,^5a we know the intensity ratio of the two gtt bands (I₁₇₁/I₂₇₅) at 114 K is equal to 2.6. Even if the (vibrational) temperature difference was taken into account (I₁₇₁/I₂₇₅ ≈ 2.1 at 390 K), the shoulder was not fully described by the 275 cm⁻¹ band. The decomposition of the 230–290 cm⁻¹ band system with the constrained I₁₇₁/I₂₇₅ ratio led to the need for the third band at 269 ± 4 cm⁻¹ to correctly describe the shoulder. These bands could have been due to either an extra conformer (e.g., tct, which has a ν₂₂ band predicted to be at 267 cm⁻¹, according to the MP2/aug-cc-pVTZ level of theory) or a strong Raman active overtone (combination mode) of one of the previously described conformations (ttt, ccc, or gtt). Note that the I₂₅₀/I₂₆₉ ratio of 7.6 ± 0.4 was found according to the three-peak deconvolution process.

Unfortunately, it was almost impossible to obtain better results with the linewidths of 20–30 cm⁻¹ that were produced at the high temperature of the experiment.⁵

The ratio of the ttt bands (I₂₀₄/I₂₅₀) had changes in the gas-phase when compared to the jet-cooled data (see Fig. 2 in ref. 5a). It seemed that a previously unobserved vibration also contaminated the 250 cm⁻¹ band. This fact supported the idea of an appearance of a tct conformation because its ν₂₃ band was predicted to be at 253 cm⁻¹ and should have changed the I₂₀₄/I₂₅₀ band intensity ratio.

A large change was observed for the gtt/ccc band intensity ratios, even after the temperature correction. The increase of the ccc signal in the jet-cooled method was unexpected because the ccc conformer was not the lowest energy structure. It could be that some glycine conformation relaxed to an almost isoenergetic ccc structure rather than to the global minimum (ttt). The same result was shown for small peptides in the jet stream.⁴ This possibility deserves further attention in both experimental and theory work.

The main advantage of the gas-phase research was its ability to provide direct quantitative information about the relative stabilities of different molecular conformers.⁵ Thermodynamic data could be extracted from the Raman band ratios according to the well-known (and widely used) van't Hoff scheme.⁷Fig. 4 shows an example of such analysis for the cccglycine conformer. It was clearly shown that the natural logarithm of the ratio of the two glycine bands linearly depended on the reverse temperature in the temperature range studied. Low-temperature points showed higher relative errors due to the lower signal-to-noise ratio (SNR) of the low-temperature spectra, which were measured at lower glycine vapor pressures. White dots represent the ratios of the higher resolution spectra (HWHM of 2.1 cm⁻¹). All points were inside the 95% confidence interval (CI, grey lines) of the linear regression model (black line).⁷

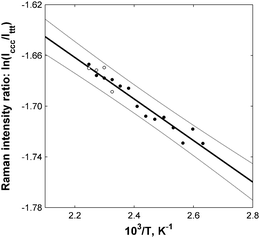Fig. 4 The dependence of the natural logarithm of the peak integral intensity ratio between cis–cis–cis (ccc) and trans–trans–trans (ttt) glycine conformers on the reverse thermodynamic temperature (circles). The linear fit (black line) is presented with 95% error bounds (gray lines). Enthalpy difference: ΔH_ccc = 0.33 ± 0.05 kcal mol⁻¹ (95%).

The data from Fig. 4 make it possible to experimentally evaluate the enthalpy difference between the ccc and tttglycine conformations (ΔH_ccc), which was determined to be 0.33 ± 0.05 (95%) kcal mol⁻¹. The inaccuracy was determined by a small change in the intensity ratios of the 303 and 204 cm⁻¹ bands within the temperature range studied.

The same analysis for the gtt conformer (Fig. 5) led to a value (ΔH_gtt) of 1.15 ± 0.07 (95%) kcal mol⁻¹. All data points were, again, inside the 95% CI. The relative accuracy for the gtt conformer energetics, when compared to the ccc conformation (6% vs. 15%), was due to the greater change in band intensities within the temperature range studied.

Fig. 5 The dependence of the natural logarithm of the peak integral intensity ratio between gauche–trans–trans (gtt) and trans–trans–trans (ttt) glycine conformers on the reverse thermodynamic temperature (circles). The linear fit (black line) is presented with 95% error bounds (gray lines). Enthalpy difference: ΔH_gtt = 1.15 ± 0.07 kcal mol⁻¹ (95%).

The experimental results presented above (0.33 ± 0.05 and 1.15 ± 0.07 kcal mol⁻¹) should be compared with the theoretical values of 0.60 and 1.15 kcal mol⁻¹.⁶ⁱ Note that a direct comparison with electronic energy differences (0.51 and 1.26 kcal mol⁻¹) was not possible due to the relatively high impact from the thermal corrections at 410 K, especially for the ccc and gtt (see Table 1). Even though the predicted energy for the gtt structure was close to the experimental value, the theoretical values should be analyzed with care. The rigid rotor–harmonic oscillator (RRHO) approximation was used for the ΔH and ΔS calculations. Unfortunately, this approximation was not readily applicable to polyatomic molecules such as glycine.^6k This was seen when analyzing data for the tct conformation. Because the lowest energy vibration for the tct structure was predicted to be at 8 cm⁻¹, the separation of vibrational and rotational motions was not possible, but it was assumed by the RRHO model. The presence of such a low-frequency vibration led to large overestimations of entropy and unrealistic tct abundance at 410 K.

Table 1 Theoretical thermodynamics of the glycine conformation equilibrium at the B3LYP/aug-cc-pVTZ theory level: the electronic energy differences, the enthalpy differences (at 410 K), the entropy differences, the Gibbs energy differences, and the conformer abundances. The FPA data extrapolated to the CCSD(T)/CBS theoretical level are shown in parentheses⁶ⁱ

Conformer	ΔEe^a	ΔHT=410 K^a	ΔST=410 K^b	ΔGT=410 K^a	x T=410 K (%)
a The values are in kcal mol^−1. b The values are in cal mol^−1 K^−1.
ttt	0	0	0	0	46
ccc	0.51 (0.64)	0.60	−1.41	1.18	11
gtt	1.26 (1.23)	1.15	−0.81	1.48	7
tct	1.63 (1.76)	1.67	3.54	0.22	[35]
gct	2.69 (2.68)	2.65	−0.64	2.91	1
ttc	4.82 (4.85)	4.72	0.03	4.71	0
tcc	5.50 (5.90)	5.27	−0.90	5.64	0
gtc	6.06 (6.10)	5.85	0.09	5.82	0

---

In general, the B3LYP treatment of biomolecules with triple-ξ basis set is not a bad choice (aug-cc-pVTZ).⁵ But it cannot be called a great one: because very few biomolecules are present in the parameterization molecule set, all the B3LYP theoretical predictions should be used with care.^5h An experimental confirmation of the method applicability and accuracy is needed.

The ccc conformer was more complicated due to the presence of the N⋯H–O hydrogen bond (HB). Its presence made theoretical treatment extremely complex and made the results highly dependent on the theory level.⁶ⁱ Note that the ccc structure had a barrier to the planarity of only 20.5 ± 5.0 cm⁻¹.^6k In a ground vibrational state, the effective structure of the ccc had a plane of symmetry.⁶ⁱ Extra theoretical treatment (e.g., higher level calculations or anharmonic vibrational analysis)⁹ was needed to clarify the difference between the predicted and observed ΔH_ccc.

Unfortunately, entropy data (ΔS) could not be extracted from the Raman spectra in the same direct way as the enthalpy data (see discussion in ref. 7). Complementary information about the Raman cross sections was needed to evaluate ΔS. This information could be provided by theory; but the use of theoretical data for relative entropy evaluation made the results less than 100% independent. The choice of theory level could alter the final values. If B3LYP/aug-cc-pVTZ Raman cross sections were used,⁷ the following ΔS values were obtained: ΔS_ccc = −2.86 ± 0.12 cal mol⁻¹ K⁻¹ and ΔS_gtt = −0.12 ± 0.16 cal mol⁻¹ K⁻¹. These results were not close to the theoretical values (−1.41 and −0.81 cal mol⁻¹ K⁻¹; see the discussion above), but the correct trend was predicted.

Formation of the N⋯H–O hydrogen bond in the ccc made the glycine geometry more rigid, which resulted in a decrease in entropy. Without this entropy factor, the ttt and ccc conformations would co-exist in almost equal concentrations at high temperatures. Entropy contributions were much less for the gtt conformation when compared with the ccc conformation.

The formation of one strong O⋯H–N hydrogen bond instead of two weak ones did not significantly change the molecular internal freedom. The gtt conformer abundance was largely determined by the enthalpy factor.^5a,6i

The use of the gas-phase Raman spectroscopy data together with the microwave spectroscopy ones¹⁰ allows the “direct observation” of hydrogen bonds: both, the interatomic distances and the conformer energetics, can be interpreted in terms of an H-bond formation. That would be of particular importance for the parametrization of the force fields used in the molecular dynamics simulations.⁶

4. Conclusions

It could be concluded that the experimental low-frequency vibrational spectra of gaseous glycine confirmed the experimental^5a and theoretical⁶ data regarding the Gly conformer structures. Using combined jet-cooled, gas-phase, and theoretical studies, three structures of the unsolvated amino acid were confirmed to co-exist at 400 K. The evidence about the existence of the fourth (tct) conformation was presented. The first experimental thermodynamic data about the enthalpy and entropy of the ccc (IIn) and gtt (IVn) conformers were presented. The enthalpy values were determined to be 0.33 ± 0.05 and 1.15 ± 0.07 kcal mol⁻¹ for the ccc and gtt, respectively; the corresponding relative entropy values were −2.86 ± 0.12 and −0.12 ± 0.16 cal mol⁻¹ K⁻¹, respectively. It was proven that the low-frequency Raman spectroscopy is capable of estimating intrinsic thermodynamic parameters of protein building blocks, such as intermolecular hydrogen bonds (ccc conformer, Fig. 1) and rotation around one of the bonds (N–C, gtt conformer). The inaccuracy of the RRHO approximation to Gly conformers was experimentally confirmed. Further studies on amino acids and simple peptides (dipeptide, tripeptides, tetrapeptides, etc.) by microwave,¹⁰ vibrational,^4,11 or other spectroscopies¹² are needed to collect a sufficient amount of experimental data that will improve our understanding of the interplay of the intrinsic intramolecular interactions in the gas-phase amino acids and their influence on AA conformational preferences in either the free form or as a part of peptides and proteins.¹

Acknowledgements

The assistance of Saint-Petersburg State University of Information Technologies, Mechanics, and Optics [IFMO] (Saint-Petersburg, Russia) and Ministry of Defense of the Russian Federation (special grant) is acknowledged. B.R.M. wishes to thank A. Borisov and I. Samoilenko for their technical and computational assistance.

References

1. (a) J. Bujnicki, Prediction of Protein Structures, Functions, and Interactions, Wiley, 1st edn, 2009; (b) M. M. Müller, M. A. Windsor, W. C. Pomerantz, S. H. Gellman and D. Hilvert, Angew. Chem., Int. Ed., 2009, 48, 922–925; (c) A. Aemissegger, V. Kräutler, W. F. Van Gunsteren and D. Hilvert, J. Am. Chem. Soc., 2005, 127, 2929–2936; (d) R. M. Balabin, J. Chem. Phys., 2010, 132, 231101; (e) D. A. Dougherty, Science, 1996, 271, 163–168.
2. (a) P. D. Schnier, W. D. Price, R. A. Jockusch and E. R. Williams, J. Am. Chem. Soc., 1996, 118, 7178–7189; (b) R. A. Jockusch, A. S. Lemoff and E. R. Williams, J. Am. Chem. Soc., 2001, 123, 12255–12265; (c) The Gordon Research Conferences “Biological Molecules in the Gas Phase” in 2001, 2003, 2005, 2007, 2009, 2011; (d) S. F. Sousa, P. A. Fernandes and M. J. Ramos, J. Phys. Chem. A, 2009, 113, 14231–14236; (e) K. Chingin, V. Frankevich, R. M. Balabin, K. Barylyuk, H. Chen, R. Wang and R. Zenobi, Angew. Chem., Int. Ed., 2010, 49, 2358; (f) P. D. McQueen, S. Sagoo, H. Yao and R. A. Jockusch, Angew. Chem., Int. Ed., 2010, 49, 9193–9196.
3. (a) A. Kamariotis, O. V. Boyarkin, S. R. Mercier, R. D. Beck, M. F. Bush, E. R. Williams and T. R. Rizzo, J. Am. Chem. Soc., 2006, 128, 905–916; (b) R. C. Dunbar, N. C. Polfer and J. Oomens, J. Am. Chem. Soc., 2007, 129, 14562–14563; (c) A. Gapeev and R. C. Dunbar, J. Am. Chem. Soc., 2001, 123, 8360–8365; (d) K. Chingin, R. M. Balabin, V. Frankevich, H. Chen, K. Barylyuk, R. Nieckarz, A. Fedorov and R. Zenobi, Phys. Chem. Chem. Phys., 2010, 12, 14121; (e) K. Chingin, R. M. Balabin, K. Barylyuk, H. Chen, V. Frankevich and R. Zenobi, Phys. Chem. Chem. Phys., 2010, 12, 11710; (f) K. Mizuse, N. Mikami and A. Fujii, Angew. Chem., Int. Ed., 2010, 49, 10119–10122.
4. (a) W. H. James, C. W. Müller and E. G. Buchanan, et al. , J. Am. Chem. Soc., 2009, 131, 14243–14245; (b) E. E. Baquero, W. H. James, H. C. Soo, S. H. Gellman and T. S. Zwier, J. Am. Chem. Soc., 2008, 130, 4795–4807; (c) V. Brenner, F. Piuzzi, I. Dimicoli, B. Tardivel and M. Mons, Angew. Chem., Int. Ed., 2007, 46, 2463–2466; (d) E. Gloaguen, B. De Courcy, J.-P. Piquemal, J. Pilmé, O. Parisel and R. Pollet, et al. , J. Am. Chem. Soc., 2010, 132, 11860–11863; (e) B. C. Dian, A. Longarte and T. S. Zwier, Science, 2002, 296, 2369–2373; (f) W. Chin, F. Piuzzi, J.-P. Dognon, I. Dimicoli, B. Tardivel and M. Mons, J. Am. Chem. Soc., 2005, 127, 11900–11901; (g) B. C. Dian, J. R. Clarkson and T. S. Zwier, Science, 2004, 303, 1169–1173.
5. (a) R. M. Balabin, J. Phys. Chem. Lett., 2010, 1, 20–23; (b) R. M. Balabin, J. Phys. Chem. B, 2010, 114, 15075; (c) A. Zehnacker and M. A. Suhm, Angew. Chem., Int. Ed., 2008, 47, 6970–6992; (d) S. Y. Ketkov, H. L. Selzle and F. G. N. Cloke, Angew. Chem., Int. Ed., 2007, 46, 7072–7074; (e) R. M. Balabin, Phys. Chem. Chem. Phys., 2010, 12, 5980; (f) G. Herzberg, Molecular Spectra and Molecular Structure. I. Spectra of Diatomic Molecules, Van Nostrand Reinhold, New York, 1950; (g) R. Lindera, M. Nispela, T. Häber and K. Kleinermanns, Chem. Phys. Lett., 2005, 409, 260–264; (h) R. M. Balabin and E. I. Lomakina, Phys. Chem. Chem. Phys., 2011, 13, 11710–11718; (i) R. M. Balabin, Mol. Phys., 2011, 109, 943; (j) K. Barylyuk, R. M. Balabin, D. Grünstein, R. Kikkeri, V. Frankevich, P. H. Seeberger and R. Zenobi, J. Am. Soc. Mass Spectrom., 2011, 22, 1167–1177.
6. (a) M. Cossi, V. Barone, B. Mennucci and J. Tomasi, Chem. Phys. Lett., 1998, 286, 253–260; (b) A. D. Mackerell, M. Feig and C. L. Brooks, J. Comput. Chem., 2004, 25, 1400–1415; (c) J. H. Jensen and M. S. Gordon, J. Am. Chem. Soc., 1995, 117, 8159–8170; (d) T. Head-Gordon, M. Head-Gordon, M. J. Frisch, C. L. Brooks and J. A. Pople, J. Am. Chem. Soc., 1991, 113, 5989–5997; (e) A. G. Császár, J. Am. Chem. Soc., 1992, 114, 9568–9575; (f) S. G. Stepanian, I. D. Reva, E. D. Radchenko, M. T. S. Rosado, M. L. T. S. Duarte, R. Fausto and L. Adamowicz, J. Phys. Chem. A, 1998, 102, 1041–1054; (g) Y. Ding and K. Krogh-Jespersen, Chem. Phys. Lett., 1992, 199, 261–266; (h) J. H. Jensen and M. S. Gordon, J. Am. Chem. Soc., 1991, 113, 7917–7924; (i) R. M. Balabin, Chem. Phys. Lett., 2009, 479, 195; (j) T. Van Mourik, P. G. Karamertzanis and S. L. Price, J. Phys. Chem. A, 2006, 110, 8–12; (k) V. Kasalová, W. D. Allen, H. F. Schaefer, E. Czinki and A. G. Császár, J. Comput. Chem., 2007, 28, 1373.
7. (a) R. M. Balabin, J. Phys. Chem. A, 2009, 113, 4910; (b) R. M. Balabin, J. Phys. Chem. A, 2009, 113, 1012.
8. Z. Xue and M. A. Suhm, J. Chem. Phys., 2009, 131, 054301.
9. (a) W. Zhuang, T. Hayashi and S. Mukamel, Angew. Chem., Int. Ed., 2009, 48, 3750–3781; (b) L. Szyc, M. Yang, E. T. J. Nibbering and T. Elsaesser, Angew. Chem., Int. Ed., 2010, 49, 3598–3610; (c) K. Ruud and R. Zanasi, Angew. Chem., Int. Ed., 2005, 44, 3594–3596; (d) K. R. Asmis and Y. Yang, et al. , Angew. Chem., Int. Ed., 2007, 46, 8691–8694; (e) C. Puzzarini, M. Biczysko and V. Barone, J. Chem. Theory Comput., 2010, 6, 828–838; (f) R. M. Balabin, J. Chem. Phys., 2010, 132, 211103; (g) R. M. Balabin, J. Phys. Chem. A, 2010, 114, 3698; (h) O. Bludský, J. Chocholoušová, J. Vacek, F. Huisken and P. Hobza, J. Chem. Phys., 2000, 113, 4629.
10. (a) P. D. Godfrey and R. D. Brown, J. Am. Chem. Soc., 1995, 117, 2019–2023; (b) J. L. Alonso, I. Peña, J. C. López and V. Vaquero, Angew. Chem., Int. Ed., 2009, 48, 6141–6143; (c) M. E. Sanz, S. Blanco, J. C. López and J. L. Alonso, Angew. Chem., Int. Ed., 2008, 47, 6216; (d) A. Lesarri, S. Mata, E. J. Cocinero, S. Blanco, J. C. López and J. L. Alonso, Angew. Chem., Int. Ed., 2002, 41, 4673; (e) J. L. Alonso, E. J. Cocinero, A. Lesarri, M. E. Sanz and J. C. López, Angew. Chem., Int. Ed., 2006, 45, 3471; (f) R. J. Lavrich, D. F. Plusquellic, R. D. Suenram, G. T. Fraser, A. R. Hight Walker and M. J. Tubergen, J. Chem. Phys., 2003, 118, 1253.
11. C. Roth, T. Peppel, K. Fumino, M. Köckerling and R. Ludwig, Angew. Chem., Int. Ed., 2011, 49, 10221–10224.
12. (a) V. Feyer, O. Plekan, R. Richter, M. Coreno, K. C. Prince and V. Carravetta, J. Phys. Chem. A, 2008, 112, 7806–7815; (b) M. L. Gordon, G. Cooper, C. Morin, T. Araki, C. C. Turci, K. Kaznatcheev and A. P. Hitchcock, J. Phys. Chem. A, 2003, 107, 6144–6159; (c) M. Okuno, H. Kano, P. Leproux, V. Couderc, J. P. R. Day, M. Bonn and H. Hamaguchi, Angew. Chem., Int. Ed., 2010, 122, 6925–6929; (d) B. G. Saar, Y. Zeng, C. W. Freudiger, Y.-S. Liu, M. E. Himmel, X. S. Xie and S.-Y. Ding, Angew. Chem., Int. Ed., 2010, 122, 5608–5611.

---