The role of the intermolecular potential on the dynamics of ethylene confined in cylindrical nanopores†
Fernando J. A. L.
Cruz
*a,
Erich A.
Müller
b and
José P. B.
Mota
a
aRequimte/CQFB, Department of Chemistry, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa, 2829-516, Caparica, Portugal. E-mail: f.cruz@dq.fct.unl.pt
bDepartment of Chemical Engineering, Imperial College London, South Kensington Campus, London, SW7 2AZ, UK
First published on 2nd August 2011
Abstract
The influence of the molecular force field upon the transport properties of ethylene is studied by molecular dynamics simulations, addressing both the bulk fluid and the confined phases within pristine single-walled carbon nanotubes. Five different molecular models with different degrees of coarse-graining were selected, spanning from a simple isotropic Lennard–Jones sphere to a fully detailed all-atom description. The fluid was probed for its self-diffusion coefficient under isochoric (0.026 ≤ ρ (mol L−1) ≤ 15.751) and isothermal (220 ≤ T (K) ≤ 340) conditions, both in the sub- and supercritical regions (Tbulkc = 282.4 K). Although the particular details of each potential model are seen to be nearly irrelevant to the bulk fluid dynamics, they are crucial to correctly describe the inhomogeneous system. The most important aspects affecting fluid transport are the existence/absence of explicit electrostatic contributions and the molecular shape. The effect of temperature on the confined fluid self-diffusion is described by the Arrhenius law, D = Aexp(−Ea/RT), and the nonlinear density dependencies of the activation energy (Ea/R) and pre-exponential factor (A) have been fitted here to empirical equations. In spite of the quasi one-dimensional confining nature of SWCNTs, the isothermal results (T = 300 K) obtained for the bulk and confined systems collapse onto a unique master curve, D = D0ρλ, suggesting that the self-diffusion coefficient of a confined fluid can be estimated from its molecular density, an easily accessible property.
1. Introduction
The confinement of fluids in nanoporous solids can be accompanied by striking effects on the molecular dynamics,1–6 which do not necessarily possess an analogy in the bulk phase. Upon confinement, molecules interact with the solid walls to an extent that markedly depends on the chemical nature of the solid and its corresponding pore size. As the dimensions of the nanopore approach those of the molecule itself, the solid–fluid interactions tend to become dominant;5,7 this is one of the main arguments used to explain why nanoconfined fluid dynamics exhibit sharp discrepancies when compared to the classical bulk phase behavior. In such situations, the most commonly accessed transport property is the self-diffusion coefficient, which apart from its fundamental and scientific importance, is of practical relevance for most industrial applications involving fluid processing such as separation and catalysis. Experimentally, however, the investigation of transport properties of nanoconfined fluids is hindered by several aspects, including the poor characterization/chemical purity of the samples, inaccurate description of surface topology, and the very small pore size. An opportunity arises here to study diffusion of fluids in confined media using classical molecular dynamics simulations (MD),8,9 thus obtaining an insight into both structural and dynamical features.As a structurally simple and well characterized model of cylindrical nanopores, single-walled carbon nanotubes (SWCNTs) are excellent candidates for theoretical studies. Their structure can be rationalized as the cylindrical folding of a graphene sheet along a particular directional vector (n,m).10,11 As the result of that folding, the carbon atoms on the solid walls may be arranged in three distinct topologies, namely armchair (n = m), zig-zag (m = 0) or chiral (n ≠ m) nanotubes. Each of those topologies exhibit different optical12 and electronic13 properties, and amongst other applications have been proposed as building blocks in composites,14 chemical sensors,15 field-effect transistors in nanoelectronics,16 biomedical devices17,18 and as separating media of organic vapors.19–21 Their hydrophobicity places them as ideal candidates to explore molecular transport through biological membranes, and therefore the dynamics of confined water has been one of the main subjects of previous work in this area.7,22,23 Recently, Liu et al.23 calculated the potential energy surfaces for zig-zag and armchair SWCNTs, and showed that those two different topologies can interact differently when put into contact with water molecules. This observation was later related to the different diffusion mechanisms observed for water confined in topologically and geometrically (10.5 < D (Å) < 22.5) distinct single-walled carbon nanotubes.
Molecular transport can be classified according to two essentially different mechanisms: i) Fickian diffusion,24 when molecules move randomly over short distances, and ii) single-file or ballistic diffusion, when molecular mobility has contributions from preferential paths. While the former is the dominant mode of transport in isotropic phases, such as bulk fluids, the latter has been observed to occur when anisotropy is introduced into the system, e.g., under the form of a nanoconfining solid surface.25 Bhatia and co-workers26 studied the diffusive and viscous transport of CH4 adsorbed into (10,10) armchair SWCNTs, and concluded that the diffusion coefficient decreases with adsorbate density. Later,2 simulations of confined H2 and CH4 indicated that the reflection of fluid molecules on SWCNT walls is essentially specular, thus mitigating momentum loss upon collision; this observation was postulated to occur when the molecular size is relatively larger than the solid lattice parameters dC–C = 1.42 Å. The dynamics of CH4 and C2H6 flowing inside a zig-zag SWCNT have been studied by Krishna et al.,27 who showed that molecules display a Fickian-type mode of transport after 100–500 ps of simulation time. Jacobtorweihen et al.28 performed extensive molecular dynamics simulations with n-alkanes (n < 6) diffusing along zig-zag nanotubes, and estimated that the corresponding self-diffusivities in the zero-loading limit decrease monotonically with the number of carbon atoms of the fluid molecule. Recently, the diffusional properties of cold argon confined inside SWCNT hexagonal bundles were probed by molecular dynamics simulations,29 and it was shown that the nanotube confined fluid exhibits Fickian diffusion, whereas molecules in the interstitial channels move according to a single-file mechanism. Bearing in mind these previous reports, it becomes clear that the diffusivity of gases and liquids within carbon nanotubes is far from being thoroughly understood and, furthermore, results are sometimes conflicting. Water and the smaller alkanes have been the generally studied fluids. However, in all those studies, there is rarely uniformity in the choice of potential models employed. We aim herein to understand the effect of the level of detail used in the description of the fluid's energetics, upon the effective observed dynamics. Much can be gained or lost in terms of computational effort and physical detail by coarse-graining molecular models; the reader is referred to recent reviews for further discussion on coarse-graining techniques.30,31 A particularly challenging issue is the mapping of the diffusivities of coarse-grained particles to those obtained from detailed atomistic descriptions.
From the point of view of molecular interactions, ethylene is an exceptionally interesting and challenging molecule, hence its selection as a prototype fluid. Geometrically, it is a planar molecule; however, the presence of a quadrupole moment, resulting from a highly anisotropic charge distribution, allows different approaches to be employed in order to model the fluid. It is the purpose of this work to study the influence of the intermolecular potential on the dynamical behaviour of ethylene, in a bulk phase, and also inside a single-walled carbon nanotube, thus subject to near one-dimensional confinement. This issue has been partially addressed by Mao and Sinnott32,33 and Cruz and Müller,34 using differently coarse-grained potentials to study the dynamics of C2H6 and C2H4. The one-dimensional self-diffusivities calculated by Mao and Sinnott, corresponding exclusively to molecular translation along the nanotube main axis, showed that ethane exhibits a slightly higher coefficient than its unsaturated analogue. On the other hand, Cruz and Müller determined effective self-diffusion coefficients, considering three-dimensional translation within the confining volume, and their calculations showed that the confined fluid density plays a paramount role upon the dynamics.
Molecular dynamics simulations are here employed along with five distinct molecular potential models, whose level of coarse-graining corresponds to different degrees of detailing the C2H4 molecule. The set of molecular models include a fully atomistic representation of the ethylene molecule,35,36 which is validated by comparison against bulk experimental data,37,38 but also simpler models with varying degrees of coarse-graining ranging down to a single isotropic Lennard–Jones sphere.39 The capabilities and drawbacks of each of these different molecular descriptors will be explored, particularly in the case of confined fluids, where, as far as we are aware, no experimental results are available in the literature. The following parts of this manuscript are organized as follows: the next section introduces the intermolecular potentials used in the calculations, for both the fluid and the solid, as well as the simulation details and methodology (Section 2). We then proceed to present the results obtained, discuss them in light of the microscopic phenomena involved (Section 3), and finally summarize the work with some concluding remarks (Section 4).
2. Molecular models and simulation details
To address the influence of intermolecular potential upon the fluid dynamical behavior, both in a bulk phase and confined into a zig-zag (16,0) SWCNT, we have chosen five different potential models, which are commonly employed in the literature to study equilibrium and transport properties of pure ethylene (Fig. 1). The selected potentials are intrinsically different physical representations of the C2H4 molecule, differing in the degree of coarse-graining and detail with which the calculations are performed. Usually, it is assumed that the more detailed the intermolecular potential, the more confident one can be about the results obtained with it. The downside to this assumption is that complexity is usually synonymous with increased computational requirements, sometimes to the extent of rendering the simulations intractable.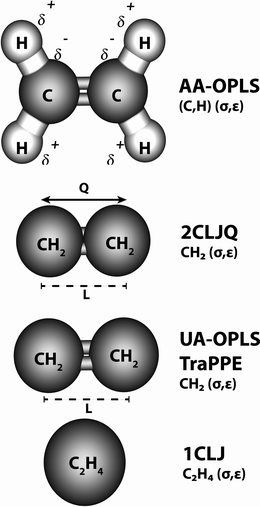 | ||
| Fig. 1 Pictorial representation of the five different intermolecular potentials used in the simulations; each sphere represents a pseudo-atom with a characteristic Lennard–Jones (σ,ε) pair. Partial electrostatic charges, δ, and a point molecular quadrupole, Q, are used in the AA-OPLS and 2CLJQ models, respectively, to calculate electrostatic interactions (see Sections 2.1–2.2 for a detailed description). In the two-center united-atom models (UA-OPLS, TraPPE), L is the chemical bond length between two CH2 (sp2) groups. | ||
In the present work, we set as benchmark a fully atomistic six-atom description of the ethylene molecule, employing partial Coulombic charges on all sites (AA-OPLS). A first level of coarse-graining adopts a model with two Lennard–Jones centers with an embedded molecular quadrupole (2CLJQ); further coarse-graining leads to the neglect of electrostatic interactions (UA-OPLS, TraPPE), and finally a simple one-site isotropic model is considered (1CLJ). All five potentials calculate the dispersive energies between two interacting particles via a (12,6) Lennard–Jones (LJ) term (eqn (1)), although the corresponding (σ,ε) pairs are obviously potential-specific.
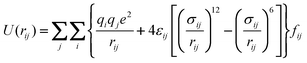 | (1) |
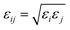 ; no attempt has been made to adjust them, as no reliable experimental data is currently available.
; no attempt has been made to adjust them, as no reliable experimental data is currently available.
2.1 All-atom OPLS (AA-OPLS)
The Jorgensen et al.35,36 parameterization of the Lennard–Jones potential is an atomistically detailed one, and is here employed for both the inter- and intramolecular interactions. It has been validated against experimental thermodynamical properties, such as heats of vaporization and liquid densities of organic and biomolecular fluids.41 Within the all-atom framework, all the atoms in the fluid molecules are described as Lennard–Jones (12,6) spheres, and explicit electrostatic charges, qi, are considered for all particles (eqn (1), Table 1). In order to take into account the 1–4 nonbonded interactions, an appropriate scaling-factor, fij = 0.5 is used, (as opposed to fixing fij = 1.0 in all other cases), thus allowing the OPLS force field to be employed for both the inter- and intramolecular interactions. The flexibility of the ethylene molecule includes explicit contributions from bond stretching and angle bending via harmonic potentials (eqn (2.1)), and also a term corresponding to 4-body interactions for the dihedral energy (eqn (2.2)). The molecular geometry, namely equilibrium bond lengths, req, and angles, θeq, and the corresponding parameters have been obtained from literature values and were adopted without further refinement. These parameter values are listed in Table 2.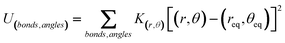 | (2.1) |
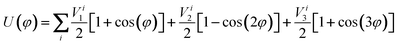 | (2.2) |
| Atom | q i | ε i /kB (K) | σ i (Å) |
|---|---|---|---|
| C | −0.230 | 38.270 | 3.55 |
| H | 0.115 | 15.107 | 2.42 |
Recently, we have successfully employed the AA-OPLS parameterization to measure the isothermal adsorption and self-diffusion of ethylene confined into an isolated SWCNT,21,34 but the systematic study of the system's dynamical behaviour under different temperature and density conditions is still lacking.
2.2 Two-center Lennard–Jones with embedded quadrupole (2CLJQ)
Vrabec et al.42 have recently modeled a large number of small organic molecules using a coarse-grained potential based on a Lennard–Jones dumbbell of variable bond length, L, which may or may not have an embedded centrally located multipole moment (dipole, quadrupole, etc.). In the case that concerns us here, ethylene is considered as a two center uncharged LJ molecule with a quadrupole moment, Q, placed at the center of mass and aligned with the chemical bond (Fig. 1). This force field has been used to study and predict vapor liquid equilibria of ethylene in fluid mixtures,43transport properties34,44 and has also been used in adsorption studies of ethylene confined in microporous carbons45 and SWCNTs.21 Briefly, the overall energy is given by the sum of the Lennard–Jones and quadrupolar interactions (eqn (3)).46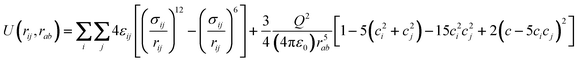 | (3) |
| Pseudo-atom | ε i /kB (K) | σ i (Å) | Q (B) | L (Å) |
|---|---|---|---|---|
| CH2 (sp2) | 76.95 | 3.7607 | 4.331 | 1.2695 |
2.3 Transferable potential for phase equilibria (TraPPE) and united-atom OPLS (UA-OPLS)
Both the TraPPE47 and UA-OPLS48 force fields are based on an united-atom (UA) description of the molecules, where the CH2(sp2) groups are treated as single interaction sites. Each pseudo-atom is separated by a distance L, corresponding to the unsaturated chemical bond length (Fig. 1). The nonbonded interactions between pseudo-atoms on different fluid molecules are governed by the Lennard–Jones (12,6) potential (eqn (1)), and electrostatic energies are neglected in both models. In these UA force fields, bond lengths are kept fixed throughout the simulations, and the fluid molecules are therefore treated as rigid entities. The corresponding bond lengths between two pseudo-atoms are given in Table 4, along with the Lennard–Jones parameters. The accuracy of the TraPPE potential in the context of fluid–solid systems was recently tested by means of Monte Carlo simulations over a wide range of fluid densities and nanotube diameters.49,50 The equilibrium thermodynamical properties thus obtained, such as isosteric heats of adsorption and Henry constants, were found to be consistent with the corresponding experimental values. We are unaware of any previous similar work employing the UA-OPLS force field.| Pseudo-atom, CH2 (sp2) | ε i /kB (K) | σ i (Å) | L (Å) |
|---|---|---|---|
| TraPPE | 85.0 | 3.675 | 1.33 |
| UA-OPLS | 70.437 | 3.850 | 1.34 |
2.4 One center Lennard–Jones (1CLJ)
Even though C2H4 is not spherically symmetrical, a large number of parameter data sets are available in the literature describing the molecule as an isotropic spherical fluid (Table 5), as this approach is simple to use and usually very cost-efficient. Calculations presented herein are based on the parameterization by Cuadros et al.,39 who forced the agreement between pressure values obtained from the empirical Soave equation of state and those obtained from computer simulations, whilst using the Pitzer acentric factor as an appropriate scaling parameter thus taking into account molecular non-sphericity.2.5 Single-walled carbon nanotubes (SWCNTs)
SWCNTs are modeled as fully atomistic solids, describing the graphitic carbon atoms as a collection of discrete Lennard–Jones centers, with parameters given by Steele:51–53ε = 28.0 K and σ = 3.4 Å. The nanotube walls are therefore treated as rigid and corrugated, i.e., all atoms in the tube are explicitly included in the calculations but are fixed in space. Johnson and co-workers54 studied the diffusivities of ideal gases (Ar, Ne) confined in carbon nanotubes, and concluded that for fluid transport within SWCNTs the potential should optimally correspond to an atomistic description with rigid bonding, such as the one employed in the present work. The validity of this approach has been discussed elsewhere.55 Additionally, the comparison of computer simulations with adsorption experiments of Xe on nanotubes suggests that the potentials developed for graphene sheets may be transferred to the case of cylindrical pores.56In a planar graphene sheet, carbon atoms are sp2 hybridized, with an overall charge distribution of electrical quadrupoles located perpendicular to the surface. When this sheet is bent to produce a nanotube, the carbon atoms' sp2 orbitals tend to be “squeezed-out” towards the tube’s external volume, and therefore the original quadrupole moments will be dislocated further away from the tube's internal pore.11 This effect becomes more and more pronounced as the SWCNT diameter decreases, and confined molecules will experience a reduced charge anisotropy. For the narrow nanotube diameter considered here, the neglect of quadrupolar interactions with the surface seems adequate, particularly for the highest temperature calculations.57 We have thus excluded contributions arising from the quadrupole moment that could be ascribed to the solid walls. This simplification has been frequently adopted before in studies involving either isolated nanotubes and/or bundled into membranes,58–63 and has a parallel with the approximations made when studying fluid adsorption on graphene sheets.64,65
Nanotube flexibility can play an important role when the carbon lattice is allowed to breathe, however, this usually leads to a dramatic increase of computer processing time. In order to address this issue, Jacobtorweihen et al.28 employed a modified version of the Lowe–Andersen thermostat, thus mimicking the breathing of (13,0) and (20,0) SWCNTs, with diameters D = 10.2 Å and D = 15.6 Å, respectively. They calculated the one-dimensional self-diffusion coefficient of confined n-alkanes (n ≤ 6) along the nanotube's main axis, and concluded that tube flexibility is only important for lighter molecules in the limit of zero-loading. Their calculations for the narrow tube (10.2 Å) considered only C4H10, but, nonetheless, indicate that tube diameter can also play an important role for lengthy molecules: the diffusion coefficient determined for the rigid lattice is roughly 27% higher than the corresponding quantity for the fully flexible structure. Similar findings have been observed by Chen et al.66 for methane confined into a (15,0) SWCNT. Only below a very low pressure threshold, p < 4 × 10−2 bar, did they identify meaningful differences in the self-diffusion coefficients calculated for the rigid and flexible lattices.
Considering all the aforementioned pieces of evidence, it is expected that for systems away from the zero-loading limit, postulating a priorinanotube rigidity would result in minor discrepancies compared to the fully flexible lattice. We have therefore modeled the nanotube walls as rigid, similar to previous studies of fluid transport inside SWCNTs.27,67–71 The carbon nanotube employed in this work has zig-zag simmetry,10,11 (n,0) with n = 16, and diameter D = 12.55 Å. We have already demonstrated that nanotube topology exerts a relatively minor influence on the self-diffusivities of confined quadrupolar fluids.34 The chirality dependency suggested in Liu's work23 can probably be ascribed to the strong electrical dipole of water molecules and the corresponding H-bonding mechanism. In line with previous works57,72 we define the nanotube effective diameter as Deff = D − δ, where D is the skeletal diameter, measured from center-to-center of opposite carbon atoms on the solid walls, and δ = 3.4 Å is the distance of closest approach between a C2H4 molecule and the SWCNT, thus taking into account the softness of the solid–fluid interaction potential. Recently, we determined the δ values for all the lightest alkanes and alkenes (C1–C3).49 As previously mentioned, the bending of a planar graphene sheet to produce a SWCNT squeezes out the π clouds towards the nanotube external space and increases the purely sp2 hybridized σ (C–C) bond length. We have thus considered a value of 1.42 Å for this latter property, in accordance with previous simulation studies.73,74
2.6 Simulation methodology
Molecular dynamics simulations were performed using version 2.18 of the DL_POLY code.75 The Verlet algorithm was used to integrate the equations of motion, fluid–fluid long-range electrostatic interactions were calculated by the Ewald summation method, and the Nosé–Hoover thermostat with a relaxation constant of f = 0.1 ps was used to control the temperature. A potential cut-off distance of 15 Å and a time step of Δt = 1 fs were used. The simulation cell consisted of a single pristine SWCNT placed along a box with dimensions 30 Å × 30 Å × 206 Å, with periodic boundary conditions applied along the tube main axis, thus effectively mimicking an infinitely long nanotube. Only endoadsorption was considered and the simulation cell was preloaded with fluid molecules that were previously equilibrated for up to 300 ps.The effect of temperature on the fluid dynamical behavior was studied over the temperature range 220 ≤ T (K) ≤ 340, by running isothermal simulations at 10 K intervals, in the canonical ensemble (NVT). The array of molecular densities considered spans a wide range, 0.242 ≤ ρ (mol L−1) ≤ 15.751, whose limits correspond to a nanotube containing only two fluid molecules (ρ = 0.242 mol L−1) and a completely filled SWCNT: ρ = 15.751 (AA-OPLS), ρ = 15.024 mol L−1 (2CLJQ, TraPPE), ρ = 14.540 mol L−1 (UA-OPLS), ρ = 11.632 mol L−1 (1CLJ).
In order to establish a comparison with the confined fluid dynamics, bulk phases were also monitored at 300 K using a supercell of 30 Å × 30 Å × 250 Å containing the pure fluid. In both cases, confined and bulk fluid, MD simulations were run for 500 ps, and, in order to avoid any non-Fickian regime,34 statistical sampling was performed after an initial 50–100 ps of simulation time.
3. Results and discussion
Self-diffusion coefficients can be deduced from the time dependent analysis of molecular trajectories, using either the Stokes–Einstein or the Green–Kubo equations, which have become the de facto method.8,9 It has been shown that both formalisms are mathematically equivalent.76 Recently, Baidakov et al. determined the self-diffusion coefficient of stable and meta-stable Lennard–Jones fluids via the particles mean-squared displacement (Einstein equation) and velocity auto-correlation functions (Green–Kubo equation), and concluded that both approaches led to self-consistent results within the calculation error (0.5–1.0%).77 A similar conclusion was obtained by Takeuchi and Okazaki when calculating the self-diffusivities of polymethylene with O2 as a solute.78 The transport data from a MD simulation was analyzed herein by calculating the fluid self-diffusion coefficient, D, using the Stokes–Einstein equation, which relates D with the mean-squared displacement of the molecular centre of mass, according to: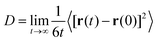 | (4) |
3.1 Bulk phases
Five coarse-grained potentials were used to probe the bulk fluid dynamical behavior in the absence of any solid heterogeneity in the system. At room temperature (T = 300 K), the calculated self-diffusion coefficients are plotted in Fig. 2 as a function of molecular density; for comparison purposes, the experimental data compiled by Férnandez et al.44 and the 1H-NMR measurements of Arends et al.37 are also indicated. There is an overlap between the experimental data and the simulation results for the AA-OPLS model, which is not observed for the other potentials. This match allows us to treat the all-atom force-field as the benchmark upon which to compare the other models. Nonetheless, there are no assurances that the AA-OPLS potential will still be suitable for other physical systems (mixtures, inhomogeneous fluids).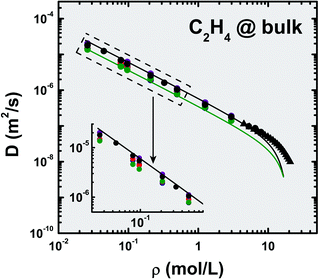 | ||
| Fig. 2 Self-diffusion coefficients, D, calculated for the bulk fluid using different potential models at T = 300 K (data for AA-OPLS, ρ < 3 mol L−1, and 2CLJQ from ref. 34). Symbols correspond to simulation (●) or experimental results (▲):37,44 AA-OPLS (black), 2CLJQ (blue), TraPPE (red), UA-OPLS (purple) and 1CLJ (green). Lines are least-squares fittings of the data using Liu's equation79 (eqn (5)) corresponding to the fully atomistic model (black, AA-OPLS) and to the one Lennard–Jones particle (green, 1CLJ). | ||
From the inspection of Fig. 2, some general trends can be established: i) the 1CLJ model leads to the overall slowest dynamics observed in the MD calculations, and ii) regardless of the specific model employed, the fluid behaves regularly, e.g., the self-diffusion coefficient decreases monotonically with increasing density. As this latter property increases, the free volume available to molecular displacement decreases, and random motion becomes progressively more restricted. Furthermore, in the low-density region, D scales linearly with (1/ρ) in agreement with the Chapman–Enskog theory.80 Jonas and co-workers38 have used spin-echo NMR to measure self-diffusivities of supercritical ethylene (ρ < 21.43 mol L−1), however, the temperatures of their experiments were far to high (323.15–398.15 K) to establish a direct comparison with our MD data. Nonetheless, their findings confirm the general behavior observed in our calculations, clearly showing a monotonical decrease of self-diffusivity with increasing bulk density. From Fig. 2 it can also be observed that, besides minor scattering of simulation results around the overall variation with ρ, the nature of the potential model does not seem to drastically influence the bulk fluid mobility under isothermal conditions. This is not surprising, bearing in mind that the models employed here have been developed from thermodynamical data for the pure bulk fluid. It is worth noting the change in slope exhibited by the experimental data, as molecular density surpasses a threshold of ρ ≈ 11–12 mol L−1. This presumably is a consequence of the enhanced importance of the π–π interactions in the very dense fluid, as C2H4 possess a significant quadrupole moment (Q = 1.3–4 B).81,82 Arends and Trappeniers37 associated this behavior with a departure from the Enskog model for hard-spheres.
The quest for a simple model to relate the self-diffusion coefficient with the corresponding fluid physical properties has been the subject of intense investigation, and is of paramount importance for both theoretical and practical applications. Amongst several others (recent discussions on the topic can be found elsewhere83,84), we have chosen the approach developed by Liu et al. because its was tested for several different pure substances and also some binary mixtures (rare gases, alkanes, alkenes, polar organics),79,85 but essentially due to its mathematical simplicity (eqn (5)). The model builds-upon the Chapman–Enskog transport theory for purely repulsive hard-spheres, DHS, as parameterized by Cohen and Turnbull,86,87 and introduces an exponential term to include the attractive interactions of a Lennard–Jones fluid, D = DHSexp(−αLJ/T*); αLJ = 0.2786 is an empirical constant fitted from molecular dynamics data and T* is the reduced temperature (T* = kBT/εLJ). Under isothermal conditions, only two parameters are required to evaluate the fluid self-diffusivity, namely the Lennard–Jones collision diameter and potential well depth, σLJ and εLJ respectively; with these two quantities at hand, Liu et al. claim that eqn (5) is able to estimate the fluid self-diffusivity under a wide range of densities (0.773–24.47 mol L−1).79 See ESI for further details.†
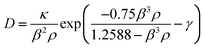 | (5) |
As previously discussed, the degree of potential coarse-graining appears to play a minor role in the bulk fluid dynamics. We have thus applied eqn (5) to the MD data obtained using two limiting potential models, AA-OPLS and 1CLJ, and the corresponding findings are indicated in Fig. 2 and Table 5. Although Liu's approach was not specifically developed for low-density fluids, it can still reasonably predict the ethylene self-diffusivities at very dilute conditions (ρ < 0.1 mol L−1). Nevertheless, its range of validity seems limited, for it slightly underestimates both experimental and simulated self-diffusion data, either with or without electrostatics. In fact, those discrepancies become significant as the fluid density increases beyond ρ > 5.6 mol L−1, and eqn (5) then predicts a much faster decrease of self-diffusivity than the experimentally observed trend. At high densities, eqn (5) becomes insensitive to the particular molecular potential details, and therefore the results obtained for the AA-OPLS and 1CLJ models are observed to converge into similar values (Fig. 2). Table 5 indicates several values for the (σLJ, εLJ) pair, obtained from different sets of thermodynamic data, as well as our own results fitted to the self-diffusivities calculated with the AA-OPLS model. It is worth noting the relatively large σLJ = 4.728 Å value obtained in this work, suggesting that molecular shape is in fact a vital property to accurately describe the fluid's dynamics.
| σ LJ (Å) | ε LJ (K) | Optimized property | Reference |
|---|---|---|---|
| 4.232 | 205 | viscosity | Hirschfelder80 |
| 4.523 | 199.2 | second virial coefficient | Hirschfelder80 |
| 4.163 | 224.7 | viscosity | Reid88 |
| 4.047 | 215.3 | self-diffusivity | Zhu89 |
| 4.155 | 225.6 | viscosity | Mourits90 |
| 4.124 | 215.8 | critical point | Müller91 |
| 4.048 | 169.1 | self-diffusivity | Liu79 |
| 4.140 | 224.2 | molecular density | Calado92 |
| 4.257 | 201.9 | viscosity | Tee93 |
| 4.433 | 202.5 | second virial coefficient | Tee93 |
| 4.589 | 200.8 | vapor pressure | Cuadros39 |
| 4.728 | 172.3 | self-diffusivity | this work |
3.2 Confined fluids
The self-diffusion coefficients calculated for ethylene confined into a (16,0) SWCNT are plotted in Fig. 3, along with results obtained for the bulk phases. We are unaware of any previous studies reporting experimental self-diffusivities of ethylene in SWCNTs. An immediate conclusion drawn from Fig. 3 is that simulation data in the whole density domain are influenced by molecular density in a very similar manner, for both the bulk and confined phases. Recently, Mittal and Truskett94 studied the effect of confining a Lennard–Jones fluid onto a slit pore of two-dimensional geometry. They interpreted their observations in terms of an effective packing fraction, φeff = NπσHS3/6AH, where σHS is the hard-sphere equivalent diameter of each LJ particle, H is the slit-pore effective width, and A is the surface area of the pore, and concluded that the dynamical data for both the inhomogeneous and bulk systems roughly collapsed onto a common master curve. A similar finding can be observed in Fig. 3, suggesting that self-diffusivities can be reasonably estimated from an easily accessible equilibrium property such as molecular density, ρ, using a simple power law, D = D0ρλ (Table 6). This is quite surprising if one bears in mind the highly restricted one-dimensional geometry characteristic of SWCNTs, which should result in stronger confinement effects compared to Mittal's two-dimensional slit–pore geometry. The deviation of our simulation data from the master-curve, observed in the high-density limit, is circumstantial; it has to do with our geometrically-based definition of molecular density, ρ = (N/NA)/Veff, where N is the number of confined molecules, NA is Avogadro's number, and Veff is the effective volume of the nanotube (cf. 2.5). At high-densities, packing effects/efficiency in the dense fluid become important and the simple use of Veff is insufficient to describe those effects. This does not, however, affect the interpretation of the results. Simulation data obtained for the two heavily coarse-grained potentials, UA-OPLS and 1CLJ, exhibit some scatter, particularly in the region where the bulk and inhomogeneous systems meet (Fig. 3).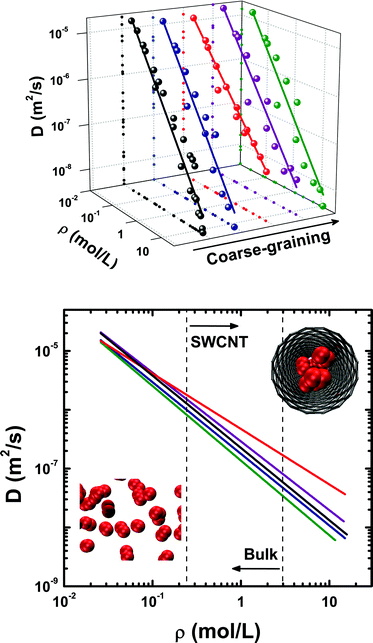 | ||
| Fig. 3 Influence of the intermolecular potential upon bulk and confined C2H4 dynamics at T = 300 K: top) Self-diffusion coefficients for ethylene in the whole density domain (data for AA-OPLS, ρ < 3 mol L−1, and 2CLJQ from ref. 34); bottom) projection onto the (D,ρ) plane, showing the two areas corresponding to a bulk (ρ ≤ 2.969 mol L−1) and confined fluid (ρ ≥ 0.242 mol L−1). Symbols are MD data and lines correspond to a power-law, D = D0ρλ (Table 6); note that, for each individual potential, both bulk and confined self-diffusivities seem to collapse onto the same master-curve (see text for details). Data points and lines are colored according to the molecular potential employed: AA-OPLS (black), 2CLJQ (blue), TraPPE (red), UA-OPLS (purple) and 1CLJ (green). In snapshots, ethylene molecules are represented as a two-center Lennard–Jones fluid and the SWCNT by its graphitic carbon mesh. | ||
| Molecular potential | D 0 × 107 | λ |
|---|---|---|
| AA-OPLS | 2.247 | 1.229 |
| 2CLJQ | 1.784 | −1.218 |
| TraPPE | 4.720 | −0.943 |
| UA-OPLS | 2.899 | −1.169 |
| 1CLJ | 1.368 | −1.269 |
Overall, it can be observed from Fig. 3 that the models with explicit electrostatic interactions (AA-OPLS and 2CLJQ) systematically lead to lower values of self-diffusivities, while on the other hand, the TraPPE and UA-OPLS that neglect Coulombic energies, exhibit the highest values. The isotropic 1CLJ potential seems to behave in a spurious fashion, leading to the lowest observed self-diffusivities. It was already demonstrated that the 1CLJ model led to the slowest dynamics observed in the bulk fluid (Fig. 2), and a similar conclusion can be extrapolated to the confined phase, where molecular displacement becomes severely restricted.
Considering the two cases in which electrostatic interactions are explicitly considered (AA-OPLS and 2CLJQ), it is observed that the differences in the corresponding self-diffusivities are rather small and approximately constant over the entire density range (Fig. 3); however, the 2CLJQ potential somehow results in smaller calculated D values. As clearly pointed out by Vrabec and co-workers,42 their parameterization of the ethylene molecule leads to a quadrupole moment which is ca. 0.331 B higher than the upper limit of the range of reported experimental values (Q = 1.3–4 B),81,82 thus artificially enhancing fluid–fluid electrostatics and possibly resulting in a slowing down of molecular translation. Because electrostatic interactions are long-ranged, the effect just mentioned should influence the results obtained not only for the dense but also for the very dilute fluid, thus explaining the constant ΔD differences between the AA-OPLS and 2CLJQ models.
The endoadsorption of quadrupolar molecules in zig-zag carbon nanotubes (7.86 ≤ D (Å) ≤ 14.89) has been addressed before using grand canonical Monte Carlo simulations.95 It was observed that, due to the strongly confining nature of such one-dimensional geometries, a strong molecular quadrupole such as CO2 (Q = 1.64–4.87 B)46 causes alignment of the fluid in a staggered configuration. In face of this, one can hypothesize the existence of molecular clusters held together by strong electrostatic coupling, which induces some local structure in the fluid that inhibits molecular translation inside the nanopore, and thus results in smaller self-diffusion coefficients compared to the potentials where electrostatics are omitted (TraPPE and UA-OPLS). In Fig. 4 we plot the radial distribution function8 of the confined dense fluids (eqn (6)), calculated for the individual carbon centres, for three representative coarse-grained potentials: AA-OPLS, TraPPE, and 1CLJ.
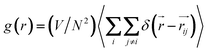 | (6) |
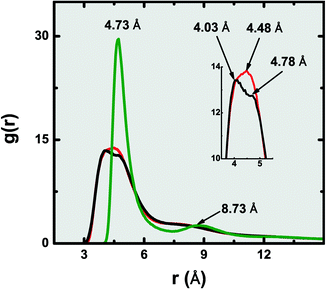 | ||
| Fig. 4 Radial distribution functions of dense confined ethylene, calculated for the individual carbon centres, at T = 300 K: AA-OPLS (black, ρ = 15.024 mol L−1), TraPPE (red, ρ = 15.024 mol L−1) and 1CLJ (green, ρ = 11.632 mol L−1). | ||
The simple one-center Lennard–Jones fluid exhibits a very sharp peak at r = 4.73 Å and a second (less intense) long-range peak located at r = 8.73 Å, indicating that molecules are densely packed together with almost no free volume between them (σ1CLJ ≈ 4.6 Å). If the fluid potential is to be increasingly refined, up to the atomistic level, a different picture can be obtained from Fig. 4. When the C2H4 molecule is described with the TraPPE model, not only does the initial g(r) peak becomes much broader, with an half-width length of Δr ≈ 1.95 Å, but it also appears closer at r = 4.48 Å; the second peak observed in the 1CLJ model is no longer clearly observable. If electrostatics are now explicitly added to the fluid molecules, via atomic partial charges (AA-OPLS), a further refinement of the initial peak takes place, as indicated by the magnification inset of Fig. 4. The r = 4.48 Å peak of the TraPPE potential essentially gets split into two contributions, r = 4.03 Å and r = 4.78 Å, suggesting the insurgence of a very short-range ordered arrangement of molecules in the AA-OPLS model, that is not present for the other potentials.
3.3 Influence of temperature
We have performed molecular dynamics isochoric calculations over a wide temperature range (220 ≤ T (K) ≤ 340), thus drafting a systematic picture of the influence of temperature on the self-diffusion coefficients of the confined fluid. For this purpose, only three different molecular potentials were selected: the two extreme situations of coarse-graining (AA-OPLS and 1CLJ) and an intermediate model (TraPPE). The results obtained are shown in Fig. 5 for three distinct molecular densities. It is observed that the response of the confined fluid to temperature is similar regardless of the temperature being above or bellow the bulk critical value, Tc = 282.4 K.40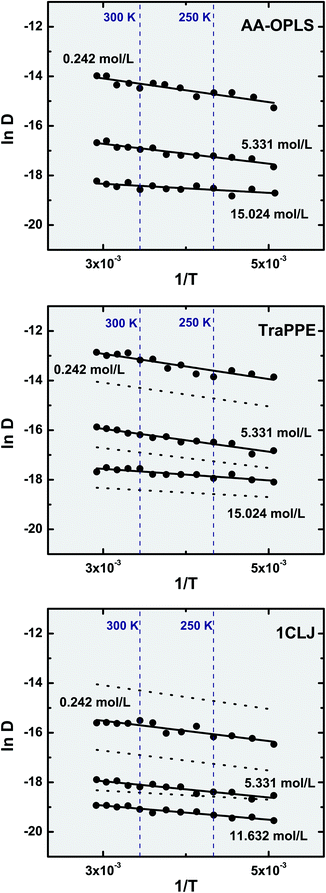 | ||
| Fig. 5 Temperature dependence of the confined fluid self-diffusion coefficient, in the range 220 ≤ T (K) ≤ 340. Symbols represent molecular dynamics results and lines correspond to an Arrhenius fit, D = Aexp(−Ea/RT). For comparison purposes, the Arrhenius plots obtained for the AA-OPLS fluid are indicated as dotted lines in both the TraPPE and 1CLJ charts. Note that the three different densities indicated include two limiting situations: when the nanotube contains only two fluid molecules (0.242 mol L−1), and when it is filled with fluid (11.632 mol L−1; 15.024 mol L−1). | ||
The isochors in Fig. 5 confirm our observations that potential coarse-graining plays a paramount role when studying the dynamics of confined ethylene. At constant density, it is observed that the self-diffusion coefficients obey a general trend: D (1CLJ) < D (AA-OPLS) < D (TraPPE). Simulation data show that a temperature rise in the system has a direct effect on the fluid dynamics, with a monotonical relationship between self-diffusivity and temperature. This effect can be interpreted on the basis of kinetic theory, considering that a temperature increase in the system has a direct consequence in terms of molecular kinetic energy, Ekin = (3/2)kBT, and thus molecular velocities respond to applied temperature according to 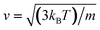 .96 We consider the temperature dependence of the self-diffusional process to be determined by an Arrhenius law:
.96 We consider the temperature dependence of the self-diffusional process to be determined by an Arrhenius law:
| D = Aexp(−Ea/RT) | (7) |
The results obtained from fitting our data to the Arrhenius equation are recorded in Table 7. It is quite interesting to observe that for each potential model studied, regardless of its own specificities and degree of molecular detail, the activation energy (Ea/R) decreases monotonically with increasing molecular density. Bhatia2 studied the transport of small molecular fluids (H2, CH4) confined in armchair nanotubes, and observed that reflection of fluid molecules on the solid walls was dominantly specular, suggesting that momentum transfer occurs essentially via fluid–fluid collisions. Because molecules in the dense fluid are highly packed, with little free volume between them, exchange of momentum via molecular collisions is highly efficient, thus dramatically increasing the self-diffusional process as a response to temperature. On the other hand, as the fluid density decreases, molecules are increasingly far away from each other, with long mean free paths between them, and thus momentum transfer is restricted. The results recorded in Table 7 highlight the hydrophobic nature of carbon nanotubes. Liu and co-workers23 determined the activation energy for water diffusion (ρ = 55 mol L−1) inside a Deff = 15.39 Å zig-zag carbon nanotube as Ea ≈ 1941 K. At an ethylene density of the same order of magnitude as Liu's, ρ(C2H4) > 11 mol L−1, the self-diffusion of ethylene has an activation energy which is ca. 5–8 times lower than that of confined water.
| Molecular potential | ρ (mol L−1) | A (m2s−1) | E a/R (K) |
|---|---|---|---|
| AA-OPLS | 0.242 | 5.160 × 10−6 | 636.95 |
| 5.331 | 2.710 × 10−7 | 533.96 | |
| 15.024 | 2.254 × 10−8 | 242.85 | |
| TraPPE | 0.242 | 1.870 × 10−5 | 678.29 |
| 5.331 | 7.508 × 10−7 | 614.64 | |
| 15.024 | 5.995 × 10−8 | 310.05 | |
| 1CLJ | 0.242 | 9.379 × 10−7 | 545.81 |
| 5.331 | 5.913 × 10−8 | 437.35 | |
| 11.632 | 1.867 × 10−8 | 380.44 | |
The activation energies and pre-exponential factors of the Arrhenius law are plotted in Fig. 6 as a function of molecular density, and a relationship seems to exist between those two properties; a more minute mapping of the [(Ea/R), A, ρ] space would be required to fully confirm this observation, ideally in the very low and ultra high density regions. Nonetheless, in the density domain accessed in the present study, both Arrhenius parameters exhibit nonlinear decays with ρ, which can be reasonably estimated with the empirical equations:
| (Ea/R) = (Ea/R)0 − bρ3/2 | (8.1) |
| lnA = lnA0 − bρ1/2 | (8.2) |
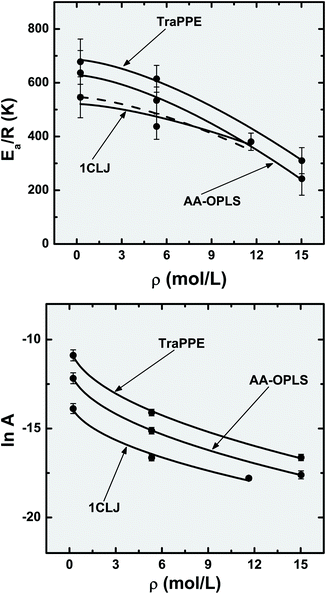 | ||
| Fig. 6 Dependence of the Arrhenius parameters, activation energy (Ea/R) and pre-exponential factor (A), with the confined fluid molecular density. Symbols are the results of fitting MD data with the Arrhenius law and lines correspond to nonlinear functions, (Ea/R) = (Ea/R)0 − bρ3/2 and lnA = lnA0 − bρ1/2. The dashed line is an extrapolation of the 1CLJ data with the parameters ((Ea/R)0,b) calculated for the upper (ρ = 5.331 mol L−1) and lower (ρ = 11.632 mol L−1) data point error intervals. | ||
The curves indicated in Fig. 6 suggest that there is an initial (small) region of molecular densities where (Ea/R) is roughly constant, corresponding to an infinitely dilute fluid, (Ea/R)0 = 546 K (1CLJ) < (Ea/R)0 = 628 K (AA-OPLS) < (Ea/R)0 = 685 K (TraPPE). After that initial region, the activation energies decrease more noticeably with density; the precise boundary is a function of the particular potential model employed. When the pre-exponential factor is considered, the data plotted in Fig. 6 indicate that the former decreases monotonically as the nanotube becomes completely filled with fluid. If we consider the slope of eqn (8.2) as a measure of susceptibility regarding molecular density (bTraPPE = 6.4, b1CLJ = 6.6, bAA-OPLS = 6.7), it can be concluded that the three potentials respond in a similar manner, within the errors associated with the corresponding fittings.
As previously mentioned, we are unaware of any experimental work reporting self-diffusion data for confined ethylene. Nonetheless, and in order to probe the simultaneous effect of confinement and temperature on the fluid dynamics, we compare in Fig. 7 our results with the bulk experimental data measured by Arends et al.37 and Baker et al.38 using the NMR spin-echo technique. Because the AA-OPLS potential is the one that best reproduces the bulk experimental measurements (Fig. 2), we proceed our discussion using this model as a benchmark for the simulation data. In the limit of complete tube filling, entropic effects are usually dominant21 and thus packing efficiency rules over energetic considerations. It is clear from Fig. 7 that, when the solid is saturated with fluid (15.024 mol L−1), the self-diffusion coefficients show a similar response to applied temperature, both in the bulk phase and under confinement. In fact, the activation energies obtained from the corresponding Arrhenius plots are (Ea/R)bulk = 214.12 K and (Ea/R)SWCNT = 242.85 K, suggesting that confinement exerts a major influence on the absolute values of the mobility constants, but not so much on their intrinsic dependence on temperature. To a reasonable approximation, the self-diffusivity differences between the bulk and confined phases can be considered as roughly constant over the entire temperature range, (Dbulk/DSWCNT)T ∈ [220![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K–340
K–340![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K] = 2.52 ± 0.13.
K] = 2.52 ± 0.13.
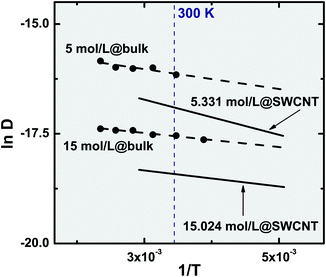 | ||
| Fig. 7 Temperature dependence of the fluid self-diffusion coefficient (220 ≤ T (K) ≤ 398.15). Symbols represent experimental data measured for bulk ethylene37,38 and lines correspond to the Arrhenius equation (eqn (7)) for the bulk (dashed) and confined (full) phases. The confined ethylene results were obtained using the AA-OPLS potential at two different densities. | ||
A totally different picture results when density is lowered, and the existence of free volume becomes a relevant aspect. The upper two isochores of Fig. 7 correspond to a bulk and confined fluid at ρ = 5 mol L−1 and ρ = 5.331 mol L−1. At those densities, free volume inside the solid corresponds to more than 50% of the total available volume, and therefore a sharp discrepancy can be observed in the slopes of the isochores, originating in activation energies that are quite different between the bulk and confined fluid, (Ea/R)bulk = 301.64 K and (Ea/R)SWCNT = 533.96 K. For those lower densities, the self-diffusivities ratio increases dramatically to (Dbulk/DSWCNT)T ∈ [220![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K–340
K–340![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K] = 10.2 ± 0.5. One can extrapolate the previous observations to a very dilute fluid, and postulate that as the free volume inside the solid increases, so do the differences in the corresponding activation energies between the bulk and confined fluid. Unfortunately, this could not be validated by comparison with experimental findings, for as far as we are aware literature data do not reach such a low density region as the one studied in the present work (ρ = 0.242 mol L−1).
K] = 10.2 ± 0.5. One can extrapolate the previous observations to a very dilute fluid, and postulate that as the free volume inside the solid increases, so do the differences in the corresponding activation energies between the bulk and confined fluid. Unfortunately, this could not be validated by comparison with experimental findings, for as far as we are aware literature data do not reach such a low density region as the one studied in the present work (ρ = 0.242 mol L−1).
Conclusions
The effect of confinement on the dynamical properties of C2H4 was observed to be dependent on the particular potential model employed to study the fluid, in a manner which is significantly different than in bulk, where the calculated D values are rather independent of the potential used (Fig. 2). The fully atomistic force field (AA-OPLS) was validated by comparing simulation results with bulk experimental data, leading to a qualitative agreement between both. As ethylene is confined into a (16,0) single-walled carbon nanotube, differences between molecular potentials are enhanced resulting in discrepancies in the observed self-diffusivities.It is generally argued that coarse-graining intermolecular potentials results in increased self-diffusivities, an effect which is commonly ascribed to a smoothing of the overall molecular shape. In the present case, if the AA-OPLS model is used as a benchmark, it becomes clear (cf.Fig. 2–3) that the effect of coarse-graining is unpredictable, and an appropriate and accurate parameterization may faithfully reproduce the self-diffusion data. Furthermore, the existence of explicit electrostatic details in the potential seems to induce short-range order in the confined fluid (Fig. 4), resulting in a slowing down of molecular mobility. In spite of the marked anisotropy introduced by the solid, both the bulk fluid and anisotropic systems diffusion data are observed to roughly collapse onto a same master curve, which in this work was described as a simple power-law dependency of the self-diffusion coefficient with molecular density, D = D0ρλ (Table 6).
In order to monitor the influence of temperature upon the confined fluids, three representative intermolecular potentials were chosen, AA-OPLS, TraPPE and 1CLJ, corresponding to different degrees of coarse-graining. It was demonstrated that the temperature induced response of the self-diffusivites, although clearly potential dependent, could be reasonably described by the Arrhenius law. The activation energies, (Ea/R), and pre-exponential factors, A, thus calculated, indicate non-linear relationships between those properties and molecular density (eqns (8.1) and (8.2)), which, as far as we are aware, have previously been unnoticed. Using the AA-OPLS potential, we determined the activation energy for ethylene self-diffusion inside the SWCNT as 242.8 ≤ (Ea/R) (K) ≤ 636.95, roughly 5–8 times smaller than the corresponding value for water.23 Finally, considering the AA-OPLS model as a benchmark for simulation data and comparing with bulk fluid experimental measurements, one concludes that: i) under isochoric conditions, the influence of temperature upon molecular diffusion can be reasonably described by the Arrhenius law, both in the bulk and confined systems, and ii) as molecular density approaches that of a very dilute fluid, the effect of confinement upon the fluid's dynamics increases, leading to a dramatic increase of the activation energies compared to the isochoric bulk phase.
Acknowledgements
This paper is dedicated to Prof. Jorge C. G. Calado on the occasion of his 73rd birthday.F.J.A.L. Cruz gratefully acknowledges financial support from FCT/MCTES (PT) through grant SFRH/BPD/45064/2008.
References
- L. D. Gelb, K. E. Gubbins, R. Radhakrishnan and M. Sliwinska-Bartkowiak, Rep. Prog. Phys., 1999, 62, 1573–1659 CrossRef CAS.
- S. K. Bhatia, Adsorpt. Sci. Technol., 2006, 24, 101–116 CrossRef CAS.
- B. Coasne, S. K. Jain and K. E. Gubbins, Mol. Phys., 2006, 104, 3491–3499 CrossRef CAS.
- S. K. Bhatia and D. Nicholson, Phys. Rev. Lett., 2008, 100, 236103 CrossRef.
- D. Nicholson and S. K. Bhatia, Mol. Simul., 2009, 35, 109–121 CrossRef CAS.
- K. E. Gubbins, Y.-C. Liu, J. D. Moore and J. C. Palmer, Phys. Chem. Chem. Phys., 2011, 13, 58–85 RSC.
- T. Nanok, N. Artrith, P. Pantu, P. A. Bopp and J. Limtrakul, J. Phys. Chem. A, 2009, 113, 2103–2108 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1990 Search PubMed.
- J. M. Haile, Molecular Dynamics Simulation: Elementary Methods, Wiley, New York, 1992 Search PubMed.
- R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes, Imperial College Press, London, 1998 Search PubMed.
- M. Meyyappan, Carbon Nanotubes: Science and Applications, CRC Press, London, 2005 Search PubMed.
- J. A. Fagan, J. R. Simpson, B. J. Bauer, S. H. De Paoli Lacerda, M. L. Becker, J. Chun, K. B. Migler, A. R. H. Walker and E. K. Hobbie, J. Am. Chem. Soc., 2007, 129, 10607–10612 CrossRef CAS.
- A. Taherpour, Fullerenes, Nanotubes, Carbon Nanostruct., 2007, 15, 279–289 CrossRef CAS.
- S. B. Sinnott and R. Andrews, Crit. Rev. Solid State Mat. Sci., 2001, 26, 145–249 CrossRef CAS.
- S. Y. Hong, G. Tobias, B. Ballesteros, F. E. Oualid, J. C. Errey, K. Doores, A. I. Kirkland, P. D. Nellist, M. L. H. Green and B. G. Davis, J. Am. Chem. Soc., 2007, 129, 10966–10967 CrossRef CAS.
- L. Zhang, S. Zaric, X. Tu, X. Wang, W. Zhao and H. Dai, J. Am. Chem. Soc., 2008, 130, 2686–2691 CrossRef CAS.
- W. Yang, P. Thordarson, J. J. Gooding, S. P. Ringer and F. Braet, Nanotechnology, 2007, 18, 412001 CrossRef.
- Y. Wu, J. A. Phillips, H. Liu, R. Yang and W. Tan, ACS Nano, 2008, 2, 2023–2028 CrossRef CAS.
- Z. Mao and S. B. Sinnott, J. Phys. Chem. B, 2001, 105, 6916–6924 CrossRef CAS.
- J. Jiang, S. I. Sandler, M. Schenk and B. Smit, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 45447 CrossRef.
- F. J. A. L. Cruz and E. A. Müller, Adsorption, 2009, 15, 1–12 CrossRef CAS.
- A. Striolo, Nano Lett., 2006, 6, 633–639 CrossRef CAS.
- Y.-C. Liu, J.-W. Shen, K. E. Gubbins, J. D. Moore, T. Wu and Q. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125438 CrossRef.
- R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport phenomena, John Wiley & Sons, New York, 2002 Search PubMed.
- Q. Chen, J. D. Moore, Y.-C. Liu, T. J. Roussel, Q. Wang, T. Wuan and K. E. Gubbins, J. Chem. Phys., 2010, 133, 094501 CrossRef.
- S. K. Bhatia, H. Chen and D. S. Sholl, Mol. Simul., 2005, 31, 643–649 CrossRef CAS.
- R. Krishna and J. M. van Baten, Fluid Phase Equilib., 2006, 45, 2084–2093 CAS.
- S. Jakobtorweihen, C. P. Lowe, F. J. Keil and B. Smit, J. Chem. Phys., 2007, 127, 24904 CrossRef CAS.
- Y.-C. Liu, J. D. Moore, T. J. Roussel and K. E. Gubbins, Phys. Chem. Chem. Phys., 2010, 12, 6632–6640 RSC.
- M. L. Klein and W. Shinoda, Science, 2008, 321, 798–800 CrossRef CAS.
- D. Sengupta, H. Leontiadou, A. E. Mark and S.-J. Marrink, Biochim. Biophys. Acta, Biomembr., 2008, 1778, 2308–2317 CrossRef CAS.
- Z. Mao and S. B. Sinnott, J. Phys. Chem. B, 2000, 104, 4618 CrossRef CAS.
- Z. Mao and S. B. Sinnott, Phys. Rev. Lett., 2002, 89, 278301 CrossRef.
- F. J. A. L. Cruz and E. A. Müller, Adsorption, 2009, 15, 13–22 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- N. A. McDonald, H. A. Carlson and W. L. Jorgensen, J. Phys. Org. Chem., 1997, 10, 563–576 CrossRef CAS.
- B. Arends, K. O. Prins and N. J. Trappeniers, Phys. A, 1981, 107, 307–318 CrossRef.
- E. S. Baker, D. R. Brown and J. Jonas, J. Phys. Chem., 1984, 88, 5425–5429 CrossRef CAS.
- F. Cuadros, I. Cachadina and W. Ahumada, Int. Rev. Phys. Chem., 1995, 14, 205–213 CrossRef CAS.
- J. S. Rowlinson and F. L. Swinton, Liquids and Liquid Mixtures, Butterworths, London, 1982 Search PubMed.
- W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670 CrossRef CAS.
- J. Vrabec, J. Stoll and H. Hasse, J. Phys. Chem. B, 2001, 105, 12126–12133 CrossRef CAS.
- J. Stoll, J. Vrabec and H. Hasse, AIChE J., 2003, 49, 2187–2198 CrossRef CAS.
- G. A. Fernández, J. Vrabec and H. Hasse, Int. J. Thermophys., 2005, 26, 1389–1407 CrossRef.
- S. Curbelo and E. A. Müller, Adsorpt. Sci. Technol., 2005, 23, 855–865 CrossRef CAS.
- C. G. Gray and K. E. Gubbins, Theory of Molecular Fluids, Clarendon Press, Oxford, 1984. Search PubMed.
- C. D. Wick, M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 2000, 104, 8008–8016 CrossRef CAS.
- W. L. Jorgensen, J. D. Madura and C. J. Swenson, J. Am. Chem. Soc., 1984, 106, 6638–6646 CrossRef CAS.
- F. J. A. L. Cruz and J. P. B. Mota, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165426 CrossRef.
- F. J. A. L. Cruz, I. A. A. C. Esteves and J. P. B. Mota, Colloids Surf., A, 2010, 357, 43–52 CrossRef CAS.
- W. A. Steele, Surf. Sci., 1973, 36, 317–352 CrossRef CAS.
- W. A. Steele, The interaction of Gases with Solid Surfaces, Pergamon Press, Oxford, 1974 Search PubMed.
- W. A. Steele, Chem. Rev., 1993, 93, 2355–2378 CrossRef CAS.
- D. M. Ackerman, A. I. Skoulidas, D. S. Sholl and J. K. Johnson, Mol. Simul., 2003, 29, 677–684 CrossRef CAS.
- V. P. Sokhan, D. Nicholson and N. Quirke, J. Chem. Phys., 2002, 117, 8531–8539 CrossRef CAS.
- V. V. Simonyan, J. K. Johnson, A. Kuznetsova and J. T. Yates, J. Chem. Phys., 2001, 114, 4180–4185 CrossRef CAS.
- K. Kaneko, R. F. Cracknell and D. Nicholson, Langmuir, 1994, 10, 4606–4609 CrossRef CAS.
- A. Heyden, T. Düren and F. J. Keil, Chem. Eng. Sci., 2002, 57, 2439–2448 CrossRef CAS.
- F. R. Hung, B. Coasne, E. E. Santiso, K. E. Gubbins, F. R. Siperstein and M. Sliwinska-Bartkowiak, J. Chem. Phys., 2005, 122, 144706 CrossRef.
- P. Kondratyuk, Y. Wang, J. K. Johnson and J. T. Yates Jr, J. Phys. Chem. B, 2005, 109, 20999–21005 CrossRef CAS.
- B. Mukherjee, P. K. Maiti, C. Dasgupta and A. K. Sood, J. Chem. Phys., 2007, 126, 124704–124711 CrossRef.
- A. I. Skoulidas, D. S. Sholl and J. K. Johnson, J. Chem. Phys., 2006, 124, 054708 CrossRef.
- A. Striolo, A. A. Chialvo, K. E. Gubbins and P. T. Cummings, J. Chem. Phys., 2005, 122, 234712 CrossRef CAS.
- A. Vernov and W. A. Steele, Langmuir, 1992, 8, 155–159 CrossRef CAS.
- X. Zhao and J. K. Johnson, Mol. Simul., 2005, 31, 1–10 CrossRef CAS.
- H. Chen, J. K. Johnson and D. S. Sholl, J. Phys. Chem. B, 2006, 110, 1971–1975 CrossRef CAS.
- D. Cao and J. Wu, Langmuir, 2004, 20, 3759–3765 CrossRef CAS.
- H. Chen and D. S. Sholl, J. Am. Chem. Soc., 2004, 126, 7778–7779 CrossRef CAS.
- H. Chen and D. S. Sholl, J. Membr. Sci., 2006, 269, 152–160 CrossRef CAS.
- A. Striolo, Nanotechnology, 2007, 18, 475704–475713 CrossRef.
- A. Alexiadis and S. Kassinos, Chem. Eng. Sci., 2008, 63, 2047–2056 CrossRef CAS.
- T. Ohba and K. Kaneko, J. Phys. Chem. B, 2002, 106, 7171–7176 CrossRef CAS.
- T. Düren, F. J. Keil and N. A. Seaton, Mol. Phys., 2002, 100, 3741–3751 CrossRef.
- J. Jiang, N. J. Wagner and S. I. Sandler, Phys. Chem. Chem. Phys., 2004, 6, 4440–4444 RSC.
- W. Smith and I. T. Todorov, Mol. Simul., 2006, 32, 935–943 CrossRef CAS.
- R. Zwanzig, Annu. Rev. Phys. Chem., 1965, 16, 67–102 CrossRef CAS.
- V. G. Baidakov and Z. R. Kozlova, Chem. Phys. Lett., 2010, 500, 23–27 CrossRef CAS.
- H. Takeuchi and K. Okazaki, J. Chem. Phys., 1990, 92, 5643–5652 CrossRef CAS.
- H. Liu, C. M. Silva and E. A. Macedo, Chem. Eng. Sci., 1998, 53, 2403–2422 CrossRef CAS.
- J. O. Hirschfelder, C. F. Curtiss and R. B. Bird, Molecular Theory of Gases and Liquids, Wiley, New York, 1964. Search PubMed.
- R. F. Borkman and J. Frank, J. Am. Chem. Soc., 1971, 93, 5640–5644 CrossRef CAS.
- W. Majer, P. Lutzmann and W. Hüttner, Mol. Phys., 1994, 83, 567–578 CrossRef CAS.
- O. Suárez-Iglesias, I. Medina, C. Pizarro and J. L. Bueno, Fluid Phase Equilib., 2008, 269, 80–92 CrossRef.
- Z. N. Gerek and J. R. Elliott, Ind. Eng. Chem. Res., 2010, 49, 3411–3423 CrossRef CAS.
- A. L. Magalhães, S. P. Cardoso, B. R. Figueiredo, F. A. D. Silva and C. M. Silva, Ind. Eng. Chem. Res., 2010, 49, 7697–7700 CrossRef.
- M. H. Cohen and D. Turnbull, J. Chem. Phys., 1959, 31, 1164–1169 CrossRef CAS.
- A. E. Nasrabad, J. Chem. Phys., 2009, 130, 024503 CrossRef.
- R. C. Reid, J. M. Prausnitz and B. E. Poling, The Properties of Gases and Liquids, McGraw-Hill, New York, 1987 Search PubMed.
- Y. Zhu, X. Lu, J. Zhou, Y. Wang and J. Shi, Fluid Phase Equilib., 2002, 194–197, 1141–1159 CrossRef CAS.
- F. M. Mourits and F. H. A. Rummens, Can. J. Chem., 1977, 55, 3007–3020 CrossRef CAS.
- E. A. Müller and L. D. Gelb, Ind. Eng. Chem. Res., 2003, 42, 4123–4131 CrossRef.
- J. C. G. Calado, P. Clancy, A. Heintz and W. B. Streett, J. Chem. Eng. Data, 1982, 27, 376–385 CrossRef CAS.
- L. S. Tee, S. Gotoh and W. E. Stewart, Ind. Eng. Chem. Fundam., 1966, 5, 356–363 Search PubMed.
- J. Mittal, J. R. Errington and T. M. Truskett, J. Phys. Chem. B, 2007, 111, 10054–10063 CrossRef CAS.
- E. A. Müller, J. Phys. Chem. B, 2008, 112, 8999–9005 CrossRef.
- S. Chapman and T. G. Cowling, The Mathematical Theory of Non-uniform Gases, Cambridge University Press, Cambridge, 1990. Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Liu's equation. See DOI: 10.1039/c1ra00019e |
| This journal is © The Royal Society of Chemistry 2011 |

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–H) = 58.615 kJ mol−1.
C–H) = 58.615 kJ mol−1.