Kinetically controlled formation of helical mesoporous silica nanostructures correlated to a ribbon intermediate phase†
Wei-Chia
Huang
a,
Li-Ling
Chang
a,
Yasuhiro
Sakamoto
b,
Ching-Yi
Lin
a,
Nien-Chu
Lai
a and
Chia-Min
Yang
*a
aDepartment of Chemistry, National Tsing Hua University, Hsinchu, 30013, Taiwan. E-mail: cmyang@mx.nthu.edu.tw; Fax: +886 3 5165521; Tel: +886 3 5731282
bNanoscience and Nanotechnology Research Center, Osaka Prefecture University, 1-2 Gakuen-cho, Naka-ku, Sakai, 599-8570, Japan
First published on 29th July 2011
Abstract
We report here the synthesis of mesoporous silica nanostructures simultaneously having helical morphology and c2mm symmetry correlated to a ribbon intermediate phase. A mixture of four types of helical nanostructures, including short-pitch (just a few lattice constants) sphere-like nanoparticles, short-pitch straight nanorods, long-pitch (hundreds of nanometres) twisted nanorods and long-pitch spiral nanorods could be produced. A formation mechanism was proposed based on the in situsmall-angle X-ray scattering (SAXS) measurements and other analyses, with the emphasis on the influences of the assembly kinetics on the structural and morphological properties of the helical nanostructures. Based on the mechanism, we further showed simple kinetic control to prepare solely short-pitch or long-pitch helical nanostructures. The present study demonstrates the possibility to tailor the helical mesostructures through kinetic control and offers prospects for the design and preparation of these types of materials.
Introduction
The advent of mesoporous M41S1,2 and FSM-16 materials3,4 sparked an enormous amount of research activity on the synthesis and applications of ordered mesoporous and mesostructured materials with controlled mesostructure, composition, functionality and morphology.5–20 Recently, the discoveries of helical mesoporous materials21–35 and the silica mesostructures36–39 corresponding to the intermediate phases in surfactant–water systems40–42 are among the most exciting advances in this research field. Intermediate phases are non-cubic phases between two-dimensional (2D)-hexagonal and lamellar liquid-crystal phases,40–42 and ribbon phases are the intermediate phases that appear closest to the hexagonal phase.40–43 The low-symmetry ribbon phases consist of non-circular micellar rods arranged on a 2D-rectangular lattice.40–43 Correspondingly, the low-symmetry mesostructured materials correlated to the ribbon phases may be regarded as deformed structures of the 2D-hexagonal mesophase (e.g. MCM-41 with p6mm symmetry) in which the cylindrical mesopores are flattened.36–38 The additional anisotropy of the resulting elliptical channels may bring unprecedented opportunities in exploring curvature-dependent chemistry and phenomena44,45 in the anisotropic nano-space.With regard to helical mesoporous silica materials, in analogy to the fascinating self-assembled helical structure in nature, they also attract great attention21–35and are promising for chiral separation, catalysis and recognition46–48 and for the template preparation of helical nanowires and nanomaterials.24,25,49 Helical mesoporous silica materials can be prepared in two-phase static systems21,22 or by confined assembly in porous anodic alumina membranes.23,24 More interestingly, helical mesostructures can be formed by a direct assembly of surfactants and inorganic precursors in a single-phase solution with low surfactant concentration.25–35 All the reported single-phase derived materials have MCM-41-like 2D-hexagonal structure, and both chiral25 and achiral surfactants26–35 could be applied to generate helical mesostructures. The formation of the helical morphology was thought to be driven by a reduction in surface free energy (ΔGS) from the straight and hexagonally packed composite micellar rods until it is balanced by an increased bending energy of the micellar rods (ΔGB).30–32 Han et al. proposed an alternative entropy-driven model for the helical silica mesostructures synthesized in a highly concentrated ammonia solution.34
Apart from the thermodynamic considerations, however, very little was reported or discussed on the influence of the assembly kinetics on the mesostructure and morphology of the helical materials. Considering a synthesis of helical mesoporous silica materials in an alkaline solution of a cationic surfactant with low concentration, the cooperative organization of ordered organic–inorganic hybrids involves: (1) hydrolysis of the tetraalkoxysilane precursor, (2) ion exchange/binding of anionic silicate species to the head groups of the surfactant molecules, (3) aggregation/elongation of the silicate-encased micellar rods to pack into a silicatropic liquid crystal, and (4) interfacial condensation/polymerization of silicate species.2,6,50–52 It is reasonable to speculate that possible modulation of the rates of these reactions/processes may also affect the structural and morphological properties of the helical mesoporous materials.
Recently, we discovered a new type of mesoporous silica materials with a mesostructure correlated to the 2D-rectangular c2mm ribbon phase.38 The materials, designated as MMT-1 (standing for Mesoporous Materials from Tsing Hua University in Taiwan), are synthesized in an alkaline and dilute solution of mixed cationic and nonionic surfactants. They have elliptical channels and can be regarded as a deformed structure of MCM-41. Furthermore, the channels in MMT-1 are coiled to form a helical mesostructure with very short helical pitch.38 We herein report the formation of a mixture of short-pitch (just a few lattice constants) and long-pitch (hundreds of nanometres) nanostructures by decreasing the injection rate of the silica source tetraethoxysilane (TEOS). In situSAXS and scanning electron microscopy (SEM) measurements were performed to study the structural and morphological evolution of the materials. Based on the results, a formation mechanism of the helical MMT-1 nanostructures was proposed with emphasis on the roles of the assembly kinetics in influencing the mesostructure and the morphology. Furthermore, we examined the proposed mechanism and successfully synthesized purely short-pitch or long-pitch MMT-1 nanostructures by simply controlling the kinetic parameters of the synthesis. Our study demonstrates the feasibility to tailor the helical mesoporous silica materials through kinetic control and offers prospects for the design and preparation of new mesostructured materials.
Experimental
Synthesis
Helical MMT-1 materials were synthesized under alkaline conditions by using cetyltrimethylammonium bromide (CTAB) and tetraethylene glycol dodecyl ether (C12EO4).38 In a typical synthesis, 0.9 g of CTAB and 0.3 g of C12EO4 were dissolved in 570 g of distilled water and 21.6 g of 0.4 M NaOH solution with stirring at 500 rpm at 308 K. After complete dissolution, 5.6 g of TEOS was injected into the surfactant solution using a syringe pump with a controlled injection rate (R) in the range of 3.0–24.0 mL h−1. The mixture was stirred at 500 rpm for 2 h and was then aged at 373 K for 48 h. The product was filtered, washed and finally dried in air. The samples are referred to as E-MMT-1(R), where R denotes the injection rate. Surfactant-free materials were obtained by calcination at 813 K in air. For some syntheses, a small amount of ethanol (EtOH) was added in the surfactant solution prior to the injection of TEOS. The resulting samples are referred to as E/E-x-MMT-1(R), where x is the molar ratio of EtOH (see below). Alternatively, TEOS was replaced by tetramethoxysilane (TMOS) and the resulting samples are referred to as M-MMT-1(R). The molar composition of the synthesis mixture was 1 TEOS (or TMOS)/0.0938 CTAB/0.0313 C12EO4/0.32 NaOH/xEtOH/1230 H2O, with x = 0–40.The Pt-infiltrated materials were prepared according to the reported procedures.53–55 0.3 g of calcined MMT-1 silica was first impregnated with 0.004 g of tetraammine platinum(II) nitrate and was heated to 573 K in a oxygen flow. The sample was then impregnated with 0.055 g of the same salt, after which it was heated to 573 K in a hydrogen flow to reduce the metal. The loading amount of Pt in the Pt/MMT-1 composites was ∼15 wt%.The host silica was dissolved by HF solution to obtain the Pt nanowires.53,54
Characterization
X-Ray diffraction (XRD) patterns were recorded on a Mac Science 18MPX diffractometer using Cu-Kα radiation. Scanning electron microscopy (SEM) images were obtained with a field emission JEOL JSM-7000F microscope operating at 10 kV. The samples were coated with Pt before SEM measurement. The transmission electron microscopy (TEM) images of the calcined pure-silica samples and the dark-field scanning transmission electron microscopy (DF-STEM) images of the Pt-infiltrated samples were taken using a field emission JEOL JEM-2100F microscope operated at 200 kV and a JEOL JEM-2010 microscope operated at 200 kV. Nitrogen sorption isotherms were measured at 77 K using a Quantachrome Autosorb-1MP instrument.The in situSAXS measurements were performed at the beamline 17B3 of the National Synchrotron Radiation Research Center (NSRRC), Taiwan, using X-rays with a photon energy of 10.0 keV. One-dimensional SAXS profiles were circularly averaged from 2D images obtained using a multiwire area detector (gas-type). The sample-to-detector distance was 1751.72 mm. The scattering wavevector Q, 4πsin(θ)/λ, defined by the scattering angle 2θ and wavelength λ, was calibrated with silver behenate, and the scattering intensity I(Q) was calibrated to the absolute intensity scale with a polyethylene sample. Each reaction for the measurement was carried out in a batch reactor. The silica source was injected with a controlled rate to the reaction mixture using a syringe pump. The reaction mixture was continuously pumped through a Kapton-sealed thin container, through which the X-ray beam passed, and then back to the reactor at a pumping rate of 40 mL min−1. Both the reactor and the container were thermostatted to a desired temperature of 35 °C.
Results and discussion
We found that changing the injection rate of the tetraalkoxysilane only slightly affected the c2mm mesostructure but had a profound influence on the morphology of the resulting MMT-1 materials. Fig. 1 shows the XRD patterns of the samples synthesized with different injection rate (R) of TEOS. All the patterns contain well-resolved reflections in the range of 2θ = 1–5°, indicating high structural order of these samples with the 2D rectangular c2mm symmetry. For the samples synthesized with R = 3.0, 7.5 and 12.0 mL h−1, all the reflections are identical in position and the unit cell parameters a and b are 11.0 nm and 4.4 nm, respectively. Upon increasing the injection rate to 16.0 and 24.0 mL h−1, the resulting samples (E-MMT-1(16.0) and E-MMT-1(24.0)) exhibit less intense and broader reflections and might have lower structural ordering. The reflections are also shifted slightly toward the small 2θ region, suggesting slightly larger unit cells (a = 11.6 nm and b = 4.5–4.6 nm) for the two samples. | ||
| Fig. 1 XRD patterns of the as-synthesized E-MMT-1(R) with R = 3.0, 7.5, 12.0, 16.0 and 24.0 mL h−1, respectively (from top to bottom). | ||
Despite having similar c2mm mesostructure, the SEM characterization revealed diverse morphologies for the MMT-1 materials synthesized with slow (R ≤ 12.0 mL h−1) or fast (R > 12.0 mL h−1) injection rates. Fig. 2 shows the SEM images of the two representative samples E-MMT-1(7.5) and E-MMT-1(16.0) (see Fig. S1 in Electronic Supplementary Information (ESI)† for the SEM images of E-MMT-1(3.0) and E-MMT-1(24.0)). The sample E-MMT-1(16.0) looks very similar to the material synthesized with fast injection rate reported in our previous study38 and solely consists of small (70–130 nm in diameter) nanoparticles (see Fig. S2 in ESI for its TEM image). On the other hand, E-MMT-1(7.5) contains four types of nanostructures with distinct morphologies. The textural properties and the fractions (based on the numbers of particles counted in the SEM images) of them are summarized in Table S1 in ESI. The majority (∼55%) of the nanostructures are sphere-like nanoparticles, followed by straight nanorods. The rest of the helical nanostructures can be identified as twisted nanorods (∼13%) with single twist axis and spiral nanorods (∼2%) with two axes, one lying outside the rod and the other at the center of the rod.29,31,34 The twisted nanorods are thinner and shorter than the spiral nanorods.
 | ||
| Fig. 2 SEM images of the as-synthesized (a) E-MMT-1(7.5) and (b) E-MMT-1(16.0). The arrows in (a) indicate a sphere-like nanoparticle, a straight nanorod, a twisted nanorod, and a spiral nanorod (from left to right). | ||
Further characterizations on the calcined E-MMT-1(7.5) reveal interesting internal structure and the relationship between the particle morphology and the helicity of the nanostructures. For the first two types of particles (sphere-like nanoparticles and straight nanorods), the corresponding electron microscopy images in Fig. 3 suggest that both of them have stripes circling the particles on the external surface. They also have nearly identical pyramidal-shaped ends connected by a cylindrical segment, and the nanoparticles could be regarded as shortened straight nanorods. The channels at the pyramidal-shaped ends are slightly tilted and distorted with a tilt angle of about 50° relative to the edge of the cylindrical segment (cf.Fig. 3g). The cylindrical segments of the two types of particles are highly ordered c2mm mesostructures with the same unit cell dimension of a = 9.5 nm and b = 4.0 nm (see Fig. S3 in ESI for the XRD pattern of the calcined sample). The major and minor axes of the elliptical channel sections are estimated to be 4.7 nm and 3.3 nm, respectively. Moreover, the channels in both types of particles are wound around a center axis parallel to the minor axis of the elliptical channel section. The helical arrangement is further confirmed by the DF-STEM images of the “whirlpool-like” Pt nanowires in the Pt-infiltrated samples. The helical pitch must be very short, probably just a few lattice constants, in order to give the images with the 2D-rectangular arrangement of the channels clearly visible on both sides of the particles.21,22 The short helical pitch in similar MMT-1 nanoparticles was confirmed in our previous study.38
 | ||
| Fig. 3 SEM and TEM images of the sphere-like nanoparticles (a, b) and the straight nanorods (d, e) in the calcined E-MMT-1(7.5). (c, f) DF-STEM images of the Pt-infiltrated sphere-like nanoparticles (c) and straight nanorods (f). Scale bar = 50 nm. (g) Schematic illustration of the arrangement of the elliptical channels at the ends of both types of nanostructures. | ||
On the other hand, the twisted nanorods and spiral nanorods have helical morphologies with relatively long helical pitches. The ratio of the right-handed and left-handed helices is about 1.0 judged from 100 nanorods in different SEM images. The pitches for the twisted and spiral nanorods are 250–300 nm and 700–900 nm, respectively, as measured from the SEM and TEM images as well as the DF-STEM images of the Pt-infiltrated sample in Fig. 4. The helical pitch for twisted and spiral nanorods is roughly proportional to the rod diameter, resulting in a nearly constant pitch-to-diameter ratio (P/D) of ∼3.5. The P/D value is much larger than that for the short-pitch particles in the same batch of the sample E-MMT-1(7.5), but it is relatively small as compared to the values (P/D > 6.0) for most reported MCM-41-like helical materials.25–35 Another interesting feature of the twisted nanorods is that the helical channels turn back at the end of the nanorods (cf.Fig. 4b). It is further confirmed by the DF-STEM image of the Pt-infiltrated twisted nanorods (Fig. 4c), in which the helical Pt nanowires are observed to form “8”-shaped loops at the end of the rod.
 | ||
| Fig. 4 SEM and TEM images of the twisted nanorods (a, b) and the spiral nanorods (d, e) in the calcined E-MMT-1(7.5). (c) DF-STEM image of the Pt-infiltrated twisted nanorods. | ||
The structural evolution during the synthesis of E-MMT-1(7.5) was studied by in situSAXS, and the morphology of the solid products obtained by quickly quenching the synthesis at different reaction times (t) was investigated by SEM. The results are shown in Fig. 5. At t = ∼20 min after the addition of TEOS, a Bragg peak appeared at Q = 0.134 Å−1 corresponding to a d-spacing (d) of 4.7 nm. The peak quickly evolved and split into two that further moved away from each other within the following 10 min and became sharper and more intense as the reaction proceeded until t = ∼60 min. Other high-order Bragg peaks appeared later at t = ∼26 min, and the SAXS patterns could be indexed assuming a 2D-rectangular c2mm lattice. At t = 120 min, the 20 and 11 peaks were at Q = 0.106 Å−1 (d20 = 5.9 nm) and Q = 0.146 Å−1 (d11 = 4.3 nm), and the unit cell parameters were calculated to be a = 11.8 nm and b = 4.6 nm (a/b = 2.57). The parameters a and b as well as their ratio (a/b) versus time are also plotted in Fig. 5. The rapid change of a/b from 1.73 (t = 20 min) to 2.57 (t = 30 min) indicated a fast structural deformation of the material. By assuming a pseudo-first-order structural deformation, the rate constant kdef was estimated to be 8.2 × 10−3s−1 from the plot of a/b versus time. Moreover, the SEM images suggested that the morphology of the nanostructures was already developed within the same period of time: while some spherical and rod-like particles started to appear at t = 20 min, four types of nanostructures could be clearly observed at t = 30 min. The particles at this stage were smaller than those in the final product (cf.Fig. 2a), and they continued to grow within the following 30 min. The solid product collected at t = 15 min only consisted of small (5–8 nm) nanoparticles that were presumably composed of the silicatropic micelles and silicate species formed at the initial stage of synthesis.
 | ||
| Fig. 5 In situ SAXS data for the synthesis of E-MMT-1(7.5). The SEM images of the samples obtained by quenching the synthesis at different reaction times are shown at the right. Inset is the temporal evolution of the cell parameters a and b and the a/b ratio. | ||
The change of the intensity of the 11 Bragg peak in the in situSAXS data was further analyzed by applying the Avrami–Erofe’ev expression,56–59 a widely used expression to model various solid-state reactions60–63 including CoAPO-562 and MCM-41:63
 | (1) |
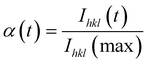 | (2) |
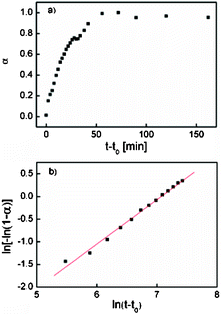 | ||
| Fig. 6 (a) Crystallization curve of E-MMT-1(7.5) obtained from the integrated values of the 11 reflection of the c2mm mesostructure as a function of time. (b) The corresponding Sharp–Hancock plot over the range 0.15 < α < 0.8. | ||
For the synthesis of helical mesoporous materials, the simultaneous formation of different types of helical morphologies is seldom observed.25–32,34 To the best of our knowledge, the only exception is that reported by Yuan et al.33 using a cationic surfactant and perfluorooctanoic acid as an additive. Therefore, the coexistence of four helical nanostructures in E-MMT-1(7.5) having the same c2mm mesostructure yet different helical morphologies with bimodal pitch distribution is unique. Concerning the formation of helical MMT-1 nanostructures, the reduction in surface free energy ΔGS is thought to be the main driving force. Moreover, the kinetic factors obviously play some role in influencing the textural properties of the materials. For the synthesis of E-MMT-1(7.5), once TEOS was injected into the synthesis solution, it readily hydrolyzed to produce anionic silicate species that diffused and adsorbed preferentially onto the cetyltrimethylammonium (CTA) cations in the spherical micelles.6 The following hydrolytic condensation of silicates (with a rate constant denoted as kin) at the interface would then pull CTA cations together and induce a segregation of the two surfactants.38 A similar segregation phenomenon was observed in a ribbon-like mesophase of mixed amphiphiles with head groups of different polarity.66 Owing to a much weaker repulsion between the nonionic head groups of C12EO4 compared to that for CTA,5,51 the parts of the micelles consisting of the segregated C12EO4 molecules would be less curved than the CTA-enriched parts, resulting in the deformed micellar rods. While the deformation proceeded, the initially formed silicate-encased micellar rods served as nuclei and continued to fuse and elongate with an apparent rate constant km. Further condensation of the silicate species located at the highly curved positions of the micellar rods may force the rods to bend and coil, against the increase in bending energy ΔGB, and finally grow into helical c2mm nanostructures. With such an effect of anisotropic silicate condensation against ΔGB, which is absent in the syntheses of MCM-41-like helical materials using a single type of surfactant or using an acid (instead of a base) as a catalyst,25–35 we speculated that the formation of much curved and short-pitch helical morphologies accompanied by a large decrease in ΔGS should be more favorable. The long-pitch nanorods in E-MMT-1(7.5), with a small fraction of ∼15%, could be regarded as kinetic products since less degree of bending of the silicate-encased micellar rods is required.
The proposed formation mechanism suggests the importance of the kinetic considerations for the formation of helical mesoporous materials and the possibility to modulate these materials by further tuning the kinetics of the reactions/processes involved in the synthesis. To examine it, we attempted to prepare structurally and morphologically “pure” samples by kinetic control. A successful example has already been demonstrated: a fast TEOS injection rate (R = 16.0 and 24.0 mL h−1) solely produced small sphere-like nanoparticles with short helical pitch (cf.Fig. 2). This may be comprehended because a fast addition of TEOS would facilitate the overall assembly process, especially the bending/coiling of the silicate-encased micellar rods triggered by the anisotropic silicate condensation, and the formation of long-pitch kinetic products was therefore not favored.
We further considered possible control over the kinetics of the hydrolytic condensation of silicate species (with rate constant kin) instead of the rate of fusion/elongation of the micellar rods (with rate constant km). Based on the proposed formation mechanism, we expected that an increase in kin would tend to produce short-pitch nanostructures that are thermodynamically more stable, while a decreased kin would favor the formation of long-pitch helical MMT-1. To increase kin, we replaced TEOS by TMOS as the silica source. Fig. 7 shows the SEM and TEM images of the resulting materials. With a TMOS injection rate of 7.5 mL h−1, the sample M-MMT-1(7.5) contains nearly 99% of short-pitch and sphere-like helical MMT-1 nanoparticles, similar to the E-MMT-1 samples with R > 12.0 mL h−1. When the TMOS injection rate was decreased, the fraction of short-pitch straight nanorods in the sample M-MMT-1(3.0) increased to ∼30%. The highly ordered c2mm mesostructure was confirmed by XRD (Fig. S5 in ESI) and the sections of the elliptical channels can also be clearly observed in their TEM images (see the insets in Fig. 7).
Alternatively, since the addition of alcohol is known to slow down the hydrolytic condensation rates of silicates,67 our strategy to decrease kin was to add a small amount of ethanol (EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O = x
H2O = x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1230, x ≤ 40) to the synthesis solution prior to the addition of TEOS. The amount of EtOH was small enough to have negligible effects on the thermodynamics of the surfactant assembly.68 As expected, we found that more long-pitch twisted nanorods were produced when adding more EtOH, and nearly 100% twisted nanorods were observed in the E/E-x-MMT-1(7.5) samples with 30 ≤ x ≤ 40. The electron microscopy images of the sample E/E-35-MMT-1(7.5) are shown in Fig. 8. The twisted nanorods are wider and much longer than those in E-MMT-1(7.5) (Table S1 in ESI). This seems that the slight decrease of kin not only favored the formation of long-pitch helical nanostructures, but also allowed slower but continuous growth into wider and longer nanorods. The c2mm mesostructure of E/E-35-MMT-1(7.5) was confirmed by XRD (Fig. S5 in ESI). Furthermore, the helical morphology and the elliptical shape of the channels in this sample were observed in the TEM images shown in Fig. 8b and 8c. The helical pitch is roughly proportional to the rod diameter, and the P/D ratio (2.0–3.5) is very close to the values for the long-pitch nanorods shown in Fig. 4.
1230, x ≤ 40) to the synthesis solution prior to the addition of TEOS. The amount of EtOH was small enough to have negligible effects on the thermodynamics of the surfactant assembly.68 As expected, we found that more long-pitch twisted nanorods were produced when adding more EtOH, and nearly 100% twisted nanorods were observed in the E/E-x-MMT-1(7.5) samples with 30 ≤ x ≤ 40. The electron microscopy images of the sample E/E-35-MMT-1(7.5) are shown in Fig. 8. The twisted nanorods are wider and much longer than those in E-MMT-1(7.5) (Table S1 in ESI). This seems that the slight decrease of kin not only favored the formation of long-pitch helical nanostructures, but also allowed slower but continuous growth into wider and longer nanorods. The c2mm mesostructure of E/E-35-MMT-1(7.5) was confirmed by XRD (Fig. S5 in ESI). Furthermore, the helical morphology and the elliptical shape of the channels in this sample were observed in the TEM images shown in Fig. 8b and 8c. The helical pitch is roughly proportional to the rod diameter, and the P/D ratio (2.0–3.5) is very close to the values for the long-pitch nanorods shown in Fig. 4.
 | ||
| Fig. 8 (a) SEM, (b) TEM and (c) cross-section TEM images of E/E-35-MMT-1(7.5). The arrow in (c) indicates the elliptical section of the mesopores. | ||
The in situSAXS measurements and analysis were again performed on the syntheses of M-MMT-1(7.5) and E/E-35-MMT-1(7.5). Fig. 9 shows the SAXS data, the XRD patterns of the aged samples, and the evolution of the calculated unit cell parameters as well as their ratio. The corresponding crystallization curves and the Sharp–Hancock plots are shown in Fig. S6 in ESI. When TMOS was used as a silica precursor, the first Bragg peak at Q = 0.140 Å−1 appeared at the reaction time t = 10 min. The peak quickly evolved and split into two peaks positioned at Q = 0.119 Å−1 and 0.150 Å−1 within 8 min, and the peaks became sharper and more intense until t = 58 min. The corresponding parameters a and b derived from the pattern at t = 58 min are 10.4 nm and 4.4 nm, respectively. Obviously, both the induction time t0 (∼10 min) and the duration of structural deformation (8 min) are shorter as compared to the corresponding values for E-MMT-1(7.5) synthesized with TEOS. The pseudo-first-order rate constant of structural deformation (kdef) for M-MMT-1(7.5) was about 2.0 × 10−2s−1, and the values of the parameters n and kc are 0.84 and 1.8 × 10−3s−1, respectively. A comparison of the derived rate constants for M-MMT-1(7.5) and E-MMT-1(7.5) indicated that an increase of the hydrolytic condensation rate of silicate (i.e. increased kin) facilitated structural deformation and materials growth. On the other hand, the synthesis of E/E-35-MMT-1(7.5) with decreased kin exhibited longer induction time, slower structural deformation and slower growth (cf.Fig. 9b), and the derived values of kdef, n and kc for E/E-35-MMT-1(7.5) are 5.6 × 10−3s−1, 1.03 and 6.0 × 10−4s−1, respectively. The fact that the degree of structural deformation of this sample was lower could be attributed to a smaller degree of surfactant segregation when EtOH was present in the synthesis solution.
 | ||
| Fig. 9 In situ SAXS patterns, the XRD patterns of the aged samples (insets), and the temporal evolution of the cell parameters a and b and the a/b ratio for (a) M-MMT-1(7.5) and (b) E/E-35-MMT-1(7.5). | ||
The formation routes of short-pitch M-MMT-1(7.5) (Route A) and long-pitch E/E-35-MMT-1(7.5) (Route B) are represented and compared in Fig. 10. The rate of fusion/elongation of the micellar rods (with rate constant km) is mainly determined by the synthesis temperature and the surfactant concentration and therefore should be roughly the same for both routes (kmA ∼ kmB).Our results show that the helicity and the morphology could be controlled by tuning the rate of the hydrolytic condensation of silicate species (with rate constant kin) (kinA > kinB).
 | ||
| Fig. 10 Schematic representation of the formation of the short-pitch M-MMT-1(7.5) (Route A) and long-pitch E/E-35-MMT-1(7.5) (Route B). kmA and kmB: rate constants for the fusion and elongation of the micellar rods; kinA and kinB: rate constants for the hydrolytic condensation of silicate species. | ||
It has to be mentioned that the MMT-1 materials with different degrees of structural deformation (i.e. different a/b ratios) would have deformed channels with different ellipticities. Unfortunately, such a difference in the shape of the channels was not large enough to give pronounced distinction in the gas physisorption isotherms of the materials.69 For example, the nitrogen physisorption isotherms of the calcined E-MMT-1(7.5), M-MMT-1(7.5) and E/E-35-MMT-1(7.5) (Fig. S7 in ESI) look slightly different, but the derived textural properties for the three samples are nearly identical. The average pore diameters, BET surface areas and total pore volumes are ∼3.8 nm, 1060–1180 m2 g−1, and 0.85–1.00 cm3 g−1, respectively.
Finally, attempts were made to prepare Pt nanowires by using the M-MMT-1(7.5) and E/E-35-MMT-1(7.5) helical nanostructures as hard templates. Fig. 11 shows typical TEM images of the silica-free samples. Most of the Pt nanowires derived from short-pitch M-MMT-1(7.5) are long (50–200 nm) and uniform in width (about 4 nm). The width matches the major axis of the elliptical channel sections observed in Fig. 7a, suggesting a true templated preparation in the confined elliptical channels of M-MMT-1(7.5). The Pt nanowires are aligned horizontally and therefore the elliptical sections could not be observed. Interestingly, Pt nanowires are packed in a concentric fashion, which seems to reflect the concentric coiling of the short-pitch helical channels in the host silica. When E/E-35-MMT-1(7.5) was used as the hard template, the resulting Pt nanowires were also uniform in width (cf.Fig. 11b). The packing of these nanowires is not so regular, but it could still reflect the long-pitch helical morphology of the silica template.
 | ||
| Fig. 11 TEM images of the Pt nanowires prepared with (a) M-MMT-1(7.5) and (b) E/E-35-MMT-1(7.5) as templates. | ||
Conclusions
Helical mesoporous MMT-1 silica nanostructures with c2mm symmetry have been synthesized by using a mixture of cationic and nonionic surfactants. A mixture of short-pitch sphere-like nanoparticles, short-pitch straight nanorods, long-pitch twisted nanorods and long-pitch spiral nanorods could be produced by decreasing the injection rate of the TEOS precursor. A formation mechanism was proposed with the emphasis on the influences of the assembly kinetics on the structural and textural properties of the helical nanostructures. Based on the mechanism, we also examined and demonstrated simple kinetic control to prepare solely short-pitch or long-pitch helical MMT-1 nanostructures. Our results demonstrate the feasibility to tailor the helical mesostructures through kinetic control and give new insights into the formation of deformed and helical materials.Acknowledgements
The authors thank U. S. Jeng, Y. H. Lai and C. H. Su (NSRRC) for their help with SAXS measurements, and the National Science Council of the Republic of China for financial support under the contract no. NSC98-2113-M-007-020-MY3. YS thanks the Swedish Research Council (VR) for financial support.References
- C. T. Kresge, M. E. Leonowicz, W. J. Roth, J. C. Vartuli and J. S. Beck, Nature, 1992, 359, 710–712 CrossRef CAS.
- J. S. Beck, J. C. Vartuli, W. J. Roth, M. E. Leonowicz, C. T. Kresge, K. D. Schmitt, C. T. W. Chu, D. H. Olson, E. W. Sheppard, S. B. McCullen, J. B. Higgins and J. L. Schlenker, J. Am. Chem. Soc., 1992, 114, 10834–10843 CrossRef CAS.
- T. Yanagisawa, T. Shimizu, K. Kuroda and C. Kato, Bull. Chem. Soc. Jpn., 1990, 63, 988–992 CrossRef CAS.
- S. Inagaki, Y. Fukushima and K. Kuroda, J. Chem. Soc., Chem. Commun., 1993, 680–682 RSC.
- Q. S. Huo, D. I. Margolese, U. Ciesla, P. Y. Feng, T. E. Gier, P. Sieger, R. Leon, P. M. Petroff, F. Schuth and G. D. Stucky, Nature, 1994, 368, 317–321 CrossRef CAS.
- U. Ciesla and F. Schüth, Microporous Mesoporous Mater., 1999, 27, 131–149 CrossRef CAS.
- M. E. Davis, Nature, 2002, 417, 813–821 CrossRef CAS.
- G. J. D. Soler-illia, C. Sanchez, B. Lebeau and J. Patarin, Chem. Rev., 2002, 102, 4093–4138 CrossRef.
- H. P. Lin and C. Y. Mou, Acc. Chem. Res., 2002, 35, 927–935 CrossRef CAS.
- C. M. Yang, H. S. Sheu and K. J. Chao, Adv. Funct. Mater., 2002, 12, 143–148 CrossRef CAS.
- A. Stein, Adv. Mater., 2003, 15, 763–775 CrossRef CAS.
- S. Che, A. E. Garcia-Bennett, T. Yokoi, K. Sakamoto, H. Kunieda, O. Terasaki and T. Tatsumi, Nat. Mater., 2003, 2, 801–805 CrossRef CAS.
- A. Taguchi and F. Schuth, Microporous Mesoporous Mater., 2005, 77, 1–45 CrossRef CAS.
- B. Hatton, K. Landskron, W. Whitnall, D. Perovic and G. A. Ozin, Acc. Chem. Res., 2005, 38, 305–312 CrossRef CAS.
- F. Hoffmann, M. Cornelius, J. Morell and M. Froba, Angew. Chem., Int. Ed., 2006, 45, 3216–3251 CrossRef CAS.
- A. H. Lu and F. Schüth, Adv. Mater., 2006, 18, 1793–1805 CrossRef CAS.
- B. G. Trewyn, II Slowing, S. Giri, H. T. Chen and V. S. Y. Lin, Acc. Chem. Res., 2007, 40, 846–853 CrossRef CAS.
- S. W. Boettcher, J. Fan, C. K. Tsung, Q. H. Shi and G. D. Stucky, Acc. Chem. Res., 2007, 40, 784–792 CrossRef CAS.
- Y. Wan, Y. F. Shi and D. Y. Zhao, Chem. Mater., 2008, 20, 932–945 CrossRef CAS.
- T. Kimura and K. Kuroda, Adv. Funct. Mater., 2009, 19, 511–527 CrossRef CAS.
- Q. S. Huo, D. Y. Zhao, J. L. Feng, K. Weston, S. K. Buratto, G. D. Stucky, S. Schacht and F. Schüth, Adv. Mater., 1997, 9, 974–978 CrossRef CAS.
- F. Marlow, B. Spliethoff, B. Tesche and D. Y. Zhao, Adv. Mater., 2000, 12, 961–965 CrossRef CAS.
- Z. L. Yang, Z. W. Niu, X. Y. Cao, Z. Z. Yang, Y. F. Lu, Z. B. Hu and C. C. Han, Angew. Chem., Int. Ed., 2003, 42, 4201–4203 CrossRef CAS.
- Y. Y. Wu, G. S. Cheng, K. Katsov, S. W. Sides, J. F. Wang, J. Tang, G. H. Fredrickson, M. Moskovits and G. D. Stucky, Nat. Mater., 2004, 3, 816–822 CrossRef CAS.
- S. Che, Z. Liu, T. Ohsuna, K. Sakamoto, O. Terasaki and T. Tatsumi, Nature, 2004, 429, 281–284 CrossRef CAS.
- B. G. Trewyn, C. M. Whitman and V. S. Y. Lin, Nano Lett., 2004, 4, 2139–2143 CrossRef CAS.
- X. W. Wu, H. Y. Jin, Z. Liu, T. Ohsuna, O. Terasaki, K. Sakamoto and S. N. Che, Chem. Mater., 2006, 18, 241–243 CrossRef CAS.
- H. Y. Jin, Z. Liu, T. Ohsuna, O. Terasaki, Y. Inoue, K. Sakamoto, T. Nakanishi, K. Ariga and S. N. Che, Adv. Mater., 2006, 18, 593–596 CrossRef CAS.
- B. Wang, C. Chi, W. Shan, Y. H. Zhang, N. Ren, W. L. Yang and Y. Tang, Angew. Chem., Int. Ed., 2006, 45, 2088–2090 CrossRef CAS.
- S. Yang, L. Z. Zhao, C. Z. Yu, X. F. Zhou, J. W. Tang, P. Yuan, D. Y. Chen and D. Y. Zhao, J. Am. Chem. Soc., 2006, 128, 10460–10466 CrossRef CAS.
- X. J. Meng, T. Yokoi, D. L. Lu and T. Tatsumi, Angew. Chem., Int. Ed., 2007, 46, 7796–7798 CrossRef CAS.
- L. Zhang, S. Z. Qiao, Y. G. Jin, L. N. Cheng, Z. F. Yan and G. Q. Lu, Adv. Funct. Mater., 2008, 18, 3834–3842 CrossRef CAS.
- P. Yuan, L. Z. Zhao, N. A. Liu, G. F. Wei, Y. H. Wang, G. J. Auchterlonie, J. Drennan, G. Q. Lu, J. Zou and C. Z. Yu, Chem.–Eur. J., 2010, 16, 1629–1637 CrossRef CAS.
- Y. Han, L. Zhao and J. Y. Ying, Adv. Mater., 2007, 19, 2454–2459 CrossRef CAS.
- G. L. Lin, Y. H. Tsai, H. P. Lin, C. Y. Tang and C. Y. Lin, Langmuir, 2007, 23, 4115–4119 CrossRef CAS.
- D. Y. Zhao, Q. S. Huo, J. L. Feng, J. M. Kim, Y. J. Han and G. D. Stucky, Chem. Mater., 1999, 11, 2668–2672 CrossRef CAS.
- H. B. Qiu, Y. Sakamoto, O. Terasaki and S. N. Che, Adv. Mater., 2008, 20, 425–429 CrossRef CAS.
- C. M. Yang, C. Y. Lin, Y. Sakamoto, W. C. Huang and L. L. Chang, Chem. Commun., 2008, 5969–5971 RSC.
- Y. Han, D. Zhang, L. L. Chng, J. Sun, L. Zhao, X. Zou and J. Y. Ying, Nat. Chem., 2009, 1, 123–127 CrossRef CAS.
- F. Husson, H. Mustacchi and V. Luzzati, Acta Crystallogr., 1960, 13, 668–677 CrossRef CAS.
- H. Hagslatt, O. Soderman and B. Jonsson, Liq. Cryst., 1992, 12, 667–688 CrossRef.
- S. Gustafsson, P. O. Quist and B. Halle, Liq. Cryst., 1995, 18, 545–553 CrossRef CAS.
- S. Gustafsson and P. O. Quist, J. Colloid Interface Sci., 1996, 180, 564–573 CrossRef CAS.
- M. K. Kidder, P. F. Britt, Z. T. Zhang, S. Dai, E. W. Hagaman, A. L. Chaffee and A. C. Buchanan, J. Am. Chem. Soc., 2005, 127, 6353–6360 CrossRef CAS.
- Y. H. Yang, G. A. Du, S. Y. Lim and G. L. Haller, J. Catal., 2005, 234, 318–327 CrossRef CAS.
- T. E. Gier, X. H. Bu, P. Y. Feng and G. D. Stucky, Nature, 1998, 395, 154–157 CrossRef CAS.
- A. E. Rowan and R. J. M. Nolte, Angew. Chem., Int. Ed., 1998, 37, 63–68 CrossRef CAS.
- D. Bradshaw, T. J. Prior, E. J. Cussen, J. B. Claridge and M. J. Rosseinsky, J. Am. Chem. Soc., 2004, 126, 6106–6114 CrossRef CAS.
- Z. An, J. He, X. Shu and Y. X. Wu, Chem. Commun., 2009, 1055–1057 RSC.
- A. Monnier, F. Schuth, Q. Huo, D. Kumar, D. Margolese, R. S. Maxwell, G. D. Stucky, M. Krishnamurty, P. Petroff, A. Firouzi, M. Janicke and B. F. Chmelka, Science, 1993, 261, 1299–1303 CAS.
- A. Firouzi, D. Kumar, L. M. Bull, T. Besier, P. Sieger, Q. Huo, S. A. Walker, J. A. Zasadzinski, C. Glinka, J. Nicol, D. Margolese, G. D. Stucky and B. F. Chmelka, Science, 1995, 267, 1138–1143 CAS.
- A. Firouzi, F. Atef, A. G. Oertli, G. D. Stucky and B. F. Chmelka, J. Am. Chem. Soc., 1997, 119, 3596–3610 CrossRef CAS.
- C. H. Ko and R. Ryoo, Chem. Commun., 1996, 2467–2468 RSC.
- C. M. Yang, B. Zibrowius, W. Schmidt and F. Schüth, Chem. Mater., 2004, 16, 2918–2925 CrossRef CAS.
- C. M. Yang, W. Schmidt and F. Kleitz, J. Mater. Chem., 2005, 15, 5112–5114 RSC.
- M. Avrami, J. Chem. Phys., 1939, 7, 1103–1112 CrossRef CAS.
- M. Avrami, J. Chem. Phys., 1940, 8, 212–224 CrossRef CAS.
- M. Avrami, J. Chem. Phys., 1941, 9, 177–184 CrossRef CAS.
- B. V. Erofe’ev, C. R. Dokl. Acad. Sci. URSS, 1946, 52, 511–517 Search PubMed.
- A. M. Fogg, S. J. Price, R. J. Francis, S. O'Brien and D. O'Hare, J. Mater. Chem., 2000, 10, 2355–2357 RSC.
- A. M. Beale and G. Sankar, Chem. Mater., 2003, 15, 146–153 CrossRef CAS.
- D. Grandjean, A. M. Beale, A. V. Petukhov and B. M. Weckhuysen, J. Am. Chem. Soc., 2005, 127, 14454–14465 CrossRef CAS.
- E. Gianotti, G. Berlier, K. Costabello, S. Coluccia and F. Meneau, Catal. Today, 2007, 126, 203–210 CrossRef CAS.
- S. F. Hulbert, J. Br. Ceram. Soc., 1969, 6, 11–20 CAS.
- J. D. Hancock and J. H. Sharp, J. Am. Ceram. Soc., 1972, 55, 74 CrossRef CAS.
- S. Alpérine, Y. Hendrikx and J. Charvolin, J. Phys. Lett., 1985, 46, 27–31 CrossRef.
- C. J. Brinker and G. W. Scherer, Sol–Gel Science, 1990 Search PubMed.
- M. T. Anderson, J. E. Martin, J. G. Odinek and P. P. Newcomer, Chem. Mater., 1998, 10, 311–321 CrossRef CAS.
- S. Lowell, J. E. Shields, M. A. Thomas, M. Thommes, Characterization of Porous Solids and Powders: Surface Area, Pore size and Density, 2004 Search PubMed.
Footnote |
| † Electronic Supplementary Information (ESI) available: A table summarising the textural properties and the fractions of different types of nanostructures in selected samples and more SEM images, TEM images, XRD patterns, nitrogen physisorption isotherms and in situSAXS patterns and analysis data of MMT-1 samples. See DOI: 10.1039/c1ra00013f/ |
| This journal is © The Royal Society of Chemistry 2011 |

