Ab initio modeling of trititanate nanotubes
Dénes
Szieberth
*a,
Anna Maria
Ferrari
a,
Philippe
D'Arco
b and
Roberto
Orlando
c
aDipartimento di Chimica IFM, Università di Torino and NIS -Nanostructured Interfaces and Surfaces - Centre of Excellence, Via P. Giuria 7, 10125, Torino, Italy Web: http://www.nis.unito.it
bUPMC Paris Univ, UPMC CNRS, UMR 7193, Inst Sci Terre Paris, Paris, France
cUniv Piemonte Orientale, Dipartimento Sci & Tecnol Avanzate, I-15121, Alessandria, Italy
First published on 4th January 2011
Abstract
Nanotubes with H2Ti3O7 stoichiometry have been studied by ab initio methods in the diameter range of ∼20–60 Å. The distribution of the protons on the unit cell surface and its effect on the structure and electronic properties of the titanium dioxide backbone has been investigated. The preferred protonation pattern was found to be the function of the diameter of the nanotube and the convexity of the surface. Trititanate tubes have been found to be more stable than lepidocrocite nanotubes at all diameters. At diameters < 50 Å the dissociation of water from the internal surface and the emergence of a new tube wall structure was observed. Band gaps were found to change only slightly with the curvature, the maximum difference from the flat slab values was ±0.5 eV.
Introduction
Nanostructured TiO2 materials have been widely utilized and investigated in the last decades.1,2 Among the potential applications are solar cells,1 photocatalytic decomposition of organic material,3 photoelectrochemical splitting of water,4 gas sensors5 and electrodes for lithium batteries.6One of the most common methods of preparation is hydrothermal treatment of titania7 in basic solutions. Despite the large number of investigations, atomic level information on the structure of nanotubes prepared in this way is still ambiguous.8 Several structures such as anatase,9–11 lepidocrocite,12 trititanate13,14 and various other titanate stoichiometries15,16 have been proposed. Structural transitions between the proposed structures have also been observed. Trititanate nanotubes were converted into anatase through the hexatitanate and TiO2(B) metastable structures during calcination.17 The conversion into anatase nanorods by dehydration was also detected in high temperature vacuum annealing experiments.18 Molecular dynamics simulations have also supported the possibility of the transition between anatase, lepidocrocite and trititanate layers.19
Although theoretical calculations can play a major role in providing information on the atomic scale, because of the size of the systems involved, only a handful of computational studies of TiO2 nanotubes appeared in the literature. Molecular mechanics calculations have been carried out for a wide range of TiO2 structures, demonstrating that trititanates possess exceptional stability.20 The structures of several anatase- and lepidocrocite-type nanotubes with varying diameter were investigated using a density functional theory-tight binding method (DFT-TB).21 The structures, strain energies,22,23 and band gaps22–25 of small-diameter anatase zigzag and armchair nanotubes were calculated using ab initio methods. In our previous study on lepidocrocite-like TiO2 nanotubes26 we have found that full ab initio methods provide different geometry reconstructions in strained structures compared to the DFT-TB method.
The DFT-TB method was also used for the study of nanotubes created from different polytitanic acid units,27 and it was counterintuitively found that titanate-based nanotubes exhibit larger strain energies than lepidocrocite tubes with the same diameters.
Flat titanate sheets—that are supposed to create the walls of titanate nanotubes by rolling up—resemble lepidocrocite-like blocks connected by divalent oxygen bridges. Titanate sheets of different stoichiometries were investigated by plane wave DFT calculations.28 It was established that the different arrangements of protons on the H2Ti3O7 trititanate surface create several minima in a 0.2 eV energy interval. It was also found that these structures can be converted easily to the lepidocrocite structure by dehydration. Nanoribbons created from hydroxylated anatase (001) sheets with different hydration states on the two sides were shown to adopt curved shapes, enabling them to act as models for nanotubes. The electronic structure of the titanate nanosheets has not been discussed here.
The aim of this study is to provide ab initio structural and electronic data for some trititanate-based nanotubes. Different protonation patterns have been considered. The trititanate structure is not only a potential constituent of nanotubes prepared by hydrothermal methods, but because of its close relationship with the lepidocrocite structure also a model for the investigation of the interaction of water with TiO2 nanotube walls. The multitude of possibilities for the positioning of the protons on the trititanate surface provides a unique conformational flexibility for this nanotube type. Our aim is to explore the conformational possibilities provided by the different proton arrangements on the tube wall surfaces. The structural and electronic changes brought about by alterations of the surface protonation patterns can provide insights into the functional properties of this type of nanotube. In our knowledge no high-level ab initio calculations were previously carried out for trititanate nanotubes.
Methods
Calculations were performed with the periodic ab initio CRYSTAL0929,30 code, using the hybrid PBE031 DFT functional. This functional was reported to give accurate structural and electronic properties for TiO2 crystals.32 All calculations have been performed using an all-electron 8-411Gd Gaussian-type basis set33 for O, and a Hay–Wadt small core ECP34 with a 411-31 (3sp2d) basis set for valence electrons22 for Ti atoms. These basis sets were proved to give results of acceptable accuracy with moderate computational cost.35 The level of accuracy in evaluating the Coulomb and the exchange series is controlled by five parameters29 for which a 8 8 8 8 16 setting was used. The convergence threshold for SCF energy was set to 10−7 Ha. The reciprocal space was sampled according to a regular sublattice determined by the shrinking factor29 10 (6 independent k-points in the irreducible part of the Brillouin zone).The DFT exchange–correlation energy is evaluated by numerical integration over the unit cell volume. In CRYSTAL, a Gauss–Legendre radial and a Lebedev angular grid of points is used. In the present calculations a (75,974) pruned grid is applied.
Structure optimizations were performed by the use of analytical derivatives of the energy with respect to atomic coordinates and unit-cell parameters within a quasi-Newton scheme. For the updating of the Hessian the BFGS scheme is used. Convergence of the geometry was checked on both gradient components and nuclear displacements for which the default criteria are chosen.29
The computation of nanotubes with large unit cells (480 atoms in case of the (20,0) nanotubes) was made possible by the exploitation of the helix roto-translational symmetry of these structures. This symmetry is used for the automatic generation of the structures, for the calculation of one and two-electron integrals (only the irreducible part of the Fock matrix is calculated then rotated by the symmetry operators of the point group to generate the full Fock matrix), and for the diagonalization of the Fock matrix where each irreducible representation is treated separately.36
Results and discussion
Selection of the slabs
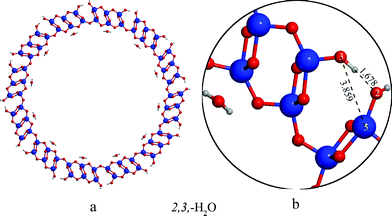
Trititanate nanotubes can be formed through the rolling up of flat H2Ti3O7 sheets. The arrangement of the protons on the sheet surfaces gives rise to several energy minima.28 The structure of the Ti3O72− skeleton and the possible sites where the protons can be positioned can be seen in Fig. 1.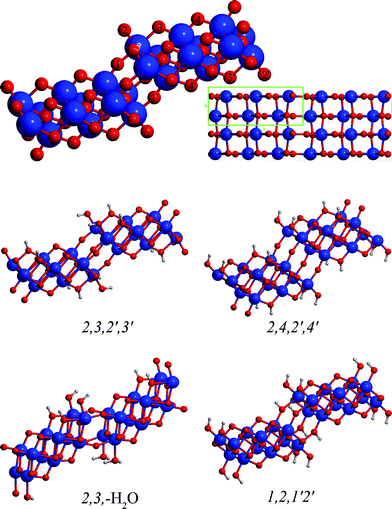 | ||
| Fig. 1 The structure of trititanate nanosheets and notation of proton binding sites. | ||
The relative energies and cell parameters of slabs with different proton arrangements are collected in Table 1 (values are referring to one H2Ti3O7 unit). Only structures having protons positioned at site 2 are considered, due to the expected superior proton affinity of this site. Plane wave DFT values from ref. 28 are also included for comparison. The geometries of representative proton arrangements can be seen on Fig. 1. The notation h,i,j′,k′ indicates, that the slab is protonated at the h and i sites on one surface, and at the j and k sites on the opposite one. In case of nanotubes the first two indexes apply to the external, while the last two to the internal surface. The –H2O notation means that the protonation results in a H2O molecule weakly bound to the surface instead of covalently bonded OH groups.
According to results reported in Table 1 the most stable trititanate slab is the 2,3,2′,3′ one. The smaller stability of the 2,3,2′,4′ (by 1.2 kcal mol−1/H2Ti3O7) and the 2,4,2′,4′ arrangement (by 2.3 kcal mol−1/H2Ti3O7) shows that protonation of site 3 is favored over site 4. The 2,3,–H2O is less stable by 3.0 kcal mol−1/H2Ti3O7, showing that the covalent binding of hydroxide groups is preferred with respect to loosely bound H2O molecules.
The 1,2,1′,2′ protonation pattern produces two minima, one, in which the stepped trititanate structure is preserved, and another one, in which the O1–Ti5 oxygen bridges open up and the trititanate sheet is separated into ribbons held together by hydrogen bonds (not depicted of Fig. 1). This latter minimum however is unsuitable for the construction of cylindrical nanotubes, therefore we excluded it from further investigations.
Among the investigated slab structures the 1,2–j′,k′, the 2,3,–H2O and the 2,3–j′,k′ surface structures can be conceived as the direct product of the heterolytic water splitting at the lepidocrocite surface (the water fragments are bound to two adjacent Ti–O sites out of three), whereas the 2,4–j′,k′ pattern requires a subsequent proton migration on the surface. The hydrated phases are more stable than the reference lepidocrocite (ranging the chemisorption energy from 6.3 to 1.8 kcal mol−1 per water molecule) irrespective to the resulting hydration pattern. This result is in line with previous calculations that reported a range from 5.7 to 3.0 kcal mol−1 for water dissociation at TiO2 surfaces and nanosheets.28
The cell parameters of the rectangular trititanate unit cell (a, b) are very close to each other for all the investigated protonation patterns: the differences are within 1% for the a vector and within 3% for the b vector (see Fig. 1 and Table 1). Moreover, the protonation pattern does not significantly affect the band gap of the flat layers: all investigated arrangements produced a band gap between 5.3 and 5.4 eV, a very similar value to the 5.4 eV determined for lepidocrocite TiO226 (the calculated bulk value of rutile with the same computational parameters is 4.1 eV). All flat trititanate slabs possess an indirect band gap.
In addition, it is worthwhile noticing that the relative energies, cell parameters, band gap behavior with respect the bulk oxide provided by the basis set/functional combination used in this paper provides results in excellent agreement with earlier studies.27,28
The relative stability of these structures are expected to change with the rolling of the nanotube. Since the curvature of the nanotube creates different strains on the internal and external surface of the tubes, different proton arrangements are expected to be preferred on the two surfaces. Furthermore, the relative stability of the different arrangements can also change with the radius of the nanotube. While at large diameters the most stable proton arrangements are expected to be similar to those of the flat sheets, both the compressive strain on the internal surface and the tensile strain on the external surface can change the proton arrangement preferences, so the most stable protonation pattern is expected to be a function of the nanotube curvature: the relative energies has to be evaluated and compared at different nanotube diameters.
Within the investigated proton arrangements we have selected two symmetric (2,3,2′,3′ and 2,4,2′,4′) and two asymmetric (2,3,2′,4′ and 2,3,–H2O) proton arrangements for the nanotube rollups, because of their larger relative stabilities in the flat surfaces (see Table 1). In particular the investigation of the 2,3,–H2O structure is motivated by the observation of weakly bound H2O molecules at the inner surface of titanate nanotubes of small diameters.27
We have only considered rollups of the (n,0) type, since the divalent oxygen bridges holding the lepidocrocite-like blocks together are pointing in the circumferential direction in this case, providing large flexibility and reducing the strain in the nanotube.
In case of the asymmetric arrangements of the protonation pattern at the two surfaces of the slab, the structure of the nanotube depends on which surface becomes the internal and which surface the external one. Therefore from the flat 2,3,2′,4′ arrangement the 2,3,2′,4′ and the 2,4,2′,3′ nanotubes are generated, the former one characterized by sites 2 and 3 protonated on the external surface of the tube and the sites 2′ and 4′ on the internal surface, while in the latter one the protonation patterns are reversed. Since the dehydration is expected to happen on the internal surface of the nanotubes,27 the 2,3,–H2O slab was only rolled keeping the weakly bound H2O molecules on the inside.
In the next section the properties of nanotubes having different protonation patterns and different dimensions (characterized by the rollup index) will be discussed. The diameters (D), relative energies (ΔE) compared to the most stable nanotube at a given rollup index, strain energies (ES), relative strain energies (ERS), and band gaps (Eg) are collected in Table 2. ES and ERS are defined in the “strain energy” paragraph.
| 8,0 | 12,0 | 18,0 | 20,0 | Flat slab | ||
|---|---|---|---|---|---|---|
| 2 ,3,2′,3′ | D | 23.5 | 35.5 | 53.0 | 60.1 | — |
| ΔE | 1.5 | 1.9 | 0.0 | 0.0 | 0.0 | |
| E S | 3.3 | 2.1 | 1.2 | 1.1 | 0.0 | |
| E RS | 1.2 | 0.0 | −0.9 | −1.0 | −2.1 | |
| E g | 5.0 | 5.1 | 5.2 | 5.3 | 5.4 | |
| 2 ,4,2′,4′ | D | 23.2 | 35.1 | — | — | — |
| ΔE | 4.0 | 6.1 | — | — | 2.2 | |
| E S | 4.5 | 3.5 | — | — | 0.0 | |
| E RS | 2.5 | 1.5 | — | — | −1.3 | |
| E g | 4.9 | 5.1 | — | — | 5.3 | |
| 2 ,3,2′,4′ | D | 23.2 | 34.4 | 51.1 | 58.5 | — |
| ΔE | 0.3 | 1.0 | 1.0 | 0.7 | 1.2 | |
| E S | 2.7 | 1.8 | 1.5 | 1.3 | 0.0 | |
| E RS | 0.6 | −0.2 | −0.6 | −0.8 | −1.7 | |
| E g | 4.8 | 4.9 | 4.9 | 5.0 | 5.3 | |
| 2 ,4,2′,3′ | D | 23.1 | 34.6 | — | — | — |
| ΔE | 4.4 | 5.9 | — | — | 1.2 | |
| E S | 4.8 | 3.5 | — | — | 0.0 | |
| E RS | 2.7 | 1.4 | — | — | −1.7 | |
| E g | 5.0 | 5.1 | — | — | 5.3 | |
| 2 ,3,−H2O | D | 26.2 | 38.0 | 56.8 | 62.9 | — |
| ΔE | 0.0 | 0.0 | 1.3 | 2.5 | 3.0 | |
| E S | 2.6 | 1.5 | 1.6 | 1.8 | 0.0 | |
| E RS | 0.5 | −0.6 | −0.5 | −0.3 | −0.6 | |
| E g | 5.8 | 5.9 | 5.9 | 5.8 | 5.3 |
(8,0) tubes
The diameters of the (8,0) nanotubes (measured as the average of the distance between the corresponding O3 and O3′ atoms on the opposite sides of the nanotube) displaying different protonation patterns is very similar (D = 23.3 ± 0.2 Å), whereas the 2,3,–H2O tube exhibits only slightly larger size (D = 26.2 Å).The relative energies reported in Table 2 show that the order of stability of the titanate nanotubes as a function of the different protonation patterns is 2,3,–H2O > 2,3,2′,4′ > 2,3,2′,3′ > 2,4,2′,4′ > 2,4,2′,3′. We can notice that: (i) at variance with the flat slabs, the 2,3,–H2O arrangement, (less stable by 3.0 kcal mol−1/H2Ti3O7 than the 2,3,2′,3′ structure in the case of the flat nanosheets) becomes now the most stable pattern (1.5 kcal mol−1/H2Ti3O7 more stable than 2,3,2′,3′); (ii) the 2,3 arrangement on the external surface is preferred over the 2,4 one: all three nanotubes possessing the 2,3 pattern are significantly more stable than those possessing the 2,4.
The differences in energy can be traced back to the geometrical reconstructions the slabs use to adapt to the curvature of the nanotube (see Fig. 2). At these small diameters the large tensile strain on the external surface of these nanotubes opens up the divalent oxygen bridges between O3 and Ti5 (dO3-Ti5 = 4.15 Å in the 2,3,2′,3′ and 4.05 Å in the 2,3,2′,4′ structure, see Fig. 2a,b and 2c,d) and increases the proton affinity of O3. As a consequence, the energy difference between the 2,3,2′,3′ and the 2,4,2′,3′ structures increases from the flat slab value of 1.2 kcal mol−1/H2Ti3O7 to 2.9 kcal mol−1/H2Ti3O7 in the (8,0) nanotubes (see Table 2).
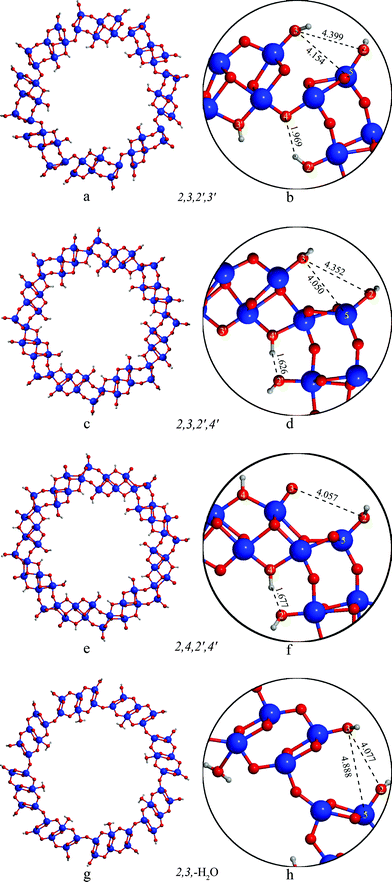 | ||
| Fig. 2 Structure of the (8,0) nanotubes with different protonation patterns. | ||
In order to explain the preference of the 2,3,2′,4′ structure over the 2,3,2′,3′ one we have to consider the protonation pattern on the internal surface. In case of the 2,3,2′,4′ structure the protons at the 4′ site create short hydrogen contacts (dH–O2′ = 1.62 Å) towards the 2′ oxygen (Fig. 2c,d). In the 2,3,2′,3′ arrangement (Fig. 2a,b) the 3′ proton cannot form hydrogen bonds towards the 2′ site; in addition the orientation of the 2′ proton hinders the effective interaction with the 4′ site, forming a somewhat longer H-bond (dH–O4′ = 1.97 Å), that accounts for the lower stability of 2,3,2′,4′ with respect to 2,3,2′,3′ (by 1.2 kcal mol−1/H2Ti3O7). The effect of the different arrangement of the protons on the internal surface propagates through the bonds of the nanotube wall and influences the geometry of the external surface as well: the distance of the O3 and Ti5 atoms differs by 0.1 Å in these two cases (cf.Fig. 2b and 2d)
The 2,3,2′,3′, 2,3,2′,4′, 2,4,2′,3′ and 2,4,2′,4′ nanotubes retain a bonding structure similar to the flat trititanate slabs in the nanotube walls. In the most stable structure of this rollup, the 2,3,-H2O nanotube, the lepidocrocite-like blocks in the nanotube walls are replaced by a structure resembling an anatase (001) layer (cf.Fig. 2a-f and 2g,h). The transformation between anatase (001) and lepidocrocite-like structures in case of thin TiO2 sheets has been described earlier.37 It is interesting to note however, that while in the case of flat TiO2 layers the lepidocrocite-like structure is favored energetically, the strain present in the (8,0) nanotubes reverses the stability order. A structure consisting of hydroxylated anatase-like segments has also been identified earlier among the possible H2Ti3O7 slabs,28 however was less stable than its lepidocrocite counterparts. The unexpected difference of the TiO2 framework from the other trititanates has not been reported in the previous but less accurate DFT-TB calculations.27 The water molecules on the internal surface of the 2,3,−H2O tube are only weakly bound to Ti sites (dO–Ti = 2.310 Å). This arrangement is slightly (0.27 kcal mol−1/H2Ti3O7) preferred over the 2,3,2′,4′ one, which is within the expected accuracy of the calculations. It is interesting to note, that the anatase-like reconstruction of the trititanate nanotube wall -similarly to the case of layers having the TiO2 stoichiometry37- is not stable in case of the flat sheets: it rearranges itself to the usual stepped lepidocrocite-like trititanate structure shown on Fig. 1.
While protons on the surface of the flat trititanate slabs are (with the exception of the 2,3,–H2O structure) positioned in the planes containing the divalent oxygen rows running on the surface, in case of the nanotubes themselves the protons are moving out of these planes. For instance, in case of the 2,3 arrangement on the external surface of the nanotubes the protons connected to these two sites can point either to the same or to different sides of the planes of the divalent oxygens, creating two different minima. The energy of these minima however differ by less than 0.1 kcal mol−1/H2Ti3O7 in all cases.
The energy ordering of the nanotubes did not change compared to the (8,0) nanotubes. The energy differences between the 2,3,2′,3′, 2,3,2′,4′, 2,4,2′,4′ and 2,4,2′,3′ tubes also did not change significantly; for instance the difference in the relative energies between the 2,3,2′,3′ and the 2,3,2′,4′ structures changed only from 0.9 to 1.2 kcal mol−1 with the increase of the diameter, showing that the two types of hydrogen bonds on the internal surface that have been found to govern the relative stabilities of these structures in the (8,0) tubes, are weakened to a similar extent by increasing the diameter of the tubes because of the larger distance between the atoms involved in hydrogen bond.
The only significant change in the relative energies is that the energy difference between the most stable 2,3,–H2O arrangement and all the other structures is larger with respect to (8,0) tubes. The reason of this extra stabilization is that the O2 and O3 atoms on the external surface point towards each other in the anatase-like structure, and as a result, the decreased O2–O3 distance (dO2–O3 = 2.668 Å in the (12,0) case compared to the 4.077 Å in the (8,0 case) allows the formation of hydrogen bridges between them (see Fig. 3a,b). The distance of the weakly bound H2O from the Ti sites on the internal surface is nearly identical to the (8,0) case (2.322 Å), showing that the stabilization is not the consequence of changes on the internal nanotube surface.
(18,0) and (20,0) tubes
Because of the demanding computational cost necessary for the calculations of these large nanotubes, (D≈50–60 Å) we have only considered the proton arrangements that were found to be the most stable at the smaller diameters: namely the 2,3,2′,3′, 2,3,2′,4′ and 2,3,–H2O structures.According to the data in Table 2 the order of stability of these structures is the following: 2,3,2′,3′ > 2,3,2′,4′ > 2,3,–H2O similarly to the relative energies of the flat slabs but reversed with respect to the smaller tubes. The most stable 2,3,2′,3′ configuration is preferred over the 2,3,2′,4′ one by 1.0 kcal mol−1/H2Ti3O7 in case of the (18,0) and by 0.7 kcal mol−1/H2Ti3O7 in case of the (20,0) tubes, close to the 1.2 kcal mol−1/H2Ti3O7 of the flat slabs (see Table 2). The preference of the 2,3,2′,3′ arrangement over the 2,3,–H2Oone is 1.3 kcal mol−1/H2Ti3O7 in case of the (18,0) and 2.5 kcal mol−1/H2Ti3O7 in case of the (20,0) rollups (see Table 2), approaching the 3.0 kcal mol−1/H2Ti3O7 energy difference in case of the flat slabs.
The relative stability of the 2,3,2′,4′ and the 2,3,2′,3′ structures is determined by several factors. On the internal surface the hydrogen bonds are weakened in both cases because of the increased O4′–O2′ distances. On the external surface the decrease of the curvature brings the O3 and Ti5 atoms closer together. In case of the 2,3,2′4′ nanotube the decreased O3–Ti5 distance allows the closing of the divalent oxygen bridges by incipient formation of the O3-Ti5 bond (d = 2.377 Å in the (18,0) tube, see Fig. 4c), while the 2,3,2′,3′ nanotube is stabilized by a hydrogen bond formed between the proton positioned at site O3 and the O2 oxygen atom, similarly to the 2,3,-H2O tube in the (12,0) rollup (cf.Fig. 4b and 3b) The resulting difference in energy between the two structures is however very small, within the accuracy of calculations.
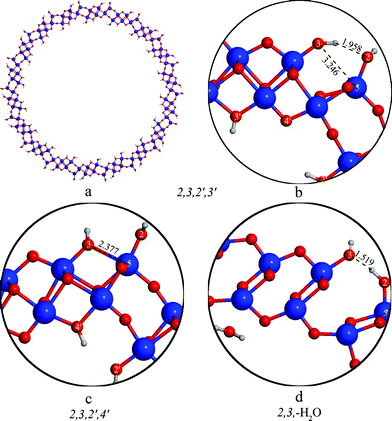 | ||
| Fig. 4 Structure of (18,0) nanotubes with different protonation patterns. | ||
Strain energies
The stability of TiO2 nanotubes is related to the ability of the structure to sustain the strain arising from the different surface tensions existing at the two sides of the rolled sheet. The strain energies ES are the difference between the energy of one formula unit (H2Ti3O7) in the fully optimized nanotube and in the corresponding optimized flat layer having the same structure, divided by the number of Ti atoms in the unit: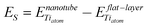 | (1) |
The computed ES values do not exceed 5 kcal mol−1/Ti atom irrespective of the size of the tubes and of the protonation pattern and smoothly decrease with the nanotube diameter, Table 2. The different degree of hydration as achieved in 2,3,–H2O nanotubes does not provide a reduced strain energy even in the range of small diameter. In addition the ES of trititanate nanotubes are considerably smaller than the values computed for lepidocrocite nanotubes of the same size26 confirming the larger flexibility of their structure. These results are in contrast with the earlier DFT-TB study where the strain energies of the lepidocrocite structure was counterintuitively found to be smaller than those of the trititanates.27
However the ES values do not allow the comparison between the relative stabilities of nanotubes of different stoichiometries. Such a comparison however – considering the several different titania and titanate structures proposed for nanotubes – is of fundamental interest in order to achieve feasible prediction of phase stability. A possible way to obtain comparable values for various dry and hydrated nanotubes having the general stoichiometry (TiO2)x(H2O)y is the combination of the strain energy, ES, (computed according to eqn (1)) with the hydration energy, EH, of the reference flat dry surface.
E H is the energy (per Ti atom in the formula unit) connected to the formation of a flat hydrated slab (with the same stoichiometry and protonation pattern of the nanotube of interest) starting from a dry lepidocrocite layer:
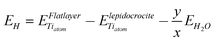 | (2) |
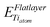 and
and 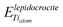 are the energy of a TiO2 unit in the nanotube like flat layer and in a lepidocrocite layer, respectively; EH2O is the energy of an isolated H2O molecule. The result of combining eqn (1) and 2 is the relative strain, ERS:
are the energy of a TiO2 unit in the nanotube like flat layer and in a lepidocrocite layer, respectively; EH2O is the energy of an isolated H2O molecule. The result of combining eqn (1) and 2 is the relative strain, ERS: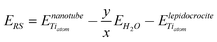 | (3) |
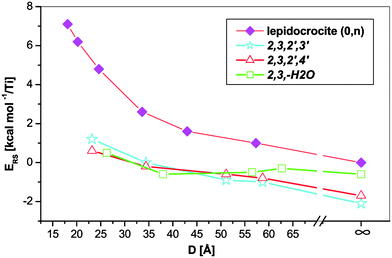 | ||
| Fig. 5 Relative strain energies of different trititanate and lepidocrocite nanotubes. The infinity symbol marks the flat slab values. | ||
The trititanate tubes are more stable than their lepidocrocite counterparts at all investigated diameters. This is in contrast with the findings of ref. 27, where only the conventional strain energies were used to compare the two types of nanotubes. The flat trititanate slabs – the values corresponding to these are marked with an infinity symbol on the rightmost side of Fig. 5 – also show larger stability with respect to lepidocrocite, indicating that the hydration of lepidocrocite slabs is thermodynamically favoured for both flat slabs and nanotubes. At any given diameter the difference between the curve corresponding to the lepidocrocite nanotube and a curve corresponding to a trititanate structure can be related to the energy gain in the hydration process. This difference converges to the value of hydration energy at the flat slab (2.1 kcal mol−1/Ti atom in case of the 2,3,2′,3′ protonation pattern). Although it can be argued that the small hydration energy can be easily overcome by entropy effects,28 the preference for hydrated (trititanate) nanotubes is increasing by decreasing the diameter, indicating that the hydration state of these nanotubes is also a function of the size of the tubes.
Band gaps
The band gaps of the individual patterns nearly monotonously approach the flat slab value with the increasing diameter (see Table 2 and Fig. 6). The nanotubes displaying the 2,3 protonation pattern on the external surface possess an indirect band gap similar to the flat layers, while the ones with the 2,4 pattern possess a direct gap. At small diameters, the band gaps of the trititanate nanotubes are smaller than those of the flat layers displaying the same protonation pattern and smaller with respect to the dry lepidocrocite tubes with the exception of the 2,3,–H2O arrangement, that has a significantly higher band gap (5.8 eV) than all other structures. However variations in the band gap are small and do not exceed a few tenths of an eV. Rationalization of values of Table 2 is not an easy task since reported structures differ not only for the protonation pattern but also for the structure of the oxide backbone (lepidocrocite, hydrated stepped lepidocrocite, hydrated stepped anatase-like arrangements). In order to try to recognize a common effect of hydration on the width and shape of band gap and edges, we have calculated the projected density of states, DOS, for selected trititanates of different diameter and compared to the DOS of dry lepidocrocite nanotubes of approximately the same size, Fig. 7. The structure of the DOS is similar in all the cases reported in Fig. 7: the top of the valence band is characterized by O 2p states and the bottom of the conduction band by Ti 3d empty states; however the presence of hydroxyls produces tails in the top of the valence states that push the edge of the band up. The net result is a reduction of the width of the band gap. However, although the variation in the width of the band gap appears to be significant only for nanotubes of small size, the presence of tails of the density of states of the valence bands and their subsequent upshift appear to be a genuine effect induced by the presence of the hydroxyls groups and not related to the diameter of the nanotubes.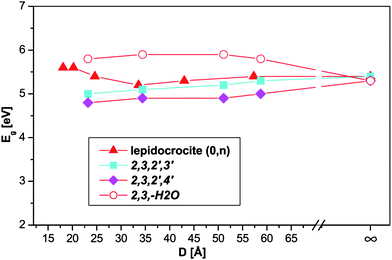 | ||
| Fig. 6 Band gap of the nanotubes plotted against the tube diameter. The infinity symbol marks the flat slab values. | ||
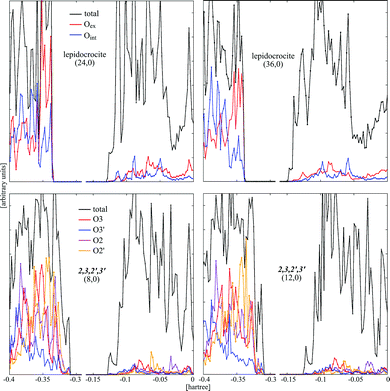 | ||
| Fig. 7 PDOS plots of selected nanotubes. | ||
Conclusions
Trititanate nanotubes have been investigated by ab initio DFT calculations up to the hitherto unavailable 60 Å diameter. The preferred protonation pattern on the surface of the nanotubes was found to be the function of the diameter, and different on the internal and the external surface of the nanotube walls. At small (<50 Å) diameters the dehydration of the internal surface was observed, and the nanotube walls adopted a new, anatase-like structure. The stability of the trititanate tubes were compared to the lepidocrocite-like TiO2 tubes calculated in an earlier work,26 and the trititanate structure was found to be more stable at all investigated diameters, indicating that the lepidocrocite TiO2 nanotubes are susceptible to hydration. The energy gain of hydration increases with decreasing diameter. The band gaps of trititanate nanotubes and nanosheets are considerable larger than bulk TiO2 (more than 1 eV) and they change with the diameter of the tubes only in a relatively narrow energy range. The presence of hydroxyl groups in trititanate nanotubes induce tails in the density of the states at the top of the valence band that pushes the edge of the band up.Acknowledgements
We acknowledge the CINECA-INSTM cofinanced Key Project for the availability of high performance computing resources and support and the CINECA-ISCRA project number HP10B5QG7W.References
- A. Motonari, J. Jinting and I. Seiji, Curr. Nanosci., 2007, 3, 285–295 Search PubMed.
- D. V. Bavykin, J. M. Friedrich and F. C. Walsh, Adv. Mater., 2006, 18, 2807–2824 CrossRef CAS.
- A. Fujishima, X. Zhang and D. A. Tryk, Surf. Sci. Rep., 2008, 63, 515–582 CrossRef CAS.
- M. Ni, M. K. H. Leung, D. Y. C. Leung and K. Sumathy, Renewable Sustainable Energy Rev., 2007, 11, 401–425 CrossRef CAS.
- Z. Tang, Y. Ji, Y. Xu, R. Xu, Z. Zhang and Z. Zhou, Sens. Lett., 2008, 6, 933–937 CrossRef CAS.
- D. Deng, M. G. Kim, J. Y. Lee and J. Cho, Energy Environ. Sci., 2009, 2, 818–837 RSC.
- T. Kasuga, M. Hiramatsu, A. Hoson, T. Sekino and K. Niihara, Langmuir, 1998, 14, 3160–3163 CrossRef CAS.
- Q. Chen and L.-M. Peng, Int. J. Nanotechnol., 2007, 4, 44–51 Search PubMed.
- Y. Q. Wang, G. Q. Hu, X. F. Duan, H. L. Sun and Q. K. Xue, Chem. Phys. Lett., 2002, 365, 427–431 CrossRef CAS.
- Z. V. Saponjic, N. M. Dimitrijevic, D. M. Tiede, A. J. Goshe, X. Zuo, X. Chen, A. S. Barnard, P. Zapol, R. Curtiss and T. Rajh, Adv. Mater., 2005, 17, 965–971 CrossRef CAS.
- G. Moglievsky, Q. Chen, H. Kulkarni, A. Kleinhammes, W. M. Mullins and Y. Wu, J. Phys. Chem. C, 2008, 112, 3239–3246 CrossRef CAS.
- T. Akita, M. Okumura, K. Tanaka, K. Ohkuma, M. Kohyama, T. Koyanagi, M. Date, S. Tsubota and M. Haruta, Surf. Interface Anal., 2005, 37, 265–269 CrossRef CAS.
- Q. Chen, W. Zhou, G. Du and L. Peng, Adv. Mater., 2002, 14, 1208–1211 CrossRef CAS.
- S. Afshar and M. Hakamizadeh, J. Exp. Nanosci., 2009, 77–86 Search PubMed.
- J. Yang, Z. Jin, X. Wang, W. Li, J. Zhang, S. Zhang, X. Guo and Z. Zhang, Dalton Trans., 2003, 3898–3901 RSC.
- D. H. Kim, Y. H. Jung, D.-K. Choi, S. J. Kim and K. S. Lee, J. Nanosci. Nanotechnol., 2009, 9, 941–945 CrossRef CAS.
- E. Morgado Jr, P. M. Jardim, B. A. Marinkovic, F. C. Rizzo, M. A. S. de Abreu, J. L. Zotin and A. S. Araùjo, Nanotechnology, 2007, 18, 495710 CrossRef.
- A. Riss, M. J. Elser, J. Bernardi and O. Diwald, J. Am. Chem. Soc., 2009, 131, 6198–6306 CrossRef CAS.
- F. Alvarez-Ramirez and Y. Ruiz-Morales, Chem. Mater., 2007, 19, 2947–2959 CrossRef CAS.
- J. N. Hart, S. C. Parker and A. A. Lapkin, ACS Nano, 2009, 3, 3401–3412 CrossRef CAS.
- A. N. Enyashin and G. Seifert, Phys. Status Solidi B, 2005, 242, 1361–1370 CrossRef CAS.
- A. V. Bandura and R. A. Evarestov, Surf. Sci., 2009, 603, L117–L120 CrossRef CAS.
- J. Wang, L. Wang, L. Maa, J. Zhao, B. Wang and G. Wang, Phys. E., 2009, 41, 838–842 CrossRef CAS.
- Z. Liu, Q. Zhang and L.-C. Qin, Solid State Commun., 2007, 141, 168–171 CrossRef CAS.
- F. Lin, G. Zhou, Z. Li, J. Li, J. Wi and W. Duan, Chem. Phys. Lett., 2009, 475, 82–85 CrossRef CAS.
- D. Szieberth, A. M. Ferrari, Y. Noel and M. Ferrabone, Nanoscale, 2010, 2, 81–89 RSC.
- A. N. Enyashin and A. L. Ivanovskii, J. Phys. Chem. C, 2009, 113, 20837–20840 CrossRef CAS.
- M. Casarin, A. Vittadini and A. Selloni, ACS Nano, 2009, 3, 317 CrossRef CAS.
- R. Dovesi, V. R. Saunders, R. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco and M. Llunell, CRYSTAL09, ( 2009) CRYSTAL09 User's Manual. University of Torino, Torino Search PubMed.
- R. Dovesi, R. Orlando, B. Civalleri, C. Roetti, V. R. Saunders and C. M. Zicovich-Wilson, Z. Kristallogr., 2005, 220, 571–573 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Labat, P. Baranek and C. Adamo, J. Chem. Theory Comput., 2008, 4, 341–352 CrossRef CAS.
- http://www.crystal.unito.it/Basis_Sets/Ptable.html .
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–273 CrossRef CAS.
- X. Dong, Master’s thesis, Materials Chemistry, University of Torino, 2009 Search PubMed.
- Y. Noel, P. D'Arco, R. Demichelis, C. M. Zicovich-Wilson and R. Dovesi, J. Comput. Chem., 2010, 31, 855–862 CAS.
- A. Vittadini and M. Casarin, Theor. Chem. Acc., 2008, 120, 551–556 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2011 |