Neutral and positively charged new purine tetramer structures: a computational study of xanthine and uric acid derivatives

Abstract

New tetramer structures, based on 9-methylxanthine (Xa), 9-methylxanthine protonated at N7 (XaH⁺) and 9-methyluric acid (Ua), were investigated by high-level density functional calculations. We have found that homo- and heterotetrads (XaH⁺)₄, (XaH⁺–Xa)₂, (XaH⁺–Ua)₂ carrying positive charges can be formed by low barrier hydrogen bonds. Systems with zero charge [(Xa)₄, (Xa–Ua)₂, (Ua)₄] were also constructed, investigated and compared to the guanine tetrad [(G)₄]. It was shown that the new tetramers can bind cations and anions without the necessity of stacking interactions. Application of the calculated systems in higher-ordered structures (e.g. quadruplexes) is promising with or without intercalating ions.

---

Introduction

Higher-ordered structures, based on self-recognition and self-assembly of simpler molecules, are of potential interest in a variety of fields ranging from structural biology to medicinal chemistry, supramolecular chemistry, nanotechnology and molecular-scale devices. Nucleic acids are prominent representatives of such simple building blocks. The guanine (G) base present in nucleic acids is well known for its ability to participate in the formation of tetrads and quadruplex structures, as well as more complex motifs, owing to its multiple hydrogen bonding pattern, stacking and ion-binding capacity.^1–5 Recently, it was found that guanosine-based quadruplexes, occurring e.g. in telomere sequences, are heavily involved in switching on and off genes. Consequently, quadruplexes may be useful anticancer drug targets as well.⁶

Since the discovery of the G tetrad, several other quadruplex structures have been reported, based on experimental results or theoretical considerations (see e.g.ref. 7, 8 and references therein). These new structures cover a wide range of changes from small modification in the guanine base to the complete substitution of the whole monomeric building block. It was also shown that in most of the cases cations play a stabilizing role in the formation of quadruplex strands by intercalating into the stacking tetrads. Negatively charged molecules (e.g. picrates) can bind to the “lateral part” of stacked structure ensuring additional stabilization.

In these situations, quadruplex structures were always neutral and according to our knowledge an intercalating anion has been reported only in one case.⁹ Charged quadruplexes can be important not just because of the intercalation of ions but they also provide new possibilities in the design of novel higher-ordered structures (e.g. nano-wires).

It was also pointed out that the G quartet is one of the most suitable structures for stacking since guanine quartets are strongly bound (there are two H-bonds between neighbouring molecules) and already posses a planar equilibrium structure.¹⁰ Other purine-based tetramers (e.g.adenine or inosine) have also been investigated,^10,11 however these structures have been found less stable and they tend to adopt non-planar geometries. This non-planarity is understandable since the nucleobases in these tetramers are connected to each other by only one H-bond which yields a flexible structure.

In the present paper, we point out that if one takes xanthine instead of hypoxanthine (which was used previously to model inosine nucleoside),¹² two H-bonds can be formed between neighbouring xanthines by low-barrier hydrogen bond (LBHB). Moreover, naturally occurring uric acid can be also involved in tetramer formation with or without xanthine. The low-barrier hydrogen bond is well characterized experimentally as well as theoretically.¹³ A possible implementation is to have a proton positioned between heteroatoms that face each other at nearly H-bond distance. Consequently, the system will have an additional positive charge and this provides a very strong interaction.

Herein, based on theoretical considerations we propose new quartet systems possessing positive or zero charge, which are composed of xanthine and uric acid derivatives. According to our expectation, these systems are capable to bind anions naturally. Moreover, since the monomers in the tetrad are connected through two H-bonds, they can form strongly bonded, planar structures. To our knowledge, this is the first example of a quartet in which the positive charge is supported by the tetramer structure itself, and not by an additional intercalating ion. This opens new possibilities in the design of novel nanostructures.

Xanthine and uric acid are naturally occurring purines. In the present work, 9-methylxanthine (Fig. 1a) and 9-methyluric acid (Fig. 1b) were considered to simulate a possible connection point to any backbone chain (e.g.sugar-phosphate chain or PNA). However, the presence of this backbone chain is not necessary for self-assembly. Moreover, the N(7) protonated form of Xa (XaH⁺) will have an important role in our systems. Thus, the appropriate choice of the pH environment is essential in the experiments.

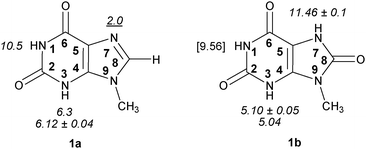Fig. 1 9-Methylxanthine (1a) and 9-methyluric acid (1b) with pK_a values. Experimental pK_a data are shown in italics, and pK_a value for protonated 1a with underlined characters.^14–19 The value predicted by the Marvin program suit²⁰ is shown in square brackets. The bold numbers within the rings show the atom numbering convention.

According to Pfleiderer and Nübel 9-methylxanthine (1a) has pK_a1 (HN3) 6.12 ± 0.04, and pK_a2 (HN1) > 13.¹⁴ Lichtenberg et al.²¹ have determined the value 5.9 for pK_a1 (HN3). Consensus pK_a values of 6.3 for pK_a1 (HN3) and 10.5 for pK_a2 (HN1) in 9-methylxanthine were given by Kulikowska et al. in their thorough and critical review (see Fig. 1).¹⁸Xanthosine and its monophosphate have slightly lower pK_a1 (HN3) values (5.7¹⁸ and 5.3 ± 0.02,²² respectively). The sites of first deprotonation in xanthine (pK_a1 = 7.53) and xanthosine (pK_a1 = 5.67) are erroneously given as N1 by Christensen et al.,²³cf. ref. 14 and 22. A recent paper also corroborates the order of deprotonation in xanthine (N3 > N7) using Raman spectra.¹⁵

9-Methyluric acid (1b) has pK_a1 (HN3) 5.10 ± 0.05¹⁶ and 5.04,¹⁹ and pK_a2 (HN7) 11.46 ± 0.1.¹⁶ Pfleiderer has also found pK_a1 (HN3) 5.27 ± 0.04, and pK_a2 (HN9) 10.90 ± 0.1 for uric acid itself.¹⁶ Additional experimental value for uric acid (pK_a1 4.9–5.45) has also been reported without specifying the site of deprotonation.¹⁷ Hargis et al. have found the value 5.53 as the first dissociation constant of uric acid.¹⁹

The pK_a for protonated guanosine (HN7⁺) has been reported to be 1.9,²³ and 2.2,¹⁸ for protonated hypoxanthine 1.8,²³ for inosine 1.0.¹⁸ The pK_a for the dissociation of N(7)-protonated 9-methylxanthine is 2.0,²¹ for xanthine this pK_a is 0.8,¹⁸ for xanthosine 1.1.¹⁸

In Fig. 2, optimized dimers are presented (with binding energy and optimal H-bond distances), which represent the principal interactions of the novel quartets. According to the pK_a values, the investigated charged structures can be formed in strongly acidic environment, but the pK_b value at the N(7) position is tunable in Xa with different functional groups in the C(8) position. For the purpose of comparison, the G dimer (as it is present in the G-quartet) is also calculated.

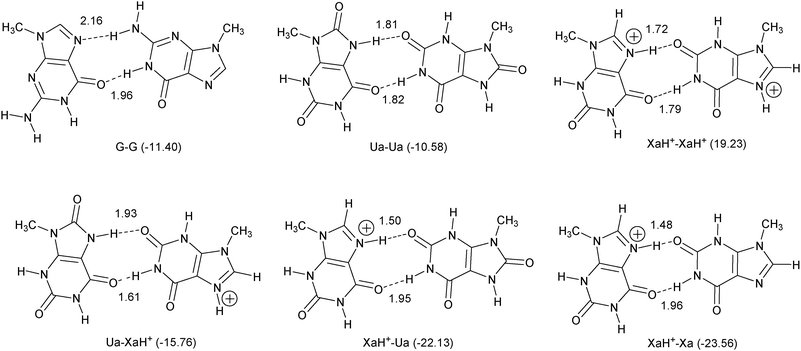Fig. 2 Basic dimer interactions for tetramer structures. The calculated bond energy values (in kcal mol⁻¹) are shown in parentheses, and the optimized H-bond length (in Å) between the proton and the acceptor heteroatom is presented near the pertinent bond.

Methods and computational details

All calculations were performed using density functional theory (DFT) as implemented in the Amsterdam Density Functional (ADF) program package developed by Baerends and others,^24–35 and the QUantum-regions Interconnected by Local Descriptions (QUILD) program by Swart and Bickelhaupt.^36,37 The Becke exchange functional³⁸ was used in combination with the correlation functional suggested by Lee et al.³⁹ The MOs were expanded using triple-ζ basis set augmented with two polarization functions (TZ2P).³² This level of computation provides good agreement with other high level calculations, as it has been shown in previous papers (e.g.ref. 40 and 41). In particular, with our TZ2P basis, the BSSE was previously shown to be in the order of 1 kcal mol⁻¹ and has therefore been neglected here.⁴¹

The interaction energy (ΔE_int) was analysed using a quantitative energy decomposition scheme first introduced in the context of DFT by Ziegler and Rauk.⁴²

The overall bond energy (ΔE_bond) was calculated as

ΔE_bond = ΔE_prep + ΔE_int (1)

where the preparation energy (ΔE_prep) is the amount of energy required to deform the separate fragments from their equilibrium structure to the geometry that they acquire in the overall complex. A detailed description of this energy decomposition scheme can be found elsewhere (see. ref. 43).

The electron density distribution is analyzed using the Voronoi deformation density (VDD) method.^44–46 The VDD charge Q_A is computed as the (numerical) integral of the deformation density Δρ(r) = ρ(r) − Σ_Bρ_B(r) associated with the formation of the molecule from its atoms in the volume of the Voronoi cell of atom A (eqn (2)). The Voronoi cell of atom A is defined as the compartment of space bound by the bond midplanes on and perpendicular to all bond axes between nucleus A and its neighboring nuclei (cf. the Wigner–Seitz cells in crystals).

Q_A = −∫_{Voronoi cell A} (ρ(r) − Σ_Bρ_B(r))dr (2)

Here, ρ(r) is the electron density of the molecule and Σ_Bρ_B(r) the superposition of atomic densities ρ_B of a fictitious promolecule without chemical interactions that is associated with the situation in which all atoms are neutral. The interpretation of the VDD charge Q_A is rather straightforward and transparent. Instead of measuring the amount of charge associated with a particular atom A, Q_A directly monitors how much charge flows, due to chemical interactions, out of (Q_A > 0) or into (Q_A < 0) the Voronoi cell of atom A, that is, the region of space that is closer to nucleus A than to any other nucleus.

Results and discussion

General trends

As one can see (Fig. 2), the dimer bonding energies are very promising especially in the presence of LBHB. The exception is the XaH⁺–XaH⁺ situation, where the bond energy (and the interaction energy as well) is positive. We have verified that a small barrier of 8.47 kcal mol⁻¹ prevents dissociation of this complex. Regarding the large binding energy difference between the XaH⁺–Xa and XaH⁺–XaH⁺ dimers, a simple explanation of the results is that the H-bonds cannot compensate the electrostatic repulsion in the XaH⁺–XaH⁺ case. Previously, however, we have found that the orbital interaction has an equally important role in the formation of the H-bond as the electrostatic interaction (see e.g.ref. 47 and ref. 3 therein). Thus, a more careful theoretical investigation seems to be appropriate but this is beyond the scope of this work.

All the structures discussed in this work are real minima, in particular also the XaH⁺–XaH⁺ dimer complex. The new dimers contain alternating H-bonds (proton donor and acceptor occur in each monomer), contrary to the G–G dimer, where all the proton donors belong to the right-handed G moiety (Fig. 2, structure G–G). This pattern of alternating hydrogen bonds enhances the planarity of the new arrangements which is important in the formation of quadruplexes because planar tetramers establish stacking structures more efficiently. According to the binding energy values, the most stable quadruplex can be formed by XaH⁺ and Ua molecules, but the homo Ua tetramer structure is also promising. In the former case, the quadruplex will be doubly positively charged, while the latter one will be neutral. Since all the dimer structures are true minima, the quadruply charged tetramer can be also constructed by XaH⁺ molecules in principle but positive interaction energy is expected without additional circumstances. It is an open question whether the (XaH⁺)₄ structure can eventually be stabilized by properly placed negative ions. Finally, although the XaH⁺–Xa dimer provides the strongest binding energy, it is not expected to form the most stable quartet since two XaH⁺–Xa units can be connected only through two H-bonds, i.e., one on each side (see Fig. 3).

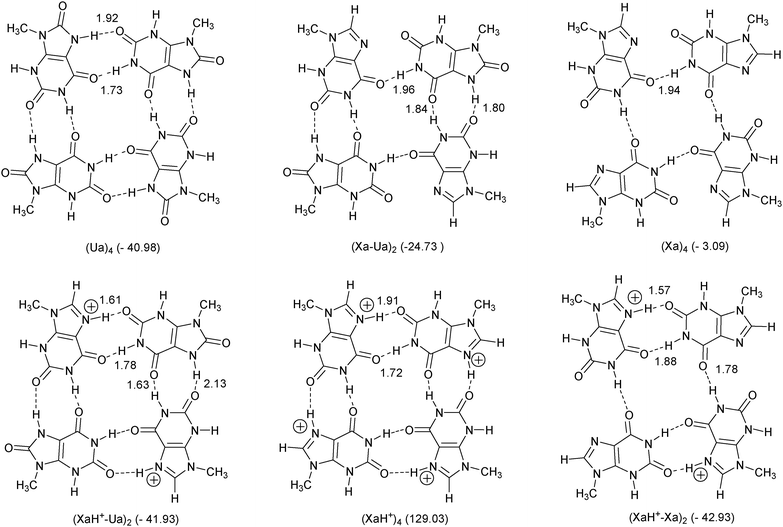Fig. 3 Tetramer structures investigated. The numbers in the parentheses show the calculated bond energy (in kcal mol⁻¹) referring to the monomer fragmentation in C(s) symmetry. Optimal bond distances are also presented (in Å).

Tetramer structures

In Fig. 3, we present tetramer structures optimized in C_s symmetry, built up from the above-mentioned dimers.

Some of them are constructed from only one type of monomer [(Ua)₄, (Xa)₄, (XaH⁺)₄] similarly to the G-tetramer, and there are systems which contain two different types of monomers. The numbers in parentheses in Fig. 3 show the calculated binding energy referring to the monomer fragmentation and the optimal bond distances are also presented analogously to the dimer case. Regarding the total charge, there are complexes with +4, +2 and zero charges, and according to the number of the H-bonds we have systems possessing 8, 6 and 4 connections, respectively.

Considering the total binding energies the quadruply charged (XaH⁺)₄ system has a positive ΔE_bond value in accordance with the dimer consideration (see above) but the bond energy of the (Xa)₄ structure (−3.09 kcal mol⁻¹) is unexpectedly weak compared to that of A₄ (−33.1 kcal mol⁻¹ at BLYP-D/TZ2P).¹⁰ This is a consequence of the steric repulsion between the N(7) and the O(2) atoms in the C_s symmetric case which cannot be compensated by the relatively long (1.94 Å) single H-bond. Moreover, frequency analyses show that the stationary point of (Xa)₄ under the constraint of C_s symmetry is a transition state, similar to the A₄ structure.¹⁰ All other complexes are in real equilibrium, even in the case of (XaH⁺–Xa)₂, in which steric repulsions can be found between the N(7) and the O(2) atoms, analogous to the situation in (Xa)₄.

For comparison, we optimized the G₄tetrad (the optimized structure can be found in Fig. 5) at the same level of theory, and the calculated total binding energy of the guanine monomers is −64.61 kcal mol⁻¹. This value is in good agreement with other calculations (see e.g.ref. 10) but a bit surprising regarding the dimer calculations. According to the preliminary dimer studies we were expecting similar or stronger interaction in certain cases [(Ua)₄, (XaH⁺–Ua)₂, (XaH⁺–Xa)₂] but the G₄tetrad shows an extra strong binding compared to our new cases. This is the consequence of a cooperative bond effect in G₄ which has been explained by Otero et al.⁴⁸ and Gilli and co-orkers⁴⁹ in terms of resonance assisted hydrogen bonding (RAHB). Here, we find that even the strong LBHB cannot compensate its absence in the present tetrads. In Fig. 4, we present the results of an alternative fragmentation scheme in which the interaction between differently chosen dimer fragments have been calculated.

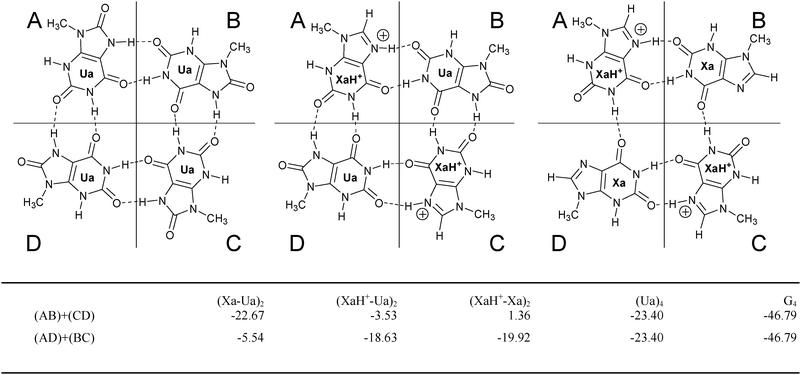Fig. 4 Dimer fragmentation. The pertinent dimers are built up from the monomers in areas A, B, C or D and the interaction energy (in kcal mol⁻¹) between the dimer fragments is summarized in the table. In the Ua₄ and G₄ cases the A, B, C, D regions are defined in the similar way.

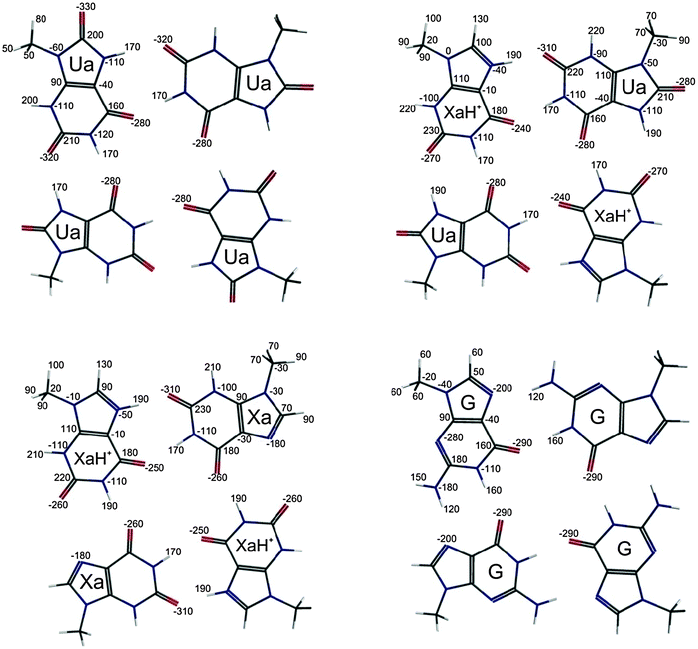Fig. 5 VDD atomic charges⁴⁶ (in milli atomic units) of the optimized structure at the (Ua)₄, (XaH⁺–Ua)₂ (XaH⁺–Xa)₂ and (G)₄ complexes.

We have two types of decomposition, namely (AB) + (CD) and (AD) + (BC) according to the introduced areas A, B, C, and D in Fig. 4. Concerning the optimized structures we found that the tetramer structures show a universal distortion in the presence of the LBHB. Namely, taking the optimized dimers as reference systems, the N(7)–O(2) distance is more elongated regarding the B–C (or A–D) fragments as compared to that of the LBHB containing A–B (or C–D) fragments. The consequence is an asymmetric dimer–dimer interaction. In particular, the fragment analyses provide 1.36 kcal mol⁻¹ (AB + CD) and −19.92 kcal mol⁻¹ (AD + BC) interaction energy in the case of (XaH⁺–Xa)₂. The positive interaction value shows that the formation of this quartet is unlikely, contrary to the interaction in the dimer (see in Fig. 3). This fact demonstrates that the interaction between the neutral and the protonated xanthine is still strong between the AD and BC dimer fragments but the H-bonds cannot compensate for the strong electrostatic repulsion between AB and CD which have both a net positive charge. Likewise, in the case of (XaH⁺–Ua)₂, we have −3.53 kcal mol⁻¹ and −18.63 kcal mol⁻¹ interaction energies for the AB + CD and AD + BC decompositions, respectively. Thus, the new H-bond is still weak between the N(7)–H group of the Ua and the O(2) atom of the XaH⁺ fragment, which is also confirmed by the relatively long H(7)⋯O(2) bond length of 2.13 Å (see Fig. 3).

The lateral and central H-bonds in the tetrad are elongated and shortened, respectively, if compared to the corresponding ones in the dimer. There is only one exception in the (XaH⁺–Ua)₂ complex, where the O(6)⋯H(1) connection between the Ua and the XaH⁺ was 1.61 Å in the dimer and 1.63 Å in the tetramer. Two effects are worth to mention in connection with this finding. First, the LBHB tends to form as short bond distance as possible while the electrostatic repulsion between the two positively charged dimer fragments tries to shift the dimers as far away as possible. These effects can cause together the different behaviour of this system. Moreover, this fragmentation proves that, in the present set of model systems, the LBHB cannot yield the same amount of energy gain as the cooperative effect (see e.g. the (AD)–(BC) interaction energies). From an electrostatic point of view it is understandable since the LBHB systems are divided into two positively charged fragments, where the interaction energy contains the electrostatic repulsion effect, too.

Finally, we have performed Voronoi Deformation Density (VDD) charge analyses⁴⁶ for the (Ua)₄, (XaH⁺–Ua)₂, (XaH⁺–Xa)₂ and (G)₄ systems, and the results are presented in Fig. 5a–d, respectively. According to the atomic VDD charges, an additional anion cannot be bound in the central position, since the four oxygen atoms carry a large negative partial charge in all the cases. However, this situation opens the possibility that if the +2 total charge of the system is compensated by anions, an additional cation can still be bound. Moreover, the largest negative charges are present at the oxygen atom in the LBHB bonds. Thus, the binding position of the anion is expected to be slightly shifted away from the LBHB region.

Comparing the VDD charges in the hydrogen bonds in the new systems we can conclude that the numbers do not account for the differences in the monomer fragmentation interaction energies. The charges are very similar in the central H-bonds (the four N–H⋯O bonds near the symmetry center of the tetrad), and the positive charges spread among the H(7), N(7), C(8) and H(8) atoms in the LBHBs at the Xa molecules. The latter result explains the similar VDD charge values of the LBHB region comparing to that of the VDD charges in the other systems with usual hydrogen bond.

Ion binding

Stacked quartets can form quadruplexes that are often further stabilized by cations (typically by potassium, sodium or ammonium), since they coordinate to the negatively charged carbonyl groups at the center of the G tetrad. The preferred G quadruplex structure adopted by a guanine-rich sequence in a DNA or RNA chain depends on the nature of the coordinating cations. VDD charge analyses point out that the central region of the new tetrads is similarly negatively charged as the G-tetramer. Hence, a Na⁺ cation was placed into the center of the tetrads. Furthermore, when LBHB was assumed in the systems, it carries a positive charge (which according to the charge analyzes spreads around the neighboring atoms) and the anion binding is expected near this area. We have to note that two anions can be present in the doubly charged systems at the same time, and we could distinguish two arrangements: the anions are on the same or on the opposite sides of a tetrad.

Taking into account these facts, we have investigated the (XaH⁺–Ua)₂ system with a Na⁺ and two F⁻ ions and the neutral (Ua)₄ system with a sodium cation. The schematic pictures of the optimizations are summarized in Fig. 6. The Na⁺ was always constrained to be on the C₄ symmetry axis, and the F⁻ ions were placed close to the LBHB region at the XaH⁺ molecule. The important role of the central cation at the (XaH⁺–Ua)₂tetrad is shown by the observation that when we tried to optimize the structures without the sodium ion, the two anions always destroyed the tetramer structures. For comparison the G-tetrad was also calculated with Na⁺ in the center and we introduced a different fragmentation of the ion binding systems in contrast to the ion-free ones. In Fig. 6, we present the results of the interaction energy calculations and the interaction values are included into the table in Fig. 6. The fragmentation schemes are as follows: (i) we calculated the interactions of the Na⁺ ion with the remaining part of a complex to reveal the strength of Na⁺ ion binding; (ii) we defined (dimer + anion + cation) and (dimer + anion) fragments in the complexes (where anions were present as well) in two ways, analogously to the corresponding situations without extra ions. This allows us to investigate how coordination of the cation affects the interactions between fragments in AB + CD and AD + BC decomposition.

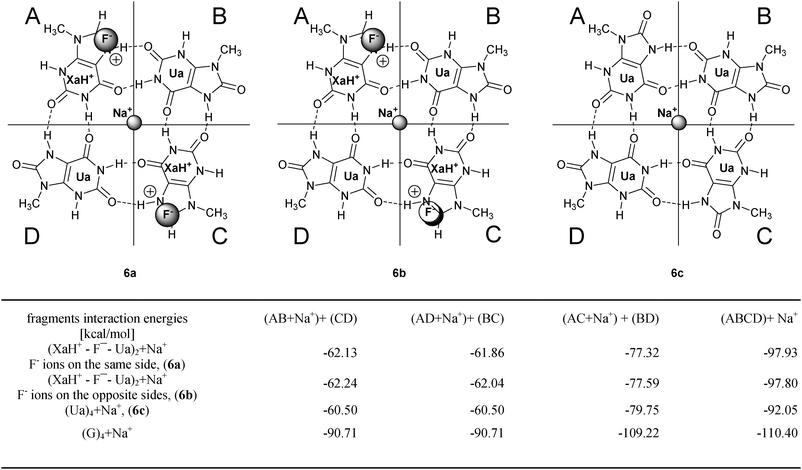Fig. 6 Investigated ionic systems with interaction energies (in kcal mol⁻¹). The definition of the different decomposition schemes can be found on the top of the columns, and in the last row the G4 system values are also presented for comparison.

In connection with the first scheme, we can conclude that the G₄ tetramer binds most strongly the sodium ion and the compensated (XaH⁺–F⁻–Ua)₂ complexes are capable to bind Na⁺ with nearly similar strength. Taking into account that the four oxygens around the sodium have very similar VDD charges in the ion free situation (Fig. 5), this shows that the metal–tetramer interaction is mainly based on the ionic interaction between Na⁺ and the four oxygen atoms. Regarding fragmentation (ii), we can see that the interaction energy differences were eliminated in the presence of a cation and anions (the (XaH⁺–Ua)₂ + 2F⁻ + Na⁺ system) which ones were found between the AB + CD and AD + BC decompositions in the situation without ion (column 3 of table in Fig. 4). The different interaction energies between the fragments are nearly equal in the ion-containing systems (see e.g. columns 2 and 3 of table in Fig. 6) and the values show a similar tendency regarding the different tetramer systems. In column 4 of the table in Fig. 6, we present dimer fragmentations [(AC + Na⁺) + (BD)] which, in principle, are similar to the A + B + C + D monomeric decomposition since it breaks all the H-bonds in the complex (there are no H bonds within AC and BD fragments). This confirms the result of the monomeric case, where the G₄tetrad displays significantly different interaction energy due to the cooperative effect. Furthermore, we can ascertain that the different positions of the anions (similar or opposite site) do not modify notably the interaction energies. The calculations were also performed with Cl⁻ ions and the results are in good accordance with the results for the F⁻ ions.

Conclusions

In the present article, we have investigated dimer and tetramer structures based on 9-methylxanthine and 9-methyluric acid by high level quantum-chemical calculations. We have found that while dimers showed very promising binding capacities (see Fig. 2), the new tetramer structures are in all cases more weakly bound than the well-known G₄tetrad (cf.Fig. 3). This is the consequence of the absence of the cooperative H-bonding in the new systems, in which G₄ provides additional stabilization. Still, the binding energies between the monomers in the new quartets are acceptable and the planarity of the latter ones is also good. The missing cooperative effect was partly compensated by strong low-barrier hydrogen bonds (LBHB) with net positive charges. The LBHB provides extra strong interaction between dimer fragments in the tetramers (see Fig. 2). The structures with positive charge are capable to bind anions. We would like to emphasize that the latter character of the new systems is very important because so far quadruplexes or higher ordered structures with anion intercalation, to our knowledge, have been investigated only in one case.⁹ The new positively charged tetramers can exist only in the presence of ions. Although in overall strongly bound the monomers without ions they easily decompose into dimer fragments. This decomposition is prevented by coordination of ions.

Finally, we would like to emphasize that either the LBHB or the cooperative effects cannot be recognized by any molecular mechanical level methods. Only quantum chemical calculation or a properly modified molecular mechanical method is suitable to investigate these systems.

Acknowledgements

This work was supported by grants OTKA 73672 and OTKA 61577, COST Action MP0802. One of the authors (G. P.) would like to thank the Hungarian Eötvös Fellowship for a secondment at the Department of Theoretical Chemistry, VU University Amsterdam. We also thank the National Research School Combination (NRSC-C) and the Netherlands Organization for Scientific Research (NWO-CW and NWO-NCF) for financial support.

References

1. S. Burge, G. N. Parkinson, P. Hazel, A. K. Todd and S. Neidle, Nucleic Acids Res., 2006, 34, 5402–5415.
2. J. T. Davis and G. P. Spada, Chem. Soc. Rev., 2007, 36, 296–313.
3. S. Lena, S. Masiero, S. Pieraccini and G. P. Spada, Chem.–Eur. J., 2009, 15, 7792–7806.
4. Quadruplex nucleic acids, ed. S. Neidle and S. Balasubramanian, The Royal Society of Chemistry, Cambridge, 2006.
5. A. Taylor, J. Taylor, G. W. Watson and R. J. Boyd, J. Phys. Chem. B, 2010, 114, 9833–9839.
6. S. Borman, Chem. Eng. News, 2009, 87, 28–30.
7. M. Franceschin, Eur. J. Org. Chem., 2009, 2225–2238.
8. S. Martic, X. Y. Liu, S. N. Wang and G. Wu, Chem.–Eur. J., 2008, 14, 1196–1204.
9. T. van der Wijst, B. Lippert, M. Swart, C. Fonseca Guerra and F. M. Bickelhaupt, JBIC, J. Biol. Inorg. Chem., 2010, 15, 387–397.
10. C. Fonseca Guerra, T. van der Wijst, J. Poater, M. Swart and F. M. Bickelhaupt, Theor. Chem. Acc., 2010, 125, 245–252.
11. B. C. Pan, K. Shi and M. Sundaralingam, J. Mol. Biol., 2006, 363, 451–459.
12. F. C. Meng and X. Zhao, THEOCHEM, 2008, 869, 94–97.
13. J. Emsley, Chem. Soc. Rev., 1980, 9, 91–124.
14. W. Pfleiderer and G. Nübel, Justus Liebigs Ann. Chem., 1961, 647, 155–160.
15. S. Gogia, A. Jain and M. Puranik, J. Phys. Chem. B, 2009, 113, 15101–15118.
16. W. Pfleiderer, Justus Liebigs Ann. Chem., 1974, 2030–2045.
17. D. Gningue and J. J. Aaron, Talanta, 1985, 32, 183–187.
18. E. Kulikowska, B. Kierdaszuk and D. Shugar, Acta Biochim. Pol., 2004, 51, 493–531.
19. R. C. Smith, J. Z. Gore, M. McKee and H. Hargis, Microchem. J., 1988, 38, 118–124.
20. ChemAxon, Marvin 5.2.6, 2009.10.19, 2009.
21. D. Lichtenberg, F. Bergmann and Z. Neiman, J. Chem. Soc. C, 1971, 1676–1682.
22. S. S. Massoud, N. A. Corfu, R. Griesser and H. Sigel, Chem.–Eur. J., 2004, 10, 5129–5137.
23. J. J. Christensen, J. H. Rytting and R. M. Izatt, Biochemistry, 1970, 9, 4907–4913.
24. E. J. Baerends, et al., ADF2008.01, Amsterdam, 2008.
25. E. J. Baerends, D. E. Ellis and P. Ros, Chem. Phys., 1973, 2, 41–51.
26. E. J. Baerends and P. Ros, Chem. Phys., 1975, 8, 412–418.
27. E. J. Baerends and P. Ros, Int. J. Quantum Chem., 1978, 169–190.
28. P. M. Boerrigter, G. T. Velde and E. J. Baerends, Int. J. Quantum Chem., 1988, 33, 87–113.
29. C. Fonseca Guerra, O. Visser, J. G. Snijders, G. te Velde and E. J. Baerends, in Methods and Techniques for Computational Chemistry, METECC-5, ed. E. Clementi and G. Corongiu, Cagliari, 1995, pp. 305–395.
30. C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403.
31. J. Krijn and E. J. Baerends, Fit-functions in the HFS-method, Vrije Universiteit, Amsterdam, 1984.
32. J. G. Snijders, P. Vernooijs and E. J. Baerends, in At. Data Nucl. Data Tables 26, 1981, pp. 483–509.
33. G. T. Velde and E. J. Baerends, J. Comput. Phys., 1992, 99, 84–98.
34. G. T. Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
35. L. Versluis and T. Ziegler, J. Chem. Phys., 1988, 88, 322–328.
36. M. Swart and F. M. Bickelhaupt, Int. J. Quantum Chem., 2006, 106, 2536–2544.
37. M. Swart and F. M. Bickelhaupt, J. Comput. Chem., 2008, 29, 724–734.
38. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
39. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789.
40. C. Fonseca Guerra and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 1999, 38, 2942–2945.
41. C. Fonseca Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, J. Am. Chem. Soc., 2000, 122, 4117–4128.
42. T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10.
43. F. M. Bickelhaupt and E. J. Baerends, Rev. Comput. Chem., 2000, 15, 1–86.
44. F. M. Bickelhaupt, N. J. R. V. Hommes, C. Fonseca Guerra and E. J. Baerends, Organometallics, 1996, 15, 2923–2931.
45. C. Fonseca Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, Chem.–Eur. J., 1999, 5, 3581–3594.
46. C. Fonseca Guerra, J. W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189–210.
47. G. Paragi, E. Szajli, F. Bogar, L. Kovacs, C. Fonseca Guerra and F. M. Bickelhaupt, New J. Chem., 2008, 32, 1981–1987.
48. R. Otero, M. Schock, L. M. Molina, E. Laegsgaard, I. Stensgaard, B. Hammer and F. Besenbacher, Angew. Chem., Int. Ed., 2005, 44, 2270–2275.
49. G. Gilli, F. Bellucci, V. Ferretti and V. Bertolasi, J. Am. Chem. Soc., 1989, 111, 1023–1028.

---