Substituent effects on BTP's basicity and complexation properties with LnIII lanthanide ions†
G.
Benay
,
R.
Schurhammer
,
J.
Desaphy
and
G.
Wipff
*
Laboratoire MSM, UMR CNRS 7177, Institut de Chimie, 4 rue B. Pascal, 67000 Strasbourg, France. E-mail: wipff@unistra.fr
First published on 11th October 2010
Abstract
Bis(1,2-4 triazin-3-yl)pyridines “BTPs” represent a new class of N-donor extracting agents that separate trivalent actinides and lanthanides from nuclear waste solutions with high An/Ln separation factors. We report here QM calculations on the effect of Rpara–BTP substituents on the protonation and complexation energies of these ligands (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes with LnIII lanthanides) in the gas phase. Both processes follow similar trends and are highly sensitive to the electron donor/acceptor character and polarizability of R. When compared to R–pyr analogues with pyridine, R–BTPs are found to be intrinsically much more basic, by ca. 20 kcal mol−1. In aqueous solution, however (modelled by the continuum PCM model), BTPs and pyridines have a similar basicity, pointing to the importance of solvent environment on their protonation states. In the optimized Ln(R–BTP)33+ complexes with Ln = La, Eu, Yb, complexation energies Ec3 increase with the intrinsic basicity of the ligands, in the order R = NMe2 > NH2 > OMe > C6H5 > tButyl > Me > H > F > Cl. Furthermore, comparison of complexes with different LnIII cations indicates that their stability increases in the order LaIII < EuIII < YbIII, by the same amount with the different R-substituents. The relative contributions of central pyridinyl and lateral triazinyl nitrogens of BTPs are shown to depend on the stoichiometry of the complex and on the LnIII size, possibly contributing to the subtle AnIII/LnIII discrimination by substituted BTPs.
3 complexes with LnIII lanthanides) in the gas phase. Both processes follow similar trends and are highly sensitive to the electron donor/acceptor character and polarizability of R. When compared to R–pyr analogues with pyridine, R–BTPs are found to be intrinsically much more basic, by ca. 20 kcal mol−1. In aqueous solution, however (modelled by the continuum PCM model), BTPs and pyridines have a similar basicity, pointing to the importance of solvent environment on their protonation states. In the optimized Ln(R–BTP)33+ complexes with Ln = La, Eu, Yb, complexation energies Ec3 increase with the intrinsic basicity of the ligands, in the order R = NMe2 > NH2 > OMe > C6H5 > tButyl > Me > H > F > Cl. Furthermore, comparison of complexes with different LnIII cations indicates that their stability increases in the order LaIII < EuIII < YbIII, by the same amount with the different R-substituents. The relative contributions of central pyridinyl and lateral triazinyl nitrogens of BTPs are shown to depend on the stoichiometry of the complex and on the LnIII size, possibly contributing to the subtle AnIII/LnIII discrimination by substituted BTPs.
1. Introduction
Heterocyclic N-donor ligands L based on the bistriazinylpyridine (BTPs) skeleton have been recently developed to separate MIII trivalent actinides from lanthanide ions by liquid–liquid extraction from nuclear solutions.1–3 For example, nPrBTP extracts AmIII from water to an alkane/2-ethylhexanol mixture with a distribution coefficient DAm of 300 and a separation factor SFAm/Eu of 130. Extracted complexes are of ML33+ type where the cation, well shielded from solvent and counterions by three BTP ligands, is coordinated to nine soft N-atoms,4–8 possibly explaining the preference for actinide over the harder lanthanide cations.9–11BTP derivatives with lateral n-alkyl chains are degraded under acidic and radiolytic conditions, but their CyMe4 derivatives (2,6-bis(5,5,8,8-tetramethyl-5,6,7,8-tetrahydrobenzo[1,2,4]triazine-3-yl) pyridines; see Fig. 1) are more stable while retaining satisfactory performance.12 So far, little is known about the basicity and complexation ability of BTPs as a function of their substituents. This led us to undertake quantum mechanical “QM” studies on substituted R–BTPs to investigate the intrinsic effect of their Rpara–pyridine substituent (R = NMe2, NH2, OMe, C6H5, tButyl, Me, H, F, Cl) in the gas phase. As a reference, we consider the protonation of R–pyr analogues in the pyridine series, well documented by experiment in the gas phase and in aqueous solution 13,14 and by simulations.15–17 Solvation effects play a major role in proton transfer, reactivity and complexation equilibria.13,18,19 When used as extractant molecules, BTPs are solubilized in the organic phase, in equilibrium with acidic aqueous solutions. This medium is more polar than an organic phase based on e.g.alkanes where basicity and complexation processes are more “gas phase like”. It is however less polar than pure water (where BTPs are quasi insoluble). Thus, in order to gain insights into solvation effects on the BTPs basicity, QM calculations were also performed “in aqueous solution” to mimic a polar phase. In the following, unless otherwise indicated, “BTP” corresponds to the Me4–BTP derivatives with four lateral Me groups. The unsubstituted H4–BTP and the CyMe4–BTP derivatives (see Fig. 1) will also be tested for comparison.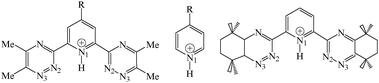 | ||
| Fig. 1 Studied R–BTP(H+) (cis–cis form) and R–pyridine(H+) analogues (R = H, Cl, F, tBut, Me, C6H6, OMe, NH2, NMe2) and CyMe4BTP. | ||
2. Methods
All structures were optimized at the DFT/B3LYP level of theory using the Gaussian03 software.20 The H, C, N, O, F and Cl atoms of the ligands were described by the 6-31G(d,p) basis set.20 As f-orbitals do not play an important role in metal–ligand bonding21 the 46 core and 4f electrons of the LaIII, EuIII and YbIII lanthanides were described by quasi-relativistic effective core potentials (ECP) of the Stuttgart group.22 For the corresponding valence orbitals the affiliated (7s6p5d)/[5s4p3d] basis set was used23 enhanced by an additional single f-function with an exponent of 0.591.24QM calculations “in aqueous solution” were conducted with the PCM model where the aqueous solvent is represented by a polarizable continuum medium with a dielectric constant of 80.25 Spheres delineated by solute atoms are defined from standard atomic radii implemented in Gaussian03, and the solvent probe sphere has a radius of 1.385 Å.20 This model does not account for specific (e.g. H-bonding) interactions with the solvent and cannot thus pretend to quantitatively predict basicities in solution, but allows for consistent comparisons within a series as a function of the R substituents. Total energies are given in Tables S1 and S2 (ESI†). For related theoretical studies on N-containing aromatic heterocyclic molecules, see e.g.ref. 15, 17 and 26.
3. Results
3.1 Protonation of R–BTPs and R–pyridines in the gas phase
Protonation energies EProt were calculated from eqn (1):| EProt: R–BTP + H+ → R–BTPH+ | (1) |
The EProt energies reported in Table 1, calculated from the cc forms show that in the gas phase, basicities of R–BTP and R–pyr are modulated by the para-pyridine substituent R and follow the same order in both series. The more attractor R is (Cl and F), the less basic R–BTP is. Conversely electron donor groups (OMe, NH2 or NMe2) enhance the basicity of R–BTP. Analysis of substituent effects in terms of several components (e.g. effects of field, electronegativity, polarizability, π-resonance)27 is beyond the scope of this paper. However, the importance of polarization28 can be seen in the higher basicity of Cl–BTP compared to F–BTP, and of NMe2–BTP compared to NH2–BTP in the gas phase. Likewise, replacing R = H by alkyl or aryl groups enhances EProt, by up to 7.9 kcal mol−1. Regarding the largest ΔEProt difference (from Cl to NMe2 substituent), it is somewhat lower in the BTP series than in the Pyr series (16.5 and 22.7 kcal mol−1, respectively), presumably due to dilution of the positive charge in the lateral rings of BTPH+s. For R–pyridines, the corresponding difference of experimental proton affinities at 300 K in the gas phase is somewhat smaller (17.9 kcal mol−1)14 than ΔEProt. More quantitative agreement with experiment would require using larger basis sets with diffuse functions.17,26 Note that the EProt energies correspond to molecules “at rest” in their energy minimum, whereas experimental proton affinities include thermodynamic contributions of rotational, vibrational and translational motions. Calculating the latter with Gaussian03 yields protonation enthalpies ΔHProt in the gas phase (see Table 1 for typical cases).29 Comparing Cl–Pyr to NH2–Pyr, one obtains a ΔΔHProt difference of 22.4 kcal mol−1, differing by only 0.3 kcal mol−1 from the ΔEProt energy. Likewise, in the R–BTP series, the ΔEProt difference between Cl–BTP and NMe2–BTP (17.0 kcal mol−1) is close to the calculated ΔΔHProt difference (16.1 kcal mol−1), indicating that the calculated changes of EProt energies in the gas phase as a function of R are meaningful.
| R | R–BTP | R–pyridines | |||||
|---|---|---|---|---|---|---|---|
| E Prot | ΔEProta | ΔHProtc | E Prot | ΔEProta | ΔHProtc | PA expd | |
| a Difference with respect to the unsubstituted H–BTP or H–pyridine. b Protonation of the NH2 group instead of the N-ring atom is calculated to be less stable by 37.5 kcal mol−1. c Calculated protonation enthalpies, assuming an enthalpy of 1.5 kcal mol−1 for H+.29 d Experimental proton affinities, based on PA(NH3) = 205.5 kcal mol−1.14 | |||||||
| Cl | −258.9 | 3.5 | −251.9 | −231.5 | 4.1 | −224.3 | 217.8 |
| F | −259.8 | 2.6 | −232.2 | 3.4 | 217.2 | ||
| H | −262.4 | 0 | −255.4 | −235.6 | 0 | −228.3 | 220.4 |
| Me | −265.4 | −2.9 | −240.1 | −4.5 | 223.7 | ||
| t But | −266.8 | −4.4 | −242.5 | −6.9 | |||
| C6H6 | −267.7 | −5.3 | −243.5 | −7.9 | |||
| OMe | −268.1 | −5.6 | −243.8 | −8.2 | 226.8 | ||
| NH2 | −272.7b | −10.3 | −250.2 | −14.6 | 231.0 | ||
| NMe2 | −275.9 | −13.5 | −268.0 | −254.2 | −18.6 | −246.7 | 235.7 |
Lateral substituents borne by the two triazinyl rings also markedly influence the BTP basicity: from H4–BTP to Me4–BTP, EProt increases in magnitude by 11.5 kcal mol−1. Likewise, from Me4–BTP to CyMe4–BTP, EProt increases further by 2.3 kcal mol−1.
3.2 Relative basicities of R–BTPs and R–pyridines in PCMwater solvent
Protonation energies EProt–Wat of R–BTP and R–pyr calculated “in water” with the PCM model are given in Table 2.| R | R–pyridine | R–BTP | ΔEProt–WatBTP/Pyr | |||||
|---|---|---|---|---|---|---|---|---|
| E Prot–Wat a | ΔEProt–Wat | pKab | ΔGexpc | ΔΔGexp | E Prot–Wat a | ΔEProt–Wat | ||
| a Calculated PCM values have been corrected by subtracting the ΔHgas→water(H+) enthalpy of −269.8 kcal mol−1 (from ref. 14). b Experimental values. From V. A. Palm, Tables of Rate and Equilibrium Constants of Heterolytic Organic Reactions, Academy of Science of the USSR, Moscow, 1976, vol. 2. c From ref. 14. | ||||||||
| Cl | −19.1 | 1.8 | 3.8 | −5.2 | 1.9 | −16.5 | 3.0 | 2.6 |
| F | −20.4 | 0.5 | −17.7 | 1.8 | 2.7 | |||
| H | −20.9 | 0.0 | 5.2 | −7.1 | 0.0 | −19.5 | 0.0 | 1.4 |
| Me | −23.5 | −2.6 | 6.0 | −8.1 | −1.0 | |||
| t But | −23.4 | −2.5 | −20.3 | −0.8 | 3.1 | |||
| C6H6 | −23.3 | −2.4 | −21.4 | −1.9 | 1.9 | |||
| OMe | −24.8 | −3.9 | −9.0 | −1.9 | −21.9 | −2.4 | 2.9 | |
| NH2 | −26.5 | −5.6 | 9.1 | −12.4 | −5.3 | −28.0 | −8.5 | −1.5 |
| NMe2 | −29.7 | −8.8 | −12.9 | −5.8 | −27.0 | −7.5 | 2.7 | |
In the pyridine series, basicities follow the same order of R-substituents in water as in the gas phase, i.e.Cl–Pyr is least basic and NMe2–Pyr is most basic. The energy gap ΔEProt–Wat between these compounds (10.6 kcal mol−1) is about half of that in the gas phase (22.7 kcal mol−1). Likewise, in the BTP series, the basicity order is similar to the one in the gas phase, with one exception in the case of NH2/NMe2 order that is reversed in solution. The calculated energy range ΔEProt–Wat (11.5 kcal mol−1) between Cl– and NMe2– derivatives is similar to the one in the pyridine series, and also about half the range calculated in the gas phase. These features are fully consistent with experimental observations in the pyridine series where, according to Aue et al., “the gas- and aqueous-phase free energies of protonation correlate roughly with one another, with an approximate twofold attenuation of the gas-phase substituent effects in the aqueous basicities”.14 A similar correlation between basicities in the gas-phase and in acetonitrile solution has been observed.30 Regarding the NH2– and NMe2– substituted pyridines, they are known to deviate from the linear relationship between water solution and gas phase complexation enthalpies.31
Comparing different types of bases (BTPs versuspyridines) is a more difficult task.31 Before doing so, we decided to test the performance of the PCM model on a challenging case, NH3versusaniline, where relative basicities in water are opposite to those in the gas phase.18 According to our simulations, aniline is indeed intrinsically more basic than NH3 (EProt = −223.5 and −218.6 kcal mol−1, respectively, in the gas phase). The difference of 5.9 kcal mol−1 is comparable to the difference in experimental proton affinities in the gas phase (6.9 kcal mol−1).32 In PCM aqueous solution, the order is inversed and NH3 is calculated to be more basic than aniline (by 13.4 kcal mol−1). Agreement with experiment is only qualitative however, since the pKa difference in water (9.25–4.62) translates to a free energy difference of 6.3 kcal mol−1, about half of the PCM value. Thus, care should be taken when comparing different types of bases with this model.33
Comparing however the PCM-calculated basicity of R–BTPs versus R–pyrs with the same R-substituent indicates that “in water”, both have similar basicities. They differ by only 1.4 to 3.1 kcal mol−1, depending on R (Table 2), indicating that BTPs and pyridines should have similar basicities. This feature can be understood from the lesser proton solvation in R–BTPH+, compared to R–pyrH+ where the proton is more accessible to the solvent and therefore better solvated. Thus, the relative basicities of R–BTP and R–pyr markedly depend on the solvent environment. In a dry apolar organic phase of low dielectric constant ε (e.g.alkanes with ε ≈ 2), relative basicities should be similar to those in the gas phase, i.e. BTPs should be much more basic than pyridines. In the extreme case of aqueous solutions, BTPs are calculated to be slightly less basic. In reality, in liquid–liquid extraction systems, the organic phase is heterogeneous and contains water, extractants, synergistic agents (e.g. diamides, alcohols), acid and extracted complexes.5 In such media or at water–oil interfaces, basicities are expected to be intermediate between those in the gas phase and in aqueous solution, and are hardly predictable from simulations only. Furthermore, as seen above, the precise nature of BTPs (e.g. lateral substituents) also markedly influences their basicity, calling for care with general conclusions. Anyway, assuming that BTP's basicities are comparable to those of pyridines, they should be protonated in the presence of nitric acid solutions.
Coming back to the R-substituent effect in the liquid–liquid biphasic extraction systems, it is expected to be somewhat larger in the organic phase than in water, but smaller than in the gas phase.
3.3 Lanthanide 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 3 complexes of R–BTPs
3 complexes of R–BTPs
We considered 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes of R–BTPs with LnIII ions (Fig. 2) to gain insights into the effect of the R-substituent on the corresponding complexation reaction energies Ec1 and Ec3 in the gas phase defined in eqn (2) and (3) and reported in Tables 3 and 4. Snapshots of 1
3 complexes of R–BTPs with LnIII ions (Fig. 2) to gain insights into the effect of the R-substituent on the corresponding complexation reaction energies Ec1 and Ec3 in the gas phase defined in eqn (2) and (3) and reported in Tables 3 and 4. Snapshots of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes are shown in Fig. S1 (ESI†).
3 complexes are shown in Fig. S1 (ESI†).| Ln(NO3)3 + R–BTP → Ln(NO3)3R–BTP | (2) |
| Ln3+ + 3 R–BTP → Ln(R–BTP)33+ | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes has been studied for EuIII and LaIII ions. The corresponding Ec1 energies range from −40.4 (Cl–BTP) to −47.0 kcal mol−1 (NMe2–BTP), indicating that the R–BTP ligands are attracted by the neutral complex, by different amounts depending on the R-substituent. The range ΔEc1, 9.5 kcal mol−1, is about half the corresponding ΔEProt range in the gas phase. Complexation energies Ec1 roughly follow the same order as the basicities, with exceptions, though, in the case of alkyl- and aryl-substituted BTPs that form less stable complexes than expected from a linear correlation (Fig. 3). As mentioned above, these R-groups are polarizable, and polarization effects are indeed weaker upon complexation of R–BTP to the neutral species Ln(NO3)3 than upon protonation.
1 complexes has been studied for EuIII and LaIII ions. The corresponding Ec1 energies range from −40.4 (Cl–BTP) to −47.0 kcal mol−1 (NMe2–BTP), indicating that the R–BTP ligands are attracted by the neutral complex, by different amounts depending on the R-substituent. The range ΔEc1, 9.5 kcal mol−1, is about half the corresponding ΔEProt range in the gas phase. Complexation energies Ec1 roughly follow the same order as the basicities, with exceptions, though, in the case of alkyl- and aryl-substituted BTPs that form less stable complexes than expected from a linear correlation (Fig. 3). As mentioned above, these R-groups are polarizable, and polarization effects are indeed weaker upon complexation of R–BTP to the neutral species Ln(NO3)3 than upon protonation.
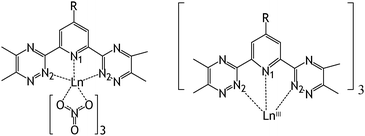 | ||
Fig. 2 Simulated 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶ ∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Ln(NO3)3(R–BTP) complexes (Ln = La, Eu) and 1 1 Ln(NO3)3(R–BTP) complexes (Ln = La, Eu) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶ ∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 Ln(R–BTP)33+ complexes (Ln = La, Eu, Yb). 3 Ln(R–BTP)33+ complexes (Ln = La, Eu, Yb). | ||
 | ||
| Fig. 3 E c1 (top) and Ec3 (bottom) complexation energies (EuIII complexes; in kcal mol−1) as a function of the protonation energies EProt. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes
1 complexes
| R | Eu | La | ||
|---|---|---|---|---|
| E c1 | ΔEc1 | E c1 | ΔEc1 | |
| Cl | −40.4 | 3.9 | −40.2 | 3.9 |
| F | −42.8 | 1.6 | −42.5 | 1.6 |
| H | −44.3 | 0.0 | −44.1 | 0 |
| Me | −44.8 | −0.5 | −44.5 | −0.5 |
| t But | −43.9 | 0.5 | −43.6 | 0.5 |
| C6H6 | −43.5 | 0.9 | −43.2 | 0.9 |
| OMe | −44.8 | −0.5 | −44.5 | −0.5 |
| NH2 | −46.7 | −2.4 | −46.7 | −2.3 |
| NMe2 | −47.0 | −2.6 | −46.7 | −2.6 |
| R | La | Eu | Yb | ΔEEu/La | ΔEEu/Yb | ||||
|---|---|---|---|---|---|---|---|---|---|
| E c3 | ΔEc3 | E c3 | ΔEc3 | E c3 PCM a | E c3 | ΔEc3 | |||
| a Calculated using the PCM energy of −34.9299 u.a. for “naked” EuIII. | |||||||||
| Cl | −608.1 | 17.4 | −656.3 | 17.5 | −173.1 | −696.8 | 17.6 | 48.2 | −40.5 |
| F | −614.4 | 11.1 | −662.5 | 11.3 | −703.0 | 11.4 | 48.1 | −40.5 | |
| H | −625.5 | 0.0 | −673.8 | 0.0 | −714.4 | 0.0 | 48.3 | −40.6 | |
| Me | −632.8 | −7.3 | −681.1 | −7.3 | −721.7 | −7.3 | 48.3 | −40.6 | |
| t But | −634.2 | −8.7 | −682.6 | −8.8 | −723.2 | −8.8 | 48.3 | −40.6 | |
| OMe | −637.3 | −11.8 | −685.7 | −11.9 | −726.3 | −11.9 | 48.3 | −40.6 | |
| NH2 | −650.7 | −25.2 | −701.0 | −27.2 | −739.7 | −25.3 | 50.3 | −38.8 | |
| NMe2 | −657.9 | −32.4 | −706.4 | −32.5 | −189.8 | −747.0 | −32.6 | 48.5 | −40.7 |
Complexation energies Ec3 corresponding to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes range from −608 to −747 kcal mol−1 (see Table 3). They are much larger in magnitude than the Ec1 energies, because each ligand formally interacts with a +3 charged instead of a neutral species, and polarization effects in the ligand should be larger in 1
3 complexes range from −608 to −747 kcal mol−1 (see Table 3). They are much larger in magnitude than the Ec1 energies, because each ligand formally interacts with a +3 charged instead of a neutral species, and polarization effects in the ligand should be larger in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes.34 As a result, for the LaIII, EuIII and YbIII complexes, the order of Ec3 energies exactly fits the order of protonation energies EProt, as sketched in Fig. 3. As for the 1
3 complexes.34 As a result, for the LaIII, EuIII and YbIII complexes, the order of Ec3 energies exactly fits the order of protonation energies EProt, as sketched in Fig. 3. As for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, the least basic Cl–BTP ligand forms the least stable 1
1 complexes, the least basic Cl–BTP ligand forms the least stable 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complex, whereas the most basic NMe2–BTP ligand forms the most stable complex. The energy difference between these complexes, ca. 50 kcal mol−1, is about twice the difference ΔEProt in protonation energies, indicating that substituent effects are magnified in complexation compared to protonation processes in the gas phase.
3 complex, whereas the most basic NMe2–BTP ligand forms the most stable complex. The energy difference between these complexes, ca. 50 kcal mol−1, is about twice the difference ΔEProt in protonation energies, indicating that substituent effects are magnified in complexation compared to protonation processes in the gas phase.
Comparing now the different lanthanide cations, one sees that, for a given R–BTP ligand, the Ec3 complexation energies decrease in magnitude in the order Yb(III) > Eu(III) > La(III), i.e. as the lanthanide cation gets bigger and less “hard”. At a more quantitative level, the preference for EuIII over LaIII is quasi independent on the R-substituent (except for R = NH2): ΔEEu/La = 48.1 to 48.5 kcal mol−1. Likewise, the preference for the hardest YbIII cation over EuIII is quasi independent on R (ΔEEu/Yb = −40.5 to −40.7 kcal mol−1). Thus, changing the R-substituent should have a minor effect on the selectivity of a given R–BTP towards different LnIII ions.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes) and S4 (1
1 complexes) and S4 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes) in ESI† reveal several interesting features. First, as expected, all Ln–N bonds shorten when the complex gets more stable, i.e. as the cation gets smaller, in the order La > Eu > Yb. This is consistent with previous computational and experimental results (see ref. 35 and references cited therein). Regarding the R-effect on Ln–N bonds, in both types of complexes, Ln–N bonds shorten when the interaction gets stronger. Ln–N1 bond with the central pyridine ring shortens by ca. 0.04 Å along the R-series (from Cl to NMe2 groups), whereas the Ln–N2 bonds with the lateral rings decrease less (by ca. 0.01 Å), as expected. Generally, for a given LnIII ion and R–BTP ligand, Ln–N1 bonds are shorter in the 1
3 complexes) in ESI† reveal several interesting features. First, as expected, all Ln–N bonds shorten when the complex gets more stable, i.e. as the cation gets smaller, in the order La > Eu > Yb. This is consistent with previous computational and experimental results (see ref. 35 and references cited therein). Regarding the R-effect on Ln–N bonds, in both types of complexes, Ln–N bonds shorten when the interaction gets stronger. Ln–N1 bond with the central pyridine ring shortens by ca. 0.04 Å along the R-series (from Cl to NMe2 groups), whereas the Ln–N2 bonds with the lateral rings decrease less (by ca. 0.01 Å), as expected. Generally, for a given LnIII ion and R–BTP ligand, Ln–N1 bonds are shorter in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 than in the 1
3 than in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, in keeping with the stronger cation–ligand interactions in the former. Comparing now the Ln–N1 to the Ln–N2 bonds reveals different trends, depending on the LnIII cation size and on the stoichiometry of the complex. In 1
1 complexes, in keeping with the stronger cation–ligand interactions in the former. Comparing now the Ln–N1 to the Ln–N2 bonds reveals different trends, depending on the LnIII cation size and on the stoichiometry of the complex. In 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, Ln–N1 bonds are longer than Ln–N2, indicating a weaker contribution of the central pyridine ring, compared to the lateral rings to the ligand binding, and this feature is most pronounced with the biggest cation. In the 1
1 complexes, Ln–N1 bonds are longer than Ln–N2, indicating a weaker contribution of the central pyridine ring, compared to the lateral rings to the ligand binding, and this feature is most pronounced with the biggest cation. In the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes, the relative bond “ordering” depends on the cation size. With the YbIII and EuIII cations, Ln–N1 distances are shorter than the Ln–N2 distances whatever the R-substituent is. With the biggest ion LaIII, the order depends on R. For the best ligands (R = NMe2 or NH2), La–N1 is shorter than La–N2, whereas for the other BTP derivatives, La–N1 is longer. This analysis makes clear that the relative contributions of the pyridine and triazinyl rings (and their derivatives) depend on the cation size and hardness, a feature that may contribute to discriminate actinideversus lanthanide ions.36,37
3 complexes, the relative bond “ordering” depends on the cation size. With the YbIII and EuIII cations, Ln–N1 distances are shorter than the Ln–N2 distances whatever the R-substituent is. With the biggest ion LaIII, the order depends on R. For the best ligands (R = NMe2 or NH2), La–N1 is shorter than La–N2, whereas for the other BTP derivatives, La–N1 is longer. This analysis makes clear that the relative contributions of the pyridine and triazinyl rings (and their derivatives) depend on the cation size and hardness, a feature that may contribute to discriminate actinideversus lanthanide ions.36,37
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, qEu = 1.37 to 1.38 e, and qLa = 1.48 e. For 1
1 complexes, qEu = 1.37 to 1.38 e, and qLa = 1.48 e. For 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes, qLa = 1.66 to 1.67 e, qEu = 1.56 to 1.57 e and qYb = 1.54 to 1.55 e. Thus, when the R-group evolves from acceptor to donor, the electron transfer to the LnIII ion remains little affected. The increased stability of the complex along the R-series seems to be rather due to polarization of the ligand, in the direction Rδ+⋯Nδ− for the pyridine moiety. Indeed, the qN1 charge is more negative in the complexes (−0.55 to −0.65 e) than in the corresponding free ligands (−0.51 to −0.55 e). Furthermore, in 1
3 complexes, qLa = 1.66 to 1.67 e, qEu = 1.56 to 1.57 e and qYb = 1.54 to 1.55 e. Thus, when the R-group evolves from acceptor to donor, the electron transfer to the LnIII ion remains little affected. The increased stability of the complex along the R-series seems to be rather due to polarization of the ligand, in the direction Rδ+⋯Nδ− for the pyridine moiety. Indeed, the qN1 charge is more negative in the complexes (−0.55 to −0.65 e) than in the corresponding free ligands (−0.51 to −0.55 e). Furthermore, in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 1
3 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes of a given LnIII ion, when R is changed from Cl to NMe2, the qN1 charge becomes more negative (by ca. 0.05 e), whereas qN2 remains quasi constant. Regarding the qLn charges for different LnIII ions, they decrease in the order La > Eu > Yb for each type of complex, indicating increased ligand to cation electron transfer in the lanthanide series as the complex becomes more stable. Comparing now qLn in the 1
1 complexes of a given LnIII ion, when R is changed from Cl to NMe2, the qN1 charge becomes more negative (by ca. 0.05 e), whereas qN2 remains quasi constant. Regarding the qLn charges for different LnIII ions, they decrease in the order La > Eu > Yb for each type of complex, indicating increased ligand to cation electron transfer in the lanthanide series as the complex becomes more stable. Comparing now qLn in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 versus 1
1 versus 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes, it is found to be lower in the former (by ca. 0.20 e with EuIII) as expected from the coordination of negatively charged nitrate ligands in Ln(NO3)3R–BTP complexes, instead of neutral ligands in Ln(BTP)33+ complexes.
3 complexes, it is found to be lower in the former (by ca. 0.20 e with EuIII) as expected from the coordination of negatively charged nitrate ligands in Ln(NO3)3R–BTP complexes, instead of neutral ligands in Ln(BTP)33+ complexes.
4. Discussion and conclusions
We report QM investigations on the effect of R-substituents on the basicity and complexation properties of R–BTPs, an important class of molecules that can discriminate between LnIII and AnIII ions, and thus of high potential for nuclear waste partitioning by liquid–liquid extraction. Intrinsically (in the gas phase), the basicity order of R–BTPs is the same as with R–pyridines, but R–BTPs are found to display a much higher protonation energy (by more than 20 kcal mol−1) and should thus be more easily protonated in apolar or weakly polar media. In aqueous solution, mimicked by the simple PCM-continuum model, the basicity sequence of R–BTPs is calculated to be the same as for R–pyr and also the same as in the gas phase (with one exception when R = NH2). R–BTPs are found to be somewhat less basic than R–pyr analogues, and those with alkyl, aryl or donor R-groups should thus be protonated in acidic aqueous solutions and, a fortiori, in organic solutions in contact with such phases.Optimizations of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes Ln(R–BTP)33+ in the gas phase reveal a quasi-linear relationship between intrinsic basicities of R–BTPs and complexation energies with trivalent lanthanides. In the 1
3 complexes Ln(R–BTP)33+ in the gas phase reveal a quasi-linear relationship between intrinsic basicities of R–BTPs and complexation energies with trivalent lanthanides. In the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, BTPs with alkyl and aryl substituents deviate from the linear correlation, presumably because of different contributions of polarization effects in protonation versus complexation processes.
1 complexes, BTPs with alkyl and aryl substituents deviate from the linear correlation, presumably because of different contributions of polarization effects in protonation versus complexation processes.
The studied alkyl lateral substituents R′lat borne by triazinyl rings also markedly influence the basicity of BTPs and should therefore also affect their complexation properties, as shown by Guillaumont (when R′lat = CH3, OCH3 and CN).9 What happens in solution cannot be predicted by QM simulations alone,38 but the latter point to the versatile acido-basic and complexing character of BTPs as a function of their substituents and call for experimental studies along these lines. In fact, recent experimental studies fully support the predicted correlation between the basicity of BTPs and their complexation properties: in the R–BTP series with R = Cl, H and OMe, the basicity of the ligand increases (estimated pKas of the protonated forms in ethanol are 2.1, 3.0 and 3.4, respectively) while the corresponding distribution ratio for EuIII extraction from water to an organic phase increases (from 0.002 to 0.59), indicating an increased stability of the Eu(R–BTP)33+ complex.39,40 Furthermore, it was found that increasing the BTP basicity enhances the An/Ln separation factor (by a factor of ca. 4 when R is changed from Cl to OMe),39 a key feature in the context of nuclear waste partitioning. Beyond the BTP series, such a correlation can be important for other polyaromatic N-donor based extractants with pyridine moieties like the bis-triazine-bipyridine (BTBP) derivatives that display remarkable actinide/lanthanide discrimination.41,42
Acknowledgements
The authors are grateful to IDRIS, CINES, Université de Strasbourg and GNR PARIS for computer resources, and to Etienne Engler for assistance. Support from the ACSEPT FP7 EEC collaborative project and Training Grant for GB is greatly acknowledged.References
- Z. Kolarik, U. Müllich and F. Gassner, Solvent Extr. Ion Exch., 1999, 17, 1155–1170 CrossRef CAS.
- Z. Kolarik, U. Müllich and F. Gassner, Solvent Extr. Ion Exch., 1999, 17, 23–32 CrossRef CAS.
- Z. Kolarik, Chem. Rev., 2008, 108, 4208–4252 CrossRef CAS.
- M. G. B. Drew, D. Guillaneux, M. J. Hudson, P. B. Iveson, M. L. Russell and C. Madic, Inorg. Chem. Commun., 2001, 4, 12–15 CrossRef CAS.
- M. Weigl, A. Geist, U. Mullich and K. Gompper, Solvent Extr. Ion Exch., 2006, 24, 845–860 CrossRef CAS.
- M. A. Denecke, A. Rossberg, P. J. Panak, M. Weigl, B. Schimmelpfennig and A. Geist, Inorg. Chem., 2005, 44, 8418–8425 CrossRef CAS.
- S. Colette, B. Amekraz, C. Madic, L. Berthon, G. Cote and C. Moulin, Inorg. Chem., 2004, 43, 6745–6751 CrossRef CAS.
- V. Hubscher-Bruder, J. Haddaoui, S. Bouhroum and F. Arnaud-Neu, Inorg. Chem., 2010, 49, 1363–1371 CrossRef CAS.
- D. Guillaumont, THEOCHEM, 2006, 771, 105–110 CrossRef CAS.
- L. Petit, L. Joubert, P. Maldivi and C. Adamo, J. Am. Chem. Soc., 2006, 128, 2190–2191 CrossRef CAS.
- L. Petit, C. Adamo and P. Maldivi, Inorg. Chem., 2006, 45, 8517–8522 CrossRef CAS.
- M. J. Hudson, C. E. Boucher, D. Braekers, J. F. Desreux, M. G. B. Drew, M. S. J. Foreman, L. M. Harwood, C. Hill, C. Madic, F. Marken and T. G. A. Youngs, New J. Chem., 2006, 30, 1171–1183 RSC.
- J.-F. Gal and P.-C. Maria, Correlation Analysis of Acidity and Basicity: From the Solution to the Gas Phase, in Physical Organic Chemistry, ed. R. W. Taft, John Wiley & Sons, Inc., New York, 1990, pp. 159–238 Search PubMed.
- D. H. Aue, H. M. Webb, W. R. Davidson, P. Toure, J. H. P. Hopkins, S. P. Moulik and D. V. Jahagirdar, J. Am. Chem. Soc., 1991, 113, 1770–1780 CrossRef CAS.
- I. Lee, C. K. Kim, I. S. Han, H. W. Lee, W. K. Kim and Y. B. Kim, J. Phys. Chem. B, 1999, 103, 7302–7307 CrossRef CAS.
- F. Blanco, D. H. O'Donovan, I. Alkorta and J. Elguero, Struct. Chem., 2008, 19, 339–352 CrossRef CAS.
- S. Hwang, Y. H. Jang and D. S. Chung, Bull. Korean Chem. Soc., 2005, 26, 585–588 CrossRef CAS.
- C. Reichardt, Solvents and Solvent Effects in Organic Chemistry, VCH, Weinheim-Basel, 1990 Search PubMed.
- J. M. Lehn, Struct. Bonding, 1973, 161, 1–69.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision B.05, Gaussian, Inc., Pittsburgh, PA, 2003 Search PubMed.
- L. Maron and O. Eisenstein, J. Phys. Chem. A, 2000, 104, 7140–7143 CrossRef CAS.
- M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1989, 75, 173–194 CrossRef CAS.
- T. H. Dunning and P. J. Hay, Gaussian basis sets for molecular calculations in Methods of Electronic Structure Theory. Modern Theoretical Chemistry 3, ed. H. F. Schaefer III, Plenum Press, New York, 1977, pp. 1–28 Search PubMed.
- A. W. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. F. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS.
- B. Kallies and R. Mitzner, J. Phys. Chem. B, 1997, 101, 2959–2967 CrossRef CAS.
- R. W. Taft, Protonic Acidities and Basicities in the Gas Phase and in Solution: Substituent and Solvent Effects in Physical Organic Chemistry, ed. R. W. Taft, John Wiley & Sons, New York, 1983, pp. 247–350 Search PubMed.
- J.-L. M. Abboud, J. Catalan, J. Elguero and R. W. Taft, J. Org. Chem., 1988, 53, 1137–1140 CrossRef CAS.
- Assuming an enthalpy of 1.5 kcal mol−1 (=2.5 RT) for the “free proton” H+ at 300 K (see I. A. Topol, G. J. Tawa, S. K. Burt and A. A. Rashin, J. Phys. Chem. A, 1997, 101, 10075 Search PubMed ).
- I. Kaljurand, T. Rodima, I. Leito, I. A. Koppel and R. Schwesinger, J. Org. Chem., 2000, 65, 6202–6208 CrossRef CAS.
- E. M. Arnett, J. Chem. Educ., 1985, 62, 385–391 CAS.
- Y. K. Lau, P. P. S. Saluja, P. Kebarle and A. W. Alder, J. Am. Chem. Soc., 1978, 100, 7328 CrossRef CAS.
- We tested DFT/B3LYP/6-31G(d,p) calculations on the sequence of alkyl amines NH3, NH2Me, NHMe2, NMe3 whose relative basicities in water are known to differ from those in the gas phase. In the gas phase, the relative calculated protonation energies EProt (in kcal/mol) are in the order NH3 (0; EProt = −218.6) < NH2Me (9.9) < NHMe2 (16.1) < NMe3 (19.8), following the experimental order (0, 12.0, 18.6 and 22.8 kcal/mol, respectively). Experimentally, in water, pKa's are 9.25, 10.66, 10.72 and 9.81, respectively, indicating that NH2Me and NHMe2 have similar basicities, higher than the NMe3 basicity. In PCM solution, the calculated protonation energy differences, with respect to NH3 are 0.4, −1.2, −1.6 kcal/mol for NH2Me, NHMe2, NMe3, respectively, indicating that NMe3 is the most basic. The PCM model thus accounts for the higher basicity of NMe3 compared to NH3 in water, but exaggerates the basicity of NMe3 relative to NHMe2 and NH2Me, presumably due to the neglect of specific H-bonding interactions in this model.
- In aqueous solution, the complexation energy would be much smaller, due to the desolvation energy of the “free” LnIII ion (see e.g. L. Maron and D. Bourissou, Organometallics, 2009, 28, 3686 Search PubMed ). The experimental dehydration enthalpy of EuIII is 839 kcal mol−1 ( I. Marcus, Ion Solvation, Wiley, New York, 1985) CrossRef CAS.
- D. Guillaumont, J. Phys. Chem. A, 2004, 108, 6893–6900 CrossRef CAS.
- G. Ionova, C. Rabbe, R. Guillaumont, S. Ionov, C. Madic, J. C. Krupa and D. Guillaneux, New J. Chem., 2002, 26, 234–242 RSC.
- Note that according to EXAFS data and QM calculations on M(BTP)33+ complexes with M = Eu and Cm, however, there is no significant difference between M–N1 and M–N2 bond distances with both cations ( M. A. Denecke, A. Rossberg, P. J. Panak, M. Weigl, B. Schimmelpfennig and A. Geist, Inorg. Chem., 2005, 44, 8418 Search PubMed ).
- As for protonation energies, substituent effects are expected to be smaller in solution than in the gas phase. According to our QM calculations, the difference in complexation energies Ec3 for NMe2–BTPversusCl–BTP to form Eu(R-BTP)33+ complexes drops from 50.0 kcal mol−1 in the gas phase to 16.7 kcal mol−1 in PCM–water (see Table 4).
- S. Trumm, G. Wipff, A. Geist, P. J. Panak and T. Fanghänel, Radiochim. Acta, 2010 Search PubMed , in press.
- S. Trumm, D. Schild, B. Schimmelpfennig, P. J. Panak, A. Geist and T. Fanghänel, 2010, private communication, publication in preparation.
- C. Ekberg, A. Fernvick, T. Retegan, G. Skarnemark, M. Foreman, M. Hudson, S. Englund and M. Nilsson, Radiochim. Acta, 2008, 96, 222–235.
- M. J. Hudson, M. G. B. Drew, M. R. S. Foreman, C. Hill, N. Huet, C. Madic and T. G. A. Youngs, Dalton Trans., 2003, 1675–1685 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Total energies of neutral, protonated and complexed ligands and structural parameters of the complexes. See DOI: 10.1039/c0nj00527d |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2011 |
