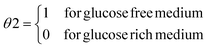A mathematical analysis of nuclear intensity dynamics for Mig1-GFP under consideration of bleaching effects and background noise in Saccharomyces cerevisiae

Abstract

Fluorescence microscopy is an imaging technique that provides insights into signal transduction pathways through the generation of quantitative data, such as the spatiotemporal distribution of GFP-tagged proteins in signaling pathways. The data acquired are, however, usually a composition of both the GFP-tagged proteins of interest and of an autofluorescent background, which both undergo photobleaching during imaging. We here present a mathematical model based on ordinary differential equations that successfully describes the shuttling of intracellular Mig1-GFP under changing environmental conditions regarding glucose concentration. Our analysis separates the different bleaching rates of Mig1-GFP and background, and the background-to-Mig1-GFP ratio. By applying our model to experimental data, we can thus extract the Mig1-GFP signal from the overall acquired signal and investigate the influence of kinase and phosphatase on Mig1. We found a stronger regulation of Mig1 through its kinase than through its phosphatase when controlled by the glucose concentration, with a constant (de)phosphorylation rate independent of the glucose concentration. By replacing the term for decreasing excited Mig1-GFP concentration with a constant, we were able to reconstruct the dynamics of Mig1-GFP, as it would occur without bleaching and background noise. Our model effectively demonstrates how data, acquired with an optical microscope, can be processed and used for a systems biology analysis of signal transduction pathways.

---

Introduction

In systems biology, mathematical modelling of signal transduction pathways aims at the understanding of biological networks. Therefore high quality and quantitative time course data are necessary.¹Fluorescence microscopy and related imaging techniques have, together with the development of fluorescent probes, become a powerful tool to assay biological structures and processes in the physiological context of intact living cells.² However, the imaging process induces both reversible quenching and irreversible photobleaching of the fluorophores. Consequently, the target molecule is still present but not detectable. Tsien et al.³ addressed this problem by developing highly photostable fluorophores of mOrange and TagRFP. Yet, those derivates are not always useful nor available. In order to address the problem of photobleaching, we use mathematical modelling. In our case study we compare the model to experimental data on Mig1-GFP shuttling.

Acting as a transcription factor in the Snf1-pathway, Mig1 plays a crucial role in the energy metabolism of Saccharomyces cerevisiae during the regulation of glucose.⁴Mig1 is controlled by its kinase Snf1 and its phosphatase Glc7/Reg1. In the presence of glucose, Snf1 is in an inactive dephosphorylated state and Mig1 represses genes such as SUC2, which encode for proteins converting other carbon sources than glucose as the primary source of energy. In this state, Mig1 resides in the nucleus. If glucose is absent, Snf1 is activated through phosphorylation and in turn phosphorylates Mig1. Mig1 is then transported out of the nucleus into the cytosol so that alternative carbon sources can be used in the metabolism of the cell.⁵

Our model describes Mig1-GFP shuttling into and out of the nucleus when the cells are repeatedly deprived and exposed to glucose. This procedure gives us an insight into the shuttling of fluorescently tagged Mig1 proteins using time lapse microscopy.⁶ Our method of analysis allows for a stepwise extraction of the information on the background and Mig1-GFP bleaching rates, the background-to-Mig1-GFP ratio, and the rates of Mig1-GFP phosphorylation and dephosphorylation. Hereby, it is possible to predict Mig-GFP shuttling as it would occur without bleaching. Our analysis demonstrates how data acquired using an optical microscope can be processed and used for mathematical modelling of signal transduction pathways.

Experimental

Details regarding the design of the microfluidic device, the positioning of the cells on the surface, and the procedure of the environmental switching are described in Eriksson et al.⁶

Microscope setup

The microscope used in the experiments was an inverted epi-fluorescence microscope, Leica DMI6000B, equipped with a motorized xy stage and a motorized microscope objective. The images were acquired using a 14 bit dynamic range EMCCD camera (C9100-12, Hamamatsu Photonics) together with a fluorescence light source, EL 6000 (Leica Microsystems), a GFP filter cube (472/30 nm exciter, 520/35 nm emitter and 495LP, Semrock IDEX Corporation) and an mCherry filter cube (560/40× exciter, 630/75m emitter and 585LP, ET-TexRed, Chroma). The optical tweezers were formed by expanding a laser beam (λ = 1070 nm, IPG Photonics) to slightly overfill the back aperture of the microscope objective (100×, NA1.3 oil, HCX PL FLUOTAR, Leica Microsystems). The same objective was also used to image the yeast cells. The trapping laser beam was introduced to the microscopevia a dichroic mirror (Omega Optical Inc.) inserted between the microscope objective and the filter cube cassette (for details regarding our optical tweezers setup see Sott et al.).⁷ The power in the laser focus was calculated to be 240 mW by measuring the transmission through the microscope objective using the dual-objective technique as described by Misawa and colleagues.⁸ The flow rates in the microchannels were controlled by syringe pumps (CMA 400, CMA Microdialysis AB). The microscope, the camera, and the microfluidic pumps were all controlled from the computer through the software OpenLab (Improvision Inc.) with custom written programs in the extension OpenLab Automator.

Microfluidic device

In order to allow for precise and reversible changes of glucose concentration around single yeast cells, a microfluidic device was constructed, on which three inlet channels were merged into one single channel containing the measurement region wherein the cells were positioned (Fig. 1). The lower inlet channel was used to introduce cells suspended in growth medium into the system. The medium flowing in the middle channel was the same growth medium as the cells were suspended in, while the medium flowing in the top channel was pure growth medium without glucose (except for the GFP bleaching experiments, see below). The two lower inlets were connected to the same syringe pump, while the upper inlet was connected to a second pump. Thus, the flow rate could be controlled independently, enabling environmental changes of the cells positioned in the measurement region. Two different flow settings were used, referred to as flow configuration 1 (FC1) and flow configuration 2 (FC2), respectively, as shown in Fig. 1. In FC1, the flow rate in the larger inlet was set to 40 nl min⁻¹, while the flow rates in the two smaller inlets were set to 80 nl min⁻¹. This configuration was used when positioning the cells on the surface and whenever glucose should be present in the measurement region. In FC2, the flow rates were instead 480 nl min⁻¹ in the larger inlet and 40 nl min⁻¹ in each of the two smaller inlets. This configuration was used to expose the cells positioned in the measurement region to stress, i.e. to remove glucose.

Fig. 1 Schematic representation of the microfluidic flow system. The lowermost channel introduces the cells, the middle channel neutral medium, and the uppermost stress medium, in this case medium without glucose. FC1 and FC2 stands for flow configuration 1 and 2, respectively, see the microfluidic device paragraph for details.

Fabrication and preparation of the microfluidic device

The microfluidic device was fabricated using soft lithography. For specific details regarding the fabrication process, we refer to Sott et al.⁷ The microfluidic device was moulded in poly(dimethylsiloxane), PDMS, and sealed to a cover glass by exposing both the PDMS and the cover glass to oxygen plasma using a plasma cleaner (Harrick Scientific). Holes were punched in the PDMS structure allowing the channels to be connected to polytetrafluoroethylene (PTFE) tubings, which in turn were attached to 250 μl glass syringes (Hamilton Company).

To enable attachment of cells, Concanavalin A (ConA), dissolved in buffer (10 mM Tris-HCl and 100 mM NaCl at pH 8.0) at a concentration of 1 mg ml⁻¹, was allowed to adsorb to the cover glass surface for one hour before the experiments.

Yeast strain, plasmid and growth conditions

The yeast strain used in all experiments was YSH2346 (BY4741 MATalpha NRD1-mCherry-hphNT1), transformed with the plasmid BM3315.⁹ The strain carries its native copy of the MIG1 gene and its only genomic alteration is the insertion of a mCherry-hphNT1 fragment, constructed using plasmid pBS35 (gift from Prof. Roger Y. Tsien) as PCR template, behind the NRD1 gene. The NRD1-mCherry construct allows detection of the nucleus in experiments using fluorescence microscopy. BM3315 is a centromeric, URA3 plasmid for expression of Mig1-GFP, driven by the endogenous MIG1 promoter.

Cells were grown in synthetic drop-out medium (Yeast Nitrogen Base, YNB, 6.7 g l⁻¹, Complete Supplement Mixture (CSM-Uracil) 0.77 g l⁻¹ pH 6), supplemented with either glucose 4% m/v plus ethanol 3% v/v or with ethanol 3% v/v as sole carbon source.⁹ Yeast cultures were grown to OD600 = 0.6 – 1.0, corresponding to mid log phase, at 30 °C in an incubation shaker (220 rpm), collected and concentrated by centrifugation (30 s, 6000 rpm).

Positioning cells within the measurement region using optical tweezers

To position the cells inside the measurement region of the microfluidic device, the microscope stage and the objective were controlled by an OpenLab automation.⁶ The coordinates of the first positioned cell, the total number of cells and the spacing between the cells were all determined by the user. The automation then positioned the trapped cells in an array one by one, by bringing them down towards the bottom surface at the desired positions in order to get attached to the coated surface. The program also allowed the user to visually approve the trapped cell before it was positioned in the measurement region. Here, only morphologically deviating cells and cells in clusters were discarded in the experiments. For each experiment, approximately 25 cells were imaged. However, some cells had to be excluded from further analysis, since they showed lack of GFP, looked unhealthy or dead, or were lost during the course of the experiment. This resulted in approximately 20 successfully analysed cells for each experiment.

Image analysis

For each time point, an image stack with seven optical sections was acquired. Each optical section was imaged using three different filter settings in order to acquire the brightfield, Mig1-GFP (green) and mCherry (red) signal. In order to keep the fluorescent labeling to a minimum, we used brightfield images to find the cell contours, while the size and position of the nuclei were determined using the fusion protein Nrd1-mCherry, which is always localized in the nucleus independent of the level of stress.

The image analysis was performed using our own software, CellStress,¹⁰ written in MATLAB (MathWorks, Inc.). The contours of the nuclei were found using the mCherry images, while the contours of the cells were identified from the brightfield images using the plug-in tool CellStat.¹¹ The fluorescence intensity of the Mig1-GFP inside the nucleus was finally measured for each individual cell (Fig. 2).

Fig. 2 S. cerevisiae cells expressing Mig1-GFP and Nrd1-mCherry in 4% glucose media. The image segmentation is performed on (a) the bright field image just below the focal plane and (b) the maximum intensity projection of the mCherry fluorescence channel. In (c) a maximum intensity projection of the GFP channel is shown. (d) and (e) show the segmentation of the bright field and the mCherry images, respectively. In (f) the contours of the cell objects and nuclear objects from the segmentations are shown as an overlay in the GFP image.

Background bleaching experiment

Every cell has autofluorescence which arises from naturally occurring molecules, such as flavins, NADH and other fluorescing biomolecules.¹⁰ The exact mechanism and nature of the background molecules are not known in this case, but bleaching is a widely familiar problem resulting in the destruction of the fluorophore and a decrease in emission intensity over time.¹² A background bleaching experiment yields information regarding the bleaching rate of naturally existing fluorescing molecules in the cell. Thus, the experiment was done using the strain BY4741 without the plasmid expressing Mig1-GFP. All other parameters, such as glucose concentration and pulse duration (intervals of 10 minutes only) are as described in the environmental change experiment (see below). Axial stacks (seven images with a spacing of 0.8 μm) of brightfield and fluorescence images (GFP and mCherry respectively) were acquired at intervals of 30 seconds.

GFP bleaching experiment

In order to distinguish between changes in signal intensity due to bleaching of GFP and those due to shuttling kinetics, experiments were performed where cells either remained in a glucose-rich medium or in a glucose-free medium during the whole course of the experiment. The aim of this experiment was to determine the background-to-Mig1-GFP ratio and to analyze the rate by which bleaching of the GFP molecules occurs and how this bleaching rate might differ from that of the naturally occurring fluorescing molecules. Axial stacks (seven images with a spacing of 0.8 μm) of brightfield and fluorescence images (GFP and mCherry respectively) were acquired at intervals of 30 seconds.

Environmental change experiment

Prior to the experiment, cells positioned in the flow chamber were exposed to growth medium containing 3% ethanol and 4% glucose to ensure that they are far away from starvation. Hence, we assume that the maximum number of Mig1-GFP molecules in the nucleus has been reached prior to the initiation of the experiment.

In the course of the experiment, the microfluidic flow settings were shifted such that the cells were exposed to medium containing 3% ethanol as sole carbon source, to only stress the cells by glucose starvation but not an overall starvation, causing Mig1-GFP to shuttle from the nucleus into the cytosol (Fig. 3). Shifts between the two media were then repeated at different time intervals (5, 10 or 20 minutes) in different experiments. In all cases, the full duration of an experiment was 40 minutes, hence four, two or one complete cycles of shifting could be monitored.

Fig. 3 Experiments with a changing environment. (a) Schematic of the change in glucose concentration and the change in GFP signal in the nucleusversus time, respectively. (b) The corresponding microscope images of a selected cell, showing the shuttling of Mig1-GFP into and out of the nucleus as a response to these changes. The leftmost image is a brightfield image and the others are fluorescence images.

Axial stacks (seven images with a spacing of 0.8 μm) of brightfield and fluorescence images (GFP and mCherry respectively) were acquired at intervals of 30 seconds.

In order to evaluate the correctness of the model, additional experiments (Fig. 9a–c) with image acquisition every 60 seconds were done.

Processing of raw data

Whereas some technologies, like Western Blotting, report the average response of a population during the experiment, single cell experiments can instead provide data on individual cells. To obtain the average dynamic behavior, it requires an averaging over all cells after the experiment.

From all three types of experiments described above, we use the intensity data measured in the nuclei. We first normalize the time series of every cell to its average value over time. The time courses now all share the same average value, which equals one. In a second step, we take the average over all normalized cells at each time point and calculate the standard deviation, thus combining approximately 60 cells out of three experiments. In a last step, we scale this averaged time course to a range between zero and one by dividing with its initial intensity. Hence, for all experiments, the initial time point has the intensity value one, see e.g.Fig. 5, 6c, and d.

Results

The intracellular response to the environmental changes results in a shuttling of Mig1-GFP between the nucleus and cytosol and can thus be monitored using fluorescence microscopy. For the mathematical model we used data acquired from time lapse fluorescence microscopy where yeast cells were exposed to repetitive environmental changes between glucose-rich and glucose-free media. The model takes into account the decrease in intensity over time due to bleaching of Mig1-GFP and autofluorescent molecules. It is based on ordinary differential equations and describes the experimental data glucose concentration, background intensities, Mig1-GFP intensities and the sum of background and GFP intensities in a dynamic environment.

Parameter estimation

Numerical simulations were carried out with Matlab (MathWorks, Inc.) and the Systems Biology Toolbox2,¹³ using the particle-swarm¹⁴ algorithm for parameter estimation. A list of all parameter values is given in Table 1.

Table 1 Overview of the parameter values used in the model ordered by the different models in the columns. The parameter values for the background bleaching experiment were taken in order to estimate the parameters for the GFP bleaching experiment, and those values are finally used for the environmental change experiments. The handing down of parameter values is indicated by the quotation marks. The non-existence of a parameter in the model is denoted by a dash. A, B ≠ 0 indicate a constant level of Mig1 (de)phosphorylation. The italicised fields highlight parameter values taken from unpublished data.¹⁷ The units for A, B, and the initial conditions, are normalized concentrations (molecules per cell), the unit for λ is (minute)⁻¹ and units for α and β are (concentration·minute)⁻¹

	BG	GFP eth	GFP glc	5 min	10 min	20 min
λ1	0.92	“	“	“	“	“
λ2	0.0002	“	“	“	“	“
BG1(0)	0.12	“	“	“	“	“
BG2(0)	0.88	“	“	“	“	“
λ3	—	0.022	0.022	“	“	“
Mig1GFPtotal(0)	—	0.30	0.54	0.55	0.55	0.48
BGprop	—	0.63	0.47	0.57	0.56	0.49
Mig1GFP(0)	—	—	—	0.41	0.49	0.46
α	—	—	—	0.35	0.35	0.35
β	—	—	—	0.50	0.50	0.50
A	—	—	—	0.03	0.03	0.03
B	—	—	—	0.06	0.06	0.06
Mig1total	—	—	—	19 000	19 000	19 000

---

Background bleaching model

In this experiment cells without the capability of expressing GFP were used. We describe the bleaching of fluorescing molecules by a decreasing exponential function, implying that the bleaching impact is proportional to the fluorescing molecules available (Fig. 4a). The experimental data of the background show a rapid initial decline within the first three minutes followed by an almost constant level, as shown in Fig. 5. Hence, we assume that the bleaching process of the background molecules is a combination of mainly two different processes: a fast and sensitive process and a slow and insensitive process.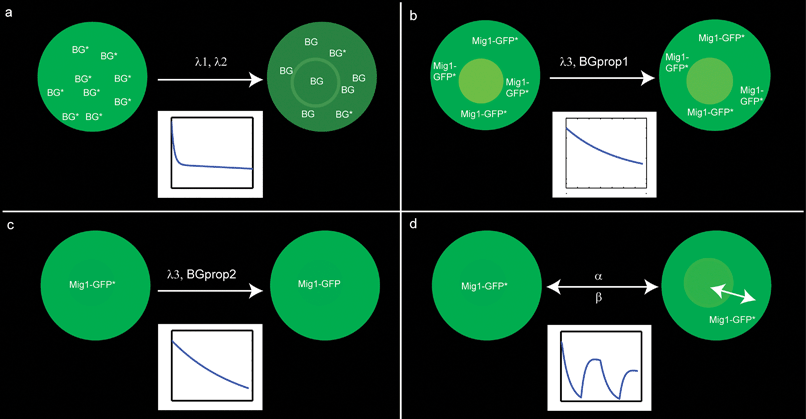

Fig. 4 Schematics illustrating the different contributions to the fluorescent signal of the nucleus. (a) Background bleaching with λ1 denoting the bleaching rate of a fast and sensitive process and λ2 of a slow and insensitive process. (b) GFP bleaching for cells residing in glucose-free media with λ3 denoting the bleaching rate and BGprop1 denoting the proportion of background to the overall intensity. (c) GFP bleaching for cells residing in glucose-rich media, λ3 and BGprop1 analogously to (b). (d) Nuclear intensity of Mig1-GFP for cells in a dynamic environment, where the surrounding media changes between glucose-rich and glucose-free media, α and β denoting the shuttling rates for Mig1-GFP. For further explanation see the section Results.

Fig. 5 Comparison of simulation and experimental data (intensities in the nucleus) of the autofluorescence in cells without GFP. Images were taken every 30 seconds. For parameter values we refer to Table 1. The background bleaching model is described in the Results section.

The background noise (BG), described as the sum of two exponentially decaying functions, can be expressed as

BG = BG1(0)·e^−λ1·t + BG2(0)·e^−λ2·t,

where

d/dt(BG1) = −λ1·BG1

d/dt(BG2) = −λ2·BG2

and λ1 and λ2 are determined through experimental measurements. The simulation is shown in Fig. 5. The values for the estimated parameters are given in Table 1.

The only parameter difference among the background bleaching experiment and the environmental change experiment was the absence of Mig1-GFP. All other parameters were kept constant. The purpose of the background bleaching experiments is to determine the bleaching effect of the autofluorescence, which for normal experiments is hidden in the sum of intensities of GFP and autofluorescence. The change in medium is, however, not considered in the background model. This simplification is reasonable because it is not expected that background molecules are affected by changes in the medium.

GFP bleaching model

To analyze GFP bleaching we designed two different experiments: one where cells were continuously exposed to a glucose-poor medium (0 g L⁻¹) resulting in Mig1-GFP residing in the cytosol (Fig. 4b), and another one where cells were continuously exposed to a glucose-rich medium (40 g L⁻¹) resulting in Mig1-GFP residing inside of the nucleus (Fig. 4c). The intensity data measured are equal to the sum of the background and Mig1-GFP intensity. The contribution of the background to the overall intensity in the nucleus will be higher when Mig1-GFP is located in the cytosol, and lower when it is located in the nucleus.

Since no confocal laser scanning imaging technique is applied, the intensity of the excitation light is assumed to be equal throughout the entire volume of the cell, resulting in a similar bleaching rate, λ3, of Mig1-GFP, regardless of Mig1-GFP localization within the cell. According to Song et al.,¹⁵ we can assume an exponential decay of the Mig1-GFP intensity, when exposed to excitation light as illustrated in Fig. 4b and c. Any qualitative differences between the two experiments is thus explained by the different contribution of the background to the measured intensity.

We further define the decrease of the total excited Mig1-GFP concentration within a cell under bleaching effects as

d/dt(Mig1GFPtotal) = −λ3·Mig1GFPtotal

such that

BGGFP = Mig1GFPtotal(0)·e^−λ3·t + BGprop·BG

where BGGFP is the intensity composed of background (BG) and Mig1-GFP fluorescent intensities, both decreasing due to bleaching. We define BGprop as the local parameter accounting for the background-to-Mig1-GFP ratio (Fig. 6a and b). The comparison between the simulation and the experimental data can be seen in Fig. 6c and d. We can therefore extract the bleaching rate for Mig1-GFP by using the information from the background bleaching data. Applying this information, we can now start to analyze the Mig1-GFP shuttling data.

Fig. 6 (a), (b) The sum of background (dashed red line) and Mig1-GFP (dotted green line) intensities representing the overall measured intensity in the nucleus (solid blue line) in glucose-poor medium (left column) and glucose-rich medium (right column) as described in the model for the GFP bleaching. Note that under glucose-poor conditions the background intensity has a higher portion of the overall measured intensity in the nucleus, since Mig1-GFP is located to the cytosol, compared to glucose-rich conditions when Mig1-GFP is located to the nucleus. (c), (d) Comparison of simulation and experimental data of Mig1-GFP and background intensities. Images were taken every 30 seconds. For parameter values we refer to Table 1. The GFP bleaching model is described in the Results section.

Environmental change model

This model analyzes changes in Mig1-GFP localization under glucose starvation stress. Fitting the model to the experimental data, the phosphatase and kinase rate constants for Mig1-GFP were determined (Fig. 4d). As shown in the previous section, the decrease in excited Mig1-GFP concentration due to bleaching can be described as the exponentially decreasing function:

Mig1GFPtotal(t) = Mig1GFPtotal(0)·e^−λ3·t

where λ3 is the bleaching rate of Mig1-GFP. We then finally insert this degradation term into the model for Mig1-GFP shuttling:

d/dt(Mig1GFP) = α·(A + θ1)·Mig1PGFP − β·(B + θ2)·Mig1GFP

where

Mig1PGFP = Mig1GFPtotal − Mig1GFP

and α and β are parameters representing the rate of Mig1-GFP dephosphorylation and phosphorylation, respectively. The term within the brackets is a switch function representing the presence of active phosphatase and kinase of Mig1, respectively. We therefore assume that the activation of Mig1's kinase and phophatase is faster than the activation and deactivation of Mig1 itself. The parameters A and B indicate a basal phosphorylation and dephosphorylation of Mig1 regardless of the glucose concentration, respectively. The Heaviside¹⁶ step functions θ1 and θ2 represent the switches among glucose-rich and glucose-free media:

The intensity of the environmental change experiments can be described as the composition of background and Mig1-GFP shuttling:

BGGFPshuttling = Mig1GFP + BGprop·BG

as shown in Fig. 7a to c for the comparison of experimental data and simulation. Fig. 7d shows the composition of background and Mig1-GFP resulting in the overall intensity.

Fig. 7 (a) to (c) Comparison of simulation (BGGFP shuttling) and experimental data of the environmental change experiment, for pulse durations of (a) 5 minutes, (b) 10 minutes, and (c) 20 minutes. Images were taken every 30 seconds. (d) Simulation of the intensity in the nucleus of a 10 minutes environmental change experiment. The intensity (solid blue line) is defined as the sum of background (dashed red line) and Mig1-GFP shuttling (dotted green line) both undergoing photobleaching during imaging. For further details see the Results section.

Since BGprop is a local parameter, we need to start a new estimation for the environmental change experiments. The result of the parameter estimation for A and B indicates that there is in addition to the glucose depending regulation a basal Mig1 (de)phosphorylation, since A, B ≠ 0. This result is supported by findings in Western blot data¹⁷ which indicate that Snf1 is never fully dephosphorylated. The values can be found in Table 1.

Due to the bleaching process, the total concentration of excited Mig1-GFP is, unlike the Mig1 concentration, not constant but decreases over time. In order to predict the rate of change for Mig1 (regardless of GFP-tagging), we use the above equation of Mig1-GFP for Mig1 by replacing Mig1GFPtotal with a constant total concentration of Mig1:

d/dt(Mig1) = α·(A + θ1)·Mig1P − β·(B + θ2)·Mig1

where Mig1P = Mig1total − Mig1 and Mig1total representing a constant.

So far our model simulated the normalized data. We now obtain a more natural view on Mig1 and Mig1-GFP shuttling dynamics, by scaling Mig1GFPtotal to 19 000 which is an approximate number of Mig1 molecules per cell.¹⁷ The simulation can be seen in Fig. 8a for Mig1 and in Fig. 8b for Mig1-GFP.

Fig. 8 Simulation of Mig1 (solid blue line) and Mig1P (dotted green line). The total concentration (dashed red line) is constant and set to 19 000 molecules per cell.¹⁶ (b) Simulation of Mig1-GFP (solid blue line) and Mig1P-GFP (dotted green line). The total concentration (dashed red line) is decreasing due to photobleaching.

Model validation

The model was validated using new experimental data acquired at 60 seconds intervals. Hence, we would expect a two-fold slower bleaching rate but the same values for parameters α, β, A, and B. Therefore we divide the bleaching rates λ1, λ2 and λ3 by two. New estimates for the local parameter BGprop and the initial conditions are required. As presented in Fig. 9, the simulation is in good agreement with the experimental data. This supports the assumption that the decrease in the intensity data is due to bleaching effect during image acquisition.

Fig. 9 Comparison of simulation and experimental data of the environmental change experiment for pulse durations of (a) 5 minutes, (b) 10 minutes, and (c) 20 minutes. Images were taken every 60 seconds. Dividing the bleaching rates for background and GFP by two and resuming parameters α, β, A, and B as estimated before leads to the successful reproduction of the data.

Discussion

All fluorophores undergo photobleaching during excitation. The lack of photostability is therefore a limiting factor during imaging, especially for time series and single cell experiments. We have developed a mathematical model that successfully describes the decrease of total excited Mig1-GFP due to photobleaching and the shuttling of Mig1-GFP. Our mathematical model takes bleaching and background noise into account and can thus extract the information on Mig1-GFP shuttling in order to predict the dynamic behavior of Mig1 during changing environmental conditions. The estimated parameter values suggest that the basal phosphorylation and dephosphorylation of Mig1 occur both independently of glucose levels, thereby supporting the findings of Western Blot data.¹⁷ Furthermore, the estimated parameter values suggest that the kinase has a greater influence on the activation status of Mig1 than the phosphatase.

The image acquisition every 60 seconds supports the assumption that the decrease in total excited Mig1-GFP is sufficiently explained by the occurrence of bleaching: Exclusively by dividing the estimated values for bleaching rates by two (since only half the number of images were taken) and assigning the local parameters for background-to-Mig1-GFP ratio, we obtain a satisfying reproduction of the data.

Our model suggests that mathematical modelling can be a complement to the extensive development of highly photostable variants of mOrange and TagRFP. It thereby demonstrates how raw data, that were generated in an optical microscope, can be processed and used for mathematical modelling of signal transduction pathways.

Acknowledgements

We thank Yvonne Schmitz for fruitful discussions and Sherry Freiesleben for careful reading of the manuscript. We thank Prof. Roger Y. Tsien, University of California, San Diego and Mark Johnston, University of Washington for plasmids.

S.F. is supported by the DFG Graduiertenkolleg 1387 – dIEM oSiRiS (Die Integrative Entwicklung von MOdellierungs- und SImulationsmethoden für Regenerative Systeme) and by EU FP6 project “Systems biology of the AMP-activated protein kinase” (AMPKIN) (Grant LSH-CT-2005-518181). O.W. and T.M. acknowledge support by the German Federal Ministry for Education and Research (BMBF) as part of the European Transnational Network—Systems Biology of Microorganisms (SysMo)—within the BaCell-SysMo and COSMIC consortia.

M.G. is supported by the Swedish Research Council and the European Commission 6th framework programme through the project AMPKIN and 7th framework programme through the project UNICELLSYS.

Notes and references

1. R. Phillips and R. Milo, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 21465–21471.
2. R. Pepperkok and J. Ellenberg, Nat. Rev. Mol. Cell Biol., 2006, 7, 690–696.
3. N. C. Shaner, M. Z. Lin, M. R. McKeown, P. A. Steinbach, K. L. Hazelwood, M. W. Davidson and R. Y. Tsien, Nat. Methods, 2008, 5, 545–551.
4. M. Carlson, B. C. Osmond, L. Neigeborn and D. Botstein, Genetics, 1984, 107, 19–32.
5. G. M. Santangelo, Microbiol. Mol. Biol. Rev., 2006, 70, 253–282.
6. E. Eriksson, K. Sott, F. Lundqvist, M. Sveningsson, J. Scrimgeour, D. Hanstorp, M. Goksör and A. Granéli, Lab Chip, 2010, 10, 617–625.
7. K. Sott, E. Eriksson and M. Goksör, in Lab-on-a-Chip Technology: Biomolecular Separation and Analysis, ed. K. E. Herold and A. Rasooly, Caister Academic Press, 2009, vol. 2, ch. 9, pp. 151–166.
8. H. Misawa, M. Koshioka, K. Sasaki, N. Kitamura and H. Masuhara, J. Appl. Phys., 1991, 70, 3829–3836.
9. M. J. De Vit, J. A. Waddle and M. Johnston, Molecular Biology of the Cell, 1997, 8, 1603–1618.
10. M. Smedh, C. Beck, K. Sott and M. Goksör, Proceedings SPIE, 2010, 7762 , to be published.
11. M. Kvarnström, K. Logg, A. Diez, K. Bodvard and M. Käll, Opt. Express, 2008, 16, 12943–12957.
12. F. W. D. Rost, Fluorescence Microscopy, Cambridge University Press, 1995.
13. H. Schmidt and M. Jirstrand, Bioinformatics, 2006, 22, 514–515.
14. A. I. F. Vaz and L. N. Vicente, J. Global Optim., 2007, 39, 197–219.
15. L. Song, E. Hennink, I. Young and H. Tanke, Biophys. J., 1995, 68, 2588–2600.
16. R. Bracewell, The Fourier Transform and Its Applications, McGraw Hill, New York, 1999.
17. R. Garcia Salcedo, private communication.

---

Footnote

† Equal contribution of senior authors.

---