A “tool box” for rational design of degradable controlled release formulations

Abstract

Controlled release technology could provide a universal solution to the problems of patient compliance and sub-optimal dosing that often plague modern pharmaceuticals. Yet, harnessing this potential requires the ability to design drug delivery formulations which satisfy specific dosing schedules. This review intends to portray how material properties, processing methods and mathematical models can serve as effective tools for rationally tuning the duration and rate of drug release from biodegradable polymer matrices.

---

Sam N. Rothstein

Sam Rothstein graduated with honors from Bucknell University in 2005, earning a BS in Chemical Engineering. He is presently a pre-doctoral fellow in the laboratory of Dr Steven R. Little at the University of Pittsburgh. His thesis research focuses on methods for rationally designing controlled release medications and the associated advances are being commercialized as part of a new pharmaceuticals company.

Steven R. Little

Dr Steven Little received his PhD in Chemical Engineering at the Massachusetts Institute of Technology in 2005. Subsequently, he served as a post-doctoral associate in the laboratories of Robert Langer, ScD. He currently holds the position of Assistant Professor and Bicentennial Alumni Faculty Fellow at the University of Pittsburgh in the Departments of Chemical Engineering, Bioengineering, Immunology, and The McGowan Institute for Regenerative Medicine. His laboratory focuses on advanced drug-delivery strategies for immunotherapeutics and tissue engineering.

---

1. Introduction

Biodegradable controlled release technology holds potential to resolve patient compliance issues and adverse effects that account for 10% to 14% of hospitalizations and $136 billion in annual medical expenses.¹ The reason for such potential is that controlled release formulations can (in concept) autonomously regulate the local and systemic administration rate of practically any drug while, at the same time, resorbing harmlessly inside the body. However, the reason that the field has not yet realized this enormous potential is that (in practice) generating a specific controlled release formulation (i.e. one customized to the dosing schedule demanded by any given medication) is extremely time consuming and costly. As such, only 11 biodegradable, controlled release formulations have reached the market.² In each case, the associated drugs have clear compliance risks (elevating the need for extended dosing) or wide therapeutic windows (relaxing the requirement for stringent control over release). Yet, these medications represent just a small fraction of drugs that could be improved with properly designed controlled release formulations. By one estimate, at least 90% of the top 100 best selling prescription medications could further advance patient quality of life if they offered reduced dosing frequency.^3,4 From this viewpoint, the field can be said to have broad therapeutic applicability, but comparatively limited implementation.

Over the past two decades, a number of studies have aimed to increase the efficiency of designing degradable drug delivery formulations. The earliest studies sought to identify key physical properties of the polymer matrices that determine release behavior.^5,6 Twenty years later, researchers are still experimenting with a variety of new formulation compositions, polymer chemistries and processing conditions in an attempt to tune this release behavior.^7–10 Over time, a number of system properties and processing conditions have emerged as potential tools for tuning the kinetics of delivery systems.^4,11 However, a standardized method of tuning remains elusive due to the complexity that arises when factors, such as polymer chemistry, alter several properties that determine release simultaneously, such as matrix crystallinity, pH, degradation rate and hydrophobicity.⁸

To better evaluate the complex mechanics of release, researchers have also attempted to implement mathematical models. For a number of years these models have been applied to experimentally acquired release data as a means of assessing their validity.^12,13 The earliest of these fitted descriptions often deviated significantly from data or focused exclusively on initial or final release.^14–16 More recently, models are beginning to accurately describe full complex release profiles, in many cases predicting aspects of the delivery kinetics without the need for optimization or “fitting”.^17–20 However, subsequent implementation remains a rare occurrence because many of these models still require parameter values that must be calculated anew from experimentally acquired release data for each drug or polymer system considered.

Overall, the combined efforts of mathematical and experimental studies have produced a wealth of data on the various behaviors of biodegradable polymer matrices. Some recent reviews have sought to summarize advances in mathematical modeling, cataloging the nuances of their approaches (empirical, Monte Carlo, mechanistic, etc.).^13,17 Still others have focused on documenting experimental techniques, such as nano/micro technologies for macromolecule delivery or the loading and release of small molecules.^4,11 Ultimately, mathematical models and heuristic, empirical methods are simply two different approaches to achieve the same ultimate goal: obtaining a desired release behavior for a given drug with minimal time and cost. Mathematical models quantify release mechanics and relate them to tunable system properties, while empirical studies uncover tunable system properties and relate them to quantifiable release mechanics. Keeping these perspectives in mind, the wealth of data on biodegradable matrix controlled release can be distilled down into a number of “design tools” (or system properties and processing conditions that can be used to predicatively tune release). As controlled release formulations often present complex release profiles, it is likely that more than one design tool will be required to achieve total control over delivery kinetics.

In this review, we will present an empirical and model-based “tool-box” containing a broad range of conditions that can be used to adjust the release behavior of biodegradable polymer matrices in various ways. We will focus primarily on the most widely studied biodegradable polymeric materials (i.e. polyesters, polyanhydrides, poly(ortho esters), etc.) given their prevalence in the literature, long history of use, and similarity of fundamental release behavior (encompassing both the underlying mechanisms and resulting kinetics). Although the techniques that can be used to control release in these systems are generally applicable to any size, shape, and orientation of a degradable matrix, we will most often refer to one of the most commonly reported configurations of these matrices, a spherical particulate system (Fig. 1). Regardless, these degradable systems are presently understood to control drug release via fundamental phenomena of diffusion (passive movement of drug), degradation (breakdown of the polymer matrix), erosion (mass loss from the polymer matrix) and dissolution (the solubilization of drug).⁸ By analysing the attempts to control these fundamental system phenomena and documenting their effects on release behavior, we can, correspondingly, identify a set of tools for rationally designing custom release behavior.

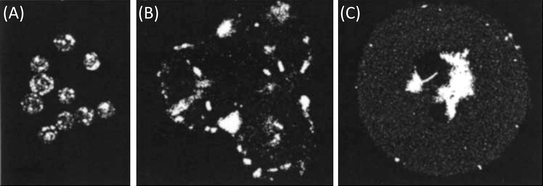
Fig. 1 Microscopy images of particle matrix cross-sections and exteriors (inset). (A) In homogenous systems (like single emulsion microparticles) the drug resides in-phase with the polymer matrix (adapted with permission from ref. 12). (B) In contiguous systems (like double or water-in-oil-in-water emulsion microparticles), the drug resides in pockets that are separated from the polymer matrix (unpublished data).

2. Experimental studies

Studies have empirically varied independent system properties (such as matrix size, degradation rate or polymer molecular weight) or processing conditions (such as emulsion type, solution osmolarity, or solvent choice) and documented their effects with in vitro assays. Each of these experimental variations can be evaluated for its potential as a design tool that a scientist or engineer can use to tune release behavior.

As a general rule, drug delivery vehicles can be tuned to provide a specific rate and duration of release independently. However, biodegradable matrices have been commonly observed to produce up to three distinct phases: (1) an initial phase (a.k.a. “initial burst”) that is typically categorized by the rapid delivery of drug upon hydration, (2) a “lag phase” marked by a near-zero rate of release for some period of time and (3) a “final phase” where measurable release resumes, typically in a Fickian fashion. Therefore, it would be useful to classify tools by their suitability for tuning the magnitude and/or duration of each individual phase in order to gain complete control over release (Fig. 2).

Fig. 2 Tri-phasic release profile depicting: (A) initial burst, (B) lag phase and (C) final release. Note that any one of these phases may or may not be apparent depending upon the properties of the release system.

2.1. Initial burst

Numerous studies have addressed the “initial burst” and a summary of findings have been the focus of two reviews in the past decade.^21,22 Both of these reviews discuss hypothetical mechanisms of “burst” release and potential strategies for preventing or eliminating it. Maintaining the theme of this review, we will focus on the impact that individual “design tools” have on the magnitude and/or kinetics of the initial burst.

2.1.1. Tools for modifying the magnitude of the initial burst. The initial burst can easily encompass all of release or even be completely eliminated. However, no one method exists for precisely targeting values across this entire range. Instead, studies put forth a variety of techniques that change burst magnitude with varying degrees of sensitivity.
2.1.1.1. Dispersion of drug in the polymer matrix. Several studies have succeeded in creating dramatic reductions in burst magnitude by forcing hydrophilic proteins to disperse in the hydrophobic polymer matrix. For example, Fu et al. eliminated the initial release of a water-soluble protein (human glial-cell line derived neurotrophic factor) by using an ionic surfactant to dissolve the hydrophilic protein in-phase with the polymer.²³ In contrast, an equivalent double emulsion formulation (with polymer entrapping pockets of aqueous protein) produced more than 70% initial release.²³ A similar approach was adopted to eliminate the burst release of insulin using PEGylation, which aided the dissolution of the protein in dichloromethane.²⁴ Practically, partitioning experiments can be used to determine if other agents will dissolve/disperse in the same phase as the polymer (e.g. organic phase) with the aid of surfactants or other modifications.²⁵ Since this design tool simply involves the dispersion of drug and polymer in a matrix, it should readily apply to any number of systems.

Interestingly, less predictable results are observed when a cosolvent is used to stabilize hydrophilic drugs in the same phase as the hydrophobic polymer matrix.^26,27 Using this approach on insulin-loaded PLGA microparticles reduced burst magnitude from 65 to 20%.²⁷ However, when applied to another protein (granulocyte colony stimulating factor), this technique actually increased the magnitude of the initial burst.²⁶ Yet both of these studies produce single emulsion systems by dissolving a protein in the cosolvent, dimethylsulfoxide before it mixing with a polymer–dichloromethane solution. It is unknown as to the source of the disparity, but it may be possible that this process may cause protein molecules to aggregate into a separate phase, giving rise to a measurable burst magnitude.

2.1.1.2. Manipulation of osmotic pressure. Subtle changes in burst magnitude have also been achieved by changing the osmotic pressure during the processing of systems that are intentionally fabricated with an internal aqueous phase (e.g. double (water-in-oil-in-water) emulsion systems, see Fig. 1B). Accordingly, Jiang et al. tuned the initial burst of bovine serum albumin (BSA) to values between 30% and 80% of total release by adding salt or sucrose to the outermost aqueous phase during microparticle fabrication.²⁸ The same technique has been used in other macromolecule-loaded systems to reduce the magnitude of the initial burst.^29–32 Within each study, the reduction in burst magnitude was proportional the amount of NaCl added to the outermost aqueous phase (i.e. the strength of the osmotic pressure gradient driving water out of the microparticles). Because osmosis is a fundamental process, this design tool should extend to a wide range of contiguous systems, and is particularly important to account for in systems where the drug itself dramatically affects the osmotic pressure (such as plasmid DNA).^33,34
2.1.1.3. Manipulation of matrix size. A number of studies have also varied matrix size to tune the magnitude of burst release in double emulsion systems.^29,35–37 While this property is particularly easy to tune during fabrication, its effectiveness at controlling the magnitude of initial release varies from agent to agent. For example, initial release of the small molecule, lidocaine, from polymeric microparticles dropped 30% as particle size increased 10 fold.³⁵ This trend is echoed over a larger size span by polyanhydride particles loaded with butorphanol.³⁷ However, the release of insulin was more sensitive to changes in particle size, dropping 35% in magnitude from just a 3 fold change in particle size²⁹ (Fig. 3). Limitations arise as matrix size is reduced to below 5 µm because such small bodies are readily cleared in vivo by the reticuloendothelial system (RES, consisting of phagocytic cells like macrophages)³⁸ or above 500 µm in diameter as matrix hydration begins to effect the kinetics of the initial burst.^19,39 However, for median sizes, this method presents an effective approach to tuning the magnitude of initial burst release.

Fig. 3 Comparison of burst magnitudes (% total release) from double emulsion microparticles when varying size. Analysis was conducted on data from three different studies: small molecule lidocaine,²⁴insulin protein²⁵ and melittin peptide.²⁶ Initial burst magnitude of each system was affected to different extents by changes in matrix size.

2.1.1.4. Manipulation of drug loading. Discrete changes in initial burst magnitude have also been produced by altering the drug loading. Working with a variety of model proteins (lysozyme, carbonic anhydrase, and alcohol dehydrogenase), Sandor et al. noted that decreasing drug loading from 7 to 1 wt% reduced the initial burst from a high of roughly 80% to just 15–40% of total release.⁴⁰ Equally dramatic reductions in burst magnitude have been observed following changes in peptide loading.^29,36 Studies on small molecule release from polyester and polyanhydride implants have also reported similar trends.^41–45 Limitations to this technique do arise at low loadings (lower payload) or high loading (breakdown of matrix structure, e.g. percolation).⁴⁶ However, the simplicity and broad applicability of this tool still make very attractive for inducing measurable changes to burst magnitude.
2.1.1.5. Manipulation of initial porosity. In some cases, controlled release matrices are fabricated to be porous instead of solid, which can noticeably influence the magnitude of the initial burst. One of the most common ways to produce such a system is to increase the ratio of drug phase to polymer phase. In fact a number of studies have even correlated scanning electron microscopy images of microparticles porosity with dramatic changes burst magnitude.^32,36,47,48 Further, this relation holds true for small molecule, peptide and protein release data, provided that the pore size is large enough to allow for free-diffusion of the agent.⁴⁹ Another approach to altering initial porosity has been to change the concentration of stabilizer or surfactant used in processing. In such studies, altering the poy(vinyl) alcohol or poloxamer concentration inversely changed burst magnitude on the order of 10–20%.^47,50 However, several reports note that stabilizer concentration also impacted matrix size which may have also accounted for observed changes as described in Section 2.1.1.3.^36,51 Finally, post-fabrication pore-closing procedures, where matrices are subject to thermal or solvent-based annealing, have also successfully decreased the magnitude of the initial burst in porous matrices.^32,47 Hence, depending on the initial state of a polymer matrix (porous or solid) altering processing conditions to change its porosity can be an effective way of either increasing or decreasing the magnitude of the initial burst.

2.1.2. Tools for tuning kinetics of the initial burst phase. Methods for altering rate (kinetics) of the initial burst may also prove useful if it can be manipulated to benefit the delivery strategy. For example, rapid delivery of an antigen might be necessary for the successful function of a controlled release vaccine. Alternatively, slowing the initial burst rate may bring the initial delivery of a prescription in line with its optimal, constant (zero order) release profile.
2.1.2.1. Controlling drug dissolution rate. One way to influence burst release kinetics is to alter the encapsulated agent's dissolution rate. This has been accomplished by co-encapsulating an agent with a variety of excipients.^52,53 Experimenting with different cyclodextrin excipients, Wang et al. were able to tune the duration of initial release of β-lapachone (a hydrophobic chemotherapeutic) to values between 1 week and 1 day by complexing it with hydrophilic cyclodextrin of varying size.⁵² This approach to increasing burst rate should also apply to other hydrophobic small molecules that readily complex with cyclodextrin or other hydrophilic agents.²²

Interestingly, reports describing the use of excipients to decrease the rate of early release (rendering hydrophilic molecules more hydrophobic) are absent from the literature, possibly because evidence suggests that these types of systems exhibit little to no initial burst.²³ Further, a study intending to reduce dissolution rate by switching from amorphous to crystalline drug reported a similar change in burst magnitude, but not kinetics.⁵⁴ However, studies comparing agents with different intrinsic dissolution rates have noted a correlation to burst kinetics in polyanhydride implants.^55,56 This suggests that methods for reducing an agent's dissolution rate could slow its burst release. However, until such methods are realized, excipients remain a reliable tool for increasing burst release rate of hydrophobic agents.

2.1.2.2. Effect of radial drug distribution. A number of different fabrication methods have been used to control the radial distribution of drug within biodegradable polymer matrices, thereby altering their initial burst kinetics. Such heterogeneous distributions have been achieved with double-walled microparticles which are formed by using multiple immiscible solvents to separate polymers of differing solubility into core and shell phases. These systems consistently show reduced protein burst kinetics when the drug is trapped in the matrix core rather than when it is in the shell or loaded throughout.^57,58 Further, the extent of this reduction is proportional to the thickness of the shell separating the drug-loaded core from the outside environment.⁵⁷ Coated implants (tablets, discs, or spheres) made from polyesters or polyanhydrides have produced similar results.^59–62 Mixed results were observed in some small molecule loaded matrices, which could be explained by the preferential partitioning of such agents into the coating shell instead of the matrix core.^63–66 Fortunately, studies have reported control over the radial distribution of small molecules through an electrospray fabrication process.^67–69Piroxicam and rhodamine loaded microparticles produced by this method showed significantly slower initial release kinetics when drug was concentrated at the matrix core than when it was distributed closer the particle surface⁶⁹ (Fig. 4). This technique was also recently applied to macromolecule loaded (rhodamine–BSA or FITC–dextran), double emulsion microparticles, but only the magnitude of the initial burst was altered,⁷⁰ as discussed in Section 2.1.1.3. Between electrospray fabricated microparticles and systems such as double-walled particles or implants, radial drug distribution can successfully modified for a diverse array of active agents.

Fig. 4 Drug distribution formed in microparticles manufactured using a novel acoustic method. Particle sizes are as follows: (A) 10 µm, (B) 50 µm, and (C) 100 µm in diameter (adapted with permission from ref. 59).

2.1.3. Initial release summary. A number of different techniques make it possible to tune the magnitude and duration of the initial release phase. By altering the processing methods, matrix size, osmotic pressure, or drug loading, the magnitude of the initial release can be tuned to nearly any value between 0 and 100%. By altering the agent dissolution rate or radial drug distribution, it is possible to tune kinetics of initial release as well. Despite the encompassing applicability and diversity of these tools for tuning burst release, future research into this phase of release may still be warranted for yet un-investigated agents.

2.2. Lag phase

Following the initial burst, a lag (or pause in release) may occur before the remaining encapsulated drug is released. By definition, this phase lacks measurable kinetics, but may possess significant duration. However, particularly slow initial release or, conversely, early onset of final release may serve to disguise this phase. Hence, the duration of the lag phase should be defined as time elapsed between day 0 (while the competing burst phase is occurring) and the onset of final release (a time denoting the resumption of drug delivery).

2.2.1. Tools for modifying the duration of the lag phase.
2.2.1.1. Setting of initial polymer molecular weight. Many studies have shown that the duration of the lag phase can be altered by varying the polymer's initial molecular weight (M_w). For example, Friess and Schlapp induced a 10 day lag phase in gentamicin loaded microparticles by switching from a 13.5 kDa PLGA to a higher molecular weight of 36.2 kDa.⁷¹ Comparable results have been reported for small molecule loaded polyester implants.⁷² This relation also holds true in peptide loaded microparticles, as well.^73–75Macromolecule release data from different studies also confirm a clear trend between lag phase duration and the molecular weight of the PLGA matrix (Fig. 5).^{23,40,75–80} This fundamental trend is only preserved within a given class of agents, suggesting that effect of polymer molecular weight is dependent, at least in part, upon some property (or properties) of the encapsulated agent.^71,73,79

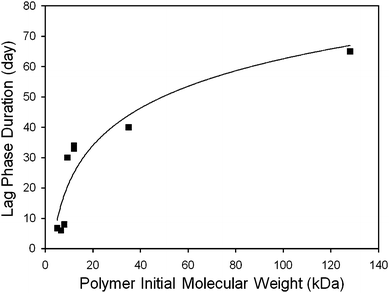Fig. 5 Relationship between polymer molecular weight and lag duration in macromolecule releasing systems. The lag phase duration (squares) was determined by analyzing release data from a number of different studies.^{25,27,42,77–81} The results fit a power expression (line, r² = 0.8565).

2.2.1.2. Controlling polymer degradation rate. Another well-documented tool that can be used to alter the duration of the lag phase is the polymer's degradation rate. For copolymers, this is simply controlled by altering the ratio of the two monomers, with degradation rate typically being inversely proportional to hydrophobicity of the resulting polymer chain. For example, in work by Cui et al. where 9.5 kDa of 50 : 50 PLGA microparticles produced a melittin release profile with an 8 day lag phase, while 10 kDa of 75 : 25 PLGA microparticles presented a 14 day lag phase.³⁶ Similarly, Wang et al. tested ethacrynic acid loaded films of 110 kDa 50 : 50 PLGA and PLA which produced lags of 1 or 6 days, respectively.⁸¹ This trend has also been echoed by polyanhydride copolymer microparticles loaded with BSA,⁸²PLGA and PLA fibers loaded with BSA⁸⁰ as well as other polyester implants loaded with small molecule drugs.^83,84 The consistent performance of the polymer degradation rate and initial molecular weight as tools for controlling lag phase duration suggests that the two may act in concert via a common property such as polymer lifespan.
2.2.1.3. Use of catalytic excipients. When a specific polymer chemistry or molecular weight is desired (and therefore not accessible as a tool to tune release), the degradation rate and, in turn, duration of the lag phase can also be modified by using an excipient. This is evident in one study where proteinase K increased the degradation rate of PLA fibers eliminating all lag from the release of paclitaxel and doxorubicin.⁸⁵ This enzyme will also catalyze the degradation of L-lactic linkages in PLGA copolymers and consequently should shorten the duration of lag phase in said systems as well.⁸⁶ An anhydride (acid) has also been used as a catalyst to hasten the degradation of poly(ortho ester) matrices, completely eliminating a 2 day lag phase.⁸⁷ This mechanism should apply equally well to polyester or polyanhydride matrices whose hydrolysis is also effected by the presence of acid.³⁹ Future work is needed to determine if acidic excipients will cause measurable damage to encapsulated peptides or proteins.
2.2.1.4. Post fabrication irradiation. The duration of the lag phase can also be reduced by γ-irradiation.^88,89 The most dramatic changes produced by this method were reported for the release of progesterone from PLA microspheres, where 100 kGY of radiation reduced the lag duration from nearly 200 days (prior to exposure) to just 50 days.⁸⁹ Working with small molecule loaded PLGA microspheres, Faisant et al. also reported a similar trend when 5-fluorouracil loaded PLGA microparticles were irradiated (4–33 kGy).⁸⁸ These changes in lag duration can likely be attributed to the cleavage of polymer chains in the encapsulating matrix (e.g.reduction in initial polymer molecular weight), a phenomenon whose effects are described earlier in this section. Interestingly, both studies also noted an increase in burst rate, phenomena not observed with other degradation-based methods of altering the duration of the lag phase. While this method for altering lag phase should apply to a wide range of polyester matrices, its utility may be limited because: (1) it simultaneously alters the kinetics of the initial burst, (2) it appears to be only capable of shortening the lag phase (not lengthening it) and (3) it may degrade sensitive agents such as peptides and proteins.

2.2.2. Lag phase summary. Controlling the duration of the lag phase can be simply a matter of tuning the encapsulating polymer's lifespan. This can be accomplished by adjusting polymer initial molecular weight or degradation rate, as well as by using a catalytic excipient or γ-irradiation. By carefully tuning the lag phase it is possible to either merge initial and final release into one seamless phase or separate them by considerable delay. As lag phases were rarely observed in system releasing small molecules (<300 Da), further study is warranted to determine how best to induce and tune this phase in such systems.

2.3. Final release phase

Control over the final release phase can help to extend drug delivery or even determine how pronounced the effects of the initial burst and lag phase will be on the overall release profile. Because this phase is responsible for the delivery of the remainder of drug in the polymer matrix, its magnitude is (by definition) predetermined by the magnitudes of the prior release phases. However, the kinetics of this phase can still be readily tuned by several different methods.

2.3.1. Modifying the kinetics of final release.
2.3.1.1. Use of polymer blends. Firstly, the rate of final release can be reduced (or its duration extended) by blending together like polymers.^{71,73,90–93} For example, by adding together equal measures of 36.2 kDa PLGA and 13.5 kDa PLGA, Friess and Schlapp were able to extend the final release of gentamicin (small molecule) from just 3 days to 7 days.⁷¹ Similar mixtures have also been used to extended the release of peptides and proteins.^73,91 This tool has even used to sustain protein (lysozyme) release from polyanhydride microspheres.⁹³ Interestingly enough, this method of reducing the final release rate extends directly from methods for tuning the lag phase duration (which also marks the time until final release). For instance, mixing together polymers with different lag phases could stagger the onset of final release, yielding an overall slower final release rate than either polymer could achieve alone. Hence this technique for modulating the rate of final release should prove effective for any matrix system with an adjustable lag phase.
2.3.1.2. Control viacopolymer ratio. Data also suggest that duration of final release in polyester systems is dependent on the copolymer ratio. Studies on melittin microparticles show that poly(lactic-co-glycolic) acid composed of equal amounts of each monomer (50 : 50 PLGA) completes final release in just 2 weeks, while 75 : 25 PLGA takes 3 weeks to deliver nearly the same amount of peptide.³⁶ A similar observation can be made for the ethacrynic acid loaded films.⁸¹ (Note: in all aforementioned cases altering copolymer ratio also adjusted the duration of the lag phase via the polymer degradation rate, as described in Section 2.2.1.2.) While, this effect appears consistent across different PLGA copolymers, further research is needed to better understand its mechanism. Tuning common factors such as polydispersity in the polymer molecular weight or semicrystallinity of the polymer matrix (which lead to variance in the polymer lifespan⁹⁴) may produce comparable effects in other polymer types.⁹⁵

2.3.2. Final release summary. A relatively limited number of techniques are able to alter the kinetics of the final release phase for a number of different systems. Both blending like polymers and altering the copolymer chemistry (for greater lactic content) decrease the rate of final release, allowing for more extended delivery. Similarly reducing polydispersity in polymer initial molecular weight or reducing the copolymer's lactic acid content can increase the rate of final release.

2.4. Summary of experimental results

Many methods for tuning the release kinetics of biodegradable polymer matrices have been tested in carefully designed experiments on a variety of different drugs. The result is a set of independent methods for tuning the magnitude or kinetics of the initial burst, the duration of the lag phase and the rate of final release. When used in combination, these design tools can produce release profiles ranging pure the Fickian diffusion to complex tri-phasic behaviors. In the latter case, when phases are distinct, it is often clear how to apply the experimental-based design tools discussed thus far. However, if phases are indistinct from one another, mathematical models are often helpful for determining the best way to control release behavior.

3. Mathematical models

In 1961, the Higuchi equation set a new standard for design by permitting diffusion and solubility-limited release to be tuned predictably through experimental system properties.⁹⁶ This equation predicted that the cumulative release of drug from planar films of cream or ointment would be proportional to the square root of time provided that a “core” of drug remained above its solubility limit. Although this model was originally designed for non-degradable and non-swellable systems, many different matrices also produce diffusion/solubility-limited release provided that other processes which influence release (e.g.degradation, erosion, etc.) occur at a much slower rate than dissolution and diffusion^84,97–101 For such systems, the Higuchi equation quantifies how agent solubility and matrix geometry effect release, making it one of the first mathematical model-based “tools” for controlled release. Over the past 50 years, mathematical models have continued to quantify the fundamental mechanics of release uncovered in experimental studies. Although past reviews^12,13 have adequately described the differences in mathematics and paradigms of existing models, analysis of their implementation (e.g. the description or prediction of experimentally acquired release data) is needed to evaluate each model's utility as a design tool.

In order to serve as an effective design tool, a mathematical model must provide a means of predicting how changes in system properties will affect the release of a given drug. This is an important distinction, as many models, through regression, will fit tri-phasic release data, while only predicting how one or two system properties will affect release. As most system properties only alter a single aspect or phase of release kinetics, this would limit a model's ability to tailor release kinetics. On the other end of the spectrum, models accounting for too many system properties can be difficult to implement as a number of different parameter values would be required for their successful solution. Thus, as design tools, models can be categorized by the phases of release that they effectively tune and then be evaluated for their accuracy, applicability and ease of implementation.

3.1. Models for tuning initial burst release

3.1.1. Agent loading and copolymer ratio. Wong et al. modeled the initial burst release of immunoglobulin G from PLGA microparticles with varying drug loading and copolymer composition.¹⁰² Analytical solutions to this diffusion–dissolution model revealed a strong agreement to the first 50 days of release data when values for the agent diffusivity and dissolution rate constant were optimized to minimize sum-squared error. The low variance in these optimized values may allow for the prediction of burst release in systems with different loadings or copolymer ratios. (As some of the collected data were lacking a lag phase, at times, both of these properties appeared to impact the initial burst kinetics.) Further work is required to determine if values for agent diffusivity and dissolution rate will have to be calculated anew when attempting to predict the burst kinetics of other proteins or polymer chemistries.

3.1.2. Agent loading, solubility. Small molecule release from PLGA has been captured by a model that combines a Monte Carlo description of dissolution and erosion with partial differential equations describing pore-mediated diffusion.¹⁰³ This model was successfully applied to 5-fluorouracil release data from 104 kDa PLGA microspheres by optimizing values for mean polymer lifespan and agent diffusivity. Importantly values for loading, drug solubility and matrix size were specified for the given microparticle system instead of being computed by regression to release data. This should allow the model to predict how changes in these system properties affect release, provided that their perturbation does not significantly alter the optimized values for mean polymer lifespan and agent diffusivity. While this predictive ability has yet to be tested, experimental studies suggest that altering the loading will effect the magnitude of the initial burst (Section 2.1.1.3) and varying drug solubility will effect burst kinetics (Section 2.1.1.4). (In like systems, matrix size has been reported to effect the polymer degradation rate and, in turn, its lifespan, while having little impact on release kinetics.¹⁰⁴) Future implementation of this model on single emulsion systems (where agent solubility and loading have been experimentally varied) would promote its utility as a design tool.

Zhang et al. have derived a detailed model for describing mono-, bi-, and tri-phasic protein release profiles.¹⁰⁵ To account for this diversity in release behavior, this model actually contains three different versions of its core equations optimized to approximate a diverse range of experimentally observed erosion behavior. Each version of the model's equations was tested on release data from systems with different erosion profiles. By fitting the model first to mass loss (erosion) data, the most appropriate version of its equations was determined and values were computed for erosion rate constants. Then release data were described by optimizing values for the initial tortuosity and dissolution rate constant. Values for the remaining system properties (agent solubility limit, initial diffusivity, microparticle radius, drug loading, initial tortuosity and initial porosity) were taken from the literature. Because sensitivity analysis shows that the erosion mechanism can have a dramatic effect on release kinetics, matrix-specific properties that are likely to effect erosion (e.g. microparticle radius, initial porosity or initial tortuosity) may prove a difficult means of precisely altering release. Fortunately, this model still accounts for agent-specific system properties such as agent loading and solubility which can be used to tune the magnitude and kinetics of the initial burst, respectively (Sections 2.1.1.3 and 0).

3.2. Models for both burst release and the lag phase

3.2.1. Initial polymer molecular weight, irradiation. Diffusion–erosion equations have been combined with empirical correlations to predict the effects of post-fabrication, γ-irradiation on release.¹⁰⁶ This model accurately fit bi-phasic release data from aclarubicin or progesterone-loaded, PLA microparticles of varying molecular weight or irradiation exposure, respectively. Optimized parameter values for agent diffusivity, degradation rate, lag duration, erosion and auto-catalysis were successfully correlated to irradiation exposure and a further regression-free prediction was made for a more heavily irradiated set of PLA microparticles. This demonstrates that the model can successfully predict the experimentally observed effects of irradiation exposure on release, namely increased burst rate and decreased lag duration. It is likely that similar predictions could be made for other agents and polyester matrix formulations if their system-specific parameters (agent diffusivity, erosion half life and degradation rate) are recalculated. With such adjustments, this model could aid in the prediction of initial burst kinetics and lag phase duration following irradiation exposure. It is possible that equivalent correlations could be developed and used to predict the effects of varying initial polymer molecular weight as well.

3.2.2. Polymer initial molecular weight, agent distribution. Raman et al. modeled the effects of polymer initial molecular weight and drug dispersion on piroxicam release from single emulsion microparticles.¹⁰⁷ The model combines diffusion–reaction expressions with a correlation relating piroxicam diffusivity to polymer molecular weight (D(M_w)) in order to predict release while only needing to optimize one constant (initial drug diffusivity), which accounts for the kinetics of initial release. Its descriptions of release were accurate for the initial burst and the lag phase, but deviated from the data as much as 15% at later points in time. This likely occurred because the D(M_w) correlation requires extrapolation for polymer molecular weights less than 5 kDa, an issue which could be resolved by gathering data from lower molecular weight polymer matrices. As implemented, this model can predict changes in burst kinetics arising from drug distribution and changes in the lag phase duration due to polymer initial molecular weight. With an agent specific D(M_w) correlation and recalculated values for initial diffusivity in place, this model could be used to predict the performance of different drugs as well.

3.3. Models for tuning tri-phasic release

3.3.1. Microparticle combinations. The aforementioned model of piroxicam release has recently been extended by Berchane et al. with an algorithm for tuning release kinetics by mixing together different microparticle formulations at different ratios.²⁰ This algorithm was used to optimize (weighted sum squared error) the component mass fractions in a mixture of piroxicam loaded microparticles with different release behaviors to produce entirely new profiles, from linear to multi-phasic patterns. This technique could readily be adapted to generating specific release profiles for any number of drugs provided that a library of formulations with suitably diverse release behaviors could be developed.

3.3.2. 19-Parameters (8 fitted and 11 measured). Batycky et al. modeled tri-phasic protein release by piecing together a number of analytical equations.¹⁰⁸ This model successfully predicted the release of glycoprotein 120 from PLGA microspheres based on measured values for 19 different parameters (Fig. 6A). Less rigorous predictions (using a number of estimated parameters) for tetanus toxin release captured the initial burst and lag phases but showed systemic deviations arising at just 15 to 45% of completion (Fig. 6B). This suggests that it is important to precisely measure or derive values for all model parameters if accurate predictions are to be made. Eight of these parameters, such as effective drug diffusivity, rate of mesopore formation or burst release fraction, can only be determined through observation of the polymer matrix during in vitrodegradation, erosion and release assays. However, the remaining eleven parameters correspond to system properties that are commonly known or readily measured, namely microparticle radius, initial porosity (micro, meso, and occlusion), pore size distribution, polymer degradation rate, monomer molecular weights, soluble oligomer number, drug radius, drug molecular weight, and drug loading. Systemic sensitivity analysis, where each of these parameters is independently varied, will help to determine which system properties specified in this model can be used to tune release.¹⁰⁹

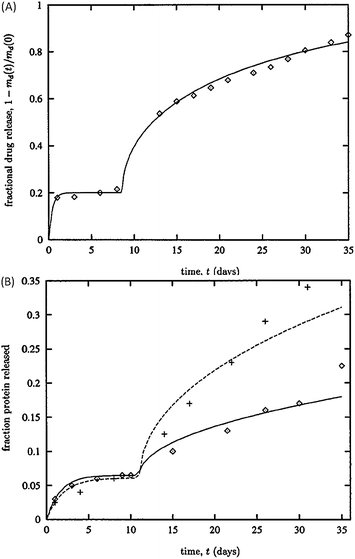Fig. 6 Predictions of protein release from PLGA and PLA microparticles. (A) Model's prediction (solid line) compares favourably with glycoprotein release data (diamonds). (B) Estimations of tetanus toxin release (solid line) capture the initial burst and lag phase of the data from PLGA (crosses) and PLA (diamonds) microparticles. Reproduced with permission of ref. 108.

3.3.3. 4–6 Parameters. More recently, Rothstein et al. have developed a model that describes up to 3 phases of release for agents ranging in size from small molecules to viruses. Initial regressive testing of this diffusion erosion model covered 10 different agents in 13 different microparticle formulations. The resulting optimized values for agent diffusivity and lag duration were accounted for with two correlations to complete a set of system properties (polymer initial molecular weight, polymer degradation rate, microparticle size, initial drug distribution, and drug molecular weight) that allow the model to be solved without regression. Subsequent regression free predictions were made for 4 different microparticle formulations with differing copolymer ratios, initial molecular weights, agent types, matrix sizes, and polymer chemistries. In all cases, these predictions capture the magnitude of the initial burst and subsequent phases of release (Fig. 7). However, the model does not account for effects of dissolution on the initial burst kinetics as evident in its prediction of BSA release from polyanhydride microparticles, which-over estimates burst rate by a factor of 5 (Fig. 7B). This shortcoming did not hamper the model's predictions for the release of hydrophilic agents from PLGA microparticles (Fig. 7A). Based on the accuracy of these predictions, this model provides means for tuning the initial burst (via initial drug distribution and matrix size), the lag phase (viapolymer molecular weight and degradation rate) and the final rate of release (viacopolymer ratio or blends).

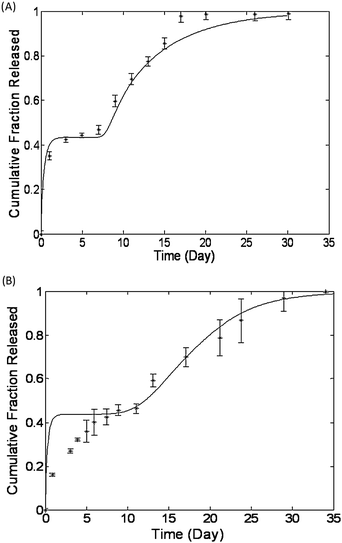Fig. 7 Regression free predictions of release data from Rothstein et al. (A) Melittin peptide release from PLGA microparticles and (B) bovine serum albumin protein release from polyanhydride microparticles. In each case the model's prediction appear as a solid line and the experimentally acquired release data are represented with asterisks. Reproduced with permission of ref. 19.

Recently, the model by Rothstein et al. has been extended to handle matrix implants and hydrophobic agents. This required additional equations accounting for matrix hydration and drug dissolution kinetics, but did not require adjustments for the model's empirical correlations. The new model was tested successfully with regression free predictions of drug release from 2 polyanhydride and 2 poly(ortho ester) implants. However, the mechanisms (hydration, dissolution, degradation, erosion and diffusion) used in this model are fundamental to PLGA and PLA matrices as well.⁸ Predictions for such implants can be made from just the 4 readily attainable parameters (degradation rate, matrix size, polymer initial molecular weight and agent molecular weight) or alternatively 6 parameters (adding on values for agent dissolution rate and maximum solubility) if release is limited by dissolution as well.

3.4. Summary of mathematical models

Mathematical models have successfully described release data from a number of different biodegradable matrix formulations. As design tools these models predict anywhere from 1 to 3 phases of release. A few of these models^18,19,108 can even be solved without requiring regression to a system's in vitro release data. By predicting how tunable system properties effect each phase of release, these models make real the possibility of rationally designing the release kinetics of biodegradable polymer matrices.

4. Conclusions

The literature presents a number of different approaches to controlling drug release from polyester and polyanhydride matrices. Empirical studies of release have produce methods for independently tuning the different aspects of the standard tri-phasic release profile. Mathematical models are beginning to successfully correlate quantitative predictions of release kinetics to physically tunable properties and conditions. Between empirical and mathematical methods a number of different tools have been developed to provide the means for precisely tuning the release kinetics of a broad range of active agents.

Challenges in drug delivery still exist, such as the design of systems with drug–materials interactions, or with rapid changes release kinetics, and it is important to continue the development of experimental and theoretical tools to handle these increasingly complex scenarios as well as new agents and polymers. Such tools may prove essential for a number of applications requiring precise temporo-spatial control, including the delivery of growth factors for regenerative medicine and the delivery of cytokines or chemokines for immunotherapy. Furthermore, to better incorporate controlled release behavior into new therapeutics, tools will also be needed for predicting in vivo performance of hydrolysable polymer matrices in various ways. Fortunately new techniques such as live animal imaging may make it easier to measure and compare in vivo release kinetics, helping researchers understand how in vitro design tools might be applied to precisely control the concentration of drug in a specific physiological compartment over time. With continued advances to the design “tool-box”, future scientists and engineers may someday tailor controlled release formulations to provide specific dosing kinetics to any given physiological compartment by simply selecting correct materials and processing methods. This would pave the way to not only to the broad-scale production of custom release systems for any application, but perhaps even to patient-specific, or “individualized”, controlled release systems that can be accompany individualized medicine in the future.

Notes and references

1. P. Clinton, Pharmaceut. Exec., 2005, 25, 21–21.
2. V. R. Sinha and A. Trehan, J. Controlled Release, 2003, 90, 261–280.
3. A. Humphreys and R. Mayer, MedAdNews, 2007, 13, 33–38.
4. R. C. Mundargi, V. R. Babu, V. Rangaswamy, P. Patel and T. M. Aminabhavi, J. Controlled Release, 2008, 125, 193–209.
5. I. M. Sanders, J. S. Kent and G. I. McRae, J. Pharm. Sci., 1984, 73, 1294–1297.
6. L. M. Sanders, B. A. Kell, G. I. McRae and G. W. Whitehead, J. Pharm. Sci., 1986, 75, 356–360.
7. S. Freiberg and X. X. Zhu, Int. J. Pharm., 2004, 282, 1–18.
8. F. Alexis, Polym. Int., 2005, 54, 36–46.
9. J. P. Jain, S. Modi, A. J. Domb and N. Kumar, J. Controlled Release, 2005, 103, 541–563.
10. S. Lakshmi, D. S. Katti and C. T. Laurencin, Adv. Drug Delivery Rev., 2003, 55, 467–482.
11. C. Wischke and S. P. Schwendeman, Int. J. Pharm., 2008, 364, 298–327.
12. J. Siepmann and A. Gopferich, Adv. Drug Delivery Rev., 2001, 48, 229–247.
13. D. Y. Arifin, L. Y. Lee and C. H. Wang, Adv. Drug Delivery Rev., 2006, 58, 1274–1325.
14. A. G. Thombre and K. J. Himmelstein, AIChE J., 1985, 31, 759–766.
15. A. Gopferich and R. Langer, AIChE J., 1995, 41, 2292–2299.
16. R. Wada, S. H. Hyon and Y. Ikada, J. Controlled Release, 1995, 37, 151–160.
17. J. Siepmann and F. Siepmann, Int. J. Pharm., 2008, 364, 328–343.
18. S. N. Rothstein, W. J. Federspiel and S. R. Little, J. Mater. Chem., 2008, 18, 1873–1880.
19. S. N. Rothstein, W. J. Federspiel and S. R. Little, Biomaterials, 2009, 30, 1657–1664.
20. N. S. Berchane, F. F. Jebrail and M. J. Andrews, Int. J. Pharm., 2010, 383, 81–88.
21. X. Huang and C. S. Brazel, J. Controlled Release, 2001, 73, 121–136.
22. S. D. Allison, Expert Opin. Drug Delivery, 2008, 5, 615–628.
23. K. Fu, R. Harrell, K. Zinski, C. Um, A. Jaklenec, J. Frazier, N. Lotan, P. Burke, A. M. Klibanov and R. Langer, J. Pharm. Sci., 2003, 92, 1582–1591.
24. K. D. Hinds, K. M. Campbell, K. M. Holland, D. H. Lewis, C. A. Piché and P. G. Schmidt, J. Controlled Release, 2005, 104, 447–460.
25. L. E. Bromberg and A. M. Klibanov, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 143–147.
26. S. H. Choi and T. G. Park, Int. J. Pharm., 2006, 311, 223–228.
27. W. Bao, J. Zhou, J. Luo and D. Wu, J. Microencapsulation, 2006, 23, 471–479.
28. G. Jiang, B. C. Thanoo and P. P. DeLuca, Pharm. Dev. Technol., 2002, 7, 391–399.
29. R. Liu, S. S. Huang, Y. H. Wan, G. H. Ma and Z. G. Su, Colloids Surf., B, 2006, 51, 30–38.
30. A. L. Gomes dos Santos, A. Bochot, A. Doyle, N. Tsapis, J. Siepmann, F. Siepmann, J. Schmaler, M. Besnard, F. Behar-Cohen and E. Fattal, J. Controlled Release, 2006, 112, 369–381.
31. J. M. Pean, M. C. Venier-Julienne, F. Boury, P. Menei, B. Denizot and J. P. Benoit, J. Controlled Release, 1998, 56, 175–187.
32. J. Kang and S. P. Schwendeman, Mol. Pharmaceutics, 2007, 4, 104–118.
33. S. R. Little, D. M. Lynn, S. V. Puram and R. Langer, J. Controlled Release, 2005, 107, 449–462.
34. S. R. Little, D. M. Lynn, Q. Ge, D. G. Anderson, S. V. Puram, J. Chen, H. N. Eisen and R. Langer, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 9534–9539.
35. D. Klose, F. Siepmann, K. Elkharraz, S. Krenzlin and J. Siepmann, Int. J. Pharm., 2006, 314, 198–206.
36. F. Cui, D. Cun, A. Tao, M. Yang, K. Shi, M. Zhao and Y. Guan, J. Controlled Release, 2005, 107, 310–319.
37. H. C. Chang and L. C. Li, Drug Dev. Ind. Pharm., 2000, 26, 829–835.
38. J. A. Champion and S. Mitragotri, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 4930–4934.
39. F. Burkersroda, L. Schedl and A. Gopferich, Biomaterials, 2002, 23, 4221–4231.
40. M. Sandor, D. Enscore, P. Weston and E. Mathiowitz, J. Controlled Release, 2001, 76, 297–311.
41. M. J. Dorta, A. Santovena, M. Llabres and J. B. Farina, Int. J. Pharm., 2002, 248, 149–156.
42. D. B. Masters, C. B. Berde, S. Dutta, T. Turek and R. Langer, Pharm. Res., 1993, 10, 1527–1532.
43. H. Onishi, M. Takahashi and Y. Machida, Biol. Pharm. Bull., 2005, 28, 2011–2015.
44. M. Ramchandani and D. Robinson, J. Controlled Release, 1998, 54, 167–175.
45. P. B. Storm, J. L. Moriarity, B. Tyler, P. C. Burger, H. Brem and J. Weingart, J. Neuro-Oncol., 2002, 56, 209–217.
46. T. Ehtezazi and C. Washington, J. Controlled Release, 2000, 68, 361–372.
47. H. K. Kim, H. J. Chung and T. G. Park, J. Controlled Release, 2006, 112, 167–174.
48. S. E. Bae, J. S. Son, K. Park and D. K. Han, J. Controlled Release, 2009, 133, 37–43.
49. N. K. Varde and D. W. Pack, J. Controlled Release, 2007, 124, 172–180.
50. Y. Y. Yang, T. S. Chung and N. Ping Ng, Biomaterials, 2001, 22, 231–241.
51. T. Feczkó, J. Tóth and J. Gyenis, Colloids Surf., A, 2008, 319, 188–195.
52. F. Wang, G. M. Saidel and J. Gao, J. Controlled Release, 2007, 119, 111–120.
53. Y. S. Nam, S. H. Song, J. Y. Choi and T. G. Park, Biotechnol. Bioeng., 2000, 70, 270–277.
54. A. Gèze, M. C. Venier-Julienne, D. Mathieu, R. Filmon, R. Phan-Tan-Luu and J. P. Benoit, Int. J. Pharm., 1999, 178, 257–268.
55. E. S. Park, M. Maniar and J. C. Shah, J. Controlled Release, 1998, 52, 179–189.
56. A. H. Shikani and A. J. Domb, Laryngoscope, 2000, 110, 907–917.
57. N. A. Rahman and E. Mathiowitz, J. Controlled Release, 2004, 94, 163–175.
58. L. E. Kokai, H. Tan, S. Jhunjhunwala, S. R. Little, J. W. Frank and K. G. Marra, J. Controlled Release, 2010, 141, 168–176.
59. A. Gopferich, J. Controlled Release, 1997, 44, 271–281.
60. Z. Xiang, P. Sarazin and B. D. Favis, Biomacromolecules, 2009, 10, 2053–2066.
61. C. M. Negrin, A. Delgado, M. Llabres and C. Evora, J. Controlled Release, 2004, 95, 413–421.
62. D. Teomim, I. Fishbien, G. Golomb, L. Orloff, M. Mayberg and A. J. Domb, J. Controlled Release, 1999, 60, 129–142.
63. W. Zheng, Int. J. Pharm., 2009, 374, 90–95.
64. C. T. Eng, R. Lin and C. H. Wang, J. Colloid Interface Sci., 2005, 291, 135–143.
65. E. J. Pollauf, K. K. Kim and D. W. Pack, J. Pharm. Sci., 2005, 94, 2013–2022.
66. C. Berkland, A. Cox, K. Kim and D. W. Pack, J. Biomed. Mater. Res., Part A, 2004, 70, 576–584.
67. C. Berkland, K. Kim and D. W. Pack, J. Controlled Release, 2001, 73, 59–74.
68. C. Berkland, M. King, A. Cox, K. Kim and D. W. Pack, J. Controlled Release, 2002, 82, 137–147.
69. C. Berkland, K. Kim and D. W. Pack, Pharm. Res., 2003, 20, 1055–1062.
70. C. Berkland, E. Pollauf, C. Raman, R. Silverman, K. Kim and D. W. Pack, J. Pharm. Sci., 2007, 96, 1176–1191.
71. W. Friess and M. Schlapp, J. Pharm. Sci., 2002, 91, 845–855.
72. W. Vogelhuber, P. Rotunno, E. Magni, A. Gazzaniga, T. Spruß, G. Bernhardt, A. Buschauer and A. Gopferich, J. Controlled Release, 2001, 73, 75–88.
73. X. Luan and R. Bodmeier, J. Controlled Release, 2006, 110, 266–272.
74. R. Bhardwaj and J. Blanchard, J. Controlled Release, 1997, 45, 49–55.
75. M. Takenaga, Y. Yamaguchi, A. Kitagawa, Y. Ogawa, Y. Mizushima and R. Igarashi, J. Controlled Release, 2002, 79, 81–91.
76. G. Wei, G. J. Pettway, L. K. McCauley and P. X. Ma, Biomaterials, 2004, 25, 345–352.
77. C. Sturesson, P. Artursson, R. Ghaderi, K. Johansen, A. Mirazimi, I. Uhnoo, L. Svensson, A. C. Albertsson and J. Carlfors, J. Controlled Release, 1999, 59, 377–389.
78. J. L. Cleland, E. Duenas, A. Daugherty, M. Marian, J. Yang, M. Wilson, A. C. Celniker, A. Shahzamani, V. Quarmby, H. Chu, V. Mukku, A. Mac, M. Roussakis, N. Gillette, B. Boyd, D. Yeung, D. Brooks, Y. F. Maa, C. Hsu and A. J. S. Jones, J. Controlled Release, 1997, 49, 193–205.
79. S. Mao, J. Xu, C. Cai, O. Germershaus, A. Schaper and T. Kissel, Int. J. Pharm., 2007, 334, 137–148.
80. B. B. Crow, A. F. Borneman, D. L. Hawkins, G. M. Smith and K. D. Nelson, Tissue Eng., 2005, 11, 1077–1084.
81. Y. Wang, P. Challa, D. L. Epstein and F. Yuan, Biomaterials, 2004, 25, 4279–4285.
82. A. S. Determan, B. G. Trewyn, V. S.-Y. Lin, M. Nilsen-Hamilton and B. Narasimhan, J. Controlled Release, 2004, 100, 97–109.
83. H. Murakami, M. Kobayashi, H. Takeuchi and Y. Kawashima, J. Controlled Release, 2000, 67, 29–36.
84. D. Sendil, D. L. Wise and V. Hasirci, J. Biomater. Sci., Polym. Ed., 2002, 13, 1–15.
85. J. Zeng, L. Yang, Q. Liang, X. Zhang, H. Guan, X. Xu, X. Chen and X. Jing, J. Controlled Release, 2005, 105, 43–51.
86. M. S. Reeve, S. P. McCarthy, M. J. Downey and R. A. Gross, Macromolecules, 1994, 27, 825–831.
87. A. Joshi and K. J. Himmelstein, J. Controlled Release, 1991, 15, 95–104.
88. N. Faisant, J. Siepmann, P. Oury, V. Laffineur, E. Bruna, J. Haffner and J. P. Benoit, Int. J. Pharm., 2002, 242, 281–284.
89. S. Yoshioka, Y. Aso and S. Kojima, J. Controlled Release, 1995, 37, 263–267.
90. M. J. Blanco-Prieto, M. A. Campanero, K. Besseghir, F. Heimgatner and B. Gander, J. Controlled Release, 2004, 96, 437–448.
91. D. K. Pettit, J. R. Lawter, W. J. Huang, S. C. Pankey, N. S. Nightlinger, D. H. Lynch, J. A. C. L. Schuh, P. J. Morrissey and W. R. Gombotz, Pharm. Res., 1997, 14, 1422–1430.
92. S. Duvvuri, K. Gaurav Janoria and A. K. Mitra, Pharm. Res., 2006, 23, 215–223.
93. P. A. Thomas, T. Padmaja and M. G. Kulkarni, J. Controlled Release, 1997, 43, 273–281.
94. G. Schliecker, C. Schmidt, S. Fuchs, R. Wombacher and T. Kissel, Int. J. Pharm., 2003, 266, 39–49.
95. A. S. Determan, J. R. Graham, K. A. Pfeiffer and B. Narasimhan, J. Microencapsulation, 2006, 23, 832–843.
96. T. Higuchi, J. Pharm. Sci., 1961, 50, 874–875.
97. N. Kunou, Y. Ogura, T. Yasukawa, H. Kimura, H. Miyamoto, Y. Honda and Y. Ikada, J. Controlled Release, 2000, 68, 263–271.
98. Y. S. Lee, J. P. Lowe, E. Gilby, S. Perera and S. P. Rigby, Int. J. Pharm., 2010, 383, 244–254.
99. H. Zhang, Y. Lu, G. Zhang, S. Gao, D. Sun and Y. Zhong, Int. J. Pharm., 2008, 351, 244–249.
100. U. Edlund and A. C. Albertsson, Adv. Polym. Sci., 2002, 157, 67–112.
101. Y. Sun, J. Wang, X. Zhang, Z. Zhang, Y. Zheng, D. Chen and Q. Zhang, J. Controlled Release, 2008, 129, 192–199.
102. H. M. Wong, J. J. Wang and C. H. Wang, Ind. Eng. Chem. Res., 2001, 40, 933–948.
103. J. Siepmann, N. Faisant and J. P. Benoit, Pharm. Res., 2002, 19, 1885–1893.
104. J. Siepmann, K. Elkharraz, F. Siepmann and D. Klose, Biomacromolecules, 2005, 6, 2312–2319.
105. M. Zhang, Z. Yang, L. L. Chow and C. H. Wang, J. Pharm. Sci., 2003, 92, 2040–2056.
106. J. He, C. Zhong and J. Mi, Drug Delivery, 2005, 12, 251–259.
107. C. Raman, C. Berkland, K. Kim and D. W. Pack, J. Controlled Release, 2005, 103, 149–158.
108. R. P. Batycky, J. Hanes, R. Langer and D. A. Edwards, J. Pharm. Sci., 1997, 86, 1464–1477.
109. D. E. Zak, J. Stelling and F. J. Doyle Iii, Comput. Chem. Eng., 2005, 29, 663–673.

---