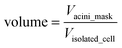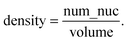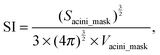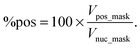Phenotypic transition maps of 3D breast acini obtained by imaging-guided agent-based modeling

Abstract

We introduce an agent-based model of epithelial cell morphogenesis to explore the complex interplay between apoptosis, proliferation, and polarization. By varying the activity levels of these mechanisms we derived phenotypic transition maps of normal and aberrant morphogenesis. These maps identify homeostatic ranges and morphologic stability conditions. The agent-based model was parameterized and validated using novel high-content image analysis of mammary acini morphogenesisin vitro with focus on time-dependent cell densities, proliferation and death rates, as well as acini morphologies. Model simulations reveal apoptosis being necessary and sufficient for initiating lumen formation, but cell polarization being the pivotal mechanism for maintaining physiological epithelium morphology and acini sphericity. Furthermore, simulations highlight that acinus growth arrest in normal acini can be achieved by controlling the fraction of proliferating cells. Interestingly, our simulations reveal a synergism between polarization and apoptosis in enhancing growth arrest. After validating the model with experimental data from a normal human breast line (MCF10A), the system was challenged to predict the growth of MCF10A where AKT-1 was overexpressed, leading to reduced apoptosis. As previously reported, this led to non growth-arrested acini, with very large sizes and partially filled lumen. However, surprisingly, image analysis revealed a much lower nuclear density than observed for normal acini. The growth kinetics indicates that these acini grew faster than the cells comprising it. The in silico model could not replicate this behavior, contradicting the classic paradigm that ductal carcinoma in situ is only the result of high proliferation and low apoptosis. Our simulations suggest that overexpression of AKT-1 must also perturb cell–cell and cell–ECM communication, reminding us that extracellular context can dictate cellular behavior.

---

Insight, innovation, integration

Epithelial morphogenesis and homeostasis is the result of a delicate balance between apoptosis, proliferation, and polarization. This statement, though shown to be true empirically, remains an intuition derived from experimental data that does not have predictive power. By providing a means to test the consequences of local interactive rules between components of a system, agent-based modeling (ABM) can reveal the emergent properties of a system as a whole. In this work, we integrate ABM with high-content image analysis of cultured mammary epithelial cells to describe how cell interactions lead to the emergent property of 3-dimensional organization. The ABM identified acceptable ranges for proliferation, apoptosis, and polarization necessary to maintain morphological homeostasis and provides novel insight into oncogenic events that disrupt morphogenesis.

Introduction

Recent experimental advances in three-dimensional organotypic in vitro culture systems have enabled the development of physiological models of epithelial morphogenesis and tissue homeostasis. For example, normal mammary epithelial cells when grown in vitro on laminin-rich extracellular matrix (ECM) form spherical organotypic ‘acinar’ structures that resemble the secretory alveoli observed in the mammary gland in vivo.¹ Three notable characteristics of normal acinar structures are the establishment of basal polarity,² the formation of a central lumen,¹ and the attainment of homeostasis characterized by a stable acinar size.³In vitro polarity is established at the cell surface in contact with an ECM rich in collagen IV and laminin-111 components that mimic the in vivobasement membrane.⁴ Markers of interaction with the basement membrane, such as various integrins (α5, α6, β4) and laminin, as well as basolateral (epithelial-epithelial) cell markers (such as E-cadherin and β-catenin) become expressed as the acini develop.⁵Cell polarization enables maintenance of a sheet-like structure that separates the basement membrane (basal side) and the lumen (apical side). Formation of the cell-free lumen¹ coincides with expression of tight-junction proteins at the apical surface of the epithelial cell layer² as well as markers of apoptosis in cells located in the center of the acinus.⁶ Mouse embryo studies suggest that apoptotic duct cavitation⁷ is the result of the interplay of two signals: (1) apoptotic signals from the outer endoderm layer inducing apoptosis in inner ectodermal cells; and (2) rescue signals that are mediated by contact with the basement membrane enabling the survival of the columnar cells lining the cavity. In tissue culture and in vivo, the basement membrane integrin beta 1 generates such an apoptosis suppressing signal.⁸ Surprisingly, many acini albeit growing, have non-cycling cells⁹ as identified by the lack of the proliferation marker Ki67. This suggests that not every cell participates in the growth of the acini.

While polarization, apoptosis, and proliferation have been identified as pivotal mechanisms driving mammary acini formation, the complex interplay of these mechanisms remains elusive. Two groups have addressed acini formation using two-dimensional agent-based models (ABM). Rejniak and colleagues have constructed an agent-based biomechanical model of mammary acinus development.^10,11 Grant, Kim and coworkers^12,13 have also created an ABM of MDCK cell acini morphogenesis consisting of agents representing epithelial cells, extracellular matrix, and luminal space on a 2D hexagonal grid. While these models have shed light into the complex changes that may occur during cancer progression, they have been limited to modeling morphogenesis in 2D. Although informative, acini formation is a three-dimensional phenomenon. We set out to create a 3D ABM of epithelial cell morphogenesis, with an initial focus on mammary acini formation. The model was parameterized and validated from experimental data on mammary acini morphogenesisin vitro. Instead of relying on sparse datasets from the literature that were not acquired with the intention of being modeled, we performed novel high-content 3D imaging that enabled direct parameterization and validation of the model to our in vitro culture system. By varying the activity levels of cell proliferation, polarization and apoptosis we derived phenotypic transition maps between normal and aberrant phenotypes. Comparing such maps with in vitro data acquired from normal and pathological breast cell lines grown in 3D allows us to identify parameter regions defining normal and various abnormal phenotypes. These regions could in turn be used to characterize the stability of homeostasis for various organs and would also highlight the various potential paths to cancer.

Materials and method

Cell culture

Human mammary epithelial (HMECs) cells, MCF10A-pER Akt, containing an inducible system for the expression of Akt/PKB (a serine/threonine kinase)⁶ were maintained according to the published protocol.¹⁴Cells were plated at a density of 6300 cells cm⁻² in 24-well culture plates in the prescribed medium along with 5% v/v laminin-rich extra-cellular matrix (lrECM) (BD Biosciences #354230). Prior to plating, a 12 mm diameter round coverslip overlaid with ∼1 mm (30 μL) of lrECM was placed at the bottom of each well. Cells were maintained at 37 °C and 5% CO2 and the culture medium was replaced every 3 days. Akt expression was induced by adding 1 μM 4-hydroxy-Tamoxifen into the culture media (after the first day of culture).

Immunofluorescence

At the appropriate time point after initial cell plating, the acini on the coverslips were fixed by washing with PBS followed by incubation at −10 °C for 1 h immersed in cold methanol:acetone (1 : 1). The coverslips were subsequently washed with PBS, and immersed in blocking solution composed of 10% v/v goat serum, 8 μg mL⁻¹ goat anti-mouse IgG (Caltag #435000) and IF buffer (0.5 g L⁻¹NaN3, 0.1% BSA, 0.2% Triton X-100, 0.05% Tween-20) and incubated at 4 °C overnight. Coverslips were then inverted onto 20 μL of primary antibodies in 10% goat serum in IF buffer and incubated at 4 °C overnight. Primary antibodies used were (i) rabbit anti-Ki67 (Abcam #16667) (at 1 : 50 dilution) and (ii) rat anti-α6-integrin (Millipore #MAB 1378) (at 1 : 300 dilution). Coverslips were washed with IF buffer (3 × 20 min) and incubated with secondary antibody at 4 °C overnight. Secondary antibodies used were (i) donkey anti-rabbit IgG Alexa 594 (Invitrogen) (at 1 : 200 dilution) and (ii) goat anti-rat IgG Alexa 488 (Invitrogen) (at 1 : 200 dilution). Acini were subsequently washed with IF buffer (3 × 1 h) and coated with vectashield (Vector labs) prior to being mounted onto glass slides, sealed with nail polish and then stored at 4 °C until imaging.

Image acquisition, processing and analysis

Cells were viewed and imaged using a Zeiss Axio Observer Z1 automated microscope (Carl Zeiss, Jena, Germany). Images were acquired using a high NA Zeiss plan-apochromat 20× (NA of 0.8) and a sensitive scientific-grade EM-CCD camera (Axiocam). In order to acquire a large number of specimens, maximizing acquisition time and simplifying analysis, the centers of individual acini were marked with the “Mark and Find” function of Axiovision and all acini were acquired at once. Z-stacks were taken with a 5 μm step width. Each time step imaged during the growth of acini was done on 100 to 200 acini in duplicate experiments. Fig. 1A shows a cross section of a normal MCF10A acinus at day 12 for biomarkers identifying the different mechanisms considered here.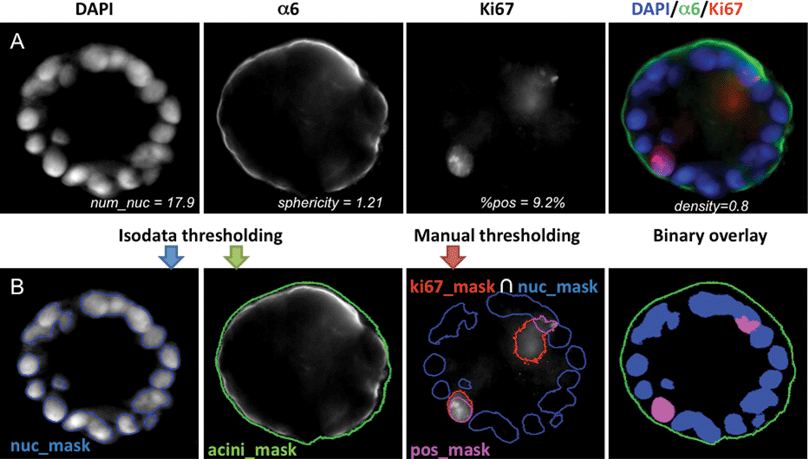

Fig. 1 Quantification of acinar properties. (A) Center slice of a 12 day MCF10A acinus grown on top of Matrigel™ is shown: DAPI for nuclear staining (blue), α6 for basement membrane staining (green) and Ki67 for proliferation marks (red). Merged image is also shown as a color image in the right panel. Values for various imaging properties are displayed for this acinus. (B) Illustration of image analysis. An overlay of the masks for the nuclei (blue mask), for the basement membrane (green contour), and for the proliferating nuclei (purple mask) are shown below each corresponding channel. An overlay of all three binary masks with their corresponding colors is shown in the right panel.

Image processing was performed under Matlab (MathWorks Inc, Natick, MA) and DIPimage (image processing toolbox for Matlab, Delft University of Technology, The Netherlands). Both nucleus and acinus were segmented by simple automatic isodata thresholding,¹⁵ resulting in two masks, nuc_mask and acini_mask, respectively (Fig. 1B). The proliferating nuclei were segmented by intersecting the mask from manually thresholding Ki67 signal with the nuclear mask resulting in a mask labeled pos_mask (Fig. 1B). As illustrated in Fig. S1A,‡ various imaging parameters characterizing an acinus were quantified automatically and were manually validated. These parameters are as follows:

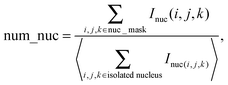
(i) The number of nuclei. Counting the number of nuclei inside an acinus is challenging due to considerable overlaps between individual nuclei. An imaging method¹⁶ we previously introduced to count objects that cannot be easily segmented was used to estimate the number of nuclei. Briefly, normalizing the total DAPI intensity contained within the nuclear mask by the mean total intensity measured for individual nuclei on single cell acini yields acceptable nuclear counts as described below:

where I_nuc(i,j,k) is the intensity at location (i,j,k). The average total intensity of 20 isolated nuclei was obtained by measuring acini containing a single cell (Fig. S1B‡). The 3D automated counts were compared to blindfolded manual counts and were found to be in excellent agreement (Fig. S1C‡).

(ii) The volume of an acinus, is estimated by the number of pixels comprised in the acinus mask (V_{acini_mask}). However, in order to be able to compare directly measured volumes to simulated volumes, one needs to normalize this volume to the volume of a single cell (V_{isolated_cell}). Single cell occupation was obtained by measuring the average volume delimited by α6 immunostaining in 20 acini with only one cell (Fig. S1B‡). Thus, the acinus volume in cell units is dimensionless and represents the maximum number of cells that can fit within an acinus:

(iii)The acinus density, is the volume percentage occupied by cells in an acinus as defined by
(iv) Sphericity index (SI) of an acinus is an invariant property of the acinus (i.e. independent from scaling and thus volume independent). It is equal to 1 for a perfect sphere and increases as the acinus becomes more deformed.¹⁷ As previously defined,¹⁸SI is the volume ratio between the acinus and a sphere, which has the same surface area as the acinus.
where S_{acini_mask} is the surface of the volume delimited by α6 immunostaining.

(v) The percentage of cycling cells marked by positive Ki67 staining in vitro is defined as the volumes ratio between the Ki67 positive mask and the nuclear mask:

Agent-based model and simulations

In agent-based models (ABM), a complex system is represented as a collection of autonomous, decision-making entities, or agents, that have a set of intrinsic state variables and predefined instructions that are executed under specific conditions. In our work, cell agents represent mammary epithelial cells whose properties and behavior are derived from wet-lab experiments and high-content image analysis. In simulations of the model, each cell surveys its local environment and assesses its intrinsic state to execute the proliferation, polarization or apoptosis program. System-level properties emerge from the interactions of multiple cells with each other and their environment. In effect, the ABM formalism allows putting mechanistic hypotheses into action and visualizing their impact on the emerging system. The system dynamics, usually unknown a priori and hence not explicitly implemented, can be surprising and non-intuitive, especially in cases involving cooperation and competition.^19,20 Agent-based models are increasingly utilized to understand system dynamics in tumor biology,^21–31 immunology and inflammation,^32–35wound healing,^36,37 vascular biology,^38–40morphogenesis,^41–44 and pharmacology/toxicology.^45–49

Repast Symphony, a non-commercial, open source software toolkit (http://repast.sourceforge.net/) was used to implement the model. Agents reside on a three-dimensional rhombic dodecahedron lattice (that provides the closest spherical-cell like packing; Fig. 2A). Each agent is represented by a dodecahedron (six pairs of opposing faces) with twelve neighbors. The model comprises three distinct agents—epithelial cells, basement membrane and lumen. Each discrete-time simulation starts at day 1.2 with a single cell agent at the center of the computational domain of 50 × 50 × 50 lattice points, which triggers population of its twelve adjacent lattice points with basement membrane objects. We introduced a 1.2 day time delay to account for the time needed for cells to settle in culture in vitro. Each simulation consists of 18 time steps equivalent to 0.6 days in real time. Therefore, we simulated a total of 12 days comparable to in vitro experiments. The following set of rules to simulate acinus growth were applied (the rules are summarized in Fig. 2B–F and the simulation parameters are summarized in Table 1):

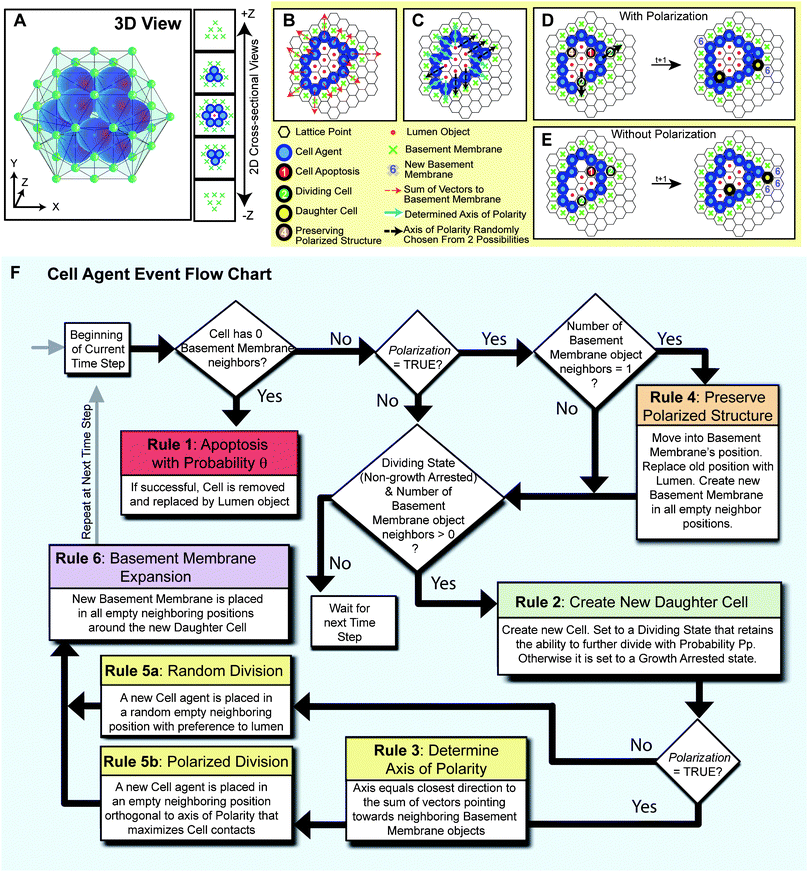Fig. 2 Depiction of the 3D lattice and the cell agent rules of interaction (A) A 3D image and 2D cross-sectional views of an example in silico acinus consisting of 12 cell agents and 1 central lumen object surrounded by 42 basement membrane objects on the lattice. (B) When the Polarization variable is set TRUE, and the rules of cell polarization are enabled, each cell agent determines its polarity direction by taking the arithmetic sum of vectors pointing towards neighboring basement membrane objects (red dashed arrows). Rules are applied in 3D, but are shown above as 2D cross-sections. (C) The closest of the twelve neighboring positions to which the vector sum points towards determines the polarity (blue arrows). If multiple directions are equally distant, polarity is chosen from these at random (black dashed arrows). (D) An example execution through a simulation time step is depicted with Polarization enabled. Numbers and colors on a cell indicate the rule it will execute based on its local environment. During polarized division, the dividing cell agent places the daughter cell agent in the direction that maximizes contacts with other cell agents, except in the two directions along its axis of polarity. (E) For comparison, an example execution through a simulation time step is also shown with Polarization disabled. During nonpolarized cell division, dividing cell agents can place daughter cell agents in any neighboring position occupied by a basement membrane or lumen object with preference towards the lumen. (F) An event flow diagram for a cell agent summarizes the 6 rules of interaction.

Table 1 Parameters for the in silico model and the range of values it can equal

Parameter	Description	Values
Proliferation potential (Pp)	Probability of a daughter cell to maintain the ability to divide. (1 − Pp is the probability of growth arrest)	[0 1]
Apoptosis efficiency (θ)	Probability that a cell will die when the apoptosis criteria is met (devoid of basement membrane contact)	[0 1]
Polarization	Whether the rules of polarity are enabled	TRUE or FALSE

---

Rule 1: Cell agents devoid of contact with basement membrane objects attempt to undergo apoptosis with probability θ.^7,8Cell agents that have undergone apoptosis are replaced by lumen objects.

Rule 2: Cell agents in contact with at least one neighboring basement membrane object can divide. To account for the low frequency of proliferating cells that is observed in growing acini,⁹cells are equipped with a proliferation potential (Pp). The proliferation potential reflects the probability of a daughter epithelial cell to retain the ability to divide or become growth arrested. If a daughter cell ends up without touching the basement membrane, it will try to undergo apoptosis per Rule 1.

Rule 3: A polarized cell has directionality and tries to maintain a sheet-like structure with its neighboring cells such that there is basement membrane on one side (basal side) and lumen in the opposing direction (apical side). Each cell agent determines its polarity direction by taking the arithmetic sum of vectors pointing towards neighboring basement membrane objects (Fig. 2B). The closest of the twelve neighboring positions to which the vector sum points towards determines the polarity axis (Fig. 2C). If multiple directions are equally distant, polarity is chosen from these at random. A boolean parameter, Polarization, determines whether cell agents in the simulation are equipped with polarity or not.

Rule 4: In order to maintain a sheet-like configuration and to maintain contacts with basement membrane, polarized cell agents that are in contact with only one basement membrane object will move and replace that basement membrane object. A lumen object will be placed in the cell's previous location. Basement membrane objects will be created in any empty neighboring positions.

Rule 5: Dividing cells with polarity place daughter cells into the site orthogonal to the polarization axis that maximizes contacts with other cell agents (Fig. 2D). Non-polarized cells place daughter cells in a neighboring position currently occupied by a lumen or basement membrane object at random, but with preference to lumen positions (Fig. 2E).

Rule 6: Newly created cell agents will create basement membrane objects in any empty neighboring positions (not currently occupied by a cell agent, basement membrane or lumen object).

Note that a sphericity index of SI = 1 indicating a perfect spherical acinus cannot be achieved in our simulations because of the discretization of space into rhombic dodecahedron units (e.g. a single cell acinus yields a SI ∼ 1.1). To compare the SI between the simulations and the experimental data, the following adjustment is applied. Pixels in an empty image (with pixel resolution identical to acinar microscope images) whose locations correspond to a simulated basement membrane agent position are marked and subsequently joined using a cubic spline fit surface contour. Applying a Gaussian filter to the binary contour mask fills remaining gaps between points along the resulting discrete basement membrane. As shown previously,⁵⁰ this results in a pseudo microscope image that can be processed using the same imaging procedure applied for real acini images.

Results

Phenotypic transition maps

In order to fully explore the different phenotypes resulting from varying proliferation potential (Pp—see Materials and method) and apoptosis efficiency (θ) levels, simulations were performed with both parameters varied over the full range of values from 0.1 to 1. Values below 0.1 were not mapped as found to be biologically unrealistic. For each distinct pair of parameters, 100 independent acini simulations were performed and results are summarized in Fig. 3 (with cell polarization) and Fig. 4 (without cell polarization). We will use these maps to identify the ranges and interplays of parameters θ and Pp that lead to different phenotypes.

Fig. 3 In silico phenotypic transition maps depicting acinar characteristics as a function of apoptosis efficiency θ and proliferation potential after 12 days in culture—polarization ON. (A) Cell count, (C) % of growth arrested acini, (F) acini volume, (H) sphericity. All simulations were performed with Polarization set to TRUE. (B,D,E,G) Example images of simulations at day 12 for four parameter sets ([θ = 0.3, Pp = 0.9], [θ = 0.3, Pp = 0.4], [θ = 0.9, Pp = 0.9], [θ = 0.9, Pp = 0.4]).

Fig. 4 In silico phenotypic transition maps depicting acinar characteristics as a function of apoptosis efficiency θ and proliferation potential after 12 days in culture—polarization OFF. (A) Cell count, (C) % of growth arrested acini, (F) acini volume, (H) sphericity. All simulations are done with polarization set to off. (B,D,E,G) Example images of simulations at day 12 for four parameter sets ([θ = 0.3, Pp = 0.9], [θ = 0.3, Pp = 0.4], [θ = 0.9, Pp = 0.9], [θ = 0.9, Pp = 0.4]).

In silico acinar formation suggests apoptosis is necessary and sufficient for lumen formation, while polarization is essential for acinar sphericity

Exploring the parameter range with our transition maps indicated that the apoptotic rule was necessary and sufficient to form a lumen independently of polarization. Representative 2D cross-sectional images of simulation results for in silico acini after 12 days for low apoptosis efficiency levels (θ = 0.3) are depicted in Fig. 3B,D when polarization is enabled and Fig. 4B,D when polarization is disabled. Low levels of apoptosis efficiency led to partially filled lumen with multiple epithelial layers (Fig. 3BD, 4BD).

In the physiologically unrealistic case where apoptosis is completely inhibited (i.e.θ = 0), lumens were filled, but contained small and sparse cavitations (Fig. S2A,B‡). These cavitations were the result of polarization as they were not observed when polarization was disabled (Fig. S2C,D‡). In contrast, high apoptosis efficiency levels (i.e.θ = 0.9) yielded acini lumen formation that resembles experimental acini with single cell layer epithelium⁹ lining the basement membrane.

Identifying normal phenotype maps and validating them with experimental data

The number of nuclei per acinus, the acinar volume in cell units, and the sphericity of the acinus delimited by α6 immunostaining are plotted as function of days in culture (Fig. 5A,B,C). Using the measurements made at the final day in culture (day 12) we inferred the parameter regions satisfying the normal phenotype by overlapping corresponding measurement maps matching these ranges (average ± one standard deviation, Fig. 5D,E). The overlapping region is small, suggesting a fine balance for maintaining acinus homeostasis. This mapping revealed that only simulations with cell polarization enabled could match experimentally measured acini properties (Fig. 5D) as removing polarization led to no overlap (Fig. 5E). The best-fit set of parameters were identified as θ = 0.9 and Pp = 0.4 (see Supplementary Movie S1 for example simulation with polarization enabled, and Supplementary Movie S2 for example simulation with polarization disabled‡). As shown in Fig. 5A,B,C, these parameters led to simulations matching all three measurements across the full time course. We also compared the percentage of proliferating cellsin silico to that observed in vitro over 12 days and identified a match for the first seven days (Fig. S3A‡). The in silico acinus eventually reached an equilibrium between cell death (22 ± 9.5%—Fig. S4C‡) and cell proliferation (35 ± 18%—Fig. S3A‡) leading to growth arrest for acini with equal rates. When measuring cell death at day 12 using ethidium homodimer-1 (LIVE/DEAD kit, Invitrogen, Inc.), excellent agreement was observed between the predicted and measured levels of death (25 ± 10%) (Fig. S4‡). However, in vitro proliferating levels were lower (11 ± 3%—Fig. S3A‡) than cell death rates. This is a surprising low number as the proliferating rate should be greater or equal to the death rate for an acinus to grow or reach a steady state, respectively. Ki67 labeling may not be detecting all dividing cells, which may be the source of the discrepancy between the measured in vitro levels of proliferation and our in silico predictions.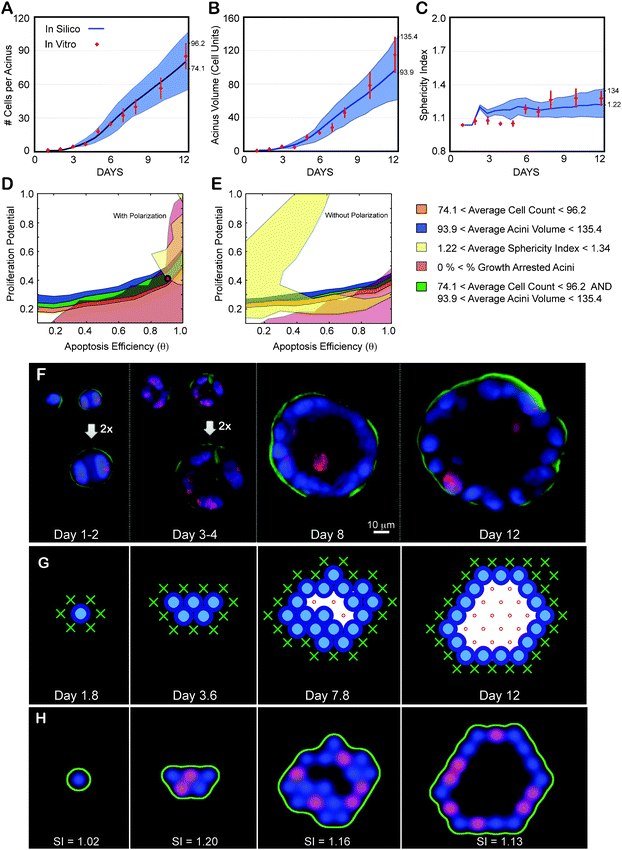

Fig. 5 Achieving a normal phenotype in silico and in vitro validation. (A–C) Experimental data as a function of days in culture. Average and standard deviations from ∼100 to 200 acini per time point are shown as red diamonds. (A) Average number of cells contained in one acinus. (B) Average acinar volume (in cell units). (C) Average acinar sphericity. (D–E) Transition maps are used to identify the parameter space that matches in vitro measurements at day 12. The average ± standard deviation of the measurements set the boundaries for each map. Overlap between the different areas delimits the parameter space matching all considered measurements. Cell number, acini volume, acini sphericity and growth arrest levels are used to delimit this space. (D) Resulting overlap with Polarization enabled maps from Fig. 3. It leads to a possible region of overlap. The red circle indicates the chosen parameter values (θ = 0.9, Pp = 0.4) within this area. The corresponding predicted in silico measurements for these parameters are displayed in panels A–C as solid blue curves with standard deviations shown as blue shadows. Note for all simulations: agent doubling time was set to 0.6 days with a 1.2 day delay for cells to reenter cycle. (E) Resulting overlap with Polarization disabled maps from Fig. 4. These maps lead to no overlap and therefore no possible fit of the experimental data. (F) Representative center slices of normal acini during the first 12 days in culture (nuclear stain with DAPI in blue, proliferation marks with Ki67 in red, basement membrane with α6 in green). (G) Example of 2D cross-sectional view of an in silico acinus with a normal phenotype obtained with parameters θ = 0.9, Pp = 0.4, and Polarization enabled. (H) 2D cross-sectional view of the same in silico acinus after transforming epithelial and basement membrane agents coordinates into pseudo microscope 3D image. Pseudo images are used to compute acini sphericity index (SI) for each simulation (displayed below each acinus). Red marks proliferating agents, green marks basement membrane agents and blue marks all epithelial agents.

Characterizing lumen formation: an imaging approach validated by in silico data

We propose a method to characterize lumen formation based on 3D imaging measurement of cell density. Cell density alone is a poor indicator of the lumen status as it naturally decreases with acinar volume. Instead, we used a simple mathematical formalism to characterize density as a function of the number of epithelial layers (β) as illustrated in Fig. 6A on a spherical acinus. Although acini are not perfect spheres, this formalism is in good agreement with the simulated data (Fig. 6B), with β values reflecting accurately the average number of epithelial layers observed in the simulations. Therefore, β can be used as a hollowness factor for the lumen, with values close to 1 for physiologically normal acini. Using the parameters defined for the normal phenotype in Fig. 5 (θ = 0.9 and Pp = 0.4), the prediction for density was in excellent agreement with the experimental data leading to an average number of epithelial layers of ∼1.05 (Fig. 6D). β was calculated for all possible pairs of parameters by fitting the volume dependency of the density of all simulated acini during their growth progression. This enabled the creation of ‘β transition maps’ either with or without polarization (Fig. 6C and Fig. S5‡).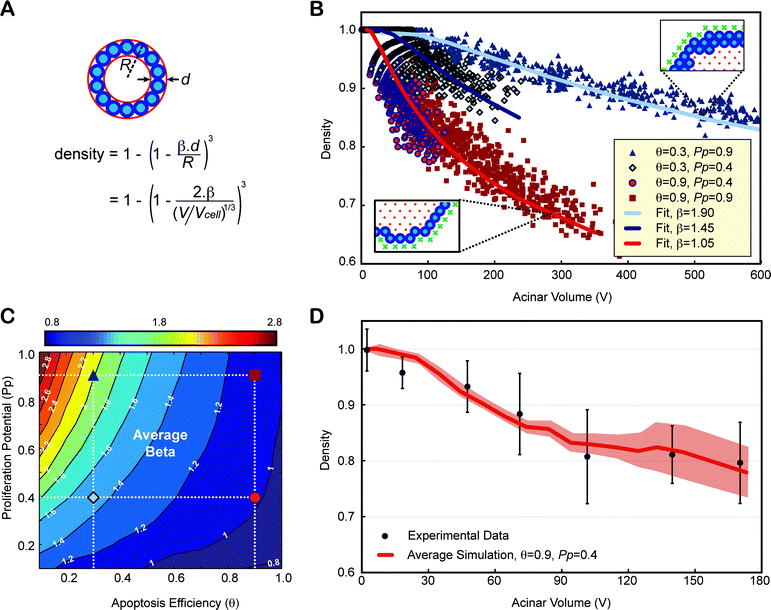

Fig. 6 Contrary to density, epithelium thickness β is an invariant property of an acinus and can be used as an indicator of lumen formation. (A) Density alone is a poor indicator of normal lumen formation, as it does not only depend on the number of epithelial layers alone (β) but also on the volume of the acinus. One can compute the theoretical density of a spherical acinus of radius R and agents of diameters d with β epithelial layers, as a function of the acinar volume (V) normalized to the cellular occupation (V_cell). (B) Four distinct simulations with different apoptotic efficiencies q and proliferation potential Pp, lead to very distinct lumen formation. Even though simulated acini are not perfectly spherical, simulated densities versus acinar volume can be fitted very accurately. (C) β transition maps. The location of the four parameters conditions whose β values were fitted in panel (B) are marked with the same symbols and colors on the map. The normal phenotype simulated in Fig. 5 is shown as a red circle. (D) The dependency of density variation versus acinar volume for simulations with θ = 0.9 and Pp = 0.4 match experimental data. Experimental densities are averaged over 7 different acini volume bins, mixing all densities from day 1 to day 12, as it was done for simulations.

Cell polarization had a noticeable effect on the β transition map. The single cell epithelial layer was well conserved across various levels of proliferation in polarized cells with sufficiently high levels of apoptosis (θ = 0.9 − β isocontours are almost vertical). In contrast, the absence of cell polarization led to an increase in the average number of epithelial layers with increasing proliferation potentials (Fig. S5‡). This suggests that apoptosis and polarization worked synergistically: once a lumen was created through apoptotic cavitation, cell polarization ensured division along the plane of the basement membrane further enhancing lumen expansion. Loss of polarization disrupted the maintenance of a single cell layer epithelium leading to non-spherical acini (Fig. 4H) and larger β values (Fig. S5B‡). Increased proliferation exacerbated this phenotype.

Phenotypic transition maps of dysplastic morphogenesis

The above derived phenotypic transition maps were parameterized and validated for non-transformed MCF10A cells and physiologically normal acini formation. We next challenged our ABM to predict how shifts in the interplay of cell proliferation, polarization and apoptosis could lead to pathological, malignant morphologies. We used the established, modified MCF10A cell line (MCF10A-pER Akt) that contains an inducible system for Akt-1/PKB expression (a serine/threonine kinase).⁶Activation of Akt-1/PKB is thought to increase proliferation whilst reducing apoptosis, inducing a shift to unchartered territory of the phenotypic maps (low θ values; large Pp values). Acini grown from MCF10A-pER Akt-cells have disrupted morphogenesis that recapitulates properties of ductal carcinoma in situ (DCIS), such as delayed lumen formation, scattered apoptosis-resistant cells within the lumen, and acinar structures that fail to growth arrest.⁶ These phenotypes were confirmed by high-content imaging (Fig. 7A,B,C). We quantified acinar size and cell number in order to localize the DCIS phenotype on the transition maps, as previously done for the normal phenotype. At day 12, acini contained an average of 127 ± 12 nuclei and had an average volume of 574 ± 107 (in cell units). Regardless of polarization state, the range of these measurements did not result in an overlapping region between the volume and nuclear number maps derived in Fig. 3 and 4 (Fig. 7D,E). The measured number of nuclei per acinus should yield much smaller acini, and, analogously, the observed acini volume should contain significantly more nuclei. In addition, the fitting of the volume dependency of density led to an average number of epithelial layers, β ∼ 0.45 (Fig. 7F). This value is much lower than any values generated in the β transition maps, with or without polarization (Fig. 5S). This low-density phenotype is a striking feature of this biological system that cannot be recapitulated with our current model. Representative cross sections of the Akt-on acini confirm this low-density effect, showing very loose epithelium and large space between cells (Fig. 7G). It is important to note here that the MCF10A-pER Akt cell line has been reported to be 46% larger in volume than the MCF10A line.⁶ However, these larger cellular volumes, that we confirmed separately (∼30–40% increase with our imaging), cannot explain the lower cell density because acini volumes are reported in “cell units” (see Materials and method). The 46% increase of the cellular volume will cancel out when computing the cell density of the acinus, and thus the lower density reflects real gaps between cells. Contrary to what we expected, in vitro measurements for proliferation in these cultures are comparable to normal acini (Fig. S3B‡). In contrast, apoptotic levels are low, as expected, being reduced 5 fold compared to normal acini (Fig. S4C‡). These results suggest that this low-density phenotype is not driven by polarization and it cannot be sufficiently explained by lowered levels of apoptosis. We conclude that additional, yet to be determined cell mechanisms are involved that lead to the observed morphology.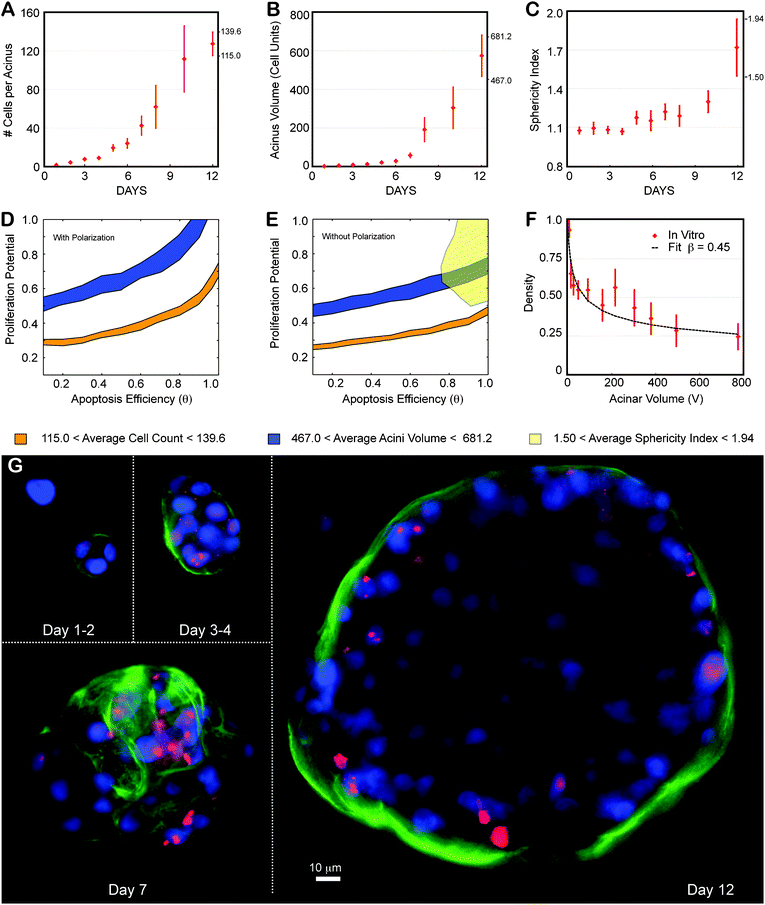

Fig. 7 Locating ductal carcinoma in situ using the transition map. The MCF10A-pER Akt, which have a compromised apoptotic pathways were grown on top of Matrigel™ and quantified similarly to normal MCF10A. (A–C) Experimental data as a function of days in culture. Average and standard deviations from ∼100 to 200 acini per time point are shown as red diamonds. (A) Average number of cells contained in one acinus. (B) Average acinar volume (in cell units). (C) Average acinar sphericity. (D) Satisfying all three measurements at day 12 is impossible with Polarization enabled, as there are no overlapping regions for the different maps. (E) When disabling polarization, there are still no overlapping regions, indicating some additional mechanism is involved. (F) Akt-on acini density decreases much faster with acinar volume compared to normal MCF10A, leading to fit for β of 0.45. (G) Representative center slices of Akt-on acini during the first 12 days in culture (nuclear stain with DAPI in blue, proliferation marks with Ki67 in red, basement membrane with α6 in green).

Discussion

We set out to develop a simple computer model that could test the synergistic effects of cell proliferation, polarization and apoptosis on epithelial acini morphogenesis. Our computational model may be generalized to other morphogenesis model systems, however we initially focused on mammary acinar formation and homeostasis. We identified a simple set of rules that were critical for the development and maintenance of the normal acinar phenotype. Our approach adds to previous work^10–13 by introducing (i) a three-dimensional model of acinar morphogenesis. To our knowledge, this is the first 3D model of mammary epithelial acinus formation. Additionally, our approach (ii) directly integrates into the model high-content three-dimensional imaging data from in vitro experiments. We further (iii) introduce a ‘β factor’ that describes the thickness of the epithelial sheet lining the basement membrane as a novel imaging parameter that reliably describes acinus lumen formation. We derived phenotypic transition maps revealing emergent synergisms underlying normal and aberrant morphological development.

Agent-based models have previously been utilized to study mammary acinar formation. The models by Grant, Kim, and coworkers^12,13 focus on establishing a unifying theory that simultaneously represents epithelial cell growth and morphogenesis in four different culture conditions: (1) the formation of stable, self-enclosed monolayer cysts when grown in 3-D embedded culture, (2) the generation of cysts with inverted polarity when grown in suspension cultures, (3) the establishment of a confluent monolayer when grown on a surface, and (4) the genesis of stable cyst-like structures when the monolayer is overlaid with Collagen I. Grant¹² established a minimal set of 9 rules essential to recapitulate all phenotypes that arise when changing only the initial simulation condition. A descendent version of the model by Kim¹³ included three more rules to describe new model behaviors and phenotypic overlap with the in vitro system. Validation of the model was based primarily on the ability to recapitulate the qualitative culture traits for the different culture conditions. The model revealed that loss of cell polarization or apoptosis leads to lumen filling characteristic of glandular epithelial cancer, suggesting that both mechanisms are necessary to form a lumen.

With their IBCell model, Rejniak and Anderson^10,11 simulate cells as very sophisticated objects. Cells are deformable where a mesh of elastic springs defines the cell shape and a viscous incompressible fluid defines cell mass. Points on the cell boundary act as receptors that sense the surrounding environment for extra-cellular matrix signals, cell signals or death signals, and the differential engagement of the various receptors determines the cellular behavior. Similar to our findings, Rejniak and coworkers found that lumen formation is primarily dependent on apoptosis. However, while in our model apoptosis results from a loss of contact to the basement membrane as suggested by experimental in vivo findings,^7,8 lumen formation in the IBCell model requires the propagation of a death signal from the outer cells to the center of the lumen. Both survival signal from the basement membrane or cell death signal from the basal cells towards the luminal cells have been proposed as a mechanism for ductal morphogenesis in mouse embryos.⁷ Interestingly, both mechanisms could recapitulate lumen formation when modeled as single death-inducing mechanism. Therefore, these two biological mechanisms are both sufficient and biologically redundant to create a lumen. Our model also proposes an emergent synergism between polarization and apoptosis, as favoring division perpendicularly to the basement membrane enhances lumen maintenance. Non apoptotic factors involved in lumen formation have been discussed in detail previously.⁵¹ In our work, as long as a cell agent has lost contact with the basement membrane, it will undergo death. However, the type of death is irrelevant to this model as it could be happening via non-apoptotic mechanisms such as autophagy or entosis.^51,52Growth arrest, another hallmark of normal acinus development, is predominantly driven by polarization in the IBCell model. This happens as agents lose their ability to proliferate when they become fully polarized upon tight junction formation. In our model, growth arrest is the result of a balance between proliferation and apoptosis. An acinus ceases to grow when all cells have insufficient space to divide or are oriented such that the progeny move into the lumen, which subsequently triggers apoptosis due to lack of contact with the basement membrane. It is interesting to note here that even though polarization was not designed as a mechanism to growth arrest the acinus in our model, it naturally emerges as an important factor for stabilizing the acini size for normal phenotype (i.e. removing polarization when θ = 0.9 and Pp = 0.4 leads to significantly less growth arrested acini: Fig. 3C and 4C). Therefore, in both models, polarization helps maintain a single cell layer epithelium leading to better growth arrest and more spherical structures. Evidence for the equilibrium between cell proliferation and death, which is unique to our model, is also suggested by Debnath and colleagues.⁹ In their work, they show when acini are fully arrested at day 20 that there are still 20% of the acini with cycling cells. In agreement with this, we also report that ∼10% of acinar cells are still cycling at day 12.

Once homeostasis is reached, one would expect to see in vitro proliferation rates similar to death rates. This was observed for our simulations at day 12 (both in silico proliferation and death rates were ∼20–30%). In contrast, the percentage of Ki67 labeled cells that were observed in vitro (∼10%) was lower than the observed death rates (25% ± 10%). Since in vitrodeath rates we report here are in good agreement with our simulation predictions, it might suggest that in vitro proliferation rates measured by Ki67 may not be including all cycling cells. Differences of rates may also be due to the difference of duration between apoptosis and the cell cycle, as the later is typically much longer. On the other hand, if we assume this difference is real, it may then imply that some cells are being growth arrested. As suggested by many studies from the Bissell lab,^1,4,53 the interaction between the basement membrane and the integrins play an important role in mediating proliferation. It would therefore be interesting to test in silico the impact of the percent contact between the basement membrane and the agents in dictating proliferation status.

Despite the success in modeling normal acinus formation, the current model is unable to reproduce in vitro morphologies of ductal carcinoma in situ (DCIS). Acinus expansion was much faster than the growth of the cell population, leading to very low cell densities and “bloated-looking” acini. Normal phenotypic transition maps show that reducing apoptosis primarily compromises lumen formation by increasing epithelial layer thickness while the acinus volume is only slightly increased. Therefore, the rapid expansion observed in the in vitro DCIS system and the low cell density are not likely the result of lower apoptosis. In contrast to the classic paradigm that DCIS is the result of high proliferation and low apoptosis,⁶ our modeling approach supports the long list of evidence^4,5,54 that microenvironment signalingvia integrin may drive the malignant phenotype and suggests the need for modeling the cell-basement membrane interaction, as other in silico studies have recently suggested.⁵⁵

Summary

We introduced an agent-based model of epithelial cell morphogenesis to explore the complex interplay between apoptosis, proliferation, and polarization. The agent-based model was parameterized and validated using novel high-content image analysis of mammary acini morphogenesisin vitro. Model simulations could be tuned to replicate the in vitro normal phenotype, revealing important properties of acinar morphogenesis. The most important findings were that apoptosis is necessary and sufficient for initiating lumen formation, but cell polarization is the pivotal mechanism for maintaining physiological epithelium morphology and acini sphericity. Furthermore, simulations highlighted that acinus growth arrest in normal acini can be achieved by controlling the fraction of proliferating cells, but also suggested that polarization has a stronger impact on enhancing growth arrest when apoptosis is fully functional. Despite the successes in modeling the normal phenotype, the model could not replicate in vitro data measured from a DCIS biological system, where apoptosis was compromised via overexpression of AKT-1. The resulting 3D acini were much larger, but cell density was much lower than observed for normal acini. This “bloated” phenotype contradicts the classic paradigm that these large in vitro DCIS are only the result of high proliferation and low apoptosis. Instead our simulations suggest that overexpression of AKT-1 must additionally lead to perturbation of cell–cell and cell–ECM communication.

Acknowledgements

This project was supported by the National Cancer Institute under Award Number U54 CA143836 for the PSOC affiliated authors and U54CA149233 for the ICBP affiliated authors. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute or the National Institutes of Health.

References

1. M. H. Barcellos-Hoff, J. Aggeler, T. G. Ram and M. J. Bissell, Development, 1989, 105, 223–235.
2. C. Plachot, L. S. Chaboub, H. A. Adissu, L. Wang, A. Urazaev, J. Sturgis, E. K. Asem and S. A. Lelievre, BMC Biol., 2009, 7, 77.
3. V. M. Weaver, A. R. Howlett, B. Langton-Webster, O. W. Petersen and M. J. Bissell, Semin. Cancer Biol., 1995, 6, 175–184.
4. O. W. Petersen, L. Ronnov-Jessen, A. R. Howlett and M. J. Bissell, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 9064–9068.
5. C. C. Park, H. Zhang, M. Pallavicini, J. W. Gray, F. Baehner, C. J. Park and M. J. Bissell, Cancer Res., 2006, 66, 1526–1535.
6. J. Debnath, S. J. Walker and J. S. Brugge, J. Cell Biol., 2003, 163, 315–326.
7. E. Coucouvanis and G. R. Martin, Cell, 1995, 83, 279–287.
8. N. Boudreau, C. J. Sympson, Z. Werb and M. J. Bissell, Science, 1995, 267, 891–893.
9. J. Debnath, K. R. Mills, N. L. Collins, M. J. Reginato, S. K. Muthuswamy and J. S. Brugge, Cell, 2002, 111, 29–40.
10. K. A. Rejniak and A. R. Anderson, Bull. Math. Biol., 2008, 70, 1450–1479.
11. K. A. Rejniak and A. R. Anderson, Bull. Math. Biol., 2008, 70, 677–712.
12. M. R. Grant, K. E. Mostov, T. D. Tlsty and C. A. Hunt, PLoS Comput. Biol., 2006, 2, e129.
13. S. H. Kim, J. Debnath, K. Mostov, S. Park and C. A. Hunt, BMC Syst. Biol., 2009, 3, 122.
14. J. Debnath, S. K. Muthuswamy and J. S. Brugge, Methods, 2003, 30, 256–268.
15. T. Ridler and S. Calvard, IEEE Trans. on Systems, Man, and Cybernetics, 1978, SMC–8, 630–632.
16. M. C. Fleisch, C. A. Maxwell, C. K. Kuper, E. T. Brown, M. H. Barcellos-Hoff and S. V. Costes, Microsc. Res. Tech., 2006, 69, 964–972.
17. R. C. Gonzalez and R. E. Woods, Digital Image Processing, Prentice Hall, Upper Saddle River, N.J., 2nd edn, 2002.
18. K. L. Andarawewa, A. C. Erickson, W. S. Chou, S. V. Costes, P. Gascard, J. D. Mott, M. J. Bissell and M. H. Barcellos-Hoff, Cancer Res., 2007, 67, 8662–8670.
19. C. Power, JASSS, 2009, 12, 8.
20. H. Enderling, A. R. Anderson, M. A. Chaplain, A. Beheshti, L. Hlatky and P. Hahnfeldt, Cancer Res., 2009, 69, 8814–8821.
21. T. Alarcón, H. M. Byrne and P. K. Maini, J. Theor. Biol., 2003, 225, 257–274.
22. P. Gerlee and A. Anderson, J. Theor. Biol., 2007, 246, 583–603.
23. K. A. Rejniak, J. Theor. Biol., 2007, 247, 186–204.
24. Z. Wang, C. Birch, J. Sagotsky and T. Deisboeck, Bioinformatics, 2009, 25, 2389–2396.
25. D. Basanta, H. Hatzikirou and A. Deutsch, Eur. Phys. J. B, 2008, 63, 393–397.
26. H. Enderling, N. R. Alexander, E. S. Clark, K. M. Branch, L. Estrada, C. Crooke, J. Jourquin, N. Lobdell, M. H. Zaman, S. A. Guelcher, A. R. Anderson and A. M. Weaver, Biophys. J., 2008, 95, 2203–2218.
27. H. Hatzikirou, L. Brusch, C. Schaller, M. Simon and A. Deutsch, Comput. Math. Appl., 2010, 59, 2326–2339.
28. M. J. Piotrowska and S. D. Angus, J. Theor. Biol., 2009, 258, 165–178.
29. J. Galle, M. Hoffmann and G. Aust, J. Math. Biol., 2009, 58, 261–283.
30. I. Ramis-Conde, M. A. Chaplain, A. R. Anderson and D. Drasdo, Phys. Biol., 2009, 6, 016008.
31. K. A. Norton, M. Wininger, G. Bhanot, S. Ganesan, N. Barnard and T. Shinbrot, J. Theor. Biol., 2010, 263, 393–406.
32. J. J. Linderman, T. Riggs, M. Pande, M. Miller, S. Marino and D. E. Kirschner, J. Immunol., 2010, 184, 2873–2885.
33. J. Tang, K. Ley and C. A. Hunt, BMC Syst. Biol., 2007, 1, 14.
34. J. Tang and C. A. Hunt, PLoS Comput. Biol., 2010, 6, e1000681.
35. A. M. Bailey, B. C. Thorne and S. M. Peirce, Ann. Biomed. Eng., 2007, 35, 916–936.
36. N. Y. Li, K. Verdolini, G. Clermont, Q. Mi, E. N. Rubinstein, P. A. Hebda and Y. Vodovotz, PLoS One, 2008, 3, e2789.
37. T. Sütterlin, S. Huber, H. Dickhaus and N. Grabe, Bioinformatics, 2009, 25, 2057–2063.
38. A. A. Qutub and A. S. Popel, BMC Syst. Biol., 2009, 3, 13.
39. S. M. Peirce, E. J. Van Gieson and T. C. Skalak, FASEB J., 2004, 18, 731–733.
40. A. M. Bailey, M. B. Lawrence, H. Shang, A. J. Katz and S. M. Peirce, PLoS Comput. Biol., 2009, 5, e1000294.
41. O. Sliusarenko, J. Neu, D. R. Zusman and G. Oster, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 1534–1539.
42. T. Sun, P. McMinn, M. Holcombe, R. Smallwood and S. MacNeil, PLoS One, 2008, 3, e2129.
43. Y. Setty, I. R. Cohen, Y. Dor and D. Harel, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20374–20379.
44. S. H. Kim, S. Park, K. Mostov, J. Debnath and C. A. Hunt, PLoS One, 2009, 4, e4819.
45. J. Wambaugh and I. Shah, PLoS Comput. Biol., 2010, 6, e1000756.
46. T. N. Lam and C. A. Hunt, Drug Metab. Dispos., 2009, 37, 231–246.
47. C. A. Hunt, G. E. Ropella, T. N. Lam, J. Tang, S. H. Kim, J. A. Engelberg and S. Sheikh-Bahaei, Pharm. Res., 2009, 26, 2369–2400.
48. R. Mukhopadhyay, S. V. Costes, A. V. Bazarov, W. C. Hines, M. H. Barcellos-Hoff and P. Yaswen, Breast Cancer Res., 2010, 12, R11.
49. S. Park, S. H. Kim, G. E. Ropella, M. S. Roberts and C. A. Hunt, J. Pharmacol. Exp. Ther., 2010, 334, 124–136.
50. S. V. Costes, A. Ponomarev, J. L. Chen, D. Nguyen, F. A. Cucinotta and M. H. Barcellos-Hoff, PLoS Comput. Biol., 2007, 3, e155.
51. M. J. Reginato and S. K. Muthuswamy, J. Mammary Gland Biol. Neoplasia, 2006, 11, 205–211.
52. M. Overholtzer, A. A. Mailleux, G. Mouneimne, G. Normand, S. J. Schnitt, R. W. King, E. S. Cibas and J. S. Brugge, Cell, 2007, 131, 966–979.
53. J. Aggeler, J. Ward, L. M. Blackie, M. H. Barcellos-Hoff, C. H. Streuli and M. J. Bissell, J. Cell Sci., 1991, 99(Pt 2), 407–417.
54. M. J. Bissell and M. H. Barcellos-Hoff, J. Cell Sci. Suppl., 1987, 8, 327–343.
55. K. A. Rejniak, S. E. Wang, N. S. Bryce, H. Chang, B. Parvin, J. Jourquin, L. Estrada, J. W. Gray, C. L. Arteaga, A. M. Weaver, V. Quaranta and A. R. Anderson, PLoS Comput. Biol., 2010, 6, e1000900.

---

Footnotes

† Published as part of an Integrative Biology themed issue in honour of Mina J. Bissell: Guest Editor Mary Helen Barcellos-Hoff.

‡ Electronic supplementary information (ESI) available: Fig. S1–S5, Movie S1 and S2. See DOI: 10.1039/c0ib00092b

---