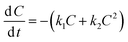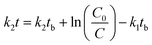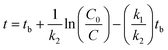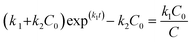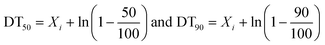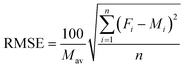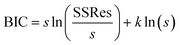Evaluation of four mathematical models to describe dissipation kinetics of 4-n-nonylphenol and bisphenol-A in groundwater–aquifer material slurry
Ajit K.
Sarmah
*a and
Maheswaran
Rohan
b
aSoil Chemical & Biological interactions, Soils and Landscape Team, Landcare Research Manaaki Whenua, Private Bag 3127, Hamilton, New Zealand. E-mail: sarmahA@LandcareResearch.co.nz; Fax: +64 7 8593701; Tel: +64 7 8593737
bResearch and Development Group, Department of Conservation, P.O. Box 516, Hamilton, New Zealand
First published on 11th November 2010
Abstract
The performance of four mathematical models (hockey stick, biexponential, first-order double exponential decay, and first-order two-compartment) was evaluated to describe the dissipation kinetics for 4-n-nonylphenol (4-n-NP) and bisphenol-A (BPA) in groundwater–aquifer material slurry under aerobic and anaerobic conditions conducted under controlled laboratory conditions. The fit of each model to the measured values under both conditions was tested using an array of statistical indices to judge the model's ability to fit the measured datasets. Corresponding 50% (DT50) and 90% (DT90) dissipation values for each compound were numerically obtained and compared against each model. The model derived DT50 values in groundwater–aquifer material ranged from 1.06 to 1.24 (4-n-NP) and 0.341 to 0.568 days (BPA) under aerobic condition, while they were 2- to 4-fold higher under anoxic condition. DT90 values for 4-n-NP ranged anywhere between 2.3 and 4.45 days under both conditions, while DT90 values for BPA ranged from around 1 day to as high as 12 days under both conditions tested. A visual examination of the measured and fitted plots as well as the statistical indices showed that, with the exception of the hockey stick model, the models performed satisfactorily. Despite having only 3 parameters, the biexponential model could describe the dissipation kinetics very well and this was supported by the statistical indices generated for each case.
Environmental impactSome industrial chemicals such as 4-nonylphenol and bisphenol-A have the potential to disrupt endocrine mechanisms and normal development in exposed organisms. Given the wide occurrence of these compounds in the environment, and their potential to cause damages to human and wildlife, understanding their fate in various environmental media is important. We demonstrated that selection and utilisation of appropriate mathematical models are capable of describing the entire dissipation kinetics for these compounds in groundwater/aquifer material media, which help in the development of appropriate dissipation end-points. These end-points which have been tested for their statistical rigor are scientifically robust, and can be confidently used as input parameters often required in many regulatory modeling exercises and for risk assessment purposes. |
Introduction
In recent times many industrial chemicals with recognised estrogenic activity have been detected in surface water, river sediments as well as in groundwater, in various parts of the world. These industrial chemicals include alkylphenols such as 4-tert-octylphenol and technical mixtures of 4-n-nonylphenol (4-n-NP), plasticizers such as phthalate esters that are incorporated into plastics, and bisphenol-A (BPA), a building block used in the manufacture of polycarbonate and epoxy resins.1 Although these xenoestrogens have estrogenic potencies lower than estrogenic steroids,2 they can be present in the environment at concentrations considerably higher than steroid estrogens3–5 and have the potential to exert a significant synergistic effect on exposed organisms.Alkylphenol ethoxylates (APEO), high-volume chemicals that have been used for more than 4 decades, make up the world's third largest group of surfactants in terms of production and have been widely used for a variety of industrial, household and commercial applications.3 Due to their poor ultimate biodegradability with the formation of nonylphenol (Fig. 1) and, to a lesser extent, octylphenol, which are considered as persistent and ubiquitous environmental pollutant,3 the nonylphenol ethoxylates (NPEO) have been replaced in household applications, mainly by the less toxic alcohol ethoxylates.6 However, for industrial applications, this replacement has not been carried out yet because of the excellent performance of APEO and their low production costs.7 These compounds can be found in groundwaters as a result of leaching or due to diffuse pollution and transport along a given aquifer. For example, the presence of nonylphenol in aquifers is related invariably to anthropogenic activities such as the discharge of sewage treatment plant effluents with concentrations averaging 790 ng L−1,8 in river samples at levels ranging from 0.1–0.8 mg L−1,3 and in stream samples in the vicinity of septic systems 1200 µg L−1.4 Other forms of anthropogenic activities such as agricultural practices also led to the presence of nonylphenol at levels ranging from 0.16–0.38 µg L−1 in aquifers,6 in landfill leachate, and in the discharge of industrial wastewater <100 to 280 ng L−1.9 The presence of APEO in pesticide formulations may also lead to leaching of nonylphenol to groundwater as a result of the high amount of pesticide applied on extensive crops.6
 | ||
| Fig. 1 Molecular structures of 4-n-nonylphenol and bisphenol-A. | ||
Bisphenol-A (2,2-bis(4-hydroxyphenyl)propane) or BPA (Fig. 1) is widely used as a monomer in the synthesis of epoxy resins and polycarbonate plastics.10Polymers containing BPA are commonly used for coating concrete and steel tanks and pipes. More than a million tons of BPA are annually produced in the world.10 The annual production of BPA in the world exceeded >900 million pounds in the early 1990s,11 and the amount subsequently increased to nearly 1.4 billion pounds in 1995.12 Due to such widespread uses and manufacture of BPA, a large quantity of BPA is eventually discharged. For example, according to the US Toxic Release Inventory (TRI), in 1995, 3600 kg of BPA were discharged to surface water following offsite or onsite treatment.13 A reconnaissance study conducted by the United States Geological Survey detected trace levels of 4 nonylphenol (median value of 0.8 µg L−1) and bisphenol-A (0.14 µg L−1) in stream samples collected across the USA.14 In a recent analysis of 47 groundwater samples from sites across 18 states of the United States, the maximum concentration of BPA was found to be 2.55 µg L−1.15 In another recent study, BPA was detected at 20% of the 25 groundwater sites that serve as drinking water sources to populations of over 8 million people in the United States.16
BPA has been identified as a weakly estrogenic chemical that modifies natural endocrine functions by binding to the estrogen receptor and, consequently, causes adverse effects on the human health and wildlife like breast cancer, endometriosis, and infertility.17 Although the compound was reported to be 4–6 orders of magnitude less potent than natural estrogen, 17β-estradiol,18,19 there is documented evidence that BPA can also act as a weak antiandrogen.20
Given the occurrence of both 4-n-NP and BPA in groundwaters across different parts of the world, and their potential to cause damage to human and wildlife, understanding their fate in environmental media such as in groundwater/aquifer material, river water or sediment is important (Fig. 2). The dissipation values of the compounds obtained in such media through laboratory studies are often used by regulatory authorities for risk assessment purposes and as input parameters in many fate models. Selection of appropriate kinetic models plays a key role in the derivation of DT50/DT90 (time for 50% or 90% of initial residues to dissipate) values for organic chemicals, and outputs of many predictive models are very sensitive to the chosen DT50/DT90 values used as inputs in fate and risk assessment models. The purpose of this work was to use 4 mathematical models to describe the kinetic of 4-n-NP and BPA dissipation in a media composed of groundwater and aquifer material and to determine their DT50 and DT90 values. Apart from graphical representation of the dissipation plots, statistical indices were also calculated to compare the performance of each model against the datasets. Finally, a discussion of the mechanistic basis for the models is provided, as are recommendations for the models' use in dissipation studies.
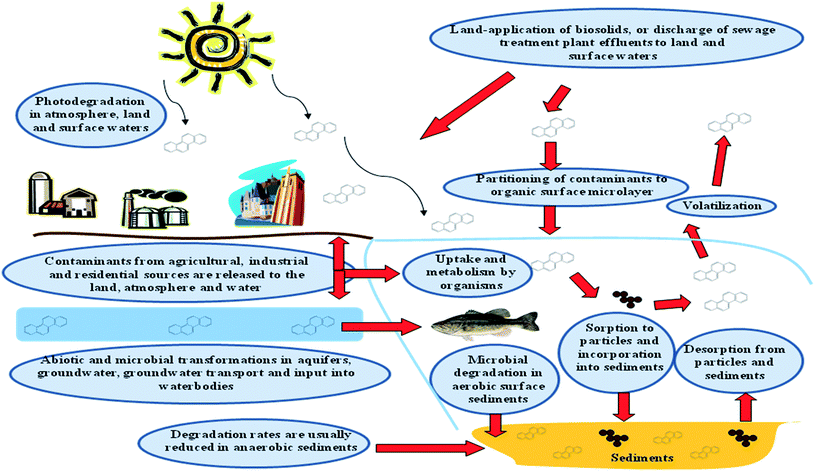 | ||
| Fig. 2 Schematic diagram showing the various fate and transport processes affecting 4-n-nonylphenol and bisphenol-A in the environment (source: adapted and modified from Newman and Unger34). | ||
Material and methods
Chemicals
Bisphenol-A (>99% purity), and deuterium-labeled bisphenol-A (bisphenol-A-d16) with 98% purity, were purchased from Sigma Aldrich (St Louis, MO, USA). 4-n-Nonylphenol (99.5% purity) was purchased from Dr Ehrenstorfer, Augsberg, Germany. High-purity Mallinkrodt solvents (>99% purity) acetonitrile, methanol, and dichloromethane of nanograde were obtained from the BioLab Group, Auckland, New Zealand.Groundwater, aquifer material and slurry preparation
Groundwater from a depth of 830 cm from the surface was collected by suction from a farmland in the Hautapu, Waikato region of New Zealand. Aquifer material consisted of underground layer of water bearing permeable sediment or unconsolidated materials (gravel, sand, silt and clay) with ∼12% of CaCO3. Aquifer material was obtained from a depth of 810 cm with a coring device that was pre-washed with water and swabbed with 70% ethanol. Both groundwater and aquifer material were immediately stored in amber Winchester bottles, placed in a freezer and transferred to the laboratory and stored at −14 °C prior to setting up the trial. To prepare the groundwater–aquifer material slurry, groundwater sample was filtered using 0.7 µm Whatman (Beckman, Sydney, Australia) glass-microfiber filter to remove particulate and algal materials. The aquifer solids were centrifuged in Beckman 250 mL polycarbonate tubes (2500 rpm for 60 minutes at 15 °C) to separate the pore water from the solids, supernatant decanted, and residue solids were combined with filtered groundwater sample and mixed in a plastic beaker thoroughly to obtain homogenous slurry.1Dissipation studies
Laboratory dissipation studies under aerobic and anaerobic conditions were carried out using a modified standard American Society for Testing and Materials method.21 Aerobic dissipation treatments were prepared in wide-mouth 100 mL screw-cap glass borosilicate bottles to provide maximum surface area for air exchange and thus maintaining the aerobic status during the entire duration of the experiment. Anaerobic studies were performed in 40 mL Pyrex glass centrifuge tubes with Teflon-lined screw caps to minimize for airspace for maintaining the anaerobic conditions. All handling and manipulations were carried out in laminar flow hood, while all equipments used in the experimental study were autoclaved on the day of use and stored under ultraviolet lamp to maintain sterility.Preparation of aerobic and anaerobic treatments was given in full details by Sarmah and Northcott.1 Briefly, appropriate amount of groundwater–aquifer material slurry was spiked with 0.1 mL of 20 µg mL−1 combined solution of BPA and 4-n-NP prepared in 0.5% (v/v) of methanol solution to each replicate (n = 3) to obtain a fortification of 2.0 µg of each compound. This resulted in the compound fortification of 100 µg L−1 in each replicate tube. Fortified samples for each treatment (sterile and non-sterile under aerobic and anaerobic conditions) were covered with aluminium foil, and placed in the dark at a temperature between 16 and 18 °C for the duration of the experiment (70 d). Anaerobic pouch boxes containing an anaeropack (Mitsubishi Gas Chemical, Tokyo, Japan) were employed to remove air along with anaerobic resazurin indicator strip (Oxoid, Cambridge, UK). Samplings were carried out on day 0, 1, 2, 4, 7, 14, 21, 30, 50 and 70 and immediately analysed or stored at −4 °C for later analysis.
The incubation time of 16–18 °C was chosen to represent the ideal temperature one likely to encounter in groundwater and aquifers within NZ's Waikato region. It is important to note that while this laboratory study was designed to represent field situations, true conditions that one might observe in the field are always very challenging to achieve under laboratory controlled experiment. Events like heavy rainfall, fluctuation of temperature, flooding or other natural hazards, which can play a role in overall dissipation of these compounds in the field, are difficult to simulate under laboratory conditions. However, experimental protocols adopted in this study does approximate near field situations one likely to observe.
Extraction and analysis
Both 4-n-NP and BPA were extracted from the groundwater–aquifer material slurry by adding 15 or 20 mL dichloromethane to the bottles/tubes, shaken for 16 h on a flatbed shaker at 350 rpm, and centrifuged (2000 rpm for 15 min). After centrifugation, 10 mL of DCM extract were passed through a column of anhydrous Na2SO4 into a glass vial. The extraction was repeated, combined, concentrated under a gentle stream of nitrogen, and reconstituted in 0.1 mL of toluene. BPA residues were derivatized following Larch and Zinn,21 to its respective trifluoroacetate by adding 10 µL of trifluoroacetic anhydride, mixed under vortex, and left (5 min) at room temperature to react. An aliquot of 0.4 mL of isooctane was added to each extract, mixed, washed with K2CO3 solution to remove any reaction by-products, and then isooctane solution was placed in GC vials for analysis by GCMS. Full details of sample analysis and GCMS operating conditions including column, oven temperature, and examples of ion and total chromatograms were provided in Sarmah and Northcott.1Dissipation models
We have selected the following models for consideration based on their relative simplicity (three and four parameters) and their potential to better fit the measured dissipation kinetics datasets for 4-n-NP and BPA that appear to be biphasic or multiphasic in nature.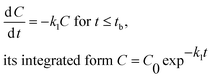 | (1) |
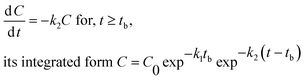 | (2) |
By solving the above first-order differential equation, we obtain
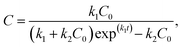 | (3) |
| C(t) = C1(t) + C2(t) = Csol exp(−k1t) + Csorb exp(−k2t) | (4) |
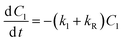 | (5) |
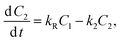 | (6) |
| C = (C1 + C2) | (7) |
After putting the values of C1 and C2 (from eqn (5) and (6)) in eqn (7), and solving for C, we get:
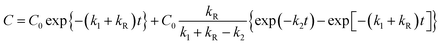 | (8) |
All four models used in this study describe non-linear dissipation kinetic, fast and slow release of organic compounds with time. Parameters for these models were obtained from the best-fit models using either Microsoft Excel Solver (Microsoft, 2003) or add-ins analysis Tool Pak of Microsoft Excel as described below.
Modelling approach
To fit the measured data for 4-n-NP and BPA by the selected models under two treatments (aerobic and anaerobic conditions), Microsoft Solver was used as a modelling tool-pack utilising the Generalized Reduced Gradient (GRG2) non-linear optimization code available within the Microsoft Excel software.We used the total concentrations of 4-n-NP and BPA measured in groundwater–aquifer slurry under both aerobic and anaerobic conditions to fit the models and extract the parameters. The eqn (2)–(4) and (8) were used to obtain the predicted values of C for each compound, and in turn subsequently used in minimisation of the residuals for each model. The parameters such as C0, k1, k2tb (HS), C0, k1, k2 (BEXP), Csol, Csorb, k1, k2 (FODED) and C0, k1, k2, kR (FOTC) are estimated iteratively by minimising the sum of squares of the residuals (SSRes), difference between measured and model-fitted values. This gives best fit for all the cases. This is an iterative algorithm, so that initial values for the parameters are defined as follows: the initial applied concentration for 4-n-NP and BPA was taken as default C0 value, which was approximately 100 µg kg−1 for both the compounds. However, for other parameters (tb, k1, k2, kR), the initial guess was by a trial and error approach. It is important to note that lower bounds for the rate constants were not set to ‘zero’ in the modelling procedure, allowing the Solver to do the required iterations to obtain the best values.
Hockey-stick (HS) model. According to eqn (1), we can derive the following:
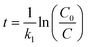 | (9) |
Similarly, according to eqn (2), we have
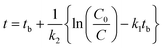 | (10) |
In eqn (9) and (10), C represents either 50% or 90% of initial concentration of the compound, while other terms are as defined earlier.
BEXP model. According to eqn (3), we can derive the following:
 | (11) |
FODED and FOTC models. The equations for both FODED and FOTC models are not in explicit form and therefore no analytical solutions are available. Thus solver was used to estimate values for DT50 and DT90 for these two models using an iterative procedure as described earlier by Sarmah and Close30 and with following equations.
where Xi is the concentration of the compound at time ‘zero’, after logarithmic transformation of eqn (4) (FODED) and (8) (FOTC).
In this procedure, right-hand sides of eqn (4) and (8) were transformed in to its natural logarithmic form, and then subtracting the values thus obtained from above equations for the respective DT50 and DT90, we get squares of deviation (devsq) that corresponds to a minimum value. Right-hand sides of above equations are taken as ‘target cell’ in Microsoft Excel, which is matched by the values obtained using eqn (3) and (8). When the value of ‘devsq’ is ‘0’ or as close as to ‘0”, corresponding values for DT50 and DT90 for each compound are obtained.
Statistical indices to derive goodness of fit
Measures of the goodness of fit for the optimised parameters and for the fitted values for each pesticide and soil type were carried out using following statistical indices.31where Mav is the average of measured value, Fi is fitted value, Mi is measured value, and n is the number of observations. The root mean square error (RMSE) calculates the average difference between fitted and measured data and value for RMSE should be as close to ‘zero’ as possible.
where err = model error which is the measurement error percentage (element of proportionality) given by the equation below:
If χ2 > tabulated χm,α2 (m = degrees of freedom, α = probability level at 5%, if otherwise stated), then the model is inappropriate at the chosen level of significance.
where s = no of measurement or sample size, SSRes = sum of squares of residuals obtained during data fitting by model, and k = no. of parameters to be estimated.
The assumption behind BIC is that the model errors are normally distributed—lower the values for BIC, fewer explanatory variables, better model fit or both.
Results and discussion
The fitted plots of 4 models (HS, BEXP, FODED and FOTC) and the measured data for nonylphenol and bisphenol-A under aerobic and anaerobic conditions are presented in Fig. 3 and 4 respectively. These models were selected for comparison based on their degree of flexibility and relative simplicity such as the numbers of parameters needed to be optimised and their individual ability to fit the measured data within reasonable iterations. The preliminary model-fitting procedure suggested that irrespective of using actual applied concentrations in the Y-axis or setting the values as 100% of the remaining initial application of the chemicals did not have any bearing on the curve fitting, and values obtained for the optimized parameters. Therefore, in the modelling procedure, the actual theoretical initial concentration was used as a starting value that is approximately 100 µg kg−1 for both 4-n-NP and BPA, and values in the Y-axis were not set to % of initial applied amount.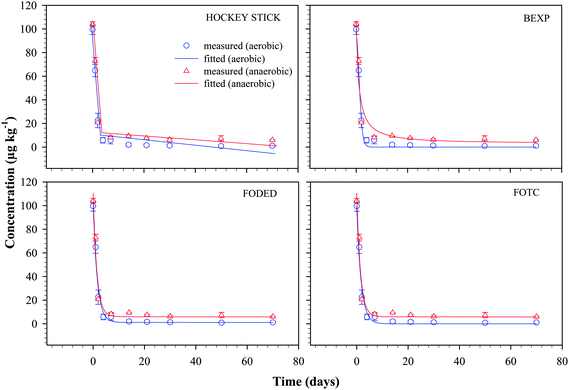 | ||
| Fig. 3 Plots of measured residues of 4-n-nonylphenol (4-n-NP) groundwater–aquifer material slurry as a function of time along with the fit for the non-linear biphasic HS, BEXP, FODED and FOTC models. Vertical error bars represent the range of duplicate results for measured values. Bars where not visible fall within the symbols. | ||
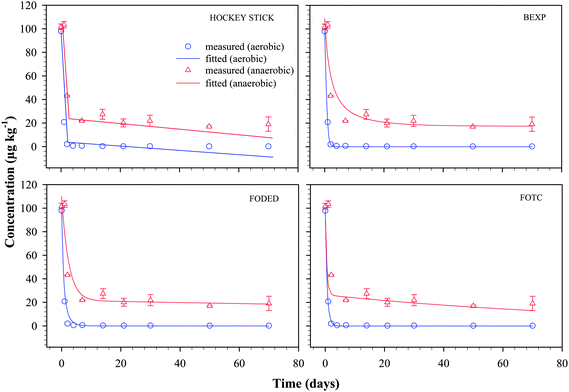 | ||
| Fig. 4 Plots of measured residues of bisphenol-A (BPA) in groundwater–aquifer material slurry as a function of time along with the fit for the non-linear biphasic HS, BEXP, FODED and FOTC models. Vertical error bars represent the range of duplicate results for measured values. Bars where not visible fall within the symbols. | ||
4-n-NP dissipation
Fig. 3 shows the measured and model fitted dissipation data for 4-n-NP under aerobic and anaerobic conditions. Good convergence to the solution was achieved in most cases and, in general, the models investigated here fit the datasets well, with the exception of the HS model, which failed to fit the 4-n-NP data under anaerobic condition, despite using a number of iterations and changing the optimized values for the parameters. It is important to note that the fit of HS model for 4-n-NP under aerobic and anaerobic conditions is far from satisfactory, with underestimation of the measured values for 4-n-NP from day 50 and day 70. The breakpoints (tb) for 4-n-NP under both conditions were similar (3.2 and 3.3, for aerobic and anaerobic conditions respectively), suggesting that corresponding DT50 values also did not differ much (Table 1).| Models | Parameters | Aerobic | Anaerobic | ||
|---|---|---|---|---|---|
| 4-n-NP | BPA | 4-n-NP | BPA | ||
| HS | k 1 | 0.6531 (0.008) | 1.605 (0.007) | 0.5997 (0.008) | 0.2782 (0.013) |
| k 2 | 0.6113 (0.005) | 1.589 (0.003) | 0.5806 (0.006) | 0.1491 (0.004) | |
| C 0 | 112.329 (0.674) | 99.970 (0.023) | 112.329 (0.577) | 100.00 (0.632) | |
| t b | 3.245 (0.318) | 3.266 (0.052) | 2.329 (0.009) | 2.6251 (0.027) | |
| BEXP | k 1 | 1.5778 (0.015) | 2.4615 (0.033) | −0.0331 (0.0001) | −0.0821 (0.001) |
| k 2 | −0.0135 (0.001) | −0.0164 (0.001) | 0.0092 (0.0008) | 0.0047 (0.0001) | |
| C 0 | 99.789 (0.459) | 97.900 (0.881) | 106.67 (1.201) | 108.782 (0.333) | |
| FODED | k 1 | 0.6273 (0.007) | 1.5896 (0.011) | 0.6810 (0.003) | 0.41852 (0.0135) |
| k 2 | 0.0009 (0.00006) | 0.58 (0.013) | 0.0004 (0.00002) | 0.0022 (0.0002) | |
| C sol | 101.194 (0.871) | 68.535 (1.154) | 104.601 (1.452) | 88.227 (0.666) | |
| C sorb | 1.173 (0.017) | 29.448 (0.577) | 6.0 (0.340) | 21.696 (0.881) | |
| FOTC | k 1 | 1.101 (0.1154) | 1.001 (0.145) | 2.102 (0.088) | 1.003 (0.145) |
| k 2 | 0.59 (0.0202) | 1.6049 (0.034) | 0.532 (0.009) | 0.1793 (0.318) | |
| k R | 51.32 (0.664) | 35.268 (1.233) | 35.385 (0.632) | 35.268 (1.344) | |
| C 0 | 99.60 (0.781) | 97.90 (0.663) | 100.00 (0.666) | 100.00 (0.881) | |
The optimised parameters for the models for each compound along with error estimates in bracket under each treatment are summarised in Table 1, while DT50 and DT90 values and the corresponding statistical indices are given in Table 2. The BEXP model fitted the 4-n-NP dissipation data best, as supported by the goodness of fit statistical indices. For example, BEXP had lowest values for SSRes (66.524), RSME (3.082), BIC (25.857), and a χ2 value of 0.157 (model error of 9.2 at 1% probability level). The box–whisker plots in Fig. 5 show that the BEXP model was superior in predicting the measured values for both 4-n-NP and BPA under aerobic condition. For example, for 4-n-NP under aerobic condition, median of the BEXP model is in excellent agreement with the zero line, followed closely by FOTC, FODED and HS model. However, under anaerobic condition, FODED model provided the closest match followed by FOTC and BEXP model. Under both aerobic and anaerobic conditions, HS model provided the poorest fit for 4-n-NP, and this also supported the earlier discussion. Overall, model derived DT50 values for 4-n-NP ranged from 1.06 to 1.21 days and 1.12 to 1.31 days for aerobic and anaerobic conditions, respectively, while DT90 values were two- to four-fold greater than the DT50 values obtained by the models under any given condition.
| Models | Parameters | 4-n-NP | BPA | ||
|---|---|---|---|---|---|
| Aerobic | Anaerobic | Aerobic | Anaerobic | ||
| HS | DT50 | 1.062 | 1.157 | 0.341 | 0.431 |
| DT90 | 2.302 | 3.525 | 1.135 | 1.434 | |
| SSRes | 191.115 | 253.732 | 255.927 | 340.00 | |
| RMSE | 25.643 | 10.438 | 20.9939 | 26.078 | |
| BIC | 38.713 | 44.444 | 43.981 | 67.5 | |
| χ 2 | 2.452 | 2.268 | 2.039 | 2.950 | |
| Model error | 16.4 | 21.011 | 24.8 | 27.0 | |
| BEXP | DT50 | 1.215 | 1.315 | 0.488 | 0.549 |
| DT90 | 2.594 | 2.632 | 1.296 | 1.339 | |
| SSRes | 66.524 | 670.82 | 1.172 | 1208.58 | |
| RMSE | 3.082 | 10.573 | 0.409 | 14.192 | |
| BIC | 25.857 | 45.393 | −12.227 | 50.691 | |
| χ 2 | 0.157 | 0.923 | 0.008 | 0.693 | |
| Model error | 9.2 | 23.4 | 2.1 | 21.4 | |
| FODED | DT50 | 1.10 | 1.123 | 0.568 | 2.315 |
| DT90 | 3.846 | 4.451 | 2.28 | 3.06 | |
| SSRes | 182.219 | 400.768 | 200.707 | 973.85 | |
| RMSE | 5.510 | 8.952 | 5.783 | 13.956 | |
| BIC | 38.236 | 42.95 | 39.202 | 50.945 | |
| χ 2 | 0.431 | 0.551 | 1.318 | 0.559 | |
| Model error | 16.0 | 18.1 | 10.0 | 17.4 | |
| FOTC | DT50 | 1.12 | 1.16 | 0.442 | 3.72 |
| DT90 | 3.89 | 3.889 | 1.445 | 12.71 | |
| SSRes | 204.497 | 653.732 | 5.657 | 953.51 | |
| RMSE | 5.838 | 11.434 | 0.971 | 2.4304 | |
| BIC | 39.39 | 47.358 | 3.514 | 6.93 | |
| χ 2 | 0.484 | 0.9 | 0.038 | 0.048 | |
| Model error | 17.0 | 24.4 | 4.8 | 5.5 | |
BPA dissipation
Fig. 4 shows the measured and model fitted plots for BPA in groundwater–aquifer material slurry. A visual examination of the 4 plots in Fig. 4 revealed that dissipation of BPA under aerobic condition is well fitted by the 4 models. However, under anaerobic conditions, HS and FOTC models could not describe the BPA dissipation kinetic and grossly underestimated the measured data from day 14 onwards. The fit of the 4 models under aerobic condition was also well supported by the statistical indices derived during the modelling procedure. For instance, among the models, BEXP gave the best fit of the measured data for BPA dissipation with a model error of 2.1 (χ2 = 0.008), while displaying the lowest values for other indices such as RMSE (0.409), a value of BIC as −12.227. This, along with the smallest SSRes (1.172) during model fitting, further signifies that the BEXP model was superior to other models in this instance. Under anaerobic condition, however, BEXP overestimated the measured data at the initial few sampling events, and this was evident in the higher values for RMSE, BIC, and model error (Table 2).While visual examination would indicate a good and almost identical match of the measured and fitted values of BPA under aerobic condition by the 4 models, a close look at the values for the statistical indices reflects the subtle differences between each of these models. The HS model's inability to predict the measured values of BPA dissipation under both aerobic and anaerobic conditions can also be observed on higher statistical indices (RMSE, BIC, χ2 and model error) as shown in Table 2. Similarly, the FODED model also showed some inconsistency in the data fitting and this can be judged from the statistical indices and from a comparison against other model. Given that the HS model also had 4 parameters like the FODED and FOTC models, the HS model gave by far the worst performance in terms of data fitting (Fig. 4 and Table 2). Box–whisker and residual plots showed that under anaerobic condition for BPA, the model FOTC is considered as a better model than the FODED model because of the two large outliers present in the FODED model (Fig. 5). However, both models performed equally well when the outliers were removed.
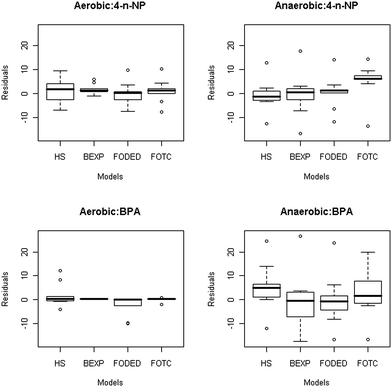 | ||
| Fig. 5 Box–whisker plots of residuals (measured–predicted) of 4-n-nonylphenol (4-n-NP) and bisphenol-A (BPA) dissipation in groundwater–aquifer slurry under aerobic and anaerobic conditions for each model. Boxes cover the medial 50% of the data with the median dividing the box. Whiskers range to the largest and smallest points within 1.5 times the interquartile distance, and outliers are shown as circles beyond the whiskers. | ||
Comparison of dissipation parameters
Table 2 depicts the values for DT50 and DT90 for 4-n-NP and BPA under both aerobic and anaerobic conditions. There was no marked variation in the DT50 and DT90 values for 4-n-NP derived from the 4 model fits with DT50 values ranging from 1.06 to 1.21 days (aerobic condition), while DT90 values ranged between 2.6 and 3.9 days under the anoxic condition (Table 2). Dissipation of BPA was relatively faster than 4-n-NP, with DT50 values of around a ½ day in the aerobic conditions, and varied between 0.34 and 4 days under anaerobic conditions. In the absence of available literature values for these compounds in the media examined (groundwater–aquifer material), a comparison is not justifiable. Given that the values for dissipation times of both compounds were generated from model fitting and the fitted models were assessed by statistical measures such as goodness of fit, the behaviour of the models to fit the measured values is dependent on the indices given in Table 2. Dissipation values (DT50) obtained in the present study are much lower than those earlier reported by Ying et al.32 while studying degradation of 4-n-NP in aquifer material collected from south-eastern Australia. Another study by the same group reported a half-life value of 1.8 days for 4-n-NP degradation in aquifer material collected from a superficial coastal aquifer near the city of Perth, Western Australia.33 However, in both cases, the authors assumed pseudo-first-order kinetics and calculated the half-lives for the compound. It is not appropriate to compare both studies with the present study in terms of how the half-life values are reported, because the experimental protocols adopted and other controlled laboratory condition may differ considerably between these studies. However, when it is assumed that decay follows first-order, in reality if the kinetic is biphasic like the study reported here, appropriate models should be used to calculate the dissipation times for the compound.Utility and mechanistic basis for biphasic models
The four biphasic models applied to fit the measured data are formulated to accommodate a biphasic dissipation mechanism, and it is worth noting that models are empirical in nature, and based on a rather putative mechanism for the observed degradation of 4-n-NP and BPA in the environmental media used. While a mechanistic explanation is not available for HS, BEXP and FODED models, the two-compartment (FOTC) model can be conceived to have some basis for a mechanistic interpretation of the data. The FOTC model provides two time-dependent rate constants separately for each compartment—slow (retained residue) and fast (deposited residue). In the ‘fast’ compartment it is assumed that compound dissipation takes place mainly through surface losses where a combination of physical, photochemical and volatilization processes takes place when the compound residues are initially deposited after application. In the ‘slow’ compartment, dissipation is assumed to take place at a much slower rate and to be affected by biotic, abiotic and enzymatic hydrolysis. In addition, there is continuous transfer of residues taking place between the two compartments, and their flow is governed by the concentration gradient in each compartment.While a two-compartment mechanism provides one explanation for a curve-linear decay pattern, the possibilities of the involvement of other mechanisms cannot be ruled out. For example, a population of microorganisms may increase or decrease over time, more than two compartments may exist in the soil, multiple mechanisms of decay may be operating, and/or the material may move between compartments over the course of the study. Without further data, except the fact that the decay pattern fits a biexponential model, there is no way to confirm a biphasic decay mechanism. Simply conforming to the model does not guarantee a specific mechanism. This is reinforced by the good fit of the non-mechanistically based models (HS, BEXP and FODED) for the datasets used in this study.
Conclusions
The following conclusions are drawn from this study:• Both 4-n-NP and BPA appear to decay rapidly in groundwater–aquifer material slurry, with a clear biphasic dissipation pattern.
• Overall, BEXP is judged as the best model for 4-n-NP and BPA under aerobic condition, however, under anaerobic condition, FODED and FOTC were the best models for 4-n-NP, and BPA respectively.
• The model-derived DT50 and DT90 values can provide useful input parameters for use in risk-assessment models and for regulatory purposes.
• The performance of the models used to fit a measured dataset should be evaluated using statistical indices in order to avoid bias in the estimation of the end-points for the compounds.
• It is recommended that model selection should be based on an understanding of the mechanisms that are contributing to a particular decay pattern, or on the fit of the model, and the lack of systematic deviations from measured values.
• It is also important to note the simplicity and interpretability of each model used, as this can often determine the model choice.
References
- A. K. Sarmah and G. L. Northcott, Environ. Toxicol. Chem., 2008, 27, 819–827 CrossRef CAS
.
- C. Sonnenschein and A. M. Soto, J. Steroid Biochem. Mol. Biol., 1998, 65, 143–150 CrossRef CAS
.
- M. Ahel, C. Schaffner and W. Giger, Water Res., 1996, 30, 37–46 CrossRef CAS
.
- R. A. Rudel, S. J. Melly, P. W. Geno, G. Sun and J. G. Brody, Environ. Sci. Technol., 1998, 32, 861–869 CrossRef CAS
.
- T. Isobe, H. Nishiyama, A. Nkashima and H. Takada, Environ. Sci. Technol., 2003, 35, 1041–1049
.
- A. Latorre, S. Lacorte and D. Barcelo, Chromatographia, 2003, 57, 111–116 CAS
.
- N. Jonkers, T. P. Knepper and P. de Voogt, Environ. Sci. Technol., 2001, 35, 335–340 CrossRef CAS
.
- L. B. Barber, E. M. Thurman, M. P. Schroeder and D. R. Leblanc, Environ. Sci. Technol., 1988, 22, 205–211 CrossRef CAS
.
- M. Ahel, Bull. Environ. Contam. Toxicol., 1991, 47, 586–593 CAS
.
- C. A. Staples, P. B. Dorn, G. M. Klecka, S. T. O'Block and L. R. Harris, Chemosphere, 1998, 36, 2149–2173 CrossRef CAS
.
- J. H. Lobos, T. K. Leib and T. M. Su, Appl. Environ. Microbiol., 1992, 58, 1823–1831 CAS
.
- P. Perez, R. Pulgar, F. Olea-Serrano, M. Villalobos, A. Rivas, M. Metzler, V. Pedraza and N. Olea, Environ. Health Perspect., 1998, 106, 167–174 CrossRef CAS
.
-
US Environmental Protection Agency, Preliminary Exposure Profile—Bisphenol A, Office of pollution Prevention and toxics (OPPT), 1994 Search PubMed
.
- D. W. Kolpin, E. T. Furlong, M. T. Meyer, E. M. Thurman, S. D. Zaugg, L. B. Barber and H. T. Buxton, Environ. Sci. Technol., 2002, 36, 1202–1211 CrossRef CAS
.
- K. K. Barnes, D. W. Kolpin, E. T. Furlong, S. D. Zaugg, M. T. Meyer and L. B. Barber, Sci. Total Environ., 2008, 402, 192–200 CrossRef CAS
.
- M. J. Focazlo, D. W. Kolpin, K. K. Barnes, E. T. Furlong, M. T. Meyer, S. D. Zaugg, L. B. Barber and E. M. Thurman, Sci. Total Environ., 2008, 402, 201–216 CrossRef CAS
.
-
T. Colborn, D. Dumanski and J. P. Meyers, Our Stolen Future: Are we Threatening our Fertility, Intelligence, and Survival? A Scientific Detective Story, Plume/Penguin Book, New York, 1996, p. 306 Search PubMed
.
- E. J. Routledge and J. P. Sumpter, Environ. Toxicol. Chem., 1996, 15, 241–248 CAS
.
- F. S. V. Saal, P. S. Cooke, D. L. Buchanan, P. Palanza, K. A. Thayer, S. C. Nagel, S. Parmigiani and W. V. Welshons, Toxicol. Ind. Health, 1998, 14, 239–260
.
- P. Sohoni and J. P. Sumpter, J. Endocrinol., 1998, 158, 327–339 Search PubMed
.
- O. Larch and P. Zinn, J. Chromatogr., A, 2003, 991, 77–91 CrossRef CAS
.
-
FOCUS, Guidance Document on Estimating Persistence and Degradation Kinetics from Environmental Fate Studies on Pesticides in EU Registration, Report of the FOCUS Work Group on Degradation Kinetics, EC Document Reference Sanco/10058/2005, version 2.0, FOCUS, Brussels, Belgium, 2006
.
- C. C. Reyes and R. L. Zimdahl, Weed Sci., 1989, 153, 65–90
.
-
M. J. Duffy, T. H. Carski and M. K. Hanafey, in Proceeding of the IX Symposium of Pesticide Chemistry: Mobility and Degradation of Xenobiotics, ed. E. D. Biagini, Piacenza, Italy, 11–13, Oct 1993, pp. 295–308 Search PubMed
.
- L. Sanchez, A. Pena, F. Sanchez-Rasero and E. Romero, Biol. Fertil. Soils, 2003, 37, 319–323 CAS
.
-
J. W. Hamaker and C. A. I. Goring, in Bound and Conjugated Pesticide Residues in Soil, ed. D. D. Kaufman, G. G. Still, G. D. Paulson and S. K. BandalAmerican Chemical Society, Washington, DC, 1976 Search PubMed
.
- J. D. Wolt, Rev. Environ. Contam. Toxicol., 1997, 153, 65–90 CAS
.
- F. F. Scherr, A. K. Sarmah, H. J. Di and K. Cameron, Environ. Toxicol. Chem., 2009, 28, 2564–2571 CrossRef CAS
.
- B. D. Hill and G. B. Schaalje, J. Agric. Food Chem., 1985, 33, 1001–1006 CrossRef CAS
.
- A. K. Sarmah and M. E. Close, J. Environ. Sci. Health, Part B, 2009, 44, 507–517 CrossRef CAS
.
- K. M. Loague and R. E. Green, J. Contam. Hydrol., 1991, 7, 51–73 CrossRef CAS
.
- G. G. Ying, R. S. Kookana and P. Dillon, Water Res., 2003, 37, 3785–3791 CrossRef CAS
.
- G. G. Ying, R. S. Kookana and P. Dillon, Ground Water Monit. Rem., 2004, 24, 102–107 CrossRef CAS
.
-
M. C. Newman and M. A. Unger, Fundamentals of Ecotoxicology, CRC/Lewis, FL. Lewis Publishers, Boca Raton, 2nd edn, 2003, p. 458 Search PubMed
.
| This journal is © The Royal Society of Chemistry 2011 |